1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 61, № 1, 2023

Теплофизика высоких температур, 2023, T. 61, № 1, стр. 98-107

Отклик газовых пузырьков в сферических кластерах на однократный импульс разрежения

А. А. Аганин 1, И. А. Аганин 1, *, А. И. Давлетшин 1, Р. И. Нигматулин 1

1 Институт механики и машиностроения – ОСП ФГБУН “Федеральный исследовательский центр “Казанский научный центр РАН”
Казань, Россия

* E-mail: aganel@gmail.com

Поступила в редакцию 20.12.2021
После доработки 27.02.2022
Принята к публикации 07.06.2022

Полный текст (PDF)

Аннотация

Изучается отклик газовых (воздушных) пузырьков в сферическом кластере на однократное импульсное косинусообразное понижение и последующее восстановление давления окружающей жидкости (водоглицериновой смеси) при длительности импульса в окрестности периода собственных колебаний кластера. Полагается, что все пузырьки в ходе отклика остаются слабонесферическими. Исследуется влияние продолжительности и амплитуды импульса возбуждения, положения пузырьков в кластере, расстояния между пузырьками, числа пузырьков в кластере. Рассматриваются кластеры кубической структуры, в которых центры пузырьков располагаются в узлах кубической сетки, а также кластеры со случайным расположением пузырьков и с пузырьками, находящимися в центре и вершинах ряда вложенных друг в друга правильных многогранников. Для оценки влияния взаимодействия между пузырьками проводится сравнение с откликом одиночного пузырька. Используется один из вариантов дискретных моделей динамики пузырьков в кластере, в котором наряду с радиальными колебаниями моделируются их пространственные перемещения и малые несферические деформации. Установлено, что при выполнении условия малости несферических деформаций пузырьков в ходе отклика максимальное повышение давления в пузырьках по отношению к его начальному значению не превосходит нескольких раз. Если игнорировать нарушение данного допущения, то можно получить и значительно большие степени сжатия пузырьков. Это обусловлено тем, что при игнорировании нарушения условия малости деформаций диапазоны рассматриваемых параметров существенно расширяются.

ВВЕДЕНИЕ

Совместная динамика пузырьков может довольно сильно отличаться от динамики одиночных пузырьков (например, [1–5]), что обусловлено их гидродинамическим взаимодействием. Так, в результате взаимодействия амплитуда радиальных колебаний пузырьков в кластерах может увеличиваться и уменьшаться [6], расширение и сжатие пузырьков могут замедляться и ускоряться [7], может меняться период колебаний пузырьков [8]. Пузырьки в кластерах могут сближаться и удаляться [9, 10]. В результате взаимодействия пузырьки могут деформироваться и разрушаться [11–13], на их поверхности могут возникать направленные внутрь высокоскоростные струи [14]. Максимальные давления (и другие параметры) во взаимодействующих пузырьках могут значительно превышать их максимальные значения, реализующиеся в этих же пузырьках при отсутствии их взаимодействия [6, 15, 16]. Считается, что взаимодействие пузырьков является одним из необходимых условий достижения сверхсжатия содержимого кавитационных пузырьков для реализации в них термоядерных актов [17, 18] и т.д.

Основные особенности динамики одиночных пузырьков и пузырьков в пузырьковых жидкостях и применяемых для их исследования моделей можно найти в монографиях [1–3]. При изучении динамики пузырьков в кластерах зачастую используются модели, в которых пузырьки считаются чисто сферическими. В частности, такое допущение применяется в континуальной модели в [6, 19–23] для изучения образования и распространения ударных волн в кластере, установления влияния неоднородности пузырьков по размерам, исследования генерируемого кластером шума. Кластер подвергается воздействию в виде уменьшения и последующего восстановления давления жидкости. Допущение о сферичности пузырьков применяется в [7, 16] в несколько иной континуальной модели при изучении динамики пузырьковых кластеров и ее зависимости от размеров пузырьков при ступенчатом уменьшении давления жидкости от 50 до 10 кПа и последующем его повышении до 50 кПа. Подобная модель применяется в [24, 25] для исследования поведения пузырькового кластера в ультразвуковом поле. Гипотеза о сферичности пузырьков используется в модели работы [26, 27], в которой кластер интерпретируется как большая капля жидкости со множеством микропузырьков и однородным давлением. Изучаются динамика и диффузионная устойчивость пузырьков такого кластера, подвергаемого воздействию акустического поля c длиной волны, гораздо большей, чем размер кластера. Пузырьки считаются сферическими в работах [28, 29], где анализируется фокусировка волн давления в тороидальных кластерах.

Дискретная модель коллективной динамики сферических пузырьков в интенсивном ультразвуковом поле [30] (в дискретных моделях движение пузырьков описывается обыкновенными дифференциальными уравнениями второго порядка относительно радиусов пузырьков и радиус-векторов их центров) применялась в [31] для изучения поведения пузырьков в кластере при их мгновенном сжатии и периодическом возбуждении. Рассматривался сферический кластер с пузырьками в центре и вершинах вложенных додекаэдров. Было обнаружено, что степени сжатия некоторых пузырьков в таком кластере весьма значительные. Модель совместной динамики сферических пузырьков, подобная той, что применялась в [31], использовалась и в [32, 33] для изучения динамики пузырьков в сферических кластерах при резком повышении давления в жидкости и внутри пузырьков. Изначально пузырьки находятся в центре, вершинах правильных многогранников и в узлах кубической сетки. Было показано, что давление в центральных пузырьках кластера может достигать значений, намного превышающих величины, реализующиеся в случае одиночных пузырьков.

Выполнение допущения о сферичности пузырьков в кластере зачастую (как, например, в перечисленных работах) никак не контролируется. Вместе с тем очевидно, что результаты исследований могут сильно зависеть от деформаций пузырьков. В частности, существенное влияние несферических деформаций пузырьков было продемонстрировано в [34], где прямое численное моделирование использовалось для изучения расширения и последующего коллапса пузырьков в полусферическом кластере около плоской твердой стенки. Деформации пузырьков рассчитывались явно. Было показано, что при использовании одного из вариантов дискретной модели, в которой пузырьки считаются сферическими, пиковые давления получаются более чем в 10 раз завышенными по сравнению с теми, что дает прямое численное моделирование.

В настоящей работе изучается отклик газовых пузырьков в сферическом кластере на импульсное изменение давления окружающей жидкости в виде его однократного косинусоидального понижения и последующего повышения до исходного значения. Подобный закон изменения давления жидкости является весьма типичным, в частности, для сужающихся и затем расширяющихся потоков жидкости (такой закон рассматривался в [6, 19–23]). Исследуется влияние амплитуды и длительности импульса, положения пузырьков в кластере, расстояния между пузырьками, числа пузырьков в кластере, структуры кластера. Рассмотрение ограничивается лишь той областью параметров воздействия на кластер и конфигурации кластера, в которой все пузырьки остаются близкими к сферическим вплоть до завершения их радиальных пульсаций после окончания изменения давления жидкости. Исследования проводятся с помощью дискретной модели [35], в которой наряду с радиальными колебаниями пузырьков моделируются также их пространственные перемещения и малые несферические деформации. Последнее позволяет непосредственно контролировать выполнение принимаемого условия малости несферических деформаций. И в этом смысле результаты настоящей работы, в отличие от работ, где при использовании допущения о сферичности пузырьков фактически никак не проверяются не только их деформации, но и разрушение, являются намного более адекватными.

Применяемая в настоящей работе модель [35] использовалась также и в [36] для контроля малости несферических деформаций. В работе [36] исследовалось влияние взаимодействия газовых пузырьков в сферическом кластере воздушных пузырьков при их переходе в новое положение равновесия в результате мгновенного повышения их внутреннего давления. Исследование проводилось с применением указанной выше модели совместной динамики пузырьков, используемой в [32, 33]. Было показано, что, если удовлетворяется условие малости несферических деформаций, то область параметров задачи сужается так, что достигаемые в ней максимальные давления в центральных пузырьках кластера оказываются намного ниже, чем значения в соответствующей области при отсутствии таких ограничений.

ПОСТАНОВКА ЗАДАЧИ

Изучаются особенности влияния межпузырькового взаимодействия на динамику газовых (воздушных) пузырьков в сферическом кластере при однократном воздействии импульсом разрежения в том случае, когда влияние несферических деформаций пузырьков мало (т.е. когда пузырьки можно считать близкими к сферическим). Рассматривается импульсное воздействие, при котором давление жидкости (водоглицериновой смеси) pL изменяется следующим образом:

(1)
$\begin{gathered} {{p}_{L}} = {{p}_{0}} + \frac{1}{2}{{p}_{a}}\left[ {\cos \left( {2\pi \frac{t}{{{{t}_{0}}}}} \right) - 1} \right] \\ {\text{при }}0 \leqslant t \leqslant {{t}_{0}}{\text{,}}\,\,\,\,{{p}_{L}} = {{p}_{0}}{\text{ при }}t > {{t}_{0}}, \\ \end{gathered} $
где t – время, p0 – статическое давление жидкости, pа – амплитуда импульса, t0 – его длительность. Согласно (1), давление жидкости сначала в течение времени t0/2 понижается от p0 до p0 − pа, а затем за время t0/2 восстанавливается до начального значения p0 и далее остается постоянным. Величины p0 и pа выбираются таким образом, чтобы минимальное давление pL min = 1 бар. Это означает, что p0 связано с pа как p0 = pL min + pа. Изначально (при t = 0) жидкость и пузырьки кластера покоятся, все пузырьки являются сферическими с радиусом R0 = 0.25 мм.

Основное внимание направлено на кластеры с кубической структурой (рис. 1), в которых центры пузырьков располагаются в узлах равномерной трехмерной сетки, причем один из центров находится в середине кластера.

Длительность импульса t0 варьируется в окрестности периода tcl = $f_{{{\text{cl}}}}^{{ - 1}}$ собственных колебаний кластера (fcl – частота собственных колебаний), начальное расстояние между центрами ближайших пузырьков кластера d0, амплитуда импульса pа и число пузырьков в кластере K варьируются от d0 = ∞, pа = 0 и K = 1 до тех значений, при которых (в случае воздействия с длительностью импульса t0 = tcl) нарушается условие малости несферических деформаций пузырьков.

Рис. 1.

Схема сферического кластера кубической структуры.

Собственная частота кластера fcl определяется следующим выражением [6, 37, 38]:

(2)
${{f}_{{{\text{cl}}}}} = {{f}_{{{\text{sing}}}}}{{\left( {1 + \frac{{12}}{{{{\pi }^{2}}}}\frac{{R_{{{\text{cl}}0}}^{2}}}{{R_{0}^{2}}}{{\alpha }_{0}}\left( {1 - {{\alpha }_{0}}} \right)} \right)}^{{ - 1/2}}},$
где Rcl0 – значение радиуса кластера Rcl при t = 0, fsing – собственная частота одиночного пузырька, α0 – объемное газосодержание при t = 0. Под радиусом кластера Rcl понимается расстояниe между центром кластера и наиболее удаленной от него точкой поверхностей периферийных пузырьков. Частота fsing и газосодержание α0 определяются как
$\begin{gathered} {{f}_{{{\text{sing}}}}} = \frac{1}{{2\pi {{R}_{0}}}}\sqrt {\frac{{3\kappa {{p}_{0}}}}{{{{\rho }_{L}}}} + \frac{{2\left( {3\kappa - 1} \right){{\sigma }}}}{{{{R}_{0}}{{\rho }_{L}}}} - \frac{{4{{\nu }^{2}}}}{{R_{0}^{2}}}} ,~ \\ {{{{\alpha }}}_{0}} = K{{\left( {\frac{{{{R}_{0}}}}{{{{R}_{{{\text{cl}}0}}}}}} \right)}^{3}}, \\ \end{gathered} $
где κ = 1.4 – показатель адиабаты газа в пузырьках, ρL = 1156 кг/м3 – плотность жидкости, σ = 0.07 Н/м – поверхностное натяжение, ν = 9.52 × 10−6 м2/с – кинематическая вязкость жидкости.

Анализируется также и влияние структуры кластера. С этой целью, наряду с кластерами кубической структуры (рис. 1), рассматриваются кластеры со случайным расположением пузырьков и с пузырьками, находящимися в центре и вершинах ряда вложенных друг в друга правильных многогранников.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Используется математическая модель взаимодействия пузырьков работы [35]. В данной модели уравнение поверхности k-го пузырька (1≤ k ≤ K) в сферической системе координат (rk, θk, φk) с началом отсчета в центре этого пузырька имеет вид

${{r}_{k}} = {{R}_{k}}\left( t \right) + \sum\limits_{n = 2}^\infty {\sum\limits_{m = - n}^n {a_{{n{\kern 1pt} k}}^{m}(t)Y_{n}^{m}\left( {{{\theta }_{k}},{{\varphi }_{k}}} \right).} } $
Здесь Rk ‒ радиус пузырька; $Y_{n}^{m}\left( {{{\theta }_{k}},{{\varphi }_{k}}} \right) = $ $ = P_{n}^{{\left| m \right|}}\left( {\cos {\kern 1pt} {{{{\theta }}}_{k}}} \right){{{\text{e}}}^{{im{{{{\varphi }}}_{k}}}}}$ – сферическая функция с номером n порядка m; $P_{n}^{{\left| m \right|}}$ – присоединенный полином Лежандра степени n порядка |m|; i – мнимая единица; $a_{{n\,k}}^{m}$ – амплитуда отклонений в виде сферических функций $Y_{n}^{m}\left( {{{\theta }_{k}},{{\varphi }_{k}}} \right)$ поверхности пузырька от сферической формы rk = Rk.

Положение k-го пузырька определяется радиус-вектором его центра ${{{\mathbf{p}}}_{k}} = {{x}_{k}}{\mathbf{i}} + {{y}_{k}}{\mathbf{j}} + {{z}_{k}}{\mathbf{k}}$, где i, j, k − направляющие векторы осей декартовых координат x, y, z c началом отсчета в центре кластера (в центре центрального пузырька). Отклонение формы k-го пузырька от сферической в виде гармоник степени n характеризуется величиной ${{\varepsilon }_{{nk}}}$, определяемой выражениями

$\begin{gathered} {{\varepsilon }_{{nk}}} = {{\varepsilon }_{{nk\max }}}{\text{ при }}{{\varepsilon }_{{nk\max }}} + {{\varepsilon }_{{nk\min }}} \geqslant 0{\text{,}} \hfill \\ {{\varepsilon }_{{nk}}} = {{\varepsilon }_{{nk\min }}}{\text{ при }}{{\varepsilon }_{{nk\max }}} + {{\varepsilon }_{{nk\min }}} < 0{\text{,}} \hfill \\ \end{gathered} $
где ${{\varepsilon }_{{nk\max }}} = \mathop {\max }\limits_{{{\theta }_{k}},{{\varphi }_{k}}} \varepsilon _{{nk}}^{ * }({{\theta }_{k}},{{\varphi }_{k}})$ – максимум положительного отклонения (высота выпуклости) поверхности пузырька от сферической поверхности ${{r}_{k}} = {{R}_{k}}$ в виде гармоник степени n, ${{\varepsilon }_{{nk\min }}} = $ $ = \mathop {\min }\limits_{{{\theta }_{k}},{{\varphi }_{k}}} \varepsilon _{{nk}}^{ * }({{\theta }_{k}},{{\varphi }_{k}})$ – максимум отрицательного отклонения (глубина вогнутости со знаком минус) поверхности пузырька от сферической поверхности ${{r}_{k}} = {{R}_{k}}$ в виде гармоник степени n, $\varepsilon _{{nk}}^{ * }({{\theta }_{k}},{{\varphi }_{k}}) = $ $ = \sum\nolimits_{m = - n}^n {\varepsilon _{{n{\kern 1pt} k}}^{m}Y_{n}^{m}\left( {{{\theta }_{k}},{{\varphi }_{k}}} \right)} $ – величина отклонения поверхности пузырька от сферической поверхности ${{r}_{k}} = {{R}_{k}}$ в точке (θk, φk) в виде гармоник степени n ($\varepsilon _{{nk}}^{ * }({{\theta }_{k}},{{\varphi }_{k}}) > 0$, если отклонение наружу пузырька, и $\varepsilon _{{nk}}^{ * }({{\theta }_{k}},{{\varphi }_{k}}) < 0$, если отклонение внутрь), $\varepsilon _{{nk}}^{m} = {{a_{{nk}}^{m}} \mathord{\left/ {\vphantom {{a_{{nk}}^{m}} {{{R}_{k}}}}} \right. \kern-0em} {{{R}_{k}}}}$. Несферические деформации пузырьков считаются малыми в том смысле, что $\varepsilon _{{nk}}^{2} \ll 1$ при любых n и k. Величина ${{\varepsilon }_{{nk}}}$ зависит только от формы пузырька. В частности, она не изменяется при повороте системы (${{r}_{k}},{{\theta }_{k}},{{\varphi }_{k}}$).

Динамика k-го пузырька кластера описывается следующими уравнениями:

(3)
(4)
$\begin{gathered} {{R}_{k}}\ddot {p}_{k}^{m} + 3{{{\dot {R}}}_{k}}\dot {p}_{k}^{m} - 2{{{\dot {R}}}_{k}}\dot {p}_{k}^{{1{\kern 1pt} '}}\varepsilon _{{2k}}^{{2{\kern 1pt} '}}\,\beta _{{211}}^{{2{\kern 1pt} '1{\kern 1pt} ' - m}} - \\ - \,\,\frac{{7\ddot {p}_{k}^{{1{\kern 1pt} '}}a_{{2k}}^{{2{\kern 1pt} '}}\beta _{{211}}^{{2'1{\kern 1pt} ' - m}}}}{6} - \frac{{3\dot {p}_{k}^{{1{\kern 1pt} '}}\dot {a}_{{2k}}^{{2{\kern 1pt} '}}\beta _{{211}}^{{2{\kern 1pt} '1{\kern 1pt} ' - m}}}}{2} + \psi _{{1\,k}}^{m} = \\ = \sum\limits_{\begin{subarray}{l} j = 1, \\ j \ne k \end{subarray}} ^K {\left[ {\frac{{3{{{\left( {{{R}_{k}}{{B}_{{0\,j}}}C_{{01{\kern 1pt} kj}}^{{0m}}} \right)}}^{'}}}}{{d_{{kj}}^{2}}}} \right.} - \frac{{3{{{\left( {{{R}_{k}}R_{j}^{3}\dot {p}_{j}^{{1{\kern 1pt} '}}C_{{11kj}}^{{1{\kern 1pt} 'm}}} \right)}}^{'}}}}{{2d_{{kj}}^{3}}} - \\ - \,\,\frac{{6{{R}_{k}}{{B}_{{0j}}}C_{{01kj}}^{{0m}}{{{\dot {d}}}_{{kj}}}}}{{d_{{kj}}^{3}}} - \frac{{5{{R}_{k}}{{B}_{{0j}}}\dot {p}_{k}^{{1{\kern 1pt} '}}C_{{0{\kern 1pt} 2kj}}^{{02{\kern 1pt} '}}\beta _{{211}}^{{2{\kern 1pt} '1{\kern 1pt} ' - m}}}}{{d_{{kj}}^{3}}} + \\ + \,\,\frac{{3{{{\left( {{{B}_{{0j}}}C_{{01{\kern 1pt} kj}}^{{01{\kern 1pt} '}}a_{{2{\kern 1pt} k}}^{{2{\kern 1pt} '}}} \right)}}^{'}}\gamma _{{211}}^{{2{\kern 1pt} '1{\kern 1pt} ' - m}}}}{{2d_{{kj}}^{2}}} - \\ \left. { - _{{_{{_{{^{{}}}}^{{^{{}}}}}}^{{}}}}^{{_{{_{{}}^{{^{{^{{}}}}}}}}^{{}}}}\frac{{{{B}_{{0j}}}\left( {\dot {a}_{{2{\kern 1pt} k}}^{{2{\kern 1pt} '}} + 2{{{\dot {R}}}_{k}}\varepsilon _{{2{\kern 1pt} k}}^{{2{\kern 1pt} '}}} \right)C_{{0{\kern 1pt} 1kj}}^{{01{\kern 1pt} '}}\beta _{{121}}^{{1{\kern 1pt} '2{\kern 1pt} ' - m}}}}{{d_{{k{\kern 1pt} j}}^{2}}}} \right]{\text{,}} \\ m = - 1,{\text{ }}0,{\text{ }}1, \\ \end{gathered} $
(5)
Здесь $p_{k}^{{ \mp 1}} = ({{x}_{k}} \pm i{{y}_{k}}){\text{/}}2$, $p_{k}^{0} = {{z}_{k}}$, pk = ${{p}_{k}} = {{p}_{{k0}}}{{\left( {{{R}_{0}}{\text{/}}{{R}_{k}}} \right)}^{{3\kappa }}} - $ давление в пузырьке; pk0 = p0 + + (2σ/R0) – его начальное значение; dk j − расстояние между центрами k-го и j-го пузырьков; $B_{{0k}}^{0} = - R_{k}^{2}{{\dot {R}}_{k}}$; точка сверху, как и штрих около выражений в круглых скобках (abc)', означает дифференцирование по времени, наличие сомножителей с повторяющимися верхними индексами со штрихами (одним или двумя) подразумевает суммирование в диапазоне значений, указываемых этими индексами, например: , $\dot {p}_{k}^{{1{\kern 1pt} '}}\dot {a}_{{s{\kern 1pt} k}}^{{s'}}\gamma _{{s{\kern 1pt} 1{\kern 1pt} n}}^{{s{\kern 1pt} '{\kern 1pt} 1{\kern 1pt} '{\kern 1pt} m}} = \sum\nolimits_{b = - 1}^1 {\sum\nolimits_{q = - s}^s {\dot {p}_{k}^{b}\dot {a}_{{s{\kern 1pt} k}}^{q}\gamma _{{s{\kern 1pt} 1n}}^{{q{\kern 1pt} bm}}} } $; $C_{{n\gamma kj}}^{{m\varsigma }} = C_{{n\gamma kj}}^{{m\varsigma }}(t) = $ $ = C_{{n\gamma }}^{{m\varsigma }}Y_{{n + \gamma }}^{{m - \varsigma }}\left( {{{\theta }_{{kj}}},{{\varphi }_{{kj}}}} \right)$, $\alpha _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }}$, $\beta _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }}$, $\gamma _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }}$, $\phi _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }}$, $C_{{n\,\gamma }}^{{m\,\varsigma }}$ − числа, определяемые следующими выражениями:
$\begin{gathered} \alpha _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }} = \frac{{2\vartheta + 1}}{{4\pi }}\frac{{\left( {\vartheta - \left| \zeta \right|} \right)!}}{{\left( {\vartheta + \left| \zeta \right|} \right)!}} \times \\ \times \,\,\int\limits_0^{2\pi } {\int\limits_0^\pi {\sin } } \theta Y_{\eta }^{\nu }\left( {\theta ,\varphi } \right)Y_{\xi }^{\psi }\left( {\theta ,\varphi } \right)Y_{\vartheta }^{\zeta }\left( {\theta ,\varphi } \right)d\theta d\varphi , \\ \beta _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }} = \frac{{\eta \left( {\eta + 1} \right) + \xi \left( {\xi + 1} \right) - \vartheta \left( {\vartheta + 1} \right)}}{2}\alpha _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }}{\text{,}} \\ \gamma _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }} = 2\alpha _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }} - \beta _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }}{\text{,}} \\ \end{gathered} $
$\begin{gathered} \phi _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }} = \frac{{2(2 - \vartheta )}}{3}\alpha _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }} - \beta _{{\eta \xi \vartheta }}^{{\nu \psi \zeta }}{\text{,}} \\ C_{{n{{\gamma }}}}^{{m{{\varsigma }}}} = {{\left( { - 1} \right)}^{{n + \frac{{\left| {m - {{\varsigma }}} \right| - \left| m \right| - \left| {{\varsigma }} \right|}}{2}}}}\frac{{\left( {n + {{\gamma }} - \left| {m - {{\varsigma }}} \right|} \right)!}}{{\left( {n - \left| {{\varsigma }} \right|} \right)!\left( {{{\gamma }} + \left| {{\varsigma }} \right|} \right)!}}. \\ \end{gathered} $
Здесь ${{\psi }_{{0k}}},\psi _{{1k}}^{m},\psi _{{тk}}^{m},{{\Delta }_{k}}$ − поправки, учитывающие влияние вязкости и сжимаемости жидкости, определяемые как
$\begin{gathered} {{\psi }_{{0k}}} = \frac{{4{{\nu }_{L}}{{{\dot {R}}}_{k}}}}{{{{R}_{k}}}},\,\,\,\,\psi _{{1k}}^{m} = \frac{{18{{\nu }_{L}}\dot {p}_{k}^{m}}}{{{{R}_{k}}}}, \\ \psi _{{n{\kern 1pt} k}}^{m} = \frac{{2(n + 1)\nu }}{{{{R}_{k}}}}\left( {(n + 2)\dot {a}_{{n{\kern 1pt} k}}^{m} + 2(n - 1){{{\dot {R}}}_{k}}\varepsilon _{{n{\kern 1pt} k}}^{m}} \right), \\ {{\Delta }_{k}} = - \frac{{{{{\dot {R}}}_{k}}}}{{{{c}_{L}}}}\left( {{{R}_{k}}{{{\ddot {R}}}_{k}} + \frac{{\dot {R}_{k}^{2}}}{2} + \frac{{{{p}_{{bk}}} - {{p}_{L}}}}{{{{\rho }_{L}}}}} \right) - \\ - \,\,\frac{{{{R}_{k}}}}{{{{c}_{L}}}}\left( {\frac{{{{{\dot {p}}}_{{bk}}} - {{{\dot {p}}}_{L}}}}{{{{\rho }_{L}}}} - \frac{{4{{\nu }_{L}}{{{\ddot {R}}}_{k}}}}{{{{R}_{k}}}}} \right), \\ \end{gathered} $
где cL – скорость звука в жидкости (cL = 1500 м/с).

Уравнения (3)–(5) получены в [35] методом сферических функций.

РЕЗУЛЬТАТЫ

Для оценки влияния взаимодействия пузырьков в кластере их динамика сравнивается с динамикой одиночных пузырьков в тех же условиях. Давление в одиночном пузырьке обозначается как pb, его начальное значение ‒ pb0. Основные особенности динамики пузырьков в кластере и их сжатия при воздействии (1) иллюстрируются на примере кластера кубической структуры (рис. 1) с начальным расстоянием между центрами соседних пузырьков d0 = 20R0 и числом пузырьков K = 57. Пузырьки кластеров кубической структуры можно разбить на несколько групп, в зависимости от начальной удаленности их центров от центра кластера rcl k, 0 = rcl k (0), где rcl k (t) – текущее расстояние между центрами k-го пузырька и кластера. Динамика пузырьков каждой из этих групп идентична: они совершают одинаковые радиальные пульсации, одинаково перемещаются вдоль прямых, проходящих через их центры и центр кластера, и одинаково деформируются. В частности, кластер с K = 57 состоит из шести таких групп с rcl k, 0 /d0 = 0 (1 пузырек), 1 (6 пузырьков), $\sqrt 2 $ (12 пузырьков), $\sqrt 3 $ (8 пузырьков), 2 (6 пузырьков), $\sqrt 5 $ (24 пузырька).

Особенности динамики пузырьков при однократном импульсном воздействии. Рис. 2 иллюстрирует динамику одиночного пузырька в ходе его отклика на импульсное возбуждение (1) в рассматриваемых условиях при длительности импульса t0 больше, равной и меньше периода tsing = 1/fsing собственных колебаний одиночного пузырька. Приведено изменение относительного давления в пузырьке (pb /pb 0 < 1 соответствуют расширению пузырьков, pb /pb 0 > 1 – их сжатию, а pb /pb 0 = 1 – равновесному состоянию). Видно, что при всех значениях t0 колебания давления в одиночном пузырьке монотонно затухают. Со временем частота этих колебаний стремится к собственной частоте fsing. Максимум амплитуды колебаний при импульсном воздействии с t0 = tsing больше, чем при меньшем и большем t0. Наряду с радиальными колебаниями пузырьков в настоящей работе рассматриваются также и их перемещения и деформации, но только такие, которые возникают в результате взаимодействия между пузырьками. Поэтому центр одиночного пузырька в ходе колебаний остается неподвижным, а его форма сохраняется сферической.

Рис. 2.

Изменения относительного давления в одиночном пузырьке (сплошные кривые) и окружающей жидкости (пунктирные кривые) при pа = 0.4pL min: (а) ‒ t0 ≈ 0.135 мс > tsing; (б) ‒ t0 = tsing = 0.07 мс; (в) ‒ t0 ≈ 0.0135 мс < tsing.

Рис. 3 демонстрирует динамику пузырьков в кластере в ходе их отклика на возбуждение (1) при длительности импульса t0 больше, равной и меньше tcl. Амплитуда возбуждения здесь такая же, как и в случае одиночного пузырька на рис. 2. Вместе с особенностями изменения относительного давления в пузырьках рис. 3 иллюстрирует также пространственные перемещения пузырьков в кластере и их несферические деформации. Изменение давления приведено только для центрального пузырька кластера, поскольку именно в этом пузырьке давление принимает свое максимальное для кластера значение. Аналогично перемещения пузырьков и их деформации показаны только для длительности импульса t0 = tcl, при которой они равны своим максимальным по t0 значениям или незначительно отличаются от них.

Рис. 3.

Изменения относительного давления в центральном пузырьке кластера при pа = 0.4pL min, d0 = 20R0, K = 57: (а) ‒ t0 ≈ 0.2 мс > tcl, (б) ‒ t0 ≈ 1/37 мс < tcl, (в) ‒ t0 = tcl ≈ 0.11 мс; (г) ‒ относительное смещение центров пузырьков кластера вдоль прямых, проходящих через эти центры и центр кластера при t0 = tcl; (д)–(ж) ‒ изменение амплитуд несферичности (приведены только те гармоники, которые соответствуют четырем максимальным значениям их амплитуды): (д) ‒ центрального пузырька кластера (rcl k, 0 /d0 = 0), (е) ‒ ближайших к нему пузырьков группы с rcl k, 0 /d0 = 1, (ж) ‒ периферийных пузырьков группы с rcl k, 0 /d0 = $\sqrt 5 $ при t0 = tcl.

Как и в случае с одиночным пузырьком, наибольшее значение максимума амплитуды колебаний давления в центральном пузырьке кластера (рис. 3а–3в) достигается при воздействии c длительностью импульса t0 ≈ tcl. По сравнению с одиночным пузырьком затухание колебаний давления в центральных пузырьках кластера при воздействии с t0 в окрестности t0 = tcl более медленное, чем у одиночных пузырьков при t0 = tsing, и имеет немонотонный характер. При этом со временем частота колебаний стремится к собственной частоте кластера, которая при каждом значении t0 оказывается несколько отличной от fcl в силу небольших перемещений пузырьков. В частности, из рис. 3г следует, что при t0 = tcl все пузырьки кластера в ходе колебаний смещаются к его центру (за исключением центрального, который остается неподвижным в силу симметричного расположения окружающих пузырьков). В результате этого радиус кластера Rcl со временем несколько уменьшается, что и приводит к изменению его собственной частоты. Сопоставление рис. 3a–3в с рис. 2 свидетельствует, что частота затухающих колебаний давления у пузырьков кластера заметно меньше, чем у одиночного пузырька, что согласуется с выражением (2), связывающим fcl с fsing. В ходе колебаний несферичность всех пузырьков сначала возрастает до некоторого максимального уровня, а затем постепенно убывает. При t0 = tcl (рис. 3д–3ж) максимум амплитуды несферичности у всех пузырьков примерно одинаковый. При этом центральный пузырек деформируется преимущественно по четвертой гармонике (рис. 3д), периферийный – по второй (рис. 3ж), а пузырьки между центром и периферией – сразу по нескольким гармоникам (рис. 3е). Такая разница во многом обусловлена различием в скорости поступательного движения пузырьков: в центре кластера она равна нулю, а по мере удаления от него имеет тенденцию к росту.

Экстремальные давления в пузырьках. Рис. 4 иллюстрирует зависимости максимальных давлений в одиночном пузырьке и пузырьках кластера от длительности импульса возбуждения t0. В случае одиночного пузырька (рис. 4а) в окрестности t0 = tsing имеется явно выраженная область, в которой максимальные давления в пузырьке оказываются заметно выше своих значений на периферии этой области. В данной (резонансной) области с ростом длительности импульса t0 до t0 ≈ tsing величина нормированных максимальных давлений pb max /pb 0 монотонно и относительно плавно возрастает до около 1.7, а затем также монотонно, но несколько более резко убывает. Справа от этой основной резонансной области можно выделить также еще одну, меньшую по размерам, область в окрестности t0 ≈ 3.7tsing с небольшим, но заметным локальным увеличением максимума давления.

Рис. 4.

Зависимости относительных максимальных давлений (а) в одиночном пузырьке и (б) пузырьках кластера (d0 = 20R0, K = 57) при pа = 0.4 pL min; точки – значения, соответствующие t0 = tsing ≈ 0.07 мс и t0 = = tcl ≈ 0.11 мс.

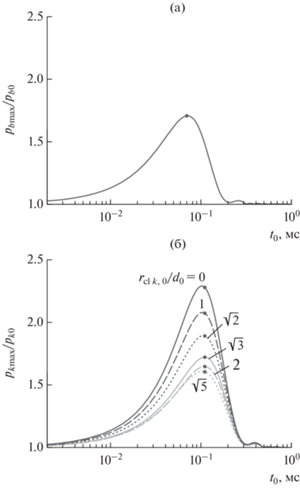
На рис. 4б видно, что указанные особенности зависимостей от t0 максимальных давлений в одиночном пузырьке имеют место и для пузырьков кластера с учетом того, что роль tsing играет здесь tcl. Вместе с тем взаимодействие между пузырьками в кластере приводит к ряду отличий. В частности, в пределах резонансной области максимальные давления монотонно возрастают по мере приближения пузырьков к центру кластера. На периферии кластера максимальные давления в пузырьках меньше, чем в случае одиночного пузырька, тогда как в пузырьках центральной области кластера они, наоборот, больше. При возбуждении кластера с t0 = tcl максимум давления в его центральном и периферийном пузырьках оказывается соответственно на 34% выше и на 6% ниже, чем в одиночном пузырьке при его возбуждении с t0= tsing.

Влияние числа пузырьков в кластере, расстояния между пузырьками, амплитуды воздействия и структуры кластера. В настоящем разделе рассматривается влияние параметров кластера K и d0, амплитуды импульса воздействия pа и структуры кластера на величину максимальных давлений в пузырьках при варьировании длительности импульса t0 в окрестности t0 = tcl. При этом значения K, d0 и pа варьируются до тех пор, пока соответствующее воздействие с длительностью t0 = tcl не нарушает условие малости несферических деформаций пузырьков. В качестве критерия малости принято неравенство $\varepsilon _{{nk}}^{2} < 0.1$.

На рис. 5 представлено изменение давления в центральном и ближайших к нему пузырьках кластера кубической структуры с d0 = 20R0, K = 57 при воздействии с длительностью импульса t0 = tcl при довольно высокой амплитуде pа = 8pL min. Деформации пузырьков не учитывались: расчет проводился по уравнениям (3), (4) с $a_{{n{\kern 1pt} k}}^{m} = 0$. Видно, что в данном случае максимальное давление в центральном пузырьке примерно в 125 раз больше, чем соответствующий максимум на рис. 4 при pа = 0.4pL min. Однако, если деформации пузырьков учитывать, то их величина у пузырьков, ближайших к центральному (rcl k, 0 /d0 = 1), становится немалой вскоре после их второго коллапса. А через малый промежуток времени данные пузырьки разрушаются (момент разрушения определяется равенством $\varepsilon _{{nk}}^{2} = 1$). Варианты, подобные приведенному на рис. 5, в настоящей работе не рассматриваются, поскольку максимальные давления в сильно несферических (а тем более в разрушенных) пузырьках могут сильно отличаться от тех, что можно получить при игнорировании несферичности пузырьков. Таким образом, принятое в настоящей работе допущение о малости несферических деформаций пузырьков кластера существенно сужает диапазоны рассматриваемых параметров кластера и воздействия на него.

Рис. 5.

Изменение давления в центральном и ближайших к нему пузырьках кластера при d0 = 20R0, K = =  57, t0 = tcl ≈ 0.44 мс, pа = 8pL min и моделировании без учета деформаций пузырьков; 1 – момент достижения предела малых деформаций пузырька ($\varepsilon _{{nk}}^{2} = 0.1$), 2 – момент его разрушения ($\varepsilon _{{nk}}^{2} = 1$) при моделировании с учетом деформаций пузырьков.

Рис. 6 иллюстрирует изменение зависимостей максимальных давлений в центральных пузырьках кластера от длительности импульса t0 в окрестности t0 = tcl при варьировании K, d0 и pа и структуры кластера в рассматриваемых условиях. Во всех случаях варьирования этих параметров зависимости максимального давления от t0 остаются качественно подобными тем, что приведены на рис. 4. Рис. 6 также свидетельствует, что с увеличением числа пузырьков в кластере наибольшие значения максимальных давлений возрастают, увеличивается ширина резонансной области. Аналогичные особенности имеют место как при уменьшении расстояния между пузырьками, так и при увеличении амплитуды воздействия.

Рис. 6.

Зависимости максимальных давлений в центральных пузырьках кластеров при ряде значений: (а) ‒ числа пузырьков в кластере K (pа = 0.4 pL min, d0 = 20R0, кластер кубической структуры), (б) ‒ расстояния между центрами пузырьков d0 (pа = 0.4pL min, K = 57, кластер кубической структуры), (в) ‒ амплитуды возбуждения pа (d0 = 20R0, K = 57, кластер кубической структуры), (г) ‒ при трех различных структурах кластера (pа = 0.4pL min, K = 57): 1 – пузырьки находятся в узлах равномерной кубической сетки, d0 = = 20R0; 2 – в центре и вершинах пяти вложенных правильных многогранников, dk j, 0 ≥ 20R0; 3 – распределены по объему случайным образом, dk j, 0 ≥ 20R0; точки – значения, соответствующие t0 = tcl.

Для оценки влияния структуры кластера результаты для кластера кубической структуры сравниваются с результатами для кластеров стохастической структуры и кластеров, состоящих из пузырьков, расположенных в центре и вершинах правильных многогранников. Стохастический кластер состоит из пузырьков со случайным начальным расположением при условии, что расстояние между центрами соседних пузырьков dk j, 0 ≥ 20R0. Кластер с пузырьками в центре и вершинах правильных многогранников состоит из 57 пузырьков, один из которых находится в центре кластера, а другие расположены на пяти концентрических сферических поверхностях, удаленных от центра кластера на расстояния d0, 1.59d0, 2d0, 2.3d0, 2.36d0 соответственно. По мере удаления от центра кластера первыми размещаются 12 пузырьков, находящихся в вершинах икосаэдра, далее – 20 пузырьков в вершинах додекаэдра, 12 пузырьков в вершинах икосаэдра, 6 пузырьков в вершинах октаэдра и 6 пузырьков в вершинах октаэдра. Многогранники ориентированы так, что минимальное расстояние между центрами пузырьков, расположенных на соседних поверхностях, составляет 20R0. На рис. 6г видно, что при изменении структуры кластера с кубической на стохастическую или при переходе к кластеру со структурой, определяемой вложенными многогранниками, зависимости максимальных давлений в центральном пузырьке кластера от t0 меняются несущественно. Рассматриваемое варьирование числа пузырьков в кластере, расстояния между пузырьками, амплитуды воздействия и структуры кластера приводит к повышению давления в пузырьках по отношению к его начальному значению не более чем в несколько раз (рис. 6).

ЗАКЛЮЧЕНИЕ

Проведено исследование влияния взаимодействия между пузырьками в сферическом кластере на величину достигаемых в них давлений в ходе отклика на однократное импульсное разрежение жидкости. Изучены зависимости этих давлений от характеристик кластера, параметров воздействия и структуры кластера. В отличие от известных работ, рассмотрение ограничивалось лишь теми вариантами, в которых все пузырьки кластера в ходе отклика сохранялись слабонесферическими. В рамках принятой модели выполнение данного условия контролировалось естественным образом по результатам расчетов несферических деформаций пузырьков. Установлено следующее.

1. В отличие от одиночного пузырька, характеризующего динамику пузырьков без учета их взаимодействия, затухание колебаний давления в пузырьках кластера в ходе отклика является более медленным и немонотонным.

2. Как и в случае одиночного пузырька, при отклике кластера на возбуждение с длительностью в окрестности значений, равных периоду собственных колебаний кластера, имеется явно выраженная (резонансная) область, в которой максимальные давления в пузырьках оказываются заметно выше соответствующих значений на периферии этой области. В пределах данной области с ростом длительности импульса величина максимальных давлений сначала монотонно и относительно плавно возрастает, а затем также монотонно, но более резко убывает. В рамках данной области максимальные давления в пузырьках по мере их приближения к центру кластера монотонно возрастают. На периферии кластера они оказываются меньше, а в центральной области кластера больше, чем в случае одиночного пузырька.

3. При варьировании числа пузырьков в кластере, расстояния между пузырьками и амплитуды воздействия характер зависимостей максимальных давлений от длительности импульса не изменяется. При этом с увеличением числа пузырьков в кластере и амплитуды воздействия, а также при уменьшении расстояния между пузырьками максимальные давления в пузырьках и ширина резонансной области возрастают.

4. При изменении структуры кластера с кубической на стохастическую (по начальному положению пузырьков) или при переходе к кластеру из пузырьков, расположенных в центре и вершинах вложенных правильных многогранников, зависимости максимальных давлений в центральном пузырьке кластера от длительности импульса меняются не сильно.

5. В рассмотренных диапазонах варьирования числа пузырьков в кластере расстояния между пузырьками, амплитуды и длительности импульса воздействия, а также в рассмотренных вариантах структуры кластера максимальное повышение давления в пузырьках по отношению к его начальному значению не превышает нескольких раз.

6. К результатам, полученным при отсутствии контроля выхода за рамки принятого допущения о том, что пузырьки в кластере сохраняются сферическими (как это зачастую делается), следует относиться с осторожностью. В частности, полученные таким образом максимальные давления в пузырьках могут оказаться сильно завышенными.

Работа выполнена при финансовой поддержке РНФ (грант № 21-11-00100).

Список литературы

  1. Нигматулин Р.И. Динамика многофазных сред. Т. 1. М.: Наука, 1987. 464 с.

  2. Нигматулин Р.И. Динамика многофазных сред. Т. 2. М.: Наука, 1987. 360 с.

  3. Кедринский В.К. Гидродинамика взрыва: эксперимент и модели. Новосибирск: Изд-во СО РАН, 2000. 434 с.

  4. Аганин А.А., Халитова Т.Ф. Деформация ударной волны при сильном сжатии несферических пузырьков // ТВТ. 2015. Т. 53. № 6. С. 923.

  5. Нигматулин Р.И., Аганин А.А., Ильгамов М.А., Топорков Д.Ю. Экстремальная фокусировка энергии при ударном сжатии парового пузырька в углеводородных жидкостях // ТВТ. 2019. Т. 57. № 2. С. 253.

  6. Brennen C.E. Bubbly Cloud Dynamics and Cavitation. Invited Lecture at the Acoustical Society of America Meeting. June 2007. Salt Lake City, Utah, 2007.

  7. Shimada M., Matsumoto Y., Kobayashi T. Dynamics of the Cloud Cavitation and Cavitation Erosion // Nippon Kikai Gakkai Ronbunshu, B-hen. 1999. V. 65. № 634. P. 1934.

  8. Ma J., Chahine G.L., Hsiao C.-T. Spherical Bubble Dynamics in a Bubbly Medium Using an Euler–Lagrange Model // Chem. Eng. Sci. 2015. V. 128. P. 64.

  9. Doinikov A.A. Translational Motion of Two Interacting Bubbles in a Strong Acoustic Field // Phys. Rev. E. 2001. V. 64. № 2. P. 026301.

  10. Harkin A., Kaper T.J., Nadim A. Coupled Pulsation and Translation of Two Gas Bubbles in a Liquid // J. Fluid Mech. 2001. V. 445. P. 377.

  11. Dear J.P., Field J.E. A Study of the Collapse of Arrays of Cavities // J. Fluid Mech. 1988. V. 190. P. 409.

  12. Blake J.R., Robinson P.B., Shima A., Tomita Y. Interaction of Two Cavitation Bubbles with a Rigid Boundary // J. Fluid Mech. 1993. V. 255. P. 707.

  13. Bremond N., Arora M., Ohl C.-D., Lohse D. Controlled Multibubble Surface Cavitation // Phys. Rev. Lett. 2006. V. 96. № 22. P. 224501.

  14. Kornfeld M., Suvorov L. On the Destructive Action of Cavitation // J. Appl. Phys. 1944. V. 15. P. 495.

  15. Chahine G.L. Pressure Generated by a Bubble Cloud Collapse // Chem. Eng. Commun. 1984. V. 28. № 4–6. P. 355.

  16. Matsumoto Y. Bubble and Bubble Cloud Dynamics // AIP Conf. Proc. 2000. V. 524. P. 65.

  17. Nigmatulin R.I., Akhatov I.Sh., Topolnikov A.S., Bolotnova R.Kh., Vakhitova N.K., Lahey R.T. Jr., Taleyarkhan R.P. Theory of Supercompression of Vapor Bubbles and Nanoscale Thermonuclear Fusion // Phys. Fluids. 2005. V. 17. № 10. P. 107106.

  18. Нигматулин Р.И., Лэхи Р.Т., Талейархан Р.П., Вест К.Д., Блок Р.С. О термоядерных процессах в кавитирующих пузырьках // УФН. 2014. Т. 184. № 9. С. 947.

  19. Wang Y.-C., Brennen C.E. Shock Wave Development in the Collapse of a Cloud of Bubbles // ASME Cavitation Multiphase Flow Forum. 1994. V. FED-194. P. 15.

  20. Wang Y.-C., Brennen C.E. The Noise Generated by the Collapse of a Cloud of Cavitation Bubbles // ASME/JSME Symp. on Cavitation and Gas-Liquid Flow in Fluid Machinery and Devices. 1995. V. FED-226. P. 17.

  21. Brennen C., Reisman G., Wang Y.-C. Shock Waves in Cloud Cavitation // 21st Symp. Naval Hydrodynamics. Washington, DC: National Acad. Press, 1997. P. 756.

  22. Reisman G.E., Wang Y.-C., Brennen C.E. Observations of Shock Waves in Cloud Cavitation // J. Fluid Mech. 1998. V. 355. P. 255.

  23. Wang Y.-C. Effects of Nuclei Size Distribution on the Dynamics of a Spherical Cloud of Cavitation Bubbles // J. Fluids Eng. 1999. V. 121. № 4. P. 881.

  24. Yoshizawa S., Sugiyama K., Matsumoto Y. Acoustic Emission from Micro Bubbles in Ultrasound Field // CAV 2001: 4th Int. Symp. on Cavitation. Pasadena, CA, USA: California Institute of Technology, 2001. Sess. A2. 003.

  25. Matsumoto Y., Yoshizawa S. Behaviour of a Bubble Cluster in an Ultrasound Field // Int. J. Numer. Me-thods Fluids. 2005. V. 47. № 6–7. P. 591.

  26. Насибуллаева Э.Ш., Ахатов И.Ш. Исследование диффузионной устойчивости пузырьков в кластере // ПМТФ. 2007. Т. 48. № 4. С. 40.

  27. Nasibullaeva E.S., Akhatov I.S. Bubble Cluster Dynamics in an Acoustic Field // JASA. 2013. V. 133. № 6. P. 3727.

  28. Галимзянов М.Н. Волны давления в трубе, заполненной жидкостью при наличии в ней пузырьковой области в форме тора // Многофазные системы. 2021. Т. 16. № 3–4. С. 112.

  29. Галимзянов М.Н., Гималтдинов И.К., Агишева У.О. О фокусировке волн давления в тороидальном пузырьковом кластере // Вестн. Башк. ун-та. 2022. Т. 27. № 2. С. 275.

  30. Doinikov A.A. Mathematical Model for Collective Bubble Dynamics in Strong Ultrasound Fields // JASA. 2004. V. 116. № 2. P. 821.

  31. Губайдуллин А.А., Губкин А.С. Особенности динамического поведения пузырьков в кластере, вызванные их гидродинамическим взаимодействием // Теплофизика и аэромеханика. 2015. Т. 22. № 4. С. 471.

  32. Aganin I.A., Davletshin A.I. Dynamics of Interacting Bubbles Located in the Center and Vertices of Regular Polyhedra // J. Phys.: Conf. Ser. 2020. V. 1588. P. 012001.

  33. Aganin I.A., Davletshin A.I. Dynamics of Gas Bubbles Inside a Ball-like Area at the Nodes of a Uniform Cubic Mesh under Sudden Liquid Pressure Rise // Lobachevskii J. Math. 2020. V. 41. № 7. P. 1148.

  34. Tiwari A., Pantano C., Freund J.B. Growth-and-collapse Dynamics of Small Bubble Clusters Near a Wall // J. Fluid Mech. 2015. V. 775. P. 1.

  35. Aganin A.A., Davletshin A.I. Equations of Interaction of Weakly Non-spherical Gas Bubbles in Liquid // Lobachevskii J. Math. 2018. V. 39. № 8. P. 1047.

  36. Aganin I.A., Davletshin A.I. Dynamics of Gas Bubbles in a Cluster under their Pressure Rise // Lobachevskii J. Math. 2021. V. 42. P. 2082.

  37. D’Agostino L., Brennen C.E. Linearized Dynamics of Spherical Bubble Clouds // J. Fluid Mech. 1989. V. 199. P. 155.

  38. Ma J., Hsiao C.T., Chahine G.L. Numerical Study of Acoustically Driven Bubble Cloud Dynamics near a Rigid Wall // Ultrason. Sonochem. 2018. V. 40. P. 944.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал