Теплофизика высоких температур, 2023, T. 61, № 2, стр. 163-169
Энергия взаимодействия в приближении Пуассона−Больцмана в корреляционной полости в асимметричной комплексной плазме
И. А. Мартынова 1, 2, *, И. Л. Иосилевский 1, 2
1 Объединенный институт высоких температур РАН
Москва, Россия
2 Московский физико-технический институт (национальный
исследовательский университет)
Долгопрудный, Россия
* E-mail: martina1204@yandex.ru
Поступила в редакцию 19.08.2022
После доработки 11.10.2022
Принята к публикации 06.12.2022
Аннотация
В работе рассматривается двухкомпонентная электронейтральная система классических макроионов конечных размеров с зарядом Z $ \gg $ 1 и точечных противоположно заряженных микроионов с единичным зарядом. В приближении Пуассона−Больцмана в корреляционной полости учтен эффект нелинейного экранирования макроионов микроионами внутри полости. Рассчитана энергия взаимодействия всех частиц системы, которая по абсолютной величине существенно превышает значения, полученные некоторыми другими авторами.
ВВЕДЕНИЕ
Данная работа посвящена изучению термодинамики комплексной плазмы. Под комплексной плазмой в настоящее время понимают достаточно много видов плазмы. Это равновесная коллоидная плазма [1, 2], неравновесная газоразрядная пылевая плазма [3, 4], плазма с конденсированной дисперсной фазой [5, 6], пылевая плазма серебристых облаков [7] и атмосферы белых карликов [8]. В данной работе рассматривается двухкомпонентная равновесная электронейтральная система макроионов с радиусом RZ и большим зарядовым числом Z $ \gg $ 1 и точечных микроионов с единичным зарядом противоположного знака. Для определенности будем считать заряд макроиона (-Ze) отрицательным, Z > 0 (далее зарядовое число Z называется “зарядом”). В работе изучается трехмерная сильно-неидельная низкотемпературная ионная система, наиболее близкая к коллоидной плазме. Характерная температура kT коллоидной плазмы комнатная (однако для некоторых результатов диапазон температур расширен), характерный заряд макроиона ‒ 103−104, его характерный радиус RZ варьируется от 0.1 до 10 мкм, характерная концентрация макроионов nZ составляет 105−109 см–3.
Термодинамика комплексной плазмы рассматривалась в большом числе работ. Например, описание однокомпонентной системы с эффективным потенциалом выполнено в [1, 6, 9, 10], многокомпонентных – в работах [11‒15]. В частности, в статье [11] рассматривались сильные корреляции точечных макроионов друг с другом в так называемом «приближении корреляционной полости». Основная идея этого приближения описана в работе [16], а позже независимо предложена в [17]. Его суть заключается в том, что в некоторой окрестности пробного макроиона (корреляционной полости) есть только микроионы, а другие макроионы отсутствуют. Это исправляет известную некорректность линеаризованного дебаевского приближения – проблему так называемой “отрицательной вероятности” (отрицательной величины концентрации макроионов на близких к пробному макроиону расстояниях). Таким образом, в пределах корреляционной полости с радиусом h концентрация макроионов полагается равной нулю, а вне полости описывается линеаризованным дебаевским приближением
(1)
$n_{Z}^{{}}(r) = \left\{ {\begin{array}{*{20}{c}} {{{n}_{Z}}\left( {1 + \frac{{Ze{{\varphi }_{{{\text{out}}}}}(r)}}{{kT}}} \right),}&{r \geqslant h,} \\ {0,}&{r \leqslant h.} \end{array}} \right.$В статье [11] были получены аналитические формулы, позволяющие построить аппроксимации численных результатов нескольких других работ для энергии взаимодействия и некоторых зависимостей, описывающих колебательные свойства системы. Для этого в [11] рассмотрено линейное экранирование макроионов микроионами и внутри, и снаружи полости. Однако здесь есть некоторые ограничения, которые связаны с изучением линейного (дебаевского) экранирования макроионов внутри полости. Во-первых, в [11] исследуется именно линеаризованное приближение, однако на достаточно близких расстояниях к макроиону условие линеаризации нарушается для характерных параметров рассматриваемой комплексной плазмы $\left| {{{e\varphi (r)} \mathord{\left/ {\vphantom {{e\varphi (r)} {(kT)}}} \right. \kern-0em} {(kT)}}} \right| > 1$, где φ(r) – средний электростатический потенциал, создаваемый внутри полости всеми микро- и макроионами. Поэтому в нашей работе будем учитывать нелинейное экранирование внутри полости в рамках приближения Пуассона−Больцмана, т.е. рассмотрим более сильные корреляции микроионов с макроионом внутри полости, чем в статье [11]. Концентрация микроионов внутри полости при этом является экспоненциальной, а не линеаризованной, как в [11]. Во-вторых, макроионы в [11] считаются точечными, в то время как в настоящей работе предполагается их конечный размер. Указанные два отличия рассмотрены в следующем разделе.
Нелинейное экранирование макроионов рассматривалось ранее и в других приближениях, например в средней сферической ячейке Вигнера−Зейтца (ВЗ) [5, 18‒20], а в статье [15] предложено аналитическое решение уравнения Пуассона−Больцмана для случаев сферической и аксиальной симметрии.
В представленной работе будет описано приближение Пуассона−Больцмана в корреляционной полости, где нелинейное экранирование рассматривается только внутри полости, затем рассчитана энергия взаимодействия всех частиц системы и продемонстрировано отличие от некоторых других работ.
ПРИБЛИЖЕНИЕ ПУАССОНА−БОЛЬЦМАНА В КОРРЕЛЯЦИОННОЙ ПОЛОСТИ
Будем рассматривать отрицательно заряженные макроионы с зарядовым числом (зарядом) −Z, где Z > 0, и радиусом RZ, а также положительные точечные микроионы с единичным зарядом.
Как отмечено во Введении, в приближении корреляционной полости концентрация макроионов внутри полости полагается равной нулю. В таком случае из условия равенства концентраций на границе полости и выражений для концентраций макроионов (1), а также средних электростатических потенциалов снаружи и внутри полости ${{\varphi }_{{{\text{out}}}}}(h) = \varphi (h)$, создаваемых всеми частицами (микро- и макроионами), получим
Так как Z $ \gg $ 1, то на границе полости выполняется условие линеаризации. Следовательно, вне полости можно рассматривать дебаевское распределение микроионов. Учитывалось нелинейное экранирование внутри полости, поэтому там распределение микроионов больцмановское. Таким образом, концентрация микроионов имеет вид
(3)
${{n}_{i}}(r) = \left\{ {\begin{array}{*{20}{c}} {{{n}_{i}}\left( {1 - \frac{{e{{\varphi }_{{{\text{out}}}}}(r)}}{{kT}}} \right),}&{r \geqslant h,} \\ {{{n}_{{i0}}}\exp \left( { - \left( {\frac{{e\varphi (r)}}{{kT}} - \frac{{e\varphi (h)}}{{kT}}} \right)} \right),}&{r \leqslant h.} \end{array}} \right.$Из условия равенства концентраций микроионов на границе полости получаем их концентрацию ${{n}_{{i0}}} = {{n}_{Z}}(Z + 1)$ на этой границе.
Средний электростатический потенциал вне полости имеет дебаевский вид
(4)
${{\varphi }_{{{\text{out}}}}}(r) = \frac{D}{r}\exp \left( { - \frac{r}{{{{r}_{{{\text{Dout}}}}}}}} \right),$(5)
${{r}_{{{\text{Dout}}}}} = {{\left( {\frac{{4\pi {{e}^{2}}}}{{kT}}{{n}_{Z}}Z(Z + 1)} \right)}^{{ - 1/2}}}.$С учетом равенства концентраций макроионов (1) на границе полости и (4) получаем
Напряженность внутри неэлектронейтральной полости
(7)
$E(r) = \frac{e}{{{{r}^{2}}}}\left( { - Z + \int\limits_{{{R}_{Z}}}^r {{{n}_{i}}(r)4\pi {{r}^{2}}dr} } \right).$С учетом
условие сшивки напряженностей на границе полости имеет следующий вид:(9)
$\frac{e}{{{{h}^{2}}}}\left( { - Z + \int\limits_{{{R}_{Z}}}^h {{{n}_{i}}(r)4\pi {{r}^{2}}dr} } \right) = - \varphi _{{{\text{out}}}}^{'}(h).$Подставляя в (9) уравнения (3)–(6), получаем уравнение для неизвестного радиуса полости h
(10)
$\begin{gathered} {{h}^{2}} + h{{r}_{{{\text{Dout}}}}} - \frac{{Z{{e}^{2}}}}{{kT}}{{r}_{{{\text{Dout}}}}} \times \\ \times \,\,\left( {Z - \int\limits_{{{R}_{Z}}}^h {{{n}_{Z}}(Z + 1)\exp \left( { - \left( {\frac{{e\varphi (r)}}{{kT}} + \frac{1}{Z}} \right)} \right)4\pi {{r}^{2}}dr} } \right) = 0. \\ \end{gathered} $Решая итерационно систему уравнений (3), (7), (9) и (10) (при условии, что на бесконечности потенциал ${{\left. {{{\varphi }_{{{\text{out}}}}}(r)} \right|}_{{x \to + \infty }}} \to 0$), находим распределение среднего электростатического потенциала φ(r) внутри полости и размер самой полости. Более подробно это приближение рассматривалось в работе [12].
ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ В ПРИБЛИЖЕНИИ КОРРЕЛЯЦИОННОЙ ПОЛОСТИ
Введем безразмерную энергию взаимодействия для всех будущих нижних индексов u = U/(kT), где U – размерная энергия взаимодействия. В приближении корреляционной полости энергию взаимодействия можно представить в виде девяти слагаемых:
(11)
$\begin{gathered} u = {{u}_{{{{i}^{{{\text{in}}}}}{{i}^{{{\text{in}}}}}}}} + {{u}_{{Z{{i}^{{{\text{in}}}}}}}} + {{u}_{{Z{{Z}^{{{\text{out}}}}}}}} + {{u}_{{{{i}^{{{\text{in}}}}}{{Z}^{{{\text{out}}}}}}}} + {{u}_{{Z{{i}^{{{\text{out}}}}}}}} + \\ + \,\,{{u}_{{{{i}^{{{\text{in}}}}}{{i}^{{{\text{out}}}}}}}} + {{u}_{{{{Z}^{{{\text{out}}}}}{{Z}^{{{\text{out}}}}}}}} + {{u}_{{{{i}^{{{\text{out}}}}}{{i}^{{{\text{out}}}}}}}} + {{u}_{{{{Z}^{{{\text{out}}}}}{{i}^{{{\text{out}}}}}}}}, \\ \end{gathered} $(12)
${{u}_{{jk}}} = \left\{ \begin{gathered} \frac{1}{{kT}}\int\limits_{{{r}_{m}}}^{{{r}_{n}}} {{{\varphi }_{j}}(r){{q}_{k}}{{n}_{k}}(r)4\pi {{r}^{2}}dr,{\text{ }}j \ne k,} \hfill \\ \frac{1}{{2kT}}\int\limits_{{{r}_{m}}}^{{{r}_{n}}} {{{\varphi }_{j}}(r){{q}_{k}}{{n}_{k}}(r)4\pi {{r}^{2}}dr,{\text{ }}j = k,} \hfill \\ \end{gathered} \right.$(13)
$\begin{gathered} {{u}_{{{{Z}^{{{\text{out}}}}}{{i}^{{{\text{out}}}}}}}} = \frac{1}{{kT}} \times \\ \times \,\,\int\limits_h^{ + \infty } {\left( {{{\varphi }_{{{{Z}^{{{\text{out}}}}}}}}(r)e{{n}_{i}}(r) + {{\varphi }_{{{{i}^{{{\text{out}}}}}}}}(r)( - Ze){{n}_{Z}}(r)} \right)2\pi {{r}^{2}}dr} , \\ \end{gathered} $Найдем потенциал ${{\varphi }_{{{{i}^{{{\text{in}}}}}}}}(r)$ при RZ ≤ r ≤ h:
(14)
${{\left. {{{\varphi }_{{{{i}^{{{\text{in}}}}}}}}(r)} \right|}_{{r \leqslant h}}} - {{\varphi }_{{{{i}^{{{\text{in}}}}}}}}(0) = \int\limits_{r < h}^0 {{{E}_{{{{i}^{{{\text{in}}}}}}}}({{r}_{1}})d{{r}_{1}}} ,$(15)
${{E}_{{{{i}^{{{\text{in}}}}}}}}({{r}_{1}}) = \left\{ \begin{gathered} {{e{{q}_{{{{i}^{{{\text{in}}}}}}}}({{r}_{1}})} \mathord{\left/ {\vphantom {{e{{q}_{{{{i}^{{{\text{in}}}}}}}}({{r}_{1}})} {r_{1}^{2}}}} \right. \kern-0em} {r_{1}^{2}}},{\text{ }}{{r}_{1}} \leqslant h, \hfill \\ {{e{{q}_{{{{i}^{{{\text{in}}}}}}}}} \mathord{\left/ {\vphantom {{e{{q}_{{{{i}^{{{\text{in}}}}}}}}} {r_{1}^{2},{\text{ }}{{r}_{1}} \geqslant h}}} \right. \kern-0em} {r_{1}^{2},{\text{ }}{{r}_{1}} \geqslant h}}, \hfill \\ \end{gathered} \right.$Найдем ${{\varphi }_{{{{i}^{{{\text{in}}}}}}}}(0) = {{\varphi }_{{{{i}^{{{\text{in}}}}}}}}({{R}_{Z}})$. Для этого запишем уравнение, аналогичное (14), но для потенциала ${{\varphi }_{{{{i}^{{{\text{in}}}}}}}}(r)$, создаваемого внутренними микроионами вне полости (при r ≥ h):
(16)
${{\left. {{{\varphi }_{{{{i}^{{{\text{in}}}}}}}}(r)} \right|}_{{r \geqslant h}}} - {{\varphi }_{{{{i}^{{{\text{in}}}}}}}}(0) = \int\limits_{r \geqslant h}^h {{{E}_{{{{i}^{{{\text{in}}}}}}}}({{r}_{1}})d{{r}_{1}}} + \int\limits_h^{{{R}_{Z}}} {{{E}_{{{{i}^{{{\text{in}}}}}}}}({{r}_{1}})d{{r}_{1}}} .$Будем считать, что потенциалы всех компонент, каждый по отдельности, на бесконечности равны нулю. Тогда из (15) и (16) получим
Это приводит к выражению для потенциала, создаваемого внутренними микроионами вне полости:
Для потенциала, создаваемого внутренними микроионами внутри полости, получаем
Найдем потенциал ${{\varphi }_{{{{Z}^{{{\text{out}}}}}}}}(r)$, создаваемый внешними макроионами, находящимися в сфере радиуса r, на поверхности этой сферы:
Так как внешние макроионы отсутствуют внутри полости, то ${{\varphi }_{{{{Z}^{{{\text{out}}}}}}}}(0) = {{\left. {{{\varphi }_{{{{Z}^{{{\text{out}}}}}}}}(r)} \right|}_{{\forall r \leqslant h}}}$. Обнуляя потенциал на бесконечности, находим
Таким образом:
По аналогии получаем потенциал, создаваемый внешними микроионами за пределами полости:
Запишем формулы для слагаемых энергии взаимодействия (11). Первое и второе слагаемые с учетом (2)
(17)
$\begin{gathered} {{u}_{{{{i}^{{{\text{in}}}}}{{i}^{{{\text{in}}}}}}}} = \frac{{{{e}^{2}}}}{{2kT}}\int\limits_{{{R}_{Z}}}^h {\left[ {\frac{{{{q}_{{{{i}^{{{\text{in}}}}}}}}}}{h} + \int\limits_{r < h}^h {\frac{{{{q}_{{{{i}^{{{\text{in}}}}}}}}({{r}_{1}})}}{{r_{1}^{2}}}d{{r}_{1}}} } \right] \times } \hfill \\ \times \,\,{{n}_{Z}}(Z + 1)\exp \left( { - \left( {\frac{{e\varphi (r)}}{{kT}} + \frac{1}{Z}} \right)} \right)4\pi {{r}^{2}}dr, \hfill \\ \end{gathered} $(18)
${{u}_{{Z{{i}^{{{\text{in}}}}}}}} = - \frac{{Z{{e}^{2}}}}{{kT}}\left( {\frac{{{{q}_{{{{i}^{{{\text{in}}}}}}}}}}{h} + \int\limits_{{{R}_{Z}}}^h {\frac{{{{q}_{{{{i}^{{{\text{in}}}}}}}}(r)}}{{{{r}^{2}}}}dr} } \right).$Сумма третьего, четвертого, пятого и шестого слагаемых, описывающих взаимодействие внутренних и внешних частиц, выглядит следующим образом:
(19)
$\begin{gathered} {{u}_{{{{i}^{{{\text{in}}}}}{{Z}^{{{\text{out}}}}}}}} + {{u}_{{{{i}^{{{\text{in}}}}}{{i}^{{{\text{out}}}}}}}} + {{u}_{{Z{{Z}^{{{\text{out}}}}}}}} + {{u}_{{Z{{i}^{{{\text{out}}}}}}}} = \\ = \,\,\frac{{{{e}^{2}}}}{{kT}}h{{r}_{{{\text{Dout}}}}}{{n}_{Z}}4\pi \left( {{{q}_{{{{i}^{{{\text{in}}}}}}}}(Z + 1) + Z(1 - Z)} \right). \\ \end{gathered} $Сумма седьмого, восьмого и девятого слагаемых, описывающих взаимодействие частиц внешних подсистем, имеет вид
(20)
$\begin{gathered} {{u}_{{{{Z}^{{{\text{out}}}}}{{Z}^{{{\text{out}}}}}}}} + {{u}_{{{{Z}^{{{\text{out}}}}}{{i}^{{{\text{out}}}}}}}} + {{u}_{{{{i}^{{{\text{out}}}}}{{i}^{{{\text{out}}}}}}}} = \frac{{{{e}^{2}}}}{{kT}}{{(Z + 1)}^{2}}{{h}^{3}}n_{Z}^{2} \times \\ \times \,\,r_{{{\text{Dout}}}}^{2}8{{\pi }^{2}}\left( {1 + \frac{{{{r}_{{{\text{Dout}}}}}}}{h}} \right) - \frac{{{{e}^{2}}}}{{kT}}{{(Z + 1)}^{2}}{{h}^{2}}n_{Z}^{2}r_{{{\text{Dout}}}}^{3}4{{\pi }^{2}} - \\ - \,\,\frac{{{{e}^{2}}}}{{kT}}{{(Z + 1)}^{2}}{{h}^{2}}n_{Z}^{2}{{r}_{{{\text{Dout}}}}}8{{\pi }^{2}}\exp \left( {\frac{{2h}}{{{{r}_{{{\text{Dout}}}}}}}} \right) \times \\ \times \,\,\left( {1 - {{{\left( {\frac{{{{r}_{{{\text{Dout}}}}}}}{h}} \right)}}^{2}}} \right) \times \\ \times \,\,\int\limits_h^{ + \infty } {r\exp \left( { - \frac{r}{{{{r}_{{{\text{Dout}}}}}}}} \right)} \left[ {\int\limits_{r > h}^\infty {\frac{1}{{{{r}_{1}}}}\exp \left( { - \frac{{{{r}_{1}}}}{{{{r}_{{{\text{Dout}}}}}}}} \right)d{{r}_{1}}} } \right]dr. \\ \end{gathered} $На рис. 1−3 приведено сравнение результатов расчетов энергии взаимодействия для нескольких вариантов наборов параметров: концентрации макроионов nZ и температуры системы kT. Для удобства линии, соответствующие одинаковым приближениям, имеют на всех трех рисунках одинаковые номера. Кривые с номером 2 (со звездами) рассчитаны авторами в приближении Пуассона−Больцмана в корреляционной полости по формулам (11), (17)−(20) и соответствуют энергии взаимодействия всех макроионов и всех микроионов друг с другом. На рис. 1 также приведена кривая 2а (с квадратами). Она соответствует части энергии взаимодействия в приближении Пуассона−Больцмана в корреляционной полости в работе [12]. Рассмотрим, чем эти расчеты в [12] отличаются от выполненных в данной работе. В [12] энергия взаимодействия была рассчитана как
(21)
$\begin{gathered} {{u}_{{{\text{prev}}}}} = \frac{1}{2}\int\limits_{{{R}_{Z}}}^h {\left( {\frac{{e\varphi (r)}}{{kT}} + \frac{{Z{{e}^{2}}}}{{rkT}}} \right){{n}_{i}}(r)4\pi {{r}^{2}}dr} - \\ - \,\,Z{{\left( {\frac{{e\varphi (r)}}{{kT}} + \frac{{Z{{e}^{2}}}}{{rkT}}} \right)}_{{r \to {{R}_{Z}}}}}. \\ \end{gathered} $Рис. 1.
Энергия взаимодействия в различных приближениях при nZ = 108 см–3, kT = 0.03 эВ, RZ = 1 мкм: 1 – все микроионы находятся на поверхности макроиона, 2 (со звездами) – приближение Пуассона–Больцмана в корреляционной полости (расчет данной работы), 2а (с квадратами) – часть энергии взаимодействия [12] (см. (21)) в приближении Пуассона–Больцмана в корреляционной полости, 3 – энергия взаимодействия в средней сферической ячейке ВЗ, 4 (штриховая) – линеаризованное дебаевское приближение в ячейке ВЗ, 5 (с кружками) – расчет по формулам [11] (см. (22)) в приближении Дебая–Хюккеля в корреляционной полости, 6 (с треугольниками) – расчет по формулам [21], 7 – равномерное распределение микроионов в ячейке ВЗ.
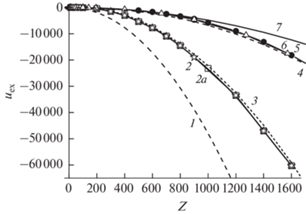
Так как φ(r) является средним потенциалом, то
Два первых слагаемых описывают взаимодействие внутренних (т.е. находящихся внутри полости) частиц друг с другом, а четыре последних представляют собой часть энергии взаимодействия внутренних и внешних (находящихся вне полости) частиц. Корреляции частиц внутри полости преобладают над корреляциями внешних частиц друг с другом и над корреляциями внешних и внутренних частиц между собой, поэтому при достаточно больших зарядах макроиона Z основной вклад в энергию взаимодействия вносит ее “внутренняя” часть (два первых слагаемых). Поэтому кривая 2а на рис. 1, соответствующая более ранним результатам [12] и рассчитанная по формуле (21), практически совпадает с результатами данной работы (кривая 2).
Сравним результаты данной работы (кривая 2) с более ранними. Например, в [11] энергия взаимодействия (кривая 5 с кружками) для двухкомпонентной системы была рассчитана как
(22)
$u_{{{\text{Khr}}}}^{{}} = \frac{{Ze}}{{2kT}}{{\left( {{{\varphi }_{{{\text{DHH}}}}}(r) - \frac{{Ze}}{r}} \right)}_{{r \to 0}}},$Рис. 2.
Энергия взаимодействия в различных приближениях при nZ = 108 см–3, kT = 0.1 эВ, RZ = 1 мкм: 1 – все микроионы находятся на поверхности макроиона, 2 – приближение Пуассона–Больцмана в корреляционной полости (данная работа), 3 – энергия взаимодействия в средней сферической ячейке ВЗ, 4 – линеаризованное дебаевское приближение в ячейке ВЗ, 5 (с кружками) – расчет по формулам [11] (см. (22)) в приближении Дебая–Хюккеля в корреляционной полости, 6 (с треугольниками) – расчет по формулам [21].
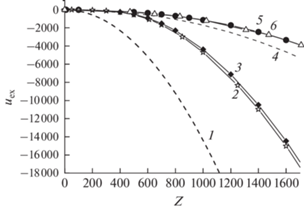
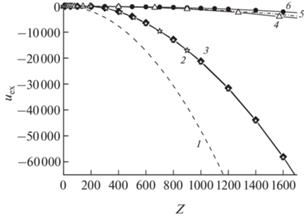
Рис. 3.
Энергия взаимодействия в различных приближениях при nZ = 106 см–3, kT = 0.03 эВ, RZ = 1 мкм: обозначения как на рис. 2.
На рис. 1–3 для сравнения представлены результаты расчетов в других приближениях в средней сферической электронейтральной ячейке ВЗ радиусом $R = {{\left( {{3 \mathord{\left/ {\vphantom {3 {(4\pi {{n}_{Z}})}}} \right. \kern-0em} {(4\pi {{n}_{Z}})}}} \right)}^{{1/3}}}$ с центральным макроионом радиусом RZ и противоположно заряженными точечными микроионами в остальной части ячейки. Эти расчеты соответствуют искусственному равномерному распределению микроионов (кривая 7 на рис. 1), линеаризованному дебаевскому распределению (штриховые кривые 4 на рис. 1−3) и больцмановскому распределению (кривые 5, приближение Пуассона‒Больцмана в ячейке). Для расчета энергии взаимодействия в указанных трех приближениях учитывалaсь энергия взаимодействия микроионов в ячейке друг с другом и микроионов с центральным макроионом. Таким образом, энергия взаимодействия в этих приближениях рассчитывалась по формулам, аналогичным (21), с той разницей, что в этих случаях радиус полости h заменялся на радиус ячейки R и подставлялись соответствующие распределения микроионов ni(r) и средний потенциал φ(r). В общем виде потенциал в линеаризованном (дебаевском) приближении выглядит следующим образом:
(23)
${{\varphi }_{{{\text{UP}}}}}(r) = \left\{ \begin{gathered} {{C}_{3}}{{r}^{2}} + \frac{{{{C}_{4}}}}{r} + {{\varphi }_{2}}{\text{, }}{{R}_{Z}} \leqslant r \leqslant R, \hfill \\ 0,{\text{ }}r \geqslant R, \hfill \\ \end{gathered} \right.$Более подробно расчет энергий взаимодействия в случае ячеечного приближения представлен в работе [12].
Для сравнения на рис. 1 приведена кривая 1, соответствующая случаю, когда все микроионы (и внутри, и снаружи полости) находятся на поверхности макроиона. Как и ожидалось, эта кривая соответствует бóльшим значениям энергии по абсолютной величине, чем в остальных расчетах.
На рис. 4 приведена зависимость заряда макроиона от размеров полости для тех же параметров системы, что и на рис. 1.
Рис. 4.
Зависимость размера полости от заряда макроиона в корреляционной полости в приближении Пуассона−Больцмана при nZ = 108 см–3, kT = 0.03 эВ, RZ = 1 мкм.
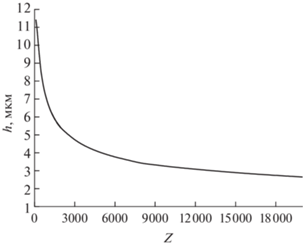
В связи с использованием в настоящей работе приближения Пуассона−Больцмана при расчете равновесного профиля заряда возникает проблема доказательства существования и единственности такого решения. Близкая проблема анализировалась в работе [15] в рамках другой постановки задачи, при решении которой соответствующий профиль заряда находился аналитически. В данной работе приближение Пуассона−Больцмана используется в рамках более сложной процедуры, включающей использование дополнительной теоретической конструкции – так называемой корреляционной полости как неэлектронейтральной ячейки переменного радиуса, величина которого находится в дополнительной итеративной процедуре. Использование приближения Пуассона−Больцмана в этой процедуре делает проблему существования и единственности искомого решения неочевидной. При более простой постановке задачи с использованием приближения Пуассона−Больцмана для нахождения равновесного профиля заряда в электронейтральной сферической ячейке ВЗ с фиксированным радиусом (см., например, [12, 22]) проблема существования и единственности искомого профиля не вызывает опасений. Действительно, как известно (см., например, [23, 24]), в этой постановке равновесный профиль заряда может быть найден в рамках вариационного подхода статистической механики (метода функционала плотности) как минимум функционала свободной энергии, когда в качестве корреляционного функционала выступает выражение, где для локального уравнения состояния флюида микроионов используется простейшее приближение идеального газа. При этом искомый профиль микроионов, обеспечивающий минимум функционала свободной энергии, локализован между двумя пределами, где указанный функционал свободной энергии заведомо завышен: а) профилем микроионов, равномерно заполняющих всю ячейку ВЗ за исключением самого макроиона, и, напротив, б) профилем, где микроионы сконцентрированы в виде тонкой (конденсированной) пленки на поверхности макроиона. Что же касается итеративной схемы настоящей работы, использующей приближение Пуассона−Больцмана только внутри корреляционной полости переменного радиуса, в то время как вне корреляционной полости применяется стандартное дебаевское приближение, то вопрос о существовании и единственности решения такой комбинированной схемы является открытым. Вместе с тем, чтобы получить по возможности содержательное сравнение с результатами аналитического подхода работы [15], где была обнаружена область параметров, в которой задача Пуассона−Больцмана формально не имела решения с конечной величиной заряда макроиона, была построена зависимость размера полости от заряда макроиона. Дело в том, что вывод об области параметров, где формально отсутствует решение, был основан на полученной в работе [15] зависимости заряда макроиона от размеров ячейки (см. рис. 1 в [15]), где при некотором размере ячейки заряд макроиона должен был стремиться к бесконечности. Полученная в настоящей работе зависимость, приведенная на рис. 4, качественно похожа на указанную выше. Однако заряд макроиона, определенный расчетами настоящей работы, должен стать слишком большим, чтобы наблюдалась указанная асимптотическая зависимость.
ЗАКЛЮЧЕНИЕ
Энергия взаимодействия, полученная в данной работе с учетом нелинейного экранирования в приближении Пуассона‒Больцмана в корреляционной полости, имеет большее по абсолютной величине значение, чем более ранние результаты [11, 21]. Основной вклад в рассчитанную энергию взаимодействия вносят слагаемые, отвечающие за взаимодействие частиц, находящихся внутри полости, т.е. энергия взаимодействия центрального макроиона полости с микроионами полости и энергия взаимодействия микроионов полости друг с другом.
Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ (соглашение с ОИВТ РАН № 075-15-2020-785 от 23 сентября 2020 г.).
Список литературы
Dijkstra M., van Roij R. Vapour-liquid Coexistence for Purely Repulsive Point-Yukawa Fluids // J. Phys. Condens. Matter. 1998. V. 10. № 6. P. 1219.
Diehl A., Barbosa M., Levin Y. Charge Renormalization and Phase Separation in Colloidal Suspensions // EPL. 2001. V. 53. № 1. P. 86.
Фортов В.Е., Храпак А.Г., Якубов И.Т. Физика неидеальной плазмы. Учеб. пособ. М.: Физматлит, 2004. 528 с.
Липаев А.М., Молотков В.И., Жуховицкий Д.И., Наумкин В.Н., Усачев А.Д., Зобнин А.В., Петров О.Ф., Фортов В.Е. Исследования пылевой газоразрядной плазмы на космической установке “Плазменный кристалл-3 Плюс” (обзор) // ТВТ. 2020. Т. 58. № 4. С. 485.
Жуховицкий Д.И., Храпак А.Г., Якубов И.Т. Ионизационное равновесие в сильно неидеальной плазме с конденсированной дисперсной фазой // ТВТ. 1984. Т. 22. № 5. С. 833.
Асиновский Э.И., Олейникова Е.Н., Хомкин А.Л. Ван-дер-ваальсова модель термической пылевой плазмы // ТВТ. 2001. Т. 39. № 6. С. 853.
Клумов Б., Морфилл Г., Попель С. Формирование структур в запыленной ионосфере // ЖЭТФ. 2005. Т. 127. № 1. С. 171.
Kenzhebekova A.I., Bastykova N.K., Kodanova S.K., Ramazanov T.S., Maiorov S.A., Moldabekov Z.A. Destruction of a Dust Particle in the White Dwarf Atmosphere // Jpn. J. Appl. Phys. 2020. V. 59. SHHA04.
Vaulina O.S., Koss X.G., Khrustalyov Yu.V., Petrov O.F., Fortov V.E. Thermodynamic and Transport Properties of Nonideal Systems with Isotropic Pair Potentials // Phys. Rev. E. 2010. V. 82. P. 056411.
Решетняк В.В., Старостин А.Н., Филиппов А.В. Теоретическое исследование равновесных свойств жидкости Юкавы в широком диапазоне параметров // ЖЭТФ. 2018. Т. 154. № 6(12). С. 1258.
Khrapak S., Khrapak A., Ivlev A., Morfill G. Simple Estimation of Thermodynamic Properties of Yukawa Systems // Phys. Rev. E. 2014. V. 89. № 2. P. 023102.
Martynova I.A., Iosilevskiy I.L. Non-linear Screening and Phase States of a Complex Plasma // Contrib. Plasma Phys. 2018. V. 58. № 2–3. P. 203.
Hynninen A.-P., Panagiotopoulos A.Z. Disappearance of the Gas−Liquid Phase Transition for Highly Charged Colloids // Phys. Rev. Lett. 2007. V. 98. № 19. P. 198301.
Мартынова И.А., Иосилевский И.Л. О сдвиге границ термодинамической неустойчивости асимметричной комплексной плазмы с учетом эффекта нелинейного экранирования // ТВТ. 2021. Т. 59. № 6. С. 817.
D’yachkov L.G. Screening of Macroions in Colloidal Plasmas: Accurate Analytical Solution of the Poisson−Boltzmann Equation // Phys. Lett. A. 2005. V. 340. P. 440.
Грязнов В.К., Иосилевский И.Л. Проблема построения интерполяционного уравнения состояния плазмы // Численные методы в механике сплошной среды. 1973. Т. 4. № 5. С. 166.
Nordholm S. Simple Analysis of the Thermodynamic Properties of the One-component Plasma // Chem. Phys. Lett. 1984. V. 105. № 3. P. 302.
Zhukhovitskiy D.I., Petrov O.F., Hyde T.W., Herdrich G., Laufer R., Dropmann M., Matthews L.S. Electrical Conductivity of the Thermal Dusty Plasma Under the Conditions of a Hybrid Plasma Environment Simulation Facility // New J. Phys. 2015. V. 17. P. 053041.
Aleksander S., Chaikin P.M., Grant P., Morales G.J., Pincus P., Hone D. Charge Renormalization, Osmotic Pressure, and Bulk Modulus of Colloidal Crystals: Theory // J. Chem. Phys. 1984. V. 80. P. 5776.
Bystrenko O., Zagorodny A. Critical Effects in Screening of High-Z Impurities in Plasmas // Phys. Lett. A. 1999. V. 255. P. 325.
Farouki R.T., Hamaguchi S. Thermodynamics of Strongly-coupled Yukawa Systems Near the One-component-plasma Limit. II. Molecular Dynamics Simulations // J. Chem. Phys. 1994. V. 101. № 11. P. 9885.
Martynova I., Iosilevskiy I., Shagayda A. Macroions Nonlinear Screening in Complex Plasma // J. Phys.: Conf. Ser. 2018. V. 946. P. 012147.
Киржниц Д.А., Лозовик Ю.Е., Шпатаковская Г.В. Статистическая модель вещества // УФН. 1975. Т. 117. С. 3.
Иосилевский И.Л., Чигвинцев А.Ю., Ногинова Л.Ю., Зорина И.Г. Аномалии профиля пространственного заряда и фазовые переходы в модифицированных моделях однокомпонентной плазмы // ТВТ. 2021. Т. 59. № 6. С. 836.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур


