Теоретические основы химической технологии, 2019, T. 53, № 1, стр. 67-77
К теории замещения метана из состава газогидрата диоксидом углерода
В. Ш. Шагапов 1, *, Г. Р. Рафикова 1, 2, М. К. Хасанов 2
1 Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Казань, Россия
2 Стерлитамакский филиал Башкирского государственного университета
Стерлитамак, Россия
* E-mail: Shagapov@rambler.ru
Поступила в редакцию 26.05.2016
После доработки 23.08.2018
Принята к публикации 19.07.2018
Аннотация
Рассмотрена плоскоодномерная теоретическая модель и получены численные решения для процесса замещения метана диоксидом углерода из состава гидрата в пласте, насыщенном метаном и его гидратом, при продувке углекислым газом. Рассмотрен случай, когда интенсивность образования гидрата диоксида углерода лимитируется диффузией углекислого газа через образовавшийся гидратный слой между потоком газовой смеси и гидратом метана. Исследована динамика основных параметров процесса и расходов инжектируемого, выходящего углекислого газа и извлекаемого метана. Проанализировано влияние величины коэффициента диффузии и значения абсолютной проницаемости на особенности процесса газозамещения.
ВВЕДЕНИЕ
В настоящее время большое внимание уделяется проблеме поиска и разработки альтернативных источников энергии. Одними из таких источников являются газогидраты, залежи которых расположены в донных отложениях мирового океана, в зонах вечной мерзлоты, а также на суше и в местах, способствующих термобарическим условиям существования гидрата. Потенциальные запасы метана в виде газогидрата превышают величину 1.5 × 1016 м3. Возникает необходимость разработки технологий, позволяющих безопасно и эффективно реализовывать добычу газа из гидратных отложений. Наиболее известные предлагаемые методы разработки таких залежей: депрессионное и тепловое воздействие на пласт [1–5], введение ингибиторов в пласт [6]. Одним из перспективных способов извлечения метана из состава гидрата является его замещение диоксидом углерода. Искусственно организованный такой круговорот, с одной стороны, позволит организовать добычу природного газа, а с другой стороны, позволит утилизировать углекислый газ до необходимых объемов с точки зрения отрицательных экологических последствий.
Эксперименты по исследованию процесса замещения метана из состава гидрата диоксидом углерода проводились в работах [7–13]. В [8–10] было установлено, что замещение метана углекислым газом в гидрате может происходить без высвобождения свободной воды при значениях давления и температуры, соответствующих стабильному существованию гидрата метана. В экспериментальных работах [10, 11] выявлено, что одним из основных механизмов процесса замещения является диффузия углекислого газа к поверхности контакта гидратов метана и двуокиси углерода. Исследование кинетики разложения газогидрата метана в пласте при закачке в него смеси диоксида углерода и азота рассмотрено в [12].
Математические модели образования гидрата углекислого газа в пласте, содержащем воду и метан в свободном состоянии, путем инжекции газообразного и жидкого диоксида углерода были рассмотрены в работах [14, 15]. Теоретическое исследование процесса нагнетания углекислого газа в пористую среду, насыщенную метаном и его гидратом, проведено в [16, 17].
В настоящей работе представлено теоретическое исследование процесса закачки газообразного диоксида углерода в пористый пласт, насыщенный гидратом метана, с последующим замещением метана в гидрате на углекислый газ. Построены численные решения, позволяющие определить основные режимы исследуемого процесса.
ОСНОВНЫЕ УРАВНЕНИЯ
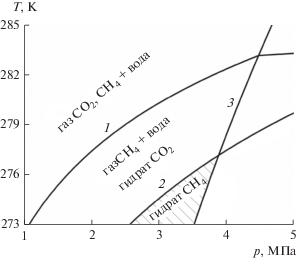
Рассмотрим в плоскоодномерном приближении процесс закачки газообразного диоксида углерода в гидратный пласт. Термобарические условия существования гидратов метана и углекислого газа представлены на фазовой диаграмме (рис. 1). Области стабильности гидратов углекислого газа и метана находятся ниже линий 1 и 2 соответственно, слева от линии 3 диоксид углерода находится в газообразном состоянии. Предполагается, что процесс замещения будет происходить в области стабильного существования гидратов метана и двуокиси углерода, а также существования CO2 в газообразном состоянии (заштрихованная область на фазовой диаграмме).
Пусть гидратный пласт в исходном состоянии состоит из трех составляющих, а именно из твердого каркаса (скелета), не участвующего в физико-химическом превращении, метана и его газогидрата. Скелет пористой среды, газогидрат (метана и диоксида углерода) полагаем неподвижными и несжимаемыми.
Запишем уравнения сохранения масс для диоксида углерода и метана, фильтрующихся через пласт:
(1)
$\begin{gathered} \frac{{\partial \left( {m{{S}_{g}}\rho _{{gd}}^{0}} \right)}}{{\partial t}} + \frac{{\partial \left( {m{{S}_{g}}{{\upsilon }_{{gd}}}\rho _{{gd}}^{0}} \right)}}{{\partial x}} = - {{J}_{{gd}}}, \\ \frac{{\partial \left( {m{{S}_{g}}\rho _{{gm}}^{0}} \right)}}{{\partial t}} + \frac{{\partial \left( {m{{S}_{g}}{{\upsilon }_{{gm}}}\rho _{{gm}}^{0}} \right)}}{{\partial x}} = {{J}_{{gm}}}. \\ \end{gathered} $Здесь m – пористость скелета (для объема, занятого газом и гидратом); ${{S}_{g}}$ – газонасыщенность; $\rho _{{gi}}^{0}$ и ${{\upsilon }_{{gi}}}\,$ (i = d, m) – парциальные плотности и скорости компонент газовой смеси; ${{J}_{{gd}}}$ и ${{J}_{{gm}}}$ – интенсивности перехода диоксида углерода в состав гидрата и вытеснения метана из состава гидрата; нижние индексы i = d, m относятся соответственно к углекислому газу и метану.
Будем полагать, что твердый гидрат состоит из двух составляющих: гидрата метана и гидрата диоксида углерода. Тогда объемную гидратонасыщенность можно представить как
где ${{S}_{{hi}}}$ – гидратонасыщенность, которая приходится к гидратам диоксида углерода (i = d) и метана (i = m).При этом
Полагая, что газогидрат неподвижен $\left( {{{\upsilon }_{{gh}}} = 0} \right),$ уравнения сохранения масс для составляющих гидратной фазы запишутся в виде [18]
(2)
$\frac{{\partial \left( {m{{S}_{{hd}}}{{G}_{d}}\rho _{{hd}}^{0}} \right)}}{{\partial t}} = {{J}_{{gd}}},\,\,\,\,\,\frac{{\partial \left( {m{{S}_{{hm}}}{{G}_{m}}\rho _{{hm}}^{0}} \right)}}{{\partial t}} = - {{J}_{{gm}}}.$Здесь $\rho _{{_{{hi}}}}^{0}$ и ${{G}_{{hi}}}$ (i = d и m) – плотность гидрата и массовое содержание газа в составе гидрата для диоксида углерода (i = d) и метана (i = m).
Кроме того, можем записать уравнение сохранения массы воды в составе гидрата в следующем виде:
(3)
$\frac{\partial }{{\partial t}}m\left( {{{S}_{{hd}}}\left( {1 - {{G}_{d}}} \right)\rho _{{hd}}^{0} + {{S}_{{hm}}}\left( {1 - {{G}_{m}}} \right)\rho _{{hm}}^{0}} \right) = 0.$Поскольку в исходном состоянии гидрат диоксида углерода отсутствует $\left( {{{S}_{{hd}}} = 0,\,\,{{S}_{{hm}}} = {{S}_{{h0}}}} \right),$ то при интегрировании уравнения (3) получим
(4)
$\begin{gathered} {{S}_{{hd}}}\left( {1 - {{G}_{d}}} \right)\rho _{{hd}}^{0} + {{S}_{{hm}}}\left( {1 - {{G}_{m}}} \right)\rho _{{hm}}^{0} = \\ = {{S}_{{h0}}}\left( {1 - {{G}_{m}}} \right)\rho _{{hm}}^{0}. \\ \end{gathered} $Здесь отметим, что для гидратов диоксида углерода и метана имеем $\rho _{{hd}}^{0} = 1117$ кг/м3, $\rho _{{hm}}^{0} = 910$ кг/м3 [19]. Наиболее распространенная структура гидратов метана и диоксида углерода KC-I, когда на одну молекулу газа приходится около шести молекул воды, в связи с чем массовые доли диоксида углерода и метана в составе гидрата соответственно равны ${{G}_{d}}$ = 0.29 и ${{G}_{m}}$ = 0.13 [20]. Следовательно, с хорошей точностью выполняется соотношение
(5)
$\left( {1 - {{G}_{d}}} \right)\rho _{{hd}}^{0} = \left( {1 - {{G}_{m}}} \right)\rho _{{hm}}^{0}.$Данное условие также означает, что в единице объема гидрата диоксида углерода и метана содержится одинаковая масса воды. С учетом вышеприведенных фактов примем, что число молекул метана, покидающего гидрат, равно числу молекул диоксида углерода, переходящих в состав гидрата, и процесс происходит без высвобождения воды из состава гидрата [8–10]. Отсюда для интенсивностей ${{J}_{{gd}}}$ и ${{J}_{{gm}}}$ выполняется следующее соотношение:
где ${{M}_{i}}$ (i = d и m) – молекулярные массы диоксида углерода и метана.Из уравнения (4) с учетом (5) следует
откуда
Для газовой смеси в целом введем среднемассовую скорость
(7)
$\rho _{g}^{0}{{\upsilon }_{g}} = \rho _{{gd}}^{0}{{\upsilon }_{{gd}}} + \rho _{{gm}}^{0}{{\upsilon }_{{gm}}},\,\,\,\,\left( {\rho _{g}^{0} = \rho _{{gd}}^{0} + \rho _{{gm}}^{0}} \right).$Сложим уравнения (1), тогда с учетом (6) и (7) будем иметь
(8)
$\frac{{\partial \left( {m{{S}_{g}}\rho _{g}^{0}} \right)}}{{\partial t}} + \frac{{\partial \left( {m{{S}_{g}}\rho _{g}^{0}{{\upsilon }_{g}}} \right)}}{{\partial x}} = {{J}_{{gd}}}\left( {\frac{{{{M}_{m}}}}{{{{M}_{d}}}} - 1} \right).$Для фильтрации и диффузионного перемешивания газовой смеси примем соответственно закон Дарси и закон Фика:
(9)
$m{{S}_{g}}{{\upsilon }_{g}} = - \frac{{{{k}_{g}}}}{{{{\mu }_{g}}}}\frac{{\partial p}}{{\partial x}},$(10)
$\begin{gathered} \rho _{{gd}}^{0}{{w}_{{gd}}} = - \rho _{{gm}}^{0}{{w}_{{gm}}} = {{D}_{g}}\frac{{\partial \rho _{{gm}}^{0}}}{{\partial x}}, \\ \left( {{{w}_{{gd}}} = {{\upsilon }_{{gd}}} - {{\upsilon }_{g}},\,\,\,\,{{w}_{{gm}}} = {{\upsilon }_{{gm}}} - {{\upsilon }_{g}}} \right). \\ \end{gathered} $Здесь ${{D}_{g}}\,$ – коэффициент диффузионного перемешивания смеси метана и диоксида углерода, ${{w}_{{gi}}}$ (i = m и d) – диффузионные скорости метана и диоксида углерода.
Будем полагать, что газовая смесь является калорически совершенной и подчиняется закону Дальтона:
(11)
${{p}_{{gd}}} = \rho _{{gd}}^{0}{{R}_{d}}T,\,\,\,\,{{p}_{{gm}}} = \rho _{{gm}}^{0}{{R}_{m}}T,\,\,\,\,p = {{p}_{{gd}}} + {{p}_{{gm}}}.$Полагая, что температура для скелета пористой среды и всех ее составляющих совпадает $\left( {{{T}_{{sk}}} = {{T}_{h}} = {{T}_{g}} = T} \right),$ запишем уравнение для изменения внутренней энергии системы, состоящей из скелета пористой среды и насыщающего вещества:
(12)
$\begin{gathered} \rho с \frac{{\partial T}}{{\partial t}} + m{{S}_{g}}\rho _{g}^{0}{{c}_{g}}{{\upsilon }_{g}}\frac{{\partial T}}{{\partial x}} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right) + \\ + \,\,m\left( {\rho _{{hd}}^{0}{{l}_{{hd}}}\frac{{\partial {{S}_{{hd}}}}}{{\partial t}} + \rho _{{hm}}^{0}{{l}_{{hm}}}\frac{{\partial {{S}_{{hm}}}}}{{\partial t}}} \right),\,\,\,\,\rho с = (1 - m)\rho _{{sk}}^{0}{{с }_{{sk}}} + \\ + \,\,m\left( {{{S}_{g}}\rho _{g}^{0}{{с }_{g}} + {{S}_{{hd}}}\rho _{{hd}}^{0}{{с }_{{hd}}} + {{S}_{{hm}}}\rho _{{hm}}^{0}{{с }_{{hm}}}} \right), \\ \rho _{g}^{0}{{с }_{g}} = \rho _{{gd}}^{0}{{с }_{{gd}}} + \rho _{{gm}}^{0}{{с }_{{gm}}}, \\ \lambda = (1 - m){{\lambda }_{{sk}}} + m\left( {{{S}_{g}}{{\lambda }_{g}} + {{S}_{{hd}}}{{\lambda }_{{hd}}} + {{S}_{{hm}}}{{\lambda }_{{hm}}}} \right). \\ \end{gathered} $Здесь ${{с }_{j}},$ ${{\lambda }_{j}}$ – удельная теплоемкость и теплопроводность фаз $\left( {j = g,h} \right),$ $\rho с ,$ $\lambda $ – удельная объемная теплоемкость и теплопроводность системы, ${{l}_{{hm}}},\,\,{{l}_{{hd}}}$ – удельные теплоты разложения и образования гидрата метана и диоксида углерода соответственно, отнесенные на единицу массы. Так как основной вклад в значения ρc и λ вносят соответствующие параметры скелета пористой среды, то будем считать их постоянными величинами.
КИНЕТИКА ЗАМЕЩЕНИЯ МЕТАНА ДИОКСИДОМ УГЛЕРОДА В СОСТАВЕ ГАЗОГИДРАТА
Будем полагать, что интенсивность замещения молекул метана молекулами диоксида углерода определяется диффузией диоксида углерода через слой гидрата диоксида углерода, образовавшийся между газом и гидратом метана.
Для построения аналитических выражений для кинетики гидратообразования диоксида углерода (или замещения молекул метана молекулами диоксида углерода) рассмотрим следующую предельную схему. Примем, что гидрат метана полностью покрывает стенки пористых каналов. Пористую среду (скелет) схематически представим как систему цилиндрических каналов радиуса а. Тогда, согласно рассматриваемой схеме, гидрат метана будет находиться в кольцевом слое между $r = a$ и $r = {{a}_{{\left( {md} \right)}}},$ гидрат диоксида углерода – в слое между $r = {{a}_{{\left( {md} \right)}}}$ и $r = {{a}_{g}},$ а газовая смесь диоксида углерода и метана – в канале радиуса $r = {{a}_{g}}.$ В рамках принятой схемы, введенные линейные размеры и относительные фазовые насыщенности будут связаны следующим образом:
(13)
$\begin{gathered} {{S}_{{hm}}} = 1 - {{\left( {\frac{{{{a}_{{\left( {md} \right)}}}}}{a}} \right)}^{2}},\,\,\,\,{{S}_{{hd}}} = {{\left( {\frac{{{{a}_{{\left( {md} \right)}}}}}{a}} \right)}^{2}} - {{\left( {\frac{{{{a}_{g}}}}{a}} \right)}^{2}}, \\ {{S}_{g}} = {{\left( {\frac{{{{a}_{g}}}}{a}} \right)}^{2}}. \\ \end{gathered} $Отметим, что в силу соотношений (4) и (5) линейный параметр ${{a}_{{\left( {md} \right)}}}$ зависит от времени, а остальные параметры – постоянные величины (a и ${{a}_{g}}$ = const).
Для процесса переноса диффундирующего газа через слой гидрата диоксида углерода запишем уравнение диффузии [21, 22]
(14)
$\frac{{\partial \rho _{{gd}}^{{0'}}}}{{\partial t}} = \frac{{{{D}_{{hd}}}}}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial \rho _{{gd}}^{{0'}}}}{{\partial r}}} \right),\,\,\,\,\,{{a}_{{\left( {md} \right)}}} > r > {{a}_{g}},$При граничных условиях
(15)
$\rho _{{gd}}^{{0'}} = \rho _{{gd\left( s \right)}}^{0},\,\,\,\,r = {{a}_{g}};\,\,\,\,\rho _{{gd}}^{{0'}} = 0,\,\,\,\,r = {{a}_{{\left( {md} \right)}}}$квазистационарное решение уравнения (14) для плотности подвижного углекислого газа в гидрате CO2 имеет следующий вид:
(16)
$\rho _{{gd}}^{'} = \rho _{{gd(s)}}^{0}\frac{{\ln ({r \mathord{\left/ {\vphantom {r {{{a}_{{\left( {md} \right)}}}}}} \right. \kern-0em} {{{a}_{{\left( {md} \right)}}}}})}}{{\ln ({{{{a}_{g}}} \mathord{\left/ {\vphantom {{{{a}_{g}}} {{{a}_{{\left( {md} \right)}}}}}} \right. \kern-0em} {{{a}_{{\left( {md} \right)}}}}})}},\,\,\,\,{{a}_{{\left( {md} \right)}}} > r > {{a}_{g}}.$Здесь $\rho _{{gd(s)}}^{0}$ – плотность подвижного диоксида углерода в составе гидрата для состояния насыщения. Второе условие в (15) означает мгновенное вытеснение молекулами диоксида углерода молекул метана при достижении молекул диоксида углерода границы $r = {{a}_{{\left( {md} \right)}}}.$ Отметим, что квазистационарное решение применимо вследствие очень малой толщины слоя газогидрата.
Запишем выражение для потока массы подвижного диоксида углерода к поверхности контакта между гидратами диоксида углерода и метана, отнесенного к единице ее площади, в следующем виде:
(17)
${{j}_{{gd}}} = - {{D}_{{hd}}}{{\left( {\frac{{\partial \rho _{{gd}}^{{0'}}}}{{\partial r}}} \right)}_{{{{a}_{{\left( {md} \right)}}}}}}.$Подставляя решение (16) в (17), получим
(18)
${{j}_{{gd}}} = \frac{{\rho _{{gd(s)}}^{0}{{D}_{{hd}}}}}{{{{a}_{{\left( {md} \right)}}}\ln ({{{{a}_{{\left( {md} \right)}}}} \mathord{\left/ {\vphantom {{{{a}_{{\left( {md} \right)}}}} {{{a}_{g}}}}} \right. \kern-0em} {{{a}_{g}}}})}}.$Чтобы связать поток ${{j}_{{gd}}}$ с интенсивностью потребления диоксида углерода ${{J}_{{gd}}},$ необходимо определить полную площадь поверхности контакта в единице объема пористой среды (удельная поверхность контакта) между гидратами СО2 и СН4. В рамках принятой схемы для этой площади можем записать
(19)
${{s}_{{md}}} = 2\pi {{a}_{{\left( {md} \right)}}}{{n}_{{\left( {md} \right)}}},\,\,\,\,{{n}_{{\left( {md} \right)}}} = \frac{{m\left( {1 - {{S}_{{hm}}}} \right)}}{{\pi a_{{\left( {md} \right)}}^{2}}},$По аналогии с законом Генри примем, что насыщенная концентрация свободного газа СО2 в составе гидрата пропорциональна величине парциального давления СО2 в газовой фазе, т.е.
где ${{\Gamma }_{d}}$ – параметр Генри. Тогда для интенсивности ${{J}_{{gd}}}$ потребления СО2 на образование гидрата в единице объема, связанной с ${{j}_{{gd}}}$ как ${{J}_{{gd}}} = {{s}_{{md}}}{{j}_{{gd}}},$ используя (18) и (19), получим(21)
${{J}_{{gd}}} = 2m\left( {1 - {{S}_{{hm}}}} \right)\frac{{\rho _{{gd(s)}}^{0}{{D}_{{hd}}}}}{{a_{{\left( {md} \right)}}^{2}\ln \left( {{{{{a}_{{\left( {md} \right)}}}} \mathord{\left/ {\vphantom {{{{a}_{{\left( {md} \right)}}}} {{{a}_{g}}}}} \right. \kern-0em} {{{a}_{g}}}}} \right)}}.$Отметим, что $\rho _{{gd(s)}}^{0}$ и ${{D}_{{hd}}}$ являются неизвестными эмпирическими параметрами. В выражение (21), следовательно, и в общую систему уравнений данные параметры входят в виде произведения. Поэтому для дальнейшего введем один эмпирический параметр, приведенный коэффициент диффузии для СО2, отвечающий в силу принятых выше допущений за кинетику образования гидрата СО2:
Подставляя (20) и первое уравнение из (11) в (22), получим
Если, по аналогии с жидкостями, коэффициент диффузии ${{D}_{{hd}}}$ и параметр Генри ${{\Gamma }_{d}}$ считать достаточно консервативными величинами (слабо зависящими от давления ${{p}_{{gd}}},$ например) и поскольку относительное изменение температуры по шкале Кельвина для рассматриваемых процессов слабо меняется $\left( {{{\Delta T} \mathord{\left/ {\vphantom {{\Delta T} {T \leqslant {{{10}}^{{ - 2}}}}}} \right. \kern-0em} {T \leqslant {{{10}}^{{ - 2}}}}}} \right),$ то введенный коэффициент D, имеющий размерность коэффициента диффузии, можно принять за постоянный эмпирический модельный параметр. Наличие небольшой доли примесей других газов в составе углекислого газа и метана может повлиять на процессы гидратообразования и разложения [20, 23, 24]. Эмпирический параметр D зависит как от структуры гидрата, так и от особенностей скелета пористой среды.
УРАВНЕНИЯ ДЛЯ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
За переменные для численного интегрирования примем $\rho _{{gd}}^{0},$ $\rho _{g}^{0},$ T и ${{S}_{{hd}}}.$
Первое уравнение из (1) с учетом (9) и (10) можно записать как
(23)
$m{{S}_{g}}\frac{{\partial \rho _{{gd}}^{0}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\rho _{{gd}}^{0}\frac{{{{k}_{g}}}}{{{{\mu }_{g}}}}\frac{{\partial p}}{{\partial x}}} \right) + m{{S}_{g}}{{D}_{g}}\frac{{{{\partial }^{2}}\rho _{{gd}}^{0}}}{{\partial {{x}^{2}}}} - {{J}_{{gd}}}.$В качестве второго уравнения используем (8), которое с учетом (9) примет вид
(24)
$m{{S}_{g}}\frac{{\partial \rho _{g}^{0}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\rho _{g}^{0}\frac{{{{k}_{g}}}}{{{{\mu }_{g}}}}\frac{{\partial p}}{{\partial x}}} \right) + {{J}_{{gd}}}\left( {\frac{{{{M}_{m}}}}{{{{M}_{d}}}} - 1} \right).$Уравнение притока тепла (12) с учетом (6) и (9) запишем в виде
(25)
$\begin{gathered} \rho с \frac{{\partial T}}{{\partial t}} = \rho _{g}^{0}{{c}_{g}}\frac{{{{k}_{g}}}}{{m{{\mu }_{g}}}}\frac{{\partial p}}{{\partial x}}\frac{{\partial T}}{{\partial x}} + \lambda \frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + \\ + \,\,\left( {\frac{{{{l}_{{hd}}}}}{{{{G}_{d}}}} - \frac{{{{M}_{m}}}}{{{{M}_{d}}}}\frac{{{{l}_{{hm}}}}}{{{{G}_{m}}}}} \right){{J}_{{gd}}}. \\ \end{gathered} $Для замыкания этой системы достаточно добавить еще одно дифференциальное уравнение, следующее из первого уравнения (2):
При этом для других переменных параметров, входящих в систему (23)–(26), с учетом (13), (21) и (22) получим
(27)
$\begin{gathered} {{J}_{{gd}}} = \frac{{4m\rho _{{gd}}^{0}D}}{{{{a}^{2}}\ln \left( {{{1 + {{S}_{{hd}}}} \mathord{\left/ {\vphantom {{1 + {{S}_{{hd}}}} {{{S}_{g}}}}} \right. \kern-0em} {{{S}_{g}}}}} \right)}}, \\ {{S}_{{hm}}} = {{S}_{h}} - {{S}_{{hd}}},\,\,\,\,\,{{S}_{g}} = 1 - {{S}_{h}}\,\,\left( {{{S}_{h}} = {\text{const}}} \right). \\ \end{gathered} $На основе (11) для давления можем получить
(28)
$p = \left( {\rho _{{gd}}^{0}\left( {{{R}_{d}} - {{R}_{m}}} \right) + \rho _{g}^{0}{{R}_{m}}} \right)T.$В соответствии с принятыми выше допущениями проницаемость для газовой смеси и радиус пористых каналов будет задаваться как
(29)
${{k}_{g}} = k{{\left( {{{{{a}_{g}}} \mathord{\left/ {\vphantom {{{{a}_{g}}} a}} \right. \kern-0em} a}} \right)}^{2}},\,\,\,\,a = \sqrt {{k \mathord{\left/ {\vphantom {k m}} \right. \kern-0em} m}} ,$Систему уравнений (23)–(29) дополним граничными и начальными условиями
(30)
$\begin{gathered} x = 0,\,\,\,\,t > 0\,:\,\,p = {{p}_{e}},\,\,\,\,\,{{p}_{{gd}}} = {{p}_{{gde}}},\,\,\,\,\,T = {{T}_{e}}, \\ x = {{x}_{0}},\,\,\,\,\,\,t > 0\,:\,\,p = {{p}_{0}},\,\,\,\,{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0em} {\partial x}} = 0, \\ 0 < x < {{x}_{0}},\,\,\,\,t = 0\,:\,\,p = {{p}_{0}},\,\,\,\,\,{{p}_{{gd}}} = 0,\,\,\,\,\,T = {{T}_{0}}, \\ \end{gathered} $РЕЗУЛЬТАТЫ
Система уравнений (23)–(29) с начальными и граничными условиями (30) была решена методом конечных разностей с применением явной схемы [25]. Для параметров системы приняты следующие значения: ${{T}_{0}} = 273$ К, ${{T}_{e}} = 273$ К, ${{p}_{0}} = 2.9$ МПа, ${{p}_{e}} = 3.3$ МПа, ${{S}_{{hm0}}} = 0.2,$ ${{x}_{0}} = 10$ м, $m = 0.1,$ k = = 10–11 м2, $\rho c = 2.5 \times {{10}^{6}}$ Дж/(м3 К), λ = 2 Вт/(м К), ${{l}_{{hm}}} = 4.37 \times {{10}^{5}}$ Дж/кг, ${{l}_{{hd}}} = 4.8 \times {{10}^{5}}$ Дж/(кг К), $\rho _{{hm}}^{0} = 910$ кг/м3, $\rho _{{hd}}^{0} = 1117$ кг/м3, ${{G}_{m}} = 0.13,$ ${{G}_{d}} = 0.29,$ Rgm = 520 Дж/(кг К), ${{R}_{{gd}}} = 189$ Дж/(кг К), ${{c}_{{gm}}} = 1560$ Дж/(кг К), ${{c}_{{gd}}} = 731$ Дж/(кг К), mgm = = 1.12 × 10–5 Па с, ${{\mu }_{{gd}}} = 1.5 \times {{10}^{{ - 5}}}$ Па с, Dg = 10–5 м2/с, $D = 5 \times {{10}^{{ - 15}}}$ м2/с.
На рис. 2 линиями 1–4 представлены распределения общего и парциальных давлений для диоксида углерода и метана (а, б, в), температуры (г), гидратонасыщенностей CO2 и СH4 (д, е) по координате в моменты времени 5, 25, 300 и 750 с соответственно. Точечная линия соответствует равновесной температуре при текущем давлении системы.
Рис. 2.
Эволюция полей общего давления $p$ (а), парциальных давлений диоксида углерода ${{p}_{{gd}}}$ (б) и метана ${{p}_{{gm}}}$ (в), температуры $T$ (г), насыщенностей гидрата диоксида углерода ${{S}_{{hd}}}$ (д) и метана ${{S}_{{hm}}}$ (е) в различные моменты времени (1 – t = 5 с, 2 – t = 25 с, 3 – t = 300 с, 4 – t = 750 с).
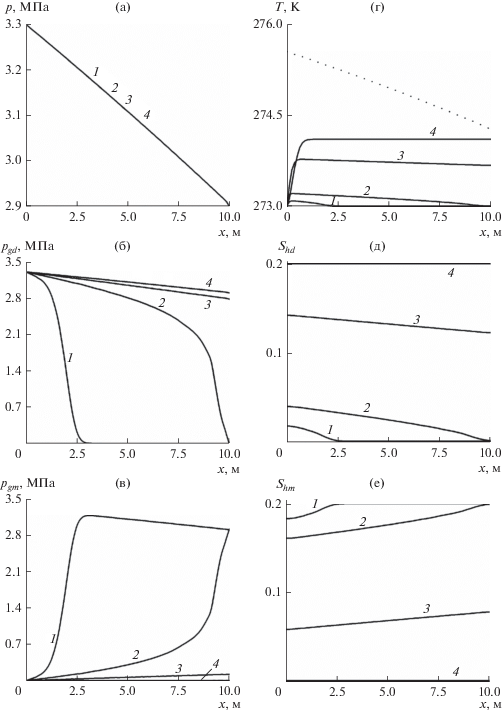
Рис. 3.
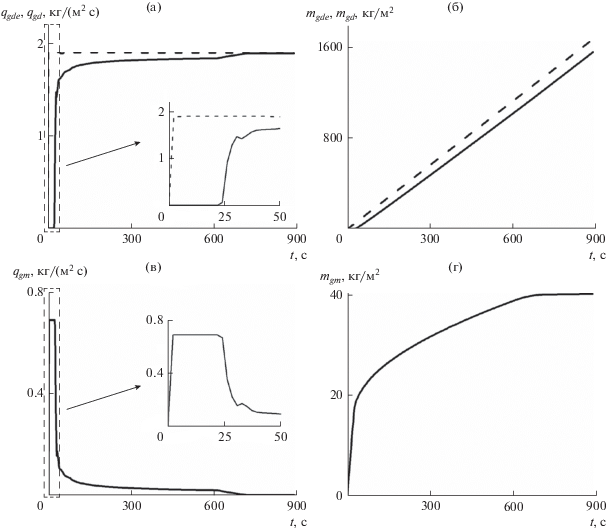
Массовые расходы и масса закачиваемого и выходящего углекислого газа (а, б), извлекаемого метана (в, г) в зависимости от времени.
Видно, что вследствие инжекции CO2 парциальное давление диоксида углерода в пласте возрастает и начинается процесс замещения метана двуокисью углерода в газогидрате. Фронт вытеснения свободного метана диоксидом углерода доходит до правой границы пласта за время около 25 с. В остальное продолжительное время вытесняется метан, полученный в результате его замещения диоксидом углерода из состава газогидрата. Процесс газозамещения в составе гидрата сопровождается повышением температуры (приблизительно на 1 К).
Массовые расходы углекислого газа и метана, отнесенные на единицу площади поперечного сечения пласта, равны
Здесь ${{q}_{{gde}}}$ – расход закачиваемого углекислого газа; ${{q}_{{gd}}},$ ${{q}_{{gm}}}$ – расходы диоксида углерода и метана на выходе.
Тогда общие массы закаченного и добытого диоксида углерода и метана, отнесенные на единицу площади поперечного сечения пласта, равны
На рис. 3 приведены зависимости массовых расходов и массы закачиваемого и выходящего диоксида углерода (а, б) и добываемого метана (в, г) от времени. Здесь штриховая линия обозначает расход и массу инжектируемого углекислого газа.
Видно, что на начальном этапе вытесняется свободный метан, затем происходит скачок расходов, часть диоксида углерода поглощается, и часть метана выделяется вследствие начала процесса газозамещения. Следующий этап характеризуется вытеснением метана, полученного в результате процесса замещения метана из состава гидрата углекислым газом. После полного извлечения метана из пласта расходы диоксида углерода на входе и выходе совпадают. В результате процесса извлекается около 40 кг/м2 метана и консервируется около 90 кг/м2 углекислого газа.
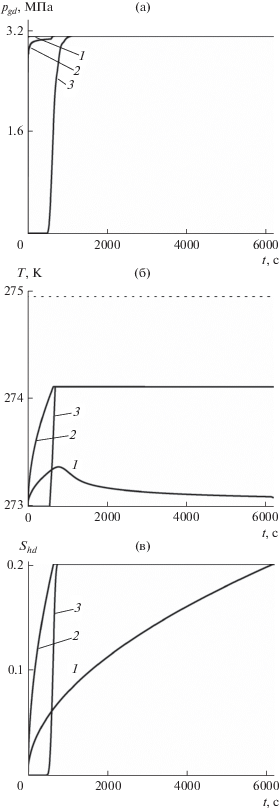
На рис. 4 линиями 1, 2 и 3 представлена динамика парциального давления диоксида углерода (а), температуры (б) и гидратонасыщенности диоксида углерода (в) в точке x = 5 м при значениях приведенного коэффициента диффузии $D = 5 \times {{10}^{{ - 14}}},$ $5 \times {{10}^{{ - 15}}}\,$ и $5 \times {{10}^{{ - 16}}}\,$ м2/с соответственно.
Рис. 4.
Осциллограммы парциального давления диоксида углерода ${{p}_{{gd}}}$ (а), температуры $T$ (б), гидратонасыщенности диоксида углерода ${{S}_{{hd}}}$ (в) в точке x = = 5 м для различных значений коэффициента диффузии: 1 – $D = 5 \times {{10}^{{ - 14}}}$ м2/с, 2 – $D = 5 \times {{10}^{{ - 15}}}$ м2/с, 3 – $D = 5 \times {{10}^{{ - 16}}}$ м2/с.
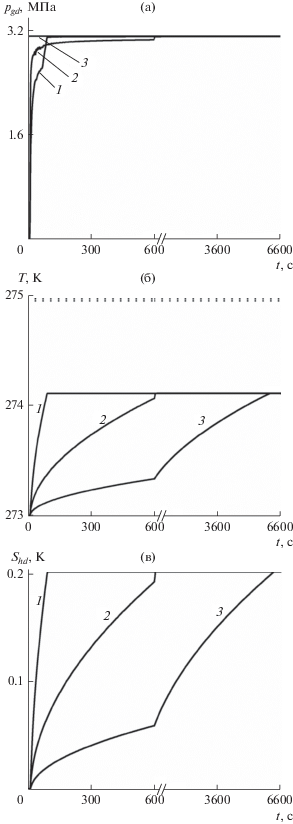
Определяющими параметрами характерных времен фильтрации ${{t}^{{(p)}}}$ (время наполнения пласта диоксидом углерода) и диффузии газа ${{t}^{{(D)}}}$ (замещение метана из состава гидрата диоксидом углерода) являются коэффициент пьезопроводности ${{\chi }^{{(p)}}}$ $\left( {{{t}^{{(p)}}} \approx {{x_{0}^{2}} \mathord{\left/ {\vphantom {{x_{0}^{2}} {{{\chi }^{{(p)}}}}}} \right. \kern-0em} {{{\chi }^{{(p)}}}}}} \right)$ и диффузии D $\left( {{{t}^{{(D)}}} \approx {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} D}} \right. \kern-0em} D}} \right).$ Если для коэффициента диффузии принять D = 5 × × 10–14 м2/с, то за время полного вытеснения метана из состава гидрата не происходит полного наполнения диоксида углерода в пласте $\left( {{{t}^{{(D)}}} < {{t}^{{(p)}}}} \right).$ Согласно рис. 4 в этом случае процесс гидратообразования происходит во фронтальном режиме. При дальнейшем уменьшении коэффициента диффузии (D = $5 \times {{10}^{{ - 15}}}$ м2/с) наблюдается примерно одинаковое значение характерных времен ${{t}^{{(D)}}} \approx {{t}^{{(p)}}}$ (кривая 2). При малых значениях коэффициента диффузии (кривая 3) процесс наполнения пласта диоксидом углерода будет происходить гораздо быстрее процесса полного замещения метана в пористой среде в составе гидрата углекислым газом $\left( {{{t}^{{(D)}}} > {{t}^{{(p)}}}} \right).$ В этом случае, согласно рис. 4, процесс гидратообразования диоксида углерода происходит в объемной области.
На рис. 5 представлены осциллограммы парциального давления диоксида углерода (а), температуры (б) и насыщенности гидрата углекислого газа (в) в точке с координатой x = 5 м при коэффициенте диффузии $D = 5 \times {{10}^{{ - 15}}}\,$ м2/с. Кривые 1, 2 и 3 соответствуют значениям проницаемости $k = {{10}^{{ - 10}}},$ ${{10}^{{ - 11}}}\,$ и $5 \times {{10}^{{ - 13}}}\,$ м2 соответственно.
Рис. 5.
Расчетные осциллограммы парциального давления диоксида углерода ${{p}_{{gd}}}$ (а), температуры $T$ (б), гидратонасыщенности диоксида углерода ${{S}_{{hd}}}$ (в) в точке x = 5 м для различных значений проницаемости: 1 – $k = {{10}^{{ - 10}}}$ м2, 2 – $k = {{10}^{{ - 11}}}$ м2, 3 – $k = 5 \times {{10}^{{ - 13}}}$ м2.
Если для значения проницаемости принять $k = {{10}^{{ - 10}}}$ м2, то время полного вытеснения метана из состава гидрата будет значительно превышать время полного наполнения диоксида углерода в пласте. В этом случае, согласно рис. 5, процесс гидратообразования углекислого газа происходит по всей длине пласта, температура успевает понижаться за счет конвективного переноса тепла. При дальнейшем уменьшении значения проницаемости ($k$ = ${{10}^{{ - 11}}}$ м2) наблюдается примерно одинаковое значение характерных времен ${{t}^{{(D)}}} \approx {{t}^{{(p)}}}.$ При более малых значениях проницаемости (кривая 3) процесс полного вытеснения метана из состава гидрата в пористой среде будет происходить быстрее процесса наполнения пласта диоксидом углерода $\left( {{{t}^{{(p)}}} > {{t}^{{(D)}}}} \right).$ В этом случае, согласно рис. 5, процесс гидратообразования диоксида углерода происходит в фронтальном режиме.
На рис. 6 линиями 1 и 2 представлены зависимости времени полного замещения метана в гидрате на диоксид углерода во всем пласте от значений абсолютной проницаемости при значениях приведенного коэффициента диффузии $D = 5 \times {{10}^{{ - 15}}}$ и $5 \times {{10}^{{ - 14}}}$ м2/с соответственно.
Рис. 6.
Влияние значения проницаемости на время полного газозамещения в составе гидрата во всем пласте при различных приведенных коэффициентах диффузии: 1 – $D = 5 \times {{10}^{{ - 15}}}$ м2/с, 2 – $D = 5 \times {{10}^{{ - 14}}}$ м2/с.
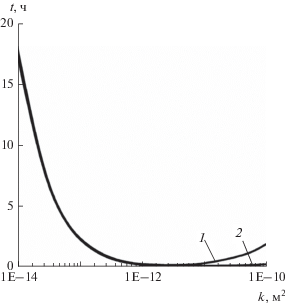
Видно, что при низких значениях проницаемости приведенный коэффициент диффузии слабо влияет на время замещения метана в гидрате на углекислый газ во всем пласте, так как в этом случае процесс лимитируется фильтрационным массопереносом. Отметим, что увеличение времени замещения в случае высокопроницаемых пористых сред обусловлено уменьшением удельной поверхности контакта между гидратами диоксида углерода и метана с ростом проницаемости.
На рис. 7 приведены зависимости времени полного замещения метана в гидрате на диоксид углерода во всем пласте от значений абсолютной проницаемости с учетом (кривая 1) и без учета (кривая 2) диффузионного перемешивания газовой смеси соответственно при коэффициенте диффузии $D = 5 \times {{10}^{{ - 14}}}\,$ м2/с.
Рис. 7.
Влияние коэффициента диффузионного перемешивания газовой смеси ${{D}_{g}}$ на время полного газозамещения в составе гидрата во всем пласте в зависимости от проницаемости: 1 – ${{D}_{g}} = {{10}^{{ - 5}}}$ м2/с, 2 – ${{D}_{g}} = 0$.

Видно, что диффузионное перемешивание влияет на полное время замещения во всем пласте только в случае низкопроницаемых пористых сред, т.е. при малых значениях интенсивности фильтрационного массопереноса.
ЗАКЛЮЧЕНИЕ
Проведено численное исследование процесса замещения метана диоксидом углерода в газогидрате при закачке углекислого газа в пористый пласт, насыщенный метаном и его гидратом, с учетом диффузионной кинетики. Показано, что при высоких значениях коэффициента диффузии углекислого газа в гидрате и низких значениях коэффициента проницаемости пласта процесс замещения будет проходить во фронтальном режиме и лимитироваться, прежде всего, фильтрационным массопереносом в пласте. В противном случае процесс газозамещения будет происходить в объемной области пласта и лимитироваться диффузией в гидрате. Также показано, что диффузионное перемешивание метана и углекислого газа оказывает влияние на время полного замещения во всем пласте только в случае низкопроницаемых сред.
ОБОЗНАЧЕНИЯ
| a | радиус, м |
| c | удельная теплоемкость, Дж/(кг К) |
| D | коэффициент диффузии, м2/с |
| G | массовая доля газа в составе гидрата |
| $J$ | интенсивность фазового перехода, отнесенная на единицу объема, кг/(м3 с) |
| $j$ | поток массы газа, отнесенный на единицу площади, кг/(м2 с) |
| k | проницаемость, м2 |
| l | удельная теплота фазового перехода, Дж/(кг К) |
| M | молекулярная масса, кг/моль |
| m | пористость |
| mg | масса газа, отнесенная на единицу площади поперечного сечения пласта, кг/м2 |
| n | число пористых каналов в единице площади пористой среды, м–2 |
| p | давление, Па |
| q | расход газа, отнесенный на единицу площади сечения пласта, кг/(м2 с) |
| R | приведенная газовая постоянная, Дж/(кг К) |
| r | радиальная координата, м |
| S | насыщенность пор |
| s | удельная площадь поверхности, м–1 |
| T | температура, К |
| t | время, с |
| $\upsilon $ | массовая скорость, м/с |
| $w$ | диффузионная скорость, м/с |
| x | координата пласта, м |
| x0 | протяженность пласта, м |
| $\Gamma $ | параметр Генри, кг/(Па м3) |
| $\lambda $ | удельная теплопроводность, В/(м К) |
| $\mu $ | динамическая вязкость, Па с |
| $\rho $ | плотность, кг/м3 |
ИНДЕКСЫ
Список литературы
Vasil'ev V.I., Popov V.V., Tsypkin G.G. Numerical investigation of the decomposition of gas hydrates coexisting with gas in natural reservoirs // Fluid Dynamics. 2006. V. 41. № 4. P. 599. [Васильев В.И., Попов В.В., Цыпкин Г.Г. Численное исследование разложения газовых гидратов, сосуществующих с газом в природных пластах // Изв. РАН. Механика жидкости и газа. 2006. № 4. С. 127.]
Цыпкин Г.Г. Течения с фазовыми переходами в пористых средах. М.: Физматлит, 2009.
Назмутдинов Ф.Ф., Хабибуллин И.Л. Математическое моделирование десорбции газа из газового гидрата // Изв. РАН. Механика жидкости и газа. 1996. № 5. С. 118.
Shagapov V.S., Khasanov M.K., Gimaltdinov I.K., Stolpovsky M.V. The features of gas hydrate dissociation in porous media at warm gas injection // Thermophysics and Aeromechanics. 2013. V. 20. № 3. P. 339. [Шагапов В.Ш., Хасанов М.К., Гималтдинов И.К., Столповский М.В. Особенности разложения газовых гидратов в пористых средах при нагнетании теплого газа // Теплофизика и аэромеханика. 2013. Т. 20. № 3. С. 347.]
Шагапов В.Ш., Мусакаев Н.Г. Динамика образования и разложения гидратов в системах добычи, транспортировки и хранения газа. М.: Наука, 2016.
Moridis G.J. Numerical studies of gas production from methane hydrates // SPE Gas Technology Symposium. SPE 75691. Calgary, 2002.
McGrail B.P., Zhu T., Hunter R.B., White M.D., Patil S.L., Kulkarni A.S. A new method for enhanced production of gas hydrates with CO2 // AAPG Hedberg Conference “Gas Hydrates: Energy Resource Potential and Associated Geologic Hazards”. Vancouver, Canada, 2004.
Espinoza N.D., Santamarina C.J. P-wave monitoring of hydrate-bearing sand during CH4–CO2 replacement // Int. J. Greenhouse Gas Control. 2011. V. 5. P. 1032.
Jung J.W., Espinoza D.N., Santamarina J.C. Properties and phenomena relevant to CH4–CO2 replacement in hydrate-bearing sediments // J. Geophysical Research: Solid Earth. 2010. V. 115. Article B10102. doi 10.1029/ 2009JB000812
Stevens J.C., Howard J.J., Baldwin B.A., Ersland G., Husebo J., Graue A. Experimental hydrate formation and gas production scenarios based on CO2 sequestration // Proc. 6th International Conference on Gas Hydrates. Vancouver, Canada, 2008.
Falenty A., Qin J., Salamatin A.N., Yang L., Kuhs W.F. Fluid composition and kinetics of the in situ replacement in CH4−CO2 hydrate system // Journal of Physical Chemistry C. 2016. V. 120. № 48. P. 27159. doi 10.1021/acs.jpcc.6b09460
Истомин В.А., Чувилин Е.М., Тохиди Б., Йанг Дж., Буханов Б.А., Маерли К.В. Кинетика разложения газогидратов метана в гидратонасыщенном пласте при закачке дымовых газов // Геомодель-2016. Геленджик, 2016.
Воронов В.П., Городецкий Е.Е. Экспериментальное исследование процесса замещения метана в газовом гидрате диоксидом углерода // Вести газовой науки. 2011. № 2 (7). С. 235.
Tsypkin G.G. Formation of carbon dioxide hydrate at the injection of carbon dioxide into a depleted hydrocarbon field // Fluid Dynamics. 2014. V. 49. № 6. P. 789. [Цыпкин Г.Г. Образование гидрата углекислого газа при его инжекции в истощенное месторождение углеводородов // Изв. РАН. Механика жидкости и газа. 2014. № 6. С. 101.]
Цыпкин Г.Г. Образование гидрата при инжекции жидкой двуокиси углерода в пласт, насыщенный метаном и водой // Изв. РАН. Механика жидкости и газа. 2016. № 5. С. 99.
Хасанов М.К. Инжекция вскипающей углекислоты в пласт, сопровождающаяся замещением метана в гидрате двуокисью углерода // Прикладная математика и механика. 2016. Т. 80. № 5. С. 553.
Хасанов М.К., Шагапов В.Ш. Разложение газогидрата метана в пористой среде при инжекции теплого углекислого газа // Инженерно-физический журнал. 2016. Т. 89. № 5. С. 1129.
Shagapov V.Sh., Musakaev N.G., Khasanov M.K. Formation of gas hydrates in a porous medium during an injection of cold gas // International Journal of Heat and Mass Transfer. 2015. V. 84. P. 1030.
Макогон Ю.Ф. Газогидраты. История изучения и перспективы освоения // Геология и полезные ископаемые Мирового океана. 2010. № 2. С. 5.
Макогон Ю.Ф. Гидраты природных газов. М.: Недра, 1974.
Шагапов В.Ш., Чиглинцева А.С., Русинов А.А., Тазетдинов Б.И. О миграции одиночного газового пузырька в воде при образовании на его поверхности стабильной газогидратной корки // Теорет. основы хим. технологии. 2017. Т. 51. № 2. С. 63.
Шагапов В.Ш., Рафикова Г.Р., Хасанов М.К. К теории образования газогидрата в частично водонасыщенной пористой среде при нагнетании метана // Теплофизика высоких температур. 2016. Т. 54. № 6. С. 911.
Rehder G., Brewer P.W., Peltzer E.T., Friederich G. Enhanced lifetime of methane bubble streams within the deep ocean // Geophysical Research Letters. 2002. V. 29. P. 21.
MgGinnis D.F., Greinert J., Artemov Y., Beaubien S. E., Wuest A. Fate of rising methane bubbles in stratified waters: How much methane reaches the atmosphere? // J. Geophysical Research. 2006. V. 111. P. 382.
Самарский А.А. Теория разностных схем. М.: Наука, 1977.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии