Теоретические основы химической технологии, 2019, T. 53, № 1, стр. 31-45
О структуре пространства состояний тепловой модели реакционно-регенерационных систем с кипящим слоем катализатора и принципах визуализации управления
А. Г. Нагиев 1, *, Г. А. Нагиев 2, Н. А. Гулиева 1
1 Сумгаитский государственный университет
Сумгаит, Азербайджан
2 Институт математики и механики Национальной академии наук Азербайджана
Баку, Азербайджан
* E-mail: alinagiev@gmail.com
Поступила в редакцию 11.10.2017
После доработки 01.10.2018
Принята к публикации 27.09.2018
Аннотация
Предложена система дифференциальных уравнений динамики тепловых состояний реакционно-регенерационных систем с мелкодисперсными катализаторами. Особое внимание обращено на существование положительных обратных связей между тепловыми и химическими процессами по двум взаимосвязанным каналам – по температуре и степени остаточной закоксованности катализатора после регенерации. Показано, что данная система модельных уравнений тепловой динамики реакционно-регенерационной системы обладает множественностью стационарных состояний в пространстве названных переменных. Проведен анализ трехмерных фазовых портретов системы, изучены бифуркации стационарных решений в области параметров. Рассмотрен вопрос оперативного контроля на основе алгоритмов визуализации структуры пространства состояний.
ВВЕДЕНИЕ
Процессы каталитического превращения углеводородов, осуществляемые в реакционно-регенерационных системах (РРС) с мелкодисперсными катализаторами, к настоящему времени характеризуются лучшими технологическими показателями и имеют большую перспективу дальнейшего развития. Крекинг остатков первичной переработки нефти, процессы дегидрирования различных углеводородов являются типичными представителями промышленных технологий, основанными на непрерывном выжиге кокса с поверхности катализатора и восстановлении активности катализаторов по целевым реакциям. Анализу специфики тепловых режимов этих систем посвящено немалое количество теоретических исследований [1–5]. Основную особенность составляет высокая скорость коксовых отложений на катализаторе, характерная для большинства химических процессов, осуществляемых в РРС. Теплота, выделяющаяся при окислительной регенерации катализатора, в ряде случаев может полностью сбалансировать энергетические затраты на осуществление целевых химических реакций. Энергетическую замкнутость этих систем и существование положительной обратной связи по тепловому каналу между реактором и регенератором принято считать основной причиной проявляющих себя разного рода критических эффектов в тепловой динамике этих систем [6]. Быстрые релаксации температуры и/или содержания кокса на катализаторе при малых изменениях внешних возмущений, внезапные потери термической устойчивости, автоколебания температуры и некоторые другие явления в тепловой динамике этих систем считаются следствиями положительных обратных связей между переменными состояния. Исследователи концентрируют внимание на разных физико-химических закономерностях, обусловливающих сложные взаимосвязи между аппаратами не только по тепловому каналу, но и по каналу баланса кокса в системе. Плохо регенерированный катализатор с большим остатком глубинного кокса в порах катализатора как следствие неполной регенерации катализатора инициирует процессы с большей интенсивностью коксообразования, замыкая цепь обратной связи также и по коксовому каналу. Образующиеся коксовые отложения на микропорах катализатора препятствуют диффузионной передаче веществ в активные центры [7–9]. Создав условия для некаталитического течения химических реакций, эти процессы усиливают тенденцию роста скоростей реакций, сопряженных с отложением кокса.
Процессы, осуществляющиеся в РРС, имеют много общих закономерностей, определяющих специфику управления технологическими режимами промышленных систем, хотя подавляющее большинство исследовательских работ из этой области посвящено каталитическому крекингу тяжелых остатков первичной переработки нефти [10, 11]. Каталитический крекинг в прямоточных реакторах трубчатого типа без использования кипящего слоя в исследованиях удобен тем, что изучение тепловой динамики этих систем можно осуществить на плоскости координат температура регенерации–остаточная закоксованность катализатора после регенерации. Процессы дегидрирования углеводородов в отличие от подавляющего большинства процессов крекинга осуществляются в псевдоожиженном слое катализатора, чем вызывается необходимость учета третьей фазовой координаты динамической системы реактор–регенератор. Этой координатой является содержание кокса на отработанном катализаторе. Большая масса катализатора, сосредоточенная в кипящем слое, превращает данный параметр в важнейшую фазовую координату динамических состояний РРС.
Целью настоящего исследования является теоретическое изучение основных закономерностей тепловой динамики промышленных процессов, осуществляющихся в РРС с псевдоожиженными слоями в обоих аппаратах. Процессы дегидрирования углеводородов, представляя названный класс, могут служить ярким примером, обладающим специфическими особенностями в управлении, связанными как с необходимостью рассмотрения трех фазовых координат, так и со спецификой кинетических зависимостей между переменными состояния.
СТРУКТУРА ДИНАМИЧЕСКИХ СВЯЗЕЙ МЕЖДУ РЕЖИМНЫМИ И КИНЕТИЧЕСКИМИ ПАРАМЕТРАМИ В ТЕПЛОВОЙ МОДЕЛИ РРС
Дифференциальные уравнения, связывающие переменные состояния с режимными и кинетическими параметрами РРС, выпишем в следующем виде:
(1)
$\begin{gathered} {{G}_{1}}\frac{{d{{C}_{1}}}}{{dt}} = {{F}_{{\text{k}}}}({{C}_{2}} - {{C}_{1}}) - {{\varphi }_{1}}({{T}_{1}},{{C}_{1}}){{G}_{1}}; \\ {{G}_{2}}\frac{{d{{C}_{2}}}}{{dt}} = {{F}_{{\text{k}}}}({{C}_{1}} - {{C}_{2}}) + {{\varphi }_{2}}({{T}_{2}},{{C}_{2}},w){{G}_{2}}; \\ {{G}_{1}}{{c}_{{\text{k}}}}\frac{{d{{T}_{1}}}}{{dt}} = {{F}_{{\text{k}}}}{{c}_{{\text{k}}}}({{T}_{2}} - {{T}_{1}}) + \\ + \,\,{{\varphi }_{1}}({{T}_{1}},{{C}_{1}}){{q}_{1}}{{G}_{1}} + {{q}_{3}}{{F}_{{{\text{fu}}}}} + {{q}_{4}}\delta {{F}_{{\text{k}}}} + \\ + \,\,{{F}_{{{\text{air}}}}}{{c}_{{{\text{air}}}}}({{T}_{{{\text{air}}}}} - {{T}_{1}}) + {{k}_{{{\text{en}}}}}{{S}_{1}}({{T}_{{{\text{en}}}}} - {{T}_{1}}); \\ {{G}_{2}}{{c}_{{\text{k}}}}\frac{{d{{T}_{2}}}}{{dt}} = {{F}_{{\text{k}}}}{{c}_{{\text{k}}}}({{T}_{1}} - {{T}_{2}}) - \\ - \,\,{{\varphi }_{2}}({{T}_{2}},{{C}_{2}},w){{q}_{2}}{{G}_{2}} + {{c}_{{{\text{raw}}}}}{{F}_{{{\text{raw}}}}}({{T}_{{{\text{raw}}}}} - {{T}_{2}}) + \\ + \,\,{{k}_{{{\text{en}}}}}{{S}_{2}}({{T}_{{{\text{en}}}}} - {{T}_{2}}), \\ \end{gathered} $в которых переменные подчинены нижеследующей классификации:
переменные состояния: ${{C}_{1}},{{C}_{2}},{{T}_{1}},{{T}_{2}}$ – весовые концентрации кокса на катализаторах в регенераторе и реакторе и соответствующие им температуры;
параметры режима: ${{F}_{k}},{{F}_{{air}}},{{F}_{{raw}}}$ – массовые скорости соответственно циркулирующего катализатора в системе, ввода воздуха в регенератор и ввода сырья; $w = {{{{F}_{{raw}}}} \mathord{\left/ {\vphantom {{{{F}_{{raw}}}} {{{G}_{2}}}}} \right. \kern-0em} {{{G}_{2}}}}$ – весовая скорость ввода сырья;
конструкционные параметры: ${{k}_{{en}}},{{S}_{1}},{{S}_{2}},{{G}_{1}},{{G}_{2}}$ – коэффициент теплопередачи в окружающую среду, площадь наружной поверхности регенератора и реактора, массы кипящих слоев в аппаратах по катализатору (предусмотренные по технологическому регламенту);
физические константы и параметры: ${{c}_{k}},{{c}_{{raw}}},{{c}_{{air}}}$ – теплоемкости катализатора, сырья и воздуха; ${{q}_{1}},{{q}_{2}},{{q}_{3}}$ – тепловые эффекты реакций горения кокса, конверсии сырья, теплотворности топливного газа и адсорбированных углеводородов;
кинетические факторы: ${{\varphi }_{1}}({{T}_{1}},{{C}_{1}}),$ ${{\varphi }_{2}}({{T}_{2}},{{C}_{2}},w)$ – функции кинетических зависимостей скорости реакции горения кокса и скорости коксотворных реакций.
Приведенная структура математической модели динамики теплового режима РРС основана на квазигомогенном представлении реакционной среды кипящего слоя катализатора без раздельного рассмотрения реакций окисления кокса, отложенного на поверхности и в порах внутри катализатора. Кроме того, для простоты кинетического описания процесса регенерации, основываясь на высокой скорости ввода воздуха – агента псевдоожижения катализатора – не учтено изменение концентрации кислорода записью соответствующих уравнений. Избыточность воздуха в отношении анализа материального баланса реакций окисления коксовых отложений принята за основу моделирования также при топливном подогреве регенератора. Обычно на этих упрощающих предположениях строят кинетическое уравнение горения коксовых отложений в процессе регенерации катализатора в виде [1–4, 12]
(2)
${{\varphi }_{1}}({{T}_{1}},{{C}_{1}}) = {{k}_{{01}}}\exp ({{ - {{E}_{1}}} \mathord{\left/ {\vphantom {{ - {{E}_{1}}} {R{{T}_{1}}}}} \right. \kern-0em} {R{{T}_{1}}}})C_{1}^{{\eta }};\,\,\eta = 1.0 - 1.4.$Однако в контексте моделирования эффекта положительной обратной связи по каналу кокса важен учет различия в кинетических закономерностях глубинных и поверхностных процессов образования и окисления кокса. Это в большей степени относится к моделированию кинетики реакций отложения кокса. Введение соответствующих фазовых координат ${{\tilde {C}}_{i}};\,\,i = 1.2$ в отдельности по каждому из названных механизмов образования кокса, как решение имеющейся проблемы, сопряжено с неоправданным увеличением размерности фазового пространства.
Другим направлением может быть стратегия, взявшая в свою основу моделирование с позиций автокатализа. Сильное влияние степени остаточной закоксованности после регенерации катализатора, а также эволюция концентрации кокса в реакционной зоне реактора в течение химического процесса создают эффект автокатализа – проявление положительной обратной связи по рассматриваемому каналу [13]. Однако существенные осложнения, связанные с учетом различий во влияниях глубинного и поверхностного кокса, и в данном случае оказываются основными препятствиями в решении задачи моделирования с приемлемой степенью сложности. Моделирование глубинного коксообразования осложнено кинетикой диффузионного торможения внутри зерна катализатора.
Надежным источником необходимой информации, касающейся проблемы обратной связи по “каналу кокса”, являются данные опытно-лабораторных исследований. В научной литературе имеется достаточное количество сведений о результатах экспериментальных исследований влияния степени закоксованности катализатора на ход химических реакций, сопряженных с реакциями отложения кокса [14–16]. Нет принципиальных препятствий и на пути использования данных функционирования промышленных установок для изучения этого влияния. Обращает на себя внимание S-образный характер кривых, выражающих эти влияния [1, 2]. При этом аппроксимацию экспериментальных характеристик оказывается удобным выразить разными видами сигмоидальных функций, такими как $y = \frac{\alpha }{{1 + {{e}^{{ - {\beta }({{C}_{2}} - C_{2}^{{{\text{nom}}}})}}}}}$ и $y = \alpha th[\beta ({{C}_{2}} - C_{2}^{{{\text{nom}}}})]$ (логистическая функция и гиперболический тангенс), в которых $C_{2}^{{{\text{nom}}}}$ – номинальное значение концентрации кокса в реакционной зоне, $\alpha ,\beta $ являются параметрами аппроксимации результатов экспериментов. Заметим, если структура формулы (2) инвариантна в отношении целевого химического процесса, осуществляемого в РРС, то модель скорости коксовых отложений определена условиями конкретного химического процесса, структурой и механизмом каталитического действия использующегося комплекса. Параметры идентификации $\alpha ,\beta ,C_{2}^{{{\text{nom}}}},$ сохраняя важные качественные свойства сигмоидальной функции в довольно широкой области, способны осуществить подстройку модели к экспериментальным данным, т.е. могут обеспечить свое применение для широкого набора процессов дегидрирования.
Выпишем обобщенную функцию скорости образования кокса с использованием сигмоидальной аппроксимации в виде
(3)
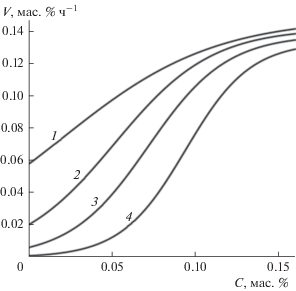
$\begin{gathered} {{\varphi }_{2}}({{T}_{2}},{{C}_{1}},w) = {{k}_{{02}}}\exp ({{ - {{E}_{2}}} \mathord{\left/ {\vphantom {{ - {{E}_{2}}} {R{{T}_{2}}}}} \right. \kern-0em} {R{{T}_{2}}}}) \times \\ \times \,\,\frac{{\alpha w}}{{1 + \exp [ - \beta \left( {{{C}_{2}} - C_{2}^{{{\text{nom}}}}} \right)}}. \\ \end{gathered} $На рис. 1 показано семейство кривых (3) при разных параметрах $\alpha ,\beta ,C_{2}^{{{\text{nom}}}},$ которые ответственны за определение скорости коксоотложения в связи с закоксованностью катализатора при произвольной температуре, учитываемой аррениусовой зависимостью.
Рис. 1.
Кривые скоростей реакций отложения кокса при разных значениях аппроксимирующих параметров $\alpha ,\;\beta ,\;C_{2}^{{{\text{nom}}}}.$ Кривые 1–4: ${{\alpha }_{i}},(i = \overline {1,4} ):$ $0.148;\,0.141;\,0.137;\,0.133;$ ${{\beta }_{i}}\;:\;22;\;34.5;\;42;\;51;$ $C_{2}^{{{\text{nom}}}}:$ $0.02;\;0.05;\;0.07;\;0.09.$
Известно, что подобный характер статической связи между переменными состояния в ряде случаев оказывается основной причиной проявления множественности стационарных состояний динамической системы и особенностей в поведении. Однако проведенный численный анализ при разных параметрах $\alpha ,\beta ,C_{2}^{{{\text{nom}}}}$ не подтверждает достаточность S-образности кривых, представленных на рис. 1, в проявлении названных особенностей в системе (1). Структура взаимосвязей в (1) характерна наличием двух перекрестных каналов, по которым устанавливаются положительные обратные связи, и, естественно, в данном случае каналу температура реактора–скорость реакций отведена завершающая роль в формировании всех особенностей структуры фазового пространства данной системы.
Число и координаты режимов равновесия несложно определить путем численного решения в некоторой ограниченной области, не выходящей за пределы адекватности моделей (1)–(3), т.е. области ${{C}_{{i\min }}} \leqslant {{C}_{i}} \leqslant {{C}_{{i\max }}};$ ${{T}_{{i\min }}} \leqslant {{T}_{i}} \leqslant {{T}_{{i\max }}};\,\,i = 1.2$ при условии $\frac{{d{{C}_{i}}}}{{dt}} = 0;\quad \frac{{d{{T}_{i}}}}{{dt}} = 0.$
Наряду с применением стандартных алгоритмов численного определения координат стационарных режимов полезен алгоритм, основанный на сравнении величин тепловыделения и теплоотвода из системы. Этот алгоритм особенно эффективен в тепловых расчетах экзотермических реакторов.
На основе первых двух уравнений системы (1) составим следующее равенство:
(4)
$\begin{gathered} C_{1}^{{\eta }}\{ 1 + \exp [ - \beta ({{C}_{2}} - {{{\bar {C}}}_{2}})\} = \\ = \frac{{{{k}_{{02}}}{{G}_{2}}}}{{{{k}_{{01}}}{{G}_{1}}}}w\exp ({{{{E}_{1}}} \mathord{\left/ {\vphantom {{{{E}_{1}}} {R{{T}_{1}}}}} \right. \kern-0em} {R{{T}_{1}}}} - {{{{E}_{2}}} \mathord{\left/ {\vphantom {{{{E}_{2}}} {R{{T}_{2}}}}} \right. \kern-0em} {R{{T}_{2}}}}). \\ \end{gathered} $Из третьего и четвертого уравнений системы при учете пренебрежительной малости отношения ${{{{q}_{2}}} \mathord{\left/ {\vphantom {{{{q}_{2}}} {{{q}_{1}}}}} \right. \kern-0em} {{{q}_{1}}}}$ выпишем соотношения
гдеНа основании (4) введем функцию невязки по координатам ${{C}_{1}},{{T}_{1}}{\text{:}}$
(6)
$\begin{gathered} P({{C}_{1}},{{T}_{1}}) = \left\{ {C_{1}^{{\eta }}[1 + \exp [ - \beta ({{C}_{2}} - {{{\bar {C}}}_{2}})] - } \right. \\ {{\left. { - \,\,\frac{{{{k}_{{02}}}{{G}_{2}}}}{{{{k}_{{01}}}{{G}_{1}}}}w\exp ({{{{E}_{1}}} \mathord{\left/ {\vphantom {{{{E}_{1}}} {R{{T}_{1}}}}} \right. \kern-0em} {R{{T}_{1}}}} - {{{{E}_{2}}} \mathord{\left/ {\vphantom {{{{E}_{2}}} {R(A{{T}_{1}} + B)}}} \right. \kern-0em} {R(A{{T}_{1}} + B)}}} \right\}}^{2}}. \\ \end{gathered} $Выпишем условие термического равновесия в форме диаграммы Ван-Хердена [17], пользуясь третьим уравнением системы (1):
(8)
${{Q}_{{rem}}} = {{q}_{1}}{{G}_{1}}{{\varphi }_{1}}({{T}_{1}},{{C}_{1}}) + {{q}_{3}}{{F}_{{fu}}} + {{q}_{4}}\delta {{F}_{k}};$(9)
$\begin{gathered} {{Q}_{{dis}}} = ({{F}_{k}}{{c}_{k}} + {{F}_{{air}}}{{c}_{{air}}} + {{k}_{{en}}}{{S}_{1}}){{T}_{1}} + {{F}_{k}}{{c}_{k}}{{T}_{2}} + \\ + \,\,{{F}_{{air}}}{{c}_{{air}}}{{T}_{{air}}} + {{k}_{{en}}}{{S}_{1}}{{T}_{{en}}}, \\ \end{gathered} $в которых ${{Q}_{{rem}}},{{Q}_{{dis}}}$ – функции теплообразования и теплоотвода.
Функция теплоотвода представляет линейную функцию температуры регенерации. Построение функции (8) упрощается при использовании итерационного алгоритма минимизации (6) по аргументу ${{C}_{1}}$:
где $(0,M]$ – некоторый достаточно широкий интервал поиска минимума (6) при произвольном ${{T}_{1}};$ $\xi $ – переменная задачи минимизации в соответствие параметру ${{C}_{1}}$ в функции невязки (6).Число и координаты стационарных состояний системы (1) можно определить, минимизируя функцию
(11)
$\Delta P({{T}_{1}}) = {{[{{Q}_{{rem}}}({{C}_{1}},{{T}_{1}}) - {{Q}_{{dis}}}({{T}_{1}})]}^{2}} \to \min $по аргументу ${{T}_{1}}$ с учетом выражения (10). При этом минимумы (11) могут достигаться в нескольких точках ${{T}_{i}};i = 1,2,..,$ соответствуя числу стационарных состояний. Очевидно, что последние являются функциями параметров системы, в том числе режимных параметров, среди которых отметим $w$ как фактор возмущения и Fk как управляющее воздействие.
ИССЛЕДОВАНИЕ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ СОСТОЯНИЙ ДИНАМИЧЕСКИХ СВОЙСТВ РРС, ОСУЩЕСТВЛЯЮЩИХ ДЕГИДРИРОВАНИЕ ПАРАФИНОВ
В технологии органического синтеза накоплен богатый производственный опыт осуществления процессов дегидрирования высших и средних парафинов в замкнутой реакционно-регенерационной системе. Механизмы образования коксовых отложений в этих процессах весьма сложны. Средние времена пребывания катализаторной массы в реакторах могут составлять несколько десятков минут. При каталитической конверсии высшие парафины больше подвержены коксообразованию, чем средние и низшие. В тепловом балансе таких систем значительную часть составляют теплота горения топочного газа и горение недесорбированной из пор катализатора массы контактного газа. Типичными представителями являются алюмохромовые катализаторы. Достаточно широкое промышленное применение находят комплексы ИМ2201 и КМД.
Модели коксообразования успешно могут быть представлены в виде формулы (4) с соответствующими параметрами $\alpha ,\beta ,{{\bar {C}}_{1}},$ первый из которых отвечает за масштаб скорости реакций, сопровождаемых отложениями кокса.
В табл. 1 приведены значения параметров тепловой модели РРС, которая ориентирована на дегидрирование изобутана в изобутилен.
Таблица 1.
Номинальные и экспериментально найденные значения параметров модели (12)
| Параметр | Единицы измерения | Номинальные значения | Значения параметра (согласно рисункам) |
Номер рисунка |
|---|---|---|---|---|
| k01 | ч–1 | 5083 | 5083 | |
| E1 | кДж/моль | 167 | 167 | |
| E2 | кДж/моль | 102 | 102 | |
| η | – | 1.2 | 1.2 | |
| k02 | ч–1 | 170 | 170 | |
| α | – | 0.137 | 0.137 | |
| β | – | 42 | 42 | |
| ${{\bar {C}}_{1}}$ | мас. % | 0.07 | 0.07 | |
| w | ч–1 | 1.6 | 1.5 | Рис. 3а, 3в |
| 1.7 | Рис. 3б, 3г | |||
| ck | кДж/(кг К) | 1.68 | 1.68 | |
| craw | кДж/(кг К) | 2.22 | 2.22 | |
| cair | кДж/(кг К) | 1.005 | 1.005 | |
| q1 | кДж/кг | 29400 | 29400 | |
| q2 | кДж/кг | 2400 | 2400 | |
| q3 | кДж/кг | 32000 | 32000 | |
| ken | Вт/(м2 К) | 5.87 | 5.87 | |
| S1 | м2 | 1080 | 1120 | |
| S2 | м2 | 941 | 941 | |
| Fk | кг/ч | 6 × 105 | 6 × 105 | Рис. 3а, |
| 7.4 × 105 | Рис. 3б | |||
| 5.9 × 105 | Рис. 3в | |||
| 9 × 105 | Рис. 3г | |||
| Fair | кг/ч | 1.6 × 105 | 1.42 × 105 | Все варианты рис. 3 |
| Fraw | кг/ч | 8000 | 8000 | |
| G1 | кг | 4 × 105 | 4 × 105 | |
| G1 | кг | 5 × 104 | 5 × 104 | |
| Traw | K | 300 | 300 | |
| Ten | K | 293 | 293 |
Использование пространства состояний для анализа поведения динамических систем, а также применение методов качественной теории дифференциальных уравнений к задачам визуализации управления предполагают в основном анализ двумерных систем. При этом естественны стремления перенесения математических приемов этого анализа в трехмерную систему координат и рассмотрение траекторий в этом пространстве. С этой точки зрения система (1) в качестве тепловой модели, очевидно, нуждается в сокращении размерности пространства до визуально представимого третьего порядка и в данном вопросе целесообразно исходить из соображений приемлемой точности такой замены. Согласно практики управления прямым путем в этой ситуации является исключение одной координаты за счет применения системы локальной стабилизации. Такой координатой может быть принята температура реакции, поскольку она, как правило, охвачена контуром локальной стабилизации с подачей азота – с одной стороны, для аэрации в целях транспортировки катализатора, а с другой стороны, для поддержания заданной температуры реакционной зоны. Возможны и другие каналы воздействия для стабилизации температуры реактора.
Приняв во внимание эту технологическую деталь, выпишем систему (1) в следующем виде:
(12)
$\begin{gathered} {{G}_{1}}\frac{{d{{C}_{1}}}}{{dt}} = {{F}_{{\text{k}}}}({{C}_{2}} - {{C}_{1}}) - {{\varphi }_{1}}({{T}_{1}},{{C}_{1}}){{G}_{1}}; \\ {{G}_{2}}\frac{{d{{C}_{2}}}}{{dt}} = {{F}_{{\text{k}}}}({{C}_{1}} - {{C}_{2}}) + {{\varphi }_{2}}({{T}_{z}},{{C}_{2}},w){{G}_{2}}; \\ {{G}_{1}}{{c}_{{\text{k}}}}\frac{{d{{T}_{1}}}}{{dt}} = {{F}_{{\text{k}}}}{{c}_{{\text{k}}}}({{T}_{z}} - {{T}_{1}}) + {{\varphi }_{1}}({{T}_{1}},{{C}_{1}}){{q}_{1}}{{G}_{1}} + \\ + \,\,{{q}_{3}}{{F}_{{{\text{fu}}}}} + {{q}_{4}}\delta {{F}_{{\text{k}}}} + {{F}_{{{\text{air}}}}}{{c}_{{{\text{air}}}}}({{T}_{{{\text{air}}}}} - {{T}_{1}}) + \\ + \,\,{{k}_{{{\text{en}}}}}{{S}_{1}}({{T}_{{{\text{en}}}}} - {{T}_{1}});\,\,\,\,{{T}_{2}} = {{T}_{z}}, \\ \end{gathered} $Метод фазовых траекторий (портретов) [18], обладая большими преимуществами в задачах принятия управленческих решений в реальном времени, во многом основывается на визуальном анализе ситуаций. В этой связи проблема размерности проявляет себя как в алгоритмизации построения фазовых портретов, так и в разработке методов управления в среде человеко-машинных систем. Прежде всего, плоскоэкранное представление трехмерных траекторий в целях оперативного контроля режимом оказывается перед бурно развивающейся технологией трехмерных компьютерных анимаций. К настоящему времени имеются заметные продвижения в решении трехмерных задач управления [18, 19], основанных на качественном анализе динамических систем [20, 21].
С другой стороны, дефект в отображении траекторий динамической системы в пространство состояний меньшей размерности, чем число контролируемых ее координат, проявляет себя в пересечениях фазовых траекторий, нарушив однозначность этого отображения. Пересекающиеся траектории – не приемлемые для проведения анализа – противоречат утверждению теоремы о единственности решений дифференциальных уравнений [20]. В то же время анализ переходных режимов системы (12) в трехмерном пространстве фазовых координат ${{C}_{1}}{\text{,}}\,\,{{C}_{2}}{\text{,}}\,\,{{T}_{1}}$ показывает приемлемость данного пространства для полного исследования топологии ее решений без учета координаты ${{T}_{2}}$. Очевидно, что в этом случае построение фазовых портретов динамической системы (12) следует выполнять при условии ${{T}_{2}} = {{T}_{z}} = {\text{const}}{\text{.}}$
В пространстве $(\theta ,{{\varepsilon }_{1}},{{\varepsilon }_{2}})$ выделим некоторый параллелепипед $D$ технологически допустимых состояний:
(13)
$\begin{gathered} [(1 - {{\chi }_{1}}) < \theta < 1 + {{\chi }_{1}}]\,\, \times \,\,[(1 - {{\chi }_{2}}) < {{\varepsilon }_{1}} < 1 + {{\chi }_{2}}] \times \\ \times \,\,[(1 - {{\chi }_{3}}) < {{\varepsilon }_{2}} < 1 + {{\chi }_{3}}], \\ \end{gathered} $В табл. 1 приведены значения параметров сокращенной модели (12), на основе которых изучен ряд статических и динамических свойств тепловой модели РРС. Найден вариант, когда в области параметров, определяемой множеством (13), может существовать от одного до трех стационарных состояний системы:
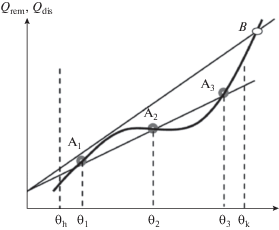
На рис. 2 приведено схематическое представление термического равновесия, наступающего при равенстве ${{Q}_{{rem}}} = {{Q}_{{dis}}}.$ Величина ${{Q}_{{dis}}}$ зависит от ряда режимных параметров, в том числе от возмущающего параметра $w$ и управляющих параметров ${{F}_{k}},{{F}_{{fu}}}.$ С точки зрения практики управления больший интерес представляют бифуркации положений равновесия. В зависимости от параметров $w,$ Fk наблюдалась бифуркация стационарных решений. С увеличением параметра ${{f}_{k}} = {{{{F}_{k}}} \mathord{\left/ {\vphantom {{{{F}_{k}}} {F_{k}^{{nom}}}}} \right. \kern-0em} {F_{k}^{{nom}}}}$ растет крутизна линии теплоотвода ${{Q}_{{dis}}}(\theta ).$
Рис. 2.
Диаграмма Ван-Хердена для графического определения положений равновесия в тепловой модели РРС.
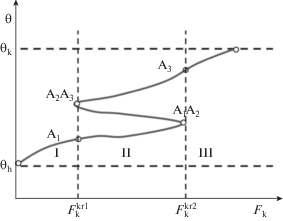
На рис. 3 показано перемещение стационарных точек ${{A}_{1}},$ ${{A}_{2}},$ ${{A}_{3}}$ относительно друг друга, с выделением трех участков, отличающихся наличием всех трех точек или исчезновением то точки ${{A}_{1}},$ то ${{A}_{2}}.$ Топологический тип каждой из стационарных точек может быть установлен путем исследования линеаризованных в их окрестности решений [22]. Полная картина структуры потоков траекторий может быть получена с использованием трехмерной компьютерной графики, основанной на данных вычислительного эксперимента на модели (12).
Рис. 3.
Бифуркация стационарных решений системы (12) в зависимости от изменения скорости циркуляции катализатора.
На рис. 4 приведены фазовые портреты системы (12) при разных параметрах режима.
Рис. 4.
Фазовые портреты РРС при разных значениях скорости циркуляции катализатора fk и весовой скорости ввода сырья $w{\kern 1pt} {\kern 1pt} :$ (а) – $w = 1.84,$ fk = 1.24; (б) – $w = 0.92,$ fk = 1.05; (в) – $w = 0.087,$ fk = 1.48; (г) – $w = 1.14,$ fk = 1.23.
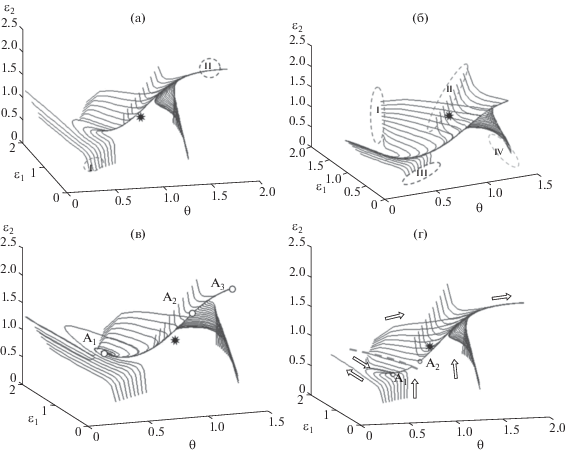
Рис. 4а соответствует режиму с высоким выходом кокса за счет большей, чем среднее значение весовой скорости ввода сырья. Увеличенная скорость циркуляции в свою очередь усиливает процессы выделения тепла. За исключением траекторий с началом из области I, все траектории из разных участков пространства состояний устремлены в некоторую “магистраль”, ведущую в высокотемпературную стационарную точку A3, которая расположена за пределами области допустимых режимов. Такой режим оказался бы аварийным.
Фазовый портрет, представленный на рис. 4б, напротив, характеризует последствия дефицита в коксовом балансе системы. Область допустимых режимов не содержит точек равновесия. Все траектории устремлены в низкотемпературную область с низким выходом кокса. В области I система в некоторое время, обладая запасом коска на катализаторе, входит в область высоких температур, затем, по мере расходования кокса, стремится в магистраль, ведущую в область меньших температур. Некоторое время высокотемпературное состояние системы поддерживается за счет высокой начальной температуры регенерации, что характерно для семейства траекторий, начавшихся из области IV. В этой области заметны малые значения остаточной закоксованности катализатора.
На рис. 4в представлен фазовый портрет с тремя состояниями равновесия, устойчивый фокус A1, седло A2 и устойчивый узел A3. Все точки равновесия расположены в области рабочих температур. Точка равновесия A1 имеет довольно обширную область притяжения. Приближаясь к ее окрестности, траектории, скручиваясь, создают колебательные изменения переменных состояния. Значительные амплитуды колебаний характеризуют эту область нестабильностью тепловых состояний системы. Варьируя параметрами $w,{{f}_{k}}$ в их малой окрестности, найден предельный цикл – режим автоколебаний.
На указанном фазовом портрете отчетливо видны также траектории, разделенные некоторой сепаратрисой, которая содержит точку равновесия A2, относящуюся к типу “седло”. Устойчивый узел A3 может считаться предпочтительным, однако в данном случае ее близость к границе недопустимых температур может создать сложности в управлении. В целом тепловой режим, характеризующийся этим фазовым портретом системы, нельзя считать эффективным как из-за колебательных переходных состояний, так и из-за множественности состояний равновесия в рабочей области.
Отличие фазового портрета, представленного на рис. 4г, в основном в преображении устойчивого аттрактора A1 из типа “фокус” в топологический тип “узел”. Предпочтительность этого отличительного признака очевидна, однако, все другие недостатки предыдущего варианта фазового портрета, связанного с плотным расположением аттракторов A1, A3 и в данном варианте сохраняются.
РАЗБИЕНИЕ ПРОСТРАНСТВА РЕЖИМНЫХ ПАРАМЕТРОВ ПО ТОПОЛОГИЧЕСКИМ ПРИЗНАКАМ ФАЗОВЫХ ПОРТРЕТОВ. ФАЗОВЫЙ ПОРТРЕТ С КОНЕЧНЫМ ЧИСЛОМ СТРАНИЦ
Проведем дискретизацию пространства параметров ($w,{{f}_{k}}$), наделяя его клеточным разбиением:
(14)
$\begin{gathered} {{w}^{{(n)}}} = {{h}_{w}}n;\,\,i = \overline {1,N;} \,\,{{h}_{w}} = {{\left( {{{w}^{{\max }}} - {{w}^{{\min }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{w}^{{\max }}} - {{w}^{{\min }}}} \right)} N}} \right. \kern-0em} N}; \hfill \\ f_{k}^{{(m)}} = {{h}_{{\text{f}}}}m;\,\,j = \overline {1,M;} \,\,{{h}_{{\text{f}}}} = {{\left( {f_{k}^{{\max }} - f_{k}^{{\min }}} \right)} \mathord{\left/ {\vphantom {{\left( {f_{k}^{{\max }} - f_{k}^{{\min }}} \right)} M}} \right. \kern-0em} M}, \hfill \\ \end{gathered} $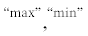 указывают на максимум и минимум названных режимных параметров. Во множестве $\Omega ,$ включающем $N \times M$ – числа результатов вычислительных экспериментов, выделим $\Lambda $ – число подмножеств однотипных фазовых портретов ${{\Omega }_{\lambda }} \subset \Omega ;\,\,\lambda = \overline {1,\Lambda } .$ Тип фазового портрета определим по признаку вхождения в $D$ точек равновесия определенных типов. Введем следующие обозначения топологических
типов:
указывают на максимум и минимум названных режимных параметров. Во множестве $\Omega ,$ включающем $N \times M$ – числа результатов вычислительных экспериментов, выделим $\Lambda $ – число подмножеств однотипных фазовых портретов ${{\Omega }_{\lambda }} \subset \Omega ;\,\,\lambda = \overline {1,\Lambda } .$ Тип фазового портрета определим по признаку вхождения в $D$ точек равновесия определенных типов. Введем следующие обозначения топологических
типов:
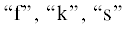 выражают соответственно фокус, узел и седло; приставки
выражают соответственно фокус, узел и седло; приставки 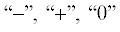 обозначают соответственно устойчивость, неустойчивость и предельный цикл. Количество
типов фазовых портретов может быть несколько большим, приведем наиболее основные типы:
обозначают соответственно устойчивость, неустойчивость и предельный цикл. Количество
типов фазовых портретов может быть несколько большим, приведем наиболее основные типы:
Отмеченные выше обозначения фазовых портретов в своем большинстве представлены на
рис. 4. Фазовые портреты, не содержащие точек равновесия, отмечены двумя разными обозначениями:
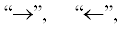 которые соответствуют направлениям проекций скорости движения на температурную ось.
Приведенное выше кодирование классификационных признаков фазовых портретов составляет
алгоритмическую основу создания глобального их хранилища, охватывающего всевозможные
их топологические типы.
которые соответствуют направлениям проекций скорости движения на температурную ось.
Приведенное выше кодирование классификационных признаков фазовых портретов составляет
алгоритмическую основу создания глобального их хранилища, охватывающего всевозможные
их топологические типы.
Число входящих в произвольную группу фазовых портретов (топологических типов) различно и отмечено через ${{z}_{\lambda }}.$ Структуры множеств, создаваемых при такой группировке, имеют особое значение с точки зрения алгоритмизации управления. Исследование этого вопроса показало, что группы ${{\Omega }_{\lambda }}$ чаще представляют собой невыпуклые множества. На рис. 5 представлено разбиение пространства параметров на области с однотипными фазовыми портретами с показом их возможной несепарабельности.
Рис. 5.
Разбиение пространства режимных параметров по топологическим типам фазовых портретов систем в РРС.
Подразумевается, что каждое подмножество ${{\Omega }_{\lambda }}$ представляет собой один фазовый портрет с количеством страниц, равным ${{z}_{\lambda }}.$ Ранжируя фазовые портреты по дискретному множеству ${{w}^{i}},\,\,f_{k}^{j};\,\,i = \overline {1,N} ,\,\,j = \overline {1,M} ,$ нумеруются страницы, соответствующие фазовым портретам при указанных параметрах.
Визуализация процесса управления согласно данному подходу сводится к действиям на двух этапах. На первом этапе, осуществляя измерение возмущающих факторов ${{w}^{i}},f_{k}^{j},$ определяется наиболее подходящее подмножество фазовых портретов ${{\Omega }_{\lambda }}$ с точки зрения их топологического типа. Поиск осуществляется по перебору реквизитных карт. Реквизиты представляют собой закодированные по вышеприведенным обозначениям сведения о качественных особенностях фазовых портретов системы. Находя то или иное подмножество, следует приступать к определению нужной страницы соответствия ${{w}^{i}},f_{k}^{j}.$ Далее на этом конкретном фазовом портрете осуществляется визуальный контроль над тепловым движением системы.
ВИЗУАЛИЗАЦИЯ КОНТРОЛЯ В СЛУЧАЕ НАЛИЧИЯ В $D$ ДВУХ АТТРАКТОРОВ. ТОМОГРАФИЧЕСКИЙ АНАЛИЗ СТРУКТУРЫ ПРОСТРАНСТВА СОСТОЯНИЙ
Рассмотрим вариант фазового портрета с наличием в $D$ двух аттракторов A1, A3, с седловой точкой A2, лежащей на сепаратрисной поверхности. Описание координат положений равновесия в зависимости от параметров режима сформулировано в виде (8)–(11). Для описания конфигурации разделяющих поверхностей в пространстве названных параметров переместим начало координат в центр притяжения одного из положений равновесия. Введем полярную систему координат:
(15)
$\begin{gathered} {{\varepsilon }_{1}} = {{\varepsilon }_{{10}}} + \rho \sin (\psi )\cos (\varphi ); \\ \theta = {{\theta }_{0}} + \rho \sin (\psi )\sin (\varphi ); \\ {{\varepsilon }_{2}} = {{\varepsilon }_{{20}}} + \rho \cos (\psi ), \\ \end{gathered} $(16)
$\begin{gathered} {{\psi }^{{(k)}}} = {{h}_{{\psi }}}k;\,\,\,k = \overline {1,K;} \,\,\,{{h}_{{\psi }}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } K}} \right. \kern-0em} K}; \\ {{\varphi }^{{(l)}}} = {{h}_{{\varphi }}}\ell ;\,\,\,\ell = \overline {1,L;} \,\,\,{{h}_{{\varphi }}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } L}} \right. \kern-0em} L}; \\ \end{gathered} $и полярного радиуса $\rho {\kern 1pt} {\kern 1pt} :$
(17)
${{\rho }^{{\left( v \right)}}} = {{h}_{{\rho }}}v;\,\,\,v = \overline {1,V;} \,\,\,{{h}_{{\rho }}} = {{\hat {\rho }} \mathord{\left/ {\vphantom {{\hat {\rho }} V}} \right. \kern-0em} V};$Две последовательности (16) при некотором радиусе $\rho $ задают сферу такого же радиуса. Исследуем решения системы (12), взявшие начала с точек, расположенных на поверхности этой сферы. Если сфера представляет достаточно близкую окрестность аттрактора ($\rho \to 0$), то, очевидно, образовавшийся шар заполнен траекториями, ведущими с поверхности сферы к центру шара. По мере увеличения $\rho ,$ т.е. отдаления этой поверхности от центра, начинают появляться траектории, выходящие из области притяжения данного центра. Разделив исследованные точки на поверхности сферы по принадлежности траекторий к рассматриваемому аттрактору, далее следует проводить фиксирование данного распределения с ранжированием по величине радиуса ρ.
На рис. 6 показан шаблон тестирующих точек на поверхности сферы радиуса $\rho .$ Показаны только две точки на поверхности этой сферы. Точка А представляет начало траектории, ведущей в аттрактор, точка В не принадлежит области притяжения этого аттрактора. Проводя циклические вычислительные процедуры по всему конечному множеству сфер с радиусами ${{\rho }_{i}} = 0,{{h}_{{\rho }}},2{{h}_{{\rho }}}...,i{{h}_{{\rho }}},...,{{\rho }_{{\max }}},$ в совокупности получим изображение некоторого трехмерного тела, геометрического места разделенных траекторий.
Рис. 6.
Сферическая система координат с центром в точке равновесия и две тестирующие точки на поверхности сферы с текущим радиусом $\rho .$
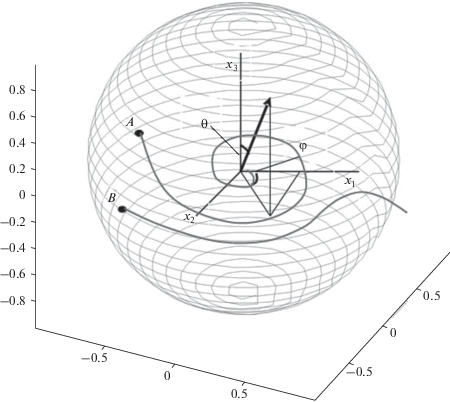
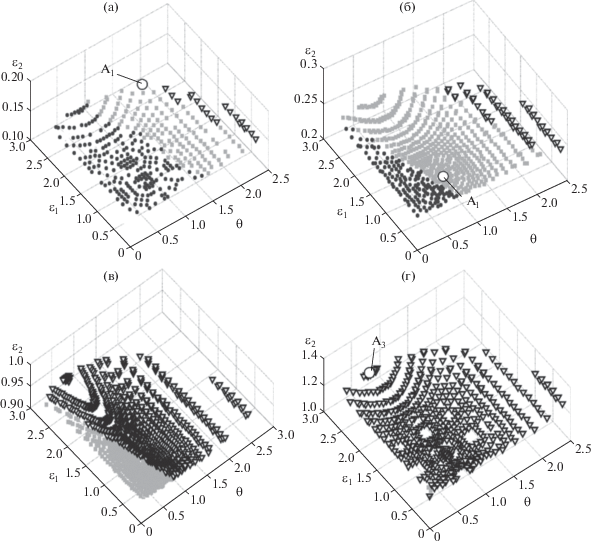
Визуализацию данного рода представления трехмерного множества проведем в томографических разрезах. На рис. 7 показаны четыре томографических слоя фазового пространства в области $D,$ содержащей поля притяжения аттракторов A1, A3, а также поле, из которого все изображающие точки входят в область спада температуры системы. Разрезы осуществлены по разным высотам по координате ${{\varepsilon }_{2}}.$ Толщина слоев во всех рисунках одинакова и составляет $\Delta {{\varepsilon }_{2}} = 0.025.$ На рис. 7а показан слой, соответствующий ${{\varepsilon }_{2}} = 0.15.$ Это есть отражение режима со значительным дефицитом теплоты в системе вследствие малого выхода кокса на отработанном катализаторе. Множество траекторий, ведущих в область спада процессов горения (изображено точечным показом поля), уступает свое место области притяжения аттрактора A1 (обозначена квадратными точками) лишь по мере увеличения $\theta $. Но это явление находит себе место только в области недопустимо высоких температур. Слой, показанный на рис. 7б (${{\varepsilon }_{2}} = 0.25$), в основном отражает граничащие области тепловой неустойчивости (области погасания) и области притяжения аттрактора А1. На рис. 7в отчетливо видна граница полей притяжения аттракторов А1 и А3. Рис. 7г отражает поле притяжения аттрактора А3 (${{\varepsilon }_{2}} = 1.25$). С увеличением координаты ${{\varepsilon }_{2}}$ наблюдается смещение области притяжения A3 влево, наблюдаются также и расширения этой области в сторону увеличения ${{\varepsilon }_{1}}.$
Рис. 7.
Томографические разрезы по разным высотам (а–г) по координате ${{\varepsilon }_{2}}$ пространства состояний, содержащей два положения устойчивого равновесия в рабочей области.
Алгоритм контроля теплового состояния РРС сводится к визуальному анализу томографических разрезов. Определение соответствующего слоя ведется по координате ${{\varepsilon }_{2}}$ изображающей точки, определяемой путем оперативного измерения. Две другие координаты этой точки высвечиваются на мониторе для контроля состояния. С практической точки зрения, учитывая большую оперативность измерения температуры, предпочтительным оказывается использование в качестве координаты прослаивания переменную $\theta .$ В то же время, согласно теории дифференциальных уравнений, выбор той или иной координаты прослаивания не влияет на точность или информативность данного анализа, хотя выбранные с этой целью координаты могут отличаться практическим удобством.
СИТУАЦИОННОЕ УПРАВЛЕНИЕ СОСТОЯНИЕМ. РАСКРАШЕННЫЕ СЕГМЕНТЫ НА СЕПАРАТНЫХ ПОВЕРХНОСТЯХ
Концепция ситуационного управления тепловым состоянием РРС связана с выбором предпочтительного фазового портрета, учитывающего возмущающий фактор $w.$ Далее должна быть решена задача стабилизации режима в области, которая отмечена на предпочтительном фазовом портрете. Предпочтительность аттрактора типа узел исходит из критерия стабильного течения непрерывного процесса. Любое свободное тепловое движение системы асимптотически направлено в центр, следовательно, оптимальным с точки зрения тепловых состояний наиболее благоприятным является режим, совпадающий по координатам с положением равновесия типа узел. Возмущения малых амплитуд обычно компенсируются действиями традиционных средств стабилизации. Возмущения с большими амплитудами могут вызвать потерю области заданного положения равновесия. Отклонение изображающей точки от положения равновесия типа узел, если оно достигает разделяющих границ аттрактора, то наступит неизбежный режим потери термической стабильности. Актуальны следующие две взаимосвязанные задачи.
А. Контроль достижения границ области притяжения аттрактора. В автоматическом режиме контроля задача сводится к определению кратчайшего расстояния между разделяющей поверхностью (или плоской кривой) и изображающей точкой. В среде человеко-машинных систем контроль следует осуществить визуально по монитору, куда заносится изображение разделяющих поверхностей (изображения томографических разрезов). Осуществляется контроль критических расстояний изображающей точки к названным поверхностям. Удобно пользоваться обычным евклидовым расстоянием.
Б. Принятие управленческих мер по предотвращению потери области притяжения заданного аттрактора. В среде человеко-машинных систем управления режимом РРС основаниями решения этой задачи служат вектор текущего состояния ${{{\mathbf{x}}}_{{\text{s}}}} = ({{\varepsilon }_{{{\text{1s}}}}},{{\theta }_{{\text{s}}}},{{\varepsilon }_{{{\text{2s}}}}}),$ вектор текущей скорости ${\mathbf{x}}_{s}^{'} = {{f}_{1}}({{{\mathbf{x}}}_{{\text{s}}}},{{{\mathbf{u}}}_{{\text{s}}}}){{\vec {\varepsilon }}_{1}}$ + ${{f}_{2}}({{{\mathbf{x}}}_{{\text{s}}}},{{{\mathbf{u}}}_{{\text{s}}}})\vec {\theta } + {{f}_{3}}({{{\mathbf{x}}}_{{\text{s}}}},{{{\mathbf{u}}}_{{\text{s}}}}){{\vec {\varepsilon }}_{2}}$ и вектор желаемого состояния на последующем шаге пошагового управления движением, т.е. вектор ${{{\mathbf{x}}}_{{\text{p}}}} = ({{\varepsilon }_{{1{\text{p}}}}},{{\theta }_{{\text{p}}}},{{\varepsilon }_{{2{\text{p}}}}}).$
Отметим два направления в пространстве состояний в виде соответствующих направляющих косинусов: желаемое направление движения, вычисляемое как разность текущего и желаемого на очередном шаге состояний:
(18)
$\frac{{({{x}_{{{\text{s}}i}}} - {{x}_{{{\text{p}}i}}})}}{{\left| {{{{\mathbf{x}}}_{{\text{s}}}} - {{{\mathbf{x}}}_{{\text{p}}}}} \right|}};\,\,\,i = \overline {1.3} $и проектированное направление, которое связывается с функциями правых частей системы дифференциальных уравнений (12) и вектором управлений, состоящим из скорости циркуляции катализатора и скорости ввода газового топлива в регенератор, т.е. ${{{\mathbf{u}}}_{{\text{s}}}} = (F_{k}^{{\text{s}}},F_{{{\text{fu}}}}^{{\text{s}}}){\kern 1pt} {\kern 1pt} {\text{:}}$
Заметим, что формулы (18), (19) представляют собой направляющие косинусы соответствующих векторов.
В человеко-машинной системе управления выбор желаемого направления движения является прерогативой управляющего персонала, а направление, проектируемое для оказания управляющего воздействия, необходимо вычислить, минимизируя следующую сумму квадратов разностей:
(20)
${{{\mathbf{u}}}_{{\text{s}}}} = \arg \mathop {\min }\limits_{u \in U} \sum\limits_{i = 1}^3 {{{{\left( {\frac{{{{f}_{i}}({{{\mathbf{x}}}_{{\text{s}}}}{\text{,}}\,{{{\mathbf{u}}}_{{\text{s}}}})}}{{\left| {{\mathbf{f}}({{{\mathbf{x}}}_{{\text{s}}}}{\text{,}}\,{{{\mathbf{u}}}_{{\text{s}}}})} \right|}} - \frac{{({{x}_{{{\text{s}}i}}} - {{x}_{{{\text{p}}i}}})}}{{\left| {{{{\mathbf{x}}}_{{\text{s}}}} - {{{\mathbf{x}}}_{{\text{p}}}}} \right|}}} \right)}}^{2}}} ,$На рис. 8 показано положение изображающей точки xs, которое достигло меры критического приближения к сепаратрисе ${{{\mathbf{S}}}_{{{\text{1}}{\text{.3}}}}}.$ Угол $\varphi $ между желаемым направлением (18) и проектированным посредством вектора us направления отвечает минимуму функции (20). Точка ${{{\mathbf{x}}}_{{{\text{s}} + 1}}}$ на (s + 1)-й итерации управления движением расположена несколько далее опасных границ.
Рис. 8.
Проектирование вектора управлений ${{{\mathbf{u}}}_{{\text{s}}}}$ в решении задачи вывода системы из состояния критически близкого расположения к опасной границе ${{S}_{{1.3}}}{\kern 1pt} {\kern 1pt} .$
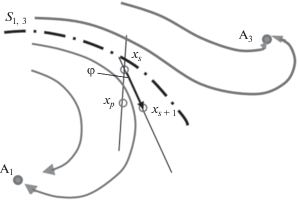
Характер возникших критических ситуаций может быть связан с положением изображающей точки относительно того или иного участка сепаратрисной поверхности ${{S}_{1}}.$ На плоских томографических изображениях (рис. 7а–7в) она представлена точечными заполнениями, разделенными с использованием различных маркеров. На рис. 7а и 7б разделены области с траекториями, ведущими в область низких температур (область погасания системы), и траекториями, ведущими в область притяжения высокотемпературного аттрактора ${{A}_{3}}.$ Различие ситуаций вызывает различие стратегий управления. В одной ситуации очевидна целесообразность топливного подогрева системы с вводом в регенератор топливного газа, с вводом в реактор катализаторного шлама из секции разделения продуктов крекинга и т.п., а в другой – принятие мер по управлению процессами десорбирования углеводородов водно-паровой обработкой катализатора. В связи с этим целесообразно применение раскрашивания как способа выделения отдельных сегментов предельной поверхности ${{S}_{1}}.$ Каждая окраска соответствует определенной технологической ситуации, для которой могут быть приготовлены специальная стратегия управления, программа контроля состояния в сопровождении оповещающей звуковой сигнализации.
ЗАКЛЮЧЕНИЕ
Реакционно-регенерационные системы как с точки зрения инженерных расчетов при проектировании разного типа химических процессов, так и с точки зрения процесса управления ими представляют собой сложные тепловые системы с большим разнообразием критических явлений в динамике. Модельное исследование этих явлений обладает высокой эффективностью в объяснении их природы, прогнозировании и нахождении рациональных управленческих мер по предотвращению неблагоприятных технологических ситуаций, а также мер по целесообразному использованию ряда специфических сторон этих явлений.
Обращает на себя внимание наличие множественности стационарных состояний, которые могут найти себе место также и в технологически регламентированной области изменения режимных параметров. Результаты проведенных исследований показали, что одна из главных причин данного нелинейного явления заключается в том, что между процессами образования кокса в результате конверсии углеводородов и процессом выжига коксовых отложений существует положительная обратная связь. Обратная связь может реализоваться как по тепловому каналу, так и по каналу кокса. Разнообразие критических явлений в тепловой динамике, выдвигая свои условия в постановках задач управления, обусловливает разработку целого ряда специальных алгоритмов анализа и формирования функций управления. К таким алгоритмам следует отнести построение трехмерных фазовых портретов по координатам “остаточная закоксованность катализатора после регенерации–температура регенератора–содержание кокса на отработанном катализаторе”. Задачами оперативного управления продиктовано решение таких проблем, как описание областей притяжения аттракторов во множестве режимных параметров, проблема визуализации этих областей, а также разработка алгоритмов контроля больших отклонений переменных состояния.
Эти задачи не только выдвигают необходимость в дальнейших исследованиях в области совершенствования вышеуказанных алгоритмов, но и стимулируют разработки новых постановок задач исследования, ориентированных на повышение эффективности в управлении тепловыми режимами РРС, применяющихся в химической технологии.
Работа выполнена при поддержке Фонда развития науки при Президенте Азербайджанской Республики (проект EİF/MQM/Elm-Təhsil-1-2016-1(26)).
ОБОЗНАЧЕНИЯ
| A1, A2, A3 | точки термического равновесия |
| A, B | безразмерные комплексы, содержащиеся в уравнении (5) |
| C | концентрация кокса на катализаторе, кг/кг |
| c | теплоемкость, кДж/(кг К) |
| D | область технологически допустимых состояний |
| E | энергия активации, кДж/моль |
| F | массовые скорости потоков веществ, кг/ч |
| G | масса катализатора в псевдоожиженном слое, кг |
| K | число делений по координате φ |
| k | константа скорости химической реакции, ч–1 |
| L | число квантов по координате ψ |
| P | безразмерная функция невязки |
| Q | скорость подвода количества теплоты, кДж/ч |
| q | тепловой эффект реакции, кДж/кг |
| R | универсальная газовая постоянная, Дж/(моль К) |
| S | наружная поверхность аппарата, м2 |
| T | температура, К |
| U | множество технологически допустимых управлений |
| V | число квантов по координате ρ |
| w | весовая скорость ввода сырья в реактор, ч–1 |
| x | нормированный вектор состояния |
| z | число страниц в многолистовом фазовом портрете |
| α, β | безразмерные аппроксимирующие коэффициенты |
| $\varepsilon $ | нормированное значение закоксованности катализатора |
| $\theta $ | безразмерная температура |
| $\rho $ | безразмерный радиус в полярной системе координат |
| $\varphi $ | аппроксимирующая функция содержания кокса на катализаторе |
ИНДЕКСЫ
| нижние | |
| 1 | регенератор |
| 2 | реактор |
| air | воздух |
| dis | теплоотвод |
| en | окружающая среда |
| fu | топливный газ |
| i | номер в последовательности дискретных значений параметра w |
| j | номер в последовательности дискретных значений параметра fk |
| k | катализатор |
| kr | критическое значение |
| nom | номинальное значение |
| max | максимальное значение |
| min | минимальное значение |
| p | желаемое состояние |
| rem | тепловыделение |
| s | текущее состояние |
| λ | номер множества однотипных фазовых портретов |
| верхние | |
| $\left. \begin{gathered} n \hfill \\ m \hfill \\ \end{gathered} \right\}$ | номера квантов дискретизации параметров $w,{{f}_{{\text{k}}}}$ |
| $\left. \begin{gathered} k = 1,2,...,K \hfill \\ \ell = 1,2,...,L \hfill \\ v = 1,2,...,V \hfill \\ \end{gathered} \right\}$ | номера квантов дискретизации полярных координат |
| $\eta $ | порядок реакции |
Список литературы
Elnashaie S.S., El-Hennawi I.M. Multiplicity of the steady state in fluidized reactors // Chem. Eng. Sci. 1979. V. 34. № 9. P. 1113.
Aliev A.M., Nagiev A.G. Statistical description of the coke balance in a reactor-regenerator system containing a fine-particle catalyst // Theor. Found. Chem. Eng. 2003. V. 37. № 2. P. 191. [Алиев А.М., Нагиев А.Г. Статистическое описание баланса кокса в системе реактор-регенератор с мелкодисперсным катализатором // Теорет. основы хим. технологии. 2003. Т. 37. № 2. С. 209.]
Wgialla R.M., Helal A.M., Elnasaie S.S. The use of mathematical and computer models to explore the applicability of fluidized bed technology for highly exothermic catalytic reactions // Math. Comput. Model. 1991. V. 15. № 1. P. 17.
Burovoi I.A., Mamedov A.A. Constructing Model Structure for Identification of Certain Class of Heterogeneous Catalytic Processes // Automation and Remote Control. 1970.V. 31. № 7. Р. 100. [Буровой И.А., Мамедов А.А. Построение структуры модели для идентификации одного класса гетерогенных каталитических процессов // Автоматика и телемеханика. 1970. Т. 31. № 7. С. 100.]
Pinheiro C.I.C., Fernandes J.L., Domingues L., Cham-bel A.J.S., Graça I., Oliveira N.M.C., Cerqueira H.S., Ribeiro F.R. Fluid Catalytic Cracking (FCC) Process Modeling, Simulation, and Control // Ind. Eng. Chem. Res. 2012.V. 51. № 1. P. 1.
Бесков В.С., Нагиев А.Г., Юсифов Р.Ю. Оптимизация ХТС с учетом множественности и устойчивости стационарных состояний // Тез. докл. Науч. конф. “Методы кибернетики химико-технологических процессов”. М.: Химия, 1984. С. 106.
Schuurman Y., Delattre C., Pitault I., Reymond J.P., Forissier M. Effect of coke deposition on transport and sorption in FCC catalysts studied by temporal analysis of products // Chem. Eng. Sci. 2005. V. 60. № 4. P. 1007.
Carabineiro H., Pinheiro I.C., Lemos F., Ribeiro F.R. Transient microkinetic modelling of n-heptane catalytic cracking over H-USY zeolite // Chem. Eng. Sci. 2004. V. 59. № 6. P. 1221.
Алиева А.А. Влияние коксоотложения в процессе каталитического крекинга на каталитическую активность смешанных Pt- металл-оксидных промоторов дожига монооксида углерода в диоксид // Процессы нефтехимии и нефтепереработки. 2001. № 3. С. 20.
Chen G.-Q., Luo Z.-H. New insights into intraparticle transfer, particle kinetics, and gas–solid two-phase flow in polydisperse fluid catalytic cracking riser reactors under reaction conditions using multi-scale modeling // Chem. Eng. Sci. 2014. V. 109. P. 38.
Moustafa T.M., Froment G.F. Kinetic Modeling of Coke Formation and Deactivation in the Catalytic Cracking of Vacuum Gas Oil // Ind. Eng. Chem. Res. 2003. V. 42. № 1. P. 14.
Shamansky V.A., Donskoy I.G. Model of carbon particle burnout in a flow reactor for thermochemical conversion of solid fuel // Theor. Found. Chem. Eng. 2017. V. 51. № 2. Р. 199. [Шаманский В.А., Донской И.Г. Модель выгорания угольной частицы в поточном реакторе для термохимической конверсии твердого топлива // Теорет. основы хим. технологии. 2017. Т. 51. № 2. С. 182.]
Шмид Р., Сапунов В.М. Неформальная кинетика. М.: Мир, 1985.
Касьянов А.А., Сухоруков А.М., Прокопюк С.Г. Опыт эксплуатации установки каталитического крекинга Г-43-107М // Нефтепереработка и нефтехимия. 1998. № 4. С. 11.
Войцеховский Б.В., Корма А. Каталитический крекинг: катализаторы, химия, кинетика. М.: Химия, 1990.
Aliev A.M., Safarov A.R., Guseinova A.M. Calculation of ethylene region of chemical technological complex for processing of cracking and pyrolysis gases // Theor. Found. Chem. Eng. 2017. V. 51. № 4. Р. 404. [Алиев А.М., Сафаров А.Р., Гусейнова А.М. Расчет этиленового региона химико-технологического комплекса по переработке газов крекинга и пиролиза // Теорет. основы хим. технологии. 2017. Т. 51. № 4. С. 397.]
Van Heerden C. The character of the stationary state of exothermic processes // Chem. Eng. Sci. 1958. V. 8. № 2. P. 13.
Copelli S., Derudi M., Rota R. Topological Criterion To Safely Optimize Hazardous Chemical Processes Involving Arbitrary Kinetic Schemes // Ind. Eng. Chem. Res. 2011. V. 50. № 3. P. 1588.
Koronaki E.D., Gakis G.P., Cheimarios N., Boudouvis A.G. Efficient tracing and stability analysis of multiple stationary and periodic states with exploitation of commercial CFD software // Chem. Eng. Sci. 2016. V. 150. P. 26.
Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. М.: Наука, 1976.
Быков В.И., Яблонский Г.С., Елохин В.И. Фазовые портреты простейших каталитических механизмов, допускающих множественность стационарных состояний поверхности // Кинетика и катализ. 1979. Т. 20. № 4. С. 1029.
Вольтер Б.В., Сальников И.Е. Устойчивость режимов работы химических реакторов. М.: Химия, 1981.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии