Теоретические основы химической технологии, 2019, T. 53, № 1, стр. 46-53
Математическое моделирование ферментативного процесса получения молочной кислоты. Обобщенная модель
Ю. Л. Гордеева 1, *, А. Г. Бородкин 2, Е. Л. Гордеева 2, Е. Г. Рудаковская 2
1 Московская государственная академия ветеринарной медицины и биотехнологии им. К.И. Скрябина
Москва, Россия
2 Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: l.s.gordeev@yandex.ru
Поступила в редакцию 21.02.2018
После доработки 15.06.2018
Принята к публикации 16.04.2018
Аннотация
Приведены результаты разработки обобщенной математической модели ферментативного метода получения молочной кислоты. Математическая модель включает нестационарные уравнения получения биомассы, потребления субстрата, получения молочной кислоты и побочных продуктов метаболизма, уравнения образования дополнительного количества основного субстрата из компонентов сырья. Результаты моделирования процесса получены с использованием констант базового варианта по результатам частных исследований. Приведены зависимости показателей процесса от времени для базового варианта и зависимость продуктивности молочной кислоты QP, г/(л ч) от времени с оценкой времени t достижения максимального значения QP (max QP). Математическая модель учитывает все возможные варианты ингибирования – биомассой, продуктом и субстратом. Результаты моделирования с учетом интенсивности ингибирования каждым фактором показали следующее. Увеличение константы ингибирования по биомассе Xmax сокращает длительность процесса; увеличение константы ингибирования по продукту Pmax несколько увеличивает длительность процесса; уменьшение значения константы ингибирования по субстрату Ki (интенсивность ингибирования возрастает) значительно увеличивает длительность процесса. Время завершения процесса tk для всех условий моделирования определялось достижением одного из условий: X = Xmax или P = Pmax или S = 0. При моделировании также установлено, что изменение констант в уравнении для образования побочных продуктов не влияет на изменение показателей процесса кроме численного значения концентрации побочных продуктов.
ВВЕДЕНИЕ
Молочная кислота первоначально рассматривалась как компонент молока. Впоследствии Пастер установил, что молочная кислота является продуктом ферментативного метаболизма определенных микроорганизмов [1].
В последние 15–20 лет значительно возрос интерес к промышленному производству молочной кислоты. Достаточно привести три обзора [2–4], в которых подробно освещены вопросы промышленного получения молочной кислоты. Приведены виды микроорганизмов, воспроизводящих молочную кислоту; сырьевые источники; технологические показатели с оценками продуктивности в периодических и непрерывных условиях культивирования; области использования молочной кислоты (в пищевой, косметической, фармацевтической и химической промышленности).
Отмеченный интерес, безусловно, затронул и научную среду исследований по биосинтезу молочной кислоты с различными видами штаммов микроорганизмов, условиями синтеза, технологическими оценками и т.д. В обзорах [5–7] приведены публикации по моделированию и оптимизации ферментативного способа синтеза молочной кислоты.
Общее число публикаций, приведенных в этих обзорах, составляет более 200 наименований.
Неординарный интерес к молочной кислоте выводит этот продукт как наиболее востребованный среди продуктов микробиологического синтеза.
Значение молочной кислоты также возросло в связи с возможностью ее использования в качестве мономера для получения биоразлагаемых полимеров (полимолочной кислоты).
Анализируя научные публикации, отметим, что большинство из них относятся к решению частных задач, т.е. изучаются конкретные штаммы микроорганизмов, отдельные виды используемых субстратов, конкретные значения технологических показателей (температура синтеза, pH и др.)
Экспериментальные исследования моделируются на основе кинетических соотношений, как правило, основанных на неструктурированном подходе.
Основные положения, объединяющие большинство научных публикаций, следующие.
Математические модели практически во всех исследованиях не противоречат биологическим основам процесса синтеза.
Виды математических моделей в разных публикациях отличаются друг от друга, однако, количество используемых математических соотношений достаточно ограничено [5–7].
Математические соотношения в той или иной степени учитывают следующие особенности процесса синтеза – возможность ингибирования субстратом, биомассой и продуктом. При этом формулы учета ингибирования могут иметь различный вид.
Еще одна особенность заключается в том, что выбор математической модели в той или иной публикации, как правило, не имеет какого-либо обоснования и осуществляется, основываясь на интуиции авторов исследования.
Целью настоящей работы является формирование обобщенной математической модели, в которой уравнения для частных исследований должны быть включены в общую систему.
УРАВНЕНИЯ ОБОБЩЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРОЦЕССА ФЕРМЕНТАТИВНОГО ПОЛУЧЕНИЯ МОЛОЧНОЙ КИСЛОТЫ
Поскольку молочная кислота является продуктом метаболизма молочнокислых микроорганизмов, основное уравнение математической модели является уравнением скорости образования этих микроорганизмов. Большинство исследований, отмеченных в обзорах [5–7], используют уравнение скорости образования биомассы в виде
где X – концентрация биомассы, г/л; t – время, ч; μ – удельная скорость роста ч–1; mX – коэффициент смертности микроорганизмов, ч–1.Выражение для удельной скорости роста в исследованиях различается.
Однако обобщенный вариант, как отмечалось выше, должен учитывать возможные эффекты торможения (ингибирования) компонентами процесса, в данном случае биомассой (X), субстратом (S) и продуктом (P). Обобщенное соотношение, учитывающее эти эффекты, имеет следующий вид:
(2)
$\begin{gathered} \mu = {{\mu }_{{\max }}}{{\left( {1 - \frac{X}{{{{X}_{{\max }}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{\max }}}}}} \right)}^{{{{n}_{2}}}}} \times \\ \times \,\,\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}}, \\ \end{gathered} $Удачность выбора соотношения (2) заключается в возможности учета частных условий ингибирования численными значениями констант. Так, если отсутствует ингибирование биомассой, то или Xmax достаточно большое или n1 близко к нулю. Отсутствие ингибирования субстратом означает, что Ki достаточно большое (Ki$ \gg $ S). Отсутствие ингибирования продуктом означает, что Pmax достаточное большое или n2 близко к нулю.
Поскольку основной продукт (молочная кислота) и возможно образуемые побочные продукты являются результатом метаболизма микроорганизмов, скорость их образования определяется растущими и нерастущими ассоциатами. Уравнения для P и B удобно записать в следующем виде [8]:
где P и B – концентрация молочной кислоты и побочного продукта соответственно, г/л; α, β, αB, βB – константы.Вообще говоря, побочных продуктов может быть несколько, и концентрация B представляет их совокупность.
Скорость потребления субстрата связана со скоростью роста микроорганизмов через стехиометрический коэффициент YX/S. Если же используется сырье, воспроизводящее субстрат в процессе ферментации, то скорость его воспроизводства вычисляется по соотношению
С учетом (1) и (5) скорость расходования субстрата может быть записана в виде
(6)
$\frac{{dS}}{{dt}} = - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{dX}}{{dt}} + {{k}_{M}}M - {{m}_{S}}X,$Таким образом, система уравнений обобщенной математической модели имеет следующий вид:
(7)
$\left\{ \begin{gathered} \frac{{dX}}{{dt}} = \mu X - {{m}_{X}}X \hfill \\ \frac{{dP}}{{dt}} = \left( {\alpha \mu + \beta } \right)X \hfill \\ \frac{{dB}}{{dt}} = \left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X \hfill \\ \frac{{dM}}{{dt}} = - {{k}_{M}}M \hfill \\ \frac{{dS}}{{dt}} = - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\left( {\mu - {{m}_{X}}} \right)X + {{k}_{M}}M - {{m}_{S}}X \hfill \\ \mu = {{\mu }_{{\max }}}{{\left( {1 - \frac{X}{{{{X}_{{\max }}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{\max }}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}} \hfill \\ \end{gathered} \right..$Поскольку процесс ферментации ориентирован на получение молочной кислоты, к системе (7) следует добавить уравнение для вычисления продуктивности QP по молочной кислоте для любого момента времени t:
Отметим также, что для большинства исследований частного характера константы mX и mS незначительны и практически не влияют на результаты моделирования.
Для моделирования процесса приведем некоторые результаты анализа системы уравнений (7). Как отмечалось ранее, ингибирование процесса как уменьшение скорости роста есть совокупный эффект влияния концентраций X, P, S на величину удельной скорости μ.
Поскольку процесс синтеза развивается во времени, с течением последнего увеличивается концентрация биомассы (предельно до величины Xmax), концентрация продукта (предельно до величины Pmax) и уменьшается концентрация субстрата S. Однако уменьшение концентрации субстрата в результате его потребления может протекать в замедленном темпе, так как имеется возможность его пополнения за счет компонента сырья M.
Таким образом, эффект ингибирования за счет X и P усиливается с течением времени и ослабляется за счет S.
Очевидно, что завершение процесса синтеза определяется моментом времени, когда или P достигает значения Pmax или S достигает значения, равного нулю.
Если же X достигает значения Xmax раньше, чем P достигает Pmax или S достигает значения, равного нулю, синтез продолжается за счет метаболизма нерастущих ассоциатов, т.е. имеет место рост концентрации P и B и уменьшение S по соотношениям (3) и (4), в которых $\alpha \mu {{X}_{{\max }}} = 0$ и ${{\alpha }_{B}}\mu {{X}_{{\max }}} = 0.$
Отсюда следует, что процесс может быть достаточно длительным по времени, при этом прирост P и B определяется численными значениями $\beta $ и ${{\beta }_{B}}.$ Однако этот прирост, как правило, невелик.
Ингибирование субстратом наиболее сильно проявляется при высокой его концентрации [составляющая ${{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}$в уравнении (2)], т.е. практически в начальной стадии процесса. При этом убывание S в силу потребления субстрата уменьшает эффект торможения. Это уменьшение может компенсироваться увеличением концентрации субстрата за счет его дополнительного образования в количестве ${{k}_{M}}M.$
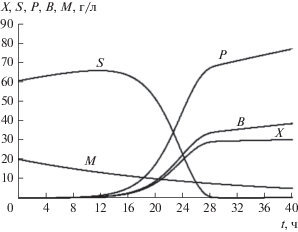
Таким образом, задача моделирования процесса заключается в получении решения системы (7) и расчета QP по (8) для различных начальных значений S0 и M0. Результаты моделирования включают получение зависимостей X(t), P(t), B(t), M(t), S(t) в цифровом или графическом виде.
Очевидно, что решение (7) ограничено выполнением условий
(9)
$1 - {X \mathord{\left/ {\vphantom {X {{{X}_{{\max }}} \geqslant 0}}} \right. \kern-0em} {{{X}_{{\max }}} \geqslant 0}},$(10)
$1 - {P \mathord{\left/ {\vphantom {P {{{P}_{{\max }}} \geqslant 0}}} \right. \kern-0em} {{{P}_{{\max }}} \geqslant 0}}.$При этом, если в (10) имеет место равенство, т.е. $P\left( {{{t}_{k}}} \right) = {{P}_{{\max }}},$ решение закончено, где ${{t}_{k}}$ − момент времени завершения процесса.
Естественно, время завершения процесса интегрирования системы (7) может задаваться пользователем.
МОДЕЛИРОВАНИЕ
Для моделирования процесса с использованием обобщенной математической модели необходимо задать численные значения констант в уравнениях системы (7).
Последние получаются при обработке экспериментальных данных по конкретной математической модели. Поскольку экспериментальные исследования по модели обобщенного типа в литературе отсутствуют, выбор значений констант проведен по данным частных исследований. Некоторые результаты оценок констант частных исследований приведены в обзорах [6, 7] и представлены в табл. 1.
Таблица 1.
Численные значения констант
| № | Ссылки | Микроорганизм | Субстрат | µmax, ч–1 | Km, г/л | Ki, г/л | Xmax, г/л | Pmax, г/л | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | [9] | Lactococcus lactis | Пшеничная мука | 0.403 | 0.79 | 164 | – | 62.5* | ||
| 2 | [10] | Lactobacillus coryniformis | Пшеничная мука | 0.28 | 0.5 | – | – | 98.6 | ||
| 3 | [14] | Lactococcus lactis | Глюкоза | 0.687 | – | – | 1.171 | – | ||
| 4 | [14] | Pediococcus acidilactici | Глюкоза | 0.230 | – | – | 1.274 | – | ||
| 5 | [11] | Lactobacillus casei | Сыворотка | 0.265 | 0.72 | – | 8.0 | 90.0 | ||
| 6 | [12] | Lactobacillus delbrueckii | Свекольная меласса | 0.831 | – | – | – | 45.0 | ||
| 7 | [13] | Lactobacillus rhamnosus | Глюкоза | 0.633 | 0.3 | – | – | 114.0 | ||
| № | n1 | n2 | α, г/г | β, ч–1 | αB, г/г | βB, ч–1 | kM, ч–1 | YX/S, г/г | mX, ч–1 | mS, ч–1 |
| 1 | – | 2.36 | 62.678* | 0.43* | 1.14* | 2.63 × 10–6* | 0.004* | – | – | 6.78 × 10–3* |
| 2 | – | 3.0 | 15.47 | – | – | – | 0.035 | 0.53 | – | – |
| 3 | 1.0 | 0.0 | 4.49 | 0.0356 | 24.08 | 0.189 | – | 0.139 | – | 0.057 |
| 4 | 1.0 | 0.0 | 4.686 | 0.06 | 185.5 | 0.001 | – | 0.149 | – | 0.086 |
| 5 | 0.5 | 0.5 | 4.0 | 0.06 | – | – | – | – | – | 0.03 |
| 6 | – | 1.0 | 0.235 | 0.087 | – | – | – | 0.27 | – | 0.09 |
| 7 | – | 2.68 | 6.6 | 0.33 | – | – | – | 1.0 | – | – |
* Значения вычислены по формулам [9] для температуры 34°С.
Разброс значений констант по частным исследованиям довольно широк. Это потребовало сформировать базовый список значений констант и использовать его для изучения различных вариантов проведения процесса.
В основу формирования базового списка положены следующие представления.
По публикациям частного характера [6, 7] коэффициент смертности микроорганизмов ${{m}_{X}}$ достаточно мал и часто просто не оценивается, так как предполагается, что смертность микроорганизмов молочнокислых бактерий невелика.
Коэффициент, определяющий расход субстрата на поддержание жизнедеятельности нерастущих микроорганизмов, ${{m}_{S}}$ также достаточно мал. Оба эти коэффициента в базовый список не включены.
Важным вопросом в формировании базового варианта является учет ингибирования.
Обращаясь к кинетическому уравнению (2), отметим, что, если Xmax достаточно большое, ингибирование биомассой наблюдается при значениях X, близких к Xmax (т.е. с момента времени, когда ингибирование заметно отражается на синтезе). Поэтому для базового варианта было принято достаточно большое Xmax = 30 г/л.
Ингибирование продуктом также имеет заметное влияние, когда концентрация P приближается к значению ${{P}_{{\max }}},$ в базовом варианте ${{P}_{{\max }}}$ принято равным 98 г/л (в соответствии с табл. 1).
Аналогичное условие для ингибирования субстратом: Ki = 164 г/л.
Численные значения остальных констант приняты, в основном, по табл. 1. Полный список констант базового варианта приведен в табл. 2.
Таблица 2.
Численные значения констант для базового варианта
| Km, г/л | Ki, г/л | μmax, ч–1 | Xmax, г/л | Pmax, г/л | n1 | n2 | YX/S, г/г | kM, ч–1 | α, г/г | β, ч–1 | αB, г/г | βB, ч–1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.2 | 164 | 0.48 | 30.0 | 98.0 | 0.5 | 0.5 | 0.4 | 0.035 | 2.2 | 0.02 | 1.1 | 0.01 |
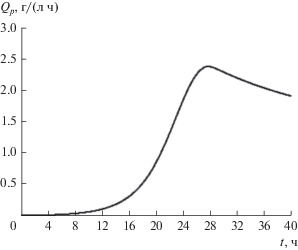
Результаты моделирования процесса в виде решения системы (7) с учетом ${{m}_{X}} = {{m}_{S}} = 0$ и использованием данных табл. 2 приведены на рис. 1 и 2.
Начальные условия для системы (7) для всех вариантов моделирования: при t = 0 P0 = B0 = 0; S0 = 60 г/л; M0 = 20 г/л.
Время завершения процесса при t = tk для всех вариантов моделирования принималось по выполнению одного из условий: X = Xmax или P = Pmax или S = 0.
В табл. 3 приведены численные значения показателей процесса при t = tk.
Таблица 3.
Значения показателей процесса в момент его завершения
| Вариант | tk, ч | X, г/л | P, г/л | B, г/л | S, г/л | M, г/л | QP, г/(л ч) |
|---|---|---|---|---|---|---|---|
| Базовый вариант | 40 | 29.942 | 76.449 | 38.225 | 0.237 | 4.932 | 1.911 |
| I | 24 | 8.0 | 18.547 | 9.273 | 51.391 | 8.634 | 0.773 |
| II | 28 | 21.342 | 49.818 | 24.909 | 19.164 | 7.506 | 1.779 |
| III | 77 | 29.989 | 74.077 | 37.039 | 3.702 | 1.351 | 0.962 |
В табл. 4 приведены максимальные значения продуктивности, в том числе и для базового варианта (рис. 2).
Таблица 4.
Максимальное значение продуктивности QP и соответствующий момент времени t
| Вариант | t, ч | max QP, г/(л ч) |
|---|---|---|
| Базовый вариант | 27.76 | 2.382 |
| I | 23.352 | 0.781 |
| II | 27.524 | 1.785 |
| III | 76.923 | 0.962 |
В табл. 2 и 3 приведены также результаты моделирования для условий, отличных от базового варианта. Эти условия позволяют оценить влияние ингибирования на показатели процесса.
Так, для варианта I значение Xmax в отличие от базового варианта было принято равным 8 г/л. В результате более сильного торможения скорости роста по сравнению с базовым вариантом оказалось, что длительность процесса tk = 28 ч (в базовом варианте 40 ч); наблюдалось также существенное уменьшение концентрации целевого продукта P и продуктивности QP.
Вариант II отличается от базового усилением эффекта ингибирования за счет изменения Pmax. В этом варианте Pmax = 50 г/л (в базовом 98 г/л).
Если в варианте I и базовом время завершения процесса определялось условием X = Xmax, то в варианте II – условием P = Pmax.
Усиление ингибирования за счет P сократило время проведения процесса с 40 до 28 ч. Существенно увеличилась концентрация продукта по сравнению с вариантом I, но уменьшилась по сравнению с базовым вариантом. Продуктивность достигла значения, близкого к значению базового варианта.
Наиболее сильное изменение в результатах моделирования наблюдалось при уменьшении константы Ki от 164 до 22 г/л, т.е. при усилении ингибирования субстратом (вариант III).
Завершение процесса, как и в базовом варианте, определялось условием X = Xmax. Длительность процесса получилась равной 77 ч (в базовом варианте 40 ч). Остаточная концентрация субстрата в базовом варианте значительно меньше, чем в варианте III, и составила 0.273 и 3.702 г/л соответственно.
Время достижения max QP во всех вариантах процесса примерно одинаковое (табл. 4).
Интересно оценить влияние использования вида сырья для синтеза (наличие или отсутствие компонента, воспроизводящего основной субстрат) и использование штамма микроорганизмов, способного или неспособного производить побочный продукт.
Исключение из сырья компонента, воспроизводящего основной субстрат, преобразует систему уравнений (7) к виду
(11)
$\left\{ \begin{gathered} \frac{{dX}}{{dt}} = \mu X - {{m}_{X}}X \hfill \\ \frac{{dP}}{{dt}} = \left( {\alpha \mu + \beta } \right)X \hfill \\ \frac{{dB}}{{dt}} = \left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X \hfill \\ \frac{{dS}}{{dt}} = - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\left( {\mu - {{m}_{X}}} \right)X - {{m}_{S}}X \hfill \\ \mu = {{\mu }_{{\max }}}{{\left( {1 - \frac{X}{{{{X}_{{\max }}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{\max }}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}} \hfill \\ \end{gathered} \right..$Использование штаммов, не продуцирующих побочные продукты, трансформирует систему уравнений обобщенной модели к виду
(12)
$\left\{ \begin{gathered} \frac{{dX}}{{dt}} = \mu X - {{m}_{X}}X \hfill \\ \frac{{dP}}{{dt}} = \left( {\alpha \mu + \beta } \right)X \hfill \\ \frac{{dS}}{{dt}} = - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\left( {\mu - {{m}_{X}}} \right)X + {{k}_{M}}M - {{m}_{S}}X \hfill \\ \frac{{dM}}{{dt}} = - {{k}_{M}}M \hfill \\ \mu = {{\mu }_{{\max }}}{{\left( {1 - \frac{X}{{{{X}_{{\max }}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{\max }}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}} \hfill \\ \end{gathered} \right..$Результаты расчетов по (11) и (12) приведены в табл. 5 и 6.
Таблица 5.
Результаты расчета показателей процесса по данным базовой модели для системы (11) и (12)
| Система | tk, ч | X, г/л | P, г/л | B, г/л | S, г/л | M, г/л |
|---|---|---|---|---|---|---|
| Система (11) | 26 | 24.01 | 55.45 | 27.72 | 7.4 × 10–4 | – |
| Система (12) | 40 | 29.942 | 76.449 | – | 0.237 | 4.932 |
Таблица 6.
Численные значения max QP
| Система | t, ч | max QP, г/(л ч) |
|---|---|---|
| Система (11) | 25.08 | 2.181 |
| Система (12) | 27.76 | 2.382 |
В табл. 6 приведены численные значения max QP и время, соответствующее этому значению.
Нетрудно видеть (табл. 5), что исключение из сырья компонента, воспроизводящего основной субстрат, существенно меняет время окончания процесса (tk = 26 ч), изменяет показатели процесса, и завершение процесса определяется значением S, которое равно 7.4 × 10–4 г/л, в то время как в базовом варианте время завершения процесса определялось величиной X = Xmax.
Время достижения max QP составило 25.08 ч (в базовом варианте 27.76 ч) и max QP = 2.182 г/(л ч) (в базовом варианте 2.382 г/(л ч)).
Исключение возможности образования побочного продукта (система (12)) практически не влияет на показатели процесса по сравнению с базовым вариантом. Последнее вполне объяснимо, так как на образование побочного продукта не влияют такие показатели синтеза, как S и P, и концентрация B исключительно продукт метаболизма X.
ЗАКЛЮЧЕНИЕ
Моделирование процесса микробиологического синтеза молочной кислоты показало следующее. Обобщенная математическая модель способна воспроизводить практически большинство частных вариантов организации процесса, опубликованных в литературе. Моделирование позволило выявить и получить количественные оценки влияния ингибирующих факторов на показатели процесса, в том числе и на условия достижения максимальной продуктивности по молочной кислоте. Экспериментально полученные оценки констант уравнений модели позволяют сравнивать различные штаммы микроорганизмов между собой, длительность процесса ферментации, возможности учета наличия в сырье компонентов, воспроизводящих основной субстрат. Отмеченные особенности могут быть использованы для организации практических технологий получения молочной кислоты.
ОБОЗНАЧЕНИЯ
| B | концентрация побочного продукта, г/л |
| Km | константа насыщения субстрата, г/л |
| Ki | константа ингибирования, г/л |
| kM | константа скорости образования субстрата из компонента сырья, ч−1 |
| M0, M | концентрация компонента сырья, из которого образуется дополнительный субстрат, в поступающем потоке и ферментере соответственно, г/л |
| mS | коэффициент, учитывающий расход субстрата на поддержание жизнедеятельности микроорганизмов, ч–1 |
| mX | коэффициент смертности микроорганизмов, ч–1 |
| n1, n2 | константы |
| P | концентрация продукта, г/л |
| QP | продуктивность, г/(л ч) |
| S0, S | концентрация субстрата в поступающем потоке и ферментере соответственно, г/л |
| t | время, ч |
| X | концентрация биомассы, г/л |
| YX/S | стехиометрический коэффициент, г/г |
| α | константа кинетического соотношения для молочной кислоты, г/г |
| αB | константа кинетического соотношения для побочного продукта, г/г |
| β | константа кинетического соотношения для молочной кислоты, ч–1 |
| βB | константа кинетического соотношения для побочного продукта, ч–1 |
| μ | удельная скорость роста, ч−1 |
ИНДЕКСЫ
Список литературы
Benninga H. A History of Lactic Acid Making: A Chapter in the History of Biotechnology (Series in Chemists and Chemistry. V. 11). N.Y.: Springer, 1990.
Hofvendahl K., Hahn-Hägerdal B. Factors affecting the fermentative lactic acid production from renewable resources // Enzyme and Microbial Technology. 2000. V. 26. P. 87.
Wee Y.-J., Kim J.-N., Ryu H.-W. Biotechnological production of lactic acid and its recent applications // Food Technol. Biotechnol. 2006. V. 44. P. 163.
Datta R., Henry M. Lactic acid: recent advances in products, processes and technologies – a review // J. Chemical Technology and Biotechnology. 2006. V. 81. P. 1119.
Bouguettoucha A., Balannec B., Amrane A. Unstructured models for lactic acid fermentation – a review // Food. Technol. Biotechnol. 2011. V. 49. P. 3.
Gordeev L.S., Koznov A.V., Skichko A.S., Gordeeva Yu.L. Unstructured Mathematical Models of Lactic Acid Biosynthesis Kinetics: A Review // Theor. Found. Chem. Eng. 2017. V. 51. № 2. P. 175. [Гордеев Л.С., Кознов А.В., Скичко А.С., Гордеева Ю.Л. Неструктурированные математические модели кинетики биосинтеза молочной кислоты. Обзор // Теорет. основы хим. технологии. 2017. Т. 51. № 2. С. 8.]
Gordeeva Yu.L., Rudakovskaya E.G., Gordeeva E.L., Borodkin A.G. Mathematical Modeling of Biotechnological Process of Lactic Acid Production by Batch Fermentation: A Review // Theor. Found. Chem. Eng. 2017. V. 51. № 3. P. 282. [Гордеева Ю.Л., Рудаковская Е.Г., Гордеева Е.Л., Бородкин А.Г. Математическое моделирование биотехнологического процесса периодической ферментации получения молочной кислоты. Обзор // Теорет. основы хим. технологии. 2017. Т. 51. № 3. С. 270.]
Luedeking R., Piret E.L. A kinetic study of the lactic acid fermentation // J. Biochem. Microbiol. 1959. V. 1. P. 393.
Åkerberg C., Hofvendahl K., Zacchi G., Hahn-Hägerdal B. Modelling the influence of pH, temperature, glucose and lactic acid concentrations on the kinetics of lactic acid production by Lactococcus lactis ssp. lactis ATCC 19 435 in whole-wheat flour // Appl. Microbiol. Biotechnol. 1998. V. 49. № 6. P. 682.
Gonzales K., Tebbano S., Lapes F., Thorigne A., Givry S., Dumar D., Pareau D. Modeling the continuous lactic acid production process from wheat flour // Appl. Microbiol. Biotechnol. 2016. V. 100. № 1. P. 147.
Altiok D., Tokatli F., Harsa Ş. Kinetic modelling of lactic acid production from whey by Lactobacillus casei (NRRL B-441) // J. Chem. Technol. Biotechnol. 2006. V. 81. № 7. P. 1190.
Monteagudo J.M., Rodriguez L., Rincón J., Fuertes J. Kinetics of lactic acid fermentation by Lactobacillus delbrueckii grown on beet molasses // J. Chem. Technol. Biotechnol. 1997. V. 68. № 3. P. 271.
Kwon S., Yoo I.K., Lee W.G., Chang H.N., Chang Y.K. High-rate continuous production of lactic acid by Lactobacillus rhamnosus in a two-stage membrane cell-recycle bioreactor // Biotechnol. Bioeng. 2001. V. 73. № 1. P. 25.
Vázquez J.A., Murado M.A. Unstructured mathematical model for biomass, lactic acid and bacteriocin production by lactic acid bacteria in batch fermentation // J. Chem. Technol. Biotechnol. 2008. V. 83. № 1. P. 91.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии