Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 229-240
Стохастическая модель совмещенных или последовательных процессов деаэрации и смешивания сыпучих сред на примере работы центробежного устройства
А. Б. Капранова *
Ярославский государственный технический университет
Ярославль, Россия
* E-mail: kapranova_anna@mail.ru
Поступила в редакцию 30.08.2016
После доработки 06.02.2017
Принята к публикации 21.12.2016
Аннотация
На основе теории марковских процессов предложена модель деаэрации сыпучих материалов в совмещенных или последовательных операциях со смешиванием с учетом степени неоднородности смеси и способа ее уплотнения. Построены функции распределения по состояниям системы твердых частиц для случайного относительного изменения выделенного деаэрируемого объема на основе одномерного или многомерного законов Пуассона. Модель проиллюстрирована совмещением указанных процессов в рабочем объеме центробежного устройства. Выполнено построение случайной порозности смеси с применением одномерного закона Пуассона (дискретного по состояниям системы и непрерывного по временному параметру) и проведена оценка соответствующих моментов методом их производящих функций.
ВВЕДЕНИЕ
Операции смешивания и деаэрации являются этапами переработки сыпучих материалов в различных отраслях промышленности. Совмещение или последовательное выполнение указанных процессов – один из способов интенсификации производства уплотненных продуктов из однородных порошковых смесей. Обычно объектами исследований являются процессы смешивания и прессования сыпучих компонентов, рассматриваемые независимо друг от друга.
В рамках теории прессования в основном не решаются задачи деаэрации (уплотнения) дисперсной среды вследствие того, что данная операция является первой стадией компактирования сыпучего материала без упругопластических деформаций его твердого скелета [1–4]. Известные статистические [5] и упругие модели деаэрации дисперсных материалов пренебрегают взаимодействием удаляемого газа с частицами твердой фазы и применимы только при изменении пористости продуктов 7–11%. Однако решение практических задач деаэрации порошков должно учитывать значительно бóльшие значения показателя их газосодержания – до 80% [4, 6]. Существующие модели смешивания сыпучих сред (регрессионные, кибернетические, потоковые, стохастические) [7] не применяются при совмещении с деаэрацией. При этом выбор критерия качества сыпучей смеси, как и его статистическая оценка, требует уточнений в соответствии с конкретной рабочей зоной аппарата.
Выделим основные причины отсутствия моделей деаэрации сыпучих материалов в совмещенных или последовательных процессах со смешиванием: (1) сложности учета в упругих моделях уплотнения – неоднородности уплотняемой смеси и стохастичность характера движения ее компонентов; (2) необходимость отражения особенностей способа деаэрации (механического, пневматического или вибрационного [1–4]); (3) обеспечение достаточных условий совместного выполнения указанных операций при наличии взаимоисключающих факторов их протекания – дополнительного насыщения газом ингредиентов при их циркуляционном движении и минимизация объема несущей фазы уплотняемой смеси без упругопластической деформации частиц. В частности, получение деаэрированного порошкового продукта возможно при совмещении смешивания порошковых компонентов и уплотнения их смеси в пределах одного центробежного устройства за счет наличия его конструктивных особенностей и наблюдаемых инерционных эффектов.
ПОСТАНОВКА ЗАДАЧИ
Методы статистической механики неравновесных процессов удачно опробованы в моделях операций переработки твердофазных систем – смешивания [7] и измельчения зернистых сред, при изучении инерции тепла в нестационарных диссипативных структурах [8] и т.п. В настоящей работе теория марковских цепей используется для описания стохастического поведения реальной физической системы (сыпучей смеси) при совмещенных или последовательных смешивании и деаэрации.
Для марковского непрерывного процесса причинная связь между событиями, произошедшими в различные моменты времени, задается соотношением для соответствующих плотностей распределения. Разделим аналогично [8] смешиваемые ингредиенты нескольких сортов на два – “ключевой” и “транспортирующий” в зависимости от их инерционных свойств. В дальнейших обозначениях верхний индекс “1” принадлежит ключевому компоненту, “2” – транспортирующему. Пусть распределение вероятностей для системы твердых частиц смеси компонентов 1 и 2 ρ(η,t) при их уплотнении определяется произведением соответствующих плотностей в ходе протекания процессов деаэрации φ(η,t) и смешивания $c_{s}^{{\text{1}}}$(η,t) в зависимости от состояния системы η и времени t:
Функция (1) для плотности распределения вероятности последовательных изменений в дисперсной системе также должна удовлетворять уравнению Фоккера–Планка [9, 10], но в пренебрежении диффузионным (флуктуационным) членом, что объясняется допущением об отсутствии явления смешивания компонентов при уплотнении смеси:
(2)
$\begin{gathered} {{\partial [\varphi (\eta ,t)c_{s}^{1}(\eta ,t)]} \mathord{\left/ {\vphantom {{\partial [\varphi (\eta ,t)c_{s}^{1}(\eta ,t)]} {\partial t}}} \right. \kern-0em} {\partial t}} = \\ = \,\,{{ - \partial [{{\beta }_{1}}(\eta ,t)\varphi (\eta ,t)c_{s}^{1}(\eta ,t)]} \mathord{\left/ {\vphantom {{ - \partial [{{\beta }_{1}}(\eta ,t)\varphi (\eta ,t)c_{s}^{1}(\eta ,t)]} {\partial \eta }}} \right. \kern-0em} {\partial \eta }}. \\ \end{gathered} $В уравнении (2) функция β1(η,t) – момент частоты переходов w(η,t), который задается выражением
(3)
${{\beta }_{1}}(\eta ,t) = \int\limits_{ - \infty }^{ + \infty } {(\eta {\text{'}} - \eta )} w(\eta {\text{'}},\eta ;t)d\eta {\text{'}}$при разложении Крамерса–Мойала основного кинетического уравнения для распределения вероятностей, полученного из уравнения Чепмена–Колмогорова–Смолуховского [11] для переходной вероятности марковского процесса. Решение уравнения Фоккера–Планка (2) может соответствовать нормальному (гауссовскому) распределению вероятностей, которое позволяет строить функцию β1(η,t) в виде разложения в ряд по состояниям системы η [12]:
Известные непрерывные марковские процессы (Винера и Орнштейна–Уленбека) не удовлетворяют уравнению (2), так как первый из них соответствует диффузии, а второй – описывается функцией распределения, зависящей от произведения двух моментов частоты переходов β1(η,t), β2(η,t), где момент β2(η,t) входит во флуктуационный член уравнения Фоккера–Планка. Считая, что деаэрация смеси компонентов 1 и 2 представляется однородным марковским процессом, а значит, стационарным, частота переходов в выражении (3) есть w(η,η').
Известно, что дискретные распределения можно записать в форме непрерывных с помощью δ-функции Дирака [11]. Допускается двойственный характер искомого распределения φ(η,t) – дискретного по состояниям системы η и непрерывного по времени t, которое в одномерном случае аппроксимируется пуассоновским (n = 0.1,…,l)
(5)
${{\varphi }_{n}} = ({{\mu _{1}^{n}} \mathord{\left/ {\vphantom {{\mu _{1}^{n}} {n!}}} \right. \kern-0em} {n!}})\exp ( - {{\mu }_{1}})$и сводится к распределению Гаусса при выполнении условия 〈n〉 = μ1 [12]. Параметр μ1 можно оценить с помощью частоты переходов w(η,η') и разности времен Δt = t' – t с числом состояний системы η, равном n [9]:
Применяя свойство δ-функции Дирака $f(\eta ) = \int\limits_{ - \infty }^{ + \infty } {f(\eta {\text{'}})\delta (\eta {\text{'}} - \eta )} d\eta {\text{'}}$ для β1(η,t) из (4), после подстановки (4) в (3) частота переходов w(η,η') равна
(7)
$w(\eta ,\eta {\text{'}}) = ({{\gamma }_{0}} + {{\gamma }_{1}}\eta {\text{'}}){{(\eta {\text{'}} - \eta )}^{{ - 1}}}\delta (\eta {\text{'}} - \eta ).$Распространяя данный подход на случай многомерного процесса Пуассона (ni = 0,1,…, li; i = = 1,…, s) по $s$ видам ηi(ni)-состояний системы, при выполнении (4) имеем
(8)
$\begin{gathered} {{\varphi }_{{{{n}_{1}}...{{n}_{s}}}}} = \left( {\prod\limits_{i = 1}^s {\frac{{\mu _{{1i}}^{{{{n}_{i}}}}}}{{{{n}_{i}}!}}} } \right) \times \\ \times \,\,\exp \left( { - \sum\limits_{i = 1}^s {{{\mu }_{{1i}}}} } \right){{\left[ {\prod\limits_{i = 2}^s {} \sum\limits_{{{n}_{i}} = 1}^{li} {\frac{{\mu _{{1i}}^{{{{n}_{i}}}}}}{{{{n}_{i}}!}}\exp ( - {{\mu }_{{1i}}})} } \right]}^{{ - 1}}}. \\ \end{gathered} $В (8) по аналогии с выражениями (6) и (7) параметр μ1i оценивается как
где ni = 0, 1, …, k – 1, k, k + 1,…, li; Δt = tk + 1– tk. Значения коэффициентов γ0 и γ1 для одномерного процесса (или γ0i и γ1i для многомерного) зависят от режима протекания операций смешивания и уплотнения.ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Реализация деаэрации дисперсной смеси с учетом ее многокомпонентности при совмещении со смешиванием. Одним из показателей степени уплотнения порошков является коэффициент динамического уплотнения (процентное отношение значений насыпных плотностей среды после и до механической деаэрации) [4, 13]. Пусть характеристическая мера случайного процесса деаэрации сыпучей смеси по смыслу совпадает с данным коэффициентом динамического уплотнения без процентного расчета и равна случайной величине fV (η,t) – отношению объемов V0 и V(η,t), занимаемых системой твердых частиц в зависимости от состояний η в начальный и конечный (промежуточный) момент времени t:
(11)
${{f}_{V}}(\eta ,t) = {{V(\eta ,t)} \mathord{\left/ {\vphantom {{V(\eta ,t)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}.$Другая характеристика процесса уплотнения дисперсной среды – порозность α2, определяемая обычно в механике гетерогенных систем отношением плотностей однородного материала из двух фаз – приведенной плотности твердого скелета ρ2 к истинной – для вещества ρT [14]. Традиционно для методов описания многофазных сред [14] нижние индексы “1” и “2” присваиваются соответственно несущей и дисперсной фазам. Пористость α1 сыпучего материала устанавливает связь между плотностями газа в порах – приведенной ρ1 и истинной ρg:
(12)
${{\rho }_{2}} = {{\alpha }_{2}}{{\rho }_{T}},\,\,\,{{\rho }_{1}} = {{\alpha }_{1}}{{\rho }_{g}},\,\,\,{{\alpha }_{1}} + {{\alpha }_{2}} = 1.$Пусть каждый твердый скелет (фазы 2) j-го компонента смеси (j = 1,…, N) имеет истинную плотность вещества ${\rho }_{T}^{j},$ массу $m_{{\text{2}}}^{j},$ объем $V_{{\text{2}}}^{j} = {{m_{{\text{2}}}^{j}} \mathord{\left/ {\vphantom {{m_{{\text{2}}}^{j}} {{\rho }_{T}^{j}}}} \right. \kern-0em} {{\rho }_{T}^{j}}},$ объемную долю (концентрацию) $c_{V}^{j} = V_{2}^{j}{{\left( {\sum\limits_{j = 1}^N {V_{2}^{j}} } \right)}^{{ - 1}}}.$ Введем для системы твердые частицы–газ понятия приведенных плотностей фаз: ρ1(η,t) = = m1/V(η,t) – для несущей фазы массой m1; ${\rho }_{2}^{j} = {{m_{{\text{2}}}^{j}} \mathord{\left/ {\vphantom {{m_{{\text{2}}}^{j}} {V({\eta },t)}}} \right. \kern-0em} {V({\eta },t)}}$ – для j-й дисперсной фазы. Значения α1 и α2 определяются в более общем случае, чем при условном разделении твердых частиц на “транспортирующую” и “ключевую” составляющие из [8], т.е. согласно (11) и (12) с учетом многокомпонентности системы твердых частиц $N$ сортов:
(13)
${{\alpha }_{1}}(c_{V}^{j},\eta ,t) = {{{{\rho }_{c}}(c_{V}^{j},\eta ,t)} \mathord{\left/ {\vphantom {{{{\rho }_{c}}(c_{V}^{j},\eta ,t)} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}},$(15)
${{\rho }_{c}}(c_{V}^{j},\eta ,t) = {{\rho }_{1}}(\eta ,t) + \frac{{\sum\limits_{j = 1}^N {c_{V}^{j}\rho _{2}^{j}(\eta ,t)} }}{N},$величина q($c_{V}^{j}$) вычисляется по формуле
(16)
$q\left( {c_{V}^{j}} \right) = N\frac{{\sum\limits_{j = 1}^N {V_{2}^{j}\rho _{T}^{j}c_{V}^{j}} }}{{\left( {\sum\limits_{j = 1}^N {\rho _{T}^{j}c_{V}^{j}} } \right)\left( {\sum\limits_{j = 1}^N {V_{2}^{j}c_{V}^{j}} } \right)}}.$По аналогии с понятием проницаемости изотропной дисперсной системы твердые частицы–газ ([$k$] = 1 Д = 10–8 см2) [4, 14] можно ввести коэффициент газопроницаемости k для многокомпонентной сыпучей смеси и согласно (12) получить следующее соотношение:
(17)
${{\alpha }_{2}}\left( {c_{V}^{j},\eta ,t} \right) = \frac{{1 - {{{({k \mathord{\left/ {\vphantom {k {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}})}}^{{{1 \mathord{\left/ {\vphantom {1 {{{n}_{k}}}}} \right. \kern-0em} {{{n}_{k}}}}}}}}}{{(1 - {{\alpha }_{{20}}})}},$Таким образом, случайная порозность сыпучей смеси α2($c_{V}^{j},$ η, t) представлена в виде нелинейного преобразования (14) для случайного относительного изменения выделенного деаэрируемого объема fV (η,t) в форме (11) с распределением вероятностей последнего φ(η,t) в виде (5) или (8) соответственно для одномерной или многомерной реализации процесса уплотнения. Требуется построить распределение вероятностей для функции α2($c_{V}^{j},$ η, t) и вычислить его основные характеристики согласно методам теории вероятностей [15] с учетом режима протекания операций смешивания и уплотнения – совмещенного или последовательного.
Оценка параметров первого момента частоты переходов. Для решения указанных задач необходимо определить неизвестные коэффициенты γ0 и γ1 в формуле (7) для распределения вероятностей φn из (5) для одномерного процесса (или γ0i и γ1i в (10) для распределения вероятностей ${{\varphi }_{{{{n}_{{}}}_{1}...{{n}_{{}}}_{s}}}}$ из (8), (9) – для многомерного). В данном изложении ограничимся одномерным случаем с возможным 1обобщением предлагаемого метода оценки параметров γ0 и γ1 на многомерную задачу. Функция φn должна удовлетворять полученному из (2) уравнению
заменяемому разностным при достижении предельной степени уплотнения сыпучей смеси в момент времени tl ≡ τ:
(18)
$\left( {1 - \frac{{{{{\left. {{{\varphi }_{n}}} \right|}}_{{{{t}_{0}}}}}}}{{{{{\left. {{{\varphi }_{n}}} \right|}}_{\tau }}}}} \right)\left( {\frac{1}{\tau } + \frac{{{{\gamma }_{0}} + {{\gamma }_{1}}{{{\left. \eta \right|}}_{\tau }}}}{{{{{\left. \eta \right|}}_{{n = l}}} - {{{\left. \eta \right|}}_{{n = l - 1}}}}}} \right) + {{\gamma }_{1}} = 0.$При совмещении процессов смешивания и деаэрации сыпучей среды $c_{s}^{{\text{1}}}$(η,t) определяется из уравнения (2), тогда согласно (4) справедливо
При последовательных указанных операциях $c_{s}^{{\text{1}}}$ не зависит от состояния η и времени t, и уравнение (18) в начальный момент времени t0 с обозначением ${{\eta }_{0}} \equiv {{\left. \eta \right|}_{{n = 0}}}$ преобразуется к виду
(20)
$ - ({{\gamma }_{0}} + {{\gamma }_{1}}{{\eta }_{0}}){{\left. {\frac{{\partial {{\varphi }_{n}}}}{{\partial \eta }}} \right|}_{{{{\eta }_{0}}}}} + {{\gamma }_{1}}{{\left. {{{\varphi }_{n}}} \right|}_{{{{\eta }_{0}}}}} = 0.$Параметры γ0 и γ1 – решения систем уравнений (18), (19) или (18), (20) согласно выбранному режиму поведения твердых частиц смеси. Комбинация ${{{{{{{\left. {{{\varphi }_{n}}} \right|}}_{{{{t}_{0}}}}}} \mathord{\left/ {\vphantom {{{{{\left. {{{\varphi }_{n}}} \right|}}_{{{{t}_{0}}}}}} {\left. \varphi \right|}}} \right. \kern-0em} {\left. \varphi \right|}}}_{r}}$ из (18) также требует определения. Случайная порозность α2($c_{V}^{j},$ η, t) – результат нелинейного преобразования (14) fV (η,t). Учитывая дифференцируемость обеих этих функций, используем свойство их распределений вероятностей ψn и φn [11, 15]
(21)
$\frac{{{{\psi }_{{k - 1}}}}}{{{{\psi }_{k}}}} = \frac{{{{\varphi }_{{k - 1}}}}}{{{{\varphi }_{k}}}}{{\left[ {\frac{{{{\alpha }_{2}}({{\eta }_{k}},{{t}_{k}})}}{{{{\alpha }_{2}}({{\eta }_{{k - 1}}},{{t}_{{k - 1}}})}}} \right]}^{2}}.$Пользуясь приближением о равновероятных соседних состояниях для распределения ψn, из выражений (21) и (17) имеем
(22)
$\frac{{{{{\left. {{{\varphi }_{n}}} \right|}}_{{{{t}_{0}}}}}}}{{{{{\left. {{{\varphi }_{n}}} \right|}}_{\tau }}}} = \alpha _{{20}}^{2}{{\left[ {1 - (1 - {{\alpha }_{{20}}}){{{\left( {\frac{{{{k}_{0}}}}{{{{k}_{l}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 {{{n}_{k}}}}} \right. \kern-0em} {{{n}_{k}}}}}}}} \right]}^{{ - 2}}}.$Применение свойства дифференцирования для связи между распределениями вероятностей ψn и φn [11, 15] в виде (21) в приближении незначительных изменений ψn для соседних состояний, близких к начальному моменту времени, позволяет рассчитать значение
(23)
${{\left. {\frac{{\partial {{\varphi }_{n}}}}{{\partial \eta }}} \right|}_{{{{\eta }_{{_{0}}}}}}} = - \frac{{2{{\varphi }_{n}}\left| {_{{{{\eta }_{{_{0}}}}}}} \right.}}{{{{\alpha }_{{2d}}}\left| {_{{{{\eta }_{{_{0}}}}}}} \right.}}{{\left. {\frac{{\partial {{\alpha }_{{2d}}}}}{{\partial \eta }}} \right|}_{{{{\eta }_{{_{0}}}}}}},$где функция порозности α2d(ηi) = ${{N}^{{ - 1}}}\sum\limits_{j = 1}^N {c_{V}^{j}\alpha _{{2d}}^{j}({{\eta }_{i}})} $ определяется значениями объемных концентраций $c_{V}^{j}$ для каждого j-го компонента и их порозностей ${\alpha }_{{{\text{2}}d}}^{j}({{{\eta }}_{i}})$ из упругой модели деаэрации порошков [16]. Тогда при подстановке выражения (23) в уравнение (20) получим
(24)
$\frac{{2{{\gamma }_{0}}}}{{{{{\left. {{{\alpha }_{{2d}}}} \right|}}_{{{{\eta }_{0}}}}}}}{{\left. {\frac{{\partial {{\alpha }_{{2d}}}}}{{\partial \eta }}} \right|}_{{{{\eta }_{0}}}}} - {{\gamma }_{1}} = 0.$Учет (23) позволяет уравнение (20) привести к более удобной форме (24). Например, решение системы (18) и (20) или (18) и (21) для последовательных смешивания и деаэрации при одномерной реализации имеет вид ${{\gamma }_{0}} = {{\eta }_{l}}({{\alpha }_{{2d}}}\left| {_{{{{\eta }_{{_{0}}}}}}} \right.){{(\tau {{H}_{0}})}^{{ - 1}}}$ и ${{\gamma }_{1}} = 2{{\eta }_{l}}{{\left. {({{\partial {{\alpha }_{{2d}}}} \mathord{\left/ {\vphantom {{\partial {{\alpha }_{{2d}}}} {\partial \eta }}} \right. \kern-0em} {\partial \eta }})} \right|}_{{{{\eta }_{{_{0}}}}}}}{{(\tau {{H}_{0}})}^{{ - 1}}},$ где обозначено ηl ≡ ≡ η|n = l; H0 ≡ $2{{\eta }_{l}}{{\left. {({{\partial {{\alpha }_{{2d}}}} \mathord{\left/ {\vphantom {{\partial {{\alpha }_{{2d}}}} {\partial \eta }}} \right. \kern-0em} {\partial \eta }})} \right|}_{{{{\eta }_{0}}}}}[{{(2 - \phi )} \mathord{\left/ {\vphantom {{(2 - \phi )} {(\phi - 1)}}} \right. \kern-0em} {(\phi - 1)}}] - {{\alpha }_{{2d}}}\left| {_{{{{\eta }_{0}}}}} \right.;$ ${{{{{\left. {\phi \equiv {{\varphi }_{n}}} \right|}}_{{{{t}_{0}}}}}} \mathord{\left/ {\vphantom {{{{{\left. {\phi \equiv {{\varphi }_{n}}} \right|}}_{{{{t}_{0}}}}}} {{{{\left. {{{\varphi }_{n}}} \right|}}_{\tau }}}}} \right. \kern-0em} {{{{\left. {{{\varphi }_{n}}} \right|}}_{\tau }}}}.$ Поиск γ0 и γ1 для совмещенных смешивания и уплотнения сыпучих сред при решении системы (18) и (19) требует уточнения вида $c_{s}^{{\text{1}}}({\eta },t)$ из соответствующей стохастической модели смешивания.
Пример совмещения смешивания и деаэрации при работе центробежного устройств. Применим данную стохастическую модель при совмещении смешивания порошков двух сортов (с объемными концентрациями $c_{V}^{{\text{1}}}$ и $c_{V}^{{\text{2}}}$) и уплотнения их смеси в центробежном устройстве с эвольветными лопастями общим числом NL при вертикальной подаче материалов (рис. 1а) [16, 17]. Пусть R0 и r0 – радиусы кожуха и цилиндра, на котором закреплены данные лопасти, ω – угловая скорость вращения рабочей ячейки. Уравнения ${{r}_{{s1}}}({\text{q}})$ и rs2(θ) дуг M1K1 и K1M2 окружностей (с центрами O1 и N1; радиусами ρs1 и ρs2) при r0≤rs1 < ${{r}_{K}}_{{_{1}}}$; ${{r}_{K}}_{{_{1}}}$ ≤ rs1 ≤ R0 для лопасти M1M2 в полярной системе координат: ${{r}_{{s1}}}$ = ${{r}_{{{{O}_{1}}}}}\cos (\theta - {{\theta }_{{{{O}_{1}}}}})$ + ${{[\rho _{{s1}}^{2} - r_{{{{O}_{1}}}}^{2}{{\sin }^{2}}(\theta - {{\theta }_{{{{O}_{1}}}}})]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}};$ ${{r}_{{s2}}}$ = = ${{r}_{{{{N}_{1}}}}}\cos (\theta - {{\theta }_{{{{N}_{1}}}}})$ + ${{[\rho _{{s2}}^{2} - r_{{{{N}_{1}}}}^{2}{{\sin }^{2}}(\theta - {{\theta }_{{{{N}_{1}}}}})]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Параметры устройства задают угловые координаты точек рабочей ячейки: ${{\theta }_{{{{O}_{1}}}}} = {{\theta }_{{{{N}_{1}}}}} + \psi ;$ ψ = arccos × × $\{ {{{\text{[}}r_{{{{O}_{1}}}}^{2} + r_{{{{N}_{1}}}}^{2} - {{{({{\rho }_{{s2}}} - {{\rho }_{{s1}}})}}^{2}}]} \mathord{\left/ {\vphantom {{{\text{[}}r_{{{{O}_{1}}}}^{2} + r_{{{{N}_{1}}}}^{2} - {{{({{\rho }_{{s2}}} - {{\rho }_{{s1}}})}}^{2}}]} {(2{{r}_{{{{O}_{1}}}}}{{r}_{{{{N}_{1}}}}})}}} \right. \kern-0em} {(2{{r}_{{{{O}_{1}}}}}{{r}_{{{{N}_{1}}}}})}}\} ;$ ${{\theta }_{{{{N}_{1}}}}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{N}_{L}}}}} \right. \kern-0em} {{{N}_{L}}}};$ ${{\theta }_{{{{M}_{1}}}}} = {{\theta }_{{{{N}_{1}}}}} + {{\theta }_{{{{M}_{3}}}}};$ ${{\theta }_{{{{M}_{2}}}}} = {{\theta }_{{{{N}_{1}}}}} + {{\theta }_{{{{M}_{4}}}}}.$ В стохастической модели для смешивания сыпучих материалов [18] при введении переменной Лагранжа tL = θ + ωt для свободной границы среды H1H2 определены: ее уравнение ${{r}_{h}}(\theta ,{{t}_{L}})$ = ${{{{{{r}_{0}}[{{r}_{b}}({{\theta }_{{{{Q}_{2}}}}},{{t}_{L}})} \mathord{\left/ {\vphantom {{{{r}_{0}}[{{r}_{b}}({{\theta }_{{{{Q}_{2}}}}},{{t}_{L}})} {{{r}_{0}}]}}} \right. \kern-0em} {{{r}_{0}}]}}}^{{{{[\theta - {{\theta }_{{{{H}_{1}}}}}({{t}_{L}})]} \mathord{\left/ {\vphantom {{[\theta - {{\theta }_{{{{H}_{1}}}}}({{t}_{L}})]} {[{{\theta }_{{{{Q}_{2}}}}} - {{\theta }_{{{{H}_{1}}}}}({{t}_{L}})]}}} \right. \kern-0em} {[{{\theta }_{{{{Q}_{2}}}}} - {{\theta }_{{{{H}_{1}}}}}({{t}_{L}})]}}}}}$ при ${{\theta }_{{{{Q}_{2}}}}} = {{\theta }_{{{{M}_{2}}}}}$ и угловые координаты точек Q2 и H1. Согласно теоретико-экспериментальным исследованиям в рабочей ячейке между последовательными лопастями наблюдаются условные зоны – отсутствия материала I, активного смешения II, а также преимущественного транспортирования и уплотнения III (рис. 1) [16, 18]. Понимание механизма движения смеси порошков в последней зоне – конечная цель настоящего изложения. Предполагается равномерное распределение вероятностей по состояниям системы η1(n1), которые соответствуют движению условной границы раздела II и III зон Q1Q2, определяемой уравнением из упругой модели деаэрации порошков [16]:
(25)
$\begin{gathered} {{r}_{b}}(\theta ,t) = \left[ {{{r}_{0}}\left( {erf\frac{{{{r}_{{s2}}}(\theta )}}{{2R(t)}} - 1} \right)\exp \left( { - \frac{{r_{0}^{2}}}{{4{{R}^{2}}(t)}}} \right)} \right. - \\ - \,\,\left. {{{r}_{s}}(\theta )\left( {erf\frac{{{{r}_{0}}}}{{2R(t)}} - 1} \right)\exp \left( { - \frac{{r_{{s2}}^{2}(\theta )}}{{4{{R}^{2}}(t)}}} \right)} \right] \times \\ \times \,\,{{\left( {erf\frac{{{{r}_{{s2}}}(\theta )}}{{2R(t)}} - erf\frac{{{{r}_{0}}}}{{2R(t)}}} \right)}^{{ - 1}}}, \\ \end{gathered} $Рис. 1.
Схемы к расчету одномерного пуассоновского распределения вероятностей по состояниям ${{{\eta }}_{1}}({{n}_{1}})$ для изменения объема двухкомпонентной смеси порошков: (а) – движение в ячейке центробежного устройства с эвольветными лопастями; (б) – распределение полярных составляющих скоростей точек среды ${{C}_{k}}$ и ${{C}_{{k + 1}}}$ в состояниях системы ${{{\eta }}_{1}}(k)$ и ${{{\eta }}_{1}}(k + 1).$
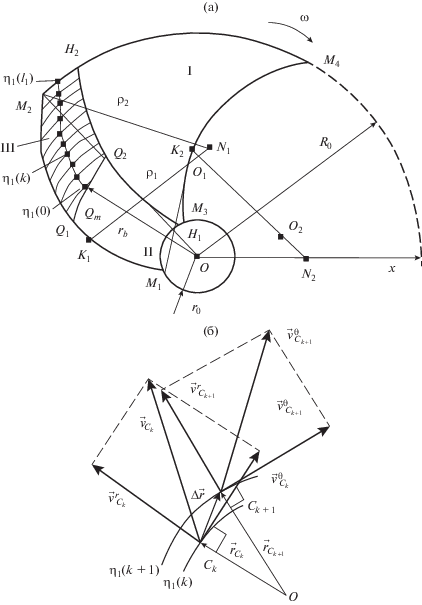
Здесь ${{\theta }_{{{{Q}_{2}}}}} \leqslant \theta \leqslant {{\theta }_{{{{Q}_{1}}}}};$ функция R = R(t) связана с коэффициентом макродиффузии D процесса смешивания двух тонкодисперсных компонентов и равна $R(t) \equiv \sqrt {2Dt} $ [16]. Применим соотношения (11) для случайной функции fV (η1,t) = V(η1,t)/V0 – отношения объемов V(η1,t) и V0, занимаемых в зависимости от изменения состояний системы при η1 $ \equiv $ η в конечный (промежуточный) и начальный моменты времени t.
Считается, что состояния системы в зоне III задаются значениями η1(n1), n1 = 0,1,…, l1 для координат точек ${{C}_{{{{n}_{1}}}}}$– середин дуг (участков окружностей радиусом ${{r}_{{C{{n}_{1}}}}} = O{{C}_{{{{n}_{1}}}}}$) между точками эвольвентной лопасти M1M2 и свободной границы среды H1H2 (рис. 1а). Точка C0 для n1 = 0 совпадает со средней точкой Qm на условной границе раздела Q1Q2 для зон II и III rb(θ,t), тогда реализация состояний ${{\eta }_{1}}({{n}_{1}}) = {{{{n}_{1}}({{R}_{0}} - {{r}_{{{{C}_{0}}}}})} \mathord{\left/ {\vphantom {{{{n}_{1}}({{R}_{0}} - {{r}_{{{{C}_{0}}}}})} {{{l}_{1}}}}} \right. \kern-0em} {{{l}_{1}}}},$ n1 = 0,1,…, l1 данной системы частиц описывается одномерным законом Пуассона (5):
(26)
${{\varphi }_{{{{n}_{1}}}}} = \left( {{{\mu _{{11}}^{{{{n}_{1}}}}} \mathord{\left/ {\vphantom {{\mu _{{11}}^{{{{n}_{1}}}}} {{{n}_{1}}!}}} \right. \kern-0em} {{{n}_{1}}!}}} \right)\exp ( - {{\mu }_{{11}}}),$(27)
$\begin{gathered} {{w}_{1}}\left( {{{\eta }_{1}}({{l}_{1}} - 1),{{\eta }_{1}}({{l}_{1}})} \right) = \\ = \frac{{{{\gamma }_{0}}_{1} + {{\gamma }_{{11}}}{{\eta }_{1}}({{l}_{1}})}}{{{{\eta }_{1}}({{l}_{1}}) - {{\eta }_{1}}({{l}_{1}} - 1)}}\delta \left( {{{\eta }_{1}}({{l}_{1}}) - {{\eta }_{1}}({{l}_{1}} - 1)} \right), \\ \end{gathered} $(28)
$\Delta t = \frac{{2\left| {\Delta {{r}_{{k,k + 1}}}} \right|}}{{{{{\left[ {{{{(v_{{Ck}}^{\theta } + v_{{Ck + 1}}^{\theta })}}^{2}} + {{{(v_{{Ck}}^{r} + v_{{Ck + 1}}^{r})}}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$Входящие в (28) модули приращения радиус-вектора Δrk, k + 1 и суммы скоростей ${{v}_{k}}$ и ${{v}_{{k + 1}}}$ точек Ck и Ck + 1 вычисляются при $v_{{Ck}}^{{\theta }} = \omega {{r}_{{Ck}}}$ и $v_{{Ck + {\text{1}}}}^{{\theta }} = {\omega }{{r}_{{Ck + {\text{1}}}}}$ согласно связи между составляющими скоростей точек уплотняемой среды $v_{{Ck}}^{{\theta }}$ = (kfωrCk + k1)/[ω(3 – – k2)] из упругой модели деаэрации порошков [16]. Коэффициенты kf, k1, k2 учитывают физико-механические характеристики деаэрируемых материалов и их трение о лопасти [17]. Обозначим Mk(rsk,Qsk) и Hk(rhk,Qhk) – выделенные наборы точек кривых: rs2(θ) – эвольвентной лопасти M1M2) и rh(θ,t') – свободной границы среды H1H2 (рис. 1). Значения углов θCk и α между линиями действия скоростей $v_{{Ck}}^{{\theta }}$ и $v_{{Ck + {\text{1}}}}^{{\theta }}$ (рис. 1б) задаются формулами θCk = (θMk + θHk)/2 и α = π – arcsin(χrCk) – arcsin(χrCk + 1), где χ = (Δr)–1sin(θCk – θCk+ 1). Модуль приращения радиус-вектора Δr0.1, когда n1 = 0 и точка C0 совпадает с Qm(rQm,θQm), равен $\left| {\Delta {{r}_{{0.1}}}} \right| = \{ {{({{r}_{{{{Q}_{m}}}}})}^{2}}$ + + ${{[{{r}_{{{{Q}_{m}}}}} + {{\eta }_{1}}(1)]}^{2}}$ – $2{{r}_{{{{Q}_{m}}}}}[{{r}_{{{{Q}_{m}}}}} + {{\eta }_{1}}(1)]\cos ({{\theta }_{{{{Q}_{m}}}}} - {{\theta }_{{C1}}}){{\} }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Таким образом, задав состояния системы при уплотнении смеси порошков в указанном устройстве при его работе в режиме совмещения со смешиванием, можно сформировать одномерное распределения вероятностей (26).
РЕЗУЛЬТАТЫ И ИХ ОБУЖДЕНИЕ
Одномерное пуассоновское распределение вероятностей для изменения объема двухкомпонентной смеси порошков. Согласно (13) и (14) с учетом (15) и (16) строятся функции для пористости ${{{\alpha }}_{{\text{1}}}}(c_{V}^{{\text{1}}},{\text{ }}c_{V}^{{\text{2}}},{\text{ }}{{{\eta }}_{{\text{1}}}},{\text{ }}t),$ порозности ${{{\alpha }}_{{\text{2}}}}(c_{V}^{{\text{1}}},{\text{ }}c_{V}^{{\text{2}}},{\text{ }}{{{\eta }}_{{\text{1}}}},{\text{ }}t)$ и плотности ${{{\rho }}_{c}}(c_{V}^{{\text{1}}},{\text{ }}c_{V}^{{\text{2}}},{\text{ }}{{{\eta }}_{{\text{1}}}},{\text{ }}t)$ указанной смеси с учетом вида fV (η,t). Оценка входящих в функцию частоты (27) параметров γ01 и γ11 при совмещенных смешивании и деаэрации связана с решением системы (18) и (19). Первое из них при значении времени $\tau = \sum\limits_{{{n}_{1}} = 0}^{{{l}_{1}}} {\Delta t({{n}_{1}})} {\text{:}}$
(29)
$\begin{gathered} {{\gamma }_{{11}}} = ({{\phi }_{1}} - 1)\left\{ {\tau {{\gamma }_{{01}}} + \left[ {{{\eta }_{1}}({{l}_{1}}) - {{\eta }_{1}}({{l}_{1}} - 1)} \right]} \right\} \times \\ \times \,\,{{\left( {\tau \left\{ {({{\phi }_{1}} - 1){{\eta }_{1}}({{l}_{1}}) - \left[ {{{\eta }_{1}}({{l}_{1}}) - {{\eta }_{1}}({{l}_{1}} - 1)} \right]} \right\}} \right)}^{{ - 1}}}, \\ \end{gathered} $Второе уравнение системы для поиска γ01 и γ11 с учетом времени смешивания ts – результат подстановки момента β1(η10,t0) в (19), тогда
(30)
${{\gamma }_{{01}}} = - \frac{{{{\partial c_{s}^{1}({{\eta }_{1}},t)} \mathord{\left/ {\vphantom {{\partial c_{s}^{1}({{\eta }_{1}},t)} {\partial t}}} \right. \kern-0em} {\partial t}}}}{{{{\partial c_{s}^{1}({{\eta }_{1}},t)} \mathord{\left/ {\vphantom {{\partial c_{s}^{1}({{\eta }_{1}},t)} {\partial {{\eta }_{1}}}}} \right. \kern-0em} {\partial {{\eta }_{1}}}}}}\left| {_{\begin{subarray}{l} {{t}_{s}} \\ {{\eta }_{{_{1}}}}(0) \end{subarray} }} \right..$Распределение плотностей вероятностей для протекания процесса смешивания $c_{s}^{{\text{1}}}({{{\eta }}_{{\text{1}}}},t)$ соответствует функции удельной концентрации ключевого компонента c(r, θ, tL) в полярных координатах (r, θ) из соответствующей стохастической модели в центробежном устройстве [15]:
(31)
$c(r,\theta ,{{t}_{L}}) = \frac{{F(r,{{t}_{L}}) - F({{r}_{b}}(\theta ,{{t}_{L}}),{{t}_{L}})}}{{F({{r}_{0}},{{t}_{L}}) - F({{r}_{b}}(\theta ,{{t}_{L}}),{{t}_{L}})}},$Таким образом, при совмещении смешивания и уплотнения порошков в центробежном устройстве с эвольвентными лопастями для случайной величины fV (η,t) с учетом (27), (29) и (30) построено одномерное распределение вероятностей ${{\varphi }_{{{{n}_{1}}}}}$ вида (26) в зависимости от непрерывного времени $t$ и дискретных состояний системы η1(n1), когда n1 = 0,1,…, l1. Для удобства анализа результатов модели выбраны следующие моменты времени t(nt) = nt τ/lt при nt = 0,1,…, lt и равенстве значений lt и li.
Предложенную модель проиллюстрируем на примере построения ${{\varphi }_{{{{n}_{1}}}}}$ при деаэрации смеси каолина ГОСТ 21235-75 и технического углерода П803 ГОСТ 7885-86 в центробежном устройстве с эвольвентными лопатками. Характеристики распределения Пуассона (26) (γ01 = 3.46 × 10–1; γ01 = = 1.278 × 101; w1 = 9.275 × 101) для случайной величины fV (η,t) представлены в табл. 1. Данные о состояниях системы приведены в табл. 2.
Таблица 1.
Характеристики одномерного распределения Пуассона ${{\varphi }_{{{{n}_{1}}}}}$ для ${{f}_{V}}({{\eta }_{1}},t)$ смеси каолина ГОСТ 21235-75 и технического углерода П803 ГОСТ 7885-86
| ${{n}_{t}}$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| $t({{n}_{t}})$, с | 5.91 | 6.34 | 7.02 | 7.19 | 7.87 | 0.98 | 8.56 | 9.29 | 10.07 |
| ${{\mu }_{{11}}}$ | 4.82 | 5.49 | 5.88 | 6.52 | 7.15 | 7.79 | 7.46 | 9.19 | 9.99 |
Таблица 2.
Расчетные данные о состояниях рассматриваемой системы твердых частиц для смеси каолина ГОСТ 21235-75 и технического углерода П803 ГОСТ 7885-86
| ${{n}_{1}}$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| ${{\eta }_{1}}({{n}_{1}}) \times {{10}^{{ - 1}}}$, с | 0.09 | 0.19 | 0.29 | 0.39 | 0.49 | 0.59 | 0.69 | 0.78 | 0.89 | 0.99 |
| ${{r}_{C}}({{n}_{1}}) \times {{10}^{{ - 1}}}$, м | 1.81 | 1.91 | 2.01 | 2.11 | 2.21 | 2.31 | 2.40 | 2.50 | 2.60 | 2.70 |
| ${{\theta }_{C}}({{n}_{1}})$, рад | 1.72 | 1.64 | 1.56 | 1.48 | 1.39 | 1.32 | 1.24 | 1.16 | 1.08 | 1.00 |
| $v_{C}^{r}({{n}_{1}})$, м/c | 2.27 | 2.26 | 2.26 | 2.26 | 2.26 | 2.26 | 2.26 | 2.26 | 2.26 | 2.26 |
| $v_{C}^{\theta }({{n}_{1}})$, м/c | 4.75 | 5.01 | 5.27 | 5.52 | 5.78 | 6.04 | 6.29 | 6.56 | 6.81 | 7.07 |
| $\Delta r \times {{10}^{{ - 1}}}$, м | – | 0.18 | 0.18 | 0.19 | 0.09 | 0.19 | 0.21 | 0.22 | 0.23 | 0.25 |
| $\Delta t({{n}_{1}}) \times {{10}^{{ - 1}}}$, с | – | 0.71 | 0.43 | 0.68 | 0.17 | 0.68 | 0.69 | 0.72 | 0.78 | 0.88 |
Физико-механические параметры смешиваемых компонентов были следующими: для каолина ${\rho }_{T}^{{\text{1}}}$ = 2.6 × 103 кг/м3; λ1 = 5.1 × 105 Па; μ1 = 3.1 × × 105 Па; для технического углерода ${\rho }_{T}^{{\text{2}}}$ = 1.875 × × 103 кг/м3; λ2 = 5.6 × 104 Па; μ2 = 3.7 × 104 Па [4]. Значения геометрических параметров ячейки аппарата с эвольвентными лопастями: R0 = 2.7 × 10–1 м; r0 = 7.0 × 10–2 м; NL = 6; ${{r}_{{{{O}_{1}}}}}$ = 1.5 × 10–1 м; ${{r}_{{{{N}_{1}}}}}$ = 1.0 × × 10–1 м; ρs1 = 1.45 × 10–1 м; ρs2 = 1.95 × 10–1 м. Режимный параметр ω = 20.6 с–1; динамические характеристики деаэрации смеси: начальная радиальная скорость vr0 = 1.85 м/с; коэффициент проскальзывания смеси вдоль лопасти β = 9.765 × × 10–6 м2/(Па с) и коэффициент газопроницаемости среды k0 = 8.7 $ \times $ 10–12 м2 при $c_{V}^{{\text{1}}} = c_{V}^{{\text{2}}} = 0.{\text{5}}$ и эмпирической константе nk = 4.1 в формуле (22) [17]. Константы имели следующие значения: kf = 6.671 × × 10–1 с–1; k1 = 3.32 × 104 с–2; k2 = 9.372 × 102. Полученные одномерные распределения вероятностей ${{\varphi }_{{{{n}_{1}}}}}$ для fV (η,t), дискретные по состояниям системы η1 и непрерывные по t, представлены на рис. 2.
Рис. 2.
Распределения вероятностей ${{{\varphi }}_{{{{n}_{1}}}}}$ случайной величины ${{f}_{V}}({{\eta }_{1}},t)$ при фиксированных значениях временного параметра $({{l}_{1}} = {{l}_{t}} = 10)$ для деаэрации смеси каолина ГОСТ 21235-75 и технического углерода П803 ГОСТ 7885-86 ($c_{V}^{1} = c_{V}^{2} = 0.5$) в центробежном устройстве с эвольвентными лопастями.
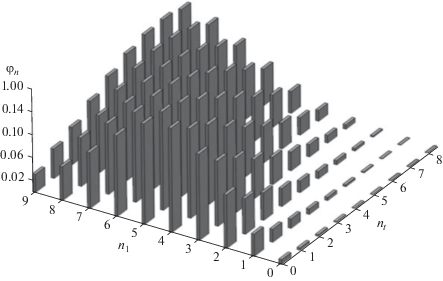
Дискретные распределения по состояниям η1(n1) для системы (n1 = 0,1,…, l1) в фиксированные моменты времени $t$, равные $t({{n}_{1}})$ при nt = = 0,1,…, lt; lt = li, показывают, с какой вероятностью будет происходить изменение некоторого объема однородной смеси порошков – ограниченного интервалом по оси абсцисс от η1(k) до η1(k + 1) при n1 = 0,1,…,k – 1, k, k + 1,…, l1 – от ${{V}_{0}} = V({{\eta }_{1}}(0),t(0))$ до $V({{\eta }_{1}}(k + 1),t(k + 1))$ при деаэрации порошковой смеси в ячейке центробежного устройства с эвольвентными лопатками. Переход смеси в зону III осуществляется при пересечении условной границы раздела зон II и III, когда начальный момент t(0) практически равен времени смешивания, а изменение объема материала, соответствующего отрезку [η1(0); η1(1)], незначительное. Вероятность изменить существенно свой объем при t(0) максимальна для срединной зоны III. С течением времени именно в этой области (${{{{n}_{1}} \sim {{l}_{1}}} \mathord{\left/ {\vphantom {{{{n}_{1}} \sim {{l}_{1}}} 2}} \right. \kern-0em} 2}$) наблюдается значительная деаэрация материала, а при t(l1) в конечном состоянии для fV (η,t), естественно, распределение вероятностей достигает своего максимума, характеризуя завершение уплотнения смеси.
Поиск основных моментов распределения вероятностей для случайной порозности смеси в центробежном устройстве. Функциональные преобразования для случайной величины α2[fV (η,t)] при η1(n1) в формах ${{\psi }_{{{{n}_{{}}}_{1}}}} = \mathop {\lim }\limits_{\Omega \to \infty } {{(2\Omega )}^{{ - 1}}}$$\int\limits_{ - \Omega }^\Omega {\exp \left\{ { - z{{\alpha }_{2}}({{n}_{1}})} \right\}} {{M}_{{_{{{{\alpha }_{2}}}}}}}(z)dz$ или $\psi ({{\eta }_{1}}) = {{(2\pi )}^{{ - 1}}}$$\int\limits_{ - \infty }^u {\exp \left\{ { - z{{\alpha }_{2}}({{\eta }_{1}})} \right\}} {{M}_{{{{\alpha }_{2}}}}}(z)dz$ определяют дискретную ${{\psi }_{{{{n}_{1}}}}}$ или непрерывную ψ(η1) функции распределения вероятностей, тогда согласно [11, 15] представление производящих функций моментов имеет вид
(32)
$\begin{gathered} {{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u) \equiv \left\langle {M\exp \left[ {u{{\alpha }_{2}}({{n}_{1}})} \right]} \right\rangle \equiv \\ \equiv \int\limits_{ - \infty }^\infty {\exp \left[ {u{{\alpha }_{2}}({{n}_{1}})} \right]d} \Phi ({{n}_{1}}) = \\ = \sum\limits_{{{n}_{1}}} {{{\varphi }_{{{{n}_{1}}}}}\exp \left[ {u{{\alpha }_{2}}({{n}_{1}})} \right]} . \\ \end{gathered} $Определим основные моменты распределения вероятностей для случайной порозности – математического ожидания 〈Mα2[fV (η,t)]〉 и дисперсии 〈Dα2[fV (η,t)]〉 нелинейного преобразования α2[fV (η,t)] случайной величины fV (n1) при условии аналитичности производящей функции моментов ${{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)$ в окрестности точки u = 0. Допустимы разложения [11] $\ln {{M}_{{{{{\alpha }}_{2}}}}}(u)$ = = $\sum\limits_{{\nu } = 1}^\infty {\left\langle {{{x}_{\nu }}} \right\rangle } {{u}^{{\nu }}}{{(\nu !)}^{{ - 1}}}$ и ${{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)$ = $\sum\limits_{{\nu } = 0}^\infty {\left\langle {{{a}_{{\nu }}}} \right\rangle } {{u}^{{\nu }}}{{(\nu !)}^{{ - 1}}},$ где 〈xr〉 = = ${{\left. {[{{{{d}^{{(r)}}}{\kern 1pt} \ln {{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)} \mathord{\left/ {\vphantom {{{{d}^{{(r)}}}{\kern 1pt} \ln {{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)} {d{{u}^{{(r)}}}}}} \right. \kern-0em} {d{{u}^{{(r)}}}}}]} \right|}_{{u = 0}}};$ 〈ar〉 = $[{{{{d}^{{(r)}}}{{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)} \mathord{\left/ {\vphantom {{{{d}^{{(r)}}}{{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)} {d{{u}^{{(r)}}}}}} \right. \kern-0em} {d{{u}^{{(r)}}}}}]{\kern 1pt} \left| {_{{u = 0}}} \right.$ – семиинварианты. Результат нелинейного преобразования fV (η1(n1),t) – при n1 = 0,1,…, l1 и изменении состояний η1(n1) – случайная порозность α2[fV (η,t)] из (32). Найдем связь между отношением объемов ${{V}_{{{{n}_{1}}0}}} \equiv {{V}_{{{{n}_{1}}}}}({{\eta }_{1}}(0),0)$ и ${{V}_{{{{n}_{1}}}}} \equiv {{V}_{{{{n}_{1}}}}}[{{\eta }_{1}}({{n}_{1}}),t({{n}_{1}})],$ занимаемых данной системой в начальный и промежуточный момент времени t на любом участке оси абсцисс от η1(k) до η1(k + 1), согласно рис. 1, если k принадлежит последовательности n1 = = 0,1,…,k – 1, k, k + 1,…, l1:
(33)
$\begin{gathered} \frac{{{{V}_{{{{n}_{1}}0}}}}}{{{{V}_{{{{n}_{1}}}}}[{{\eta }_{1}}(k),t(k)]}} = \\ = \frac{{{{\theta }_{{{{N}_{1}}}}}\left\{ {{{{[{{r}_{b}}(k) + \Delta {{\eta }_{1}}(k + 1)]}}^{2}} - {{{[{{r}_{b}}(k) + \Delta {{\eta }_{1}}(k)]}}^{2}}} \right\}}}{{\Delta {{\theta }_{{sh}}}(k)[{{r}_{b}}(k) + \Delta {{\eta }_{1}}(k + 1)] + {{2}^{{ - 1}}}\Delta {{\eta }_{1}}\Delta {{\delta }_{{sh}}}(k)}}. \\ \end{gathered} $В (33), учитывая вид кривых rs2(θ), rh(θ,t') и rb(θ,t), справедливо следующее: ${{r}_{{{{n}_{1}}}}} = {{r}_{{{{Q}_{m}}}}}$ – ‒ n1[η1(l1) – η1(l1 – 1)]; rb(n1) ≡ rb(θ(n1),t(n1)); Δη1≡ ≡ η1(l1) – η1(l1 – 1); Δθsh(n1) ≡ θs2(n1) – θh(n1); Δδsh(n1) ≡ δs2 – δh; δs2≡ 2rk sin{2–1[θs2(rk) – θs2(rk + 1)]}; δh≡ 2rk sin{2–1[θh(rk) – θh(rk + 1)]}.
После разложения в ряд Маклорена зависимостей Δδsh, δs2 и δh от n1 в пренебрежении квадратичными членами случайная порозность согласно (14), (16) и (33) представляется в форме
(34)
${{\alpha }_{2}}({{n}_{1}}) = \frac{{q{{b}_{0}}({{b}_{1}} + {{n}_{1}})}}{{{{b}_{2}} + {{n}_{1}}({{b}_{3}} + {{n}_{1}})}},$(35)
$\begin{gathered} {{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u) = \exp ( - {{\mu }_{{11}}}) \times \\ \times \,\,\sum\limits_{{{n}_{1}}} {\left( {\frac{{\mu _{{11}}^{{{{n}_{1}}}}}}{{{{n}_{1}}!}}} \right)} \exp [uq{{b}_{0}}\varepsilon ({{n}_{1}})], \\ \end{gathered} $где комбинация (b1 + n1)/[b2 + n1(b3 + n1)] ≡ ε(n1) после разложения в ряд Маклорена при введении ${{R}_{{{{n}_{1}}}}} = \sum\limits_{r = 2}^\infty {{{(r!){{d}^{r}}\varepsilon ({{n}_{1}})} \mathord{\left/ {\vphantom {{(r!){{d}^{r}}\varepsilon ({{n}_{1}})} {dn_{1}^{r}}}} \right. \kern-0em} {dn_{1}^{r}}}} $ допускает представление
(36)
$\varepsilon ({{n}_{1}}) = \frac{{{{b}_{1}} - (1 - {{b}_{1}}{{b}_{3}}){{n}_{1}}}}{{{{b}_{2}}}} + {{R}_{{{{n}_{1}}}}}.$Оценка ${{b}_{1}}{{b}_{2}} \sim ({{b}_{2}} + {{b}_{1}}{{b}_{3}}){{b}_{3}}$ позволяет пренебречь слагаемым ${{R}_{{{{n}_{1}}}}}$ в (36). Пользуясь (36) и $\sum\limits_{{{n}_{1}} = 1}^\infty {{{\mu _{{11}}^{{{{n}_{1}}}}} \mathord{\left/ {\vphantom {{\mu _{{11}}^{{{{n}_{1}}}}} {{{n}_{1}}}}} \right. \kern-0em} {{{n}_{1}}}}!} = \exp ({{\mu }_{{11}}}),$ при обозначении ξ1 ≡ qb0b1/b2 и ξ2≡ qb0(1 – b1b3)/$b_{{\text{2}}}^{{\text{2}}}$ получим приближение для (35):
(37)
${{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u) = \exp \{ u{{\xi }_{1}} + {{\mu }_{{11}}}[\exp (u{{\xi }_{2}}) - 1]\} .$Последовательность производящих функций в выражении (37) сходится к непрерывной относительно переменной u производящей функции моментов ${{M}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)$ для α2(n1) в виде (37), что позволяет согласно обратной предельной теореме [11] считать, что существует некоторая функция распределения ψ(u), к которой также сходится последовательность функций распределения ψ(η1(n1)), определяемая формулой обращения
(38)
$\begin{gathered} \psi (u) = {{(2\pi )}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\int\limits_{ - \infty }^u {\exp \{ z{{\xi }_{1}} + {{\mu }_{{11}}}[\exp (z{{\xi }_{2}}) - 1]\} dz} . \\ \end{gathered} $Математическое ожидание, дисперсия, семиинвариант порядка r = 3 для ${{\alpha }_{2}}({{n}_{1}})$ с учетом вида производящей функции (37) и функции распределения (38) равны
(39)
$\begin{gathered} \left\langle {M{{\alpha }_{2}}[{{f}_{V}}({{n}_{1}})]} \right\rangle = \left\langle {{{a}_{1}}} \right\rangle = \\ = \,\,\left\langle {{{x}_{1}}} \right\rangle = {{\xi }_{1}}\left[ {1 + {{\mu }_{{11}}}(1 - {{b}_{1}}{{b}_{3}})} \right], \\ \end{gathered} $(40)
$\begin{gathered} \left\langle {D{{\alpha }_{2}}[{{f}_{V}}({{n}_{1}})]} \right\rangle = \left\langle {{{x}_{2}}} \right\rangle = {{\mu }_{{11}}}\xi _{2}^{2}, \\ \left\langle {{{x}_{3}}} \right\rangle = {{\left. {\frac{{{{d}^{3}}\ln {{{\text{M}}}_{{{{{\alpha }}_{{\text{2}}}}}}}(u)}}{{d{{u}^{3}}}}} \right|}_{{s = 0}}} = {{\mu }_{{11}}}\xi _{2}^{3}. \\ \end{gathered} $Основные расчетные параметры, используемые при получении уравнений искомых поверхностей (рис. 3) для зависимостей 〈Mα2[fV(n1)]〉 и 〈Dα2[fV(n1)]〉 из (39), (40) приведены в табл. 3. Анализ указанных поверхностей показывает, что они расположены в порядке смены ${{n}_{1}}$ – состояния системы. Необходимо отметить существенное влияние объемных концентраций компонентов смеси на величину 〈Mα2[fV(n1)]〉 и удовлетворительное согласие полученных данных и опытных показателей [18] деаэрации смеси с относительной ошибкой, не превышающей 9.8%. Результаты моделирования позволяют прогнозировать значения порозности смеси порошков в зависимости от объемных концентраций ее компонентов.
Рис. 3.
Зависимости основных моментов от объемных концентраций для деаэрации смеси каолина ГОСТ 21235-75 и технического углерода П803 ГОСТ 7885-86 в центробежном устройстве с эвольвентными лопастями: (а) – математическое ожидание $\left\langle {M{{\alpha }_{2}}[{{f}_{V}}({{n}_{1}})]} \right\rangle $; (б) – дисперсия $\left\langle {D{{\alpha }_{2}}[{{f}_{V}}({{n}_{1}})]} \right\rangle $, ${{n}_{1}} = 0$ (1, 1'); ${{n}_{1}} = 5$ (2, 2 '); ${{n}_{1}} = 9$ (3, 3 ') .
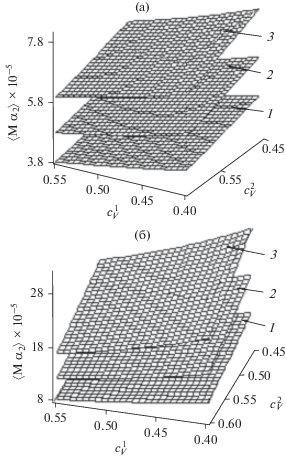
Таблица 3.
Основные коэффициенты для расчета зависимостей $\left\langle {M{{\alpha }_{2}}[{{f}_{V}}({{n}_{1}})]} \right\rangle $ и $\left\langle {D{{\alpha }_{2}}[{{f}_{V}}({{n}_{1}})]} \right\rangle $
| ${{v}_{1}} \times {{10}^{{ - 1}}}$, м | ${{v}_{2}} \times {{10}^{{ - 2}}}$, м | ${{g}_{1}} \times {{10}^{{ - 3}}}$ | ${{g}_{2}} \times {{10}^{{ - 4}}}$ | ${{c}_{0}} \times {{10}^{{ - 2}}}$, м | ${{c}_{1}} \times {{10}^{{ - 3}}}$, м | ${{c}_{3}} \times {{10}^{{ - 3}}}$, м | ${{\theta }_{{{{N}_{1}}}}},$ рад |
|---|---|---|---|---|---|---|---|
| 3.53 | 1.97 | 5.78 | 1.96 | 2.71 | –9.01 | –2.24 | 1.047 |
ЗАКЛЮЧЕНИЕ
Предложенная модель деаэрации сыпучих материалов в совмещенных или последовательных процессах со смешиванием обладает следующими особенностями: (1) описывает поведение системы твердых частиц от ее состояния и времени; (2) учитывает неоднородность уплотняемой среды и взаимодействия удаляемого газа с частицами твердого скелета; (3) применима при различных способах смешивания и деаэрации сыпучих материалов (механическом, вибрационном и пневматическом).
Кроме того, исследован механизм поведения твердых дисперсных сред на примере совмещения их смешивания и деаэрации в объеме центробежного устройства.
Полученные результаты могут быть использованы в качестве теоретической базы при разработке инженерных методов расчета нового оборудования с последовательным или совмещенным выполнением операций смешивания и деаэрации порошковых смесей, например, механических аппаратов различных типов (центробежных устройств с криволинейными лопастями, валково-ленточных агрегатов и т.д.).
В частности, метод оптимизации конструктивно-режимных параметров устройства для совмещения операций смешивания и деаэрации порошков, приведенный в работе [19], может быть дополнен результатами настоящей работы при формировании трех видов функции цели с достижением: (1) максимальных значений степени уплотнения смеси сыпучих компонентов и давления газа в ее порах; (2) максимальной производительности и минимальной мощности привода; (3) максимальной производительности и минимального коэффициента неоднородности смеси. При этом последние две целевые функции моделируются с одинаковым режимным параметром – угловой скоростью вращения рабочей ячейки центробежного устройства. Разбивая на несколько стадий расчет указанных целевых функций по их числу, в зависимости от оценки случайной порозности получаемой смеси сыпучих компонентов с учетом, с одной стороны, коэффициента газопроницаемости, а с другой, параметра макродиффузии смешиваемых компонентов, последовательно в каждом случае проводится отыскание локализации точки оптимума градиентным методом.
Указанный способ моделирования совмещенных процессов смешивания и деаэрации сыпучих компонентов и их смесей может быть использован для оценки случайной порозности: при упаковке таких материалов, как сажа, каолин, различного рода тонкодисперсных химических средств защиты растений, строительных порошковых продуктов; при изготовлении уплотненных гранул-сфер в производстве сажи, сухих красок, компонентов асфальтобетона; при деаэрации сыпучих смесей.
ОБОЗНАЧЕНИЯ
| 〈ar〉 | момент порядка r |
| c | концентрация ключевого компонента |
| $c_{s}^{{\text{1}}}({\eta },t)$ | плотность вероятности распределения системы твердых частиц (смеси компонентов 1 и 2) при смешивании в зависимости от ee состояния η и времени t |
| $c_{V}^{j}$ | объемная доля (концентрация) j-го компонента смеси |
| D | коэффициент макродиффузии, м2/c |
| 〈Dα2〉 | дисперсия случайной функции порозности |
| fV (η,t) | характеристическая мера случайного процесса деаэрации сыпучей смеси |
| k | коэффициент газопроницаемости, м2 |
| k0 | начальное значение коэффициента газопроницаемости, м2 |
| l (li) | число состояний системы для одномерного (многомерного) пуассоновского распределения при n = 0,1,…, l (при ni = 0,1,…, li) |
| m1 | масса несущей фазы 1 смеси, кг |
| mj2 | масса j-го компонента смеси как фазы 2 ее твердого скелета, кг |
| 〈Mα2〉 | математическое ожидание случайной функции порозности |
| ${{M}_{{{{{\alpha }}_{{\text{2}}}}}}}$ | производящая функция моментов для порозности смеси |
| N | число компонентов смеси |
| NL | число эвольвентных лопастей центробежного устройства |
| n | номер состояния системы в одномерном пуассоновском распределении |
| ni | i-й номер состояния системы ηi(ni) для многомерного процесса Пуассона |
| R0 (r0) | радиусы кожуха (цилиндра, на котором закреплены лопасти) центробежного устройства, м |
| r | радиальная координата в полярной системе |
| rs1(θ) и rs2(θ) | уравнение дуг M1K1 и K1M2 эвольвентной лопасти, м |
| rh(θ,tL) | уравнение свободной границы H1H2 смеси, м |
| rb(θ,t) | уравнение условной границы Q1Q2 для раздела зон движения смеси II и III в рабочем объеме центробежного устройства, м |
| s | число видов состояний ηi(ni) системы с номером ni для многомерного процесса Пуассона (i = 1,…,s) |
| t | время, с |
| tL | переменная Лагранжа tL = θ + ωt, рад |
| ts | время смешивания, с |
| Δt | промежуток времени, например, (Δt=t' – t) между соседними состояниями системы η и η', с |
| V(η,t) | объем, занимаемый системой твердых частиц в зависимости от состояний η в конечный (промежуточный) момент времени t |
| V0 | объем, занимаемый системой твердых частиц в начальный момент времени t |
| $V_{{\text{2}}}^{j}$ | объем j-го компонента смеси как фазы 2 ее твердого скелета, м3 |
| $v$ | скорость, м / с |
| w(η,t) | частота переходов системы |
| 〈xr〉 | семиинвариант порядка r |
| α1(α2) | пористость (порозность) дисперсной системы |
| α2d | порозность дисперсной системы из упругой модели деаэрации |
| β | коэффициент проскальзывания, м2/(Па с) |
| β1(η,t) | момент частоты переходов w(η,t) системы, линейный по ее состояниям η |
| β2(η,t) | момент частоты переходов w(η,t) системы, входящий во флуктуационный член уравнения Фоккера–Планка |
| γ0, γ1 | параметры разложения для момента β1(η,t) по состояниям системы η |
| δ | функция Дирака |
| η | состояния системы твердых частиц смеси компонентов 1 и 2 |
| ηi | i-е состояние системы |
| ηi(ni) | i-е состояние системы с номером ni для многомерного процесса Пуассона |
| θ | угловая координата в полярной системе, рад |
| λi, μi | коэффициенты Ламе для i-го компонента смеси, Па |
| μ1(μ1i) | параметр одномерного (многомерного) пуассоновского распределения для системы (i-го вида ее состояния) |
| ρ(η,t) | распределение вероятностей для системы твердых частиц (для смеси компонентов 1 и 2) при их уплотнении в зависимости от состояния системы η и времени t |
| ρ1(ρ2) | приведенная плотность несущей (дисперсной) фазы, кг/м3 |
| ρ1 (η,t) | приведенная плотность несущей фазы 1 смеси в зависимости от состояния системы η и времени t, кг/м3 |
| ${\rho }_{{\text{2}}}^{j}({\eta },t)$ | приведенная плотность j-го компонента смеси как ее дисперсной фазы 2 в зависимости от состояния системы η и времени t, кг/м3 |
| ρc | плотность смеси, кг/м3 |
| ρg(ρT) | истинная плотность газа (материала), кг/м3 |
| ρs1(ρs2) | радиус дуги M1K1 (K1M2) эвольвентной лопасти, м |
| ${\rho }_{T}^{j}$ | истинная плотность j-го компонента смеси, кг/м3 |
| τ | момент времени, когда достигается предельное значение степени уплотнения сыпучей смеси, с |
| φ(η,t) | плотность вероятности для системы твердых частиц (для смеси компонентов 1 и 2) при деаэрации в зависимости от состояния системы η и времени t |
| φn | одномерное пуассоновское распределение вероятностей по состояниям системы с номером n для случайной величины fV |
| ${{\varphi }_{{{{n}_{1}}...{{n}_{s}}}}}$ | многомерное пуассоновское распределение вероятностей по s видам состояний системы с номерами ni, i = 1,…,s |
| ψn | одномерное распределение вероятностей по состояниям системы с номером n для случайной порозности α2 |
| ω | угловая скорость, с–1 |
ИНДЕКСЫ
| верхние | |
| –1, ±1/2, 2, 3, n1, 1/nk, $v$ | степень |
| j | номер компонента смеси (j = 1,…,N) |
| r | радиальная составляющая |
| θ | окружная составляющая, рад |
| нижние | |
| 0 | начальные условия |
| 1 | несущая фаза |
| 2 | дисперсная фаза |
| с | смесь |
| i | номер вида состояния ${{\eta }_{i}}({{n}_{i}})$ системы для многомерного процесса Пуассона (i = 1,…,s) |
| n, ni | номер состояния системы |
| t | время |
| T | твердый скелет |
| V | объем |
Список литературы
Akiyama T., Miyamoto Y., Yamanaka N., Zhang J.Q. Densification of Powders by Means of Air, Vibratory and Mechanical Compactions // Powder Technol. 1986. V. 46. P. 173.
Генералов М.Б., Классен П.В., Степанова А.Р., Шомин И.П. Расчет оборудования для гранулирования минеральных удобрений. М.: Машиностроение, 1984.
Генералов М.Б. Механика твердых дисперсных сред в процессах. Калуга: Изд-во Н. Бочкаревой, 2002.
Капранова А.Б., Зайцев А.И. Механическое уплотнение тонкодисперсных материалов. М.: Экон-информ, 2011.
Kovalev O.B., Kovaleva I.O Simulation of random packing of the bulk layer of polydisperse spherical particles // J. Appl. Mech. Tech. Phys. 2014. Т. 55. № 4. P. 184. [Ковалев О.Б., Ковалева И.О. Моделирование случайной упаковки насыпного слоя полидисперсных сферических частиц // ПМТФ. 2014. Т. 55. № 4. С. 184.]
Kapranova A.B., Zaitsev A.I., Nikitina T.P. Calculating the degree of compaction of a powder in a screw compactor taking into account slip and friction // Theor. Found. Chem. Eng. 2000. V. 34. № 6. P. 649. [Капранова А.Б., Зайцев А.И., Никитина Т.П. Расчет степени уплотнения порошка в шнековой машине с учетом проскальзывания и трения // Теорет. основы хим. технологии. 2000. Т. 34. № 6. С. 649.]
Селиванов Ю.Т., Першин В.Ф. Расчет и проектирование циркуляционных смесителей сыпучих материалов без внутренних перемешивающих устройств. М.: Машиностроение-1, 2004.
Протодьяконов Н.О., Богданов С.Р. Статистическая теория явлений переноса в процессах химических технологии. Л.: Химия, 1983.
Репке Г. Неравновесная статистическая механика. Пер. с нем. М.: Мир, 1990.
Кайзер Дж. Статистическая термодинамика неравновесных процессов. Пер. с англ. М.: Мир, 1990.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. Пер. с англ. М.: Наука, 1984.
Рейф Ф. Берклеевский курс физики. Статистическая физика. Т. 5. Пер. с англ. М.: Наука, 1986.
Андрианов Е.И. Методы определения структурно-механических характеристик порошкообразных материалов. М.: Химия, 1982.
Нигматулин Р.И. Основы механики гетерогенных сред. М.: Наука, 1978.
Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука, 1974.
Капранова А.Б. Метод определения коэффициента макродиффузии в процессе смешения твердых дисперсных сред в центробежном аппарате // Математическое моделирование. 2009. Т. 21. № 3. С. 83.
Kapranova A.B. Powder densification process in a centrifugal apparatus with curvilinear blades // Mathematical Models and Computer Simulations. 2010. V. 2. № 1. P. 63. [Капранова А.Б. Процесс уплотнения порошков в центробежном аппарате с криволинейными лопастями // Математическое моделирование. 2009. Т. 21. № 4. С. 44.]
Kapranova A.B., Zaitzev A.I., Lebedev A.E. Estimation of the layer thickness of the bulk material by its “falling down” the curvilinear blade of the centrifugal breaker // Czasopismo techniczne. Mechanika. Krakov, Poland, 2012. V. 109. № 6. P. 183.
Капранова А.Б., Верлока И.И., Зайцев А.И. Оптимизация параметров устройства для совмещения смешивания и деаэрации порошков // Изв. вузов. Химия и хим. технология. 2015. Т. 58. № 12. С. 66.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


