Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 196-204
Моделирование аэродинамики закрученного турбулентного течения в центробежном аппарате
А. В. Шваб 1, *, Р. Р. Турубаев 1, **
1 Национальный исследовательский Томский государственный университет
Томск, Россия
* E-mail: avshvab@inbox.ru
** E-mail: roma.turubaev@gmail.com
Поступила в редакцию 07.09.2017
После доработки 05.04.2018
Принята к публикации 21.02.2018
Аннотация
Представлено численное моделирование аэродинамики закрученного турбулентного течения в вихревой камере комбинированного пневматического аппарата c расположенным в верхней части ротором, состоящим из системы вращающихся лопаток. Численный анализ закрученного турбулентного течения позволил определить основные закономерности в поведении несущей среды в аппарате. В результате была предложена модификация формы лопаток ротора, которая позволила вносить необходимые изменения в распределение поля радиальной скорости. Численные исследования показали перспективность такого подхода для управления радиальной составляющей скорости в роторе, что является необходимым условием для эффективной работы сепаратора. Достоверность проведенных численных расчетов подтверждается тестовыми исследованиями и сравнением их с опытными данными.
ВВЕДЕНИЕ
В настоящее время аэро- и гидродинамика закрученных турбулентных потоков является одним из перспективных и интенсивно развивающихся направлений науки. Авиация, химическая технология, энергетика и энергомашиностроение, атомная промышленность и многое другое – все базируется на основных закономерностях закрученных потоков [1–3]. Существующее математическое моделирование процессов в пневматических центробежных аппаратах порошковых технологий в основном базируется на экспериментальных исследованиях и полуэмпирических моделях. Без фундаментальных исследований турбулентных закрученных течений в этих технологиях невозможно совершенствовать существующие установки [4–8]. Помимо аддитивных технологий, которые сейчас активно развиваются, данные аппараты могут быть использованы в порошковой металлургии, химической, атомной и других отраслях промышленности.
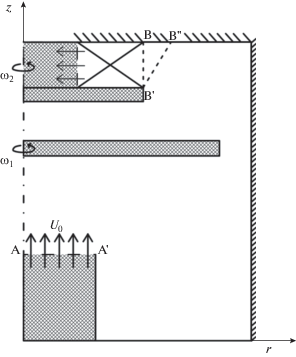
При прямоугольной форме ротора профиль радиальной составляющей скорости в выходной части аппарата имеет неравномерный характер. В качестве решения вышеизложенной проблемы было предложено численное решение задачи с модифицированной геометрической формой ротора, а именно преобразование прямоугольной формы к трапецеидальной.
Данный аппарат используется для дробления крупных частиц на более мелкие и дальнейшего их разделения по заданному размеру. Процесс отсеивания крупной фракции от мелкой происходит в два этапа. Первый этап отсеивания происходит в средней части аппарата, где расположен вращающийся дисковой элемент, крупные частицы отбиваются об него и падают вниз для дальнейшего измельчения, мелкие частицы его облетают.
Второй этап отсеивания имеет место в выходной части рабочей области, где разделение происходит с помощью ротора, который благодаря центробежной силе отбрасывает крупные частицы на периферию для повторного измельчения.
Целью данной работы является получение более равномерного профиля радиальной компоненты вектора скорости при входе в ротор за счет изменений формы лопаток ротора.
ФИЗИКО-МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Вихревая камера представляет собой цилиндрическую область, внутри которой имеется вращающийся диск, центр которого совпадает с осью цилиндра и в верхней части ротор, состоящий из большого числа вращающихся лопаток на выходе из рабочей камеры. Газ поступает через сечение А–А' (рис. 1) в вихревую камеру с постоянной осевой скоростью U0 и под действием перепада давления обтекает вращающийся диск с угловой скоростью w1 и поступает в ротор, в котором вращается вместе с лопатками с угловой скоростью w2. Большое количество вращающихся лопаток в роторе позволяет использовать приближение, при котором окружная составляющая скорости в роторе имеет распределение по закону вращения твердого тела. Как известно, от распределения радиальной составляющей скорости существенно зависит процесс сепарации порошков.
Моделирование аэродинамики в вихревой камере проводится в цилиндрической системе координат на основе уравнений Рейнольдса.
Замыкание системы уравнений Рейнольдса осуществляется на основе обобщенной гипотезы Буссинеска, согласно которой рейнольдсовы напряжения считаются пропорциональными скорости деформации осредненного течения с точностью до коэффициента турбулентной вязкости. В результате в безразмерной форме уравнения переноса импульса и неразрывности можно привести к виду
(1)
$\begin{gathered} \frac{{\partial {{u}_{r}}}}{{\partial \tau }} + \frac{{\partial \left( {{{u}_{r}}{{u}_{r}}} \right)}}{{\partial r}} + \frac{{\partial \left( {{{u}_{r}}{{u}_{z}}} \right)}}{{\partial z}} - \\ - \,\,\frac{1}{{\operatorname{Re} }}\left\{ {\frac{\partial }{{\partial r}}\left[ {\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{r}}}}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{r}}}}{{\partial z}}} \right]} \right\} + \\ + \,\,\frac{{u_{r}^{2}}}{r} - \frac{{u_{{\varphi }}^{2}}}{r} = - \frac{{\partial p}}{{\partial r}} + \frac{1}{{\operatorname{Re} }} \times \\ \times \,\,\left[ {\frac{1}{r}\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{r}}}}{{\partial r}} - \left( {1 + {{\nu }_{t}}} \right)\frac{{{{u}_{r}}}}{{{{r}^{2}}}} + \frac{{\partial {{\nu }_{t}}}}{{\partial r}}\frac{{\partial {{u}_{r}}}}{{\partial r}} + \frac{{\partial {{\nu }_{t}}}}{{\partial z}}\frac{{\partial {{u}_{z}}}}{{\partial r}}} \right]; \\ \end{gathered} $(2)
$\begin{gathered} \frac{{\partial {{u}_{z}}}}{{\partial \tau }} + \frac{{\partial \left( {{{u}_{r}}{{u}_{z}}} \right)}}{{\partial r}} + \frac{{\partial \left( {{{u}_{z}}{{u}_{z}}} \right)}}{{\partial z}} - \\ - \,\,\frac{1}{{\operatorname{Re} }}\left\{ {\frac{\partial }{{\partial r}}\left[ {\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{z}}}}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{z}}}}{{\partial z}}} \right]} \right\} + \\ + \,\,\frac{{{{u}_{r}}{{u}_{z}}}}{r} = - \frac{{\partial p}}{{\partial z}} + \frac{1}{{\operatorname{Re} }} \times \\ \times \,\,\left[ {\frac{1}{r}\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{z}}}}{{\partial r}} + \frac{{\partial {{\nu }_{t}}}}{{\partial r}}\frac{{\partial {{u}_{r}}}}{{\partial z}} + \frac{{\partial {{\nu }_{t}}}}{{\partial z}}\frac{{\partial {{u}_{z}}}}{{\partial z}}} \right]; \\ \end{gathered} $(3)
$\begin{gathered} \frac{{\partial {{u}_{{\varphi }}}}}{{\partial \tau }} + \frac{{\partial \left( {{{u}_{r}}{{u}_{{\varphi }}}} \right)}}{{\partial r}} + \frac{{\partial \left( {{{u}_{z}}{{u}_{{\varphi }}}} \right)}}{{\partial z}} - \frac{1}{{\operatorname{Re} }} \times \\ \times \,\,\left\{ {\frac{\partial }{{\partial r}}\left[ {\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{{\varphi }}}}}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{{\varphi }}}}}{{\partial z}}} \right]} \right\} + \\ + \,\,\frac{{2{{u}_{r}}{{u}_{{\varphi }}}}}{r} = \frac{1}{{\operatorname{Re} }}\left[ {\frac{1}{r}\left( {1 + {{\nu }_{t}}} \right)\frac{{\partial {{u}_{{\varphi }}}}}{{\partial r}} - \left( {1 + {{\nu }_{t}}} \right)\frac{{{{u}_{{\varphi }}}}}{{{{r}^{2}}}} + \frac{{\partial {{\nu }_{t}}}}{{\partial r}}{{u}_{{\varphi }}}} \right]; \\ \end{gathered} $(4)
$\frac{{\partial {{u}_{r}}}}{{\partial r}} + \frac{{\partial {{u}_{z}}}}{{\partial z}} + \frac{{{{u}_{r}}}}{r} = 0.$Здесь безразмерная форма уравнений получена с использованием входной скорости U0; масштаба длины, в качестве которого был выбран радиус входного сечения R0; плотности газа ρ, которая в силу небольших скоростей считается постоянной; Re = U0R0/ν – число Рейнольдса, где ν – коэффициент кинематической вязкости. В уравнениях (1)–(4) учтено, что рассматриваемая задача является осесимметричной и, следовательно, производные по окружной координате равны нулю.
Существуют различные методы для моделирования турбулентной вязкости. В работе использовалась известная модель турбулентности Уилкокса. Согласно этой модели турбулентности, записываются два дополнительных уравнения переноса для кинетической энергии турбулентности k и удельной скорости диссипации кинетической энергии ω. В цилиндрической системе координат в безразмерной форме с учетом осевой симметрии эти уравнения будут иметь следующий вид [8]:
(5)
$\begin{gathered} \frac{{\partial k}}{{\partial \tau }} + \frac{{\partial \left( {{{u}_{r}}k} \right)}}{{\partial r}} + \frac{{\partial \left( {{{u}_{z}}k} \right)}}{{\partial z}} - \frac{1}{{\operatorname{Re} }} \times \\ \times \,\,\left\{ {\frac{\partial }{{\partial r}}\left[ {\left( {1 + {{\nu }_{t}}\sigma {\text{*}}} \right)\frac{{\partial k}}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {1 + {{\nu }_{t}}\sigma {\text{*}}} \right)\frac{{\partial k}}{{\partial z}}} \right]} \right\} + \frac{{{{u}_{r}}k}}{r} = \\ = \frac{1}{{\operatorname{Re} }}\left[ {\frac{1}{r}\left( {1 + {{\nu }_{t}}\sigma {\text{*}}} \right)\frac{{\partial k}}{{\partial r}}} \right] + G - r\beta {\text{*}}kw{\kern 1pt} {\kern 1pt} ; \\ \end{gathered} $(6)
$\begin{gathered} \frac{{\partial \omega }}{{\partial \tau }} + \frac{{\partial \left( {{{u}_{r}}\omega } \right)}}{{\partial r}} + \frac{{\partial \left( {{{u}_{z}}\omega } \right)}}{{\partial z}} - \frac{1}{{\operatorname{Re} }} \times \\ \times \,\,\left\{ {\frac{\partial }{{\partial r}}\left[ {\left( {1 + {{\nu }_{t}}\sigma } \right)\frac{{\partial \omega }}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {1 + {{\nu }_{t}}\sigma } \right)\frac{{\partial \omega }}{{\partial z}}} \right]} \right\} + \frac{{{{u}_{r}}\omega }}{r} = \\ = \frac{1}{{\operatorname{Re} }}\left[ {\frac{1}{r}\left( {1 + {{\nu }_{t}}\sigma } \right)\frac{{\partial \omega }}{{\partial r}}} \right] + \alpha \frac{\omega }{k}G - r\beta {{\omega }^{2}} - \beta r\omega \left| {\mathbf{\Omega }} \right|; \\ \end{gathered} $Здесь
Для получения единственного решения ставятся следующие граничные условия. На входе в исследуемую область задается безразмерная осевая компонента скорости, равная единице. В качестве граничных условий для тангенциальных составляющих вектора скорости на стенке используется условие частичного скольжения [9], причем коэффициент скольжения определяется с помощью известного закона стенки для турбулентного течения вблизи твердой поверхности, при этом значение кинетической энергии на стенке принимается равным нулю. В соответствии с работой [9], на стенках нормальные составляющие скорости полагаются равными нулю. Задание нулю касательных составляющих вектора скорости приводит к занижению нормального градиента продольной составляющей скорости на стенке и неправильной передаче здесь напряжения трения. Используя методику работы [9], удается рассчитывать напряжение трения на стенке, соответствующее известному логарифмическому закону стенки, что позволяет использовать больший шаг разностной сетки вблизи твердой поверхности. Подробности реализации этих условий можно найти в работе [9]. На основании этой работы имеем
Граничные условия на входе для кинетической энергии турбулентных пульсаций и удельной скорости диссипации турбулентной энергии определяются из экспериментальных данных. На выходе из рассматриваемой области ставится условие Неймана для всех переменных. На оси используется условие симметрии. Безразмерная форма граничных условий для окружной скорости приводит к появлению двух дополнительных критериев Rg1 и Rg2:
Здесь w1, w2 – угловые скорости диска и ротора соответственно. Полученные критерии фактически являются обратными числами Россби.
Таким образом, система (1)–(7) является замкнутой и описывает закрученное турбулентное течение в рассматриваемой области.
МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ
Рассматриваемая задача решалась численно в переменных скорость–давление на основе метода физического расщепления полей скорости и давления. В результате расщепления по времени задача разбивается на 2 этапа:
(8)
$\frac{{{\mathbf{u}}{\text{*}} - {{{\mathbf{u}}}^{n}}}}{{\Delta \tau }} + \left( {{\mathbf{u}}\nabla } \right){\mathbf{u}}* = \frac{1}{{\operatorname{Re} }}{{\nabla }^{2}}{\mathbf{u}}{\text{*}} - \nabla {{p}^{n}},$(9)
$\frac{{{{{\mathbf{u}}}^{{n + 1}}} - {\mathbf{u}}{\text{*}}}}{{\Delta \tau }} = - \nabla \left( {\delta p} \right).$Умножая скалярно на градиент зависимость (9) и учитывая, что на (n + 1)-м слое выполняется уравнение неразрывности, в результате получим уравнение Пуассона для определения поправки к давлению:
Исследуемая задача является стационарной, поэтому уравнение Пуассона для численного решения можно представить в виде нестационарного уравнения
(10)
$\frac{{\partial \left( {\delta p} \right)}}{{\partial {{\tau }_{f}}}} = {{\nabla }^{2}}\left( {\delta p} \right) - \frac{{\nabla {\mathbf{u}}}}{{\Delta \tau }}.$Из решения системы уравнений (8) определяется промежуточный сеточный вектор скорости u*. Затем из решения нестационарного уравнения Пуассона (10) определяется поправка к давлению и далее с помощью формулы (9) определяется вектор скорости на (n + 1)-м слое:
На всех границах для поправки к давлению используется условие Неймана [12].
Полученная система уравнений состоит из нестационарных уравнений переноса, решение которых проводится эволюционным методом до установления по времени. Каждое уравнение переноса решается обобщенным неявным методом переменных направлений в дельта-форме [13]. Суть метода заключается в расщеплении шага по времени с целью построения многомерной неявной схемы, в которой требуется обращение только к трехдиагональной матрице. Метод обладает вторым порядком точности по времени, решение которого проводится следующим образом:
Разностные аналоги конвективно-диффузионных слагаемых расписывались на разнесенной разностной сетке с использованием экспоненциальной схемы [12], которая снимает ограничение на сеточное число Рейнольдса.
АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ
При анализе результатов ламинарной задачи, полученных в работе [7], было выявлено несколько случаев образования вихревых структур в непосредственной близости с ротором, что впоследствии препятствовало формированию равномерного профиля радиальной компоненты скорости на входе в ротор. Для устранения подобных структур форма ротора была изменена на трапецеидальную.
Анализ численного исследования турбулентного закрученного течения в вихревой камере показал, что изменением угла наклона границы ротора можно влиять на распределение радиальной составляющей вектора скорости в выходном сечении. Это влияние продемонстрировано на рис. 2.
Рис. 2.
Влияние угла наклона ротора на профиль скорости ${{u}_{r}}$ в сечении В–В': 1 – угол наклона 90°; 2 – 77°; 3 – 45°.
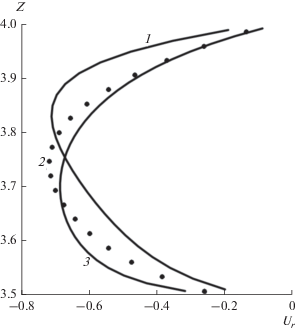
Из рис. 2 видно, что, уменьшая угол наклона границы ротора, можно получить равномерный профиль радиальной составляющей скорости. Дальнейшее уменьшение угла наклона приводит к неравномерности профиля радиальной составляющей скорости. Таким образом, выбором угла наклона границы ротора можно влиять на радиальную составляющую вектора скорости, которая, как известно, играет важную роль в процессе сепарации частиц.
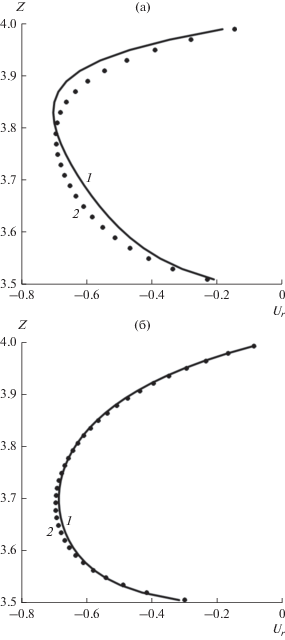
На рис. 3 показано влияние числа Рейнольдса на профиль радиальной составляющей скорости на входе в ротор. Отметим, что при трапецеидальной форме ротора (рис. 3б) увеличение числа Рейнольдса оказывает не такое сильное влияние, как при прямоугольной форме (рис. 3а). Следовательно, трапецеидальная форма ротора менее чувствительна к изменению числа Рейнольдса, что свидетельствует о перспективности изменения формы ротора для аэродинамики вихревой камеры.
Рис. 3.
Влияние числа Рейнольдса на профиль скорости ${{u}_{r}}$ в сечении В–В': 1 – Re = 5000; 2 – Re = 10 000; (а) – прямоугольная форма ротора; (б) – трапецеидальная форма ротора.
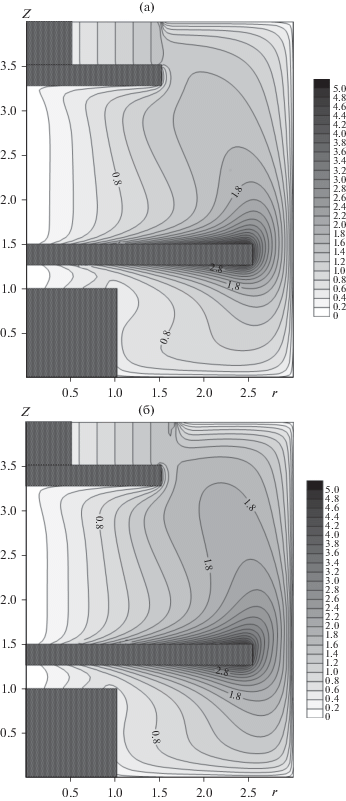
На рис. 4 и 5 представлены изолинии турбулентной вязкости и кинетической энергии турбулентности при трапецеидальной форме ротора с углом наклона границы 70°.
Существенно меняется картина течения изолиний окружной компоненты вектора скорости в выходной области вихревой камеры, что наглядно продемонстрировано на рис. 6 для случаев с прямоугольным ротором и трапецеидальным с углом наклона границы 70°.
Рис. 6.
Распределение изолиний окружной компоненты скорости: (а) – прямоугольная форма ротора; (б) – трапецеидальная форма ротора.
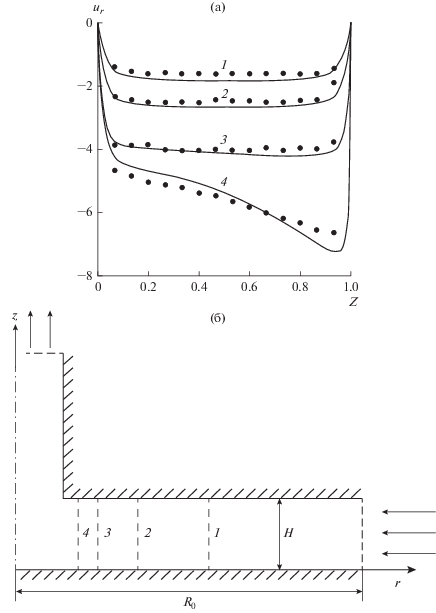
Достоверность проведенных исследований подтверждается путем сравнения решения ламинарной задачи в переменных вихрь–функция тока и скорость–давление [7], а также тестовыми исследованиями и сравнением численных результатов с экспериментальными данными [14] (рис. 7).
Рис. 7.
Сравнение численных расчетов с экспериментальными данными при параметрах течения Re = 2204 и R0/H = 10: 1 – R/R0 = 0.6; 2 – 0.4; 3 – 0.275; 4 – R/R0 = 0.185. Точками показаны экспериментальные данные [10].
ЗАКЛЮЧЕНИЕ
В настоящей работе представлено численное моделирование аэродинамики закрученного турбулентного течения в вихревой камере пневматического комбинированного аппарата. Исследованы характерные особенности в распределении полей окружной скорости, турбулентной вязкости и кинетической энергии. На основе численных исследований показана возможность изменением формы лопаток оказывать существенное влияние на радиальную составляющую скорости в роторе и тем самым управлять балансом центробежных и аэродинамических сил для повышения эффективности процесса сепарации порошков.
ОБОЗНАЧЕНИЯ
| F | безразмерный источник в уравнении переноса |
| G | безразмерное слагаемое, отвечающее за генерацию турбулентности |
| k | безразмерная кинетическая энергия турбулентности |
| p | безразмерное давление |
| $\delta p$ | безразмерная поправка к давлению |
| R | текущее значение радиуса, м |
| r, φ, z | безразмерные координаты цилиндрической системы |
| U0 | скорость потока на входе, м/с |
| w | угловая скорость, 1/с |
| α, β, β*, σ, σ* | константы двухпараметрической дифференциальной модели турбулентности Уилкокса |
| γ | безразмерный коэффициент скольжения для определения скорости на стенке |
| θ | безразмерная искомая функция в уравнении переноса |
| ν | коэффициент кинематической вязкости, м2/с |
| νt | безразмерный коэффициент турбулентной вязкости |
| τ | безразмерное время |
| ${{\tau }_{f}}$ | фиктивное время, играющее роль итерационного параметра |
| χ | константа турбулентности, равная 0.4 |
| Ω | безразмерный вектор завихренности |
| ω | безразмерная удельная скорость диссипации |
| Re | число Рейнольдса |
| Rg | обратное число Россби |
ИНДЕКСЫ
Список литературы
Scagliarini A., Einarsson H., Gylfason A., Toschi F. Law of the wall in an unstably stratified turbulent channel flow // J. Fluid Mech. 2015. V. 781. R5.
Волков К.Н., Емельянов В.Н. Течения и теплообмен в каналах и вращающихся полостях М.: Физмалит, 2010.
Bailly C., Comte-Bellot G. Turbulence (Series in Experimental Fluid Mechanics). Cham, Switzerland: Springer, 2015.
Pakhomov M.A., Terekhov V.I. Numerical simulation of turbulent swirling gas-dispersed flow behind a sudden tube expansion // Thermophys. Aeromech. 2015. V. 55. № 5. P. 597. [Пахомов М.А., Терехов В.И. Численное моделирование турбулентного закрученного газодисперсного потока за внезапным расширением трубы // Тепл. и аэромеханика. 2015. Т. 22. № 5. С. 621.]
Кафаров В.В., Дорохов И.Н. Системный анализ процессов химической технологии. М.: Наука, 1976.
Зятиков П.Н., Росляк А.Т., Шваб А.В., Демиденко А.А., Романдин В.И., Брендаков В.Н. Способ газовой центробежной классификации и измельчения порошков. Пат. 2522674 РФ. 2014.
Турубаев Р.Р., Шваб А.В. Численное исследование аэродинамики закрученного потока в вихревой камере комбинированного пневматического аппарата // Вестник Том. гос. ун-та. Мат. и мех. 2017. № 47. С. 87.
Shvab A.V., Evseev N.S. Studying the separation of particles in a turbulent vortex flow // Theor. Found. Chem. Eng. 2015. V. 49. № 2. P. 191. [Шваб А.В., Евсеев Н.С. Исследование процесса сепарации частиц в турбулентном закрученном потоке // Теорет. основы хим. технологии. 2015. Т. 49. № 2. С. 197.]
Кузьминов А.В., Лапин В.Н., Черный С.Г. Метод расчета турбулентных течений несжимаемой жидкости на основе двухслойной (k–ε) модели // Выч. техн. 2001. Т. 6. № 5. С. 73.
Wilcox D.C. Reassessment of the scale-determining equation for advanced turbulence models // Amer. Inst. of Aeron. and Astron. 1988. V. 26. № 11. P. 1299.
Shvab A.V., Khairullina V.Yu. Swirling turbulent flow between rotating profiled discs // Theor. Found. Chem. Eng. 2011. V. 45. № 5. P. 646. [Шваб А.В., Хайруллина В.Ю. Исследование закрученного турбулентного течения между вращающимися профилированными дисками // Теорет. основы хим. технологии. 2011. Т. 45. № 5. С. 557.]
Патанкар С.В. Численные методы решения задач теплообмена и динамики жидкости. Пер. с англ. М.: Энергоатомиздат, 1984.
Пейре Р., Тейлор Т.Д. Вычислительные методы в задачах механики жидкости. Пер. с англ. Л.: Гидрометеоиздат, 1986.
Singh A, Vyas B.D., Powle U.S. Investigations on inward flow between two stationary parallel disks // Int. J. Heat and Fluid Flow. 1999. V. 20. № 4. P. 395.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии