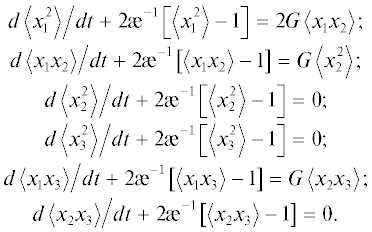Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 189-195
Возникновение и развитие эластической турбулентности в полимерных потоках
В. И. Попов *
Институт теплофизики им. С.С. Кутателадзе СО РАН
Новосибирск, Россия
* E-mail: vipopov@itp.nsc.ru
Поступила в редакцию 11.10.2017
После доработки 05.04.2018
Принята к публикации 23.03.2018
Аннотация
Исследованы условия возникновения и развития эластической турбулентности в полимерных потоках. Установлено, что для полимерной системы возникновение и развитие эластической турбулентности зависит от соотношения диссипативных и эластичных сил деформируемого потока.
ВВЕДЕНИЕ
Растворы и расплавы полимеров, их наполненные системы наделены сложной внутренней структурой и вследствие этого имеют особые физико-химические свойства. В процессе деформирования они проявляют нелинейно-вязкие свойства, частично запасают подводимую из вне энергию и релаксируют напряжения. Характерная особенность таких сред состоит в том, что в процессах их получения и переработки (экструзия, формование, шприцевание, соэкструзия и т.п.) они проявляют эластическую турбулентность (нестабильность потока).
Эластическая турбулентность проявляется уже при малых числах Рейнольдса в возникновении мелко- и крупномасштабных вихревых структур на входе в фильеру, шприц-головку (переходные условия деформирования), в раздутии, пульсации и искажении формы струи на выходе насадка (эффект Баруса). В каналах сложной геометрической формы (отличной от круглой) возникают симметричные вихревые структуры, поперечные к основному потоку.
Установлено [1, 2], что на характер нестабильного режима течения влияют геометрия входа, форма канала, температура потока, скорость деформирования. В пристенной области формующего канала возможны течения типа “stick–slip”, что проявляется в шероховатости формующего изделия на выходе насадка. Эластическая турбулентность является причиной неоднородного распределения красителей, пластификаторов, наночастиц и других наполнителей при их внедрении в полимерный поток.
Эластическая турбулентность является сдерживающим фактором повышения производительности и качества полимерных изделий при их экструзионном формовании. Исключить это нежелательное явление, чувствительное к нарушению технологических параметров, возможно лишь при соблюдении оптимальных режимных параметров формования [2, 3].
Несмотря на значительное число публикаций, направленных на выявление условий возникновения и развития эластической турбулентности, большей частью по внешним признакам проявления, проблема все еще остается не решенной. Не решен вопрос условий возникновения и развития эластической турбулентности, когда внутреннее состояние полимерной системы зависит не только от внешних параметров, но и начальных значений внутренних (структурных) параметров потока. Остается не решенным вопрос о совокупных параметрах, управляющих процессом.
В настоящей работе на основе опытных данных в рамках локально-неравновесной термодинамики с использованием феноменологических и структурно-статистических подходов дается условие возникновения и развития эластической турбулентности как совокупное действие диссипативных и эластичных (энтропийных) сил.
Общепринятым условием возникновения и развития эластической турбулентности считается наличие эластичных свойств полимерных систем. Вследствие эластичности полимерных систем при их деформировании возникают касательные и разности (первая и вторая) нормальных компонент тензора напряжений, которые релаксируют к новому равновесному состоянию не мгновенно, а во времени, которое зависит от внутренних структурных перестроек полимерной системы (времени релаксации). Следует заметить, что время релаксации определяет запаздывающие явления переноса не только импульса, но и тепла, массы, контролирующих и управляющих скоростью химических реакций.
Для характеристики полимерных потоков, в том числе для приближенной оценки возникновения эластической турбулентности, было предложено несколько новых (по отношению к обычным жидкостям) критериев подобия. Важнейшими из них, имеющими физическую интерпретацию, являются критерии Вейссенберга We = G$\unicode{230} $ и Деборы De = ${\unicode{230} \mathord{\left/ {\vphantom {\unicode{230} t}} \right. \kern-0em} t}.$
Критерий Вейссенберга считается мерой относительной важности касательных и нормальных напряжений, возникающих при деформировании полимерных систем по направлению h со скоростью сдвига G = w/h. Критерий De характеризует влияние начальных значений внутренних параметров деформируемой системы на ее состояние. Величина t – характерный временной масштаб, за который полностью меняются кинематические условия движения материальной точки (событий) [3, 4].
Известно, что даже вблизи равновесия движение высокополимерных систем протекает в условиях локально-неравновесной термодинамики [5–7]. В этом случае внутреннее состояние системы зависит не только от внешних термодинамических параметров, но и от начальных значений внутренних (структурных) параметров. В связи с этим классические (феноменологические) подходы локально-равновесной термодинамики применительно к исследованию условий возникновения и развития эластической турбулентности в полимерных потоках оказываются неадекватными. Наиболее приемлемым подходом решения проблемы может служить сочетание феноменологических и структурно-статистических подходов, для которых уравнение состояния в функциональной форме имеет вид F(P, ρ, T, 〈xixj〉) = 0. Величина 〈xixj〉 – внутренний структурно-статистический параметр.
Основная идея, заложенная в настоящей работе, состоит в том, что эластическая (вязкоупругая) турбулентность полимерных систем, определяется внутренними релаксационными процессами и возникает вследствие определенного соотношения диссипативных и эластичных сил, проявляющихся в процессе деформирования полимерных систем.
Эластические силы в полимерных системах имеют не энергетическую природу, а так же как диссипативные тепловую (энтропийную [8, 9]) природу. Разбаланс между рассеянным теплом и эластичной энергией деформирования приводит ее к релаксационному высвобождению – проявлению эластической турбулентности. Возможно возникновение инерционной турбулентности низкомолекулярных сред, когда учитываются инерционные члены в определении скорости движения внутренних параметров среды, – имеет тот же механизм и зависит от разбаланса уже инерционных и диссипативных сил.
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ВОЗНИКНОВЕНИЯ И РАЗВИТИЯ ЭЛАСТИЧЕСКОЙ ТУРБУЛЕНТНОСТИ
На рис. 1 и 2 представлены опытные данные переходного (динамического) и установившегося режимов при однородном деформировании концентрированного раствора полиакриламида (ПАА) в воде. Экспериментальные результаты получены на реометре типа Instron-3250, определяющие реодинамические свойства растворов полимеров, необходимые в дальнейшем для обоснования условий возникновения эластической турбулентности в каналах.
Мгновенная реометрическая деформация поля скоростей в полимерной системе, как на передней кромке при входе в канал, приводит к возникновению и развитию с разной скоростью во времени сдвиговых (касательных) и первой разности нормальных напряжений (рис. 1). При малых деформациях превалируют сдвиговые напряжения. Однако с ростом скорости сдвига первая разность нормальных компонент тензора напряжений начинает превышать сдвиговые напряжения. При прекращении деформирования (G = 0), как на выходе струи из канала, все напряжения релаксируют до своих равновесных состояний, причем с разной скоростью (рис. 2).
Рис. 1.
Переходной режим деформирования 1% раствора полиакриламида в воде: 1, 4, 6 – первая разность нормальных компонент тензора напряжений σ1 (скорость сдвига соответственно G = 1.3, 8.3, 20.8 с–1); 2, 3, 5 – сдвиговая компонента тензора напряжений τ (скорость сдвига соответственно G = 1.3, 8.3, 20.8 с–1).
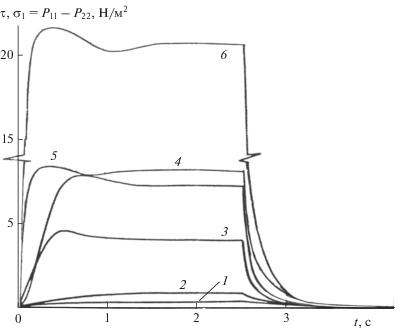
Рис. 2.
Зависимость первой разности нормальных компонент тензора напряжений (1) и касательных напряжений (2) от скорости сдвига для 1% водного раствора полиакриламида в установившемся режиме течения.
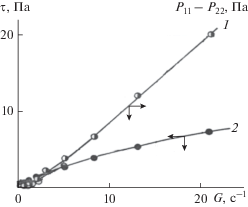
Зависимость касательных и первой разности нормальных компонент тензора напряжений от скорости сдвига для водных растворов полиакриламида в установившихся режимах течения (временная область t = 1–2.5 с, рис. 1) представлены на рис. 2.
Опыты по возникновению и развитию эластической турбулентности раствора ПАА проведены в прозрачном щелевом канале горизонтальной ориентации высотой h = 2.5 мм и длиной L = 250 мм с прямоугольным входом. Оптическая визуализация потока на входе в канал и измерение мгновенных полей скоростей по сечению и длине канала при различных условиях деформирования проводились методом стробоскопической визуализации [1] и представлены на рис. 3 и 4. Цифры 1–10 соответствуют средним расстояниям от входа в канал по величине Х/Dэ, где эквивалентный диаметр Dэ = 2h.
На рис. 3 представлен характер стабильного режима течения 1% раствора ПАА со средней мгновенной скоростью 2 см/c по длине канала (1–3). В предвходовой области канала (переходной режим деформирования) формируются два стабильно вращающиеся против часовой стрелки вихря, не возмущающие поля мгновенных скоростей по сечениям и длине канала. На выходе из канала (вид сверху) истечение падающей вниз струи имеет обычную форму. На этом же рисунке (4, 5) представлены первые признаки несимметричности мгновенных профилей скоростей с возникновением нестабильного режима течения со средней мгновенной скоростью 10 см/c. В переходной области течения, отмеченные выше два вихря, уже попеременно перемещаются по вертикали навстречу друг другу, периодически возмущая предвходовую зону канала. Измеренные поля скоростей на входе в канал (4) дают количественное представление этого возмущения. На значительном расстоянии от входа (5) имеет место относительно слабое влияние входовых явлений на профили скоростей. На выходе из канала наблюдаются небольшие продольные пульсации струи выходящего потока с незначительными поперечными волнами релаксации, которые более очевидны при больших скоростях течения (рис. 4). Первая разность нормальных компонент тензора напряжений σ1 = P11 – P22 отвечает в этом случае за раздутие выходящей струи насадка, вторая разность нормальных компонент тензора напряжений σ2 = = P22 – P33 отвечает за возникновение поперечных волн релаксации. Незначительные поперечные волны релаксации обусловлены известным результатом, что ${{{\sigma }}_{1}} \gg {{{\sigma }}_{2}}$ [6, 10].
Рис. 3.
Характер стабильного и начального возникновения нестабильного режима течения раствора полимера в предвходовой области прямоугольного канала с развитием мгновенных профилей скорости по его длине: 1 – Х/Dэ = 0.12; 2 – 0.37; 3 – 0.162; 4 – 0.25; 5 – Х/Dэ = 10.2.
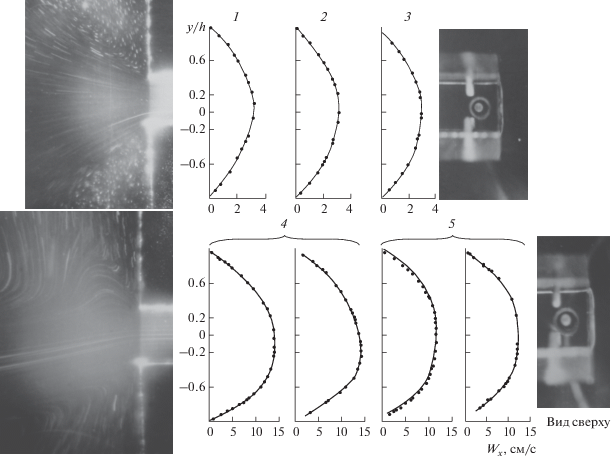
Рис. 4.
Нестабильный режим течения раствора полимера в предвходовой области и на выходе из прямоугольного канала с развитием мгновенных профилей скорости по его длине: 6 – Х/Dэ = 0.1; 7 – 0.25; 8 – 0.37; 9 – 0.62; 10 – Х/Dэ = 50.
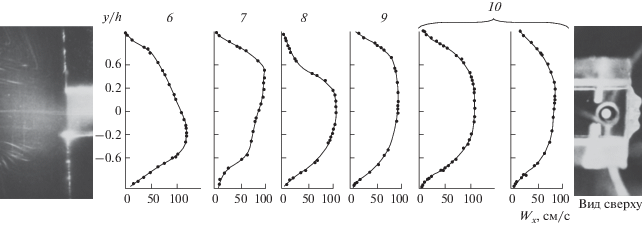
Развитый нестабильный режим течения представлен на рис. 4 со средней мгновенной скоростью течения 55 см/c. В этом случае колебательное движение вышеописанных вихрей, имеющих уже относительно мелкую структуру, усиливается и оказывает существенное влияние на структуру потока, как по сечению и длине канала, так и на выходе из него. При этом профили скоростей приобретают специфическую форму, с точкой перегиба, как известно, неустойчивые к внешним возмущениям.
Таким образом, нестабильный режим течения полимерных жидкостей характеризуется изменением кинематических характеристик течения в канале, в его предвходовой зоне и на выходе. При деформировании с изменением поля скоростей изменяются также динамические характеристики потока (компоненты и разности нормальных компонент тензора напряжений).
РЕОДИНАМИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ
Систему уравнений для теоретического анализа условий возникновения эластической турбулентности можно представить в следующем виде [5, 6]. Для внешних параметров, характеризующих внутреннее состояние полимерной системы, уравнение непрерывности, уравнение для момента импульса и определяющее уравнение имеют вид
(1)
$\begin{gathered} {\text{div}}{{\nu }_{i}} = 0,\,\,{{\partial {{P}_{{ij}}}} \mathord{\left/ {\vphantom {{\partial {{P}_{{ij}}}} {\partial {{x}_{j}}}}} \right. \kern-0em} {\partial {{x}_{j}}}} = 0, \\ {{P}_{{ij}}} = \quad\, - {{P}_{0}}{{\delta }_{{ij}}} + \varepsilon (\left\langle {{{x}_{i}}{{x}_{j}}} \right\rangle --{{\delta }_{{ij}}}). \\ \end{gathered} $Уравнение движения для внутреннего моментного параметра $\left\langle {{{x}_{i}}{{x}_{j}}} \right\rangle = \int\limits_{ - \infty }^\infty {{{x}_{i}}{{x}_{j}}{{W}_{i}}} {{d}^{3}}x{\text{,}}$ полученное из уравнения сохранения функции распределения для плотности вероятности микросистемы [11],
имеет следующий вид:
(2)
$\begin{gathered} {\text{De}}{{d\left\langle {{{x}_{i}}{{x}_{j}}} \right\rangle } \mathord{\left/ {\vphantom {{d\left\langle {{{x}_{i}}{{x}_{j}}} \right\rangle } {dt}}} \right. \kern-0em} {dt}} = {\text{We}}(\left\langle {{{x}_{i}}{{x}_{k}}} \right\rangle {{{{\dot {\nu }}}}_{{kj}}} + \\ + \,\,\left\langle {{{x}_{j}}{{x}_{k}}} \right\rangle {{{\dot {\nu }}}_{{ki}}}) - (\left\langle {{{x}_{i}}{{x}_{j}}} \right\rangle - {{\delta }_{{ij}}}). \\ \end{gathered} $Здесь ${{{\bar {\nu }}}_{i}}$ – среднестатистическая скорость узла сеточной модели полимерной среды относительно системы координат, начало которой помещено в центр масс узлов ближайшего окружения (эта скорость находится из условия безынерционного баланса механических, энтропийных и диффузионных сил, действующих на выделенный узел).
Для мгновенного возмущения системы, например, в момент t = 0, после которого движение начинается с градиентом скорости G, из (2) находим систему уравнений для моментов:
Из системы неоднородных уравнений (3), методом вариации произвольных постоянных, находятся изменения во времени моментов для внутреннего параметра 〈xixj〉, начальные значения которых при t = 0: $\left\langle {x_{1}^{2}} \right\rangle $ = $\left\langle {x_{1}^{2}} \right\rangle = \left\langle {x_{2}^{2}} \right\rangle = \left\langle {x_{3}^{2}} \right\rangle = 1;$ $\left\langle {{{x}_{3}}{{x}_{1}}} \right\rangle = \left\langle {{{x}_{1}}{{x}_{2}}} \right\rangle = \left\langle {{{x}_{2}}{{x}_{3}}} \right\rangle = 0,$ имеют следующий вид:
(4)
$\begin{gathered} \left\langle {{{x}_{1}}{{x}_{2}}} \right\rangle = 0.5G\unicode{230} \left( {1 - {\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right)} \right), \\ \left\langle {x_{1}^{2}} \right\rangle = 1 + 0.5{{G}^{2}}{{\unicode{230} }^{2}}\left[ {1 - {\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right) - } \right. \\ \left. { - \,\,2{{\unicode{230} }^{{ - 1}}}t{\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right)} \right]. \\ \end{gathered} $Уравнения (4) отражают структурные изменения полимерной системы во времени в процессе деформирования. Градиент скорости деформирует компоненту тензора 〈x1x2〉 и эластично растягивает компоненту $\left\langle {x_{1}^{2}} \right\rangle $ относительно начальных значений $\left\langle {x_{1}^{2}} \right\rangle - 1.$ При мгновенном изменении поля скоростей (например, на входе в канал) или при прекращении деформирования (например, на выходе канала) моменты эластично релаксируют к своим равновесным значениям, к состоянию максимума энтропии. Видно (2), что значения для моментов с сеточной структурой в переходных условиях деформирования, так же как для линейных полимеров [12, 13], характеризуются числом Вейссенберга We = $G\unicode{230} $ и дополнительно числом Деборы De = ${\unicode{230} \mathord{\left/ {\vphantom {\unicode{230} t}} \right. \kern-0em} t}.$
Из определяющего уравнения (1) находим соотношения экспериментально определяемых (рис. 1, 2) компонент тензора напряжений:
(5)
$\begin{gathered} {{{\tau }}_{{12}}} = \frac{{{\varepsilon }G\unicode{230} }}{2}\left( {1 - {\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right)} \right), \\ {{P}_{{11}}} - {{P}_{{22}}} = \frac{{{\varepsilon }G{{\unicode{230} }^{2}}}}{2}\left[ {1 - {\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right) - } \right. \\ \left. { - \,\,2{{\unicode{230} }^{{ - 1}}}t{\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right)} \right]. \\ \end{gathered} $В соотношениях (5) ε = 2η${{\unicode{230} }^{{ - 1}}}$ – модуль эластичности, η – эффективная стационарная сдвиговая вязкость, определяемая как τ/G (рис. 2).
Сопоставляя τ12 и P11 – P22 при одном и том же значении изменения поля скоростей за время релаксации ($G\unicode{230} $), имеем
(6)
$\begin{gathered} \frac{{{{{\tau }}_{{12}}}G}}{{{{P}_{{11}}} - {{P}_{{22}}}}} = \\ = \frac{{{{\unicode{230} }^{{ - 1}}}{{{\left( {1 - {\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right)} \right)}}^{2}}}}{{1 - {\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right) - 2{{\unicode{230} }^{{ - 1}}}t{\text{exp}}\left( { - 2{{\unicode{230} }^{{ - 1}}}t} \right)}}. \\ \end{gathered} $Соотношение (6) представляет собой временную связь между механической энергией диссипации (теплового рассеяния) и энергией эластической деформации. Вследствие энтропийной (тепловой) природы релаксации структурных изменений в полимерных системах при их деформировании эластическая энергия деформации высвобождается с некоторым запаздыванием, соответствующим времени релаксации. Это обстоятельство является причиной возникновения эластической турбулентности в локально-неравновесных условиях деформирования полимерных систем.
На малых временах процесса деформирования t < $\unicode{230} $ (локально-неравновесное деформирование, например, на входе в канал) в пристенной зоне эластического деформирования идет интенсивная диссипация механической энергии [6]. Эксперимент (4 на рис. 3) показал, что начальное возникновение эластической турбулентности происходит при мгновенной средней скорости потока порядка 10 см/c. Это соответствует линейной скорости деформации в пристенной зоне эластического деформирования жидких частиц, определенной по эквивалентному диаметру, равной G = 20–1. В этом случае τ12G = 150 Па с–1, а первая разность нормальных напряжений P11 – P22 = = 19.5 Па (рис. 1, 2). Следовательно, возникновение эластической турбулентности в опытах происходило при превышении энергии диссипации над энергией эластического деформирования в 7.7 раза.
При малых значений ${{\unicode{230} }^{{ - 1}}}t$ (большие числа Деборы) из соотношения (6), для начальных моментов времени возникновения эластической турбулентности, следует, что $\frac{{{{{\tau }}_{{{\text{12}}}}}G}}{{{{P}_{{11}}} - {{P}_{{12}}}}} = {1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0em} t}.$ Величина f = 0.13 Гц характеризует начальную частоту однородных колебаний потока от возмущающего действия предвходовых вихрей, обусловленных релаксационными процессами. Этот результат согласуется с опытными данными, полученными нами ранее [1] по исследованию спектральных характеристик колебательного движения при нестабильных режимах течения растворов полимеров в различных условиях их проявления.
Из соотношения (6) следует, что $t \to \infty $ вдали от входа в канал), имеем $\frac{{{{{\tau }}_{{{\text{12}}}}}G}}{{{{P}_{{11}}} - {{P}_{{22}}}}} = \frac{1}{\unicode{230} }.$ В этих условиях (локально-равновесного деформирования) идет запасание в полимерных потоках эластической энергии при балансировании с диссипируемой энергией деформации с последующим ее высвобождением на выходе канала в виде характерных нерегулярностей. Отношение $\frac{{{{{\tau }}_{{{\text{12}}}}}}}{{{{P}_{{11}}} - {{P}_{{22}}}}}$ характеризует динамические свойства конкретной полимерной системы и гидродинамические условия процесса течения полимерной среды.
Из приведенных выше соотношений видно, что с ростом частоты времени релаксации роль диссипативного фактора повышается. Однако в связи со значительным снижением времени релаксации с ростом скорости сдвига и температуры потока роль этого фактора может повышаться [1–3]. В связи с этим настоящая работа имеет перспективу развития в части разработки термомеханических методов высокоскоростной экструзии полимерных систем.
ЗАКЛЮЧЕНИЕ
Эластическая турбулентность инициируется начальными условиями локально-неравновесного деформирования полимерных сред, при которых их состояние зависит не только от внешних, но и внутренних значений параметров задачи. Условием возникновения и развития эластической турбулентности является фактор превышения (на порядок) энергии диссипации (теплового рассеяния) над энергией эластической деформации.
ОБОЗНАЧЕНИЯ
| D | диаметр канала, м |
| G | скорость сдвига, с–1 |
| L | длина канала, м |
| P0 | гидростатическое давление, Па |
| P11 – P22 | первая разность нормальных напряжений, Па |
| P22 – P33 | вторая разность нормальных напряжений, Па |
| t | время, с |
| Wi | конфигурационная функция распределения плотности вероятности узлов сеточной модели (вероятность конфигурационного состояния) |
| X | координата, м |
| 〈xixj〉 | статистические моменты конфигурационной функции распределения |
| ${\delta }$ij | единичная матрица |
| ε | модуль эластичности, Па |
| $\unicode{230} $ | время релаксации, с |
| η | вязкость, Па с |
| τ12 | касательное напряжение сдвига, Па |
| De = ${\unicode{230} \mathord{\left/ {\vphantom {\unicode{230} t}} \right. \kern-0em} t}$ | число Деборы |
| We = $G\unicode{230} $ | число Вейссенберга |
ИНДЕКСЫ
Список литературы
Хабахпашева Е.М., Попов В.И., Груздева И.М., Ивакина Э.Л., Карстен В.М., Бахтияров С.И. Некоторые результаты исследования реологических потоков оптическими методами // Реодинамика и тепломассообмен. Новосибирск: СО РАН, 1979. С. 63.
Хан Ч.Д. Реология в процессах переработки полимеров. М.: Химия, 1979.
Астарита Дж., Марруччи Дж. Основы гидромеханики неньютоновских жидкостей. М.: Мир, 1978.
Bird R.B., Armstrong R.C., Hassger O. Dynamics of Polymeric Liquids: Fluid Mechanics. N.Y.: Wiley-Interscience, 1987.
Попов В.И. Метод релаксационных моментов для исследования нелинейных локально-неравновесных процессов переноса полимерных систем // Инж.-физ. журн. 2015. Т. 88. № 1. С. 261.
Попов В.И. Роль эффектов нелокальности и запаздывания в процессах переноса в средах с микроструктурой // Журн. прикл. механики и техн. физики. 2002. Т. 43. № 6. С. 151.
Соболев С.Л. Локально-неравновесные модели процессов переноса // Успехи физ. наук. 1997. Т. 167. № 10. С. 1095.
Волькенштейн М.В. Конфигурационная статистика полимерных цепей. М.: АН СССР, 1959.
Попов В.И. Исследование эволюции химически активных полимерных структур в поле механических, энтропийных и диффузионных сил // Теорет. основы хим. технологии. 2011. Т. 45. № 5. С. 519.
Ladge A.S., Schieber J.D., Bird R.B. The Weissenberg effects at finite rod-rotation speed // J. Chem. Phys. 1988. V. 88. № 6. P. 401.
Терлецкий Я.П. Статистическая физика. М.: Высш. школа, 1966.
Штейнберг В. Эластическая турбулентность: хаос в растворах полимеров [Электронный ресурс] // Видеолекции Физтеха: Лекторий МФТИ. 2016. URL: http://lectoriy.mipt.ru/lecturer/SteinbergV (дата обращения: 11.09.2017).
Burnishev Y., Steinberg V. Influence of polymer additives on turbulence in von Karman swirling flow between two disks. II // Physics of Fluids. 2016. V. 28. № 3. P. 033101.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии