Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 123-130
РАСПРЕДЕЛЕНИЕ ТЯЖЕЛЫХ ИЗОТОПОВ ВОДОРОДА И КИСЛОРОДА ПРИ РЕКТИФИКАЦИИ ВОДЫ
Э. П. Магомедбеков 1, *, И. Л. Растунова 1, И. Л. Селиваненко 1, Н. Н. Кулов 2
1 Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
2 Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
* E-mail: eldar@rctu.ru
Поступила в редакцию 20.11.2018
После доработки 30.11.2018
Принята к публикации 26.11.2018
Аннотация
Показана возможность высокоточного определения массообменных характеристик насадок из нержавеющей стали при разделении изотопов водорода и кислорода методом ректификации воды под вакуумом в колоннах диаметром 60−250 мм. Представлен алгоритм расчета параметров процесса разделения и профиля концентраций дейтерия и кислорода-18 при их одновременном разделении в установке “закрытого” типа с отбором продукта методом ректификации воды под вакуумом.
ВВЕДЕНИЕ
Ректификация воды под вакуумом является одним из наиболее распространенных способов разделения изотопов водорода и кислорода [1]. Несмотря на низкие значения однократного разделительного эффекта, неоспоримыми достоинствами метода являются простота аппаратурного оформления процесса, отсутствие проблем токсичности, коррозии и взрывоопасности и практически неограниченные запасы сырья. Вследствие этого, в середине ХХ в. ректификация воды использовалась для решения задачи получения тяжелой воды (D2O) из природного сырья, а затем – на стадии конечного концентрирования дейтерия при переработке некондиционной тяжелой воды [1–4]. В последние годы ректификация воды является единственным промышленным способом производства тяжелокислородной $\left( {{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}} \right)$ и так называемой легкой воды (deuterium-depleted water – DDW) с пониженным содержанием тяжелого изотопа водорода – дейтерия, которые находят применение в исследованиях медицинского и биологического направлений [5–7].
Процесс разделения изотопов методом ректификации основан на фазовом равновесии между жидкостью и паром. Реакция изотопного обмена водорода и кислорода описывается уравнениями (1) и (2), причем тяжелые изотопы концентрируются в жидкой фазе [1, 3]:
(1)
${\text{HD}}{{{\text{O}}}_{{\left( {\text{п }} \right)}}} + {{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}_{{\left( {\text{ж }} \right)}}} \Leftrightarrow {{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}_{{\left( {\text{п }} \right)}}} + {\text{HD}}{{{\text{O}}}_{{\left( {\text{ж }} \right)}}},$(2)
${\text{H}}_{{\text{2}}}^{{{\text{18}}}}{{{\text{O}}}_{{\left( {\text{п }} \right)}}} + {\text{H}}_{{\text{2}}}^{{{\text{16}}}}{{{\text{O}}}_{{\left( {\text{ж }} \right)}}} \Leftrightarrow {\text{H}}_{{\text{2}}}^{{{\text{16}}}}{{{\text{O}}}_{{\left( {\text{п }} \right)}}} + {\text{H}}_{{\text{2}}}^{{{\text{18}}}}{{{\text{O}}}_{{\left( {\text{ж }} \right)}}}.$Термодинамическое равновесие в этих системах характеризуется коэффициентом разделения α, равным отношению относительных концентраций тяжелого изотопа в обогащенной и обедненной фазах:
В данном уравнении применительно к процессу ректификации переменная x означает концентрацию (атомная доля) тяжелого изотопа (D или 18O) в жидкой воде, а y – в паре.
Для бинарных смесей значения коэффициентов разделения могут быть рассчитаны с использованием парциальных давлений изотопных модификаций молекул воды, а также эмпирических уравнений, справедливых в диапазоне температур 273–403 К [1, 8]:
(4)
${{\alpha }_{{{\text{H}} - {\text{D}}}}} = \frac{{P_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}}}{{P_{{{\text{HDO}}}}^{0}}} = \sqrt {\frac{{P_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}}}{{P_{{{{{\text{D}}}_{{\text{2}}}}{\text{O}}}}^{0}}}} ,$(5)
${{\alpha }_{{{\text{Н }}_{{\text{2}}}^{{{\text{16}}}}{\text{O}} - {\text{H}}_{{\text{2}}}^{{18}}{\text{O}}}}} = \frac{{P_{{{\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}}}^{0}}}{{P_{{{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}}}^{0}}},$(6)
${\text{ln}}\frac{{P_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}}}{{P_{{{{{\text{D}}}_{{\text{2}}}}{\text{O}}}}^{0}}} = \frac{{26398.8}}{{{{T}^{2}}}} - \frac{{89.6065}}{T} + 0.075802,$(7)
${\text{ln}}{{\alpha }_{{{}^{{16}}{\text{O}} - {}^{{18}}{\text{O}}}}} = \frac{{{\text{1037}}}}{{{{T}^{2}}}} - \frac{{0.4156}}{T} - 0.00207.$Из анализа приведенных в табл. 1 значений коэффициентов разделения для изотопных систем H2O–D2O и ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ видно, что величина однократного разделительного эффекта для кислорода существенно меньше, чем для водорода. С увеличением температуры наблюдается снижение α, вследствие чего процесс проводят под вакуумом. При этом оптимальным считается давление на уровне 0.02–0.03 МПа, что соответствует температурам 60–70°С [1, 3].
Таблица 1.
Температурная зависимость коэффициента разделения при ректификации воды [1]
| Изотопная система | 323 К | 333 К | 343 К | 353 К | 363 К |
|---|---|---|---|---|---|
| H2O–D2O | 1.053 | 1.047 | 1.041 | 1.035 | 1.030 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.0078 | 1.0068 | 1.0063 | 1.0058 | 1.0053 |
Малые значения коэффициента обогащения (ε = α–1) при ректификации воды, особенно при разделении изотопов кислорода, обусловливают необходимость создания противоточных разделительных аппаратов с большим числом теоретических ступеней разделения. При этом очевидно, что разделению будут подвергаться две изотопные смеси H2O–HDO и ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}.$ Поскольку расчеты разделительной аппаратуры обычно проводится с использованием общей теории тонкого разделения, в которой учитывается только одна изотопная система, представляется интересным определить закономерности изменения концентраций дейтерия и кислорода-18 при их одновременном разделении в процессе ректификации воды под вакуумом.
ПАРАМЕТРЫ РАЗДЕЛЕНИЯ ИЗОТОПОВ ВОДОРОДА И КИСЛОРОДА В БЕЗОТБОРНОМ РЕЖИМЕ
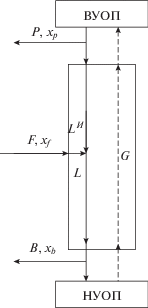
Экспериментальное исследование разделения изотопов водорода и кислорода в процессе ректификации проводилось при испытании высокоэффективных насадок из нержавеющей стали, изготовленных в РХТУ им. Д.И. Менделеева. Эксперименты проводились на экспериментальных стендах, включающих в себя ректификационные колонны диаметром 60, 120 и 250 мм и высотой насадочной части H = 1 м, испаритель и конденсатор − соответственно нижний (НУОП) и верхний (ВУОП) узлы обращения потоков, системы отбора проб, вакуумирования, контроля и автоматического управления параметрами процесса [9, 10]. Установка с колонной диаметром 250 мм была снабжена системой рекуперации тепла с использованием теплового насоса на основе фреонового цикла [11]. Исследования проводились с использованием деионизованной воды природного изотопного состава. Изотопный анализ проб проводился с использованием спектрального жидкостного изотопного анализатора T-LWIA-45-EP, предназначенного для анализа воды на уровне природного содержания изотопов с погрешностью измерения ±0.0001 ат. % (1 млн–1).
По результатам анализа концентраций дейтерия или 18O внизу (xн) и вверху (xв) колонны рассчитывали величину степени разделения (К), числа теоретических ступеней разделения (ЧТСР, N) и высоты эквивалентной теоретической ступени разделения (ВЭТС, h) по следующим уравнениям [1, 3]:
(8)
$K = \frac{{{{x}_{{\text{н }}}}\left( {1 - {{x}_{{\text{в }}}}} \right)}}{{{{x}_{{\text{в }}}}\left( {1 - {{x}_{{\text{н }}}}} \right)}},$В табл. 2 и 3 представлены результаты определения массообменных характеристик насадок в безотборном режиме при давлении 0.02 МПа при удельной нагрузке по жидкости (Lуд, кг/(м2 ч)), равной 80% от предельной. Были испытаны образцы спирально-призматической насадки (СПН) с размерами элементов 4 × 4 × 0.25 мм, 6 × 6 × 0.4 мм, 8 × 8 × 0.4 мм (табл. 2). В табл. 3 представлены результаты испытаний регулярной рулонной ленточно-винтовой насадки (РЛВН) высотой 1000 мм, изготовленной из гофрированной нержавеющей сетки с ячейкой 0.76 мм из проволоки 0.27 мм 12Х18Н10Т со следующими характеристиками: тип гофра исходных лент – прямой; ширина исходной ленты – 47 мм; ширина гофрированной полосы – 40 мм; высота гофра сетки для намотки блока – 5 мм; намотка – с зазором между витками 3 мм; слой по 4 параллельные полосы. По высоте блока устанавливались “юбочки” из прямых лент нержавеющей сетки на расстоянии 200 мм друг от друга, причем диаметр блока был примерно на 10 мм меньше диаметра царги для того, чтобы при установке в колонну “юбочки” в расправленном состоянии обеспечивали контакт между насадкой и стенкой царги. Загрузка, запуск и обработка насадки осуществлялись по оригинальным методикам, разработанным в РХТУ им. Д.И. Менделеева [9, 10].
Таблица 2.
Массообменные характеристики СПН при ректификации воды под вакуумом при давлении 0.02 МПа
| Изотопная система | α | Lуд, кг/(м2 ч) |
Концентрация тяжелого изотопа, млн–1 | К | h, см | |
|---|---|---|---|---|---|---|
| xн | xв | |||||
| Колонна диаметром 60 мм | ||||||
| Z = 4 мм | ||||||
| H2O–HDO | 1.046 | 1600 | 142 | 45 | 3.16 | 3.9 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1965 | 1692 | 1.16 | 4.0 | |
| Z = 6 мм | ||||||
| H2O–HDO | 1.046 | 2450 | 141 | 74 | 1.90 | 7.0 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1964 | 1801 | 1.09 | 6.9 | |
| Колонна диаметром 120 мм | ||||||
| Z = 4 мм | ||||||
| H2O–HDO | 1.046 | 1600 | 140 | 49 | 2.84 | 4.3 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1966 | 1699 | 1.16 | 4.1 | |
| Z = 6 мм | ||||||
| H2O–HDO | 1.046 | 2450 | 140 | 74 | 1.88 | 7.1 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1965 | 1810 | 1.08 | 7.3 | |
| Z = 8 мм | ||||||
| H2O–HDO | 1.046 | 3100 | 141 | 92 | 1.53 | 10.5 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1965 | 1855 | 1.06 | 10.4 | |
Таблица 3.
Массообменные характеристики РЛВН при ректификации воды под вакуумом при давлении 0.02 МПа
| Изотопная система | α | Lуд, кг/(м2 ч) |
Концентрация тяжелого изотопа, млн–1 | К | h, см | |
|---|---|---|---|---|---|---|
| xн | xв | |||||
| Колонна диаметром 60 мм | ||||||
| H2O–HDO | 1.046 | 5280 | 140 | 106 | 1.320 | 16.2 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1965 | 1893 | 1.038 | 16.0 | |
| Колонна диаметром 120 мм | ||||||
| H2O–HDO | 1.046 | 5440 | 141 | 109 | 1.285 | 17.9 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1965 | 1901 | 1.033 | 18.2 | |
| Колонна диаметром 250 мм | ||||||
| H2O–HDO | 1.046 | 5420 | 142 | 114 | 1.250 | 20.2 |
| ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | 1.006 | 1966 | 1907 | 1.031 | 19.8 | |
Из представленных данных видно, что для СПН повышение пропускной способности и ВЭТС примерно пропорционально увеличению размера элемента насадки. При этом увеличение диаметра колонны в 2 раза приводит к росту ВЭТС в среднем в 1.11 раза, т.е. пропорционально отношению диаметров в степени 0.17. Это хорошо согласуется с литературными данными, в соответствии с которыми для мелких высокоэффективных насадок при равномерном многоточечном орошении показатель степени, рекомендуемый для оценки коэффициента масштабного перехода, принят равным 0.2 [3]. Для насадки РЛВН значение коэффициента масштабного перехода, выраженного как отношение ВЭТС, оказалось пропорциональным отношению диаметров колонн в степени 0.156.
Наиболее значимым результатом с точки зрения исследования профилей концентраций в процессе разделения является то, что значения ВЭТС, полученные для изотопных систем H2O–HDO и ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ при их одновременном разделении, совпадают с высокой точностью. Это свидетельствует о том, что в безотборном режиме профили концентраций дейтерия и кислорода-18 будут одинаковыми.
РАЗРАБОТКА АЛГОРИТМА РАСЧЕТА ПРОФИЛЕЙ КОНЦЕНТРАЦИЙ ИЗОТОПОВ ВОДОРОДА И КИСЛОРОДА В РЕЖИМЕ С ОТБОРОМ ПРОДУКТА
С практической точки зрения важным является решение вопроса о распределении изотопных концентраций при одновременном разделении смесей H2O–HDO и ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ в режимах с отбором продукта для “закрытой” схемы (рис. 1). Разработка алгоритма расчета проводилась с использованием общей теории тонкого разделения смесей для области малых концентраций тяжелого изотопа [1].
На первом этапе на основе исходных данных определяют внешние потоки и концентрации в них целевого изотопа (например, дейтерия) с использованием уравнений материального баланса:
где xf, xp, xb – концентрация тяжелого изотопа (ат. д.) в потоках питания (F), отвала (P) и продукта (B) соответственно.Далее задаются величиной рабочего давления (температуры) вверху и внизу колонны с учетом предполагаемого гидравлического сопротивления, и для среднего значения по уравнениям (4), (6) рассчитывают величину коэффициента разделения для изотопной системы H–D. После этого произвольно задаются величиной относительного отбора (θ).
Расчет концентрирующей части разделительной установки проводится по следующим рекуррентным соотношениям:
(13)
${{K}_{{\text{K}}}} = \frac{{{{x}_{b}}\left( {1 - {{x}_{f}}} \right)}}{{{{x}_{f}}\left( {1 - {{x}_{b}}} \right)}},$(14)
${{\lambda }_{{{\text{K}}\,{\text{min}}}}} = \frac{{{{x}_{b}} - {{x}_{f}}}}{{{{x}_{b}} - \frac{{{{x}_{f}}}}{{\alpha - \varepsilon {{x}_{f}}}}}},$(15)
${{L}_{{{\text{K}}\,{\text{min}}}}} = \frac{{B\left( {{{x}_{b}} - \frac{{{{x}_{f}}}}{\alpha }} \right)}}{{\frac{\varepsilon }{\alpha }{{x}_{f}}\left( {1 - {{x}_{f}}} \right)}},$(16)
$\theta = \frac{{{{L}_{{{\text{K}}\,{\text{min}}}}}}}{{{{L}_{{\text{K}}}}}} = \frac{{1 - {{\lambda }_{{\text{K}}}}}}{{1 - {{\lambda }_{{{\text{K}}\,{\text{min}}}}}}},$(18)
${{N}_{{\text{K}}}} = \frac{{{\text{ln}}\frac{{{{K}_{{\text{K}}}}\left( {\alpha - 1} \right){{\lambda }_{{\text{K}}}}}}{{\alpha - {{\lambda }_{{\text{K}}}} - {{K}_{{\text{K}}}}\left( {1 - {{\lambda }_{{\text{K}}}}} \right)\alpha }}}}{{{\text{ln}}\frac{\alpha }{{{{\lambda }_{{\text{K}}}}}}}},$Далее проводится расчет исчерпывающей части колонны:
(19)
${{K}_{{\text{И }}}} = \frac{{{{x}_{f}}\left( {1 - {{x}_{p}}} \right)}}{{{{x}_{p}}\left( {1 - {{x}_{f}}} \right)}},$(22)
${{\lambda }_{{{\text{И max }}}}} = \frac{{{{x}_{f}} - {{x}_{p}}}}{{\frac{{{{x}_{f}}}}{{\alpha - \varepsilon {{x}_{f}}}} - {{x}_{p}}}},$(23)
${{N}_{{\text{И }}}} = \frac{{\ln \left[ {{{K}_{{\text{И }}}}\left( {1 - \theta } \right)} \right]}}{{\ln \frac{\alpha }{{{{\lambda }_{{\text{И }}}}}}}},$Концентрация целевого изотопа в потоке пара (y) в любом сечении колонны рассчитывается с использованием уравнений рабочих линий для концентрирующей или исчерпывающей частей колонны:
После этого может быть проведена оптимизация по θ с использованием в качестве параметра оптимизации минимального значения суммарного потока (J), характеризующего объем разделительного оборудования:
Для расчета профиля концентраций второй изотопной системы (например, 16O–18O) в качестве исходных параметров используется его концентрация в питающем потоке xf,O, величина коэффициента разделения, рассчитанная по уравнениям (5), (7), исходя из условий процесса, а также значения потоков, полученные в результате расчетов целевой системы.
Задаваясь произвольным значением относительного отбора (θO), определяется величина степени разделения в концентрирующей части установки (KKO) с использованием полученного ранее значения NK и рассчитанного по уравнению (9) значения максимальной степени разделения (KmKO) из соотношения
(27)
${\text{1}} - {{\theta }_{{\text{O}}}} = \frac{{{{K}_{{{\text{KO}}}}} - 1}}{{{{K}_{{{\text{mKO}}}}} - 1}}.$Далее по уравнениям (13)–(16) проводится расчет параметров процесса разделения в колонне для исследуемой системы. Затем, варьируя значения θO, методом последовательных итераций проводится расчет до того, чтобы значение мольного отношения потоков (λK,O) для определяемой системы совпало с рассчитанным ранее (λK) для целевого изотопа. После этого по уравнению (18) рассчитывается значение ЧТСР (NK,O), необходимое для достижения значения концентрации тяжелого изотопа в потоке В, равном хb,O. Из уравнений рабочих линий (24) и (25) определяются концентрации тяжелого изотопа в потоке пара (yf,O) в сечении точки ввода питания и в отвале (xp,O) соответственно. После этого по соотношениям (19) и (23) определяют соответственно значения степени разделения и ЧТСР в исчерпывающей части колонны.
В качестве примера рассмотрим задачу определения профиля концентраций дейтерия и кислорода-18 в колонне, работающей по “закрытой” схеме при следующих условиях: концентрация дейтерия в питающем потоке xf = 0.01, в концентрате xb = 0.0125 и в отвале xp = 0.007; поток питания F = 1 кмоль/ч; концентрация кислорода-18 в потоке F xf,O = 0.001966; среднее давление в колонне 0.03 МПа (Тср = 342 К), для которого значения коэффициентов разделения составили αH–D = 1.040 и α16О–18О = 1.00568. Оптимальное значение относительного отбора для системы H–D составило θ = 0.78. Параметры колонны представлены в табл. 4. В предположении, что колонна заполнена насадкой РЛВН, характеристики которой представлены в табл. 3 и работе [9], диаметр колонны составил 150 мм, а высоты концентрирующей и исчерпывающей частей (при h = 18 см) – 2.1 и 3.4 м соответственно.
Таблица 4.
Параметры процесса одновременного разделения изотопов водорода и кислорода при ректификации воды (давление 0.03 МПа, F = 1 кмоль/ч, В = 0.5455 кмоль/ч, P = 0.4545 кмоль/ч)
| Параметр | Концентрирующая часть | Исчерпывающая часть | ||
|---|---|---|---|---|
| H2O–HDO | ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | H2O–HDO | ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ | |
| Относительный отбор θ | 0.78 | 0.5836735 | 0.78 | 0.5836735 |
| Мольное отношение потоков λ | 0.896868 | 1.10576 | ||
| Поток воды L, кмоль/ч | 5.2977 | 4.2977 | ||
| Степень разделения | 1.25 | 1.0263 | 1.4286 | 1.033 |
| Концентрация вверху колонны, ат. д. | 0.01 | 0.001966 | 0.007 | 0.00190387 |
| Концентрация внизу колонны, ат. д. | 0.0125 | 0.002018 | 0.01 | 0.001966 |
| Число теоретических ступеней разделения N | 11.7 | 7.8 | 18.8 | 8.9 |
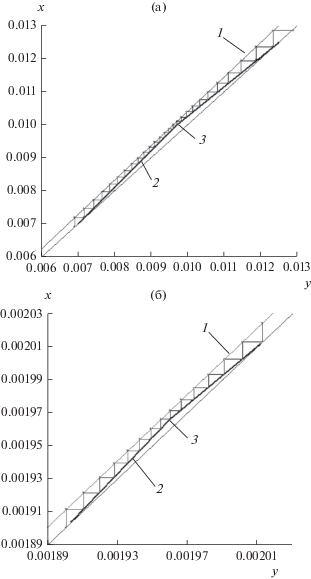
Из представленных данных видно, что параметры разделения этих изотопных смесей существенно различаются, при этом ЧТСР, необходимое для достижения балансовых значений концентраций в концентрате и отвале, для системы 16O–18O оказывается меньше, чем для системы H–D. Это подтверждается методом расчета “от ступени к ступени”, результаты которого в виде ЧТСР на диаграмме у–х, представлены на рис. 2.
Рис. 2.
Рабочая диаграмма у–х установки разделения изотопов водорода (а) и кислорода (б): 1 – равновесная линия, 2 – рабочая линия, 3 – точка ввода питания.
Полученные данным методом ожидаемые профили концентраций дейтерия и кислорода-18 в концентрирующей и исчерпывающей частях колонны представлены на рис. 3.
Рис. 3.
Профили концентраций дейтерия и кислорода-18 в концентрирующей (а) и исчерпывающей (б) частях колонны.
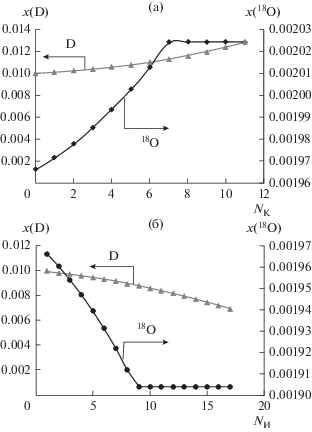
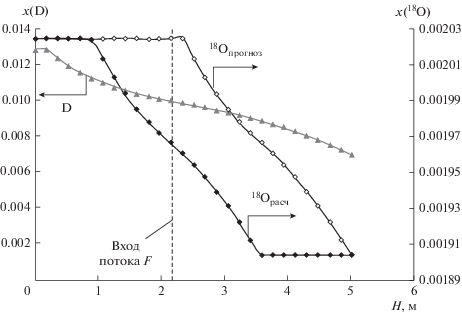
Из рисунка видно, что часть ступеней как в исчерпывающей, так и в концентрирующей частях не будет участвовать в процессе разделения. Следует отметить, что подобная зависимость наблюдалась при детритизации некондиционной тяжелой воды методом химического изотопного обмена в системе вода–водород на опытной установке в РХТУ им. Д.И. Менделеева, когда, несмотря на то, что соотношение высот концентрирующей и исчерпывающей частей составляло 1 : 5, практически вся установка была заполнена концентрированной тяжелой водой, а снижение концентрации дейтерия происходило только в последней исчерпывающей колонне. При этом профиль концентрации трития соответствовал расчетным параметрам [12]. Таким образом, можно ожидать, что в нашем случае также будет происходить перераспределение нецелевого изотопа 18O в сторону увеличения концентрирующей части, причем в точке ввода питания будет происходить смешение концентраций изотопов кислорода. На рис. 4 представлен прогнозируемый профиль концентраций 18O по высоте колонны, построенный в предположении начала отсчета ЧТСР от верхнего конца колонны без учета смешения концентраций.
Из рисунка видно, что прогнозируемый профиль концентраций 18O существенно отличается от расчетного и от профиля по дейтерию. При этом в точке ввода питания разница концентраций 18O во внутреннем потоке жидкости и потоке F будет отличаться пропорционально степени разделения КК. Таким образом, можно полагать, что с увеличением степени концентрирования по дейтерию исчерпывающая часть по кислороду-18 будет уменьшаться.
ЗАКЛЮЧЕНИЕ
На основании приведенных данных можно сделать заключение о том, что определение числа теоретических ступеней в колонне с верхним и нижним узлами обращения потоков может быть проведено при одновременном разделении изотопов водорода и кислорода в безотборном режиме.
Разработан алгоритм оценки профиля концентраций изотопов водорода и кислорода при их одновременном разделении в ректификационной колонне, основанный на принципах общей теории процессов тонкого разделения смесей для области малых концентраций. На примере одновременного разделения изотопов в смесях H2O–HDO и ${\text{H}}_{{\text{2}}}^{{{\text{16}}}}{\text{O}}--{\text{H}}_{{\text{2}}}^{{{\text{18}}}}{\text{O}}$ показано, что в колонне, работающей по “закрытой” схеме с отбором продуктов, величина относительного отбора и числа теоретических ступеней разделения для дейтерия и кислорода-18 различаются. Следствием этого будет являться различный характер зависимостей профиля концентраций этих изотопов по высоте колонны.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-13-00475).
ОБОЗНАЧЕНИЯ
| G | мольный поток пара, кмоль/ч |
| H | высота насадочной части колонны, м |
| h | высота эквивалентной теоретической ступени разделения, см |
| J | минимальное значение суммарного потока, кмоль/ч |
| К | степень разделения |
| L | поток жидкости, кмоль/ч |
| Lуд | удельная нагрузка по жидкости, кмоль/ч |
| N | число теоретических ступеней разделения |
| х | концентрация тяжелого изотопа (D или 18O) в жидкой воде, ат. д. |
| y | концентрация тяжелого изотопа (D или 18O) в паре, ат. д. |
| α | коэффициент разделения |
| ε | коэффициент обогащения |
| θ | величина относительного отбора |
| λ | мольное отношение потоков |
ИНДЕКСЫ
Список литературы
Andreev B.M., Magomedbekov E.P., Raitman A.A., Rozenkevich M.B., Sakharovsky Yu.A., Khoroshilov A.V. Separation of Isotopes of Biogenic Elements in Two-Phase Systems. Amsterdam: Elsevier, 2007.
Heavy Water Reactors: Status and Projected Development (Technical Reports Series № 407). Vienna: International Atomic Energy Agency, 2002.
Андреев Б.М., Зельвенский Я.Д., Катальников С.Г. Тяжелые изотопы водорода в ядерной технике. М.: Энергоатомиздат, 1987.
Магомедбеков Э.П., Растунова И.Л., Розенкевич М.Б. Современные технологии разделения изотопов водорода // Вопросы атомной науки и техники. Серия: Материаловедение и новые материалы. 2014. № 3(78). С. 70.
Полевой А.С. Состояние работ в области производства стабильных изотопов кислорода // VII Всероссийская (Международная) научная конференция “Физико-химические процессы при селекции атомов и молекул”. Сборник докладов. М.: ЦНИИАТОМНИНФОРМ, 2002. С. 280.
Андреев Б.М., Селиваненко И.Л., Григорьев А.И., Синяк Ю.Е., Тимаков А.А. Перспективы получения и использования воды с пониженной концентрацией тяжелых изотопов водорода и кислорода для профилактики и лечения болезней человека // 7-я Всероссийская (Международная) научная конференция “Физико-химические процессы при селекции атомов и молекул”, Сборник докладов. М.: ЦНИИАТОМНИНФОРМ, 2002. С. 325.
Легкая вода – основа качества жизни и долголетия: теория и практика. Сборник материалов Международной научно-практической конференции. Астана, 2018.
Van Hook W.A. Vapor pressures of the isotopic waters and ices // The Journal of Physical Chemistry. 1968. V. 72. № 2. P. 1234.
Magomedbekov E.P., Belkin D.Yu., Selivanenko I.L., Rastunova I.L. Characteristics of the Mass Transfer of Structured Rolled Ribbon-Screw Packings in Isotope Exchange Columns during Vacuum Water Distillation // Theor. Found. Chem. Eng. 2016. V. 50. № 4. P. 398.
Magomedbekov E.P., Belkin D.Yu., Selivanenko I.L., Rastunova I.L. Mass-transfer Characteristics of Spiral Prismatic Packings in Isotope Exchange Columns of Vacuum Water Distillation // Theor. Found. Chem. Eng. 2016. V. 50. № 5. P. 684.
Разумовский Г.Н., Селиваненко И.Л. Применение компрессионного теплового насоса для рекуперации энергии в процессе ректификации воды под вакуумом // Химическая промышленность сегодня. 2017. № 2. С. 17.
Андреев Б.М., Магомедбеков Э.П., Пак Ю.С., Розенкевич М.Б., Сахаровский Ю.А., Селиваненко И.Л. Детритизация водных потоков и концентрирование трития изотопным обменом в системах с молекулярным водородом (H2–H2O, H2–Pd) // Радиохимия. 1999. Т. 41. № 2. С. 131.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии