Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 349-360
Развитие теории работы однотрубной пневмотранспортной установки
В. П. Тарасов 1, *, К. А. Мухопад 1
1 Алтайский государственный технический университет им. И.И. Ползунова
Барнаул, Россия
* E-mail: mapp.tar@mail.ru
Поступила в редакцию 10.02.2017
После доработки 21.06.2017
Принята к публикации 30.08.2017
Аннотация
На основе теории взаимодействующих взаимопроникающих континуумов предлагается уточненная физико-математическая модель пневмотранспортной установки сыпучих материалов с учетом работы ее на переходных и неустановившихся режимах. При этом пневмотранспортная установка рассматривается как система связанного законами механики взаимовлияющего оборудования. Предлагаемая модель нагнетающей пневмотранспортной установки позволяет определять изменение параметров работы системы во времени и по длине трассы транспортирования, выбирать пневмотранспортное оборудование с наиболее рациональными характеристиками. Адекватность модели подтверждается экспериментальными исследованиями.
ВВЕДЕНИЕ
Известные преимущества пневматического способа транспортирования позволяют с успехом использовать его при решении многих практических задач, особенно для перемещения сыпучих материалов. Однако неполнота знаний о существе некоторых физических явлений, происходящих при пневмотранспортировании, и, как следствие, нерешенность двуединой задачи – обеспечения устойчивости работы систем пневмотранспорта с минимальными энергозатратами сдерживают его еще более широкое применение. Одной из основных причин этого является сложность процесса, что предполагает делать многочисленные допущения при разработке моделей. В частности, многие исследователи систем пневмотранспорта считают процесс стационарным, а его параметры неизменными во времени. Но такое допущение можно делать лишь для отдельных случаев, да и то только в определенные периоды работы установки. Это подтверждают наши исследования [1, 2] и результаты некоторых других работ [3–5]. Часто также предполагается, что многие параметры пневмотранспортирования (скорости материала и воздуха, коэффициент скольжения, плотность воздуха, концентрация материала в аэросмеси и др.) неизменны по длине трассы. Если подходить более строго, то это тоже можно обосновать только для отдельных случаев.
Кроме того, явления, происходящие в материалопроводе, зачастую рассматриваются в отрыве от процессов в других элементах пневмотранспортной установки (воздуходувной машине, приемно-питающем устройстве и др.). Такой подход упрощает решение задачи, однако не позволяет рассматривать процесс как совокупность взаимосвязанных явлений, что, в свою очередь, не дает возможности получить более объективную информацию о нем. Делаются и другие допущения, приводящие к искажению существа происходящих при пневмотранспортировании явлений.
Принятие сразу всех, отдельных из них или какой-либо комбинации допущений приводит к тому, что полученная физико-математическая модель пневмотранспортной установки может сильно отличаться от действительности, а ее анализ не позволит увидеть причины низкой эффективности системы пневмотранспорта. Разработанные на основе таких моделей методики расчета и проектирования заведомо предполагают многочисленные эмпирические коэффициенты, а область их применения ограничена рамками выполненных экспериментов. Фактические же показатели работы пневмотранспортных систем могут существенно отличаться от расчетных. Дальнейшее совершенствование систем пневматического транспорта немыслимо без уточнения физико-математических моделей и их последующего анализа. Уточнение моделей позволит понять сущность происходящих при пневмотранспортировании явлений, разработать дополнительные рекомендации к расчету и проектированию, предложить пути к совершенствованию как процесса, так и пневмотранспортного оборудования.
Ранее в [2] предпринята попытка такого рода уточнения физико-математической модели нагнетающей пневмотранспортной установки. На основании этой модели разработана методика расчета однотрубных систем пневмотранспорта и компьютерная программа для ее реализации [6]. Однако применение предложенной модели и разработанной на ее основе методики расчета и проектирования систем пневмотранспорта существенно ограничено. Это связано как со сложностью и многообразием происходящих при пневмотранспортировании явлений и неполнотой их учета, так и некоторыми неточностями в изложении модели.
Целью настоящей работы является уточнение модели, описывающей работу нагнетающей пневмотранспортной установки, и расширение границ (области) ее применения. В частности, уточняются принятые ограничения; учитываются особенности взаимодействия несущего потока с ограничивающей стенкой в условиях стесненного движения дисперсного потока; уточняются и приводятся к более удобному для использования виду характеристики пневмотранспортного оборудования; приводятся результаты апробирования модели и компьютерной программы для ее реализации; устраняются некоторые ранее допущенные неточности, а материал излагается в более строгой логической последовательности.
ФИЗИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Предлагаемые физическая и математическая модели базируются на так называемом континуальном подходе [3, 7], на основе которого разработаны и с успехом используются на практике методики расчета различных систем пневмотранспорта, например [8]. В рамках континуальной теории однородной двухфазной средой называют такую среду, в которой размеры частиц и расстояния между ними несоизмеримы с размерами ограничивающего их пространства. В такой среде можно считать, что концентрация твердой фазы изменяется в пространстве и во времени монотонно от какой-то начальной величины до конечной или бесконечно малой. Эта физическая модель позволяет представить твердую фазу как непрерывный континуум и использовать для описания взаимопроникающего движения одни и те же законы: уравнения сохранения количества движения, неразрывности, сохранения массы и энергии. При этом модель строится на основе следующих основных положений и ряда допущений.
1. Пневмотранспортная установка представляется системой, состоящей из отдельного оборудования: материалопровода; источника гидравлической энергии (в большинстве случаев в этом качестве выступает воздуходувная машина); воздухоподводящего оборудования (элементов пневмотранспортной установки, расположенных между воздуходувной машиной и материалопроводом); приемно-питающих устройств; оборудования, расположенного после материалопровода (для нагнетающей установки) и оборудования, расположенного перед приемно-питающим устройством (для всасывающей установки). В качестве основного оборудования принимается материалопровод. Именно в нем изменение параметров процесса рассматривается как во времени, так и по длине. Однако явления, происходящие в других элементах, считаются также тесно связанными физическими законами, как между собой, так и с процессами в материалопроводе.
2. Воздуходувная машина – это основной источник гидравлической энергии, обеспечивающий транспортирование материала. Кроме того, энергия, создаваемая воздуходувной машиной, иногда может расходоваться и на другие операции (подачу материала в трубопровод, доставку воздуха к материалопроводу, отделение транспортируемого материала от воздуха и очистку последнего от пыли и др.), а также теряться в виде утечек или присосов.
3. Приемно-питающее устройство подает материал из области с одним в область с другим давлением, смешивает его с воздухом и направляет в материалопровод.
4. Воздухоподводящее оборудование обеспечивает передачу и трансформацию гидравлической энергии, а также выполняет некоторые другие функции (очистку воздуха, накопление гидравлической энергии и пр.).
5. Процесс пневмотранспортирования нельзя считать установившимся, а его параметры неизменными во времени по ряду причин, обоснованных ранее [1]. Параметры процесса пневмотранспортирования изменяются как во времени, так и (или) по длине трассы (прежде всего это скорости воздуха и материала, коэффициент скольжения, концентрация материала в аэросмеси, массовые расходы воздуха и материала, плотность воздуха, производительность воздуходувной машины, давление воздуха и др.).
6. Все оборудование обладает гидравлическим сопротивлением и объемом внутренних полостей. Внутренние объемы оборудования (кроме материалопровода) считаются сосредоточенными. Сопротивления оборудования принимаются расположенными до или после соответствующего объема.
7. В материалопроводе параметры изменяются не только во времени, но и (или) по длине. При этом материалопровод представляется в виде суммы участков (горизонтальных, вертикальных, наклонных, отводов и др.), характер изменения сопротивления на которых постоянен.
8. Сопротивления движению воздуха через элементы пневмотранспортной установки из-за относительно небольшой длительности происходящих изменений описываются законами стационарного движения, т.е. коэффициенты сопротивления (местные и по длине) остаются неизменными (влияние нестационарности процесса на величины коэффициентов изучено недостаточно; известные работы по этому вопросу противоречивы; убедительных доказательств изменчивости коэффициентов сопротивлений нет).
9. Считается, что концентрационные, силовые и скоростные поля несущей среды и перемещаемого материала по сечениям воздуховодов и материалопроводов не изменяются, а частицы движутся по параллельным траекториям. Это предполагает квазиоднородность и позволяет избавиться от учета взаимодействия отдельных частиц друг с другом (дискретность потока учесть не просто, в частности, из-за наличия большого количества частиц неправильной формы).
10. Силы сопротивления компонентов аэросмеси при движении их вдоль стенок материалопровода учитываются эмпирическими зависимостями.
11. Температура воздуха и частиц транспортируемого материала в элементах пневмотранспортного оборудования принимается постоянной. Теплообмен и массообмен между материалопроводом и окружающей средой отсутствует. Это допущение позволяет считать процессы изотермическими и существенно упростить вид получаемых функций и их дальнейший анализ.
12. Взаимосвязь параметров системы и составляющих ее фаз (жидкой и твердой) рассматривается на основании свойств аддитивности термодинамических функций, что позволяет осуществлять прямое алгебраическое сложение соответствующих величин.
13. Силы вязкого сопротивления, ввиду их относительно малой значимости, поскольку несущей средой является воздух, не учитываются.
14. Все частицы принимаются одинакового размера и формы. Учесть все многообразие размеров частиц пока не представляется возможным. Считается, что в материалопроводе находится достаточно большое количество частиц, поэтому учет их размера по эквивалентному диаметру не приведет к значительному искажению результатов.
15. Аэросмесь представляется состоящей из двух фаз: несущей (жидкой) – воздуха и твердой (дисперсной) – перемещаемого материала. Движение частиц материала в трубе осуществляется за счет сил межфазного взаимодействия. При этом возможны три случая:
а) скорость материала υм меньше скорости воздуха υв (${{\upsilon }_{{\text{м }}}} < {{\upsilon }_{{\text{в }}}}$); в этом случае вектор аэродинамической силы направлен в сторону движения материала;
б) ${{\upsilon }_{{\text{м }}}} > {{\upsilon }_{{\text{в }}}},$ при этом вектор аэродинамической силы направлен в сторону противоположную движению материала;
в) ${{\upsilon }_{{\text{м }}}} = {{\upsilon }_{{\text{в }}}}$ – межфазное взаимодействие отсутствует.
Все три случая могут иметь место в определенные моменты на отдельных участках материалопровода. Принимая во внимание вышесказанное, на рис. 1 показаны силы взаимодействия компонентов смеси между собой и с ограждающими стенками материалопровода на выделенном участке длиной dx (в соответствии с п. 15а). Здесь и далее все силы приведены к единице объема выделенного участка трубопровода, т.е. являются объемными.
Рис. 1.
Схема сил взаимодействия компонентов дисперсного потока между собой и с ограничивающими движение стенками: D – диаметр канала; α – угол наклона оси канала; υв – скорость воздуха; υм – скорость материала; dx – элементарная длина участка канала; Р – статическое давление; dP – приращение статического давления на выделенном участке dx; Fс и Rс – силы аэродинамического сопротивления движению материала и воздуха со стороны стенок канала соответственно; Fa и Ra – силы аэродинамического сопротивления, действующие на частицы материала со стороны воздуха и на несущую фазу со стороны транспортируемого материала соответственно; Fд. в и Fд. м – удельные силы давления, действующие на несущую и дисперсную фазы соответственно; Fт. в и Fт. м – удельные силы тяжести, действующие на несущую и дисперсную фазы соответственно.
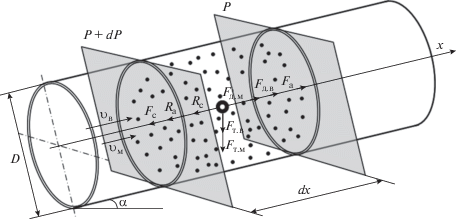
Поскольку воздух и материал движутся, а ограничивающие стенки материалопровода неподвижны, то со стороны стенок на воздушный поток будут действовать удельные (объемные) силы аэродинамического сопротивления движению воздуха Rс и материала Fc. Величина силы Rс определяется известным соотношением
(1)
${{R}_{{\text{с }}}} = \lambda \frac{{{{\rho }_{{\text{в }}}}\upsilon _{{\text{в }}}^{2}}}{{2D}},$Экспериментальным определением силы сопротивления движению материала о стенки трубопровода занимались многие исследователи. Предложены и используются на практике сотни выражений, пригодных для конкретных узких условий проведения эксперимента. В качестве варианта можно воспользоваться выражением, предложенным в [1, 9],
(2)
${{F}_{{\text{с }}}} = \frac{{{{G}_{{\text{м }}}}}}{S}\left( {\frac{{acos\alpha }}{{{{\upsilon }_{{\text{м }}}}}} + b{{\upsilon }_{{\text{м }}}}} \right),$Со стороны воздушного потока на дисперсную фазу действует аэродинамическая сила Fa, зависящая от относительной скорости фаз ${{\upsilon }_{{\text{о }}}} = {{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}},$ плотности воздуха, размера частиц дисперсной фазы, содержания дисперсной фазы в потоке и коэффициента аэродинамического взаимодействия фаз С:
(3)
${{F}_{{\text{a}}}} = \frac{3}{4}{{\rho }_{{\text{в }}}}C\sigma \frac{{\left| {{{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}}} \right|\left( {{{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}}} \right)}}{{{{d}_{{\text{э }}}}}},$Реакция дисперсной фазы Rа на воздушный поток будет численно равна аэродинамической силе Fа, но направлена в противоположную сторону, т.е. Rа = −Fа.
Вследствие разности давлений dP на границах выделенного участка dx на “жидкую” и дисперсную фазы будут действовать удельные силы давления Fд. в и Fд. м соответственно:
где ε – относительное объемное содержание воздуха в двухкомпонентном потоке (порозность аэросмеси); Р – статическое давление, Па; х – координата, м,Силы тяжести фаз Fт. в и Fт. м (соответственно воздуха и материала) выделенного объема аэросмеси определяются выражениями
где ρм – плотность частиц твердой фазы, кг/с; g – ускорение свободного падения, м/с2.Движение воздуха будет обеспечиваться за счет разности давлений с учетом изменения количества движения. К силам сопротивления движению воздуха будут относиться силы гидравлического трения воздуха о стенки материалопровода, силы взаимодействия его с частицами твердой фазы, а на наклонных и вертикальных участках и силы тяжести. Движение транспортируемого материала будет происходить также вследствие разности давлений с учетом изменения количества движения и под действием аэродинамической силы со стороны воздушного потока. В качестве сил сопротивления будут выступать силы взаимодействия транспортируемого материала со стенкой материалопровода, а на участках подъема еще и сила тяжести.
На основании принятого континуального подхода к описанию движения дисперсного потока в материалопроводе пневмотранспортной установки и изложенных выше допущений уравнения неразрывности и уравнения движения без учета сил вязкости отдельно для непрерывной и дисперсной фаз при одномерном движении запишутся следующим образом.
Уравнение неразрывности для дисперсионной фазы (воздуха)
(8)
$\frac{\partial }{{\partial t}}\left( {\varepsilon {{\rho }_{{\text{в }}}}} \right) + \frac{\partial }{{\partial x}}\left( {\varepsilon {{\rho }_{{\text{в }}}}{{\upsilon }_{{\text{в }}}}} \right) = 0,$уравнение неразрывности для дисперсной фазы (перемещаемого сыпучего материала)
(9)
${{\rho }_{{\text{м }}}}\frac{\partial }{{\partial t}}\left( \sigma \right) + {{\rho }_{{\text{м }}}}\frac{\partial }{{\partial x}}\left( {\sigma {{\upsilon }_{{\text{м }}}}} \right) = 0,$уравнение движения для дисперсионной фазы
(10)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {\varepsilon {{\rho }_{{\text{в }}}}{{\upsilon }_{{\text{в }}}}} \right) + \frac{\partial }{{\partial x}}\left( {\varepsilon {{\rho }_{{\text{в }}}}\upsilon _{{\text{в }}}^{2}} \right) = - \varepsilon \frac{{\partial P}}{{\partial x}} - \varepsilon {{\rho }_{{\text{в }}}}gsin\alpha - \\ - \,\,\lambda \frac{{{{\rho }_{{\text{в }}}}\upsilon _{{\text{в }}}^{2}}}{{2D}} - \frac{3}{4}{{\rho }_{{\text{в }}}}C\sigma \frac{{\left| {{{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}}} \right|\left( {{{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}}} \right)}}{{{{d}_{{\text{э }}}}}}, \\ \end{gathered} $уравнение движения для дисперсной фазы
(11)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {\sigma {{\rho }_{{\text{м }}}}{{\upsilon }_{E}}} \right) + \frac{\partial }{{\partial x}}\left( {\sigma {{\rho }_{{\text{м }}}}\upsilon _{{\text{м }}}^{2}} \right) = - \sigma \frac{{\partial P}}{{\partial x}} - \\ - \,\,\sigma {{\rho }_{{\text{м }}}}gsin\alpha - \frac{{{{G}_{{\text{м }}}}}}{S}\left( {\frac{{acos\alpha }}{{{{\upsilon }_{{\text{м }}}}}} + b{{\upsilon }_{{\text{м }}}}} \right) + \\ + \,\,\frac{3}{4}{{\rho }_{{\text{в }}}}C\sigma \frac{{\left| {{{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}}} \right|\left( {{{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}}} \right)}}{{{{d}_{{\text{э }}}}}}. \\ \end{gathered} $Обе фазы полностью занимают выделенный объем материалопровода, поэтому
Изложенные выше положения и допущения, а также полученные на их основе зависимости с учетом конкретных особенностей относятся к любой пневмотранспортной установке (всасывающей, нагнетающей, разветвленной, однотрубной, комбинированной и пр.). В дальнейшем с целью конкретизации и упрощения изложения процесс рассматривается на примере нагнетающей однотрубной системы пневмотранспорта с ограниченным количеством входящего в ее состав оборудования, в том числе питателем непрерывного действия (барабанный, винтовой и др.). При этом сопротивление отделителя и воздухоочистительных устройств не учитывается. Схема такой пневмотранспортной установки представлена на рис. 2.
Рис. 2.
Схема нагнетающей однотрубной пневмотранспортной установки: 1 – воздуходувная машина; 2 – ресивер; 3 – вентиль; 4 – воздуховод (2, 3, 4 – воздухоподводящее оборудование); 5 – питатель; 6 – материалопровод; 7 – отделитель.
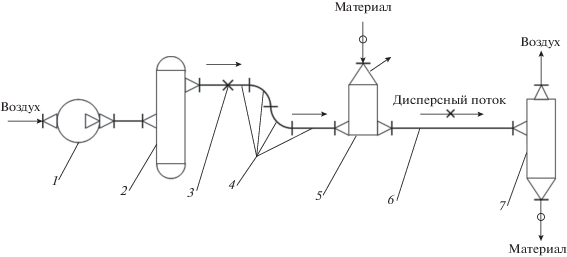
Объем воздухоподводящего оборудования в соответствии с допущением 6 считается сосредоточенным в ресивере 2, а его сопротивление – в вентиле 3. Объем ресивера и температура воздуха в нем принимаются постоянными. Принимается также, что утечки воздуха имеют место только в приемно-питающем устройстве. Сделанные упрощения позволяют избавиться от суммирования участков материалопровода, объемов и сопротивлений воздухоподводящего оборудования, утечек воздуха. При этом существо происходящих явлений сохраняется.
В соответствие с принятой физической моделью и сделанными допущениями уравнение неразрывности несущей среды для всей системы (пневмотранспортной установки) запишется в виде
(13)
${{G}_{{{\text{в м }}}}} = {{G}_{{{\text{в }}{\text{.т }}}}} + {{G}_{{\text{у }}}} + \frac{V}{{RT}}\frac{{d{{P}_{{{\text{в м }}}}}}}{{dt}},$Производительность воздуходувной машины в любой момент времени можно определить из ее характеристики (зависимости производительности от создаваемого давления). Для многих воздуходувных машин с учетом частоты движения их рабочего органа эту зависимость можно представить в виде
(14)
${{G}_{{{\text{в м }}}}} = \left( {{{G}_{{{\text{н о м }}}}} + c\left( {{\text{1}} - {{{\left( {\frac{{{{P}_{{{\text{в м }}}}}}}{{{{P}_{{{\text{н о м }}}}}}}} \right)}}^{d}}} \right)} \right){{\left( {\frac{\nu }{{{{\nu }_{{{\text{н о м }}}}}}}} \right)}^{h}},$Давление, создаваемое воздуходувной машиной, будет численно равно сумме потерь давления во всех элементах установки. Для нашего случая
(15)
${{Р }_{{{\text{в м }}}}} = {\Delta }{{Р }_{{{\text{в о }}}}} + {\Delta }{{Р }_{{{\text{п и т }}}}} + Р {\text{,}}$Потери давления в воздухоподводящем оборудовании (вентиле) ΔРво и питателе ΔРпит определяются по известным для местных сопротивлений выражениям
(16)
${\Delta }{{Р }_{{{\text{в о }}}}} = {{\xi }_{{{\text{в о }}}}}\frac{{{{{\rho }}_{{{\text{в о }}}}}{\upsilon }_{{{\text{в о }}}}^{2}}}{{\text{2}}},$(17)
${\Delta }{{Р }_{{{\text{п и т }}}}} = {{\xi }_{{{\text{п и т }}}}}\frac{{{{{\rho }}_{{{\text{п и т }}}}}{\upsilon }_{{{\text{п и т }}}}^{2}}}{{\text{2}}},$Следует заметить, что если сопротивление воздухоподводящего оборудования или питателя рассредоточено по нескольким элементам, то в выражениях (16) и (17) появится знак суммы, учитывающий общее сопротивление составляющих.
Поскольку материалопровод считается воздухонепроницаемым, массовый расход воздуха в любом сечении материалопровода при установившемся режиме движения можно определить, исходя из значений его скорости, площади поперечного сечения материалопровода, порозности и плотности в любой момент времени по формуле
Плотность воздуха ρв в оборудовании определяется давлением P и температурой воздуха Т в нем и может быть рассчитана по закону Менделеева–Клапейрона
(19)
${{\rho }_{{\text{в }}}} = \frac{{\left( {{{P}_{{{\text{aт м }}}}} + \Delta P} \right)}}{{RT}},$Утечки воздуха, как правило, имеют место только в приемно-питающем устройстве и могут быть учтены выражением
(20)
${{G}_{{\text{у }}}} = k{{\left( {\frac{{{{P}_{{{\text{п и т }}}}}}}{{{{P}_{{{\text{а т м }}}}}}}} \right)}^{u}},$Массовый расход материала в любой точке материалопровода при установившемся режиме движения определяется соотношением
При неустановившемся режиме движения силы гидродинамического взаимодействия фаз будут отличаться от сил при установившемся режиме. Причинами этого является изменяющийся режим обтекания частиц дисперсного материала, в результате которого следовало бы учитывать силу Бассе, наличие которой связано с изменением количества движения обтекающей среды, и силу инерции присоединенной массы. В [4] общую силу F, действующую на частицу в условиях нестационарного обтекания, предлагается определять по формуле
где Fa – сила аэродинамического воздействия при стационарном режиме обтекания, Н; Fм – cила инерции присоединенной к частице массы жидкости, Н; FБ – нестационарная сила (сила Бассе), вызванная переформированием пограничного слоя, Н.Учет влияния силы Бассе (предыстории движения) связан со значительными трудностями из-за недостаточной изученности ее природы и влияющих факторов. Однако для слабонестационарных процессов (к каковым можно отнести, по мнению [4], и процесс пневмотранспортирования) ею можно пренебречь.
Сила инерции присоединенной массы определяется уравнением
(23)
${{F}_{{\text{м }}}} = \frac{{\pi d_{{\text{э }}}^{3}}}{{12}}{{\rho }_{{\text{в }}}}\frac{{d{\text{(}}{{{\upsilon }}_{{\text{в }}}} - {{{\upsilon }}_{{\text{м }}}}{\text{)}}}}{{dt}}.$Если сравнить ее с силой инерции сферической частицы ${{F}_{{\text{и }}}} = \frac{{\pi d_{{\text{э }}}^{3}}}{6}{{\rho }_{{\text{м }}}}\frac{{d{{{\upsilon }}_{{\text{м }}}}}}{{dt}},$ то, вследствие того, что ρв$ \ll $ ρм, и по причине соизмеримости градиентов скоростей материала и воздуха, этой силой в большинстве случаев также можно пренебречь.
Коэффициент сопротивления λ движению воздуха со стенкой канала в выражении (1) с учетом вышесказанного можно определить по одной из известных зависимостей, например по формуле Блазиуса [11]. При этом за определяющий размер D, входящий в критерий Рейнольдса Re, будет логично принимать эквивалентный диаметр порового канала dк, который зависит от размера частиц транспортируемого материала, его концентрации в потоке, геометрических размеров канала и его формы. Ранее в [10] для трубопроводов круглого поперечного сечения получено выражение для расчета эквивалентного диаметра порового канала
(24)
${{d}_{{\text{к }}}} = \frac{{\varepsilon D{{d}_{{\text{э }}}}f}}{{\left( {{{d}_{{\text{э }}}} + 1.5\sigma D} \right)}},$Коэффициент аэродинамического сопротивления движению шарообразной частицы Сш зависит от числа Рейнольдса и определяется по одной из известных формул, например, как в [11]:
(25)
${{С }_{{\text{ш }}}} = \frac{{24}}{{{{{\operatorname{Re} }}_{{\text{м }}}}}} + 0.67\sqrt {{{C}_{{\text{ш }}}}} .$При этом число Рейнольдса Reм следует находить по относительной скорости воздуха ${{\upsilon }_{{\text{о }}}} = {{\upsilon }_{{\text{в }}}} - {{\upsilon }_{{\text{м }}}}$ и эквивалентному диаметру частицы dэ, учитывающему отличие ее формы от шарообразной, а за величину скорости воздуха υв принимать фактическое (действительное) ее значение с учетом стесненности потока, т.е. скорость воздуха в поровых каналах. Кроме того, в реальных условиях в потоке находится большое количество частиц, поэтому следует вносить поправки, например, как в [11], с помощью коэффициента стеснения потока Ест и эквивалентного диаметра dэ. С учетом этого коэффициент сопротивления С и коэффициент стеснения Ест рассчитываются по выражениям
(27)
${{E}_{{{\text{с т }}}}} = {{\left( {1 - {{{\left( {\frac{{{{d}_{{\text{э }}}}}}{D}} \right)}}^{2}}} \right)}^{{\frac{3}{2}}}}{{\varepsilon }^{3}}.$Изменение массового расхода транспортируемого материала в начале материалопровода определяется соответствующей характеристикой приемно-питающего устройства, а также предшествующей питающему устройству машиной. Наши опытные данные [12], исследования и испытания промышленных установок показали, что для многих приемно-питающих устройств эту зависимость можно представить в виде
(29)
${{G}_{{\text{м }}}} = {{G}_{0}}\left( {1 - {{{\text{e}}}^{{ - mt}}}} \right) + {\Delta }{{G}_{1}}\sin \left( {\omega t} \right) + \Delta {{G}_{2}},$Слагаемое ${{G}_{0}}{{{\text{e}}}^{{ - mt}}}$ выражения (29) учитывает изменения в подаче материала в трубопровод, вызванные пуском приемно-питающего устройства. Здесь следует учитывать, что для некоторых видов питателей (например, для камерного и некоторых разновидностей винтовых) ΔG1 зависит еще и от давления воздуха Р.
В соответствии с физической моделью скорость воздуха в дросселирующем устройстве должна определяться с учетом утечек воздуха через питающее устройство и накопления (высвобождения) воздуха в объеме предшествующего оборудования. Эту скорость можно определить из соответствующего массового расхода и площади поперечного сечения местного сопротивления. Для рассматриваемой пневмотранспортной установки с учетом принятых допущений массовый расход воздуха в местном сопротивлении (вентиле)
(30)
${{G}_{{{\text{в в }}}}} = {{G}_{{{\text{в м }}}}} - \frac{V}{{RT}}\frac{{d{{P}_{{{\text{в м }}}}}}}{{dt}}.$При определении аэродинамического сопротивления питателя по выражению (17) массовый расход воздуха в нем и соответствующая ему скорость принимаются равными их величинам в материалопроводе, если доминирующее сопротивление расположено после места утечек. Если доминирующее сопротивление питателя расположено до места утечек, то расход воздуха в питателе будет равным расходу воздуха в дросселирующем устройстве. Если сопротивление питателя нельзя считать сосредоточенным (складывается из суммы двух и выше указанных составляющих), то каждой из составляющих будет соответствовать свой расход.
АПРОБИРОВАНИЕ МОДЕЛИ
На основании уточненной физико-математической модели работы пневмотранспортной установки разработаны методика и программы расчета систем пневматического транспорта сыпучих материалов с учетом переходных и неустановившихся режимов [6, 13]. С их помощью можно отслеживать изменения основных параметров пневмотранспортирования как по длине трассы, так и во времени.
Экспериментальные исследования по проверки адекватности предложенной модели выполнены на стендах в условиях лаборатории пневматического транспорта Алтайского государственного технического университета им. И.И. Ползунова и при испытаниях промышленных систем пневматического транспорта на предприятиях пищевой промышленности. Предметом исследований являлись нагнетающие пневмотранспортные установки. Условия проведения лабораторных и промышленных испытаний сведены в табл. 1.
Таблица 1.
Диапазоны значений основных параметров систем пневмотранспортирования
| Параметр | Лабораторная установка | Промышленная установка |
|---|---|---|
| Транспортируемый материал | Мука, отруби, комбикорма, соль, оболочки крупяных культур и подсолнечника | Мука, отруби, комбикорма, соль, пшеница, оболочки крупяных культур и подсолнечника, технический углерод |
| Диаметр материалопровода, мм | 15–70 | 30–150 |
| Массовая концентрация материала в аэросмеси, кг/кг | 10–250 | 20–150 |
| Скорость транспортирующего воздуха, м/с | 1.5–20 | 4–30 |
| Потери давления, кПа | до 200 | до 250 |
В качестве примера на рис. 3, 4 приведены некоторые результаты экспериментальных исследований – диаграммы изменений избыточного давления воздуха Рвм (кривые 4) и объемного расхода воздуха Qвм (кривые 1), создаваемых воздуходувной машиной с течением времени, а также результаты расчета по предложенной модели (кривые 3 и 2 соответственно). На диаграммах отражены изменения основных параметров нагнетающей пневмотранспортной установки при транспортировании муки на расстояние 25 м. Производительность приемно-питающего устройства составляла 0.8 кг/с, а диаметр материалопровода – 38 мм. На рис. 3 представлен вариант работы пневмотранспортной установки при равномерной подаче материала в материалопровод, а на рис. 4 – при периодической подаче с учетом ΔG1 в уравнении (29).
Рис. 3.
Диаграммы изменения избыточного давления и объемного расхода воздуха, создаваемых воздуходувной машиной, при равномерной подаче материала в материалопровод: 1, 4 – расход воздуха и избыточное давление соответственно (эксперимент); 2, 3 – расход воздуха и избыточное давление соответственно (расчет по модели).
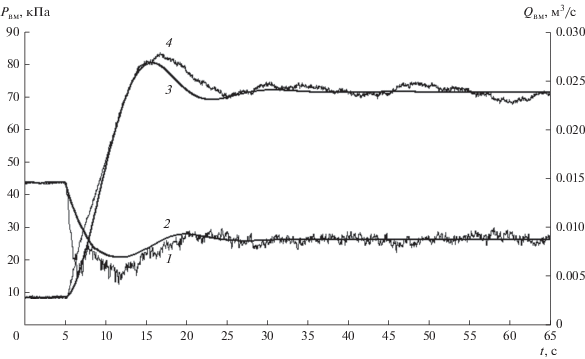
Рис. 4.
Диаграммы изменения избыточного давления и объемного расхода воздуха, создаваемых воздуходувной машиной, при периодической подаче материала в материалопровод: 1, 4 – расход воздуха и избыточное давление соответственно (эксперимент); 2, 3 – расход воздуха и избыточное давление соответственно (расчет по модели).
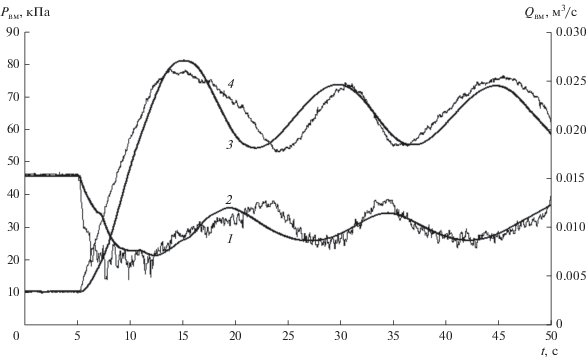
При пуске воздуходувной машины (t = 0, рис. 3, 4) избыточное давление Рвм, создаваемое воздуходувной машиной, увеличивается от 0 до давления, равного сопротивлению элементов пневмотранспортной установки движению воздушного потока. При пуске питателя (t = 5 c, рис. 3, 4, кривые 3 и 4) давление воздуха Рвм сначала возрастает, а потом стабилизируется и становится равным сопротивлению движения аэросмеси в установившемся режиме. Объемный расход воздуха Qвм при загрузке материала (рис. 3, 4, кривые 1 и 2) уменьшается вследствие четырех причин: 1) из-за роста давления и связанного с этим увеличением плотности воздуха; 2) по причине снижения производительности воздуходувной машины в соответствии с ее характеристикой; 3) из-за накопления воздуха в воздухоподводящем оборудовании; 4) по причине увеличения утечек воздуха из питающего устройства в соответствии с ростом давления.
Сравнение экспериментальных и расчетных данных (рис. 3, 4, кривые 1, 2 и 3, 4 соответственно) свидетельствует о том, что предлагаемая модель вполне адекватно описывает процессы, происходящие при пневмотранспорте сыпучего материала, как на стационарных режимах работы, так и на переходных.
Сделанные ранее сравнения результатов расчета по предложенной модели [14] и выполненным по другим методикам, а также с экспериментальными данными, полученными с применением средств непрерывного контроля, например в [15], показывают удовлетворительное соответствие. Промышленные испытания систем пневмотранспорта, разработанных на основе предлагаемой модели, например [15], также вполне удовлетворительно согласуются с результатами расчетов.
ЗАКЛЮЧЕНИЕ
Несмотря на сделанные в физико-математической модели пневмотранспортной установки допущения и упрощения, полученная система уравнений во многом отражает существо происходящих при пневмотранспорте явлений и позволяет:
определять локальные мгновенные значения параметров аэросмеси и ее компонентов;
отслеживать изменение параметров аэросмеси и ее компонентов по длине и во времени;
анализировать процесс с различными характеристиками применяемого оборудования и выбирать пневмотранспортное оборудование с характеристиками, обеспечивающими устойчивое транспортирование на рациональных режимах;
осуществлять поиск наиболее рациональных режимов транспортирования;
формулировать требования к пневмотранспортному оборудованию и организации процесса;
делать выбор рациональных способов пневмотранспортирования с конкретным оборудованием.
Экспериментальные исследования и опыт внедрения промышленных систем пневматического транспорта позволяют утверждать, что разработанные на основе результатов исследований установки отличаются повышенными технико-экономическими показателями, а параметры их работы вполне удовлетворительно соответствуют расчетным значениям.
Разработанная на основании предлагаемой модели компьютерная программа [6] позволяет прогнозировать изменение параметров работы систем пневмотранспорта. Результаты такого компьютерного расчета (табличные данные и диаграммы) дают проектировщику обширную информацию о параметрах процесса пневмотранспортирования (в том числе в переходных и неустановившихся режимах работы системы). Они позволяют учесть дополнительные факторы, оказывающие влияние на работу пневмотранспортной установки, подобрать рациональные виды оборудования, разработать системы с повышенными технико-экономическими показателями, предусмотреть мероприятия, позволяющие избежать появления неустойчивости процесса.
ОБОЗНАЧЕНИЯ
| a | коэффициент, учитывающий физико-механические свойства транспортируемого материала и трубопровода, м/с2 |
| b | коэффициент, учитывающий физико-механические свойства транспортируемого материала и трубопровода, 1/м |
| С | коэффициент аэродинамического взаимодействия между фазами |
| Сш | коэффициент аэродинамического сопротивления движению шарообразной частицы |
| с | коэффициент расхода, кг/с |
| D | диаметр материалопровода, м |
| d | показатель степени |
| dк | эквивалентный диаметр порового канала, м |
| dэ | эквивалентный диаметр частиц, м |
| Ест | коэффициент стеснения потока |
| F | сила, действующая на частицу материала в условиях нестационарного обтекания, Н |
| Fa | сила аэродинамического воздействия при стационарном режиме обтекания частицы, Н |
| FБ | нестационарная сила (сила Бассе), вызванная переформированием пограничного слоя, Н |
| Fc | сила аэродинамического сопротивления движению материала со стороны стенок материалопровода, Н/м3 |
| Fи | cила инерции частицы, Н |
| Fм | cила инерции присоединенной к частице массы жидкости, Н |
| Fa | удельная аэродинамическая сила, действующая на дисперсную фазу со стороны воздушного потока, Н/м3 |
| Fт. в, Fт. м | удельные силы тяжести, действующие на выделенный объем воздуха и материала на участке dx, Н/м3 |
| Fд. в, Fд. м | удельные силы давления, действующие на воздушный поток и дисперсную фазу на участке dx, Н/м3 |
| f | коэффициент формы частиц |
| G0 | средняя производительность пневмоустановки в установившемся режиме работы, кг/с |
| ΔG1 | изменения производительности, вызванные неравномерностью работы приемно-питающего устройства или предшествующей машиной, кг/с |
| ΔG2 | возмущения в подаче материала, вызванные случайными факторами, кг/с |
| Gв, Gм | массовый расход воздуха и материала, кг/с |
| Gвм | производительность (массовый расход) воздуходувной машины, кг/с |
| Gвт | массовый расход воздуха в материалопроводе, кг/с |
| Gном | номинальное (паспортное) значение массового расхода воздуходувной машины, кг/с |
| Gу | утечки воздуха через приемно-питающее устройство, кг/с |
| g | ускорение свободного падения, м/с2 |
| h | показатель степени |
| k | коэффициент утечек воздуха из приемно-питающего устройства, кг/с |
| m | коэффициент, зависящий от типа приемно-питающего устройства, 1/с |
| Р | статическое давление, Па |
| Ратм | атмосферное давление, Па |
| Pвм | избыточное давление воздуха в ресивере (при сделанных допущениях численно равно давлению воздуха, создаваемому воздуходувной машиной), Па |
| Pном | номинальное (паспортное) значение давления, создаваемое воздуходувной машиной при номинальном массовом расходе, Па |
| ΔР | потери давления в материалопроводе, Па |
| ΔРво | потери давления в воздухоподводящем оборудовании (вентиле), Па |
| ΔРпит | потери давления в приемно-питающем устройстве, Па |
| R | газовая постоянная воздуха, Дж/(кг К) |
| Ra | удельная аэродинамическая сила, действующая на воздушный поток со стороны дисперсной фазы, Н/м3 |
| Rс | удельная сила аэродинамического сопротивления движению воздуха со стороны стенок материалопровода, Н/м3 |
| S | площадь поперечного сечения материалопровода, м2 |
| Т | температура, К |
| t | время, с |
| u | показатель степени |
| V | объем воздухоподводящего оборудования (ресивера), м3 |
| х | координата, м |
| α | угол наклона материалопровода, град |
| ε | порозность аэросмеси |
| λ | коэффициент аэродинамического сопротивления движению воздуха |
| μ | динамическая вязкость воздуха, Па с |
| ν | частота движения рабочего органа воздуходувной машины, 1/с |
| νном | номинальная частота движения рабочего органа воздуходувной машины, 1/с |
| ξво | коэффициент сопротивления вентиля |
| ξпит | коэффициент сопротивления питателя |
| ρв | плотность воздуха, кг/м3 |
| ρво | плотность воздуха в вентиле, кг/м3 |
| ρм | плотность частиц материала, кг/м3 |
| ρпит | плотность воздуха в питателе, кг/м3 |
| σ | объемное содержание материала в аэросмеси |
| υв | скорость воздуха, м/с |
| υм | скорость материала, м/с |
| υо | относительная скорость воздуха, м/с |
| υпит | скорость воздуха в питателе, м/с |
| ω | частота изменения возмущающего фактора, 1/с |
| $\operatorname{Re} = \frac{{{{\upsilon }_{{\text{в }}}}D{{\rho }_{{\text{в }}}}}}{\mu }$ | число Рейнольдса |
| ${{\operatorname{Re} }_{{\text{м }}}} = \frac{{{{\upsilon }_{{\text{о }}}}{{d}_{{\text{к }}}}{{\rho }_{{\text{в }}}}}}{\mu }$ | число Рейнольдса для частиц материала |
Список литературы
Тарасов В.П. Совершенствование работы нагнетающих пневмотранспортных установок. Дис. … канд. техн. наук. М.: Московский технологический институт пищевой промышленности, 1986.
Тарасов В.П. Элементы теории работы однотрубной пневмотранспортной установки // Известия вузов. Пищевая технология. 2005. № 5–6. С. 82.
Островский Г.М. Пневматический транспорт сыпучих материалов в химической промышленности. Л.: Химия, 1984.
Островский Г.М. Прикладная механика неоднородных сред. СПб.: Наука, 2000.
Гусев М.В. Снижение энергоемкости процесса транспортирования зернопродуктов в мельничных пневмотранспортных установках. Дис. … канд. техн. наук. М.: ВНИИЗ, 1983.
Мухопад К.А., Яковлев А.В., Кошелев К.Б., Тарасов В.П. Расчет пневмотранспортной установки. Свидетельство о государственной регистрации программы для ЭВМ № 2012616372. 2012.
Нигматулин Р.И. Основы механики гетерогенных сред. М.: Наука, 1978.
Смоловик В.А., Росляк А.Т. Расчет низкоскоростного пневмотранспорта при высокой концентрации сыпучего материала // Теорет. основы хим. технологии. 2004. Т. 38. № 2. С. 202.
Ярославцев Д.Е., Тарасов В.П. Потери давления в материалопроводе при пневмотранспортировании муки [Электронный ресурс] // Горизонты образования. Научно-образовательный журнал АлтГТУ. 2007. Вып. 9. URL: http://edu.secna.ru/media/f/pp2.pdf
Тарасов В.П., Курилов А.Н. Об определении размера канала (эквивалентного диаметра) в двухфазных системах // Материалы международной научно-практической конференции “Современные проблемы техники и технологии пищевых производств”. Барнаул, 2016. С. 148.
Альтшуль А.Д., Киселев П.Г. Гидравлика и аэродинамика (основы механики жидкости). М.: Стройиздат, 1975.
Мухопад К.А., Яковлев А.В., Тарасов В.П., Кошелев К.Б. Анализ работы однотрубной нагнетающей пневмотранспортной установки // Вестник КрасГАУ. 2007. № 6. С. 184.
Яковлев А.В., Мухопад К.А., Кошелев К.Б., Тарасов В.П. Расчет всасывающей многотрубной пневмотранспортной установки. Свидетельство о государственной регистрации программы для ЭВМ № 2012661433. 2012.
Мухопад К.А., Тарасов В.П., Ярославцев Д.Е. Автоматизированный расчет нагнетающих пневмотранспортных установок с учетом неустановившихся режимов транспортирования // Сб. тр. XI научно-практической конференции “Современные проблемы техники и технологии пищевых производств”. Барнаул, 2008. С. 364.
Береснев С.В., Тарасов В.П. Анализ работы пневмотранспортных установок новосибирского КХП № 1 с учетом переходных и неустановившихся режимов [Электронный ресурс] // Горизонты образования. Научно-образовательный журнал АлтГТУ. 2012. Вып. 14. URL: http://edu.secna.ru/media/f/mapp___pdf
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


