Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 97-104
Производительность осевых мешалок в смесителях с отражательными перегородками
И. В. Доманский a, *, А. И. Мильченко b, В. А. Некрасов a, Н. В. Воробьев-Десятовский b
a Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия
b АО “ПОЛИМЕТАЛЛ ИНЖИНИРИНГ”
Санкт-Петербург, Россия
* E-mail: domanskij.iv@gmail.com
Поступила в редакцию 18.05.2019
После доработки 06.09.2019
Принята к публикации 18.09.2019
Аннотация
На основе уравнения момента импульса получена аналитическая связь критерия производительности осевой мешалки с критерием мощности. Это соотношение выведено при допущении о неизменности поля тангенциальных скоростей по высоте смесителя. На основе имеющихся в литературе экспериментально найденных полей скоростей получено уравнение для расчета коэффициента пропорциональности между производительностью мешалки и циркуляционным расходом. Приведено сопоставление опубликованных опытных значений критерия производительности мешалки и критерия циркуляционного расхода с расчетными по предложенным уравнениям.
ВВЕДЕНИЕ
Типовые смесители с отражательными перегородками и осевыми мешалками относятся к основному виду технологического оборудования многих современных производств химической, гидрометаллургической, биотехнологической и пищевой промышленности [1–5].
Расход жидкости, проходящий через зону мешалки (производительность мешалки), Q1 и полный расход жидкости в циркуляционном контуре смесителя (циркуляционный расход) Q – важнейшие технологические характеристики процесса перемешивания. Совместно с критерием мощности NР, широко представленным в специальной литературе [1–16], они определяют выбор параметров мешалки, привода и других конструктивных элементов механического перемешивающего устройства. От циркуляционного расхода Q зависит кратность циркуляции в смесителе и степень равномерности распределения компонентов в перемешиваемой среде, а следовательно, и интенсивность протекающих в ней технологических процессов [5–7, 16]. Знание производительности мешалки Q1 позволяет вычислить и такую важную, по мнению авторов работ [15, 16], характеристику процесса перемешивания, как поток импульса, проходящий через зону мешалки.
Циркуляционный расход жидкости можно представить в виде двух составляющих [6, 8, 9, 19, 20]
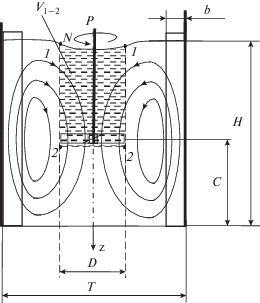
Составляющая Q2 – дополнительный поток, увлекаемый потоком Q1 в направлении циркуляции – обычно по оси аппарата вниз (down-pumping) [1–7]) (рис. 1), а часто – по оси аппарата вверх (up-pumping).
При использовании осевых мешалок в аппарате с перегородками создается один циркуляционный контур. При этом в работах [8–12, 18, 19] экспериментально показано, что в зоне расположения осевой мешалки площади поперечных сечений нисходящего и восходящего потоков примерно равновелики, поэтому площадь сечения потока Q можно вычислить по формуле
где Т – диаметр аппарата, м.В настоящее время в научно-технической литературе опубликовано большое число работ [1–6, 8, 9, 11–16, 18–23], в которых приводятся опытные данные как о производительности Q1 осевых мешалок различных конструкций, так и о циркуляционном расходе Q в смесителях с отражательными перегородками. Одной из важнейших характеристик смесителей является критерий мощности Np:
численное значение которого в анализируемых далее работах обычно изменялось в диапазоне 0.5÷2.4.
Цель работы. Обобщение накопленных опытных данных по оценке Q, Q1, необходимой для практики, возможно на основе разработки научно обоснованного математического описания этой важной прикладной задачи.
Так, в работах [1, 6, 13] приведен анализ баланса подводимой энергии, необходимой для создания насосного эффекта мешалки, и энергии, которая затрачивается при циркуляции жидкости в смесителе. Этот упрощенный подход позволил на базе ряда допущений установить ориентировочную связь критерия расхода
с критерием мощности мешалки Np в виде
(5)
${{{\text{N}}}_{{{{{\text{Q}}}_{{\text{1}}}}}}} = {{\left( {k{{{\text{N}}}_{{\text{p}}}}} \right)}^{{0.33}}}.$Уравнение (5) содержит экспериментально найденный коэффициент k = 0.51÷0.73, который справедлив для случая применения трех типов широко применяемых осевых мешалок с плоскими и изогнутыми лопастями [13]. Критерий мощности изменялся при этом в диапазоне Np = 0.2÷2.0.
Непостоянство коэффициента k свидетельствует о том, что соотношение (5) лишь частично учитывает (через критерий мощности Np) существенное влияние на искомый параметр NQ1 клиренса осевых мешалок C, а также числа и типоразмеров отражательных перегородок сосуда.
В работах [15, 16] для целого ряда типов осевых мешалок с применением лазерной техники для измерения полей скоростей получена зависимость
(6)
${\text{Mo}} = \left( {1.43{\kern 1pt} \div {\kern 1pt} 1.46} \right){\text{N}}_{{{{{\text{Q}}}_{1}}}}^{2},$устанавливающая связь критерия производительности NQ1 с важным для оценки макроперемешивания [16] критерием потока импульса
(7)
${\text{Mo}} = \frac{{\int\limits_0^{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0em} 2}} {\rho u_{{\text{z}}}^{2}2\pi rdr} }}{{\rho {{N}^{2}}{{D}^{4}}}}.$Отметим, что, если уравнение импульсов решить совместно с уравнением (6), то можно найти связь критерия производительности с осевой силой, действующей на осевую мешалку. Однако наличие решения в таком виде не представляет интереса, поскольку в настоящее время объем исследований осевой силы весьма ограничен.
Постановка задачи. В данной работе предлагается более полное математическое описание указанной выше задачи, которое позволяет обобщить результаты опытов ряда исследователей при помощи новых расчетных зависимостей для вычисления как производительности мешалки Q1, так и циркуляционного расхода жидкости Q в смесителе. Эти зависимости позволили обобщить результаты опытов ряда исследователей. Последующий анализ выполнен на основе уравнения момента импульса, которое является преобразованной формой второго закона Ньютона [17].
ПРОИЗВОДИТЕЛЬНОСТЬ ОСЕВОЙ МЕШАЛКИ
Уравнение момента импульса [17] в случае его применения к описанию поведения жидкости, находящейся в произвольном по величине объеме V с площадью поверхности S, имеет вид
в котором момент импульса L и поток момента импульса J рассчитываются соответственно по формулам
Поскольку при установившемся режиме перемешивания ∂L/∂τ = 0, то уравнение (8) в проекции на вертикальную ось z имеет вид
гдеПри решении поставленной задачи в качестве контрольного объема примем круговой цилиндр V1–2 диаметром D, равным диаметру мешалки, и высотой Н–С (рис. 1). Контрольный объем V1–2 ограничивают следующие три поверхности:
1. Свободная поверхность S1 перемешиваемой жидкости.
2. Боковая поверхность цилиндра с образующей 1–2 S1–2 = πD(H–C).
3. Плоская поверхность S2 = πD2/4, расположенная под мешалкой.
Таким образом, в формуле (12) необходимо учитывать поток момента импульса через поверхность контрольного объема
В рассматриваемом случае очевидно, что на поверхности S1 вертикальная составляющая скорости un = 0. Следовательно, согласно уравнению (12) и поток момента импульса J1 = 0.
Уравнение (12) при нахождении потока момента импульса, входящего через боковую поверхность цилиндра S1–2, можно представить в виде
где β1–2 – поправочный коэффициент для входящего в выделенный объем жидкости потока момента импульса.При известных полях тангенциальных ut и радиальных скоростей ur на поверхности S1–2 значение коэффициента β1–2 можно вычислить с учетом (12) и (14) по формуле
(15)
${{\beta }_{{1 - 2}}} = \frac{{2\pi {{R}_{{\text{M}}}}}}{{{{Q}_{1}}{{u}_{{\text{M}}}}}}\int\limits_0^{H - C} {{{u}_{{\text{r}}}}{{u}_{{\text{t}}}}dz} .$Если принять, что ut при r = RM не зависит от z и равна uM, то из (15) можно найти ориентировочное значение β1–2 = 1.
Уравнение для расчета потока момента импульса, выходящего через поверхность S2, расположенную непосредственно под мешалкой, можно представить в виде
где β2 – поправочный коэффициент для выходящего из выделенного объема жидкости потока момента импульса.При известных полях тангенциальных ut и осевых скоростей uz в сечении 2 (рис. 1) значение коэффициента β2 можно вычислить с учетом (12) и (16) по формуле
(17)
${{\beta }_{2}} = \frac{{2\pi }}{{{{Q}_{1}}{{u}_{{\text{M}}}}{{R}_{{\text{M}}}}}}\int\limits_0^{{{R}_{M}}} {{{u}_{{\text{z}}}}{{u}_{{\text{t}}}}{{r}^{2}}dr} .$Таким образом, суммарный поток момента импульса, входящий в уравнение (12), можно описать с учетом (14) и (16) выражением
(18)
${{J}_{z}} = ({{\beta }_{2}}--{{\beta }_{{1 - 2}}})r{{Q}_{1}}{{u}_{{\text{M}}}}{{R}_{{\text{M}}}}.$Следует найти также и составляющие момента Mz, которые действуют на выделенный объем жидкости V1–2. Это момент на валу мешалки MM и моменты сил, действующих на поверхностях выделенного объема S1, S1–2 и S2:
При известной величине мощности на перемешивание Р момент, передаваемый от мешалки к перемешиваемой жидкости, составляет
Момент силы трения на свободной поверхности S1 жидкости можно принять равным нулю, т.е.
В рассматриваемом смесителе с отражательными перегородками крутящий момент на валу мешалки уравновешивается в основном моментом силы сопротивления, возникающей при обтекании перегородок [5]. В связи с этим малый момент M2, передаваемый посредством перемешиваемой жидкости на дно аппарата, в первом приближении можно также принять равным нулю.
Примем, что крутящий момент от жидкости, находящейся в зоне действия мешалки, к жидкости, непосредственно примыкающей к этой зоне, как сверху, так и снизу, передается в равной мере. В таком случае выражение для расчета момента силы трения на боковой поверхности S1–2 выделенного объема можно вычислить по формуле
а суммарный момент (19) с учетом (20)–(22) получить в виде
После подстановки (18) и (23) в (11) получим уравнение для расчета расхода жидкости через зону мешалки (производительность мешалки) в виде
(24)
${{Q}_{1}} = \frac{{0.5{{M}_{{\text{M}}}}}}{{\Delta \beta \rho {{u}_{{\text{M}}}}{{R}_{{\text{M}}}}}},$Для вычисления Q1 по (24) необходимо знать величину средней тангенциальной составляющей скорости жидкости uM при r = RM. Для нахождения ее величины воспользуемся данными работы [5], в которой принято, что крутящий момент на валу мешалки уравновешивается в основном моментом силы сопротивления, возникающей при обтекании перегородок:
(26)
$\zeta {{k}_{{\text{B}}}}bh\left( {{{R}_{{\text{V}}}} - 0.5b} \right)\frac{{\rho u_{{{\text{TB}}}}^{2}}}{2} = {{M}_{{\text{M}}}}.$При этом поле тангенциальных скоростей при r > RM, т.е. вне зоны прямого взаимодействия мешалки и жидкости, как правило, принимается в виде уравнения для свободного вихря utr = const, или
С учетом соотношения (25) уравнение (27) можно записать в виде
(28)
${{u}_{{\text{M}}}}{{R}_{{\text{M}}}} = {{\left( {\frac{{\pi {{M}_{{\text{M}}}}}}{{2\rho ZD}}} \right)}^{{0.5}}},$(29)
$Z = \frac{\pi }{2}\zeta {{k}_{{\text{п}}}}\frac{b}{T}\frac{h}{H}\frac{{{{\Gamma }_{{\text{H}}}}}}{{\left( {1 - {b \mathord{\left/ {\vphantom {b T}} \right. \kern-0em} T}} \right)}}.$С учетом (28) и (29) выражение (24) примет вид
(30)
${{Q}_{1}} = \frac{1}{{\Delta \beta }}{{\left( {\frac{{2{{M}_{{\text{M}}}}Z}}{{\pi \rho }}D} \right)}^{{0.5}}},$или в безразмерном виде с учетом (3), (4) и (20)
(31)
${{{\text{N}}}_{{\text{Q}}}}_{{_{{\text{1}}}}} = \frac{1}{{2\pi \cdot \Delta \beta }} \cdot {{\left( {\frac{{{{{\text{N}}}_{{\text{P}}}}Z}}{{{{\Gamma }_{{\text{D}}}}}}} \right)}^{{0.5}}}.$Таким образом, уравнение (31) с учетом (4) теоретически обоснованно описывает влияние весьма широкого круга конструктивных и энергетических параметров смесителя с отражательными перегородками на производительность осевых мешалок по сравнению с равенством (5).
РАСЧЕТ ПРОИЗВОДИТЕЛЬНОСТИ ЦИРКУЛЯЦИОННОГО КОНТУРА СМЕСИТЕЛЯ
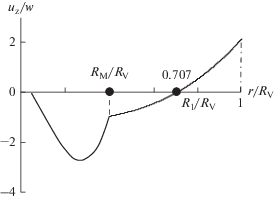
Для расчета производительности мешалки Q1 и циркуляционного расхода Q воспользуемся экспериментальными полями скоростей [12, 18] на уровне расположения мешалки. Опыты, представленные в [12], показали, что в безразмерных координатах для осевых мешалок различных конструкций поля скоростей практически совпадают. Количество лопастей в этом исследовании изменялось от 2 до 6 (5 значений), а угол их наклона составлял от 20° до 45° (6 значений). Поле осевых скоростей в безразмерном виде, если в качестве масштаба скорости принять среднюю расходную скорость в циркуляционном контуре w = Q/S1, представлено на рис. 2.
Для нахождения отношения Q/Q1 достаточно знать распределение скоростей в периферийной зоне аппарата, в области RM < r < RV. Обработка опытных данных [12] в этой области позволила получить уравнение в виде
(32)
$\frac{{{{u}_{{\text{z}}}}}}{w} = 3.3{{\left( {\frac{r}{{{{R}_{{\text{V}}}}}}} \right)}^{3}} - 1.17.$В соответствии с равенством (32) при r = R1 = = 0.707RV скорость uz = 0, т.е. при r > R1 = 0.707RV на уровне расположения мешалки наблюдается восходящее течение (up-pumping), а при r < R1 – нисходящее (down-pumping).
Отношение циркуляционного расхода Q к уже найденному согласно (30) расходу через зону мешалки Q1 можно вычислить по формуле
(33)
$\gamma = \frac{Q}{{{{Q}_{1}}}} = \frac{{{{{\text{N}}}_{Q}}}}{{{{{\text{N}}}_{{{{Q}_{1}}}}}}} = \frac{Q}{{Q - {{Q}_{2}}}} = \frac{{\int\limits_{{{R}_{1}}}^{{{R}_{{\text{V}}}}} {{{u}_{{\text{z}}}}rdr} }}{{\int\limits_{{{R}_{{\text{M}}}}}^{{{R}_{{\text{V}}}}} {{{u}_{{\text{z}}}}rdr} }}.$Вычисления, которые выполнены по уравнению (33) с учетом соотношения (32), позволили установить, что параметр γ зависит лишь от симплекса ГD и при 0.25 < Г < 0.5 может быть вычислен по упрощенной формуле
Критерий же циркуляционного расхода NQ можно рассчитать с учетом соотношения (33) по простой зависимости
Таким образом, в результате теоретического анализа получено уравнение для расчета критерия производительности мешалки (31) и формула (35) для расчета критерия циркуляционного расхода в смесителе. Эти уравнения содержат коэффициент Δβ, численное значение которого можно вычислить по (25) с учетом (15) и (17), если известны поля скоростей на поверхности S1–2 и S2 (см. рис. 1).
Если предположить, что поля тангенциальных и осевых скоростей в безразмерном виде остаются неизменными, то и численное значение Δβ было бы также неизменным. Однако, как показали выполненные далее вычисления, решение оказалось более сложным.
РАСЧЕТ КОЭФФИЦИЕНТА Δβ
Нахождение расчетной зависимости для определения Δβ и проверка справедливости уравнений (31) и (35) проведены далее на основе опытных данных, имеющихся в литературе [8, 9, 11–14, 16, 19–23].
В этих работах безразмерные переменные, входящие в уравнение (31), изменялись в следующих диапазонах:
− критерий мощности Np = 0.5–2.4 (минимальное значение при использовании трехлопастной мешалки с углом атаки α = 20°; максимальное – шестилопастной мешалки с углом атаки α = 45°);
− симплексы ΓD = 0.25–0.5 и ΓC = 0.25–0.33;
− конструктивные параметры сосуда, определяющие величину переменной Z (количество отражательных перегородок kb = 4; высота перегородок h = T = H; относительная ширина перегородок b/T = 1/15; 1/12; 1/10), что соответственно приводит в итоге к следующим значениям переменной Z = 0.09; 0.14; 1.4.
Опытные значения коэффициента Δβоп вычислялись на основе (31) по формуле
(36)
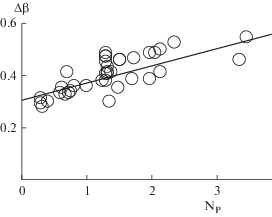
$\Delta {{\beta }_{{{\text{оп}}}}} = \frac{{\text{1}}}{{2\pi {{{\text{N}}}_{{{{{\text{Q}}}_{{\text{1}}}}\left( {{\text{оп}}} \right)}}}}}{{\left( {\frac{{{{{\text{N}}}_{{\text{P}}}}Z}}{{{{{\text{Г}}}_{{\text{D}}}}}}} \right)}^{{0.5}}}.$Результаты расчетов, приведенные на рис. 3, показывают, что численное значение коэффициента Δβ изменяется в узком диапазоне и зависит от критерия мощности Np. Применение метода наименьших квадратов позволяет аппроксимировать опытную зависимость уравнением
СОПОСТАВЛЕНИЕ ОПЫТНЫХ И РАСЧЕТНЫХ ДАННЫХ
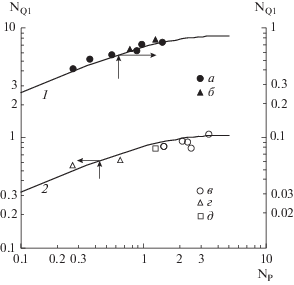
Уравнение (31) с учетом зависимости (37) позволяет вычислить критерий производительности мешалки. На рис. 4 приведено сопоставление опытных и расчетных данных для двух типов аппаратов с параметрами:
I. – при ГD = 0.41, ГС= 0.33, Z = 1.14;
II. – при ГD = 0.33, ГС = 0.33, Z = 1.4.
В обоих случаях наблюдается уменьшение степени роста критерия производительности NQ1 с ростом критерия мощности NР. Если аппроксимировать представленную на рис. 4 зависимость степенным одночленом, то при низких значениях NP показатель степени окажется равным 0.5. Если же NP = 0.8–2.6, то показатель составит –0.33, что соответствует часто применяемой [6, 13] эмпирической зависимости (5).
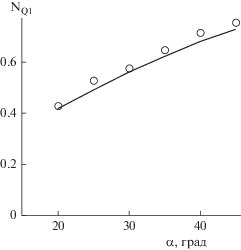
Данные работы [12], представленные на рис. 5, подтверждают, что критерий мощности NР мешалки в полной мере учитывает влияние угла наклона α лопастей на критерий циркуляционного расхода.
Рис. 5.
Зависимость критерия производительности мешалки NQ1 от угла наклона стандартных лопастей α: линия – расчет по формуле (31); точки – опытные данные [12].
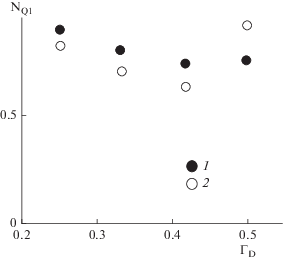
Сопоставление опытных и расчетных данных, представленное на рис. 6, свидетельствует о том, что уравнение (31) правильно отражает влияние симплекса ГD на критерий производительности мешалки.
Рис. 6.
Зависимость критерия производительности мешалки NQ1 от ГD: линия – расчет по (31); точки – опытные данные [21].
На рис. 7 приведено сопоставление значений коэффициента пропорциональности между критерием циркуляционного расхода и критерием производительности мешалки в зависимости от симплекса ГD. Линия построена на основе уравнения (34), а точки являются результатом вычисления отношения опытных значений NQ(оп) к найденному значению NQ1 по уравнению (31), т.е.
(38)
${{\gamma }_{{{\text{оп}}}}} = {{{{{\text{N}}}_{{{\text{Q(оп)}}}}}} \mathord{\left/ {\vphantom {{{{{\text{N}}}_{{{\text{Q(оп)}}}}}} {{{{\text{N}}}_{{{{{\text{Q}}}_{{\text{1}}}}}}}}}} \right. \kern-0em} {{{{\text{N}}}_{{{{{\text{Q}}}_{{\text{1}}}}}}}}}.$Рис. 7.
Зависимость коэффициента γ от симплекса подобия ГD: линия – расчет по формуле (34); точки – на основе опытных данных [8, 19].
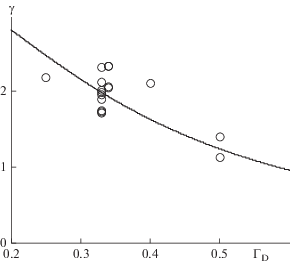
Приведенное сопоставление подтверждает справедливость уравнения (34).
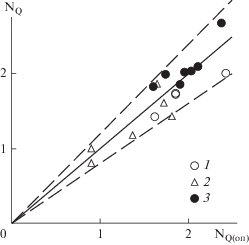
И, наконец, на рис. 8 приведена общая корреляция результатов расчета критерия циркуляционного расхода по уравнению (35) и опытных данных [8, 9, 12, 19, 20, 22].
Разброс в пределах 12–15% на итоговых графиках (рис. 3–8) изученных параметров смесителей можно считать приемлемым для практики в связи со сложностью и недостаточной освоенностью лазерных экспериментов и другой применявшейся измерительной техники. Отметим также, что на значительные расхождения различных литературных данных по оценке производительности мешалок указывается, например, в монографии [2].
ЗАКЛЮЧЕНИЕ
На основе теоретического анализа и экспериментальных данных в опубликованных исследованиях получены уравнения для расчета критерия производительности осевой мешалки и критерия циркуляционного расхода смесителя. Эти уравнения обобщают опытные данные для осевых мешалок различной геометрии, учитывают влияние на циркуляционный расход целого ряда конструктивных параметров смесителя, позволяют более обосновано подойти к выбору конструкции смесителя.
ОБОЗНАЧЕНИЯ
| b | ширина отражательных перегородок, м |
| C | клиренс мешалки, м |
| D | диаметр мешалки, м |
| H | высота заполнения аппарата, м |
| h | высота отражательной перегородки, м |
| J | поток момента импульса, Н м |
| Jz | поток момента импульса в проекции на ось z через поверхность S, Н м |
| kB | число перегородок |
| L | момент импульса, Н м с |
| M | крутящий момент, Н м |
| Mz | суммарный момент, Н м |
| Mo | критерий импульса |
| N | частота вращения, с–1 |
| NР | критерий мощности мешалки |
| NQ | критерий циркуляционного расхода в смесителе |
| NQ1 | критерий производительности мешалки |
| P | мощность перемешивания, Вт |
| Q | циркуляционный расход жидкости, м3/c |
| Q1 | производительность мешалки, м3/c |
| Q2 | расход жидкости через кольцевое сечение с радиусами RM, R1, м3/с |
| R1 | радиус реверса осевого течения жидкости, м |
| RM | радиус мешалки, м |
| RV | радиус сосуда, м |
| r | текущий радиус, м |
| T | диаметр сосуда, м |
| ut | окружная скорость жидкости, м/с |
| uTB | окружная скорость набегания потока на перегородку, м/с |
| uz | осевая скорость жидкости, м/с |
| w | средняя скорость в циркуляционном контуре, м/с |
| α | угол наклона лопастей к горизонту, град |
| β1–2 | поправочный коэффициент для входящего в выделенный объем жидкости потока момента импульса |
| β2 | поправочный коэффициент для выходящего из выделенного объема жидкости потока момента импульса |
| ζ | коэффициент сопротивления лопасти мешалки |
| ρ | плотность жидкости, кг/м3 |
| ΓC = C/T | симплекс геометрического подобия |
| ΓD = D/T | симплекс геометрического подобия |
| ΓH = H/D | симплекс геометрического подобия |
Список литературы
Strek F. Michani a michaci zarizeni. Prelozili a dopolnili I. Fort, J. Kratky, J. Vlcek. Praha, 1977.
Kraume M. Homohenisieren in Ruhrbehaltern // Mischen und Ruhren. Grundlagen und moderne Ferfahren / Herausgegeben von Matthias Kraume. Weinheim: Wiley-VCH, 2003.
Oldshue J.Y. Fluid Mixing Technology. New York: McGraw-Hill, 1983.
Hemrajani R.R., Tatterson G.B. Mechanically Stirred Vessels // Handbook of Industrial Mixing: Science and Practice / Eds. Paul E.L., Atiemo-Obeng V.A., Kresta S.M. Hoboken, N.J.: Wiley, 2004.
Брагинский Л.Н., Бегачев В.И., Барабаш В.М. Перемешивание в жидких средах. Физические основы и инженерные методы расчета. Л.: Химия, 1984.
Nienow A.W. On impeller circulation and mixing effectiveness in the turbulent flow regime // Chem. Eng. Sci. 1997. V. 52. № 15. P. 2557.
Roussinowa V., Kresta S. Comparison of continuums blend time and residence time distribution models for a stirred tank // Ind. Eng. Chem. Res. 2008. V. 47. № 10. P. 3532.
Ranade V.V., Joshi J.B. Flow generated by pitched blade turbines I: Measurements using laser Doppler anemometer // Chem. Eng. Commun. 1989. V. 81. № 1. P. 197.
Aubin J., Mavros P., Fletcher D.F., Bertrand J., Xuereb C. Effect of axial agitator configuration (up-pumping, down-pumping, reverse rotation) on flow patterns generated in stirred vessels // Chem. Eng. Res. Des. 2001. V. 79. P. 845.
Павлушенко И.С., Костин Н.М., Ячкула Б.Н. Изучение процесса перемешивания. Сообщение 1 и 2 // Труды Ленинградского технологического института имени Ленсовета. Вып. XLI. Л.: Госхимиздат, 1957. С. 118.
Wu J., Pullum L. Performance Analysis of Axial-Flow Mixing Impellers // AIChE J. 2000. V. 46. P. 489.
Wu J., Zhu Y., Pullum L. The Effect of Impeller Pumping and Fluid Rheology on Solids Suspension in a Stirred Vessel // Can. J. Chem. Eng. 2001. V. 79. P. 177.
Fort I., Medek J. Hydraulic and energetic efficiency of impellers with inclined blades // Proc. 6th European Conference on Mixing. Pavia, Italy, 1988.
Fort I., Kysela B., Jirout T. Flow characteristics of axial high speed impellers // Chem. Process Eng. 2010. V. 31. P. 661.
Brown D.A.R. Mixer performance characteristics: impeller and process efficiency // Mixing XXII. Victoria, BC, Canada, 2010.
Machado M.B., Nunhez J.R., Nobes D., Kresta S.M. Impeller Characterization and Selection: Balancing Efficient Hydrodynamics with Process Mixing Requirements // AIChE J. 2012. V. 58. № 8. P. 2573.
Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1994.
Pianko-Oprych P., Nienow A.W., Barigou M. Positron emission particle tracking (PEPT) compared to particle image velocimetry (PIV) for studying the flow generated by a pitched-blade turbine in single phase and multi-phase systems // Chem. Eng. Sci. 2009. V. 64. P. 4955.
Kumaresan T., Joshi J.B. Effect of impeller design on the flow pattern and mixing in stirred tanks // Chem. Eng. J. 2006. V. 115. P. 173.
Mishra V.P., Dyster K.N., Jaworski Z., Nienow A.W., Mckemmie J. A study of an Up- and a Down-Pumping wide blade hydrofoil impeller: Part I // Can. J. Chem. Eng. 1998. V. 76. P. 577.
Hicks R.W., Morton J.R., Fenic J.G. How to design agitators for desired process response // Chem. Eng. April 1976. P. 102.
Shaw J.A. Succeed at solids suspension // Chem. Eng. Prog. May 1992. P. 34.
Jaworsky Z., Nienow A.W., Dyster K.N. An LDA study of turbulent flow field in a baffled vessel agitated by an axial, down pumping hydrofoil impeller // Can. J. Chem. Eng. 1996. V. 74. P. 3.
Grenville R.K., Giacomelli J.J., Padron G., Brown D.A.R. Mixing: Impeller Performance in Stirred Tanks // Chem. Eng. August 2017. P. 42.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии