Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 176-184
Смена режимов диффузия–конвекция в тройных смесях с газом-разбавителем
В. Н. Косов a, b, *, О. В. Федоренко b, М. К. Асембаева b, В. Мукамеденкызы b
a Казахский национальный педагогический университет им. Абая
Алматы, Республика Казахстан
b Научно-исследовательский институт экспериментальной и теоретической физики
при Казахском национальном университете им. аль-Фараби
Алматы, Республика Казахстан
* E-mail: kosov_vlad_nik@list.ru
Поступила в редакцию 07.12.2018
После доработки 06.09.2019
Принята к публикации 16.09.2019
Аннотация
Экспериментально изучены особенности диффузии гелия и оксида азота, в равной степени разбавленных пропаном, при различных давлениях и содержании газа-разбавителя в смеси. Обнаружено, что при определенном давлении в системе возникают конвективные течения, усиливающие парциальный массоперенос, что не типично для диффузии. Возрастание давления интенсифицирует смешение компонентов смеси. Увеличение содержания газа-разбавителя в смеси приводит к стабилизации конвективных режимов. Решение уравнений диффузии показывает, что в системах с балластным газом реализуются условия для нелинейного распределения концентраций компонентов смеси по длине канала, которые могут приводить к возникновению экстремума плотности смеси (т.е. инверсии градиента плотности смеси), вызывающего возникновение конвективных течений. Численным образом исследована устойчивость механического равновесия тройной смеси в вертикальном цилиндрическом канале при действии силы тяжести и заданных градиентах концентрации компонентов. Определена граница кинетического перехода диффузия–конвекция. В координатах числа Рэлея и давления проведено сравнение опытных и численных результатов.
ВВЕДЕНИЕ
В газовых смесях наличие нескольких механизмов переноса тепла и массы приводит к возникновению особенностей, влияющих на различные режимы многокомпонентного массопереноса. Примерами могут служить эксперименты по изучению диффузии бинарной смеси паров растворов в инертный газ [1], изотермического смешения газов при различных давлениях и составах [2, 3], которые показали, что в системах могут возникать конвективные течения, приводящие к значительному росту парциальных потоков компонентов.
Опыты по изучению диффузии в тройных газовых смесях [3, 4] показали, что для систем, у которых коэффициенты взаимной диффузии (КВД) компонентов существенно отличаются друг от друга, возникшие конвективные течения существенным образом интенсифицируют суммарный массоперенос. Определенные значения давления и концентрации компонента с наибольшим молекулярным весом в смеси способствуют переходу системы из диффузионной области в конвективную. Самопроизвольное возникновение конвекции в [1–4] связывалось с тем, что молекулярная диффузия за счет неравенства в КВД компонентов приводит к формированию по вертикальной оси характерных областей с различными плотностями. При определенных условиях такое расположение в поле силы тяжести может быть неустойчивым с последующим возникновением конвекции.
Появление конвекции можно предсказывать в рамках традиционных представлений тепловых задач Рэлея [5, 6]. Исследования, проведенные в [7], показали, что в бинарных смесях нереагирующих компонентов за счет неоднородности температуры и состава возможно проявление конвективной неустойчивости с последующим нарушением молекулярного переноса. Дальнейшее изучение термоконцентрационной конвекции в бинарных системах в геометрических каналах различной формы показало ее существенное влияние на ожидаемое при неизотермической диффузии смешение [8–10].
Вместе с тем необходимо отметить, что распространение подходов [8–10] на случай смешения изотермических тройных газовых смесей ограничено особенностями регистрации смены режимов диффузия–конвекция, отмеченными в [1–3]. Экспериментально, кинетические переходы реализуются не в традиционных условиях, соответствующих тепловым задачам Рэлея [5, 6] и Рэлея–Тейлора [11], а возникают при начальной гидростатически устойчивой стратификации, которая предполагает убывание плотности смеси с высотой. В этой ситуации необходимо оценить роль перекрестных эффектов [12, 13], которые в силу специфики рассматриваемых в [9, 10] задач, не были приняты во внимание.
В настоящей работе экспериментальным образом при различных давлениях исследуется диффузия бинарной смеси в третьем газе-растворителе. Определение границы смены режимов диффузия–конвекция проводится численным образом в рамках анализа на устойчивость для соответствующей опыту геометрии.
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
Смена кинетических режимов изучалась при смешении гелия и оксида азота, в равной степени разбавленных пропаном. В отличие от опытов [1–4], в рассматриваемом случае градиент концентрации одного из компонентов в начальный момент времени практически равен нулю и это позволяет выявить специфические особенности переноса при взаимной диффузии основных смешивающихся компонентов He и N2O. Изучение смешения при разных составах C3H8 также позволяет оценить влияние газа-разбавителя на суммарный массоперенос компонентов смеси. При дальнейших рассуждениях условимся, что в смеси He (1) + C3H8 (2)–N2O (3) + C3H8 (2) цифры перед химическим элементом соответствуют начальной концентрации компонента, а числа в скобках после химического элемента определяют их нумерацию. На момент начала смешения изучаемая смесь является гидростатически устойчивой, а градиент концентрации газа-разбавителя (пропана) практически равен нулю. В данной системе молекулярные веса оксида азота и пропана одинаковы, а КВД при Т = 298.0 К и p = 0.1 МПа составляют: ${{D}_{{{\text{He}} - {{{\text{C}}}_{{\text{3}}}}{{{\text{H}}}_{{\text{8}}}}}}}$ = 0.409 × 10–4 м2/c, ${{D}_{{{\text{He}} - {{{\text{N}}}_{{\text{2}}}}{\text{O}}}}}$ = = 0.608 × 10–4 м2/c, ${{D}_{{{{{\text{N}}}_{{\text{2}}}}{\text{O}} - {{{\text{C}}}_{{\text{3}}}}{{{\text{H}}}_{{\text{8}}}}}}}$ = 0.086 × 10–4 м2/c [14]. Такое же соотношение между КВД сохраняется и при более высоких давлениях.
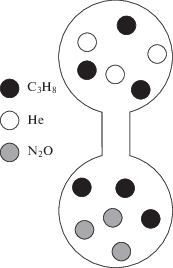
Парциальный перенос компонентов изучался на опытном устройстве, реализующем метод двух колб, соединенных вертикальным каналом [15]. Опыты проводились в диапазоне давлений от 0.2 до 1.7 МПа при температуре 298.0 К. Схема экспериментального стенда и процедура работы на нем была детально описана в [3, 4], поэтому на рис. 1 приведено только схематическое изображение диффузионной ячейки, которое проясняет некоторые специфические особенности проведения опыта. Геометрические характеристики аппарата следующие: Vu = Vl = (55.5 ± 0.5) × 10–6 м3 – объемы верхней и нижней колб, r = (2.00 ± 0.05) × 10–3 м и L = (64.00 ± 0.05) × 10–3 м – радиус и длина соединительного капилляра. Продолжительность опыта составляла 2–4 ч, что позволяло получить информацию о характерных особенностях массопереноса.
Методика проведения эксперимента была апробирована в [2, 3] и предполагала следующие процедуры. Верхняя Vu и нижняя Vl колбы аппарата заполнялись исследуемыми смесями газов до давления опыта. Затем с помощью специального устройства соединяющий колбы канал открывался и одновременно фиксировалось время начала процесса смешения. По окончании опыта канал перекрывался и регистрировалось время окончания смешения. Анализ газовых смесей из каждой колбы осуществлялся на хроматографе с погрешностью в измерении концентрации до ±0.5%. Во всех опытах в верхней колбе аппарата располагалась бинарная смесь гелия и пропана, а в нижней – пропана и оксида азота.
На рис. 2 и 3 приведены концентрации основных продиффундировавших компонентов при различных давлениях для смесей: 0.293He (1) + + 0.707С3Н8 (2) – 0.697С3Н8 (2) + 0.303N2O (3) и 0.570He (1) + 0.430С3Н8 (2) – 0.403С3Н8 (2) + + 0.597N2O (3). Обратим внимание на следующие особенности парциального переноса. Для двух основных диффундирующих компонентов явно прослеживается нелинейная зависимость суммарного переноса от давления. Зависимости, изображенные на рис. 2 и 3, являются нетипичными для диффузии, при которой наблюдается монотонное уменьшение интенсивности смешения с ростом давления. Не соответствуют общепринятому представлению диффузии зарегистрированные максимумы по интенсивности смешения для He и N2O, которые при уменьшении состава газа-разбавителя в тройной смеси смещаются в область более высоких значений давления.
Рис. 2.
Концентрации гелия, перешедшие в нижнюю колбу аппарата при различных давлениях: (а) – 0.293He + 0.707С3Н8–0.697С3Н8 + 0.303N2O, точки: 1 – 0.487 МПа; 2 – 0.582; 3 – 0.683; 4 – 0.780; 5 – 0.926 МПа; (б) – 0.570He + 0.430С3Н8–0.403С3Н8 + 0.597N2O, точки: 1 – 0.583 МПа; 2 – 0.876; 3 – 1.074; 4 – 1.27; 5 – 1.467; 6 – 1.565 МПа.
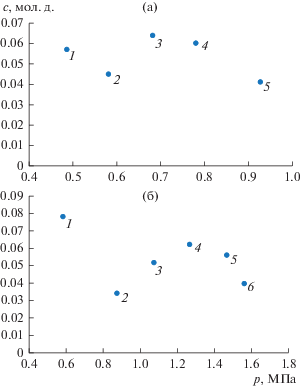
Рис. 3.
Концентрации закиси азота, перешедшие в верхнюю колбу аппарата в зависимости от давления: (а) – 0.293He + 0.707С3Н8–0.697С3Н8 + 0.303N2O, точки: 1 – 0.487 МПа; 2 – 0.582; 3 – 0.683; 4 – 0.780; 5 – 0.926 МПа; (б) – 0.570He + 0.430С3Н8–0.403С3Н8 + + 0.597N2O, точки: 1 – 0.583 МПа; 2 – 0.876; 3 – 1.074; 4 – 1.27; 5 – 1.467; 6 – 1.565 МПа.
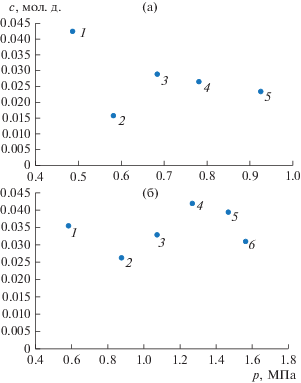
Если говорить о поведении пропана, то перенос газа-разбавителя имеет сложный характер, что проиллюстрировано на рис. 4. Для системы 0.293He (1) + 0.707С3Н8 (2)–0.697С3Н8 (2) + + 0.303N2O (3) (рис. 4а) до давления 0.68 МПа наблюдается уменьшение концентрации пропана в нижней и увеличение в верхней колбах аппарата. Такое поведение связано с проявлением реверсивной диффузии, которая, как и другие особенности многокомпонентного молекулярного переноса, была описана Туром в [16] и детализирована, например, в [17, 18]. Дальнейшее увеличение давления р > 0.68 МПа приводит к изменению отмеченной тенденции у газа-разбавителя в обеих колбах ячейки, что говорит о возникновении новых механизмов переноса, не описанных в [17]. Соизмеримо с реверсивной диффузией изменение концентрации газа-разбавителя, временами ее одновременный рост или падение в колбах аппарата может быть связано с циркуляцией при конвекции, которая отчетливо регистрируется по зависимостям для He и N2O, изображенным на рис. 2 и 3. Поведение пропана в системе 0.570He (1) + 0.430С3Н8 (2)–0.403С3Н8 (2) + 0.597N2O (3) изображено на рис. 4б. В дополнение к особенностям, описанных для предыдущего состава, отметим, что уменьшение содержания газа-разбавителя в смеси оказывает дестабилизирующее влияние. Так, уже начиная с давления 0.6 МПа и выше отмечается волнообразная зависимость интенсивности пропана от давления, связанная, по-видимому, с различным вкладом молекулярной и конвективной составляющей переноса в приграничных областях смены режимов диффузия–конвекция. Такой характер смешения нетипичен для парциального переноса, связанного с присутствием особых диффузионных режимов [16–18], которые были отмечены для этой смеси, но с большим содержанием С3Н8 в ней. Начиная с давлений 1.3–1.4 МПа и выше отмечается устойчивый рост концентрации пропана в нижней колбе, что говорит о сформировавшемся типе конвективных течений. Это может быть связано с появлением существенного градиента концентрации газа-разбавителя и возникновением встречного (по отношению к конвективному) переносу его за счет диффузии и выталкиванием некоторой части смеси газов из нижней колбы в верхнюю, тем самым поддерживая циркуляцию С3Н8.
Рис. 4.
Зависимость концентрации пропана от давления в системах: (а) – 0.293He + 0.707С3Н8–0.697С3Н8 + + 0.303N2O; (б) – 0.570He + 0.430С3Н8–0.403С3Н8 + + 0.597N2O; 1 – концентрация пропана в нижней колбе; 2 – концентрация пропана в верхней колбе.
Таким образом, из проведенных исследований следует, что в системах с балластным газом наблюдается концентрационная конвекция, вызванная неустойчивостью механического равновесия смеси. При этом интенсивность процесса зависит от концентрации газа-разбавителя и давления в системе.
ТЕОРЕТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ГРАНИЦЫ СМЕНЫ РЕЖИМОВ ДИФФУЗИЯ–КОНВЕКЦИЯ В СИСТЕМАХ С ГАЗОМ-РАЗБАВИТЕЛЕМ
Как отмечалось в [19], обобщенное описание диффузионного переноса, сопровождаемого конвекцией, для многокомпонентных смесей представляется сложной задачей. Однако для смешения вблизи границы смены режимов диффузия–конвекция возможны некоторые допущения, которые позволяют выполнять численные расчеты по определению характерных особенностей парциального массопереноса. Параметры, определяющие кинетический переход от диффузионного смешения к конвективному, получим в рамках теории устойчивости [7] для случая изотермической тройной газовой смеси. Для условия независимой диффузии $\sum\limits_{i = 1}^3 {{{{\mathbf{j}}}_{i}}} = 0;$ $\sum\limits_{i = 1}^3 {{{с}_{i}}} = 1$ макроскопическое движение смеси описывается системой уравнений гидродинамики, которая включает в себя уравнения Навье–Стокса, сохранения числа частиц смеси и компонентов [3, 4]:
(1)
$\begin{gathered} \rho \left[ {\frac{{\partial u}}{{\partial t}} + \left( {u\nabla u} \right)} \right] = - \nabla p + \eta {{\nabla }^{2}}u + \\ + \,\,\left( {\frac{\eta }{3} + \xi } \right)\nabla {\text{div}}u + \rho g{\text{,}}\,\,\,\,\frac{{\partial n}}{{\partial t}} + {\text{div}}\left( {nv} \right) = 0, \\ \frac{{\partial {{c}_{i}}}}{{\partial t}} + v\nabla {{c}_{i}} = - {\text{div}}{{j}_{i}},\,\,\,\,{{j}_{1}} = - \left( {D_{{11}}^{*}\nabla {{c}_{1}} + D_{{12}}^{*}\nabla {{c}_{2}}} \right), \\ {{j}_{2}} = - \left( {D_{{21}}^{*}\nabla {{c}_{1}} + D_{{22}}^{*}\nabla {{c}_{2}}} \right). \\ \end{gathered} $Уравнения (1) дополняются уравнением $1$состояния среды
(2)
$\rho = \rho \left( {{{с}_{1}}{\text{,}}{{с}_{2}}{\text{,}}р} \right),\,\,\,T = {\text{const}}{\text{.}}$Перед дальнейшим преобразованием системы уравнений (1), (2) необходимо отметить, что результаты вычислительного эксперимента по изучению особенностей неэквимолярной диффузии в тройных парогазовых смесях, проведенных в [20] на основе решений уравнения Стефана–Максвелла, показали существование в системах немонотонных изоконцентрационных распределений. Такие распределения являются нетипичными для бинарной диффузии и показывают сложное взаимодействие молекулярного и конвективного механизмов переноса, которое может привести к аномальным режимам смешения. Поэтому при преобразовании системы уравнений (1), (2) и последующем их решении необходимо учитывать нелинейное распределение концентраций компонентов в диффузионном канале, которое позволит определить парциальные градиенты концентраций в координатах, наиболее “опасных” с точки зрения смены режимов и соответствующих максимальной величине градиента плотности смеси.
Для решения системы уравнений (1), (2) применим метод малых возмущений [7], который позволяет представить ci и p следующим образом:
где $\langle {{c}_{i}}\rangle ,$ $\langle p\rangle $ – постоянные средние значения, принимаемые в качестве начала отсчета, а $c_{i}^{/},$ p/ – возмущенные величины, которые не приводят к существенному отклонению плотности ρ/ от среднего значения ρ0. Далее полагаем, что при выполнении условия $L \gg {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ различия между возмущениями среднечисловой $v$ и среднемассовой $u$ скоростей в уравнении Навье–Стокса будут несущественны [3, 4]. Тогда уравнения (1), (2) можно свести к системе уравнений для возмущений, обезразмеренных относительно заданных масштабов: расстояния – d, времени – d2/ν, скорости – ${{D_{{{\text{22}}}}^{*}} \mathord{\left/ {\vphantom {{D_{{{\text{22}}}}^{*}} d}} \right. \kern-0em} d},$ концентрации i-го компонента – Aid, давления – ${{{{\rho }_{0}}\nu D_{{{\text{22}}}}^{*}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}\nu D_{{{\text{22}}}}^{*}} {{{d}^{{\text{2}}}}}}} \right. \kern-0em} {{{d}^{{\text{2}}}}}}.$ Окончательно система возмущенных безразмерных уравнений (штрихи опущены) принимает вид(3)
$\begin{gathered} {{\Pr }_{{22}}}\frac{{\partial {{c}_{1}}}}{{\partial t}} - \left( {u{\mathbf{\gamma }}} \right) = {{\tau }_{{11}}}{{\nabla }^{2}}{{c}_{1}} + \frac{{{{A}_{2}}}}{{{{A}_{1}}}}{{\tau }_{{12}}}{{\nabla }^{2}}{{c}_{2}}, \\ {{\Pr }_{{22}}}\frac{{\partial {{c}_{2}}}}{{\partial t}} - \left( {u{\mathbf{\gamma }}} \right) = \frac{{{{A}_{1}}}}{{{{A}_{2}}}}{{\tau }_{{21}}}{{\nabla }^{2}}{{c}_{1}} + {{\nabla }^{2}}{{c}_{2}}, \\ \frac{{\partial u}}{{\partial t}} = - \nabla p + {{\nabla }^{2}}u + \left( {R{{a}_{1}}{{\tau }_{{11}}}{{c}_{1}} + R{{a}_{2}}{{c}_{2}}} \right)\gamma , \\ divu = 0, \\ \end{gathered} $Система уравнения (3) имеет частные решения, зависящие от времени по экспоненциальному закону [7]:
где λ – временной декремент возмущений. В случае вещественного декремента λ возмущения изменяются со временем монотонно. Для устойчивости механического равновесия необходимо, чтобы вещественные части декрементов всех нормальных возмущений были положительными. Если в спектре имеется хотя бы одно возмущение с отрицательным действительным декрементом λ, то это свидетельствует о неустойчивости равновесия по отношению к данному возмущению.Потеря устойчивости газовой смеси означает, что декременты λ некоторых характеристических возмущений при определенном числе Рэлея меняют знак. Обращение в нуль декремента определяет условия, при которых возмущение нейтрально [3, 7], т.е. не нарастает и не затухает. Это условие и характеризует границу устойчивости механического равновесия относительно данного возмущения. Таким образом, для определения границы монотонной неустойчивости нейтральное возмущение должно быть стационарным (или квазистационарным).
Рассмотрим квазистационарное смешение смеси в вертикальном диффузионном канале конечной длины. С учетом граничных условий
решение диффузионных уравнений в (1) имеет вид [20]
(4)
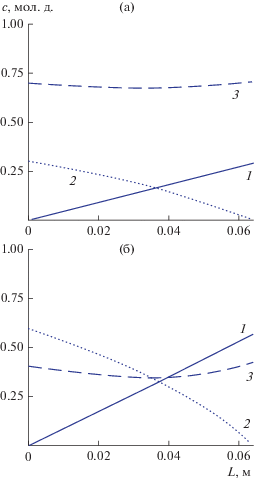
$\begin{gathered} {{c}_{1}}(z) = - B\left[ {{{j}_{1}}\left( {{{X}_{3}}z - {{X}_{1}} + \frac{A}{B}} \right) - {{X}_{2}}{{K}_{1}}\exp \left( {\frac{z}{B}} \right)} \right], \\ {{c}_{3}}(z) = - B\left[ {{{j}_{3}}\left( {{{X}_{3}}z - {{X}_{1}} - \frac{A}{B}} \right) + {{X}_{2}}{{K}_{3}}\exp \left( {\frac{z}{B}} \right)} \right], \\ {{c}_{2}}(z) = 1 - {{c}_{1}}(z) - {{c}_{3}}(z), \\ \end{gathered} $Рис. 5.
Распределение концентраций по длине канала: (а) – 0.293He + 0.707С3Н8–0.697С3Н8 + 0.303N2O; (б) – 0.570He + 0.430С3Н8–0.403С3Н8 + 0.597N2O; 1 – гелий; 2 – закись азота; 3 – пропан.
Для определения границы монотонной устойчивости рассматриваемой задачи умножим скалярно третье уравнение системы (3) на вектор u и проинтегрируем по всему объему V цилиндрического диффузионного канала конечной высоты при условиях, что $\nabla p = 0,$ $\frac{{\partial u}}{{\partial t}} = 0$ [4]:
(5)
$\int {{\mathbf{u}}{{\nabla }^{2}}{\mathbf{u}}dV} + R{{a}_{1}}{{\tau }_{{11}}}\int {{{u}_{z}}{{c}_{1}}dV} + R{{a}_{2}}\int {{{u}_{z}}{{c}_{2}}dV} = 0.$В работе [4] приведены выражения для компонент скорости, а также процедура нахождения ci в уравнении (5). Выражения для u и ci позволяют вычислить критическое число Рэлея с помощью интегрального соотношения
(6)
$R{{a}_{1}} = - \frac{{\int {u{{\nabla }^{2}}udV} }}{{{{\tau }_{{11}}}\int {{{u}_{z}}{{c}_{1}}dV} }} - \frac{{\int {{{u}_{z}}{{c}_{2}}dV} }}{{{{\tau }_{{11}}}\int {{{u}_{z}}{{c}_{1}}dV} }}R{{a}_{2}}.$Критическое число Рэлея для основной моды возмущения вычисляется из уравнения (6) с помощью стандартного пакета программы MathCad. Для системы 0.570He (1) + 0.430С3Н8 (2)–0.403С3Н8 (2) + 0.597N2O (3) (при Ra2 = 0) оно будет равным Ra1 = 86.99.
Уравнение (5) определяет на плоскости (Ra1, Ra2) граничную линию, разделяющую области диффузии (затухающие возмущения) и концентрационной конвекции (нарастающие возмущения) в координате z = L (рис. 6). Этот подход позволяет определить критическое число Рэлея каждого компонента, зависящее от термодинамических параметров. Для частного случая смешения двух компонентов, растворенных в третьем газе, граничную линию можно определить в координатах (Rai, p).
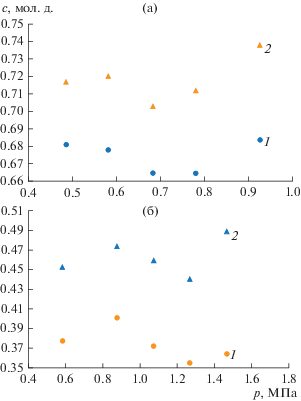
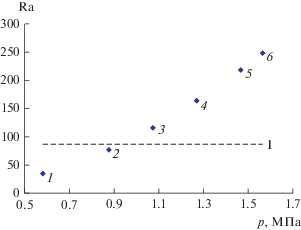
Рис. 6.
Зависимость парциального числа Рэлея от давления для системы 0.570He + 0.430С3Н8–0.403С3Н8 + + 0.597N2O. Точки – экспериментальные числа Рэлея при различных давлениях: 1 – 0.583 МПа, 2 – 0.876, 3 – 1.074, 4 – 1.27, 5 – 1.467, 6 – 1.565 MPa. I – критическая линия.
Для сравнения результатов по определению областей устойчивости и неустойчивости представим опытные данные, приведенные, например, на рис. 2б, в виде парциальных чисел Рэлея. Парциальные числа Рэлея в соответствии с (3) в применении к цилиндрическому диффузионному каналу с радиусом r и длиной L можно записать следующим образом [21]:
(7)
${\text{R}}{{{\text{a}}}_{1}} = \frac{{gn{{r}^{4}}\Delta {{m}_{1}}}}{{\rho \nu D_{{11}}^{*}}}\frac{{\partial {{c}_{1}}}}{{\partial z}}{\text{,}}\,\,{\text{R}}{{{\text{a}}}_{2}} = \frac{{gn{{r}^{4}}\Delta {{m}_{2}}}}{{\rho \nu D_{{22}}^{*}}}\frac{{\partial {{c}_{2}}}}{{\partial z}}{\text{,}}$Параметры ρ, ν, $D_{{{\text{11}}}}^{*},$ $D_{{{\text{22}}}}^{*},$ входящие в определение парциальных чисел Рэлея (7), зависят от р, Т и среднего состава смеси, который реализуется после полного смешения. Распределения концентраций компонентов вдоль диффузионного канала рассчитаны по формулам (4). Для определения градиентов концентраций в (7) были вычислены первые производные от распределения концентраций компонентов (4) по координате z.
На рис. 6 приведены восстановленные экспериментальные числа Рэлея и критическая линия для системы 0.570He + 0.430С3Н8–0.403С3Н8 + + 0.597N2O при различных давлениях. Точки, расположенные ниже линии I, соответствуют диффузии, а лежащие выше линии I – неустойчивому режиму с нарастающими конвективными возмущениями. Сравнительный анализ рис. 2б, 3б и 6 свидетельствует о том, что смена режимов для системы 0.570He + 0.430С3Н8–0.403С3Н8 + 0.597N2O происходит в интервале давлений от p = 0.88 МПа до p = 1.074 МПа, т.е. наблюдается переход от диффузионного процесса смешения к конвективному, соответствующему антисимметричному критическому движению (цилиндрический диффузионный канал делится вертикальной плоскостью, проходящей через ось, на две части, в одной из которых газ поднимается, а в другой – опускается).
Таким образом, результаты расчета показывают, что неустойчивый диффузионный процесс происходит в тройных системах с газом-растворителем при увеличении давления.
ЗАКЛЮЧЕНИЕ
Экспериментальное изучение диффузии гелия и оксида азота, растворенных в пропане, при различных составах показало, что в системе при определенном давлении возникают конвективные течения, интенсифицирующие суммарный массоперенос. Возрастание интенсивности парциального переноса компонентов от давления наблюдается для гелия и оксида азота. Влияние давления на перенос газа-разбавителя (пропана) не настолько значительно как для других компонентов смеси, однако перенос все равно превышает значения концентраций, характерных для диффузионного массопереноса. Полученные распределения концентраций компонентов по длине канала имеют немонотонный характер, вызывающий конвективную неустойчивость. Граница смены режимов диффузия–концентрационная гравитационная конвекция была получена в рамках теории устойчивости, распространённой на случай изотермического смешения тройных газовых смесей. Сравнение с опытом показало удовлетворительное согласие по определению областей диффузии и конвекции, что позволяет использовать предлагаемую модель для расчетов параметров, определяющих кинетический переход между режимами смешения для смесей с газами-разбавителями.
Работа выполнена в рамках проекта № AP05130986 “Особые режимы и возникновение пространственно-временных конвективных формирований при диффузии в многокомпонентных газовых смесях” Комитета науки Министерства образования и науки Республики Казахстан.
ОБОЗНАЧЕНИЯ
| Ai | парциальный градиент концентрации i-го компонента, мол. д./м |
| ci | концентрация i-го компонента, мол. д. |
| 〈ci〉 | постоянное среднее значение концентрации i-го компонента, принимаемое в качестве начала отсчета, мол. д. |
| $c_{i}^{'}$ | возмущенное значение концентрация i-го компонента, мол. д. |
| Dij | коэффициент взаимной диффузии, м2/с |
| $D_{{ij}}^{*}$ | практические коэффициенты диффузии, м2/с |
| d | характерный линейный масштаб, м |
| g | ускорение силы тяжести, м2/с |
| g | вектор ускорения силы тяжести, м2/с |
| ji | парциальная плотность диффузионного потока i-го компонента, м/с |
| n | мода возмущений |
| р | давление, Па |
| 〈р〉 | постоянное среднее значение давления, принимаемое в качестве начала отсчета, Па |
| р' | возмущенное значение давления, Па |
| Т | температура, К |
| t | время, с |
| u | вектор среднемассовой скорости тройной смеси, м/с |
| Vl | объем нижней колбы диффузионного аппарата, м3 |
| Vu | объем верхней колбы диффузионного аппарата, м3 |
| v | вектор среднечисловой скорости тройной смеси, м/с |
| βi | коэффициент линейной зависимости плотности i-го газового компонента от концентрации |
| γ | единичный вектор, направленный вертикально вверх |
| η | коэффициент динамической вязкости, Па с |
| ν | кинематическая вязкость смеси, м2/с |
| ξ | объемная вязкость, Па с |
| ρ | плотность смеси, кг/м3 |
| ρ0 | среднее значение плотности смеси, кг/м3 |
| ρ' | возмущенное значение плотности смеси, кг/м3 |
| τij | безразмерный параметр, определяющий соотношение между практическими коэффициентами диффузии |
| Prii | число Прандтля i-го компонента |
| Rаi | парциальное число Рэлея i-го компонента |
ИНДЕКСЫ
Список литературы
Dil'man V.V., Lipatov D.A., Lotkhov V.A., Kaminskii V.A. Instability in unsteady-state evaporation of binary solutions into an inert gas // Theor. Found. Chem. Eng. 2005. V. 39. № 3. P. 566. [Дильман В.В., Липатов Д.А., Лотхов В.А., Каминский В.А. Возникновение неустойчивости при нестационарном испарении бинарных растворов в инертный газ // Теор. осн. хим. технол. 2005. Т. 39. № 3. С. 600.]
Kosov V.N., Seleznev V.D., Zhavrin Yu.I. Separation of components during isothermal mixing of ternary gas systems under free convection conditions // Tech. Phys. 1997. V. 42. № 10. P. 1236. [Косов В.Н., Селезнев В.Д., Жаврин Ю.И. Эффект разделения компонентов при изотермическом смешении тройных газовых систем в условиях свободной конвекции // Журн. тех. физ. 1997. Т. 67. № 10. С. 139.]
Zhavrin Yu.I., Kosov V.N., Fedorenko O.V., Akzholova A.A. Some features of isothermal multicomponent mass transfer in the convective instability of gas mixture // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 171. [Жаврин Ю.И., Косов В.Н., Федоренко О.В., Акжолова А.А. Некоторые особенности изотермического многокомпонентного массопереноса при конвективной неустойчивости газовой смеси // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 177.]
Kosov V.N., Kul’zhanov D.U., Zhavrin Yu.I., Fedorenko O.V. Emergence of convective flows during diffusional mass transfer in ternary gas systems: The effect of component concentrations // Russ. J. Phys. Chem. A. 2017. V. 91. № 6. P. 984. [Косов В.Н., Кульжанов Д.У., Жаврин Ю.И., Федоренко О.В. Влияние концентрации компонентов смеси на возникновении конвективных режимов смешения при диффузии в тройных газовых смесях // Журн. физ. хим. 2017. Т. 91. № 6. С. 931.]
Гершуни Г.З. Гидродинамическая неустойчивость. Изотермические течения // Соросовский образ. журн. 1997. № 2. С. 99.
Ermolenko A.N. Rayleigh–Benard problem for an anomalous fluid // J. Appl. Mech. Tech. Phys. V. 48. № 2. P. 166. [Ермоленко А.Н. Задача Рэлея–Бенара для аномальной жидкости // Прикл. мех. тех. физ. 2007. Т. 48. № 2. С. 27.]
Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972.
Lücke M., Barten W., Büchel P., Fütterer C., Hollenger St., Jung Ch. Pattern formation in binary fluid convection and in system with throughflow // Lect. Notes Phys. 1998. V. 55. P. 127.
Ryzhkov I.I., Shevtsova V.M. On the cross-diffusion and Soret effect in multicomponent mixtures // Microgravity Sci. Technol. 2009. V. 21. № 1–2. P. 37.
Любимова Т.П., Зубова Н.А. Устойчивость механического равновесия тройной смеси в квадратной полости при вертикальном градиенте температуры // Вычисл. мех. сплошных сред. 2014. Т. 7. № 2. С. 200.
Ruev G.A., Fedorov A.V., Fomin V.M. Description of the anomalous Rayleigh-Taylor instability on the basis of the model of dynamics of a three-velocity three-temperature mixture // J. Appl. Mech. Tech. Phys. 2009. V. 50. № 1. P. 49. [Руев Г.А., Федоров А.В., Фомин В.М. Описание аномальной неустойчивости Рэлея–Тейлора на основе модели динамики трехскоростной температурной смеси // Прикл. мех. тех. физ. 2009. Т. 50. № 1. С. 58.]
Шашков А.Г., Абраменко Т.Н. Перекрестные эффекты в газовых смесях. Минск: Наука и техника, 1976.
Cussler E.L. Diffusion: Mass Transfer in Fluid Systems. Cambridge: Cambridge Univ. Press, 2009.
Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Старс, 2006.
Dunlop P., Bignell C.M. Diffusion and thermal diffusion in binary mixtures of hydrogen with noble gases // J. Chem. Phys. 1987. V. 6. P. 2922.
Toor H.L. Diffusion in three-component gas mixture // AIChE J. 1957. V. 3. № 2. P. 198.
Dil'man V.V., Kashirskaya O.A., Lotkhov V.A. Specific features of multicomponent diffusion // Theor. Found. Chem. Eng. 2010. V. 44. № 4. P. 379. [Дильман В.В., Каширская О.А., Лотхов В.А. Особенности многокомпонентной диффузии // Теор. осн. хим. технол. 2010. Т. 44. № 4. С. 396.]
Kaminskii V.A. Special modes of three-component diffusion in gases // Russ. J. Phys. Chem. A. 2011. V. 85. № 12. P. 2203. [Каминский В.А. Особые режимы трехкомпонентной диффузии в газах // Журн. физ. хим. 2011. Т. 85. № 12. С. 2359.]
Kaminskii V.A. Determining the diffusion flows and concentration distribution of ternary diffusion // Russ. J. Phys. Chem. A. 2011. V. 85. № 11. P. 1986. [Каминский В.А. Расчет диффузионных потоков и распределения концентраций для трехкомпонентной диффузии // Журн. физ. хим. 2011. Т. 85. № 11. С. 2127.]
Косов В.Н., Мукамеденкызы В., Федоренко О.В. Некоторые особенности смешения тройных газовых смесей на границе смены режимов “диффузия – концентрационная гравитационная конвекция” в квазистационарных условиях // Вестн. Моск. гос. обл. унив. Сер.: Естеств. науки. 2018. № 2. С. 125.
Kossov V., Krasikov S., Fedorenko O. Diffusion and convective instability in multicomponent gas mixtures at different pressures // Eur. Phys. J.: Spec. Top. 2017. V. 226. № 6. P. 1177.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии