Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 144-162
Метод автоматизированного синтеза оптимальных систем теплообмена на основе принципа закрепления переменных
Н. Н. Зиятдинов a, *, И. И. Емельянов a, Т. В. Лаптева a, А. А. Рыжова a, А. Н. Игнатьев a
a Казанский национальный исследовательский технологический университет
Казань, Россия
* E-mail: nnziat@yandex.ru
Поступила в редакцию 18.11.2019
После доработки 20.11.2019
Принята к публикации 21.11.2019
Аннотация
Предлагается новый подход к синтезу многостадийных систем теплообмена, в основе которого лежит принцип закрепления переменных, позволяющий свести задачу дискретно-непрерывного программирования к последовательности задач линейного и нелинейного программирования. Для их формализации предлагается новый вариант организации суперструктуры системы теплообмена, включающий все возможные схемы движения материально-тепловых потоков. Вычислительный эксперимент доказал многоэкстремальность решаемой задачи. Вертикальная декомпозиция суперструктуры позволила снизить число локальных минимумов экономического критерия и сократить вычислительную трудоемкость задачи синтеза, что соответствует запросам крупномасштабных технологических систем. Работоспособность предлагаемого алгоритма продемонстрирована на ряде модельных примеров в сравнении с эффективным программным пакетом SYNHEAT.
ВВЕДЕНИЕ
Оптимальная теплоинтеграция материально-тепловых потоков является важным способом повышения энергетической эффективности технологических установок [1, 2]. Ее сложный комбинаторный характер и большая размерность привели к разработке ряда подходов, методов и их комбинаций, позволяющих существенно снизить энергоемкость химико-технологических систем. Наиболее полный обзор дается в статьях [3–5]. Рассмотренные в них идеи применяются для решения задач синтеза оптимальных систем теплообмена одновременно с оптимизацией технологического процесса [6], с сетями водораспределения и водоочистки [7–9], при интеграции нескольких процессов, связанных водно-энергетическими потоками [10–12], при оптимальной организации холодильных циклов [13], периодических и полунепрерывных процессов [14], комплексной генерации и регенерации энергии [15, 16]. Дальнейшее развитие подходов к масштабной интеграции технологических процессов требует разработки эффективных методов синтеза оптимальных систем теплообмена (СТО). Использование их в качестве автоматизированной процедуры при оптимальном проектировании сложных химико-технологических систем (ХТС) позволит решать задачи синтеза разнородных подсистем в их взаимосвязи и взаимозависимости. В связи с этим в последнее время разрабатываемые методы синтеза СТО оцениваются исходя из двух основных требований: 1) метод должен обеспечивать нахождение глобального минимума (или близкого к нему решения) многоэкстремальной задачи оптимизации; 2) метод должен позволять решать задачи больших масштабов за приемлемое время. Если первое требование во многом зависит от развития методов глобальной детерминированной и стохастической оптимизации, второе требование предлагается выполнять путем декомпозиции задачи и ее упрощения с использованием эвристических и термодинамических подходов.
Термодинамический подход позволяет синтезировать оптимальную СТО, обеспечивающую предельно возможное количество рекуперируемой энергии [17, 18], минимально возможные потери тепловой энергии за счет необратимости процесса теплопередачи [19, 20] и т.д. Однако полученное решение может приводить к заведомо неоптимальной структуре по экономическому критерию вследствие сложной топологии и избыточности аппаратов теплообмена. Применение методов математического программирования на основе строгих математических моделей теплообменного оборудования характеризуется высокой сложностью вследствие необходимости решения задачи смешанного дискретно-непрерывного нелинейного математического программирования. Однако именно алгоритмические методы в общем случае позволяют получить лучшие решения по критерию суммарных приведенных капитальных и эксплуатационных затрат.
Наиболее эффективный метод интегрального синтеза с использованием суперструктуры, предложенный в работе [21] и развитый для изотермических материально-тепловых потоков в [22], позволяет достичь хороших результатов, но только для задач небольших размерностей. Попытки уменьшить трудоемкость задачи и снизить вероятность попадания в локальные минимумы привели к разработке множества модификаций самого алгоритма [23–25] и к использованию методов глобальной оптимизации [26–29].
Одним из способов снижения трудоемкости задачи является ее структурная и целевая декомпозиция. Так, метод декомпозиционного синтеза, предложенный на основе транспортной модели в работах [30, 31] и модели с промежуточными пунктами в [32], строится на трехуровневом алгоритме, включающем задачи: 1) минимизации потребления внешних энергоносителей; 2) минимизации числа теплообменников; 3) минимизации капитальных затрат или суммарной площади поверхностей теплообмена. Однако эвристическая природа данного подхода сужает поисковую область задачи синтеза, а вычислительная сложность NP-задачи второго уровня также затрудняет его использование для крупномасштабных проблем. В работе [33] для минимизации числа аппаратов предлагаются более жесткие формулировки задачи линейного программирования с уменьшенными периодами релаксации, а также подходы к повышению эффективности использования метода ветвей и границ для получения точного глобального оптимума за меньшее время. В одной из последних работ [34] представлен двухшаговый MILP/MINLP – алгоритм решения крупномасштабных задач синтеза.
В работах [35, 36] предложен метод синтеза систем теплообмена на основе задачи о назначениях. Метод основан на разбиении суперструктуры СТО на блоки теплообмена, для каждого из которых решается задача нелинейного программирования с экономическим критерием. Полученная матрица оценок используется для нахождения оптимальной структуры СТО, строящейся на основе оптимальной комбинации структурных блоков. Настоящая статья посвящена развитию метода для случаев многократного обмена теплом горячих и холодных материально-тепловых потоков технологических установок.
МЕТОД СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ ТЕПЛООБМЕНА НА ОСНОВЕ ЗАДАЧИ О НАЗНАЧЕНИЯХ
Предположим, что мы построили математическую модель ХТС без тепловой интеграции. Имеется:
1) Мh “горячих” потоков $S_{i}^{{\text{h}}}$, (i = 1,…, Мh) и Мc “холодных” потоков $S_{j}^{{\text{c}}}$, (j = 1,…, Мc);
2) массовые расходы $F_{i}^{{\text{h}}},$ $F_{j}^{{\text{c}}};$
3) начальные температуры $T_{i}^{{{\text{h,in}}}},$ (i = 1,…, Мh), $T_{j}^{{{\text{c,in}}}},$ (j = 1,…, Мc);
4) удельные изобарные теплоемкости $c_{i}^{{\text{h}}},$ $c_{j}^{{\text{c}}}$ соответственно.
Необходимо найти:
1) структуру СТО горячих и холодных потоков, содержащую рекуперативные теплообменники, холодильники на горячих потоках и нагреватели на холодных;
2) тепловые нагрузки рекуператоров ${{Q}^{{{\text{he}}}}},$ нагревателей ${{Q}^{{{\text{reb}}}}}$ и холодильников ${{Q}^{{{\text{col}}}}};$
3) значения поверхностей теплообмена рекуперативных теплообменников Ahe, нагревателей Areb и холодильников Acol;
4) расходов холодного теплоносителя $F_{{}}^{{{\text{cu}}}}$ в холодильниках и горячего теплоносителя $F_{{}}^{{{\text{hu}}}}$ в нагревателях, при которых температуры горячих и холодных потоков после СТО будут равны заданным значениям
и будет обеспечен отбор необходимого количества теплоты $\Delta H_{i}^{{\text{h}}}$ от горячих потоков, и передано необходимое количество теплоты $\Delta H_{j}^{{\text{c}}}$ холодным потокам, а критерий суммарных приведенных капитальных и операционных затрат примет минимальное значение.
Трудность решения поставленной задачи заключается в наличии как непрерывных (расходы внешних теплоносителей и хладагентов, тепловые нагрузки теплообменников и т.д.), так и дискретных переменных (наличие или отсутствие теплообменников на материально-тепловых потоках, связей между теплообменниками в структуре системы). Многовариантность задачи синтеза оптимальных СТО и многообразие процессов химической технологии послужили основой для разработки классификации структурных элементов СТО. Нами предлагается выделять следующие схемы организации теплообмена в ХТС:
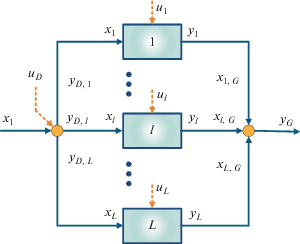
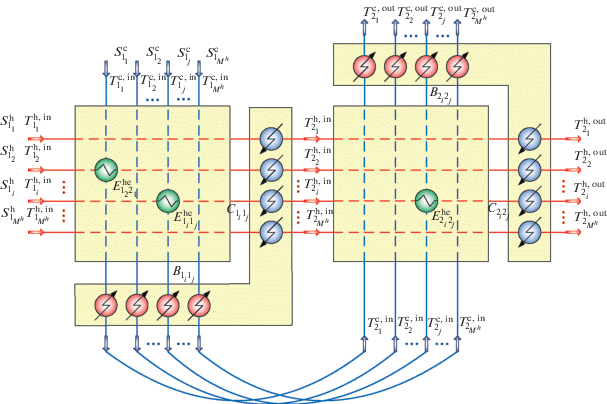
1. Схема многостадийного теплообмена, в которой для каждого горячего/холодного потока организуется последовательный рекуперативный теплообмен с несколькими холодными/горячими потоками (рис. 1). Вектор управляющих переменных uq в общем случае включает:
1) структурные переменные, определяющие топологию организации теплообмена на каждой стадии;
2) конструктивные переменные аппаратов, входящих в состав схемы теплообмена;
3) режимные переменные работы каждого теплообменника.
2. Схема теплообмена с разделением материально-тепловых потоков, где каждая часть любого потока может параллельно обмениваться теплом с другими потоками или их частями (рис. 2). После прохождения СТО все L частей каждого потока поступают в смеситель. Здесь возможно как изотермическое, так и неизотермическое смешение, разбивающие имеющееся множество схем на два класса, исходя из характера математических моделей и установленных ограничений задач оптимизации. Отметим, что в вектор uD в этом случае добавляется управление режимом работы делителя D.
Приведенные схемы, согласно принципу иерархичности технологических систем, могут рассматриваться как составные элементы структурной схемы более высокого уровня иерархии. К примеру, организация теплообмена в блоке 1 схемы с разделением потоков возможна посредством многостадийной схемы, а схема на рис. 2 может выступать структурным элементом на одной из стадий многостадийной схемы.
Итоговая схема синтезируемой системы теплообмена будет включать ряд конечных блоков, возможные варианты организации которых нами предлагается определять для каждой совокупности горячего и холодного потоков. В работе [36] рассмотрен метод поиска оптимальной структуры и режима работы каждого q-го и l-го конечных блоков на приведенных на рис. 1 и 2 структурных схемах соответственно. Однако в этой задаче векторы входных переменных x и выходных переменных y считались известными ввиду отсутствия делений потоков по энергетическим уровням на стадии и по расходам и энтальпиям на параллельные ветви. Очевидно, что для решения задачи синтеза на приведенных структурных схемах необходимо задать (N – 1) управление для распределения нагрузок между N стадиями и (L – 1) управление для делителя D в структурной схеме на рис. 2. Их совокупность определим как множество закрепляемых переменных V. Каждый численно определенный набор этих переменных определяет оптимальную по структуре и свободным управляющим переменным систему теплообмена. В работе [37] нами предложен декомпозиционный метод и итерационный алгоритм решения задачи, суть которого заключается в декомпозиции суперструктуры на отдельные элементы, оптимальная интеграция которых, с учетом заданных требований на отбор и передачу заданного количества теплоты, позволяет найти новое численное приближение к оптимальным значениям элементов множества V. Метод решения предлагается основывать на итерационной последовательности трех локальных задач:
1) поиска оптимальных оценок на теплообмен каждой пары горячего и холодного материально-тепловых потоков;
2) поиска оптимальной структуры системы теплообмена;
3) поиска оптимальных коэффициентов распределения тепловых нагрузок для найденной на втором этапе структуры СТО.
Решение задачи первого этапа будем основывать на суперструктуре блоков теплообмена каждой совокупности i-го горячего потока и j-го холодного потоков. Задачу оптимизации суперструктуры блока теплообмена опишем моделью нелинейного математического программирования. На втором этапе решением задачи линейного программирования “о назначениях” будем определять оптимальную структуру СТО как совокупности найденных оптимальных блоков по аддитивному критерию суммарных приведенных капитальных и эксплуатационных затрат. На третьем этапе решением задачи нелинейного программирования на найденной оптимальной структуре определим новые распределения тепловых нагрузок по стадиям СТО. Рассмотрим описанные задачи на k-й итерации работы метода.
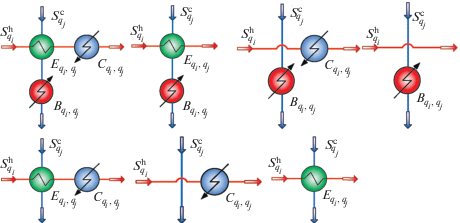
Этап 1. Поиск оптимальных оценок на теплообмен двух потоков. Рассмотрим структурную схему многостадийной системы теплообмена. В ней определим конечные структурные блоки, в которых организуется рекуперативный теплообмен между парой qi-го горячего и qj-го холодного потоков, и будем называть их элементарным блоками системы теплообмена (ЭБСТ), а потоки назовем элементарными. Множество возможных схем организации ЭБСТ между этими потоками приведено на рис. 3.
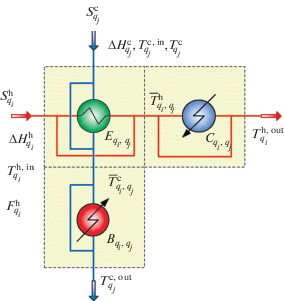
Все представленные схемы могут быть представлены в виде суперструктуры (рис. 4), включающей: 1) рекуперативный теплообменник ${{E}_{{{{q}_{i}},{{q}_{j}}}}},$ в котором могут обмениваться теплом qi-й горячий и qj-й холодный потоки; 2) холодильник ${{C}_{{{{q}_{i}},{{q}_{j}}}}},$ установленный на qi-м горячем потоке на выходе из рекуперативного теплообменника; 3) нагреватель ${{B}_{{{{q}_{i}},{{q}_{j}}}}}$ на выходе qj-го холодного потока.
Для описания входящих в состав ЭБСТ рекуперативного теплообменника, нагревателя и холодильника будем использовать математические модели, основанные на расчете среднелогарифмической разности температур. Для простоты изложения предлагаемого подхода к теплоинтеграции в используемых математических моделях теплообменников примем следующие допущения:
1) температуры входных и выходных горячих и холодных теплоносителей системы известны;
2) движение потоков в теплообменниках противоточное;
3) гидродинамические структуры потоков – идеального вытеснения;
4) суммарное термическое сопротивление стенки теплообменника пренебрежимо мало;
5) используется усредненное значение удельной изобарной теплоемкости.
Назначим каждому потоку на каждой стадии теплообмена коэффициенты $\alpha _{{{{q}_{i}}}}^{{\text{h}}},$ $\alpha _{{{{q}_{j}}}}^{{\text{с}}} \in (0,1),$ такие, что выполняется равенство
(1)
$\sum\limits_{{{q}_{i}} = 1}^{{{N}_{i}}} {\alpha _{{{{q}_{i}}}}^{{{\text{h}},(k)}}} = 1,\,\,\,\,\sum\limits_{{{q}_{j}} = 1}^{{{N}_{j}}} {\alpha _{{{{q}_{j}}}}^{{{\text{с}},(k)}}} = 1.$С учетом требования на однократность рекуперативного теплообмена для каждого ЭБСТ задача нахождения оптимальной структуры СТО может быть сведена к нахождению минимума суммарных приведенных капитальных и эксплуатационных затрат на теплообмен всех возможных паросочетаний qi-го горячего и qj-го холодного потоков. Она формализуется в виде (2)–(18) и имеет эффективные методы решения (отметим, что ее решение не потребует больших вычислительных затрат ввиду малой размерности):
(2)
$\mathop {\min }\limits_{Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}} f_{{{{q}_{i}},{{q}_{j}}}}^{{(k)}},\,\,\,\,{{q}_{j}} = 1,...,N_{j}^{{\text{c}}},\,\,\,\,{{q}_{i}} = 1,...,N_{i}^{{\text{h}}}.$1. Целевая функция:
(3)
$\begin{gathered} f_{{{{q}_{i}},{{q}_{j}}}}^{{(k)}} = \left[ {\tilde {m}_{1}^{{{\text{he}}}} + \tilde {m}_{2}^{{{\text{he}}}}{{{\left( {\frac{{Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}}}{{U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}}}}\Delta t_{{\ln }}^{{{\text{he}},(k)}}}}} \right)}}^{{{{{\gamma }}^{{{\text{he}}}}}}}}} \right] + \\ + \,\,\left[ {\tilde {m}_{{\text{1}}}^{{{\text{reb}}}} + \tilde {m}_{{\text{2}}}^{{{\text{reb}}}}{{{\left( {\frac{{Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}},(k)}}}}{{U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}}}}\Delta t_{{\ln }}^{{{\text{reb}},(k)}}}}} \right)}}^{{{{{\gamma }}^{{{\text{reb}}}}}}}} + {{{\hat {m}}}^{{{\text{reb}}}}}Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}},(k)}}} \right] + \\ + \,\,\left[ {\tilde {m}_{{\text{1}}}^{{{\text{col}}}} + \tilde {m}_{{\text{2}}}^{{{\text{col}}}}{{{\left( {\frac{{Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col,(k)}}}}}}{{U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}}}}\Delta t_{{\ln }}^{{{\text{col}},(k)}}}}} \right)}}^{{{{{\gamma }}^{{{\text{col}}}}}}}} + {{{\hat {m}}}^{{{\text{col}}}}}Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}},(k)}}} \right]. \\ \end{gathered} $2. Коэффициенты теплопередачи:
(4)
$\begin{gathered} U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}}}} = \frac{1}{{\frac{1}{{\chi _{{{{q}_{i}}}}^{{\text{h}}}}} + \frac{1}{{\chi _{{{{q}_{j}}}}^{{\text{c}}}}}}},\,\,\,\,U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}}}} = \frac{1}{{\frac{1}{{\chi _{{{{q}_{i}}}}^{{\text{h}}}}} + \frac{1}{{{{\chi }^{{{\text{cu}}}}}}}}}, \\ U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}}}} = \frac{1}{{\frac{1}{{{{\chi }^{{{\text{hu}}}}}}} + \frac{1}{{\chi _{{{{q}_{j}}}}^{{\text{c}}}}}}}, \\ \end{gathered} $3. Уравнения теплового баланса:
(5)
$\begin{gathered} Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}},(k)}} = \Delta H_{{{{q}_{j}}}}^{{{\text{c}},(k)}} - Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}, \\ Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}},(k)}} = \Delta H_{{{{q}_{i}}}}^{{{\text{h}},(k)}} - Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}, \\ \end{gathered} $(6)
$\Delta H_{{{{q}_{j}}}}^{{{\text{c}},(k)}} = \alpha _{{{{q}_{j}}}}^{{{\text{c,}}(k)}}\Delta H_{j}^{{\text{c}}},\,\,\,\,\Delta H_{{{{q}_{i}}}}^{{{\text{h}},(k)}} = \alpha _{{{{q}_{i}}}}^{{{\text{h}},(k)}}\Delta H_{i}^{{\text{h}}}.$4. Температуры на выходе рекуперативного теплообменника:
(7)
$\bar {T}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{c}},(k)}} = \frac{{Q_{{{{{\text{q}}}_{i}},{{{\text{q}}}_{j}}}}^{{{\text{he}},(k)}}}}{{F_{{{{q}_{j}}}}^{{{\text{c}},(k)}}c_{j}^{{\text{c}}}}} + T_{{{{{\text{q}}}_{j}}}}^{{{\text{c}},{\text{in}}}},\,\,\,\,\bar {T}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{h,}}(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,in}}}} - \frac{{Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}}}{{F_{{{{q}_{i}}}}^{{{\text{h}},(k)}}c_{i}^{{\text{h}}}}}.$5. Выходные температуры qj-го холодного и qi-го горячего потоков:
(8)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,out}}}} = \frac{{\Delta H_{j}^{{\text{c}}}\sum\limits_{{{n}_{j}} = 1}^{{{q}_{j}}} {\alpha _{{{{q}_{j}}}}^{{{\text{c}},(k)}}} }}{{F_{{{{q}_{j}}}}^{{{\text{c}},(k)}}c_{j}^{{\text{c}}}}} + T_{{{{q}_{j}}}}^{{{\text{c,in}}}}, \\ T_{{{{q}_{i}}}}^{{{\text{h,out}}}} = T_{{{{q}_{i}}}}^{{{\text{h,in}}}} - \frac{{\Delta H_{i}^{{\text{h}}}\sum\limits_{{{n}_{i}} = 1}^{{{q}_{i}}} {\alpha _{{{{q}_{i}}}}^{{{\text{h}},(k)}}} }}{{F_{{{{q}_{i}}}}^{{{\text{h}},(k)}}c_{i}^{{\text{h}}}}}, \\ {{q}_{j}} = 1,...,\left( {N_{j}^{{\text{c}}} - 1} \right),\,\,\,\,{{q}_{i}} = 1,...,\left( {N_{i}^{{\text{h}}} - 1} \right). \\ \end{gathered} $6. Уравнения связей по входным и выходным переменным ЭБСТ:
(9)
$F_{{{{q}_{i}}}}^{{{\text{h}},(k)}} = F_{i}^{{\text{h}}},\,\,\,\,F_{{{{q}_{j}}}}^{{{\text{c}},(k)}} = F_{j}^{{\text{c}}},$(10)
$T_{{{{q}_{j}}}}^{{{\text{c}},in}} = T_{j}^{{{\text{c,in}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,in}}}} = T_{i}^{{{\text{h,in}}}},\,\,\,\,q = 1,$(11)
$T_{{{{q}_{j}}}}^{{{\text{c,out}}}} = T_{j}^{{{\text{c,out}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,out}}}} = T_{i}^{{{\text{h,out}}}},\,\,\,\,q = N,$(12)
$\begin{gathered} T_{{{{q}_{i}} + 1}}^{{{\text{h,in}},(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,out}},(k)}},\,\,\,\,T_{{{{q}_{j}} + 1}}^{{{\text{c,in}},(k)}} = T_{{{{q}_{j}}}}^{{{\text{c,out}},(k)}}, \\ {{q}_{i}} = 1,...,\left( {N_{i}^{{\text{h}}} - 1} \right),\,\,\,\,{{q}_{j}} = 1,...,\left( {N_{j}^{{\text{c}}} - 1} \right). \\ \end{gathered} $7. Среднелогарифмическая разность температур:
(13)
$\begin{gathered} \Delta t_{{\ln }}^{{p,(k)}} = \frac{{dt_{1}^{{p,(k)}} + dt_{2}^{{p,(k)}}}}{{\ln \frac{{dt_{1}^{{p,(k)}}}}{{dt_{2}^{{p,(k)}}}}}},\,\,\,\,\forall p \in \Omega , \\ {\text{если}}\,\,\,\,dt_{1}^{{p,(k)}} \ne dt_{2}^{{p,(k)}}, \\ \end{gathered} $(14)
$\begin{gathered} \Delta t_{{\ln }}^{{p,(k)}} = dt_{1}^{{p,(k)}} = dt_{2}^{{p,(k)}},\,\,\,\,\forall p \in \Omega , \\ {\text{если}}\,\,\,\,dt_{1}^{{p,(k)}} = dt_{2}^{{p,(k)}}, \\ \end{gathered} $(15)
$dt_{1}^{{{\text{he}},(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,in}}}} - \bar {T}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{c}},(k)}},\,\,dt_{2}^{{{\text{he}},(k)}} = \bar {T}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{h}},(k)}} - T_{{{{q}_{j}}}}^{{{\text{c,in}}}},$(16)
$dt_{1}^{{{\text{col}},(k)}} = \bar {T}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{h}},(k)}} - {{T}^{{{\text{cu,out}}}}},\,\,dt_{2}^{{{\text{col}},(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,out}}}} - {{T}^{{{\text{cu,in}}}}},$(17)
$dt_{1}^{{{\text{reb}},(k)}} = {{T}^{{{\text{hu,in}}}}} - T_{{{{{\text{l}}}_{j}}}}^{{{\text{c,out}}}},\,\,dt_{2}^{{{\text{reb}},(k)}} = {{T}^{{{\text{hu,out}}}}} - \bar {T}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{c}},(k)}}.$8. Ограничения на физическую реализуемость процесса теплообмена:
(18)
$\begin{gathered} dt_{1}^{{p,(k)}} - \Delta {{T}_{{\min }}} \geqslant 0,\,\,\,\,dt_{2}^{{p,(k)}} - \Delta {{T}_{{\min }}} \geqslant 0, \\ \Delta Q_{{q_{i}^{{}},q_{j}^{{}}}}^{{p,(k)}} \geqslant 0,\,\,\,\,\forall p \in \Omega , \\ \end{gathered} $Отметим, что при алгоритмизации метода решения задачи выражения (13) и (14) могут быть заменены на аппроксимацию Чена:
(19)
$\Delta t_{{\ln }}^{{p,(k)}} = {{\left( {dt_{1}^{{p,(k)}}dt_{2}^{{p,(k)}}\frac{{dt_{1}^{{p{\text{,}}(k)}} + dt_{2}^{{p,(k)}}}}{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},\,\,\,\,\forall p \in \Omega .$Этап 2. Поиск оптимальной структуры системы теплообмена. Задачу синтеза оптимальной СТО мы сведeм к задаче оптимизации суперструктуры, включающей все возможные варианты организации многостадийной СТО. В статье [37] нами рассмотрены два варианта ее организации, характеризующиеся прямоточным и противоточным способами движения материально-тепловых потоков. При их построении для каждой стадии теплообмена положены следующие правила:
1) каждую стадию представим состоящей из подсистемы рекуперативных теплообменников, посредством которых возможен рекуперативный теплообмен i-го горячего потока со всеми холодными потоками, и подсистемы концевых нагревателей и холодильников, устанавливаемых на выходе каждого i-го горячего потока и j-го холодного элементарных потоков;
2) любая пара i-го горячего потока и j-го холодного потоков на каждой стадии могут обмениваться теплом только один раз (при наличии минимально допустимой разности температур $\Delta {{T}_{{{\text{min}}}}}$).
Рассмотрим варианты организации суперструктуры в соответствии с описанными положениями, которые характеризуются различным движением потоков в СТО. Для простоты рассмотрим их для двух стадий (рис. 5, 6).
На основе полученных экономических оценок $f_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{opt,(}}k)}}$ формализуем задачу нахождения оптимальной структуры СТО. Для этого введем двоичную переменную ${{z}_{{{{q}_{i}},{{q}_{j}}}}},$ характеризующую наличие (отсутствие) ЭБСТ в структуре СТО. Тогда для каждой q-й стадии эта задача примет вид
(20)
${{Ф}^{{{\text{opt}},(k)}}} = \mathop {\min }\limits_{z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} \sum\limits_{i = 1}^{{{M}^{{\text{h}}}}} {\sum\limits_{j = {\text{1}}}^{{{M}^{{\text{c}}}}} {f_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{opt,(}}k)}}z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} } ,$(21)
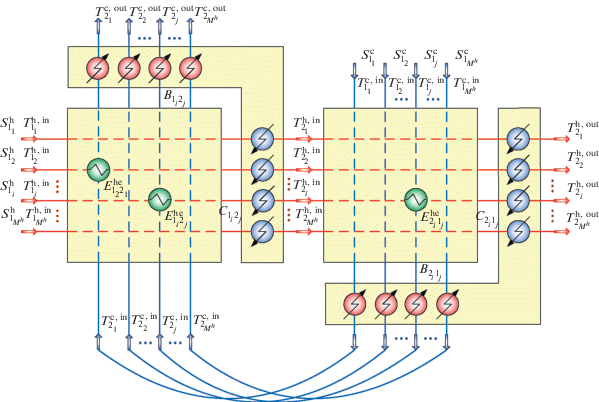
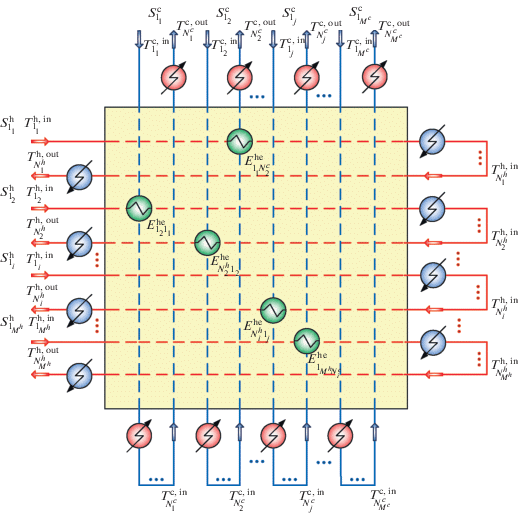
$\sum\limits_{i = 1}^{{{M}^{{\text{h}}}}} {z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} = 1,\,\,\,\,\sum\limits_{j = 1}^{{{M}^{{\text{c}}}}} {z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} = 1,\,\,\,\,{{z}_{{{{q}_{i}},{{q}_{j}}}}} \in \left\{ {0,1} \right\},$Рассмотренные варианты организации суперструктуры, в сущности, нарушают свойство эмерджентности при синтезе СТО. Это может привести к попаданию в локальный минимум задачи, так как оптимальность решения определяется независимо исходя из аддитивности найденных оптимальных решений для множества потоков каждой q-й стадии. Введем в рассмотрение вариант, позволяющий сводить множество задач о назначениях, решаемых последовательно, к одной задаче более высокой размерности, объединяющей в постановке преимущества рассмотренных глобальных схем теплообмена. Предлагаемая суперструктура синтезируемой СТО интегрирует в одной матрице все входные, выходные и промежуточные потоки и принимает вид рис. 7. Очевидно, что приведенная суперструктура расширяет поисковую область задачи оптимизации и характеризуется возможностью организации как прямоточной, так и противоточной схемы движения технологических потоков.
В таком случае формализованная постановка задачи поиска оптимальной структуры принимает вид
(22)
$\begin{gathered} {{{\text{Ф}}}^{{{\text{opt}},(k)}}} = \mathop {\min }\limits_{z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} \sum\limits_{i = 1}^{{{M}^{{\text{h}}}}} {\sum\limits_{{{q}_{i}} = 1}^{N_{i}^{{\text{h}}}} {\sum\limits_{j = 1}^{{{M}^{{\text{c}}}}} {\sum\limits_{{{q}_{j}} = 1}^{N_{j}^{{\text{c}}}} {f_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{opt,(}}k)}}z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} } } } , \\ z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}} \in \{ 0,1\} , \\ \end{gathered} $(23)
$\begin{gathered} \sum\limits_{i = 1}^{{{M}^{{\text{h}}}}} {\sum\limits_{{{q}_{i}} = 1}^{N_{i}^{{\text{h}}}} {z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} } = 1,\,\,\,\,\sum\limits_{j = 1}^{{{M}^{{\text{c}}}}} {\sum\limits_{{{q}_{j}} = 1}^{N_{j}^{{\text{с}}}} {z_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{(}}k)}}} } = 1, \\ i = 1,...,{{M}^{{\text{h}}}},\,\,\,\,i = 1,...,{{M}^{{\text{c}}}}, \\ {{q}_{i}} = 1,...,N_{i}^{{\text{h}}},\,\,\,\,{{q}_{j}} = 1,...,N_{j}^{{\text{c}}}. \\ \end{gathered} $Этап 3. Поиск новых приближений по коэффициентам распределения тепловых нагрузок. Полученная структура СТО оптимальна лишь для закрепленных значений переменных $\alpha _{{{{q}_{i}}}}^{{{\text{h}},(k)}},$ $\alpha _{{{{q}_{j}}}}^{{{\text{c}},(k)}}.$ Новые приближения по этим переменным определим путем оптимизации схемы, структура которой была получена на втором этапе. Эта задача формализуется в виде (24)–(42) как задача нелинейного математического программирования. Целевая функция (24) включает стоимости всех теплообменников, нагревателей и холодильников, установленных для совокупности qi-го горячего и qj-го холодного потоков, для которых ${{z}_{{{{q}_{i}},{{q}_{j}}}}} = 1.$ Их множество на k-й итерации определим как ${{Z}^{{(k)}}}{\text{:}}$
(24)
$\begin{gathered} {{{{\tilde {Ф}}}}^{{{\text{opt}},(k)}}} = \mathop {\min }\limits_{{\alpha }_{{{{q}_{i}}}}^{{{\text{h}},(k)}},\,\,{\alpha }_{{{{q}_{j}}}}^{{{\text{c}},(k)}},\,\,Q_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}} {{{{\tilde {Ф}}}}^{{(k)}}}, \\ \forall ({{q}_{i}},{{q}_{j}}) \in {{Z}^{{(k)}}},\,\,\,\,\forall \alpha _{{{{q}_{i}}}}^{{\text{h}}} \in V,\,\,\,\,\forall \alpha _{{{{q}_{j}}}}^{{\text{c}}} \in V. \\ \end{gathered} $1. Целевая фукция:
(25)
$\begin{gathered} {{{{\tilde {Ф}}}}^{{(k)}}} = \sum\limits_{{{q}_{i}}}^{L_{i}^{{\text{h}}}} {\sum\limits_{{{q}_{j}}}^{L_{j}^{{\text{c}}}} {\left[ {\left[ {\tilde {m}_{{\text{1}}}^{{{\text{he}}}} + \tilde {m}_{{\text{2}}}^{{{\text{he}}}}{{{\left( {\frac{{\tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}}}{{U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}}}}\Delta \tilde {t}_{{\ln }}^{{{\text{he}},(k)}}}}} \right)}}^{{{{{\gamma }}^{{{\text{he}}}}}}}}} \right]} \right.} } + \\ + \,\,\left[ {\tilde {m}_{{\text{1}}}^{{{\text{reb}}}} + \tilde {m}_{{\text{2}}}^{{{\text{reb}}}}{{{\left( {\frac{{\tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}},(k)}}}}{{U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}}}}\Delta \tilde {t}_{{\ln }}^{{{\text{reb}},(k)}}}}} \right)}}^{{{{{\gamma }}^{{{\text{reb}}}}}}}} + {{{\hat {m}}}^{{{\text{reb}}}}}\tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}},(k)}}} \right] + \\ + \,\,\,\,\left. {\left[ {\tilde {m}_{{\text{1}}}^{{{\text{col}}}} + \tilde {m}_{{\text{2}}}^{{{\text{col}}}}{{{\left( {\frac{{\tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}},(k)}}}}{{U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}}}}\Delta \tilde {t}_{{\ln }}^{{{\text{col}},(k)}}}}} \right)}}^{{{{{\gamma }}^{{{\text{col}}}}}}}} + {{{\hat {m}}}^{{{\text{col}}}}}\tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}},(k)}}} \right]} \right]. \\ \end{gathered} $2. Коэффициенты теплопередачи:
(26)
$\begin{gathered} U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}}}} = \frac{1}{{\frac{1}{{\chi _{{{{q}_{i}}}}^{{\text{h}}}}} + \frac{1}{{\chi _{{{{q}_{j}}}}^{{\text{c}}}}}}},\,\,\,\,U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}}}} = \frac{1}{{\frac{1}{{\chi _{{{{q}_{i}}}}^{{\text{h}}}}} + \frac{1}{{{{\chi }^{{{\text{cu}}}}}}}}}, \\ U_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}}}} = \frac{1}{{\frac{1}{{{{\chi }^{{{\text{hu}}}}}}} + \frac{1}{{\chi _{{{{q}_{j}}}}^{{\text{c}}}}}}}. \\ \end{gathered} $3. Уравнения теплового баланса:
(27)
$\begin{gathered} \tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{reb}},(k)}} = \Delta \tilde {H}_{{{{q}_{j}}}}^{{{\text{c}},(k)}} - \tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}, \\ \tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{col}},(k)}} = \Delta \tilde {H}_{{{{q}_{i}}}}^{{{\text{h}},(k)}} - \tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}, \\ \end{gathered} $(28)
$\Delta \tilde {H}_{{{{q}_{j}}}}^{{{\text{c}},(k)}} = \alpha _{{{{q}_{j}}}}^{{{\text{c}},(k)}}\Delta H_{j}^{{\text{c}}},\,\,\,\,\Delta \tilde {H}_{{{{q}_{i}}}}^{{{\text{h}},(k)}} = \alpha _{{{{q}_{i}}}}^{{{\text{h}},(k)}}\Delta H_{i}^{{\text{h}}}.$4. Температуры на выходе рекуперативного теплообменника:
(29)
$\tilde {\bar {T}}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{c}},(k)}} = \frac{{\tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}}}{{F_{{{{q}_{j}}}}^{{{\text{c}},(k)}}c_{j}^{{\text{c}}}}} + \tilde {T}_{{{{q}_{j}}}}^{{{\text{c,in}}}},\,\,\,\,\tilde {\bar {T}}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{h}},(k)}} = \tilde {T}_{{{{q}_{i}}}}^{{{\text{h,in}}}} - \frac{{\tilde {Q}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{he}},(k)}}}}{{F_{{{{q}_{i}}}}^{{{\text{h}},(k)}}c_{i}^{{\text{h}}}}}.$5. Выходные температуры qi-го горячего и qj -го холодного потоков:
(30)
$\begin{gathered} \tilde {T}_{{{{q}_{j}}}}^{{{\text{c,out}}}} = \frac{{\Delta H_{j}^{{\text{c}}}\sum\limits_{{{n}_{j}} = 1}^{{{q}_{j}}} {\alpha _{{{{q}_{j}}}}^{{{\text{c}},(k)}}} }}{{F_{{{{q}_{j}}}}^{{{\text{c}},(k)}}c_{j}^{{\text{c}}}}} + \tilde {T}_{{{{q}_{j}}}}^{{{\text{c,in}}}}, \\ \tilde {T}_{{{{q}_{i}}}}^{{{\text{h,out}}}} = \tilde {T}_{{{{q}_{i}}}}^{{{\text{h,in}}}} - \frac{{\Delta H_{i}^{{\text{h}}}\sum\limits_{{{{\text{n}}}_{i}} = 1}^{{{q}_{i}}} {\alpha _{{{{q}_{i}}}}^{{{\text{h}},(k)}}} }}{{F_{{{{q}_{i}}}}^{{{\text{h}},(k)}}c_{i}^{{\text{h}}}}}, \\ {{q}_{i}} = 1,...,\left( {N_{i}^{{\text{h}}} - 1} \right),\,\,\,\,{{q}_{j}} = 1,...,\left( {N_{j}^{{\text{c}}} - 1} \right). \\ \end{gathered} $6. Уравнения связей по входным и выходным переменным ЭБСТ:
(31)
$F_{{{{q}_{i}}}}^{{{\text{h}},(k)}} = F_{i}^{{\text{h}}},\,\,\,\,F_{{{{q}_{j}}}}^{{{\text{c}},(k)}} = F_{j}^{{\text{c}}},$(32)
$T_{{{{q}_{j}}}}^{{{\text{c,in}}}} = T_{j}^{{{\text{c,in}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,in}}}} = T_{i}^{{{\text{h,in}}}},\,\,\,\,q = 1,$(33)
$T_{{{{q}_{j}}}}^{{{\text{c,out}}}} = T_{j}^{{{\text{c,out}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,out}}}} = T_{i}^{{{\text{h,out}}}},\,\,\,\,q = N,$(34)
$\begin{gathered} T_{{{{q}_{i}} + 1}}^{{{\text{h,in}},(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,out}},(k)}},\,\,\,\,T_{{{{q}_{j}} + 1}}^{{{\text{c,in}},(k)}} = T_{{{{q}_{j}}}}^{{{\text{c,out}},(k)}}, \\ {{q}_{i}} = 1,...,\left( {N_{i}^{{\text{h}}} - 1} \right),\,\,\,\,{{q}_{j}} = 1,...,\left( {N_{j}^{{\text{c}}} - 1} \right), \\ i = 1,...,{{M}^{{\text{h}}}},j = 1,...,{{M}^{{\text{с}}}},\,\,\,\,{{q}_{i}} = 1,...,N_{i}^{{\text{h}}}, \\ {{q}_{j}} = 1,...,N_{j}^{{\text{c}}}. \\ \end{gathered} $7. Среднелогарифмическая разность температур:
(35)
$\begin{gathered} \Delta \tilde {t}_{{\ln }}^{{{\text{p}},(k)}} = \frac{{d\tilde {t}_{1}^{{{\text{p}},(k)}} + d\tilde {t}_{2}^{{{\text{p,}}(k)}}}}{{\ln \frac{{d\tilde {t}_{1}^{{{\text{p}},(k)}}}}{{d\tilde {t}_{2}^{{{\text{p}},(k)}}}}}},\,\,\,\,\forall p \in \Omega , \\ если\,\,\,\,d\tilde {t}_{1}^{{{\text{p,}}(k)}} \ne d\tilde {t}_{2}^{{{\text{p}},(k)}}, \\ \end{gathered} $(36)
$\begin{gathered} \Delta \tilde {t}_{{\ln }}^{{{\text{p}},(k)}} = d\tilde {t}_{1}^{{{\text{p}},(k)}} = d\tilde {t}_{2}^{{{\text{p}},(k)}},\,\,\,\,\forall p \in \Omega , \\ {\text{если}}\,\,\,\,d\tilde {t}_{1}^{{{\text{p}},(k)}} = d\tilde {t}_{2}^{{{\text{p}},(k)}}, \\ \end{gathered} $(37)
$d\tilde {t}_{1}^{{{\text{he}},(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,in}}}} - \bar {\bar {T}}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{c}},(k)}},\,\,\,\,d\tilde {t}_{2}^{{{\text{he}},(k)}} = \bar {\bar {T}}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{h}},(k)}} - T_{{{{q}_{j}}}}^{{{\text{c,in}}}},$(38)
$\begin{gathered} d\tilde {t}_{1}^{{{\text{col}},(k)}} = \bar {\bar {T}}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{h}},(k)}} - {{T}^{{{\text{cu,out}}}}}, \\ d\tilde {t}_{2}^{{{\text{col}},(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,out}}}} - {{T}^{{{\text{cu,in}}}}},\,\,\,\,\forall \left( {q_{i}^{{\text{h}}},q_{j}^{{\text{c}}}} \right) \in {{Z}^{{(k)}}}, \\ \end{gathered} $(39)
$d\tilde {t}_{1}^{{{\text{reb}},(k)}} = {{T}^{{{\text{hu,in}}}}} - T_{{{{q}_{j}}}}^{{{\text{c,out}}}},\,\,d\tilde {t}_{2}^{{{\text{reb}},(k)}} = {{T}^{{{\text{hu,out}}}}} - \tilde {T}_{{{{q}_{i}},{{q}_{j}}}}^{{{\text{c}},(k)}}.$8. Ограничения на физическую реализуемость процесса теплообмена:
(40)
$\begin{gathered} d\tilde {t}_{1}^{{{\text{p}},(k)}} - \Delta {{T}_{{\min }}} \geqslant 0,\,\,\,\,d\tilde {t}_{2}^{{{\text{p}},(k)}} - \Delta {{T}_{{\min }}} \geqslant 0, \\ \Delta \bar {Q}_{{q_{i}^{{\text{h}}},q_{j}^{{\text{c}}}}}^{{{\text{p}},(k)}} \geqslant 0,\,\,\,\,\forall p \in \Omega . \\ \end{gathered} $9. Ограничения на сумму коэффициентов распределения нагрузок по стадиям:
(41)
$\sum\limits_{{{l}_{j}} = 1}^{{{L}_{j}}} {\alpha _{{{{q}_{j}}}}^{{{\text{c}},(k)}}} - 1 = 0,\,\,\,\,\sum\limits_{{{l}_{i}} = 1}^{{{L}_{i}}} {\alpha _{{{{q}_{i}}}}^{{{\text{h}},(k)}}} - 1 = 0,$Алгоритм поиска оптимальной структуры системы теплообмена. Укрупненный алгоритм решения этой задачи заключается в следующем.
Шаг 1. Положить k = 1. Задать начальные приближения коэффициентов $\alpha _{{{{q}_{i}}}}^{{(k)}}$ и $\alpha _{{{{q}_{j}}}}^{{(k)}}.$
Шаг 2. Определить оптимальные экономические оценки для каждого ЭБСТ qi-го горячего и qj-го холодного потоков решением задачи (2)–(18).
Шаг 3. Решить задачу о назначениях (22)–(23) с целью определения оптимальной структуры для текущих приближений коэффициентов распределения нагрузок.
Шаг 4. На найденной структуре СТО решить задачу оптимизации (24)–(42) в пространстве нагрузок по всем теплообменникам многостадийной СТО.
Шаг 5. Определить новые значения $\alpha _{{{{q}_{i}}}}^{{(k + 1)}}$ и $\alpha _{{{{q}_{j}}}}^{{(k + 1)}}{\text{:}}$
(43)
$\alpha _{{{{q}_{i}}}}^{{{\text{h}},(k + 1)}} = \frac{{\Delta \tilde {H}_{{{{q}_{i}}}}^{{{\text{h}},(k)}}}}{{\Delta H_{i}^{{\text{h}}}}},\,\,\,\,\alpha _{{{{q}_{j}}}}^{{c,(k + 1)}} = \frac{{\Delta \tilde {H}_{{{{q}_{j}}}}^{{c,(k)}}}}{{\Delta H_{j}^{{\text{c}}}}}.$Шаг 6. Если |Φ(k) – Φ(k– 1)| ≥ ξ, то положить k = = k + 1. Перейти к шагу 2. В противном случае закончить процедуру вычислений.
Предположим, что среди Mh горячих потоков имеется R потоков, входная температура которых больше температуры j-го холодного потока на величину большую, чем принимаемая допустимая разность температур ΔTmin:
(44)
$T_{{{{r}_{j}}}}^{{{\text{h,in}}}} - T_{j}^{{{\text{c,in}}}} \geqslant \Delta {{T}_{{\min }}},\,\,\,\,{{r}_{j}} = 1,...,{{R}_{j}}.$Пусть также и среди ${{M}^{{\text{c}}}}$ холодных потоков имеется K потоков, входная температура которых меньше температуры i-го горячего потока на величину большую, чем принимаемая допустимая разность температур ΔTmin:
(45)
$T_{i}^{{{\text{h,in}}}} - T_{{{{g}_{i}}}}^{{{\text{c,in}}}} \geqslant \Delta {{T}_{{\min }}},\,\,\,\,{{g}_{i}} = 1,...,{{K}_{i}}.$Тогда при синтезе оптимальной многостадийной системы теплообмена примем максимально возможное число стадий теплообмена j-го холодного потока за Nj = Rj. Для i-го горячего потока примем ${{N}_{i}} = {{K}_{i}}.$
СИНТЕЗ ОПТИМАЛЬНОЙ СИСТЕМЫ ТЕПЛООБМЕНА С РАЗДЕЛЕНИЕМ МАТЕРИАЛЬНО-ТЕПЛОВЫХ ПОТОКОВ
Рассмотрим задачу синтеза оптимальных СТО с возможностью разделения материально-тепловых потоков. На каждом входном горячем (холодном) потоке поставим делители потоков $D_{i}^{{\text{h}}}$ и $D_{j}^{{\text{c}}}.$ Они будут делить i-й горячий поток $S_{i}^{{\text{h}}}$ на $L_{i}^{{\text{h}}}$ элементарных потоков $S_{{{{l}_{i}}}}^{{\text{h}}}$ (i = 1, …, Мh, $l_{i}^{{\text{h}}} = 1,...,L_{i}^{{\text{h}}}$) и j-й холодный поток $S_{j}^{{\text{c}}}$ на $L_{j}^{{\text{c}}}$ элементарных потоков $S_{{{{l}_{j}}}}^{{\text{c}}},$ (j = 1, …, Мc, $l_{j}^{{\text{c}}} = 1,...,L_{j}^{{\text{c}}}$) соответственно. Расходы $F_{{{{l}_{i}}}}^{{\text{h}}},$ $F_{{{{l}_{j}}}}^{{\text{c}}}$ потоков $S_{{{{l}_{i}}}}^{{\text{h}}}$ и $S_{{{{l}_{j}}}}^{{\text{c}}}$ будут равны $\beta _{{{{l}_{i}}}}^{{\text{h}}}F_{{{{l}_{i}}}}^{{\text{h}}},$ $\beta _{{{{l}_{j}}}}^{{\text{c}}}F_{{{{l}_{j}}}}^{{\text{c}}}$ соответственно, где $\beta _{{{{l}_{i}}}}^{{\text{h}}},$ $\beta _{{{{l}_{j}}}}^{{\text{c}}}$ – коэффициенты разделения, удовлетворяющие условиям
(46)
$\sum\limits_{{{l}_{i}} = 1}^{L_{i}^{{\text{h}}}} {\beta _{{{{l}_{i}}}}^{{\text{h}}}} = 1,\,\,i = 1,...,{{M}^{{\text{h}}}},\,\,\sum\limits_{{{l}_{j}} = 1}^{L_{j}^{{\text{c}}}} {\beta _{{{{l}_{j}}}}^{{\text{c}}}} = 1,\,\,j = 1,...,{{M}^{{\text{c}}}}.$Ясно, что температуры потоков $S_{{{{l}_{i}}}}^{{\text{h}}}$ и $S_{{{{l}_{j}}}}^{{\text{c}}}$ (li = 1, …, $L_{i}^{{\text{h}}},$ ${{l}_{j}} = 1,...,L_{j}^{{\text{h}}}$) равны температурам входных потоков $S_{i}^{{\text{h}}}$ и $S_{j}^{{\text{c}}}$ соответственно. После прохождения системы теплообменников потоки, полученные разделением i‑го горячего и j-го холодного потоков, поступают в смесители $G_{i}^{{\text{h}}}$ и $G_{j}^{{\text{c}}}$ соответственно. Используя уравнения теплового и материального баланса смесителя, получим
(47)
$\begin{gathered} \Delta H_{i}^{{\text{h}}} = \sum\limits_{{{l}_{i}} = 1}^{L_{i}^{{\text{h}}}} {\Delta H_{{{{l}_{i}}}}^{{\text{h}}}} ,\,\,\,\,F_{i}^{{{\text{h,out}}}} = \sum\limits_{{{l}_{i}} = 1}^{L_{i}^{{\text{h}}}} {F_{{{{l}_{i}}}}^{{\text{h}}}} , \\ i = 1,...,{{M}^{{\text{h}}}},\,\,\,\,{{l}_{i}} = 1,...,L_{i}^{{\text{h}}}, \\ \end{gathered} $(48)
$\begin{gathered} \Delta H_{j}^{{\text{c}}} = \sum\limits_{{{l}_{j}} = 1}^{L_{j}^{{\text{c}}}} {\Delta H_{{{{l}_{j}}}}^{{\text{c}}}} ,\,\,\,\,F_{j}^{{{\text{c,out}}}} = \sum\limits_{{{l}_{j}} = 1}^{L_{j}^{{\text{c}}}} {F_{{{{l}_{j}}}}^{{\text{c}}}} , \\ j = 1,...,{{M}^{{\text{c}}}},\,\,\,\,{{l}_{j}} = 1,...,L_{j}^{{\text{h}}}. \\ \end{gathered} $Несложно показать, что в этом случае задача синтеза оптимальной СТО принимает аналогичный вид, включая уравнения теплового и материального баланса делителя:
(49)
$\Delta H_{{{{l}_{j}}}}^{{c,(k)}} = \beta _{{{{l}_{j}}}}^{{c,(k)}}\Delta H_{j}^{{\text{c}}},\,\,\,\,\Delta H_{{{{l}_{i}}}}^{{{\text{h}},(k)}} = \beta _{{{{l}_{i}}}}^{{{\text{h}},(k)}}\Delta H_{i}^{{\text{h}}},$(50)
$F_{{{{l}_{i}}}}^{{{\text{h}},(k)}} = \beta _{{{{l}_{i}}}}^{{{\text{h}},(k)}}F_{i}^{{\text{h}}},\,\,\,\,F_{{{{l}_{j}}}}^{{c,(k)}} = \beta _{{{{l}_{j}}}}^{{c,(k)}}F_{j}^{{\text{c}}}$и условия изотермического смешения потоков:
(51)
$\begin{gathered} T_{{{{l}_{i}}}}^{{{\text{h,out}}}} - T_{i}^{{{\text{h,out}}}} = 0,\,\,\,\,T_{{{{l}_{j}}}}^{{{\text{c,out}}}} - T_{j}^{{{\text{c,out}}}} = 0, \\ i = 1,...,{{M}^{{\text{h}}}},\,\,\,\,{{l}_{i}} = 1,...,L_{i}^{{\text{h}}},\,\,\,\,j = 1,...,{{M}^{{\text{c}}}}, \\ {{l}_{j}} = 1,...,L_{j}^{{\text{h}}}. \\ \end{gathered} $В случае неизотермического смешения потоков условия (51) будут иметь вид
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Работоспособность и эффективность предложенного подхода рассмотрим на трех модельных примерах с использованием различных суперструктур. Для решения задачи нелинейного программирования на шагах 2 и 4 будем использовать метод последовательного квадратичного программирования. Одним из эффективных методов решения задачи о назначениях на шаге 3 является венгерский алгоритм, который будем использовать для нахождения оптимальной структуры системы теплообмена.
Пример 1. Начальные и конечные температуры, количество теплоты, отбираемое от “горячих” и передаваемое “холодным” технологическим потокам, представлены в табл. 1.
Таблица 1.
Исходные данные
| Горячий поток | $T_{i}^{{{\text{h,in}}}},$ К | $T_{i}^{{{\text{h,out}}}},$ К | FCp, кВт/К | Холодный поток | $T_{j}^{{{\text{c,in}}}},$ К | $T_{j}^{{{\text{c,out}}}},$ К | FCp, кВт/К |
|---|---|---|---|---|---|---|---|
| H1 | 650 | 370 | 10 | C1 | 410 | 650 | 15 |
| H2 | 590 | 370 | 20 | C2 | 350 | 500 | 13 |
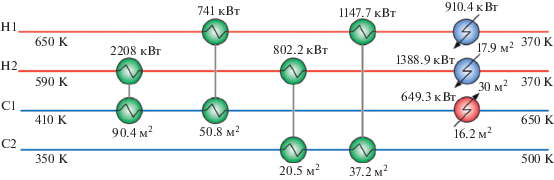
По исходным данным была найдена оптимальная структура системы теплообмена. Результаты синтеза СТО в виде диаграммы представлены на рис. 8.
В табл. 2 определены режимы эксплуатации каждого теплообменного аппарата, найденные в результате синтеза оптимальной СТО на суперструктуре смешанного тока.
Таблица 2.
Результаты решения задачи оптимального синтеза на суперструктуре смешанного тока (B − нагреватель; C − холодильник; E − рекуператор)
| Теплообменный аппарат | Q, кВт | $T_{i}^{{{\text{h,in}}}},$ К | $T_{i}^{{{\text{h,out}}}},$ К | $T_{j}^{{{\text{c,in}}}},$ К | $T_{j}^{{{\text{c,out}}}},$ К | A, м2 |
|---|---|---|---|---|---|---|
| E21 | 2208 | 590 | 479.5 | 410 | 557.2 | 90.4 |
| E11 | 741.8 | 650 | 575.8 | 557.2 | 606 | 50.8 |
| Е22 | 802.2 | 479.5 | 440 | 350 | 411.7 | 20.5 |
| Е12 | 1147.7 | 575.8 | 461 | 411.7 | 500 | 37.2 |
| С21 | 910.4 | 461 | 370 | 300 | 320 | 17.9 |
| С22 | 1388.9 | 440 | 370 | 300 | 320 | 30 |
| В11 | 649.3 | 680 | 679 | 606 | 650 | 16.2 |
В табл. 3 представлен сравнительный анализ результатов решения с использованием различных методов и алгоритмов. Структура СТО, найденная с помощью разработанного алгоритма, показала экономически более выгодные результаты по сравнению со структурой, найденной интегральным подходом с помощью программы SYNHEAT [38], и по сравнению с прямоточной и противоточной структурами многостадийного теплообмена.
Таблица 3.
Сравнительный анализ результатов решения с использованием различных методов и алгоритмов
| Параметры | Прямо- точная суперструктура |
Противоточная суперструктура |
Суперструктура смешанного тока | Результат в SYNHEAT |
|---|---|---|---|---|
| Рекуперируемая энергия, кВт | 4894.98 | 4894.97 | 4899.7 | 4894.26 |
| Подводимая энергия, кВт | 655.02 | 655.015 | 649.3 | 655.74 |
| Отводимая энергия, кВт | 2305.01 | 2305.014 | 2299.3 | 2305.74 |
| Число рекуперативных теплообменников | 3 | 3 | 4 | 3 |
| Число нагревателей | 1 | 1 | 1 | 1 |
| Число холодильников | 2 | 2 | 2 | 2 |
| Суммарные приведенные затраты, у.е. | 200 183 | 200 183 | 196 692 | 200 246 |
На рис. 9 представлена диаграмма структуры оптимальной СТО, полученной с использованием программы SYNHEAT, прямоточной и противоточной системы теплообмена.
Пример 2. Начальные и конечные температуры, количество теплоты, отбираемое от горячих и передаваемое холодным технологическим потокам, представлены в табл. 4.
Таблица 4.
Исходные данные
| Горячий поток | $T_{i}^{{{\text{h,in}}}},$ К | $T_{i}^{{{\text{h,out}}}},$ К | FCp, кВт/К | Холодный поток | $T_{j}^{{{\text{c,in}}}},$ К | $T_{j}^{{{\text{c,out}}}},$ К | FCp, кВт/К |
|---|---|---|---|---|---|---|---|
| H1 | 403 | 383 | 40 | C1 | 333 | 373 | 80 |
| H2 | 433 | 353 | 15 | C2 | 363 | 393 | 27 |
| H3 | 470 | 350 | 250 | C3 | 373 | 453 | 200 |
| H4 | 505 | 335 | 150 | C4 | 413 | 503 | 300 |
По данным материально-тепловых потоков были построены горячая и холодная композитные кривые, представленные на рис. 10.
Рис. 10.
Горячая (верхняя) и холодная (нижняя) композитные кривые на температурно-энтальпийной диаграмме (пример 2).
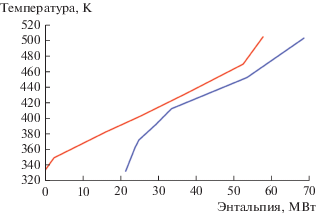
Получены следующие результаты пинч-анализа:
| Суммарное количество энергии, которую необходимо снять с горячих потоков, кВт | 57 500 |
| Суммарное количество энергии, которую необходимо передать холодным потокам, кВт | 47 010 |
| Максимально возможное количество рекуперируемой энергии, кВт | 36 210 |
| Минимальное количество энергии, отводимой холодными теплоносителями, кВт | 21 290 |
| Минимальное количество энергии, подводимой горячими теплоносителями, кВт | 10 800 |
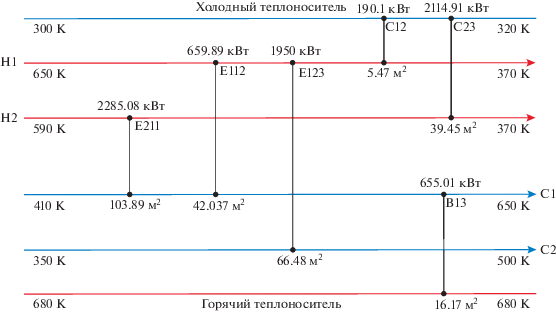
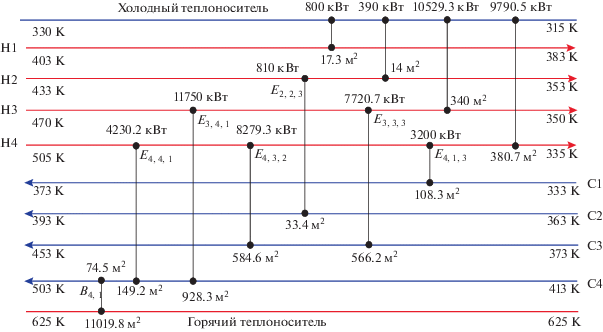
По исходным данным была найдена оптимальная структура системы теплообмена. Диаграмма оптимальной СТО представлена на рис. 11.
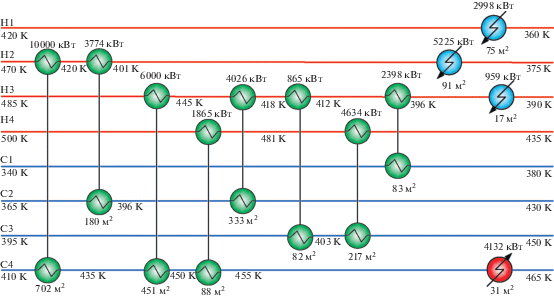
Структура СТО, найденная с помощью разработанного алгоритма на суперструктуре смешанного тока, характеризуется экономически более выгодными результатами по сравнению со структурой, найденной с помощью программы SYNHEAT, и повторяет результаты, полученные с использованием противоточной суперструктуры (табл. 5).
Таблица 5.
Сравнительный анализ результатов решения с использованием различных методов и алгоритмов
| Параметры | Прямоточная суперструктура |
Противоточная суперструктура |
Суперструктура смешанного тока | Результат в SYNHEAT |
|---|---|---|---|---|
| Рекуперируемая энергия, кВт | 32 310 | 35 990.2 | 35 988.76 | 20 010 |
| Подводимая энергия, кВт | 14 700 | 11 019.8 | 11 021.2 | 27 000 |
| Отводимая энергия, кВт | 25 190 | 21 509.8 | 21 511.3 | 37 300 |
| Число рекуперативных теплообменников | 5 | 6 | 6 | 4 |
| Число нагревателей | 1 | 1 | 1 | 1 |
| Число холодильников | 3 | 4 | 4 | 3 |
| Суммарные приведенные затраты, у.е. | 1 985 404 | 1 745 027 | 1 745 606 | 3 147 181 |
На рис. 12 представлена оптимальная структура СТО, полученная в программе SYNHEAT.
Пример 3. Рассмотрим еще один пример размерности $4{\text{H}} \times 4{\text{C}}{\text{.}}$
Начальные и конечные температуры, количество теплоты, отбираемое от горячих и передаваемое холодным технологическим потокам, представлены в табл. 6.
Таблица 6.
Исходные данные
| Горячий поток | $T_{i}^{{{\text{h,in}}}},$ К | $T_{i}^{{{\text{h,out}}}},$ К | FCp, кВт/К | Холодный поток | $T_{j}^{{{\text{c,in}}}},$ К | $T_{j}^{{{\text{c,out}}}},$ К | FCp, кВт/К |
|---|---|---|---|---|---|---|---|
| H1 | 420 | 360 | 50 | C1 | 340 | 380 | 60 |
| H2 | 470 | 375 | 200 | C2 | 365 | 430 | 120 |
| H3 | 485 | 390 | 150 | C3 | 395 | 450 | 100 |
| H4 | 500 | 435 | 100 | C4 | 410 | 465 | 400 |
По данным материально-тепловых потоков были построены композитные кривые, представленные на рис. 13.
Рис. 13.
Горячая (верхняя) и холодная (нижняя) композитные кривые на температурно-энтальпийной диаграмме (пример 3).
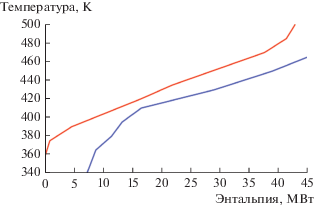
Результаты пинч-анализа:
| Суммарное количество энергии, которую необходимо снять с горячих потоков, кВт | 42 750 |
| Суммарное количество энергии, которую необходимо передать холодным потокам, кВт | 37 700 |
| Максимально возможное количество рекуперируемой энергии, кВт | 35 550 |
| Минимальное количество энергии, отводимой холодными теплоносителями, кВт | 7200 |
| Минимальное количество энергии, подводимой горячими теплоносителями, кВт | 2150 |
В ходе исследования были построены графики (рис. 14) зависимости оптимальных значений суммарных приведенных капитальных и эксплуатационных затрат от коэффициентов распределения тепловых нагрузок между стадиями суперструктуры СТО. Рассмотрим полученные решения.
Рис. 14.
Графики зависимости оптимального значения приведенных затрат от коэффициентов распределения тепловых нагрузок.
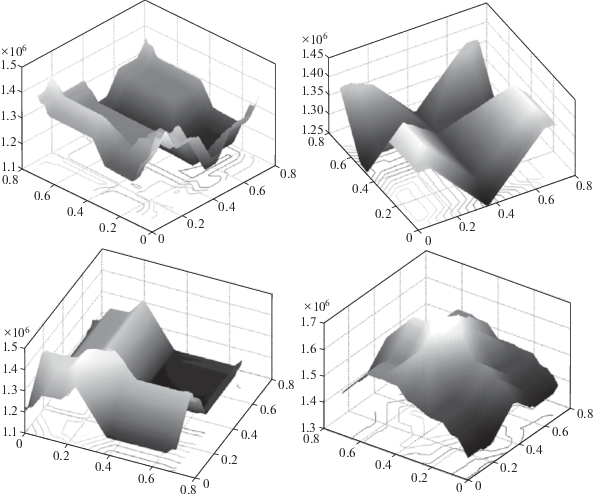
Каждая точка выделенного трехмерного пространства характеризует оптимальную структуру системы теплообмена и режимы работы входящих в ее состав теплообменников при фиксированных значениях коэффициентов распределения нагрузок. Анализируя построенные графики, можно утверждать о наличии множества экстремумов целевой функции. Поэтому проблема многоэкстремальности препятствует нахождению оптимального решения методами интегрального синтеза, к примеру с использованием программы SYNHEAT. Предлагаемый в настоящей статье метод частично решает данную проблему за счет сведения задачи оптимизации структуры стадии к задаче линейного программирования о назначениях.
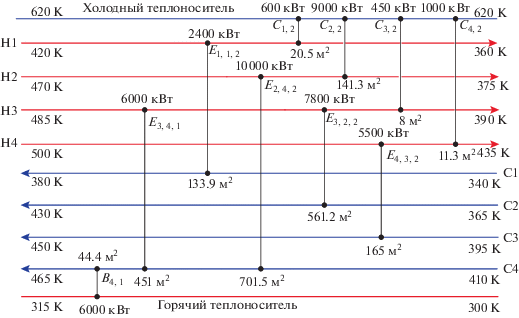
По исходным данным была найдена оптимальная структура системы теплообмена. Результаты синтеза СТО и ее диаграмма представлены в табл. 7 и на рис. 15.
Таблица 7.
Сравнительный анализ результатов решения с использованием различных методов и алгоритмов
| Число стадий в суперструктуре СТО | Прямоточная суперструктура | Противоточная суперструктура | Суперструктура смешанного тока | Результат в SYNHEAT |
|---|---|---|---|---|
| Рекуперируемая энергия, кВт | 31 200 | 31 700 | 33 532 | 23 150 |
| Подводимая энергия, кВт | 6500 | 6000 | 4132 | 9050 |
| Отводимая энергия, кВт | 11 550 | 11 050 | 9182 | 14 100 |
| Число рекуперативных теплообменников | 5 | 5 | 8 | 5 |
| Число нагревателей | 1 | 1 | 1 | 2 |
| Число холодильников | 4 | 4 | 3 | 3 |
| Суммарные приведенные затраты, у.е./год | 829 491 | 785 739 | 616 907 | 1 098 914 |
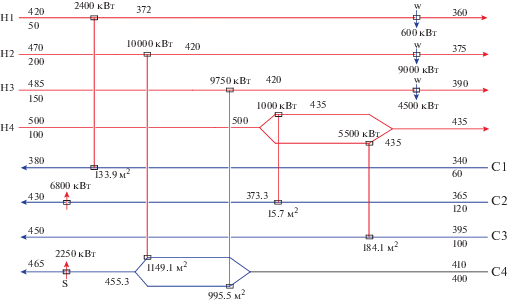
В табл. 8 представлен сравнительный анализ результатов решения с использованием различных методов и алгоритмов. Структура СТО, найденная с помощью суперструктуры смешанного тока, показала экономически более выгодные результаты по сравнению со структурой, найденной с помощью программы SYNHEAT, с прямоточной и противоточной структурами многостадийного теплообмена.
Оптимальные структуры прямоточной, противоточной системы теплообмена и структура СТО, найденная с помощью программы SYNHEAT, представлены на рис. 16, 17 и 18 соответственно.
ЗАКЛЮЧЕНИЕ
В настоящей работе показано, что предлагаемый метод автоматизированного синтеза оптимальных систем теплообмена на основе принципа закрепления переменных дает лучшие результаты за счет структурной и целевой декомпозиции задачи синтеза. Предложенная суперструктура смешанного тока позволяет расширить поисковую область оптимального значения критерия суммарных приведенных капитальных и эксплуатационных затрат на организацию системы теплообмена. Среди преимуществ предлагаемого метода можно выделить следующие:
сведение задачи синтеза оптимальных СТО к хорошо зарекомендовавшим себя методам оптимизации (линейного и нелинейного математического программирования);
частичная ликвидация локальных минимумов экономического критерия за счет отбрасывания неперспективных структурных элементов, порождающих многоэкстремальность задачи, по их экономическим оценкам, найденным в результате решения задач с поисковым пространством малой размерности;
использование структурно-модульного принципа оптимального проектирования, позволяющего минимизировать вычислительные и временные затраты, решать задачи больших размерностей реальных промышленных масштабов.
Полная автоматизация разработанного метода позволит использовать его в качестве составной процедуры многоуровневых методов автоматизированного синтеза оптимальных систем разделения многокомпонентных систем, каскада реакторов и т.д. Предлагаемый вариант декомпозиции дает возможность для последующей реализации методов проектирования оптимальных гибких систем теплообмена как с учетом неопределенности в составах и параметрах сырьевых потоков технологических установок, так и требований на качество получаемой продукции.
ОБОЗНАЧЕНИЯ
| A | площадь поверхности теплообмена, м2 |
| c | удельная изобарная теплоёмкость, (кВт ч)/(кг К) |
| F | массовый расход, кг/ч |
| f | суммарные приведенные капитальные и операционные затраты, у.е./год |
| H | теплосодержание, кВт |
| $\hat {m}_{1}^{{}}$ | приведенные ценовые коэффициенты затрат, у.е./год |
| $\hat {m}_{2}^{{}}$ | приведенные ценовые коэффициенты затрат, у.е./(год м2) |
| $\tilde {m}$ | цена единицы расхода горячего или холодного теплоносителей, у.е./кг |
| Q | количество теплоты, кВт |
| T | температура потока, К |
| ΔTmin | минимально допустимая разность температур, К |
| U | коэффициент теплопередачи, (кВт ч)/(м2 К) |
| $Z_{{}}^{{(k)}}$ | совокупности пар горячих и холодных потоков, для которых определен элементарный блок, входящий в схему системы теплообмена на k-й итерации |
| γ | корреляционный коэффициент |
| Φ | сумма приведенных капитальных затрат и операционных затрат СТО, у.е./год |
ИНДЕКСЫ
| aut | автономный теплообмен |
| с | холодный поток |
| col | холодильник/конденсатор |
| h | горячий поток |
| he | рекуперативный теплообменник |
| i | номер “горячего” потока |
| j | номер “холодного” потока |
| k | номер итерации |
| l | элементарный поток, полученный разделением исходного потока |
| q | номер стадии теплообмена |
| reb | нагреватель/кипятильник |
Список литературы
Tovazhnyanskii L.L., Kapustenko P.A., Ul’ev L.M., Boldyrev S.A., Arsen’eva O.P., Tarnovskii M.V. Thermal process integration in the AVDU A12/2 crude distillation unit during winter operation // Theor. Found. Chem. Eng. 2009. V. 43. № 6. P. 906. [Товажнянский Л.Л., Капустенко П.А., Ульев Л.М., Болдырев С.А., Арсеньева О.П., Тарновский М.В. Интеграция тепловых процессов на установке первичной переработки нефти АВТ Ф12/2 при работе в зимнее время // Теор. осн. хим. технол. 2009. Т. 43. № 6. С. 665.]
Мешалкин В.П., Товажнянский Л.Л., Ульев Л.М., Мельниковская, Л.А., Ходченко С.М. Энергоресурсоэффективная реконструкция установки нефтепереработки на основе пинч-анализа с учетом внешних тепловых потерь // Теор. осн. хим. технол. 2012. Т. 46. № 5. С. 491.
Klemeš J.J., Kravanja Z. Forty years of heat integration: pinch analysis (PA) and mathematical programming (MP) // Curr. Opin. Chem. Eng. 2013. V. 2. № 4. P. 461.
Morar M., Agachi P.S. Review: Important contributions in development and improvement of the heat integration techniques // Comput. Chem. Eng. 2010. V. 34. № 8. P. 1171.
Furman K.C., Sahinidis N.V. A critical review and annotated bibliography for heat exchanger network synthesis in the 20th century // Ind. Eng. Chem. Res. 2002. V. 41. № 10. P. 2335.
Quirante N., Caballero J.A., Grossmann I.E. A Novel Disjunctive Model for the Simultaneous Optimization and Heat Integration // Comput. Chem. Eng. 2018. V. 108. P. 217.
Ahmetović E., Ibrić N., Kravanja Z., Grossmann I.E. Water and energy integration: A comprehensive literature review of non-isothermal water network synthesis // Comput. Chem. Eng. 2015. V. 82. P. 144.
Ahmetović E., Kravanja Z. Simultaneous synthesis of process water and heat exchanger networks // Energy. 2013. V. 57. P. 236.
Bagajewicz M., Rodera H., Savelski M. Energy efficient water utilization systems in process plants // Comput. Chem. Eng. 2002. V. 26. № 1. P. 59.
Wang Y., Chang C., Feng X. A systematic framework for multi-plants heat integration combining direct and indirect heat integration methods // Energy. 2015. V. 90. P. 56.
Laukkanen T., Tveit T.-M., Fogelholm C.-J. Simultaneous heat exchanger network synthesis for direct and indirect heat transfer inside and between processes // Chem. Eng. Res. Des. 2012. V. 90. P. 1129.
Song R., Chang C., Tang Q., Wang Y., Feng X., El-Halwagi M.M. The implementation of inter-plant heat integration among multiple plants. Part II: The mathematical model // Energy. 2017. V. 135. P. 382.
Boldyryev S.A., Garev A.O., Klemeš J.J., Tovazhnyansky L.L., Kapustenko P.O., Perevertaylenko O.Yu., Arsenyeva O.P. Heat integration of ammonia refrigeration cycle into buildings heating systems in buildings // Theor. Found. Chem. Eng. 2013. V. 47. № 1. P. 39. [Болдырев С.А., Гарев А.О., Клемеш Й.Й., Товажнянский Л.Л., Капустенко П.А., Перевертайленко А.Ю., Арсеньева О.П. Тепловая интеграция аммиачного холодильного агрегата в коммунальную систему зданий // Теор. осн. хим. технол. 2013. Т. 47. № 1. С. 45.]
Zhao X.G., O’Neill B.K., Roach J.R., Wood R.M. Heat Integration for Batch Processes: Part 2: Heat Exchanger Network Design // Chem. Eng. Res. Des. 1998. V. 76. № 6. P. 700.
Klemeš J.J., Varbanov P.S. Heat Integration Including Heat Exchangers, Combined Heat and Power, Heat Pumps, Separation Processes and Process Control // Appl. Therm. Eng. 2012. V. 43. P. 1.
Holiastos K., Manousiouthakis V. Minimum hot/cold/ electric utility cost for heat exchange networks // Comput. Chem. Eng. 2002. V. 26. P. 3.
Linnhoff B. Pinch analysis–A state-of-the-art overview: Techno-economic analysis // Chem. Eng. Res. Des. 1993. V. 71. № 5. P. 503.
Ul'ev L.M., Vasil’ev M.A. Heat and power integration of processes for the refinement of coking products // Theor. Found. Chem. Eng. 2015. V. 49. № 5. P. 676. [Ульев Л.М., Васильев М.А. Теплоэнергетическая интеграция процессов переработки продуктов коксования // Теор. осн. хим. технол. 2015. Т. 49. № 5. С. 582.]
Цирлин А.М., Ахременков А.А., Григоревский И.Н. Минимальная необратимость, оптимальное распределение поверхности и тепловой нагрузки теплообменных систем // Теор. осн. хим. технол. 2008. Т. 42. № 1. С. 1.
Цирлин А.М., Ахременков А.А. Оптимальный теплообмен при изменении фазового состояния хладагента // Теор. осн. хим. технол. 2018. Т. 52. № 5. С. 541.
Yee T.F., Grossmann I.E. Simultaneous optimization models for heat integration – II. Synthesis of heat exchanger networks // Comput. Chem. Eng. 1990. V. 14. № 10. P. 1165.
Ponce-Ortega J., Jimenez-Gutierrez A., Grossmann I. Optimal synthesis of heat exchanger networks involving isothermal process streams // Comput. Chem. Eng. 2008. V. 32. P. 1918.
Bogataj M., Kravanja Z. An alternative strategy for global optimization of heat exchanger networks // Appl. Therm. Eng. 2012. V. 43. P. 75.
Pettersson F. Synthesis of large-scale heat exchanger networks using a sequential match reduction approach // Comput. Chem. Eng. 2005. V. 29. P. 993.
Zhang C., Cui G., Chen S. An efficient method based on the uniformity principle for synthesis of large-scale heat exchanger networks // Appl. Therm. Eng. 2016. V. 107. P. 565.
Bergamini M.L., Scenna N.J., Aguirre P.A. Global Optimal Structures of Heat Exchanger Networks by Piecewise Relaxation // Ind. Eng. Chem. Res. 2007. V. 46. P. 1752.
Faria D.C., Kim S.Y., Bagajewicz M.J. Global Optimization of the Stage-wise Superstructure Model for Heat Exchanger Networks // Ind. Eng. Chem. Res. 2015. V. 54. № 5. P. 1595.
Björk K.-M., Westerlund T. Global optimization of heat exchanger network synthesis problems with and without the isothermal mixing assumption // Comput. Chem. Eng. 2002. V. 26. P. 1581.
Agarwal A., Gupta S.K. Multiobjective Optimal Design of Heat Exchanger Networks Using New Adaptations of the Elitist Nondominated Sorting Genetic Algorithm, NSGA-II // Ind. Eng. Chem. Res. 2008. V. 47. P. 3489.
Cerda J., Westerberg A.W., Mason D., Linnhoff B. Minimum utility usage in heat exchanger network synthesis: A transportation problem // Chem. Eng. Sci. 1983. V. 38. № 3. P. 373.
Cerda J., Westerberg A.W. Synthesizing heat exchanger networks having restricted stream/stream matches using transportation problem formulations // Chem. Eng. Sci. 1983. V. 38. № 10. P. 1723.
Papoulias S.A., Grossmann I.E. A structural optimization approach in process synthesis. II. Heat recovery networks // Comput. Chem. Eng. 1983. V. 7. № 6. P. 707.
Chen Y., Grossmann I.E., Miller D.C. Computational Strategies for Large-Scale MILP Transshipment Models for Heat Exchanger Network Synthesis // Comput. Chem. Eng. 2015. V. 82. P. 68.
Nemet A., Isafiade A., Klemeš J., Kravanja Z. Two-step MILP/MINLP approach for the synthesis of large-scale HENs // Chem. Eng. Sci. 2018. V. 197. P. 432.
Ostrovskii G.M., Ziyatdinov N.N., Emel’yanov I.I. Synthesis of Optimal Systems of Simple Distillation Columns with Heat Recovery // Dokl. Chem. 2015. V. 461. № 2. Р. 89. [Островский Г.М., Зиятдинов Н.Н., Емельянов И.И. Синтез оптимальных систем простых ректификационных колонн с рекуперацией тепла // Докл. Акад. наук. 2015. Т. 461. № 2. С. 189.]
Ziyatdinov N.N., Ostrovskii G.M., Emel’yanov I.I. Designing a Heat–Exchange System upon the Reconstruction and Synthesis of Optimal Systems of Distillation Columns // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 178. [Зиятдинов Н.Н., Островский Г.М., Емельянов И.И. Построение системы теплообмена при реконструкции и синтезе оптимальных систем ректификационных колонн // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 184.]
Ziyatdinov N.N., Emel’yanov I.I., Tuen L.Q. Method for the Synthesis of Optimum Multistage Heat Exchange Networks // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 614. [Зиятдинов Н.Н., Емельянов И.И., Туен Л.К. Метод синтеза оптимальных многостадийных систем теплообмена // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 614.]
Yee T.F., Grossmann I.E., Kravanja Z. Simultaneous optimization models for heat integration — III. Process and heat exchanger network // Comput. Chem. Eng. 1990. V. 14. № 11. P. 1185.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии