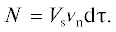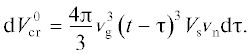Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 135-143
Кинетика реагентного осаждения: общие эволюционные закономерности различных моделей
С. К. Мясников a, *, А. Ю. Тихонов a, Н. Н. Кулов a
a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
* E-mail: msk@igic.ras.ru
Поступила в редакцию 20.09.2019
После доработки 08.10.2019
Принята к публикации 15.10.2019
Аннотация
Рассмотрены тенденции, общие закономерности и стадии эволюционных процессов, в частности эволюции твердого вещества в процессах кристаллизации. Показана роль логистической (сигмоидальной) функции в описании кинетики эволюционных процессов. Проведено математическое моделирование процесса реагентного осаждения малорастворимых солей с учетом скоростей нуклеации и роста кристаллов. Установлено, что различные модели приводят к S-образной зависимости одного вида, адекватно описывающей процесс образования кристаллических осадков малорастворимых солей кальция из пересыщенных водных растворов.
ВВЕДЕНИЕ
Реагентное (химическое) осаждение – один из важнейших кристаллизационных процессов, широко применяемый для получения неорганических веществ и материалов, при умягчении и очистке воды. Отличительная особенность процесса – кристаллизация из сильно пересыщенных растворов [1, 2], образующихся в результате быстрых химических реакций исходных компонентов при низкой растворимости конечных продуктов. Пересыщение – движущая сила кристаллизации, а его “создание – основная причина эволюционных процессов в твердой фазе” [3]. С ростом пересыщения быстро возрастает скорость нуклеации (зарождения) и количество образующихся кристаллов. Эти качества процесса позволяют использовать его в производстве новых (в том числе наноразмерных) функциональных материалов [3, 4]. Количество статей и патентов в области технологий таких материалов исчисляется шестизначными цифрами и быстро растет, причем этот рост по многим направлениям имеет экспоненциальный характер, что соответствует общим эволюционным закономерностям [3–7].
Наука, как генератор новых идей и направлений, и новые технологии развиваются по общим эволюционным законам. Один из основателей наукометрии, Д. Прайс, показал, что 300 лет научное знание экспоненциально росло со скоростью 4.7% в год, удваиваясь каждые 15 лет и удесятеряясь каждые полвека. С момента, когда в 17-м веке появились первые научные статьи, объем знаний человечества увеличился в миллион раз [8, 9]. По тому же закону до недавнего времени росло число научных журналов и научных работников. П.Л. Капица объяснял интенсивное развитие науки тем, что “всякий процесс, который следует экспоненциальному закону, в конечном итоге всегда приобретает характер взрыва” [10].
В монографии Д.А. Николаева и Л.П. Холпанова [6] показано, что широкий спектр эволюционных процессов в химической технологии и других областях науки можно описать единой экспоненциальной зависимостью.
На практике экспоненциальные тенденции не длятся вечно. Причина – ограниченность любых ресурсов. Некоторое снижение темпов роста научных знаний отмечено в последние десятилетия. Эту тенденцию замедления науки отмечали еще С. Лем и В.В. Налимов, которые предположили, что экспоненциальный рост должен перейти в логистическую S-образную кривую насыщения [11, 12]. Тем не менее, экспоненциальный рост может продолжаться в течение длительных периодов времени, если есть соответствующие условия для взрывного развития. С этой точки зрения научные знания, по мнению многих ученых, имеют неоспоримые преимущества по сравнению с материальными ресурсами – фундаментом предыдущих этапов развития общества [13].
Проблему экспоненциального роста объема знаний можно решить при эффективном использовании информационных ресурсов [8, 9, 11, 12]. При этом В.В. Налимов отмечал, что химик-исследователь тратит на информационную деятельность в среднем 50% рабочего времени [12]. По мнению Д. Прайса, основным фактором, определяющим закон экспоненциального роста объема знаний, является организация передачи информации. Чем эффективнее она осуществляется, тем в более широком масштабе и интенсивнее развивается наука [8, 9].
Но все-таки, рано или поздно, в связи с ограниченностью ресурсов, эволюционный рост должен замедлиться, все более отклоняясь от экспоненциального по мере приближения к максимально возможной величине, которую способна поддерживать внешняя среда. Соответствующая кинетическая кривая имеет S-образный вид (сигмоида). Общий эволюционный тренд может состоять из серии последовательных S-образных технологических циклов. Например, когда рост какой-то технологии замедляется, начинается зарождение и рост новой (двойная логистическая функция).
“Вопрос об эволюции твердого вещества нельзя оторвать от эволюционной проблематики в целом” [3]. В общем случае причина эволюции в материальном мире – воздействие окружающей среды или, более конкретно, приток веществ и энергии из внешней среды. Процесс приспособления вещества к изменяющейся обстановке составляет сущность его эволюции [3].
Разным эволюционным процессам присущи не только общие закономерности, но и одинаковые стадии развития. Это зарождение, рост, стабилизация (насыщение), и затухание вплоть до разрушения (смерти). Такие стадии можно выделить в процессе исторического развития различных технологий и техники, в том числе кристаллизационных технологий и соответствующего им оборудования [14].
Несложно заметить, что подобные стадии проходит и твердое вещество в процессе своей эволюции. “В закрытых системах свойства вещества изменяются во времени по единому эволюционному маршруту, состоящему в смене стадий зарождения, роста, структурного упорядочения и агрегирования его частиц” [3, 4]. При кристаллизации из растворов пересыщение почти постоянно на стадии зарождения, значительно быстрей снижается на стадии роста и существенно медленнее – на стадии упорядочения и агрегации. Соответственно количество образующейся твердой фазы или степень кристаллизации η ведет себя “зеркально”, т.е. увеличивается во времени t вдоль S-образной кинетической кривой η = f(t) [3, 15–17].
Основы теории кристаллизации были заложены в конце XIX в. работами Дж. Гиббса, Д.К. Чернова, Г.Г. Таммана. Термодинамическая теория зарождения новой фазы предложена Дж. Гиббсом (1876–1878 гг.) и значительно позднее развита М. Фольмером (1939 г.) (флуктуационная теория). Д.К. Чернов (1878 г.) установил основные стадии процесса кристаллизации: зарождение первичных зародышей – центров кристаллизации и последующий рост кристаллов из них. Г.Г. Тамман (1897–1898 гг.) изучил кинетику кристаллизации и влияние температуры на скорость нуклеации. Более современная молекулярно-кинетическая теория роста кристаллов предложена В. Косселем и И.Н. Странским (1927 г.).
Современные математические модели, характеризующие процесс кристаллизации из расплавов, предложены в работах А.Н. Колмогорова, В. Джонсона, Р. Мела и М. Аврами (1937–1941 гг.) [18–22]. Разработанные ими модели изотермической трансформации фаз (обобщенно модель JMAK) широко применяются и в настоящее время. Однако все авторы JMAK, чтобы получить конечную модель, принимают определенные допущения. Основные постулаты JMAK: объем зародышей бесконечно мал в сравнении с объемом всей системы (всего материала); центры кристаллизации возникают случайно и равномерно с постоянной интенсивностью на единицу маточного объема; все они имеют одинаковую выпуклую (шаровую) форму и ориентацию, не меняющиеся во времени, и растут с одинаковой и постоянной линейной скоростью.
При этом Р. Мел и В. Джонсон рассматривают фиктивный механизм кристаллизации, при котором центры кристаллизации возникают во всем объеме, в том числе и в сконденсированной фазе (затвердевшей ранее массе), а зародыши растут, не сталкиваясь, как взаимопроникающие сферы, т.е. не замечая друг друга.
М. Аврами, в свою очередь, доказывал, что необходимо учитывать уменьшение объема, доступного для зарождения новых центров, т.е. фактическая скорость образования зародышей зависит от времени и описывается экспоненциальным уравнением, полученным из эксперимента. Для решения проблемы Аврами использовал концепцию расширенного объема – объема новой фазы, который сформировался бы, если бы весь образец все еще не преобразовывался. Реальна только часть этого расширенного объема, другая лежит на ранее преобразованном материале и является виртуальной.
Только подход (статистический метод) А.Н. Колмогорова является математически строгим, а формулы оказываются следствием исходных логических допущений [23]. Полученная А.Н. Колмогоровым модель и зависимости JMAK до сих пор остаются эффективным теоретическим и практическим средством, они хорошо описывают экспериментальные данные, когда все вещество полностью преобразуется из жидкого состояния в твердое [24], включая случай топохимических реакций.
При кристаллизации из водных растворов объем закристаллизованной части значительно меньше объема всего раствора (особенно при осаждении малорастворимых солей), а движущая сила процесса постоянно уменьшается во времени, поэтому для подходов, предложенных авторами JMAK, требуется соблюдение дополнительных условий.
Среди первых работ, в которых проводились исследования и моделирование кинетики процесса кристаллизации из водных пересыщенных растворов, можно выделить работы С.З. Рогинского и О.М. Тодеса [25], Н.В. Дерябиной и К.П. Мищенко [26]. Авторы допускают, что рост кристаллов происходит с одинаковой скоростью только на зародышах, которые образовались к концу индукционного периода, и подчиняется уравнению первого порядка относительно пересыщения. Если принять, что весь процесс кристаллизации проходит в две стадии: первая – образование N зародышей, вторая – их рост, то уравнение снятия пересыщения, полученное Н.В. Дерябиной и К.П. Мищенко, описывает только вторую стадию.
Теоретически найденная С.З. Рогинским и О.М Тодесом кинетическая зависимость отвечает характерной S-образной кривой [25]. Экспериментально это подтверждено на примере кристаллизации гипса [27, 28]. Такой же ход кривых изменения относительного пересыщения во времени получен по модели, предложенной Л.Б. Берлинером (принявшем степенную зависимость скорости нуклеации от пересыщения), в его работах с И.В. Мелиховым [29, 30].
В дальнейшем исследования кинетики кристаллизации солей из водных растворов развивались широким фронтом. Их результаты можно найти в основных монографиях и справочниках по кристаллизации и материалах регулярных симпозиумов по промышленной кристаллизации (последний – XX International Symposium on Industrial Crystallization, Dublin, 2017) и конференций по кинетике и механизму кристаллизации (последняя – X Международная научная конференция “Кинетика и механизм кристаллизации”, Суздаль, 2018).
В последнее время особое внимание уделялось гранулометрическому составу полученных кристаллов с учетом их агрегации и агломерации и исследованию механизма этих явлений [31–34].
Среди российских ученых в этой области можно отметить работы Л.Н. Матусевича [2, 35], О.М. Тодеса [27], И.В. Мелихова [33, 36], О.Д. Линникова [34]. В работе [33] показано, как проходит объединение образовавшихся из зародышей гексагональных нанокристаллов CaSO4 ⋅ 0.5H2O в агрегаты, имеющие аналогичную форму. О.Д. Линниковым [34] предложена модель процесса образования и трансформации кристаллов, учитывающая теорию коагуляции Смолуховского [37] и механизм срастания Полака [38], которая хорошо описывает экспериментальные данные. Однако, как и в [26], модель О.Д. Линникова не учитывает процессы, проходящие в индукционный период кристаллизации, и вторичное зародышеобразование.
Для полного моделирования процесса кристаллизации солей из водных растворов необходимо учесть множество факторов: 1) первичное зародышеобразование в течение индукционного периода кристаллизации; 2) вторичное зародышеобразование в течение всего процесса кристаллизации; 3) различную скорость роста образованных зародышей из-за постоянного снижения пересыщения; 4) агрегирование и срастание кристаллов; 5) перерастворение и разрушение кристаллов; 6) наличие примесей в водных растворах и др.
Учесть все явления и факторы, в том числе и случайные, практически невозможно, поэтому при разработке моделей приходится применять ряд допущений. В результате, попытка учесть максимальное количество влияющих факторов может дать обратный эффект и ухудшить точность расчетов. Кроме того, усложнение модели ведет к возрастанию числа необходимых эмпирических параметров и утрате ее предсказательной возможности [39]. Схожие мысли по поводу моделирования высказывал и О.М. Тодес: “Имеет определенный смысл составление и анализ лишь упрощенных математических моделей кинетики массовой кристаллизации для получения определенных качественных выводов” [27]. А Я.Е. Гегузин в своей книге “Живой кристалл” [40], писал: “на трудном пути к знанию почти все испытывают потребность в упрощенной модели”, от которой требуется “хотя бы доля правды о явлении”.
В свете вышесказанного целью настоящей работы является:
1. Моделирование кинетики реагентного осаждения с учетом рассмотренных выше общих закономерностей эволюционных процессов и особенностей кристаллизации малорастворимых солей из растворов.
2. Разработка достаточно простых математических моделей разного типа, предполагающих различный физический или химический механизм зарождения и роста кристаллов.
3. Сравнение кинетических кривых трансформации твердой фазы и снятия пересыщения, полученных в рамках существующих и предлагаемых моделей.
ОСНОВНАЯ ЧАСТЬ
В этом разделе рассматриваются математические модели, представляющие реагентное осаждение (precipitation) либо как физический процесс затвердевания жидкой фазы (условно физическая модель), либо как химический процесс реагентной кристаллизации (условно химическая модель).
Физическая модель. Модель JMAK [18–20], как уже говорилось, описывает процесс кристаллизации твердого вещества из его расплава, когда весь исходный объем жидкой фазы переходит в твердое состояние. Кривая изменения количества твердой фазы во времени имеет сигмоидальный вид, на котором можно выделить стадии образования зародышей, активный рост кристаллов и окончание процесса, когда почти весь исходный материал преобразован.
Если рассматривать преобразование ионов кальция из водного раствора в нерастворимый кристаллический осадок P, состоящий из катионов кальция и анионов соответствующих малорастворимых солей, то процесс кристаллизации будет связан с образованием зародышей со скоростью vn = const на единицу объема раствора и их постоянным ростом в сферические частицы со скоростью vg = const. Во временном интервале 0 < < τ < t зарождение и рост могут происходить только из растворенного количества кальция.
По аналогии с выводом Аврами решить поставленную задачу и определить зависимость P = f(t) легче при помощи концепции расширенного объема. Поскольку в случае водных растворов кристаллизуется лишь растворенное вещество, то будем рассматривать не весь исходный объем, а только объем закристаллизованного вещества. Таким образом, расширенный объем – объем закристаллизованного вещества, который больше реального, так как учитывает постоянный и беспрепятственный рост всех образованных зародышей с постоянной скоростью на протяжении всего времени процесса кристаллизации.
Во временном интервале dτ количество зародышей N, которые появляются в объеме раствора Vs, будет определяться как
Допустим, каждый образовавшийся зародыш растет в сфере радиуса r:
Таким образом, расширенный объем $V_{{{\text{cr}}}}^{0}$ кристаллического продукта P за счет ядер, образовавшихся в интервале времени, будет равен
Интегрирование уравнения (3) при условиях $V_{{{\text{cr}}}}^{0}$(τ = 0) = 0 и $V_{{{\text{cr}}}}^{0}$(τ = t) = $V_{{{\text{cr}}}}^{0}$ позволяет найти общий расширенный объем:
(4)
$V_{{{\text{cr}}}}^{0} = \frac{{\pi }}{3}{{{v}}_{{\text{g}}}}^{3}{{t}^{4}}{{V}_{{\text{s}}}}{{{v}}_{{\text{n}}}}.$В случае растворов очевидно, что только малая часть этого объема реальна, остальная часть является виртуальной и появляется за счет предположения о росте образовавшихся ядер с неизменной скоростью. Поэтому реальная доля расширенного объема, формирующаяся при каждом приращении времени, будет пропорциональна доле незакристаллизованного вещества (иными словами, пересыщению):
(5)
$\frac{{{\text{d}}{{V}_{{{\text{cr}}}}}}}{{{\text{d}}V_{{{\text{cr}}}}^{0}}} = 1 - \frac{{{{V}_{{{\text{cr}}}}}}}{{{{V}_{{{\text{cr}}\,{\text{m}}}}}}},$(6)
${{V}_{{{\text{cr}}\,{\text{m}}}}} = \frac{{({{C}_{{\text{m}}}} - {{C}_{0}}){{V}_{{\text{s}}}}}}{{{{\rho }_{{{\text{cr}}}}}}},$Проинтегрировав дифференциальное уравнение (5), получаем
(7)
$\ln \left( {1 - \frac{{{{V}_{{{\text{cr}}}}}}}{{{{V}_{{{\text{cr}}\,{\text{m}}}}}}}} \right) = \frac{{ - V_{{{\text{cr}}}}^{0}}}{{{{V}_{{{\text{cr}}\,{\text{m}}}}}}}.$Подставляя (4) и (5) в (6), где ${\eta } = \frac{{{{V}_{{{\text{cr}}}}}}}{{{{V}_{{{\text{cr}}\,{\text{m}}}}}}}$ – доля кальция, перешедшего в твердую фазу, получим
(8)
$\ln \left( {1 - {\eta }} \right) = \frac{{ - \frac{{\pi }}{3}{v}_{{\text{g}}}^{3}{{t}^{4}}{{{v}}_{{\text{n}}}}{{{\rho }}_{{{\text{cr}}}}}}}{{{{C}_{{\text{m}}}} - {{C}_{0}}}}.$Упростим (8), подставив: ${{k}_{{\text{A}}}} = \frac{{ - \frac{{\pi }}{3}{{{v}}_{{\text{g}}}}^{3}{{{v}}_{{\text{n}}}}{{{\rho }}_{{{\text{cr}}}}}}}{{{{C}_{{\text{m}}}} - {{C}_{0}}}},$ а показатель степени при времени 4 выразим в более общем виде через nA.
Тогда уравнение (8) примет вид
О.М. Тодес, используя аналогию с моделью Колмогорова, показал, что при кристаллизации из растворов общая масса кристаллов и падение пересыщения на начальном участке кинетической кривой также пропорциональны четвертой степени времени [27].
В случае кристаллизации солей из растворов скорость зародышеобразования vn и скорость роста vg зависят от движущей силы в виде пересыщения S раствора или концентрации растворенного вещества С:
(10)
${{{v}}_{{\text{n}}}} = f\left( S \right),\,\,\,\,{{{v}}_{{\text{n}}}} = f\left( {C - {{C}_{0}}} \right),$(11)
${{{v}}_{{\text{g}}}} = f\left( S \right),\,\,\,\,{{{v}}_{{\text{g}}}} = f\left( {C - {{C}_{0}}} \right),$В практике массовой кристаллизации эти зависимости часто используются в степенном виде [1, 41, 42]:
где kn – константа скорости зародышеобразования в растворе, kg – константа скорости роста кристаллов, n – показатель степени в уравнении скорости зародышеобразования, g – показатель степени в уравнении скорости роста кристаллов (c химической точки зрения n и g – порядок соответствующих реакций).Проведенные нами эксперименты, результаты которых будут представлены в следующей работе, подтверждают степенной вид (12) и (13) для карбоната и сульфата кальция.
В работах О.Д. Линникова [34, 43] предложена модель, учитывающая теорию коагуляции Смолуховского и зависимости для скорости спонтанной кристаллизации из [25, 26]. Модель Линникова имеет ряд предположений: гранулометрический состав кристаллов формируется за счет роста кристаллов и их агрегации между собой; срастание кристаллов происходит в соответствии с теорией А.Ф. Полака [38]; влияние зародышеобразования незначительно, а после индукционного периода в растворе образуется начальное количество кристаллов, которое со временем может только уменьшиться; рост кристаллов подчиняется степенной зависимости [26].
Математическая модель процесса кристаллизации в [34, 43] описывается системой дифференциальных уравнений, которая может быть решена численно методом Рунге–Кутты.
Первое уравнение в этой системе описывает изменение концентрации ионов в растворе:
(14)
$\frac{{ - {\text{d}}C~}}{{{\text{d}}t}} = 3.3{{{\psi }}^{{ - 1}}}{{\left( {{\pi }{{{\rho }}_{{{\text{cr}}}}}} \right)}^{{\frac{1}{3}}}}N_{{{\text{cr}}}}^{{\frac{1}{3}}}{{k}_{{\text{g}}}}{{\left( {{{C}_{{\text{m}}}} - C} \right)}^{{\frac{2}{3}}}}{{\left( {C - {{C}_{0}}} \right)}^{g}},$Хотя агрегация частиц может в некоторых случаях начаться уже на стадии роста, она проходит относительно медленно и становится заметной при завершении роста частиц [3]. Существенного вклада в изменение общей массы кристаллов и, соответственно, снижение пересыщения [3, 44] – она не дает (так же как и стадия Освальдова созревания). Поэтому для описания кинетики изменения массы кристаллов и снятия пересыщения в растворе достаточно уравнения (14).
Чтобы упростить дальнейшие выводы, введем массовые концентрации P и Pm для суспензии:
$P = {{C}_{{\text{m}}}} - C$ – масса кристаллического вещества в объеме суспензии;
${{P}_{{\text{m}}}} = {{C}_{{\text{m}}}} - {{C}_{0}}$ – максимальная движущая сила или максимальная масса кристаллического вещества в объеме суспензии.
Упростим уравнение (14), подставив P, Pm, ${{k}_{L}} = 3.3{{{\psi }}^{{ - 1}}}{{\left( {{\pi \rho }} \right)}^{{\frac{1}{3}}}}N_{{{\text{cr}}}}^{{\frac{1}{3}}}{{k}_{{\text{g}}}}.$
Тогда для образующейся твердой фазы P выражение (14) примет вид
(15)
$\frac{{{\text{d}}P}}{{{\text{d}}t}} = {{k}_{L}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{g}}{{P}^{{\frac{2}{3}}}}.$В модели Линникова не рассматривается стадия зарождения кристаллов, а только их изотропный трехмерный рост и последующее преобразование [39].
Для более полного описания процесса спонтанной кристаллизации можно учесть изменение массы кристаллов в суспензии за счет образования зародышей:
(16)
$\begin{gathered} \frac{{{\text{d}}P}}{{{\text{d}}t}} = {{V}_{{\text{s}}}}{{{v}}_{{\text{n}}}}{{m}_{{\text{n}}}} \times \frac{1}{{{{V}_{{\text{s}}}}}} = {{k}_{{\text{n}}}}{{m}_{{\text{n}}}}{{\left( {C - {{C}_{0}}} \right)}^{n}} = \\ = {{k}_{{\text{n}}}}{{m}_{{\text{n}}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{n}}, \\ \end{gathered} $Изменение массы образовавшихся кристаллов за счет их роста:
(17)
$\begin{gathered} \frac{{{\text{d}}P}}{{{\text{d}}t}} = {{{v}}_{{\text{g}}}}{{S}_{{{\text{cr}}}}}{{{\rho }}_{{{\text{cr}}}}} \times \frac{1}{{{{V}_{{\text{s}}}}}} = {{k}_{{\text{g}}}}{{S}_{{{\text{cr}}}}}{{{\rho }}_{{{\text{cr}}}}}\frac{1}{{{{V}_{{\text{s}}}}}}{{\left( {C - {{C}_{0}}} \right)}^{g}} = \\ = {{k}_{{\text{g}}}}{{S}_{{{\text{cr}}}}}{{{\rho }}_{{{\text{cr}}}}}\frac{1}{{{{V}_{{\text{s}}}}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{g}}, \\ \end{gathered} $Общее выражение, учитывающее изменение массы кристаллов на протяжении всего процесса, имеет вид
(18)
$\frac{{{\text{d}}P}}{{{\text{d}}t}} = {{k}_{{\text{n}}}}{{m}_{{\text{n}}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{n}} + {{k}_{{\text{g}}}}{{S}_{{{\text{cr}}}}}{{{\rho }}_{{{\text{cr}}}}}\frac{1}{{{{V}_{{\text{s}}}}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{g}}.$Так как рост кристаллов происходит на образовавшихся зародышах, то поверхность растущих кристаллов в растворе может быть выражена через начальную поверхность зародышей следующим эмпирическим выражением [45]:
(19)
$\begin{gathered} S = N{{S}_{n}}{{\left( {\frac{{{{m}_{{{\text{cr}}}}}}}{{N{{m}_{{\text{n}}}}}}} \right)}^{d}} = N{{S}_{{\text{n}}}}{{\left( {\frac{{\left( {{{C}_{{\text{m}}}} - C} \right){{V}_{{\text{s}}}}}}{{N{{m}_{{\text{n}}}}}}} \right)}^{d}} = \\ = N{{S}_{{\text{n}}}}{{\left( {\frac{{P{{V}_{{\text{s}}}}}}{{N{{m}_{{\text{n}}}}}}} \right)}^{d}}, \\ \end{gathered} $Степень d в уравнении (19) характеризует пространственную ориентацию роста граней кристалла. Для трехмерного роста d = 2/3 [46]. Значения d от 0 до 1/2 характерны для роста кристалла по одному или двум направлениям [47].
Подставив (19) в (18), получим
(20)
$\begin{gathered} \frac{{{\text{d}}P}}{{{\text{d}}t}} = {{k}_{{\text{n}}}}{{m}_{{\text{n}}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{n}} + \\ + \,\,{{k}_{{\text{g}}}}{{N}^{{\left( {1 - d} \right)}}}{{S}_{{\text{n}}}}V_{{\text{s}}}^{{\left( {d - 1} \right)}}{{m}_{{\text{n}}}}^{{ - d}}{{{\rho }}_{{{\text{cr}}}}}{{P}^{d}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{g}}. \\ \end{gathered} $На протяжении всего процесса кристаллизации в той или иной степени может происходить зарождение новых центров, агрегация и перерастворение уже имеющихся кристаллов в суспензии. Роль этих факторов (кроме вторичной нуклеации) возрастает в сильно пересыщенных растворах, которые не так уж редко образуются в практике реагентного осаждения. При очень больших пересыщениях все процессы зарождения и трансформации твердой фазы могут проходить одновременно и их сложно учесть [42]. Отмеченные факторы влияют, главным образом, на форму и размеры кристаллов. Однако в изменение общей массы кристаллов (степени кристаллизации) малорастворимых солей кальция их вклад обычно достаточно мал и может не учитываться.
Образованные на конец индукционного периода зародыши кристаллов служат своего рода затравкой, на поверхности которой в основном осуществляется дальнейший рост кристаллов (особенно при низких пересыщениях раствора) [48]. Влияние зародышеобразования после индукционного периода незначительно. Поэтому число растущих кристаллов можно приравнять числу зародышей на конец индукционного периода.
В упрощенном виде уравнение (20) будет выглядеть как
(21)
$\frac{{{\text{d}}P}}{{{\text{d}}t}} = {{k}_{{01}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{n}} + {{k}_{{10}}}{{P}^{d}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{g}},$Если рассматривать только стадию роста кристаллов и d = 2/3, выражение (21) принимает вид (15).
Химическая модель. Химическая реакция становится автокаталитической, если ее продукт действует как катализатор и ускоряет процесс [49]. Для процесса реагентного осаждения можно провести аналогию с автокаталитической реакцией. Таким образом, зародыши карбоната и сульфата кальция, полученные после химической реакции, становятся катализатором для кристаллизации солей кальция за счет собственного роста.
Схема протекания реакции по некаталитическому пути имеет вид
Схема протекания реакции по каталитическому пути имеет вид
где P – продукт реакции, малорастворимая соль кальция.Скорость реакции по некаталитическому пути представляет собой скорость зародышеобразования:
(22)
${{{v}}_{{\text{n}}}} = {{k}_{{02}}}{{\left[ {{\text{C}}{{{\text{a}}}^{{2 + }}}} \right]}^{n}},$Скорость реакции по каталитическому пути представляет собой скорость роста кристаллов:
(23)
${{{v}}_{{\text{g}}}} = {{k}_{{20}}}{{\left[ {{\text{C}}{{{\text{a}}}^{{2 + }}}} \right]}^{g}}\left[ {\text{P}} \right],$Учитывая, что реакция протекает по обоим путям одновременно, дифференциальное уравнение изменения концентрации имеет вид
С учетом движущей силы кристаллизации в виде разницы между текущей концентрацией растворенного вещества и его концентрацией в насыщенном растворе, уравнение (24) преобразуется:
(25)
$\frac{{ - {\text{d}}C}}{{{\text{d}}t}} = {{k}_{{02}}}{{\left( {C - {{C}_{0}}} \right)}^{n}} + {{k}_{{20}}}{{\left( {C - {{C}_{0}}} \right)}^{g}}\left( {{{C}_{{\text{m}}}} - C} \right)$или для продукта реакции Р:
(26)
$\frac{{{\text{d}}P}}{{{\text{d}}t}} = {{k}_{{02}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{n}} + {{k}_{{20}}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{g}}P.$Общая модель процесса кристаллизации. Сравнивая полученные уравнения (21) и (26), очевидно, что они приводят к одному общему упрощенному дифференциальному уравнению, описывающему образование кристаллического осадка в растворе:
(27)
$\frac{{{\text{d}}P}}{{{\text{d}}t}} = {{k}_{0}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{n}} + {{k}_{1}}{{\left( {{{P}_{{\text{m}}}} - P} \right)}^{g}}{{P}^{d}},$Получить аналитическое решение эволюционного дифференциального уравнения (27) очень сложно. Однако, чтобы наглядно показать сигмоидальный вид протекания процесса, упростим задачу, приняв первый порядок реакций нуклеации n = 1 и роста кристаллов g = 1, а также фактора d = 1. В этом случае решение (27) принимает вид
(28)
$P = {{P}_{{\text{m}}}} - \left( {{{P}_{{\text{m}}}} + \frac{{{{k}_{0}}}}{{{{k}_{1}}}}} \right)\frac{{{{P}_{{\text{m}}}}}}{{{{P}_{{\text{m}}}} + \frac{{{{k}_{0}}}}{{{{k}_{1}}}}{\text{exp}}\left[ {{{k}_{1}}t\left( {{{P}_{{\text{m}}}} + \frac{{{{k}_{0}}}}{{{{k}_{1}}}}} \right)} \right]}}.$Выразим степень кристаллизации η (0 < η < 1):
(29)
${\eta } = \frac{P}{{{{P}_{{\text{m}}}}}} = \frac{{{{C}_{{\text{m}}}} - C}}{{{{C}_{{\text{m}}}} - {{C}_{0}}}}.$На рис. 1 показаны теоретические эволюционные зависимости доли закристаллизованного продукта, полученные по разным моделям. Кинетическая кривая 1 построена для случая, когда индукционного периода практически нет, и быстрый рост кристаллов начинается на первой минуте процесса. А кривая 2 – при tind ≈ 5 мин. Точками показаны результаты расчета для этих двух случаев. На первой кривой: а – по уравнению (9) при коэффициенте kA = 0.033 и степени nA = 1.1; б – по уравнению (28) при коэффициентах k0 и k1, равных 0.038 и 1.9 соответственно; в – по модели Линникова [43]. На второй кривой: г – по уравнению (9) при коэффициенте kA = 0.00023 и степени nA = 1.9; д – по уравнению (28) при коэффициентах k0 и k1, равных 0.003 и 3.5 соответственно; е – по модели Мелихова [3] при Pe = 0.01.
Рис. 1.
Теоретические зависимости изменения степени кристаллизации во времени: 1, 2 – кинетические кривые; а, г – значения по уравнению (9); б, д – по уравнению (28); в – по модели Линникова [43]; е – значения по модели Мелихова [3].
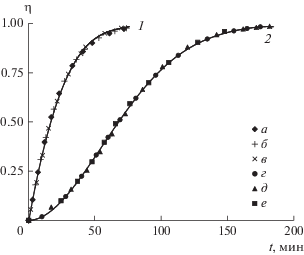
Все зависимости схожи между собой, и для каждого случая сводятся практически в одну линию, что свидетельствует об адекватном отражении реального процесса трансформации вещества предложенными моделями, и общих закономерностях эволюционных процессов физического и химического характера.
ЗАКЛЮЧЕНИЕ
Эволюционные процессы в материальном мире и обществе проходят по единым траекториям с типичными стадиями развития. Отмечено, что наука в целом и новые технологии развиваются по общим эволюционным законам. Кратко рассмотрены основные вехи исторического развития теоретических основ кристаллизации и, в частности, математического моделирования этого процесса. Сопоставлены основные эволюционные модели процесса, в первую очередь учитывающие стадии зарождения и роста кристаллов, а также их агрегации. Показано, что большинство кинетических моделей образования и роста кристаллов описываются логистической функцией и имеют S-образный вид, а в некоторых (частных) случаях сводятся к экспоненциальным зависимостям.
Полученные зависимости могут использоваться для проверки и аппроксимации экспериментальных данных по кристаллизации, прогнозирования хода эволюционных кривых по начальному участку, а также для определения продолжительности и производительности процесса реагентного осаждения при заданных технологических условиях. Зная значения основных физических величин для кристаллизуемого соединения, коэффициенты и порядок реакций нуклеации и роста, можно спрогнозировать весь процесс кристаллизации.
Работа выполнена в рамках государственного задания ИОНХ РАН в области фундаментальных научных исследований.
ОБОЗНАЧЕНИЯ
| С | массовая концентрация растворенной соли в растворе, кг/м3 |
| С0 | массовая концентрация растворенной соли в насыщенном растворе, кг/м3 |
| Сm | массовая концентрация растворенной соли в растворе в начальный момент времени, кг/м3 |
| d | значение показателя степени, характеризующее пространственную направленность роста кристаллов |
| g | показатель степени в уравнении скорости роста кристаллов |
| kA | константа в уравнении, полученном по модели Аврами |
| kL | константа в уравнении Линникова |
| kn | константа скорости зародышеобразования в растворе |
| kg | константа скорости роста кристаллов |
| k0, k01, k02 | константа, характеризующая скорость зародышеобразования |
| k1, k10, k20 | константа, характеризующая скорость роста кристаллов |
| mcr | масса образующихся кристаллов, кг |
| mn | критическая масса зародыша, кг |
| N | количество зародышей, шт |
| Ncr | общее количество кристаллов в растворе, шт |
| n | степень в уравнении скорости зародышеобразования |
| nA | степень в уравнении, полученном по модели Аврами |
| P | массовая концентрация кристаллического вещества в суспензии, кг/м3 |
| Pm | максимальная массовая концентрация кристаллического вещества в суспензии, кг/м3 |
| r | радиус растущего зародыша сферической формы, м |
| S | пересыщение раствора |
| Scr | площадь поверхности кристаллов, м2 |
| Sn | площадь поверхности зародыша кристалла, м2 |
| t | текущее время процесса кристаллизации, с |
| tind | индукционный период зарождения кристаллов, с |
| $V_{{{\text{cr}}}}^{0}$ | расширенный объем кристаллов, м3 |
| Vcr m | максимально возможный объем кристаллической фазы, м3 |
| Vs | объем раствора, м3 |
| ${{v}_{{\text{n}}}}$ | скорость нуклеации (зародышеобразования), с–1 |
| ${{v}_{{\text{g}}}}$ | линейная скорость роста кристаллов, м/с |
| η | степень кристаллизации |
| ρcr | плотность кристаллического вещества, кг/м3 |
| τ | время образования зародышей в модели Аврами, с |
| ψ | коэффициент сферичности кристаллов |
ИНДЕКСЫ
Список литературы
Mullin J.W. Crystallization. Oxford: Butterworth-Heinemann, 2001.
Матусевич Л.Н. Кристаллизация из растворов в химической промышленности / Под ред. Лебедевой И.В. М.: Химия, 1968.
Мелихов И.В. Физико-химическая эволюция твердого вещества. М.: БИНОМ, 2009.
Melikhov I.V., Tret’yakov Y.D. Approaches to the mesokinetic theory of search for the optimal technological route for conversion of a raw material into the desired material // Theor. Found. Chem. Eng. 2013. V. 47. № 1. P. 36. [Мелихов И.В., Третьяков Ю.Д. Подходы к мезокинетической теории поиска оптимального технологического маршрута превращения сырья в материал // Теор. осн. хим. технол. 2013. Т. 47. № 1. С. 42.]
Melikhov I.V. Strategy and tactics in the search for materials technology // Theor. Found. Chem. Eng. 2011. V. 45. № 6. P. 801. [Мелихов И.В. Стратегия и тактика поиска оптимальных технологий новых материалов // Теор. осн. хим. технол. 2011. Т. 45. № 6. С. 611.]
Николаев Д.А., Холпанов Л.П. Закон эволюции: математическая форма. М.: Наука, 1999.
Корнеева Е.С., Мурашова Н.М., Юртов Е.В. Анализ динамики публикаций в области наноматериалов с использованием базы данных “Sciencedirect” // Усп. хим. хим. технол. 2012. Т. XXVI. № 7. С. 77.
Price D.J.S. Little Science, Big Science. New York: Columbia University Press, 1963.
Price D.J.S. Networks of Scientific Papers // Science. 1965. V. 149. № 3683. P. 510.
Капица П.Л. Эксперимент. Теория. Практика. М.: Наука, 1987.
Лем С. Сумма технологии / Под ред. Бирюкова Б.В., Широкова Ф.В. М.: Мир, 1968.
Налимов В.В., Мульченко З.М. Наукометрия. Изучение развития науки как информационного процесса. М.: Наука, 1969.
Музяков С.И. Информационная среда и условия экспоненциального роста объема знаний в современном обществе // Власть. 2012. Т. 4. С. 42.
Jancic S.J. Techniques of Industrial Crystallization. State of the Business // Vestn. Slov. Kem. Drus. 1991. V. 38. № 3. P. 459.
Rabizadeh T., Stawski T.M., Morgan D.J., Peacock C.L., Benning L.G. The Effects of Inorganic Additives on the Nucleation and Growth Kinetics of Calcium Sulfate Dihydrate Crystals // Cryst. Growth Des. 2017. V. 17. № 2. P. 582.
Halevy S., Korin E., Gilron J. Kinetics of Gypsum for Designing Interstage Crystallizers for Concentrate in High Recovery Reverse Osmosis // Ind. Eng. Chem. Res. 2013. V. 52. P. 14647.
Кекин П.А. Кристаллизация карбоната кальция в технологических водных системах. Дис. … канд. техн. наук. М.: РХТУ им. Д.И. Менделеева, 2017.
Колмогоров А.Н. К статистической теории кристаллизации металлов // Изв. Акад. наук СССР. Сер. мат. 1937. Т. 1. № 3. С. 355.
Johnson W., Mehl R. Reaction Kinetics in Processes of Nucleation and Growth // Trans. Am. Inst. Min. 1939. V. 135. P. 416.
Avrami M. Kinetics of Phase Change. I General Theory // J. Chem. Phys. 1939. V. 7. P. 1103.
Avrami M. Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei // J. Chem. Phys. 1940. V. 8. P. 212.
Avrami M. Granulation, Phase Change, and Microstructure Kinetics of Phase Change. III // J. Chem. Phys. 1941. V. 9. P. 177.
Беленький В.З. Геометрико-вероятностные модели кристаллизации. М.: Наука, 1980.
Торнер Р.В. Теоретические основы переработки полимеров (механика процессов). М.: Химия, 1977.
Рогинский С.З., Тодес О.М. Зависимость законов распределения кристаллов по дисперсности // Изв. Акад. наук СССР. ОХН. 1942. Т. 3. С. 331.
Дерябина Н.В., Мищенко К.П. О скорости кристаллизации гипса из водных растворов некоторых солей // Пробл. кинет. катал. 1949. Т. 7. С. 122.
Тодес О.М., Себало В.А., Гольцикер А.Д. Массовая кристаллизация из растворов. Л.: Химия, 1984.
Ратинов В.Б., Тодес О.М. О спонтанной кристаллизации диссоциированных солей // Докл. Акад. наук СССР. 1960. Т. 132. № 2. С. 402.
Мелихов И.В., Берлинер Л.Б. Кристаллизация солей из пересыщенных растворов. Кинетический режим // Теор. осн. хим. технол. 1979. Т. 13. № 4. С. 530.
Берлинер Л.Б., Мелихов И.В. Метод определения кинетических параметров периодической кристаллизации // Теор. осн. хим. технол. 1985. Т. 19. № 1. С. 24.
Melia T.P., Moffitt W.P. Crystallization from aqueous solution // J. Colloid Sci. 1964. V. 19. P. 433.
Dirksen J.A., Ring T.A. Fundamentals of crystallization: Kinetic effects on particle size distribution and morphology // Chem. Eng. Sci. 1991. V. 46. № 10. P. 2389.
Melikhov I.V., Bozhevol’nov V.E. Variability and self-organization // J. Nanopart. Res. 2003. V. 5. № 5–6. P. 465.
Linnikov O.D., Rodina I.V., Grigorov I.G., Polyakov E.V. Kinetics and Mechanism of Spontaneous Crystallization of Potassium Nitrate from Its Supersaturated Aqueous Solutions // Cryst. Struct. Theory Appl. 2013. V. 2. P. 16.
Матусевич Л.Н., Шабалин К.Н. Интенсивность размешивания раствора и крупность получаемых кристаллов // Журн. прикл. хим. 1952. Т. 25. С. 1157.
Мелихов И.В., Михеева И.В., Рудин В.Н. Механизм кристаллизации полугидрата сульфата кальция в условиях, моделирующих получение фосфорной кислоты полугидратным способом // Теор. осн. хим. технол. 1985. Т. 19. № 6. С. 742.
Smoluchowski M. Versucheiner Mathematischen Theorie der Koagulations Kinetic Kolloider Lousungen // Z. Phys. Chem. 1917. V. 92. P. 129.
Полак А.Ф. Твердение мономинеральных вяжущих веществ. М.: Стройиздат, 1966.
Linnikov O.D. Mechanism of precipitate formation during spontaneous crystallization from supersaturated aqueous solutions // Russ. Chem. Rev. 2014. V. 83. № 4. P. 343. [Линников О.Д. Механизм формирования осадка при спонтанной кристаллизации солей из пересыщенных водных растворов // Усп. хим. 2014. Т. 83. № 4. С. 343.]
Гегузин Я.Е. Живой кристалл. М.: Наука, 1981.
Mersmann A. Crystallization Technology Handbook. N.Y.: Marcel Dekker, 2001.
Myerson A.S. Handbook of Industrial Crystallization. Stoneham, Mass.: Butterworth-Heinemann, 2002.
Linnikov O.D. Spontaneous crystallization of potassium chloride from aqueous and aqueous-ethanol solutions; Part 3: Model of the crystallization process // Cryst. Res. Technol. 2006. V. 41. № 10. P. 988.
Мелихов И.В., Михеев Н.Б., Кулюхин С.А. Динамика образования твердого вещества в сильно пересыщенных средах // Физ. хим. 2010. Т. 84. № 8. С. 1417.
Christoffersen J., Christoffersen M.R. The kinetics of dissolution of calcium sulfate dihydrate in water // J. Cryst. Growth. 1976. V. 35. P. 79.
Van Oosterhout G.W., van Rosmalen G.M. Analysis of kinetics experiments on growth and dissolution of crystals in suspension // J. Cryst. Growth. 1980. V. 48. P. 464.
Barone J.P., Nancollas G.H., Yoshikawa Y. Crystal growth as a function of seed surface area // J. Cryst. Growth. 1983. V. 63. P. 91.
Verdoes D., Kashchiev D., van Rosmalen G.M. Determination of nucleation and growth rates from induction times in seeded and unseeded precipitation of calcium carbonate // J. Cryst. Growth. 1992. V. 118. P. 401.
Шмид Р., Сапунов. В.Н. Неформальная кинетика. В поисках путей химических реакций. М.: Мир, 1985.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии