Теоретические основы химической технологии, 2020, T. 54, № 3, стр. 286-298
Термодинамико-топологический анализ фазовых диаграмм четырехкомпонетных систем с внутренними особыми точками
А. В. Фролкова a, *, Т. Е. Ососкова a, А. К. Фролкова a
a МИРЭА – Российский технологический университет (Институт тонких химических технологий
им. М.В. Ломоносова)
Москва, Россия
* E-mail: frolkova_nastya@mail.ru
Поступила в редакцию 16.07.2019
После доработки 12.09.2019
Принята к публикации 12.09.2019
Аннотация
Представлен обзор иностранной и отечественной литературы по экспериментальному исследованию фазового равновесия, методикам анализа и предсказания структур диаграмм, проблемам моделирования парожидкостного равновесия (ПЖР) четырехкомпонентных систем, содержащих внутренние особые точки. Для четырех систем ацетон–хлороформ–этанол–вода, ацетон–хлороформ–пропанол-2–вода, хлороформ–этанол–циклогексан–вода, этилацетат–метилэтилкетон–циклогексан–пропанол-2 получен полный набор параметров, позволяющий адекватно описывать равновесие жидкость–пар и жидкость–жидкость. Проиллюстрирована методика определения структуры диаграммы ПЖР и предсказания наличия внутреннего азеотропа в исследуемых системах, а также одной модельной системы, содержащей бинарные и четырехкомпонентный азеотроп. Показаны возможные пути эволюционного изменения структуры диаграммы ПЖР при варьировании давления, определены индексы Пуанкаре граничных однократных и двукратного тангенциального азеотропа.
ВВЕДЕНИЕ
В производствах продуктов основного органического синтеза, фармацевтической продукции, полимерных материалов и других смежных отраслей часто приходится сталкиваться не только с разделением реакционных смесей с целью выделения целевых продуктов, но и регенерацией растворителей, используемых на различных стадиях производства. Причем, как правило, разделению подвергаются многокомпонентные смеси. Опыт многолетних экспериментальных исследований фазовых равновесий показывает, что систем с поведением, близким к идеальному, практически нет. Большинство смесей характеризуется наличием азеотропов разной компонентности и типа (узлы, седла). Точки седловидного типа в фазовой диаграмме многокомпонентной системы порождают сепаратрические многообразия разной размерности, что приводит к невозможности выделения всех компонентов обычной ректификацией. В этих случаях применяют специальные методы (экстрактивная ректификация, варьирование давления, сочетание различных процессов), возможность применения которых можно оценить только на основе анализа полной структуры диаграммы фазового равновесия. В то же время число методик исследования структур фазовых диаграмм крайне ограничено, что связано с многомерностью объектов и сложностью интерпретации полученных результатов.
Настоящая работа посвящена аналитическому обзору работ в указанной области, исследованию закономерностей формирования структур фазовых диаграмм и сепаратрических многообразий четырехкомпонентных сложной физико-химической природы.
СОВРЕМЕННОЕ СОСТОЯНИЕ ИССЛЕДОВАНИЙ МНОГОКОМПОНЕНТНЫХ СИСТЕМ
Публикации за последние 10 лет в области исследования многокомпонентных жидких смесей можно условно разбить на три основные тематики: получение новых экспериментальных данных о фазовом равновесии (жидкость–жидкость, жидкость–жидкость–пар, жидкость–пар при определенных условиях: давление или температура); разработка методов корреляции экспериментальных данных (проверки на термодинамическую согласованность), выявление областей применимости различных моделей (локальных составов, групповой модели); синтез схем разделения с применением различных методов (ректификация, экстракция, мембранное разделение и т.д.).
Если говорить о четырехкомпонентных системах, то объектами исследования преимущественно выступают смеси растворителей производства полупроводников [1], эмалей [2], фармацевтической продукции [3, 4]; смеси, образующиеся в результате процесса этерификации уксусной, пропионовой, молочной кислот низшими спиртами (метанолом, этанолом, н-бутанолом) [5–8]. Отдельно следует выделить объекты (системы), образованные путем добавления растворителя к базовой трехкомпонентной системе, например, в процессе экстракции кислот и спиртов из водного раствора: бинарный растворитель метилацетат + + п-ксилол [9]; растворитель ионная жидкость 1-butyl-1-methylpyrrolidinium bis(trifluoromethylsulfonyl) imide [10]; растворитель циклопентилметиловый эфир [11] или гетероазеотропной осушки спиртов: растворитель бензол [2]. Большинство систем содержат воду и, как следствие, характеризуются ограниченной взаимной растворимостью компонентов. Данные равновесия жидкость-жидкость приводятся, как правило, при нормальной (20–30°С) температуре, реже повышенной [6, 9, 11–13]. В системах 2-бутанол–н-гептан–тетрагидрофуран–циклогексан [14], метилацетат–метанол–изопропанол–изопропилацетат [7], этилэтаноат–этанол–пропилэтаноат–пропанол [15], ацетон–вода–окись мезитила–диацетоновый спирт [16], вода–этанол–циклогексан–толуол [17] получены данные парожидкостного равновесия (ПЖР). В работе [15] также экспериментально исследовано химическое равновесие (процесс переэтерификации). Все приведенные выше ссылки содержат данные о равновесии не только в бинарных и тройных составляющих, но и в четырехкомпонентной системе.
Полученные экспериментальные данные должны пройти проверку на термодинамическую согласованность. Одним из наиболее часто используемых является метод, основанный на алгоритме Wisniak–Tamir test [18]. В работе [19] предложен метод проверки согласованности экспериментальных данных, основанный на уравнении Гиббса–Дюгема.
Математическое моделирование фазового равновесия проводится с использованием известных моделей локальных составов (NRTL, UNIQUAC, а также WILSON для гомогенных систем). Модель NRTL и ее модификации (NRTL-SAC [20]) используется более чем в 80% случаев. В работах [7–9, 20] проведен сравнительный анализ результатов описания фазового равновесия с использованием разных моделей: при описании равновесия жидкость–жидкость, жидкость–жидкость–пар модели NRTL и UNIQUAC в целом дают близкие по ошибкам показатели, однако, при описании ряда систем [7, 8, 20] NRTL дает более точные результаты. В отношении модели групповых составов UNIFAC можно отметить: чем сложнее фазовая диаграмма многокомпонентной системы, тем ниже вероятность точного предсказания различного рода свойств с использованием этой модели. Так, если в системе имеется одна область двухфазного расслаивания и отсутствуют внутренние особые точки, UNIFAC позволяет достаточно точно спрогнозировать и особенности структуры диаграммы ПЖР, и составы равновесных жидких слоев в области двухфазного расслаивания [5, 11, 20, 21]. Если же система характеризуется сильным отклонением от идеального поведения (наличие четырехкомпонентного азеотропа, области трехфазного расслаивания), прогностические возможности модели резко снижаются.
Для разделения многокомпонентных жидких смесей в основном используются процессы ректификации и экстракции [9, 10, 21, 22]. Недостатком последнего является необходимость доочистки экстракта (рафината) с получением продукта товарного качества [11], в этом случае чаще всего прибегают также к ректификационным методам. Работ, посвященных установлению закономерностей разделения четырех- и более компонентных смесей, крайне мало, что связано, в первую очередь, с увеличением размерности решаемой задачи и сложностью анализа многомерных фазовых диаграмм. А между тем, диаграмма парожидкостного равновесия, будучи топологически подобной диаграмме процесса ректификации (при бесконечном флегмовом числе), содержит информацию (термодинамические ограничения, возможные предельные составы продуктовых потоков), необходимую для проектирования технологических схем разделения многокомпонентных неидеальных смесей. Наличие в системе азеотропов и сепаратрических многообразий разной размерности обуславливает необходимость применения специальных ректификационных методов: использование дополнительных веществ, повышающих относительную летучесть компонентов [1, 23–25] или образующих гетероазеотропы [2, 11, 17, 26], сочетание ректификации и расслаивания [27–29].
Стадии синтеза принципиальной технологической схемы разделения предшествует термодинамико-топологический анализ (ТТА) диаграммы фазового равновесия. Для трехкомпонентных моноазеотропных систем область исследования диаграмм ПЖР (построение и анализ) хорошо разработана, в то время как количество методик, позволяющих изучать фазовые диаграммы многокомпонентных смесей, ограничено. Поскольку объектами настоящей работы выступают многокомпонентные системы, рассмотрим основные методы исследования структуры диаграммы фазового равновесия четырех- и более компонентных систем. В 1997 г. [30] была предпринята попытка разработки метода определения числа возможных наборов продуктовых потоков для многокомпонентных систем. Однако метод был применим для ограниченного класса трехкомпонентных систем как составляющих многокомпонентной системы: рассматривались только те классы и типы диаграмм, которые на тот момент были подтверждены экспериментально. Данный метод получил развитие в работах [31, 32], в которых для анализа диаграмм ПЖР привлекалась теория орграфов (построение матриц смежности, матриц достижимости). Метод имеет ограничения, в частности он применим для систем, содержащих не более двух устойчивых и неустойчивых узлов.
Учеными университета Штутгарта [33] на основе известных подходов рассмотрен метод анализа структуры диаграммы посредством исследования ее эволюции через бифуркационные состояния (от диаграммы зеотропной смеси, через появление бинарных, тройных и далее четырехкомпонентного азеотропа), названный авторами “эволюционным”. Такой метод можно использовать и для систем с большим числом компонентов, однако, он достаточно трудоемок. Данный подход проиллюстрирован авторами на примере одной системы: ацетон–хлороформ–этанол–гексан, содержащей четырехкомпонентный азеотроп.
В работе [34] предложен метод, позволяющий локализовать сепаратрическую поверхность внутри концентрационного тетраэдра (определение границы области дистилляции внутри симплекса). Алгоритм построен на предпосылках ранее описанных методов, основанных на построении матриц смежности и инцидентности, и проиллюстрирован на примере пяти четырехкомпонентных систем различной сложности, в том числе содержащих четырехкомпонентный азеотроп (ацетон–хлороформ–метанол–циклогексан).
В 2011 г. венгерскими учеными предложен новый алгоритм определения возможных наборов продуктовых потоков в зависимости от расположения точки состава исходной смеси [35]. Метод основан на анализе температур кипения особых точек (чистых компонентов и азеотропов), составах азеотропов, не требует построения полной диаграммы ПЖР и применим для систем любой размерности. Авторами введены следующие допущения: сепаратрические поверхности прямолинейны (линии, плоскости, гиперплоскости), четырехкомпонентный азеотроп не является устойчивым узлом, в системе отсутствует пятикомпонентный азеотроп, трехкомпонентные составляющие системы относятся к классам и типам, подтвержденным реальными системами, в каждой подсистеме может присутствовать не более двух устойчивых и неустойчивых узлов. В основу заложены подходы, ранее описанные в работе [31] (построение матриц смежности). На первом этапе на основе анализа температур кипения особых точек определяются структуры трехкомпонентных систем (из заданных в ограниченном атласе структур – 16 из 26 известных), далее формируются структуры для составляющих большей размерности (четырех-, пяти- и т.д. компонентности). Второй этап подразумевает построение матрицы смежности, ее анализ, выявление недостающих границ (построение полного графа) и определение последовательности выделения компонентов для смеси различного состава. Предложенный алгоритм реализован в виде авторской программы. Апробация метода проведена на примере двух систем ацетон–хлороформ–метанол–этанол–бензол и метанол–тетрагидрофуран–этилацетат–этанол–изопропиловый спирт–вода.
Обсуждаемый метод не лишен недостатков, что, в первую очередь, связано с большим количеством допущений, приведенных выше. В то же время в настоящее время экспериментально [36] подтверждено наличие пятикомпонентного азеотропа в системе вода–нитрометан–1,1,2,2-тетрахлорэтан–1-пропанол–октан. Существование четырехкомпонентного азеотропа типа устойчивый узел (с максимальной температурой кипения) термодинамически обосновано и, следовательно, его обнаружение – лишь вопрос времени. Даже среди бинарных систем отрицательные отклонения встречаются значительно реже по сравнению с положительными, но это не является основанием для их дискриминации в исследованиях. Следует также отметить, что авторы [35] исходят из наличия полных данных о составах и температурах кипения всех компонентов и азеотропов. Если учесть возможности современного программирования (в части построения и анализа диаграмм трехкомпонентных систем (AspenPlus, ChemCad и т.д.), четырехкомпонентных систем – преимущественно авторские программы), и условие отсутствия в n-компонентной системе азеотропов с числом компонентов больше четырех, то анализ многомерной диаграммы, в части определения типов особых точек, выделения областей дистилляции не представляет трудности.
На сегодняшний день наиболее востребованным методом исследования фазового равновесия многокомпонентных систем является термодинамико-топологический анализ [37–39]. Данный метод был успешно применен при синтезе схем разделения промышленных многокомпонентных смесей производства таких веществ как циклогексанон [40], эпихлоргидрин [41], метилизобутилкетон [42], при разделении растворителей производства эмалей, полупроводников, фармпродукции, о которых говорилось ранее [1–3].
На основе ТТА предложен метод построения и анализа диаграммы ПЖР четырех- [43] и пятикомпонентных [44] систем, позволяющий предсказывать наличие в системе n-компонентного азеотропа. Данный метод был успешно апробирован более чем на 20 четырехкомпонентных системах и 10 пятикомпонентных. В табл. 1 приведен список систем с четырехкомпонентным азеотропом (подтвержденным натурным или полученным вычислительным экспериментом).
Таблица 1.
Системы с четырехкомпонентным азеотропом
| Система |
|---|
| Вода–ацетон–хлороформ–этанол * [4, 45] |
| Вода–муравьиная кислота–уксусная кислота–гексан* [46] |
| Вода–муравьиная кислота–уксусная кислота–петролейный эфир* [47] |
| Вода–нитрометан–1,1,2,2-тетрахлорэтан–1-пропанол, вода–нитрометан–1,1,2,2-тетрахлорэтан–октан, вода–нитрометан–1-пропанол–октан, вода–1,1,2,2-тетрахлорэтан –1-пропанол–октан* [48] |
| Вода–этанол–кротоновый альдегид–углеводороды* [49] |
| Вода–этанол–бензол–циклогексан* [50–52] |
| Вода–этанол–бензол–гептан, вода–этанол–бензол–октан* [50] |
| Вода–изопропанол–толуол–октан* [53] |
| Вода–2-метил-1-пропанол–толуол–углеводороды* [54] |
| Ацетон–хлороформ–метанол–бензол [55] |
| Ацетон–хлороформ–этанол–гексан [33] |
| Ацетон–метилацетат–метанол–гексан [56] |
| Циклогексан–2-пропанол–этилацетат–метилэтилкетон* [57] |
| Этанол–метилциклопентан–бензол–гексан [54] |
| Уксусная кислота–пиридин–этилбензол–нонан* [58–60] |
В настоящей работе в качестве объектов исследования выбраны четыре четырехкомпонентные системы: ацетон–хлороформ–этанол–вода (I), ацетон–хлороформ–пропанол-2–вода (II), хлороформ–этанол–циклогексан–вода (III), этилацетат–метилэтилкетон–циклогексан–пропанол-2 (IV). В системах I и IV экспериментально подтверждено существование четырехкомпонентного азеотропа [4, 45, 57].
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ФАЗОВОГО РАВНОВЕСИЯ
Вычислительный эксперимент проводился с использованием математического моделирования в программном комплексе AspenPlus V. 10.0. Для описания фазового равновесия расслаивающихся систем I–III выбрано уравнение NRTL, для гомогенной системы IV – уравнение Wilson. Выбор моделей определяется относительной ошибкой описания равновесий жидкость–пар и жидкость–жидкость.
При подборе параметров бинарного взаимодействия отдавалось предпочтение качественному описанию составов и температур кипения тройных и четырехкомпонентного азеотропа по сравнению с бинарными. Для систем I и IV наборы параметров, описывающих парожидкостное равновесие в бинарных составляющих с минимальными относительными ошибками (до 3%), не воспроизводили в системах четырехкомпонентные азеотропы. По этой причине для систем, содержащих одинаковые пары компонентов, проводили переоценку параметров бинарного взаимодействия и их значения для повторяющихся пар различаются (табл. 2).
Таблица 2.
Параметры бинарного взаимодействия уравнения NRTL (Aij, Aji, Вij, Bji, Cij) и уравнения Wilson (Aij, Aji, Вij, Bji)
| Бинарная система | Aij | Aji | Bij | Bji | Сji | Δyотн | ΔTотн |
|---|---|---|---|---|---|---|---|
| Система I Ацетон (А)–хлороформ (ХЛФ)–этанол (Э)–вода (В) | |||||||
| А-ХЛФ | 0.3343 | 1.8160 | –529.967 | –383.045 | 0.1606 | 1.45 | 0.14 |
| А-Э | –3.8181 | –4.2751 | 1353.14 | 1657.82 | 0.9716 | 0.49 | 0.10 |
| А-В | 6.2617 | –0.4896 | –1837.85 | 701.615 | 0.4042 | 4.70 | 0.65 |
| ХЛФ-Э | 4.7349 | –4.1577 | –1163.04 | 1461.16 | 0.5773 | 2.14 | 0.26 |
| ХЛФ-В | –7.3519 | 8.8436 | 3240.69 | –1140.12 | 0.2 | 3.71* | 0.10* |
| Э-В | –7.3282 | 9.4181 | 2707.98 | –2770.44 | 0.5931 | 0.69 | 0.20 |
| Система II Ацетон (А)–хлороформ (ХЛФ)–пропанол-2 (ИПС)–вода (В) | |||||||
| А-ХЛФ | 0.9646 | 0.5382 | –590.026 | –106.422 | 0.3 | 2.95 | 0.31 |
| А-ИПС | –2.4106 | 2.4494 | 822.489 | –583.345 | 0.3 | 5.31 | 1.12 |
| А-В | 0.0 | 0.0 | 317.554 | 602.558 | 0.534 | – | – |
| ХЛФ-ИПС | 2.4013 | –0.0131 | –297.232 | 89.6465 | 1.158 | 2.15 | 1.03 |
| ХЛФ-В | –7.3519 | 8.8436 | 3240.69 | –1140.12 | 0.2 | 3.71* | 0.10* |
| ИПС-В | –1.3115 | 6.8284 | 426.398 | –1483.46 | 0.3 | 3.91 | 0.49 |
| Система III Хлороформ (ХЛФ)–этанол (Э)–циклогексан (ЦГ)–вода (В) | |||||||
| ХЛФ-Э | 4.7732 | –4.1572 | –1175.63 | 1460.76 | 0.5768 | 2.14 | 0.26 |
| ХЛФ-В | –7.3519 | 8.8436 | 3240.69 | –1140.12 | 0.2 | 3.71* | 0.10* |
| Э-ЦГ | –1.716 | –4.9021 | 948.35 | 2354.83 | 0.4066 | 3.66 | 0.33 |
| Э-В | –7.9081 | 13.2001 | 2707.98 | –3965.6 | 0.2705 | 0.72 | 0.12 |
| ЦГ-В | –10.4585 | 13.1428 | 4954.9 | –1066.98 | 0.2 | 4.72* | 0.02* |
| ХЛФ-ЦГ | 0 | 0 | 247.309 | –61.3363 | 0.3 | – | – |
| Система IV Этилацетат (ЭА)–метилэтилкетон (МЭК)–циклогексан (ЦГ)–пропанол-2 (ИПС) | |||||||
| ЭА-МЭК | 0 | 0 | 63.9382 | –129.285 | – | 3.25 | 0.24 |
| ЭК-ЦГ | 0.767 | 1.7951 | –510.331 | –730.232 | – | 1.84 | 0.51 |
| ЭА-ИПС | 1.2785 | 1.3220 | –516.12 | –625.657 | – | 0.02 | 0.03 |
| МЭК-ЦГ | 0 | 0 | –346.14 | –109.405 | – | 1.23 | 0.32 |
| МЭК-ИПС | 0 | 0 | –45.0361 | –184.584 | – | 2.58 | 0.85 |
| ЦГ-ИПС | 0 | 0 | –221.836 | –731.24 | – | 2.53 | 0.45 |
Адекватность моделирования проверяли путем сопоставления экспериментальных и расчетных значений, состава и температуры кипения азеотропов (табл. 3).
Таблица 3.
Сравнение экспериментальных [61–72] и расчетных данных по температуре кипения и составу бинарных и тройных азеотропов при 101.3 кПа
| Азеотропы | $x_{{1(2)}}^{{\exp }}$, мол. д. | $x_{{1(2)}}^{{{\text{cal}}}}$, мол. д. | $\Delta x_{{1(2)}}^{{{\text{rel}}}}$ | Т exp, °С | Т c al, °С | ΔТ rel |
|---|---|---|---|---|---|---|
| А-ХЛФ (I) | 0.3394 | 0.3449 | 1.62 | 64.47 | 64.15 | 0.50 |
| А-ХЛФ (II) | 0.3394 | 0.3542 | 4.36 | 64.47 | 64.52 | 0.08 |
| ХЛФ-Э | 0.8350 | 0.8394 | 0.49 | 59.20 | 59.49 | 0.52 |
| ХЛФ-ИПС | 0.9210 | 0.9343 | 1.43 | 60.78 | 60.41 | 0.61 |
| ХЛФ-В | 0.8397 | 0.8360 | 0.44 | 56.08 | 56.14 | 0.11 |
| ИПС-В | 0.6880 | 0.6728 | 2.21 | 80.06 | 80.18 | 0.15 |
| МЭК-ИПС | 0.6221 | 0.6345 | 1.99 | 76.99 | 76.55 | 0.57 |
| МЭК-ЭА | 0.7508 | 0.7491 | 0.23 | 76.80 | 76.84 | 0.05 |
| МЭК-ЦГ | 0.5101 | 0.5197 | 6.08 | 71.73 | 71.77 | 0.06 |
| ЭА-ИПС | 0.6593 | 0.6858 | 4.02 | 75.13 | 75.16 | 0.04 |
| ИПС-ЦГ | 0.4113 | 0.3916 | 4.79 | 69.49 | 69.31 | 0.26 |
| ЭА-ЦГ | 0.5216 | 0.5359 | 2.74 | 71.55 | 72.06 | 0.71 |
| Э-ЦГ | 0.454 | 0.4467 | 1.6 | 64.8 | 64.86 | 0.09 |
| ЦГ-В | 0.6998 | 0.6690 | 0.11 | 69.5 | 69.49 | 0.01 |
| Э-В | 0.894 | 0.8846 | 1.05 | 78.17 | 78.06 | 0.14 |
| Э-В (II) | 0.894 | 0.8964 | 0.27 | 78.17 | 78.16 | 0.01 |
| А-ХЛФ-В (I) | 0.4841 (0.3533) | 0.4619 (0.3508) | 4.58 (0.71) | 60.40 | 60.25 | 0.25 |
| А-ХЛФ-В (II) | 0.4841 (0.3533) | 0.4553 (0.3603) | 5.95 (1.98) | 60.40 | 59.72 | 1.13 |
| А-ХЛФ-Э | 0.3500 (0.4600) | 0.3497 (0.4461) | 0.09 (3.11) | 63.15 | 62.88 | 0.43 |
| А-ХЛФ-ИПС | – | 0.3469 (0.6318) | – | – | 64.13 | – |
| ХЛФ-В-Э | 0.7490 (0.1290) | 0.7525 (0.1487) | 0.47 (15.3) | 55.25 | 55.53 | 0.50 |
| ХЛФ-В-Э (II) | 0.7490 (0.1290) | 0.7599 (0.1497) | 1.45 (16.04) | 55.25 | 55.61 | 0.65 |
| ХЛФ-В-ИПС | 0.8280 (0.1600) | 0.7889 (0.1596) | 3.51 (0.25) | 55.50 | 55.83 | 0.59 |
| ХЛФ-Э-ЦГ | – | 0.7862 (0.1700) | – | – | 59.49 | – |
| Э-ЦГ-В | – | 0.3250 (0.5211) | – | – | 62.27 | – |
| ИПС-МЭК-ЦГ | 0.3020 (0.1730) | 0.2958 (0.1688) | 2.05 (2.43) | 68.90 | 68.84 | 0.09 |
| ИПС-ЦГ-ЭА | – | 0.2958 (0.1688) | – | 68.3 | 68.80 | 0.73 |
| ЭА-МЭК-ЦГ | – | 0.2461 (0.2796) | – | – | 71.47 | – |
| ЭА-МЭК-ИПС | – | 0.6090 (0.0918) | – | – | 75.13 | – |
В системах I, III и IV присутствуют четырехкомпонентные азеотропы следующего состава (в скобках указаны относительные ошибки сравнения с экспериментальными данными): I – xА = = 0.5406 (0.48%); xХЛФ = 0.2517 (4.49%); xЭ = 0.0297 (1.01%); Т = 60.17°С (2.5%); III – xХЛФ = 0.7417 (–); xэ = 0.0939 (–); xЦГ = 0.0152 (–); T = 55.61°С (–); IV – xМЭК = 0.0896 (11.44%); xЦГ = 0.5158 (5.55%); xИПС = 0.2911 (4.98%); Т = 68.53°С (0.39%).
В табл. 4 приведены результаты описания равновесных жидких слоев в системе хлороформ–вода.
Таблица 4.
Сравнение экспериментальных [73, 74] и расчетных данных по составам равновесных жидких слоев в системе хлороформ–вода при 20°С
| Система | Эксп. данные | Расч. данные | Отн. ошибки | |||
|---|---|---|---|---|---|---|
| $x_{1}^{'}$ | $x_{1}^{{''}}$ | $x_{1}^{'}$ | $x_{1}^{{''}}$ | $\Delta x_{1}^{'}$ | $\Delta x_{1}^{{''}}$ | |
| ХЛФ-В | 0.9956 | 0.0012 | 0.9958 | 0.0012 | 0.02 | 0.00 |
| ЦГ-В | 0.9999 | 0.9995 | 0.9999 | 0.9996 | 0 | 0.01 |
Относительные ошибки описания разного вида фазовых равновесий в указанных системах одним набором параметров в большинстве случаев не превышают 6%. Ошибка в 11.44% связана с малым значением концентрации метилэтилкетона в четырехкомпонентном азеотропе.
ТЕРМОДИНАМИКО-ТОПОЛОГИЧЕСКИЙ АНАЛИЗ ДИАГРАММ ФАЗОВОГО РАВНОВЕСИЯ
На рис. 1 приведены развертки и полные структуры диаграмм фазового равновесия исследуемых систем. Для каждой из систем определены типы и индексы особых точек и доказана выполнимость правила азеотропии относительно границы и полной структуры [37–39] концентрационного тетраэдра.
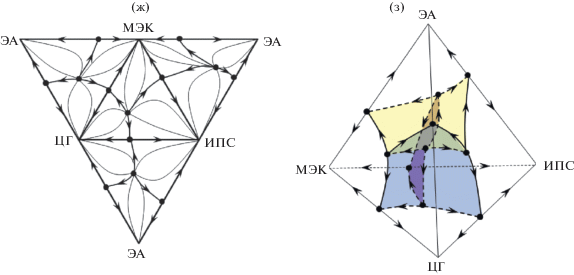
Рис. 1.
Двухмерные развертки и концентрационные тетраэдры исследуемых систем I–IV.
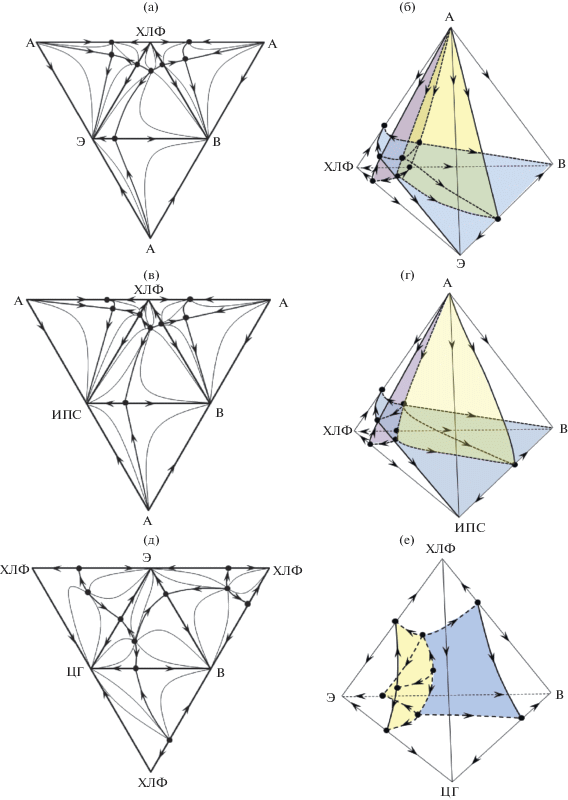
Рис. 1.
Окончание
Системы I и II характеризуются качественно одинаковой структурой развертки, но в системе с этанолом имеется четырехкомпонентный азеотроп, а в системе с пропанолом-2 он отсутствует. Анализ двухмерной развертки тетраэдра с точки зрения прогноза наличия в системе четырехкомпонентного азеотропа или его возможного появления мало информативен. Для этих целей (установления факта наличия внутреннего азеотропа) необходимо определить знак недостающих характеристических корней [43] для тройных азеотропов (исследовать температуру кипения сопряженных тройным азеотропам составов), и определить сумму индексов граничных особых точек. Если данная сумма принимает значение равное “+2” или “–2”, в системе присутствует четырехкомпонентный азеотроп; если сумма равна нулю, то внутреннего азеотропа нет. Тип азеотропа зависит от структуры сепаратрических поверхностей. Для системы I азеотроп представляет собой особую точку типа седло второго порядка.
На рис. 2 приведены структуры сепаратрических поверхностей второй размерности (S2), которые делят концентрационные тетраэдры систем I и II на 6 областей дистилляции (ректификации при бесконечном флегмовом числе).
Данные поверхности включают внутренние и граничные элементы (S1), являющиеся элементами пересечений сепаратрис S2 внутри тетраэдра и их следами на границах (развертке) тетраэдра. Чтобы определить возможные эволюционные изменения диаграммы при варьировании давления, необходимо проанализировать структуры данных многообразий. Бифуркация диаграммы ПЖР (появление/исчезновение внутреннего азеотропа) возможна только в том случае, если термодинамически разрешен переход [75–79] между структурами сепаратрических многообразий, порожденными одними и теми же седловидными точками. Так, например, в системе I четырехкомпонентный азеотроп не сможет исчезнуть ни в одном из трехкомпонентных (через стадию однократно тангенциального азеотропа) до тех пор, пока не исчезнет один из тройных азеотропов. Расчет ПЖР при пониженном давлении (50–10 кПа) показал, что в системе I при уменьшении давления сначала исчезает тройной азеотроп хлороформ–этанол–вода и только затем четырехкомпонентный исчезает в тройном ацетон–хлороформ–вода (рис. 3); индекс Пуанкаре граничного тангенциального азеотропа при этом равен +1 (i = ${\text{2}}i\left( {{\text{С}}_{{\text{4}}}^{ + }} \right)$ + $i\left( {{\text{С}}_{{\text{3}}}^{--}} \right)$ = +2 – 1 = +1). Причем трансформация азеотропа С4 в тройной азеотроп ацетон–хлороформ–вода наблюдается и на двух других сепаратрических многообразиях.
Рис. 3.
Эволюция структуры сепаратрических многообразий в системе ацетон (А)–хлороформ (ХЛФ)–этанол (Э)–вода (В) при уменьшении давления с 760 до 20 мм рт. ст.
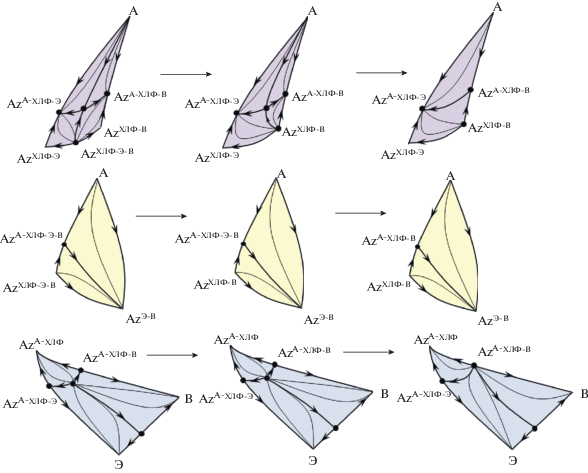
Пример систем I и II показывает, что, несмотря на то, что развертки качественно одинаковы, переход между полными структурами концентрационных тетраэдров термодинамически невозможен. При изменении давления фазовая диаграмма системы I никогда не будет топологически подобна диаграмме системы II.
Системы III и IV содержат четырехкомпонентный азеотроп узлового типа; диаграммы ПЖР разбиваются двумя и тремя сепаратрическими многообразиями на три и четыре области дистилляции, соответственно. Бифуркация четырехкомпонентного азеотропа через стадию образования граничного тангенциального азеотропа (с индексом Пуанкаре –1: i = ${\text{2}}i\left( {{\text{N}}_{{\text{4}}}^{--}} \right)$ + $i\left( {С_{{\text{3}}}^{ + }} \right)$ = –2 + 1 = –1) возможна в любом из тройных азеотропов.
В приведенных выше примерах одномерные границы (S1) сепаратрических многообразий (S2) присутствуют на двухмерной развертке тетраэдра, и формируют вокруг точек устойчивых узлов замкнутую кривую, состоящую из последовательно соединенных линий S1. Более сложным является случай, когда в концентрационном симплексе присутствуют такие S2, границы которых совпадают с ребрами тетраэдра [80]. Пример приведен на рис. 4.
Рис. 4.
Структура диаграммы ПЖР и сепаратрических многообразий четырехкомпонентной системы, содержащей бинарные азеотропы: (а) – система с четырехкомпонентным азеотропом; (б) – без внутреннего азеотропа.
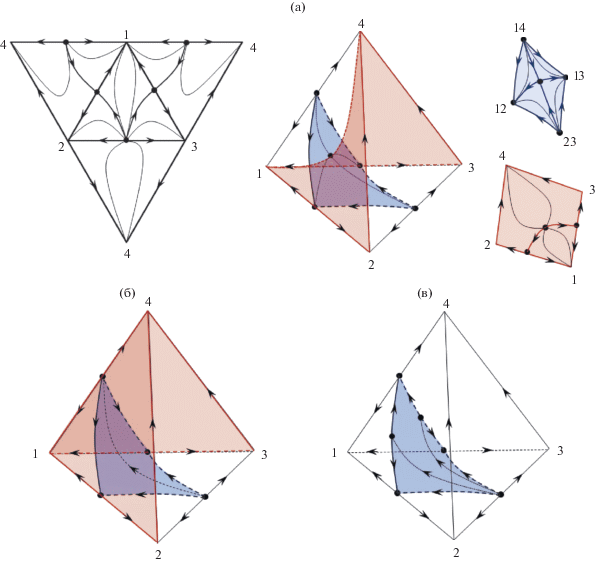
Данная система интересна еще и тем, что без построения полной структуры тетраэдра можно предсказать наличие в системе четырехкомпонентного азеотропа. Двухмерная развертка тетраэдра позволяет получить полную информацию о знаках трех характеристических корней особых точек, отвечающих точкам чистых компонентов и бинарных азеотропов. Сумма индексов особых точек равна “–2”, следовательно, в системе имеется четырехкомпонентный азеотроп с индексом +1 (седло второго порядка). Диаграмма разбивается двумя сепаратрическими поверхностями на четыре области дистилляции. Внутренний азеотроп может появиться (исчезнуть) в системе только через стадию двухкратного тангенциального азеотропа (индекс Пуанкаре равен +1: i = ${\text{2}}i\left( {{\text{C}}_{{\text{4}}}^{ + }} \right)$ + + $i\left( {{\text{N}}_{{\text{2}}}^{--}} \right)$ = +2 – 1 = +1), реализуемого в точке бинарного азеотропа 14 (сепаратрические поверхности на рис. 4).
ЗАКЛЮЧЕНИЕ
В настоящей работе представлен обзор иностранной и отечественной литературы по экспериментальному исследованию фазового равновесия, методикам анализа и предсказания структур диаграмм, проблемам моделирования ПЖР четырехкомпонентных систем, содержащих внутренние особые точки. На примере четырех реальных систем ацетон–хлороформ–этанол–вода, ацетон–хлороформ–пропанол-2–вода, хлороформ–этанол–циклогексан–вода, этилацетат–метилэтилкетон–циклогексан–пропанол-2, а также одной модельной показаны возможные пути эволюционного изменения структуры диаграммы ПЖР при варьировании давления, определены индексы Пуанкаре граничных однократных и двукратного тангенциального азеотропа.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 19-19-00620).
ОБОЗНАЧЕНИЯ
ИНДЕКСЫ
Список литературы
Yus D., Moonyong L. Distillation design and optimization of quaternary azeotropic mixtures for waste solvent recovery // J. Ind. Eng. Chem. 2018. V. 67. P. 255.
Клейменова М.Н., Комарова Л.Ф., Лазуткина Ю.С. Создание ресурсосберегающих технологий в производстве кремнийорганических эмалей на основе ректификации // Хим. интересах устойч. развит. 2013. Т. 21. С. 211.
Mujtaba I.M. Batch Distillation: Design and Operation. London: Imperial College Press, 2004.
Фролкова А.В., Фролкова А.К., Челюскина Т.В. Разделение четырехкомпонентной системы ацетон–хлороформ–этанол–вода автоэкстрактивно-гетероазеотропной ректификацией // Вестн. МИТХТ. 2010. Т. 5. № 6. С. 27.
Toikka M., Trofimova D., Samarov A. Liquid-liquid equilibrium and critical states for the quaternary system propionic acid–n-butanol–n-butyl propionate–water at 303.15 K // Fluid Phase Equilib. 2018. V. 460. P. 17.
Samarov A., Toikka M., Toikka A. Liquid–liquid equilibrium and critical states for the system acetic acid + n-butanol + n-butyl acetate + water at 308.15 K // Fluid Phase Equilib. 2015. V. 385. P. 129.
Xiao L., Wang Q., Wang H. Isobaric vapor–liquid equilibrium data for the binary system methyl acetate + isopropyl acetate and the quaternary system methyl acetate + methanol + isopropanol + isopropyl acetate at 101.3 kPa // Fluid Phase Equilib. 2013. V. 344. P. 79.
Osorio-Viana W., Duque-Bernal M., Quintero-Arias J.D., Dobrosz-Gomez I., Fontalvo J., Gomez-Garcia M.A. Activity model and consistent thermodynamic features for acetic acid–isoamyl alcohol–isoamyl acetate–water reactive system // Fluid Phase Equilib. 2013. V. 345. P. 68.
Harvianto G.R. Liquid–liquid equilibrium data and correlation for quaternary systems of acetic acid + water + + methyl acetate + p-xylene at 313.2 K // J. Ind. Eng. Chem. 2016. V. 35. P. 369.
Requejo P. Comparative study of the LLE of the quaternary and ternary systems involving benzene, n-octane, n-decane and the ionic liquid [BMpyr][NTf2] // J. Chem. Thermodyn. 2016. V. 98. P. 56.
Hongxun Z. Liquid–liquid phase equilibria of the quaternary system {water (1) + acrylic acid (2) + acetic acid (3) + cyclopentyl methyl ether (4)}: Measurement, correlation, and comparative study // Fluid Phase Equilib. 2015. V. 403. P. 23.
Toikka M., Samarov A., Trofimova M., Golikova A., Tsvetov N., Toikka A. Solubility, liquid–liquid equilibrium and critical states for the quaternary system acetic acid–ethanol–ethyl acetate–water at 303.15 K and 313.15 K // Fluid Phase Equilib. 2014. V. 373. P. 72.
Toikka M., Samarov A., Toikka A. Solubility, liquid–liquid equilibrium and critical states for the system acetic acid + n-propanol + n-propyl acetate + water at 293.15 K and 303.15 K // Fluid Phase Equilib. 2014. V. 375. P. 66.
Liebergesell B., Brands T., Koss H.-J., Bardow A. Quaternary isothermal vapor-liquid equilibrium of the model biofuel 2-butanone + n-heptane + tetrahydrofuran + cyclohexane using Raman spectroscopic characterization // Fluid Phase Equilib. 2018. V. 472. P. 107.
Pavlicek J., Bogdani G., Wichterle I. Vapour–liquid and chemical equilibria in the ethyl ethanoate + ethanol + + propyl ethanoate + propanol system accompanied with transesterification reaction // Fluid Phase Equilib. 2012. V. 328. P. 61.
Кулов Н.Н., Слайковская Н.П., Лотхов В.А. Исследование фазового равновесия в четырехкомпонентной системе ацетон–вода–окись мезитила–диацетоновый спирт // Теор. осн. хим. технол. 2012. Т. 46. № 2. С. 147.
Pequenin A., Asensi J., Gomis V. Vapor–liquid–liquid equilibrium and vapor–liquid equilibrium for the quaternary system water–ethanol–cyclohexane–toluene and the ternary system water–cyclohexane–toluene. Isobaric experimental determination at 101.3 kPa // Fluid Phase Equilib. 2011. V. 309. P. 62.
Wisniak J., Tamir A. Vapor-liquid equilibriums in the ternary systems water–formic acid–acetic acid and water–acetic acid–propionic acid // J. Chem. Eng. Data. 1987. V. 32. P. 291.
Fernandez J., Wisniak J. New computational tool to evaluate experimental VLE and VLLE data of multicomponent systems // Comput. Chem. Eng. 2017. V. 106. P. 437.
Sheikholeslamzadeh E., Rohani S. Vapour–liquid and vapour–liquid–liquid equilibrium modeling for binary, ternary, and quaternary systems of solvents // Fluid Phase Equilib. 2012. V. 333. P. 97.
Young-Kyu K., Dong-Won P. Liquid–liquid equilibrium for the quaternary system water + tetrahydrofuran + n-heptane + butyl acetate mixture at 25°C and atmospheric pressure // J. Ind. Eng. Chem. 2008. V. 14. № 5. P. 602.
Hussain A., Lee M. Feasibility Study of Reactive Distillation Configuration for 2-methoxy – 2-methylheptane // Chem. Eng. Trans. 2018. V. 69. P. 625.
Тимофеев В.С., Серафимов Л.А., Тимошенко А.В. Принципы технологии основного органического и нефтехимического синтеза. М.: Высш. шк., 2010.
Фролкова А.К. Разделение азеотропных смесей. Физико-химические основы и технологические приeмы. М.: ВЛАДОС, 2010.
Gerbaud V., Rodriguez-Donis I., Hegely L., Lang P., Denes F., You X.Q. Review of extractive distillation. Process design, operation, optimization and control // Chem. Eng. Res. Des. 2019. V. 141. P. 229.
Pequenin A., Gomis V. Quaternary isobaric (vapor + liquid + liquid) equilibrium and (vapor + liquid) equilibrium for the system (water + ethanol + cyclohexane + + heptane) at 101.3 kPa // J. Chem. Thermodyn. 2011. V. 43. № 8. P. 1097.
Frolkova A.K., Oshanina I.V., Frolkova A.V., Maevskii M.A. Cyclohexanone: The Main Methods of Obtaining and Extracting Target Products from a Reaction Mixture // Theor. Found. Chem. Eng. 2018. V. 52. № 4. P. 653.
Frolkova A.K., Akishina A.A., Maevskii M.A., Ablizin M.A. Flowsheets of multicomponent multiphase systems separation and material balance calculation features // Theor. Found. Chem. Eng. 2017. V. 51. № 3. P. 313.
Frolkova A.V., Frolkova A.K., Akishina A.A., Balbenov S.A. Phase equilibrium in the system water–acetonitrile–cyclohexene–cyclohexanone // Russ. Chem. Bull. 2015. V. 64. № 10. P. 2330.
Safrit B.T., Westerberg A.W. Algorithm for generating the distillation regions for azeotropic multicomponent mixtures // Ind. Eng. Chem. Res. 1997. V. 36. P. 1827.
Ahmad B.S., Zhang Y., Barton P.I. Product Sequences in Azeotropic Batch Distillation // AIChE J. 1998. V. 44. № 5. P. 1051.
Rooks R.E., Doherty M.F., Malone M.F., Julka V. Structure of distillation regions for multicomponent azeotropic mixtures // AIChE J. 1998. V. 44. № 6. P. 1382.
Blagov S., Hasse H. Topological analysis of vapor–liquid equilibrium diagrams for distillation process design // Phys. Chem. Chem. Phys. 2002. № 4. P. 896.
Popken T., Gmehling J. Simple Method for Determining the Location of Distillation Region Boundaries in Quaternary Systems // Ind. Eng. Chem. Res. 2004. V. 43. P. 777.
Hegely L., Lang P. A new algorithm for the determination of product sequences in azeotropic batch distillation // Ind. Eng. Chem. Res. 2011. V. 50. № 22. P. 12757.
Огородников С.K., Лестева T.M., Коган В.Б. Азеотропные смеси. Справочник / Под ред. Когана В.Б. Л.: Химия, 1971.
Серафимов Л.А. Термодинамико-топологический анализ и проблемы разделения многокомпонентных полиазеотропных смесей // Теор. осн. хим. технол. 1987. Т. 21. № 1. С. 74.
Серафимов Л.А. Термодинамико-топологический анализ диаграмм гетерогенного равновесия многокомпонентных смесей // Журн. физ. хим. 2002. Т. 76. № 8. С. 1351.
Серафимов Л.А. Современное состояние термодинамико-топологического анализа фазовых диаграмм // Теор. осн. хим. технол. 2009. Т. 43. № 3. С. 70.
Акишина А.А., Фролкова А.К., Фролкова А.В. Способ выделения циклогексанона из реакционной смеси вода–ацетонитрил–циклогексен–циклогексанон. Патент 2618273 РФ. 2017.
Охлопкова Е.А., Серафимов Л.А., Фролкова А.В. Разделение многокомпонентной системы, образующейся в производстве эпихлоргидрина // Тонкие хим. технол. 2016. Т. 11. № 6. С. 36.
Frolkova A.V., Frolkova A.K. The separation of five-component mixture formed in the production of methyl-isobutyl ketone // 43rd International Conference of SSCHE. Tatranske Matliare, 2016. P. 502.
Серафимов Л.А., Фролкова A.B., Медведев Д.В. Определение структуры диаграммы четырeхкомпонентной смеси на основе еe развeртки // Теор. осн. хим. технол. 2012. Т. 46. № 2. С. 154.
Serafimov L.A., Frolkova A.V. Determination of vapor-liquid equilibrium diagrams of multicomponent systems // Chem. Pap. 2016. V. 70. P. 1578.
Фролкова А.К., Павленко Т.Г., Бабич С.В., Береговых В.В., Львов С.В. Способ разделения смеси ацетон–хлороформ–этанол–вода. А. с. 1100819 СССР // Бюлл. изобрет. 1984. № 4.
Блюмберг Э.А., Чижов Е.Б., Эмануэль Н.М. Способ очистки уксусной кислоты. А. с. 136356 СССР // Бюлл. изобрет. 1961. № 5.
Блюмберг Э.А., Чижов Е.Б., Гельперин Н.И. Способ очистки уксусной кислоты. А. с. 149772 СССР // Бюлл. изобрет. 1962. № 17.
Malesinska B. Quinary Heteroazeotrope n-Octane Tetrachloroethylene–Nitromethane–n-Propanol–Water // Bull. Acad. Pol. Sci. 1964. V. 12. № 12. P. 853.
Engel K.H. Azeotropic distillation of hydrocarbon oils. Patent 2376870 USA. 1945.
Swietoslawski W., Galska A. A method for determining the composition of quaternary heteroazeotropes // Bull. Acad. Pol. Sci. 1954. V. 2. № 10. P. 479.
Zieborak K. On the Quaternary Azeotropes Formed by Paraffinic and Naphthenic Hydrocarbons with Benzene, Ethanol and Water // Rocz. Chem. 1951. V. 25. № 3. P. 388.
Zieborak K., Galska A. A method for determining the composition of quaternary azeotropes and the position of heteroazeotropic lines // Bull. Acad. Pol. Sci. 1955.V. 3. № 7. P. 379.
Kominek-Szczepanik M. Four-Component Azeotropes // Rocz. Chem. 1959. V. 33. № 2. P. 553.
Kominek-Szczepanik M. About polyazeotropic toluene systems from a series of homologous paraffin hydrocarbons contained in gasoline boiling at 100-130°C and butanol // Rocz. Chem. 1955. V. 29. № 2–3. P. 945.
Harding S.T., Maranas C.D., McDonald C.M., Floudas C.A. Locating All Azeotropes in Homogeneous Azeotropic Systems // Comput. Chem. Eng. 1996. V. 20. P. 413.
Imamura I., Kutsuwa Y., Matsuyama H. Reduction of the Existing Region of a Quaternary Azeotrope by Use of a Topological Condition // Kagaku Kogaku Ronbunshu. 1992. V. 18. № 4. P. 535.
Wang Q., Yan X.-H., Chen G.-H., Han S.-J. Measurement and Prediction of Quaternary Azeotropes for Cyclohexane + 2-Propanol + Ethyl Acetate + Butanone System at Elevated Pressures // J. Chem. Eng. Data. 2003. V. 48. P. 66.
Galska-Krajewska A., Zieborak K. Quaternary positive-negative azeotrope // Rocz. Chem. 1962. V. 36. № 1. P. 119.
Swietoslawski W. New Kinds of Azeotropes // Bull. Acad. Pol. Sci. 1955. V. 7. № 1. P. 13.
Zieborak K., Galska-Krajewska A. Quaternary Positive-Negative Azeotrope // Bull. Acad. Pol. Sci. 1959. V. 7. № 4. P. 253.
Vahdat N., Sather G.A. Prediction of multicomponent azeotrope composition and temperature // Chem. Eng. J. 1985. V. 31. № 2. P. 83.
Ryland G.A. Contribution to the Study of Liquid Mixtures of Constant Boiling-Point // Am. Chem. J. 1899. V. 22. P. 384.
Hanumantha R.G., Subbarao B.V. Isobaric vapor-liquid equilibria: chloroform + isopropanol, tertiary butanol + + toluene, and tertiary // Indian J. Technol. 1974. V. 12. P. 292.
Conti J.J., Othmer D.F., Gilmont R.J. Composition of Vapors from Boiling Binary Solutions. Systems Containing Formic Acid, Acetic Acid, Water // J. Chem. Eng. Data. 1960. V. 5. P. 301.
Lin Y.-F., Tu C.-H. Isobaric vapor–liquid equilibria for the binary and ternary mixtures of 2-propanol, water, and 1,3-propanediol at P = 101.3 kPa: Effect of the 1,3-propanediol addition // Fluid Phase Equilib. 2014. V. 368. P. 104.
Gu F., Hou Y.J. Salt Effects on the Isobaric Vapor-Liquid Equilibrium for Four Binary Systems // J. Chem. Eng. Data. 2000. V. 45. P. 467.
Gultekin N.J. Vapor-Liquid Equilibria for Binary and Ternary Systems Composed of Acetone, 2-Propanol, and 1-Propanol // J. Chem. Eng. Data. 1989. V. 34. P. 168.
Морачевский А.Г., Рабинович Р.Ш. Равновесие жидкость-пар в системе хлороформ этиловый спирт // Журн. прикл. хим. 1959. Т. 32. № 2. С. 458.
Reinders W.J., de Minjer C.H. Vapour-liquid equilibria in ternary systems. VI. The system water-acetone-chloroform // Recl. Trav. Chim. 1947. V. 66. № 9. P. 573.
Equilibrium-Stage Separation Operations in Chemical Engineering / Eds. Henley E.J., Seader J.D. N.Y.: Wiley, 1981.
Kudryavtseva L.S., Kivia Kh.L., Susarev M.P. Calculation of the Composition of Ternary Heteroazeotropes of the Type Hydrocarbon (Halogenoderivative of Hydrocarbon)–Water–Alcohol. Moscow: VINITI, 1971.
Yan X.H., Wang Q., Chen G. Azeotropes at elevated pressures for systems involving cyclohexane, 2-propanol, ethyl acetate, and butanone // J. Chem. Eng. Data. 2001. V. 46. P. 1235.
Stephenson R.M. Mutual solubilities: water–ketones, water–ethers, and water–gasoline–alcohols // J. Chem. Eng. Data. 1992. V. 37. P. 80.
Буданцева Л.С., Лестева Т.М., Немцов М.С. Равновесия жидкость–жидкость в системах метанол–вода–парафиновые углеводороды С7, С8. М.: ВНИИЭгазпром, 1976.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. VIII. Общие закономерности тангенциальной азеотропии // Журн. физ. хим. 1971. Т. 45. № 5. С. 1140.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. IX. Тангенциальная азеотропия и общее соотношение между особыми точками разных типов // Журн. физ. хим. 1971. Т. 45. № 6. С. 1473.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. Х. Двукратно тангенциальные азеотропы // Журн. физ. хим. 1971. Т. 45. № 7. С. 1620.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. XI. Тангенциальная азеотропия в трёхкомпонентных смесях и цепи топологических структур // Журн. физ. хим. 1971. Т. 45. № 10. С. 2448.
Бедретдинов Ф.Н., Челюскина Т.В. Исследование различных изомногообразий в четырехкомпонентных системах, содержащих биазеотропные бинарные составляющие // Тонкие хим. технол. 2018. Т. 13. № 1. С. 45.
Жаров В.Т., Серафимов Л.А. Физико-химические основы дистилляции и ректификации. Л.: Химия, 1975.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии