Теоретические основы химической технологии, 2020, T. 54, № 3, стр. 335-344
Термодинамические основы системного информационного подхода к организации сложных технологических объектов
В. А. Налетов a, *, В. А. Колесников a, М. Б. Глебов a
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: jacen23@yandex.ru
Поступила в редакцию 20.09.2019
После доработки 25.09.2019
Принята к публикации 30.09.2019
Аннотация
На основе моделей макро- и микроуровней представлены термодинамические основы системного информационного подхода к организации сложных технологических объектов с иерархической структурой на примере химико-технологических систем. Показано, что иерархическая структура химико-технологической системы представлена тремя уровнями: система как единое целое, химико-технологические процессы (элементы системы) и микросостояния (результаты превращений). При этом организация элементов системы интерпретируется на основании термодинамической модели микроуровня, которая при определенной формализации технологических превращений характеризует процесс получения информации. Организация химико-технологической системы на макроуровне описывается моделью стохастического процесса флуктуаций средних уровней энергии процессов, которая позволяет установить согласованный вариант взаимодействия элементов в системе в соответствии с нулевым началом термодинамики. Сформулирована минимаксная задача оптимальной организации сложного технологического объекта на основании объединения трех начал термодинамики: первого, второго и нулевого, которые обеспечивают достижение свойств эмерджентности системы как единого целого.
ВВЕДЕНИЕ
В соответствии с общей теорией систем Людвига фон Берталанфи [1], к классу объектов, обладающих системными свойствами, можно отнести как биологические, так и социальные, а также сложные технические системы, т.е. объекты, которые характеризуются иерархической структурой. Примерами сложных технических систем являются, в частности, химико-технологические системы (ХТС), обладающие сложной топологией и дискретной элементной структурой. В мировоззренческом плане работы Берталанфи базировались на идее общности принципов построения вышеуказанного класса объектов на основе изоморфизма законов живой материи. При этом общая теория систем представлена в его работах как фундаментальная наука, направленная на изучение и создание (конструирование, синтез) объектов на основе раскрытия таких понятий, как система, структура, связь, иерархическое строение системы, организованность, целостность, взаимодействие и ряд других.
Одним из перспективных научных направлений общей теории систем и системного анализа Берталанфи считает подход, основанный на теории информации К. Шеннона и У. Уивера [2, 3], в основе которого лежит понятие информации как меры упорядочивания или организации [4]. Однако при этом отмечалось, что работ по применению теории информации применительно к проблематике общей теории систем и ее прикладным аспектам крайне мало. Большая часть этих работ посвящена теории передачи сигналов, механизмам распознавания образов и ряду других вопросов. В частности, У.Р. Эшби [5] рассматривает организацию динамических систем как функцию взаимодействия между ее частями, обусловленную информационными потоками. Работы М.М. Бонгарда, например [6], относятся к теории распознавания образов. Связь между информацией с одной стороны и ее термодинамическим содержанием с другой представлена в работе Л. Бриллюэна, который установил корреляцию между неопределенностью элементарных состояний системы, их вероятностью и энтропией, а также ввел понятие негэнтропии: “Любая добавленная информация увеличивает негэнтропию системы. Это приводит к важному соображению: мы можем установить количественную меру информации через соответствующий прирост негэнтропии” [7].
Термодинамике процессов информации и мышления посвящена работа Н.И. Кобозева [8]. Прикладными аспектами теории информации являются, в частности, исследования в области моделирования, оптимизации и синтеза объектов химической технологии.
Работы школы В.П. Майкова впервые были посвящены применению теории информации к математическому моделированию процессов химической технологии [9, 10]. Однако в этих работах прослеживается полная идентичность количественных выражений для информационной и термодинамической энтропии.
В работах школы химической кибернетики В.В. Кафарова по применению теории информации в химической технологии [11, 12] объектами исследования являлись уже сложные химико-технологические системы с иерархической структурой.
Целью настоящей работы является представление термодинамических основ информационного подхода к оптимальной организации ХТС на основе моделей микро- и макроуровней объекта в рамках развития прикладного научного направления общей теории систем на базе теории информации.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Вначале обратимся к смысловым трактовкам понятия энтропии, которое в ходе своей эволюции имело разный физический смысл. За более чем двухсотлетнюю историю понятие энтропии существенно изменилось. Если в первоначальной форме, данной Р. Клаузиусом, энтропия имела “тепловой” (а точнее, теплоемкостный) смысл и размерность Дж/(моль К), то в трудах Л. Больцмана она получила уже иное, вероятностное толкование, причем Н – функция Больцмана была сначала безразмерной и имела обратный знак с энтропией, поскольку относилась к раскрытию неопределенности посредством выбора. Привычный вид энтропии Больцмана придал М. Планк, введя константу k, придавшую энтропии Больцмана размерность.
В дальнейшем сложилось представление об энтропии как о мере неупорядоченности и неопределенности любой системы в виде статистической энтропии. При этом статистическая энтропия, выраженная в виде S = $ - \sum\limits_i {{{p}_{i}}\ln {{p}_{i}}} ,$ вновь утратила размерность и относилась к неупорядоченности (неопределенности) произвольной системы, которая необязательно связана только с тепловым хаосом. В этом выражении рi – вероятность i-го дискретного (квантового) состояния системы. По смыслу статистическая энтропия является функцией состояния стохастической системы.
Во второй половине XX столетия появилась новая смысловая трактовка энтропии – энтропия информации, как меры упорядоченности системы. Энтропия информации являлась также безразмерной, но, в отличие от статистической энтропии, стала функцией процесса упорядочивания. Эта функция была введена К. Шенноном. Энтропия информации Шеннона H имеет аналогичное выражение, как и статистическая энтропия, но вероятности несут другой физический смысл, в силу чего другой физический смысл имеет и энтропия информации:
где K – безразмерная положительная постоянная, рi – вероятность i-го исхода.Выражение (1) справедливо для случая, когда число исходов конечно, но не определено. Понятие исхода, предложенное в работе [8], указывает на принадлежность к процессу получения информации, а вероятность в выражении энтропии информации Шеннона i-го исхода указывает на возможный конечный результат процесса, который можно определить как выбор из ряда альтернатив (исходов) единственного решения или как процесс упорядочивания (организации).
Зависимость (1) имеет максимум при равновероятном осуществлении всех исходов, т.е. когда р1 = р2 = р3 = … = рi = … и обращается в нуль при значении вероятности какого-либо исхода, равной единице, а всех остальных – равными нулю. Таким образом, раскрывается неопределенность в организации объекта.
В целом в ХТС наблюдается два вида неопределенности: неопределенность того, в какой элемент системы должны быть направлены те или иные потоки или неопределенность топологии, и неопределенность того, какие изменения (превращения) произойдут с этими потоками в элементах, что обусловлено вариантами организации собственно химико-технологических процессов (ХТП). Неопределенность организации отдельных процессов раскрывается на микроуровне, а неопределенность топологии системы – на макроуровне.
Представим процесс получения информации на микроуровне с позиции термодинамики.
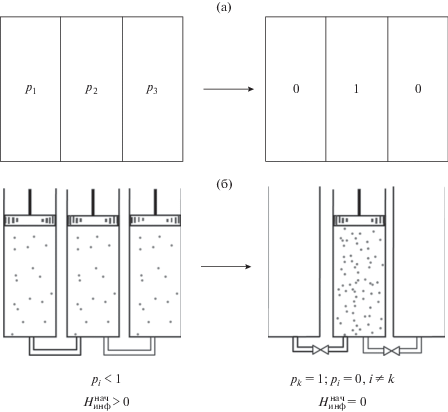
На рис. 1а представлен информационный процесс как выбор из 3 возможных исходов, имеющих вероятности соответственно р1, р2, р3, единственного решения, которое характеризуется достижением вероятности выбранного решения, равной 1.
На рис. 1б представлена термодинамическая модель информационного процесса, которая отображает процесс упорядочивания или организации на микроуровне.
Каждой ячейке на рис. 1а ставится в соответствие камера с невесомым поршнем, в которой содержится идеальный газ или “шанс-газ” в терминологии автора работы [8]. Камеры соединены каналами, по которым газ при воздействии на поршни может перемещаться из камеры в камеру.
При этом для фиксации определенного состояния термодинамической системы (рис. 1б) каналы в камерах могут быть перекрыты.
Оценим исходное и конечное состояния термодинамической системы, обобщив вывод для Z камер. Термодинамическая концентрация частиц идеального газа в i-й камере опосредованно определяет вероятность данного возможного исхода:
где mi – число частиц в i-й камере, $M = \sum\limits_{i = {\text{1}}}^Z {{{m}_{i}}} $ – общее число частиц.В этой модели наибольшей неопределенности, а следовательно, и наибольшей энтропии отвечает случай, когда камеры сообщаются друг с другом и содержат одинаковое число частиц M/Z.
Вероятность i-го исхода в этом случае будет равна
Такую информационную систему называют Z-кратно вырожденной. Энтропия вырожденной системы максимальна и равна
Выбор из Z-альтернативных состояний одного из них уменьшает неопределенность или энтропию до нуля. На термодинамической модели (рис. 1б) это означает перемещение идеального газа в одну камеру постоянного объема при неизменной температуре из других камер путем совершения работы.
Рассмотрим два состояния системы (исходное и конечное) в термодинамической модели (рис. 1б) и вычислим работу изотермического процесса по перемещению (сжатию) частиц идеального газа из Z – 1 камер в одну камеру при неизменном ее объеме. Согласно молекулярно-кинетической теории давление идеального газа при неизменной температуре пропорционально числу частиц газа в камере (p = kmT).
Тогда работа изотермического процесса при условии неизменности объема камеры, в которую перекачивается идеальный газ из других камер, будет равна
(5)
$\begin{gathered} A = MRT\ln \frac{{{{p}_{1}}}}{{{{p}_{2}}}} = MRT\ln \frac{{{M \mathord{\left/ {\vphantom {M Z}} \right. \kern-0em} Z}}}{M} = \\ = \,\, - MRT\ln Z. \\ \end{gathered} $Приведем эту работу к безразмерному виду, разделив ее на RT и приняв, что число частиц М равно числу Авогадро. Тогда безразмерная работа 1 моля вещества будет равна соответствующему безразмерному изменению свободной энергии (знак минус указывает, что работа затрачивается на повышение свободной энергии):
На аналогичную величину уменьшается и энтропия:
Таким образом, при изохорно-изотермическом сжатии идеального газа имеем
Следовательно, уменьшить исходную неопределенность и получить информацию возможно только посредством затрат обобщенной работы.
Уравнение (7) является термодинамическим аналогом уравнения Шеннона–Винера с точностью до замены безразмерной работы на количество информации Винера:
Таким образом, количество информации Винера I0 характеризует процесс получения информации или организацию путем выбора конкретного исхода и равно по абсолютной величине энтропии информации Шеннона. Из сопоставления уравнения (8) с уравнением Гиббса–Гельмгольца, представляющего зависимость изменения полной энергии как сумму изменений свободной (аналог количества информации) и связанной (аналог изменения энтропии) форм энергии, можно заключить, что процесс упорядочивания или организации на микроуровне осуществляется в условиях постоянства полной энергии или изоэнергетичности.
При этом можно заключить, что если любой информационный процесс можно представить в терминах термодинамики, то справедливо и обратное: любой термодинамический процесс, сопровождающийся изменением термодинамических характеристик, можно представить в терминах теории информации.
Для этого необходимо определенным образом формализовать технологический процесс, приняв следующее [12].
1. Каждый технологический поток является носителем информации о его возможных состояниях (возможных результатах технологического процесса или исходах) и поэтому может рассматриваться как поток информационный. При этом возможные состояния технологического потока представляются на основе корпускулярной и квантовой теорий о дискретности превращений вещества и энергии. Каждому дискретному состоянию ставится в соответствие вероятность данного исхода.
2. Ансамбль возможных состояний технологического потока или исходов характеризует объем информационного процесса, который опосредованно определяется альтернативными способами его организации, в силу чего данные возможные состояния являются статистически независимыми.
3. Преобразованию информационных потоков в аппарате ставится в соответствие решение некоторой информационной задачи, заключающейся в выборе определенного исхода из возможных альтернатив путем уменьшения исходной неупорядоченности в соответствии с уравнением Шеннона–Винера при условии постоянства полной или внутренней энергии преобразования. Уменьшение исходной неупорядоченности характеризует процесс упорядочивания или организации. При этом собственно информация является решением информационной задачи.
4. За точку отсчета для решения информационной задачи принимается безэнтропийное состояние на выходе Нвых = 0. Этому состоянию, которое принимается за эталон, ставятся в соответствие предельные случаи преобразования вещества и энергии в процессах и соответственно максимальное количество информации I0. Реальное количество информации IН всегда меньше максимального вследствие необратимости процесса, которая определяется, с одной стороны, необратимым характером протекания процесса, а с другой – невозможностью в один прием достичь желаемого результата.
С учетом потерь количества информации ΔIH уравнение Шеннона–Винера можно преобразовать следующим образом:
или
Основываясь на вышеперечисленных положениях, можно представить иерархическую структуру ХТС с позиции теории информации (рис. 2).
Рис. 2.
Иерархическая структура ХТС: L, Q – работа и теплота соответственно; U – внутренняя (полная) энергия; K – структурные параметры (доли потоков вещества или энергии, направляемые на вход соответствующего элемента); ΔГμ – объем информационного процесса (статистический вес системы на микроуровне).
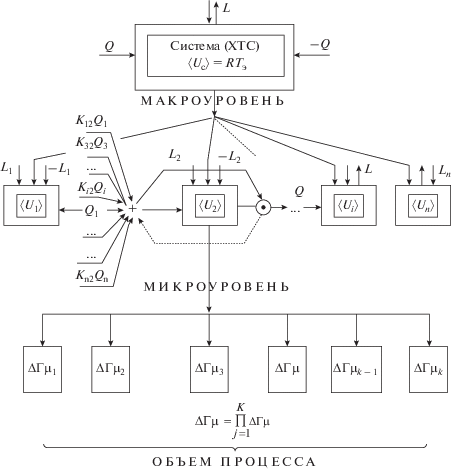
Микроуровень представлен ансамблем возможных состояний технологического потока или объемом информационного процесса, которые определяются возможными режимными и конструкционными характеристиками аппаратов.
Макроуровень представлен возможными вариантами топологии системы, которые в задаче организации ХТС на макроуровне можно идентифицировать с оптимальной дифференциацией (распределением) функций системы между ее элементами.
На рис. 3 представлены характеристики обратимого и необратимого информационных процессов на микроуровне.
Рис. 3.
Характеристики обратимого и необратимого информационного процессов на микроуровне (S – изменение термодинамической энтропии).
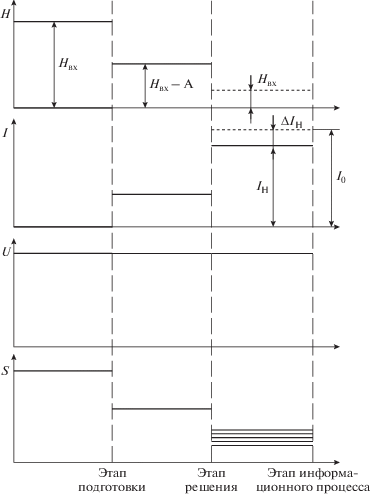
Информационным критерием совершенства технологического процесса является информационный КПД, оценивающий достижение стоящей перед ним цели в виде выражения
Пределы изменения ηинф от 0 до 1, причем повышение эффективности процесса за счет увеличения его информационного КПД характеризуется уменьшением выходной неупорядоченности, достигающей условно нулевого значения в случае решения информационной задачи.
По виду выражение (10) аналогично выражению эксергетического КПД, где в числителе и знаменателе стоят идентичные количествам информации эквиваленты работы.
Верхнюю позицию в представленной иерархии ХТС (рис. 2) занимает система как единое целое, характеризуемая дискретной элементной структурой.
В соответствии с условием изоэнергетичности информационного процесса ХТС в целом и ее элементы – ХТП должны быть помещены в “воображаемые термостаты”, согласно представлениям о замкнутых термодинамических системах. Средний интегральный уровень энергии ХТС как единого целого 〈Uс〉 определяется внешними источниками и стоками энергии (теплоты и работы). В свою очередь, взаимодействие элементов системы друг с другом на макроуровне определяется рассогласованием их средних уровней внутренней энергии 〈Ui〉 (i = 1, 2, …I), которые обусловлены топологией системы и параметрами потоков.
Рассмотрим организацию системы на верхнем иерархическом уровне (макроуровне).
Каждый процесс “решает” информационную задачу на своем постоянном уровне полной (внутренней) энергии, в общем случае отличающемся от уровня ХТС в целом. Причем чем больше рассогласование уровней, тем существенней взаимодействие элементов.
Для описания организации ХТС на макроуровне можно использовать термодинамическую модель стохастического процесса (рис. 4), которая позволяет описать все возможные варианты расположения средних уровней энергии процессов по отношению к уровню ХТС как единого целого, которые, в свою очередь, определяются возможными вариантами топологии системы.
Рис. 4.
Термодинамическая модель флуктуаций средних уровней энергии процессов на макроуровне: (а) – переход в неустойчивое состояние; (б) – переход в равновесное состояние.
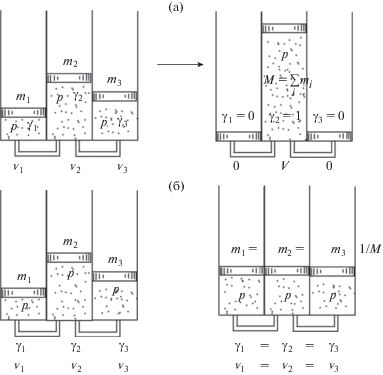
Положим, что в ячейках, которые сверху ограничены невесомыми поршнями, содержится несжимаемый идеальный газ, характеризуемый числом частиц в ячейке m, термодинамической концентрацией γ, объемом v и давлением p, которые определяют некоторый средний уровень энергии газа в ячейке.
Ячейки соединены каналами, позволяющими перетекать газу из одной ячейки в другую. При этом каналы не имеют запорных устройств. Общее число частиц в газе постоянно.
Примем, что процесс перетекания газа из ячейки в ячейку осуществляется в изобарно-изотермических условиях при постоянстве общего объема газа, что адекватно тому, что все возможные варианты распределения газа между ячейками будут обладать одним и тем же уровнем полной энергии системы или изоэнергетичностью.
В случае некоторого малого воздействия на поршни в системе могут возникнуть флуктуации, которые в условиях изоэнергетичности рассматриваемой модели могут привести либо к концентрированию газа в одной ячейке (рис. 4а, правая система) – маловероятный случай, либо к установлению равновесия (рис. 4б, правая система) – наиболее вероятный случай.
Поскольку состояние равновесия располагается между исходным и предельным неустойчивым состоянием, определим изменение энтропии в стохастической, колеблющейся системе.
Для этого сначала запишем энтропию левой системы на рис. 4а:
(11)
${{H}_{{\text{I}}}} = {{m}_{1}}\ln {{v}_{1}} + {\text{ }}{{m}_{2}}\ln {{v}_{2}} + \ldots + {\text{ }}{{m}_{Z}}\ln {{v}_{Z}} + M{{g}_{0}},$Так как в общем объеме системы ${{V}_{c}} = \sum\limits_{i = {\text{1}}}^Z {{{v}_{i}}} $ давление р и число частиц M постоянны, то
откуда
Величина γi является термодинамической концентрацией идеального газа в ячейке и одновременно термодинамическим аналогом вероятности i-го макросостояния, определяемого средним уровнем энергии данного процесса в силу того, что число частиц газа согласно распределению Больцмана пропорционально среднему уровню энергии:
Тогда
(13)
$\begin{gathered} {{H}_{{\text{I}}}} = M\sum\limits_{i = {\text{1}}}^Z {{{n}_{i}}{\text{ln}}{{n}_{i}}V} + M{{g}_{{\text{0}}}} = \\ = M\sum\limits_{i = {\text{1}}}^Z {{{n}_{i}}{\text{ln}}{{n}_{i}}} + M{\text{ln}}V + M{{g}_{{\text{0}}}}. \\ \end{gathered} $Энтропия правой системы на рис. 4а для газа, собранного в одну ячейку, при тех же обозначениях будет равна
Превышение энтропии левой системы над правой (рис. 4а), отнесенное к 1 молю идеального газа, выразится следующим образом:
Выражение энтропии (15) отображает стохастический процесс флуктуаций средних уровней энергии на макроуровне, поэтому в дальнейшем ей приписывается индекс “м” и название – макроэнтропия.
Устойчивому состоянию стохастической колеблющейся системы (правая система на рис. 4б) соответствует максимум макроэнтропии согласно (15). Кроме того, организация ХТС на макроуровне означает оптимальное распределение средних энергетических уровней элементов системы в соответствии с нулевым началом термодинамики [13], при котором энергетическое взаимодействие между элементами минимальное.
Понимая под организацией объекта определенную процедуру оптимизации, можно считать, что в процессе оптимальной организации степень организованности объекта должна повышаться.
Следовательно, оптимальная организация сложной технологической системы, каковой является ХТС, представляется как минимаксная задача, для которой на макроуровне энтропия максимизируется, а на микроуровне – минимизируется, что в целом является следствием действия трех объективных начал термодинамики: первого, второго и нулевого.
При этом действие трех начал термодинамики обеспечивает повышение степени организованности системы и, как следствие, повышение степеней ее макроскопичности, целостности, автономности и устойчивости, что исключает необходимость в частных постановках задачи и позволяет достигать эмерджентных свойств системы как единого целого.
РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
В качестве примера на рис. 5 представлено техническое решение мультифункциональной установки (энергоблока тригенерации) на основе совмещения подсистемы цикла Ренкина (ЦР) на низкокипящем рабочем теле и подсистемы холодильного цикла (ХЦ), разработанное на основе системного информационного подхода к организации сложных технических систем [14].
Рис. 5.
Технологическая схема энергоблока тригенерации для улавливания и выделения диоксида углерода из очищенных дымовых газов (потоки, обозначенные кружочками, объединены): 1 – испаритель; 2 – пароперегреватель; 3 – паровая турбина; 4 – конденсатор; 5 – насос; 6 – парциальный конденсатор (удаление воды); 7 – промежуточный теплообменник; 8 – трехступенчатый компрессор с промежуточным охлаждением; 9 – десублиматор; 10 – газовая турбина.
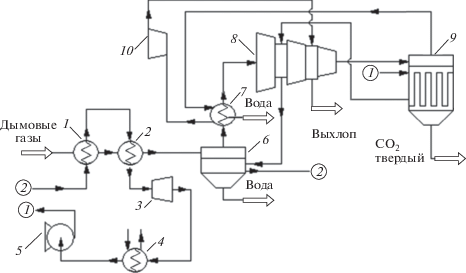
В разработанной системе осуществляется глубокая рекуперация теплоты очищенных дымовых газов теплоэнергетических систем с выработкой электроэнергии, холода и товарного диоксида углерода в твердом или газообразном состоянии [15].
Разработанное техническое решение адаптировано к любым видам природных топлив и может быть использовано как замыкающее звено промышленных теплоэнергетических систем.
В табл. 1 приведены данные сравнительного анализа системы с раздельными подсистемами и оптимально интегрированной системы – энергоблока тригенерации. В качестве критерия был выбран эксергетический КПД системы.
Таблица 1.
Сравнение показателей эффективности технических решений
| Техническое решение | Система, объединяющая раздельные подсистемы | Энергоблок тригенерации | ||
|---|---|---|---|---|
| подсистема ЦР | подсистема ХЦ | система | ||
| Эксергетический КПД, % | 70.63 | 50.31 | 35.53 | 73.56 |
Из результатов сравнительного анализа (табл. 1) следует, что в разработанном энергоблоке тригенерации достигается синергетический эффект по отношению к системе с раздельными способами, когда эксергетический КПД оптимально организованной системы оказался больше наибольшего значения эксергетического КПД отдельной подсистемы.
ЗАКЛЮЧЕНИЕ
В настоящей работе представлены термодинамические основы системного информационного подхода к оптимальной организации сложных технологических объектов на примере химико-технологических систем, которые отображаются моделями микро- и макроуровней в иерархической структуре системы.
На основании термодинамической модели микроуровня показано, что с позиции теории информации каждый элемент системы может рассматриваться как комплекс упорядочивающих операций, направленных на выбор одного из возможных состояний технологического потока или исхода, т.е. на решение некоторой информационной задачи по уменьшению исходной неопределенности. При этом количество информации, полученное в ходе решения информационной задачи для реального процесса, меньше, чем для эталонного в силу необратимости преобразования.
На основании термодинамической модели макроуровня, которая характеризует взаимодействие элементов внутри системы, было показано, что оптимальному согласованию элементов системы соответствует максимум макроэнтропии, выраженной через вероятности флуктуаций средних энергетических уровней процессов по отношению к уровню энергии ХТС как единого целого. Условие оптимальности на макроуровне является следствием нулевого начала термодинамики, отражающего стремление любой системы к устойчивому состоянию, которое характеризуется минимальными притоками свободной энергии в систему извне.
Таким образом, можно сделать вывод, что оптимальная организация сложных технологических объектов, какими являются ХТС, является минимаксной задачей, в которой на макроуровне энтропия максимизируется, а на микроуровне – минимизируется, что является следствием трех начал термодинамики: первого, второго и нулевого. Эти объективные закономерности позволяют повышать степень макроскопичности объектов, достигая при этом эмерджентности их свойств как единого целого, что является развитием информационного подхода в прикладной области общей теории систем и системного анализа.
ОБОЗНАЧЕНИЯ
| Ā | безразмерная работа |
| H | энтропия информации |
| I | количество информации |
| ΔI | потери информации; |
| k | постоянная Больцмана, Дж/К |
| m | число частиц газа |
| n | весовой коэффициент (вероятность) |
| p | вероятность (в теории информации), давление (в термодинамике) |
| R | универсальная газовая постоянная, Дж/(моль К) |
| S | термодинамическая энтропия, Дж/(моль К) |
| T | температура, К |
| $v$ | объем газа |
| Z | число исходов |
| ηинф | информационный КПД |
| Δφ | безразмерное изменение свободной энергии |
ИНДЕКСЫ
Список литературы
фон Берталанфи Л. Общая теория систем: критический обзор // Исследования по общей теории систем: сборник переводов / Под ред. Садовского В.Н., Юдина Э.Г. М.: Прогресс, 1969. С. 23.
Shannon C., Weaver W. The Mathematical Theory of Communication. Urbana: University of Illinois Press, 1949.
Шеннон К. Работы по теории информации и кибернетике. М: Изд-во иностранной литературы, 1963.
Information Theory in Biology / Ed. Quastler H. Urbana: University of Illinois Press, 1955.
Эшби У.Р. Введение в кибернетику. М.: Прогресс, 1959.
Бонгард М.М. Проблема узнавания. М.: Наука, 1967.
Бриллюэн Л. Научная неопределённость и информация. М.: Мир, 1966.
Кобозев Н.И. Исследование в области термодинамики процессов информации и мышления. М.: МГУ, 1971.
Майков В.П. Энтропийные методы моделирования в химической технике. М.: Московский институт химического машиностроения, 1981.
Балунов А.И., Майков В.П. Расчет составов продуктовых потоков сложных ректификационных систем на основе принципа максимальной энтропии // Изв. высш. учебн. завед. Хим. хим. технол. 2003. № 9. С. 94.
Naletov V.A., Gordeev L.S., Glebov M.B., Naletov A.Yu. Information-Thermodynamic Principle of the Organization of Chemical Engineering Systems // Theor. Found. Chem. Eng. 2011. V. 45. № 5. P. 631. [Налетов В.А., Гордеев Л.С., Глебов М.Б., Налетов А.Ю. Информационно-термодинамический принцип организации химико-технологических систем // Теор. осн. хим. технол. 2011. Т. 45. № 5. С. 541.]https://doi.org/10.1134/S0040579511050289
Naletov V.A., Kolesnikov V.A., Glebov M.B., Naletov A.Yu. Information-Probabilistic Approach to the Structuring of a Binary Distillation Process // Theor. Found. Chem. Eng. 2019. V. 53. № 3. P. 410. [Налетов В.А., Колесников В.А., Глебов М.Б., Налетов А.Ю. Информационно-вероятностный подход к оптимальной организации процесса бинарной ректификации // Теор. осн. хим. технол. 2019. Т. 53. № 3. С. 410.]https://doi.org/10.1134/S004057951902012X
Рейф Ф. Статистическая физика. Берклеевский курс физики. Т. 5. М.: Наука, 1977.
Налетов В.А., Глебов М.Б., Налетов А.Ю. Улавливание диоксида углерода из дымовых газов в энергоблоке тригенерации // Экол. пром. производ. 2013. Вып. 4(84). С. 6.
Налетов В.А., Глебов М.Б., Налетов А.Ю. Получение электроэнергии, холода и диоксида углерода из дымовых газов. Патент 2482406 РФ. 2013.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии