Теоретические основы химической технологии, 2020, T. 54, № 3, стр. 383-391
Контроль качества моделей химической кинетики при решении задачи оптимизации процесса получения 4-трет-бутилпирокатехина
С. И. Спивак a, О. Г. Кантор b, *, Н. Д. Морозкин c
a Институт нефтехимии и катализа РАН
Уфа, Россия
b Уфимский государственный нефтяной технический университет
Уфа, Россия
c Башкирский государственный университет
Уфа, Россия
* E-mail: o_kantor@mail.ru
Поступила в редакцию 20.11.2018
После доработки 12.10.2019
Принята к публикации 22.10.2019
Аннотация
Исследуется обратная задача определения констант скоростей реакции на основе экспериментальных данных в рамках принятой модели процесса получения 4-трет-бутилпирокатехина с позиций достижения заданного качественного уровня математического описания. По результатам численной реализации разработанного метода параметрической идентификации для двух температурных режимов определены интервалы значений констант скоростей реакции, обеспечивающие достижение заданных качественных характеристик. Представленный метод также позволяет выявлять опытные данные, подлежащие уточнению. На основе использования полученных кинетических моделей решена задача оптимизации исследованного химического процесса, что позволило определить режим подачи окислителя, обеспечивающий увеличение выхода 4-трет-бутилпирокатехина, и получить необходимые количественные оценки концентраций наблюдаемых веществ.
ВВЕДЕНИЕ
Практическая востребованность 4-трет-бутилпирокатехина (4-ТБПК) объясняется возможностью его применения в качестве стабилизатора непредельных альдегидов и этилцеллюлозных искусственных смол, ингибитора полимеризации диеновых углеводородов, антиоксиданта животных жиров, масел, восков [1–3] и пр.
Известные способы синтеза 4-ТБПК основаны на алкилировании пирокатехина олефинами или спиртами в присутствии неорганической кислоты, в качестве которой преимущественно используют серную. Промышленный процесс получения 4-ТБПК включает две стадии: на первой получают пирокатехин при помощи щелочного плавления о-хлорфенола или о-фенилсульфокислоты, на второй – полученный пирокатехин алкилируют на катионите КУ-2 с изобутиловым спиртом. Недостатками такого процесса, помимо его сложности, являются образование ди- и триалкилпроизводных пирокатехина, а также нежелательных сточных вод [3].
Альтернативным способом получения 4-ТБПК является [4] селективное окисление 4-трет-бутилфенола (4-ТБФ) растворами пероксида водорода в присутствии титаносиликатных катализаторов, используемых в промышленном масштабе [5–7], что обусловлено их подтвержденной на практике способностью обеспечивать устойчивость и повышать селективность в реакциях окисления различных органических субстратов с использованием именно пероксида водорода. Из литературных источников [2, 8, 9] известно, что дробная подача окислителя, под которой в данном случае понимается введение пероксида водорода порционно в определенные моменты времени, способна оказывать влияние на эффективность реакции (в частности, может обеспечиваться сокращение расхода окислителя). Это обусловливает целесообразность определения оптимального режима дробной подачи пероксида водорода с позиций достижения заданных целевых критериев, в качестве которых в работе рассматривается максимизация выхода 4-ТБПК при минимальном расходе окислителя.
Решение поставленной задачи проводилось на основе численных экспериментов с кинетической моделью исследуемой реакции, что априори предполагало осуществление структурной и параметрической идентификации соответствующей модели химической кинетики. При этом специфика экспериментальных данных существенно ограничивала доступный инструментарий. Таким образом, цель настоящей работы состояла в разработке метода параметрической идентификации кинетической модели исследуемого процесса получения 4-трет-бутилпирокатехина, позволяющего уже на стадии определения констант скоростей реакции контролировать качество получаемой модели химической кинетики, с последующим определением на ее основе оптимального режима дробной подачи окислителя.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Эксперименты осуществлялись в лаборатории приготовления катализаторов Института нефтехимии и катализа РАН [4] на лабораторной установке с изотермическим реактором периодического действия, снабженным мешалкой, совершающей 200 оборотов в минуту, обратным холодильником и термометром. В реактор загружали 5 мл растворителя ацетонитрила, 0.09 г 4-ТБФ (начальная концентрация 4-ТБФ составляла 0.12 моль/л), 0.4 г катализатора (аморфный мезопористый титаносиликат, характеристики которого следующие: удельная поверхность 505 м2/г, объем мезопор 0.92 см3/г, диаметр пор 4 нм). При перемешивании термостатировали до заданной температуры, после чего дозировали требуемое количество 35% водного раствора Н2О2, начальная концентрация которого составляла 0.08 моль/л, и фиксировали время начала реакции. С интервалом в 20 мин после начала реакции в реактор равными порциями по 0.08 моль/л дважды добавлялся пероксид водорода. В эти же моменты времени, а также через 1 ч после начала эксперимента, брались пробы реакционной смеси для определения содержания 4-ТБФ, пероксида водорода и 4-ТБПК.
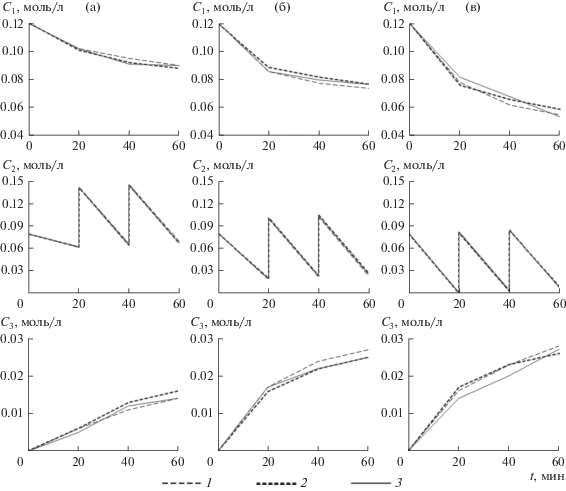
В соответствии с представленным описанием была проведена серия из трех независимых экспериментов при 35, 50 и 75°С (рис. 1), каждый из которых включал по три опыта.
СТРУКТУРНАЯ ИДЕНТИФИКАЦИЯ КИНЕТИЧЕСКОЙ МОДЕЛИ
Процесс получения 4-ТБПК является сложной химической реакцией, стехиометрические уравнения которой имеют следующий вид [10]:
(1)
$\begin{gathered} {{{\text{C}}}_{{{\text{10}}}}}{{{\text{H}}}_{{{\text{14}}}}}{\text{O}} + {{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}_{2}} = {{{\text{C}}}_{{{\text{10}}}}}{{{\text{H}}}_{{{\text{14}}}}}{{{\text{O}}}_{2}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}}, \\ 2{{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}_{2}} = 2{{{\text{H}}}_{{\text{2}}}}{\text{O}} + {{{\text{O}}}_{2}}. \\ \end{gathered} $Введем следующие обозначения: C1 – концентрация 4-ТБФ (C10H14O), C2 – концентрация пероксида водорода (H2O2), C3 – концентрация 4-ТБПК (C10H14O2), C4 – концентрация воды (H2O), C5 – концентрация кислорода (O2). Тогда матрица стехиометрических коэффициентов Г и молекулярная матрица A будут иметь вид
Кинетические уравнения реакции (1) записываются следующим образом:
где $C = {{\left\{ {{{C}_{1}},{{C}_{2}},{{C}_{3}},{{C}_{4}},{{C}_{5}}} \right\}}^{T}}$ – вектор концентраций, а $w = {{\left\{ {{{w}_{1}},{{w}_{2}}} \right\}}^{T}}$ – вектор скоростей.Справедливо следующее балансное соотношение:
В данном случае оно равносильно системе трех уравнений с пятью неизвестными:
С учетом исходных данных: а1 = 1.2 моль/л, а2 = 1.68 моль/л, а3 = 0.12 моль/л. (При проведении всех расчетов справедливость балансных соотношений контролировалась.) В силу переопределенности данной системы любые две переменные могут быть независимыми. В качестве таковых были выбраны первые две. Таким образом, используя выражения для скоростей реакции w1 и w2, система (2) представима в виде
где k1 и k2 – константы скорости реакции.МЕТОД ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ КИНЕТИЧЕСКОЙ МОДЕЛИ
Кинетическую модель реакции (1) можно считать построенной, если будут определены константы скоростей k1 и k2, что предполагает осуществление параметрической идентификации системы уравнений (3) на основании имеющихся экспериментальных данных. Подобные задачи, значительный интерес к которым проявляли классики физической химии [11], и сегодня привлекают большое внимание исследователей [12–19], в том числе в части анализа исходных данных [20–22]. В данном случае количество экспериментальных данных крайне мало – по четыре для каждого опыта, включая начальные данные, что обусловливает актуальность реализации контроля качества идентифицируемых зависимостей, на степень которого могут влиять как достигнутое качество математического описания, так и качество исходных данных.
В настоящей работе представлен нестатистический подход к построению математических моделей химической кинетики, в рамках которого параметрическая идентификация систем дифференциальных уравнений (3) осуществляется с учетом предъявляемых требований на значения показателей (критериев качества), отождествляемых с такими качественными характеристиками, как точность и устойчивость.
В самом общем случае под задачей определения качества модели химической кинетики будем подразумевать задание некоторого числового критерия и алгоритм его идентификации, позволяющего ответить на вопрос, описывает ли модель изучаемую химическую систему с требуемым уровнем качества [18], что соответствует попаданию значений введенного критерия качества внутрь заданного интервала. Единого подхода к выбору такого критерия не существует, однако, как правило, его вид определяется, исходя из целей исследования, и главным требованием к нему должна являться прозрачность трактовки [23]. С этих позиций и в соответствии с использованным в настоящем исследовании принципом равномерного приближения данных, критерии качества определялись на основе анализа невязок – модулей разности расчетных и экспериментальных данных.
Была поставлена следующая задача: найти интервалы значений констант скоростей $\left[ {k_{j}^{{min}},k_{j}^{{max}}} \right],$ j = 1, 2, которые обеспечивают приемлемые качественные характеристики кинетической модели, а именно – значения критериев, характеризующих точность и устойчивость.
Критерий точности по каждому уравнению системы (3) оценивался величиной средней ошибки аппроксимации:
Соответствующие критерии качества задавались неравенствами
где $\bar {A}_{1}^{*}$ и $\bar {A}_{2}^{*}$ – определяемые экспертно пороговые значения.При формировании критерия, характеризующего устойчивость, авторы исходили из того, что по результатам параметрической идентификации модели (3), проводимой по данным каждого отдельного опыта (при одинаковой температуре), интервалы значений констант скоростей не должны существенно отличаться, исходя из чего вид соответствующего критерия был определен следующим образом:
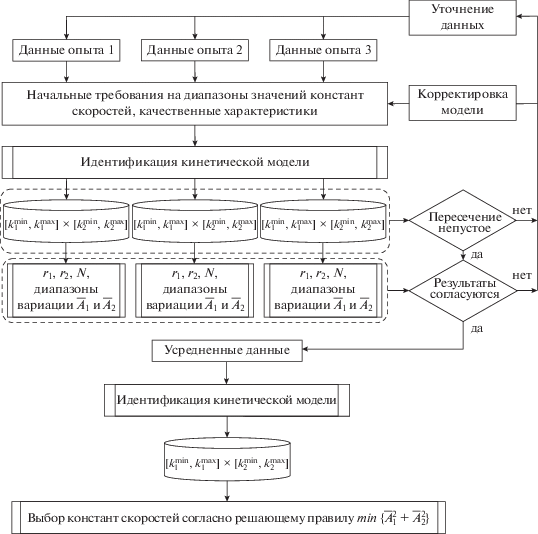
где rj – отношение длины отрезка, полученного в результате пересечения интервалов значений j-й константы скорости, рассчитанных по данным каждого отдельного опыта, к длине интервала начальных значений этой константы, выраженное в процентах, $r_{j}^{*}$ − минимально приемлемое значение критерия rj.В целях дополнительного контроля в рамках проведения анализа устойчивости осуществлялся подсчет количества узловых точек (N), попавших во множество значений констант скоростей, обеспечивающих заданные качественные характеристики кинетической модели (3), $\left[ {k_{1}^{{min}},k_{1}^{{max}}} \right]$ × $\left[ {k_{2}^{{min}},k_{2}^{{max}}} \right]$ (рис. 2).
Рис. 2.
Схема контроля качества в рамках идентификации кинетических моделей (3) при фиксированной температуре.
При использовании описанного выше подхода выполнение критерия точности, по сути, обеспечивает качество математического описания в рамках выбранной спецификации модели, а выполнение критерия устойчивости во многом определяется качеством исходных данных.
Параметрическая идентификация системы (3) проводилась на основе численного решения. В расчетах задавались пороговые значения $\bar {A}_{1}^{*},$ $\bar {A}_{2}^{*},$ $r_{1}^{*},$ $r_{2}^{*}$ и начальные диапазоны вариации констант скоростей, внутри которых вводились равномерные дискретные сетки.
РЕЗУЛЬТАТЫ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ
Полученные результаты (табл. 1) показали, что значения констант скоростей реакции из множеств $\left[ {k_{1}^{{min}},k_{1}^{{max}}} \right]$ × $\left[ {k_{2}^{{min}},k_{2}^{{max}}} \right]$, полученных на основе опытных данных при температуре 35 и 50°С, позволяют получить кинетические модели, обладающие хорошими качественными характеристиками: качество математического описания подтверждается приемлемыми значениями критерия точности, качество исходных данных – значениями критериев r1, r2 и N. Это позволило осуществить идентификацию модели (3) по совокупности всей имеющейся экспериментальной информации на основании усредненных данных серии опытов при одинаковой температуре с использованием введенного решающего правила (рис. 2).
Таблица 1.
Результаты параметрической идентификации модели (3)
| T, °С | Параметр/ критерий | Начальные диапазоны/ условия | Источник исходных данных | |||
|---|---|---|---|---|---|---|
| опыт 1 | опыт 2 | опыт 3 | усредненные данные | |||
| 35 | k1 | [0.01, 0.20] | [0.037, 0.111] | [0.044, 0.116] | [0.042, 0.116] | [0.040, 0.115] |
| k2 | [0.08, 0.24] | [0.118, 0.178] | [0.122, 0.179] | [0.125, 0,184] | [0.122, 0.181] | |
| ${{\bar {A}}_{1}}$, % | ≤12% | [5.23, 12.00] | [6.02, 12.00] | [6.74, 12.00] | [5.98, 12.00] | |
| ${{\bar {A}}_{2}}$, % | ≤12% | [8.48, 12.00] | [8.66, 12.00] | [8.71, 12.00] | [8.67, 12.00] | |
| r1, % | ≥30% | 35.3 | 39.5 | |||
| r2, % | ≥30% | 33.1 | 36.9 | |||
| N | – | 760 | 720 | 713 | 737 | |
| 50 | k1 | [0.13, 0,27] | [0.168, 0.270] | [0.137, 0.259] | [0.151, 0.256] | [0.151, 0.267] |
| k2 | [0.42, 0.70] | [0.476, 0.700] | [0.431, 0.672] | [0.448, 0.678] | [0.451, 0.689] | |
| ${{\bar {A}}_{1}}$, % | ≤12% | [10.62, 12.00] | [9.88, 12.00] | [11.06, 12.00] | [10.25, 12.00] | |
| ${{\bar {A}}_{2}}$, % | ≤12% | [0.54, 12.00] | [1.61, 12.00] | [1.06, 12.00] | [0.63, 12.00] | |
| r1, % | ≥30% | 62.9 | 82.9 | |||
| r2, % | ≥30% | 70.0 | 85.0 | |||
| N | – | 4279 | 4506 | 3824 | 4286 | |
| 75 | k1 | [1.0, 2.5] | [1.765, 2.215] | [1.975, 2.080] | [1.135, 1.810] | [1.510, 1,990] |
| k2 | [1.8, 3.0] | [2.112, 3.000] | [2.484, 2.736] | [1.810, 2.990] | [1.848, 2.952] | |
| ${{\bar {A}}_{1}}$, % | ≤33% | [24.12, 33.00] | [31.71, 33.00] | [13.48, 33.00] | [22.49, 33.00] | |
| ${{\bar {A}}_{2}}$, % | ≤33% | [22.46, 33.00] | [31.09, 33.00] | [14.56, 33.00] | [21.51, 33.00] | |
| r1, % | ≥30% | – | 32.0 | |||
| r2, % | ≥30% | 21.0 | 92.0 | |||
| N | – | 1211 | 69 | 2709 | 1470 | |
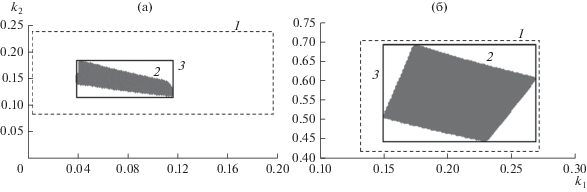
Для усредненных опытных данных при 35°С оптимальные значения констант скоростей k1 = 0.063, k2 = 0.168 (соответствующие средние ошибки аппроксимации ${{\bar {A}}_{1}} = 6.00{\text{\% }}$ и ${{\bar {A}}_{2}} = 11.87{\text{\% }}$), для усредненных опытных данных при 50°С – k1 = = 0.233, k2 = 0.535 (${{\bar {А}}_{1}} = 10.39{\text{\% ,}}$ ${{\bar {А}}_{2}} = 0.87{\text{\% }}$) (рис. 3).
Рис. 3.
Геометрическая интерпретация результатов идентификации модели (3) при T = 35 (а) и 50°С (б): 1 − границы начального приближения констант скоростей, 2 − множество значений констант скоростей, обеспечивающих достижение заданных качественных характеристик, 3 − границы этого множества.
Расчет констант скоростей k1 и k2 при 75°С с использованием уравнения Аррениуса
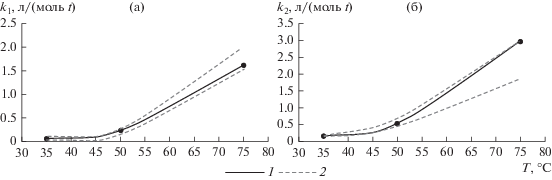
позволил установить, что полученные значения (${{k}_{1}}\left( {75^\circ {\text{С}}} \right) = 1.604,$ ${{k}_{2}}\left( {75^\circ {\text{С}}} \right) = 2.952$) в целом согласуются с интервалами, рассчитанными с применением представленного в статье метода параметрической идентификации, о чем свидетельствует их попадание в интервалы, рассчитанные по усредненным данным (табл. 1, рис. 4).
Рис. 4.
Анализ значений констант скоростей k1 (а) и k2 (б): 1 − кривые Аррениуса, 2 − границы областей значений констант скоростей согласно представленному методу параметрической идентификации.
Таким образом, было установлено, что идентификация модели (3) на основе данных при температуре 75°С не может быть осуществлена в силу недостаточно хорошего качества исходных данных. Именно по этой причине не удалось достичь удовлетворительных качественных характеристик, несмотря на то, что расчеты проводились при высоких (более 30%) пороговых значениях $\bar {A}_{i}^{*}$ для критериев точности (их уменьшение приводило к пустому интервалу значений констант скоростей для модели, описывающей данные второго опыта).
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО РЕЖИМА ПОДАЧИ ОКИСЛИТЕЛЯ
Решение задачи оптимизации дробной подачи пероксида водорода в исследованной реакции получения 4-ТБПК при 35 и 50°С осуществлялось на основе численных экспериментов с построенными кинетическими моделями.
Суть проводимых экспериментов состояла в том, чтобы оценить количество расходуемых 4-ТБФ и пероксида водорода в зависимости от того, какими порциями осуществляется подача окислителя в моменты времени 0, 20 и 40 мин. Целью являлось определение таких режимов, при которых как можно меньше расходуется пероксид водорода и как можно больше 4-ТБФ, количество которого в обратной пропорции влияет на выход 4-ТБПК.
В численных экспериментах количество подаваемого пероксида водорода варьировалось от 0.01 до 0.17 моль/л с шагом 0.01 моль/л. Таким образом, общее количество наборов режимов дробной подачи окислителя, подлежащих рассмотрению при каждой температуре, составило 173 = 4913.
По результатам численных экспериментов с кинетической моделью, построенной для данных при 35°С, было установлено, что даже незначительное сокращение концентраций 4-ТБФ и пероксида водорода в момент времени 60 мин возможно только за счет заметного увеличения количества подаваемого окислителя. Таким образом, при 35°С можно ставить вопрос только о суммарном сокращении расхода H2O2, при этом заметного увеличения расхода 4-ТБФ, а значит, и роста выхода 4-ТБПК не произойдет. Расчеты показали, что существует 6 режимов подачи окислителя, обеспечивающих его минимальный суммарный расход в количестве 0.22 моль/л (табл. 2).
Таблица 2.
Характеристика расчетных режимов дробной подачи окислителя с минимальным общим расходом H2O2 при 35°С
| C1, моль/л | C2 при t = 60 мин, моль/л | |||||
|---|---|---|---|---|---|---|
| при подаче | при t = 60 мин | абсолютное значение | изменение к фактическому среднему | |||
| t = 0 | t = 20 мин | t = 40 мин | абсолютное значение | изменение к фактическому среднему | ||
| 0.1400 | 0.0600 | 0.0200 | 0.0499 | –0.0184 (–26.9%) | 0.0893 | 0 |
| 0.1300 | 0.0700 | 0.0200 | 0.0507 | –0.0177 (–25.9%) | 0.0893 | 0 |
| 0.1400 | 0.0700 | 0.0100 | 0.0470 | –0.0213 (–31.2%) | 0.0892 | –0.0001 (–0.1%) |
| 0.1500 | 0.0600 | 0.010 | 0.0462 | –0.0221 (–32.4%) | 0.0892 | –0.0001 (–0.1%) |
| 0.1300 | 0.0800 | 0.0100 | 0.0478 | –0.0205 (–30.0%) | 0.0893 | 0 |
| 0.1600 | 0.0500 | 0.0100 | 0.0452 | –0.0231 (–33.8%) | 0.0893 | 0 |
Аналогичные численные эксперименты с кинетической моделью, построенной для данных при 50°С, также показали, что добиться к концу наблюдения реакции одновременного значимого увеличения расходов 4-ТБФ и пероксида водорода при сокращении суммарного расхода окислителя не представляется возможным. В данном случае были выявлены режимы с суммарным расходом окислителя от 0.14 до 0.36 моль/л. Однако в режимах с малыми значениями суммарного расхода пероксида водорода наблюдался незначительный расход 4-ТБФ. Наибольшего внимания, на взгляд авторов, заслуживают режимы с суммарным расходом H2O2 0.23 моль/л, обеспечивающие сокращение содержания 4-ТБФ и пероксида водорода в растворе к концу наблюдений (табл. 3).
Таблица 3.
Характеристика расчетных режимов дробной подачи окислителя с суммарным общим расходом 0.23 моль/л при 50°С, моль/л
| C1, моль/л | C2 при t = 60 мин, моль/л | |||||
|---|---|---|---|---|---|---|
| при подаче | при t = 60 мин | абсолютное значение | изменение к фактическому среднему | |||
| t = 0 | t = 20 мин | t = 40 мин | абсолютное значение | изменение к фактическому среднему | ||
| 0.1200 | 0.0900 | 0.0200 | 0.0181 | –0.0086 (–32.2%) | 0.0649 | –0.0111 (–14.6%) |
| 0.1100 | 0.100 | 0.0200 | 0.0183 | –0.0084 (–31.5%) | 0.0649 | –0.0111 (–14.6%) |
| 0.1200 | 0.0800 | 0.0100 | 0.0199 | –0.0068 (–25.5%) | 0.0646 | –0.0114 (–15.0%) |
| 0.130 | 0.0700 | 0.0100 | 0.0198 | –0.0069 (–25.8%) | 0.0647 | –0.0113 (–14.9%) |
Минимальное содержание 4-ТБФ в момент времени t = 60 мин при 35°С составляет 0.0746 моль/л, при 50°С – 0.0456 моль/л. Достигаются эти значения концентраций при максимально возможной подаче окислителя, т.е. по 0.17 моль/л через каждые 20 мин. При этом количество неизрасходованного пероксида водорода в конце наблюдений составило 0.0915 моль/л при 35°С и 0.0329 моль/л при 50°С, что существенно превышает фактические средние значения (в 6.2 раза и 1.3 раза соответственно).
ЗАКЛЮЧЕНИЕ
Представленный метод параметрической идентификации кинетических моделей с учетом их качественных характеристик позволил решить задачу оптимизации рассмотренного процесса получения 4-ТБПК и, как следствие, выявить недостаточную согласованность опытных данных, полученных при 75°С, и режимы подачи окислителя при 35 и 50°С, обеспечивающие сокращение концентраций 4-ТБФ и пероксида водорода к концу наблюдения реакции, при которых суммарный расход окислителя на 0.02 и 0.01 моль/л соответственно оказался меньше того, который имел место при проведении опытов.
Таким образом, можно утверждать, что представленный метод параметрической идентификации может быть рекомендован как метод многокритериальной оптимизации соответствующих процессов, применение которого позволяет в том числе анализировать качество опытных данных, что, в свою очередь, может составить основу стратегии планирования экспериментов в целях уточнения информационной базы исследования.
ОБОЗНАЧЕНИЯ
| A | молекулярная матрица |
| ${{\bar {A}}_{i}}$ | средняя ошибка аппроксимации i-го уравнения кинетической модели (3) (i = 1, 2) |
| $\bar {A}_{i}^{*}$ | пороговое значение средней ошибки аппроксимации ${{\bar {A}}_{i}};$С – вектор концентраций веществ |
| Ci | концентрация i-го вещества (i = 1, …, 5), моль/л |
| $C_{{i,t}}^{{эксп}}$ | экспериментальное значение концентрации Ci в момент времени t |
| $C_{{i,t}}^{{расч}}$ | расчетное значение концентрации Ci в момент времени t |
| kj | константа скорости реакции (j = 1, 2), л/(моль с) |
| $\left[ {k_{j}^{{min}},k_{j}^{{max}}} \right]$ | диапазон вариации значений константы скорости реакции |
| N | количество узловых точек в множестве $\left[ {k_{1}^{{min}},k_{1}^{{max}}} \right]$ × $\left[ {k_{2}^{{min}},k_{2}^{{max}}} \right]$ |
| rj | отношение длины отрезка, полученного в результате пересечения интервалов значений j-й константы скорости, рассчитанных по данным каждого отдельного опыта, к длине интервала начальных значений этой константы, выраженное в процентах |
| $r_{j}^{*}$ | минимально приемлемое значение rj |
| T | температура, °С |
| t | время, мин |
| w | вектор скоростей реакции |
| wi | скорость реакции, моль/(л с) |
| Г | матрица стехиометрических коэффициентов |
ИНДЕКСЫ
Список литературы
Гоготов А.Ф., Амосов В.В., Иванова А.В., Баранов О.И., Пученин Е.В., Вавилов А.В., Станкевич В.К. Промышленные испытания трет-бутилпирокатехина в качестве ингибитора в производствах ЭП-300 и “Пиротол” Ангарского завода полимеров // Нефтеперераб. нефтехим. 2004. № 3. С. 31.
Желовицкая А.В., Ермолаева Е.А., Дресвянников А.Ф. Окисление органических соединений с помощью гидроксид-радикала, генерируемого в растворах химическим и электрохимическими методами // Вестн. Казан. технол. унив. 2008. № 6. С. 211.
Хамис И., Назек И. Алкилирование пирокатехина // Хим. пром-сть. 1964. № 14. С. 245.
Talipova R.R., Kharrasov R.U., Agliullin M.R., Badikova A.D., Kutepov B.I. Selective oxidation of 4-tert-butylphenol by hydrogen peroxide in the presence of titanosilicates // Appl. Petrochem. Res. 2016. № 6. P. 419.
Arends I.W.C.E., Sheldon R.A. Activities and stabilities of heterogeneous catalysts in selective liquid phase oxidations: recent developments // Appl. Catal., A. 2001. V. 212. № 1–2. P. 175.
Liquid Phase Oxidation via Heterogeneous Catalysis: Organic Synthesis and Industrial Applications / Eds. Clerici M.G., Kholdeeva O.A. Hoboken, N.J.: Wiley, 2013.
Wu P., Kubota Y., Yokoi T. A career in catalysis: Takashi Tatsumi // ACS Catal. 2014. V. 4. P. 23.
Сложенко Е.Г., Соболева Н.М., Гончарук В.В. Применение каталитической системы H2O2 – ${\text{Fe}}_{2}^{ + }$(${\text{Fe}}_{3}^{ + }$) при очистке воды от органических соединений // Хим. технол. воды. 2004. Т. 26. № 3. С. 219.
Pignatello J.J. Dark and photoassisted iron(3+)-catalyzed degradation of chlorophenoxy herbicides by hydrogen peroxide // Environ. Sci. Technol. 1992. V. 26. № 5. P. 944.
Физическая химия. Теоретическое и практическое руководство / Под ред. Никольского Б.П. Л.: Химия, 1987.
Вант-Гофф Я.Г. Очерки по химической динамике. Л.: ОНТИ-Химтеорет, 1936.
Spivak S. Inverse problems of chemical kinetics and thermodynamics // Syst. Anal. Model. Simul. 1995. V. 18–19. P. 107.
Шаталов М.Ю., Демидов А.С., Федотов И.А. Оценка параметров уравнений химической кинетики по частичной информации об их решении // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 153.
Писаренко Е.В., Писаренко В.Н., Пономарев А.Б. Моделирование каталитического процесса изомеризации циклогексана в метилциклопентан // Теор. осн. хим. технол. 2017. Т. 51. № 2. С. 189.
Писаренко Е.В., Мазуренко А.А., Писаренко В.Н. Оптимизация процесса очистки этилена в этан-этиленовой фракции пирогаза // Усп. хим. хим. технол. 2016. Т. 30. № 4(173). С. 80.
Писаренко Е.В., Пономарев А.Б., Писаренко В.Н. Моделирование процесса гидроизомеризации н-пентана в 2-метилбутан на палладийсодержащем морденитном катализаторе // Теор. осн. хим. технол. 2018. Т. 52. № 4. С. 442.
Алиев А.М., Сафаров А.Р., Гусейнова А.М. Расчет химико-технологического комплекса по переработке газов крекинга и пиролиза на основе кинетических моделей процессов // Теор. осн. хим. технол. 2017. Т. 51. № 5. С. 569.
Сагдеев А.М., Галимова А.Т., Хазипов М.Р., Гумеров Ф.М., Саримов Н.Н. Математическое моделирование кинетики сверхкритической флюидной экстракционной регенерации гетерогенного катализатора // Теор. осн. хим. технол. 2018. Т. 52. № 1. С. 45.
Кантор О.Г., Спивак С.И., Талипова Р.Р. Параметрическая идентификация математических моделей химической кинетики // Сист. средства инф. 2017. Т. 27. № 3. С. 145.
Спивак С.И., Горский В.Г. Неединственность задачи восстановления кинетических констант // Докл. Акад. наук СССР. 1981. Т. 257. № 2. С. 412.
Горский В.Г., Спивак С.И. Степень полноты экспериментальной информации при восстановлении кинетических и равновесных констант сложных химических реакций // Математические методы химической термодинамики. Новосибирск, 1982. С. 139.
Спивак С.И., Горский В.Г. О полноте доступных кинетических измерений при определении констант скоростей сложной химической реакции // Хим. физ. 1982. № 2. С. 237.
Моисеев Н.Н. Математические задачи системного анализа М.: Наука, 1981.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии