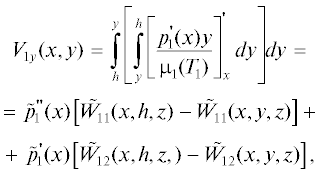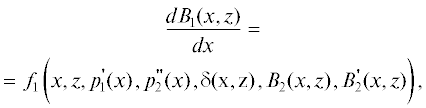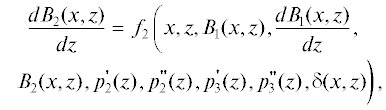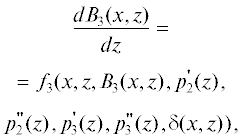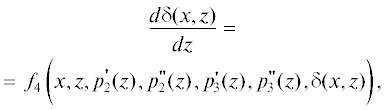Теоретические основы химической технологии, 2020, T. 54, № 4, стр. 463-474
Моделирование сопряженного тепломассообмена при пленочной конденсации
Ф. Г. Ахмадиев a, *, М. И. Фарахов b, А. А. Ахмитшин b
a Казанский государственный архитектурно-строительный университет
Казань, Россия
b ООО “Инженерно-внедренческий центр “Инжехим”
Казань, Россия
* E-mail: Akhmadiev@kgasu.ru
Поступила в редакцию 31.01.2020
После доработки 07.02.2020
Принята к публикации 14.02.2020
Аннотация
Построена математическая модель пленочной конденсации, полученная на основе уравнений сохранения массы, импульса и энергии, для хладагента в ограниченной области стекающей по поверхности стенки теплообменника пленки конденсата и газовой фазы, в двухмерной постановке. В уравнениях сохранения импульса данной модели учитывается изменение физических свойств хладагента и пленки конденсата в зависимости от температуры. Граничные условия сопряжения записаны для областей на внутренней стенке области течения хладагента, на внешней стенке, по которой течет пленка конденсата, а также на границе раздела пленка–газ. Полученная краевая задача решается приближенными и численными методами совместно с условием для определения неизвестной толщины пленки для различных постановок гидродинамической задачи. Проведены вычислительный и физический эксперименты с целью изучения основных параметров и закономерностей процесса.
ВВЕДЕНИЕ
Тепломассообменные процессы при конденсации и испарении (кипении) широко используются в различных областях техники и технологии при охлаждении различных рабочих поверхностей в технологических процессах, энергетике и др. Конденсация принадлежит к одному из наиболее распространенных технологических процессов. Процессы с конденсацией занимают большой удельный вес в химической технологии и смежных отраслях промышленности. Изучению различных аспектов процессов конденсации посвящены многочисленные работы, в том числе обзорные работы [1–6].
В зависимости от возможных механизмов образования конденсата различают следующие режимы конденсации [1]: пленочная, гомогенная и капельная конденсации; конденсации при непосредственном контакте и конденсация паров несмешивающихся жидкостей. Наиболее распространенным видом режимов в промышленных аппаратах является пленочная конденсация.
Успех в разработке и внедрении в промышленную практику принципиально новых технологических схем конденсации и высокоэффективных аппаратов, а также интенсификация работы существующих, возможны только при наличии современных точных и надежных методов их расчета, которые строятся на основе математических моделей соответствующих процессов. Математическое моделирование процессов тепломассообмена при конденсации представляет собой сложную задачу. В реальных конденсаторах имеет место сочетание различных гидродинамических режимов течения газа и пленки конденсата, например, происходит последовательное изменения режимов их течения. Математические модели тепломассопереноса при конденсации можно условно разделить на четыре класса [2].
К первой группе принадлежат решения систем сопряженных дифференциальных уравнений массы, импульса и энергии в приближениях теории пограничного слоя, которые дают возможность рассчитать профили температур, скоростей и концентраций в обеих фазах. В большинстве случаев это двухмерные плоские или осесимметричные задачи. Такая постановка задачи, видимо, является наиболее обоснованной и полной, хотя её решение вызывает большие математические трудности, и результаты решения трудно использовать непосредственно для практических целей. Развитие современных численных методов, программных продуктов и ЭВМ позволяет преодолеть многие возникающие трудности.
Ко второму классу относятся модели, предназначенные для инженерных расчетов реальных теплообменных аппаратов. При этом наиболее удобными в практике являются одномерные модели, описывающие изменения по длине осредненных по сечению характеристик потока жидкой фазы. Такие модели нередко получают на основе интегральных формулировок законов сохранения. Данный подход является определенным приближением описания процесса (“быстрый алгоритм”) и может служить основой для предварительных расчетов и дальнейшего развития теории.
К третьему классу можно отнести модели в приближении пограничного слоя с “отсосом”, когда рассматриваются параметры газового потока, а процесс конденсации моделируется отводом жидкости с поверхности твердой стенки [7, 8]. Они занимают как бы промежуточное положение между моделями первого и второго класса.
Модели четвертого класса представляют собой решения уравнений только для пленки конденсата, а воздействие газового потока в них учитывается заданием соответствующих граничных условий. Данный подход служит базой для сравнения с более поздними уточненными решениями и для дальнейшего развития методов расчета пленочной конденсации.
Первой теоретической работой по теплообмену при пленочной конденсации является работа Нуссельта [9], выполненная при целом ряде упрощающих допущений. В результате определялись толщины пленки, коэффициент теплоотдачи и количество сконденсированного газа (расход конденсата). Данная работа дала вполне удовлетворительные результаты и послужила базой для дальнейшего развития теории расчета плёночной конденсации. В работе [9] не учитывались выделение теплоты аккумуляции при охлаждении пленки, неизотермичность поверхности охлаждения и изменение физических свойств жидкости.
Впервые в постановке сопряженных пограничных слоев задачу конденсации исследовал Г.Г. Чёрный для случая вынужденного движения чистого пара [10], в которой также имеется строгий вывод граничных условий на поверхностях разрыва в произвольной сплошной среде из общих законов сохранения. Позднее данный подход был использован в других работах. Например, в [11] в сопряженной постановке численно решена задача нестационарного тепло- и массообмена в пленке стекающей жидкости в щелевом канале при сформулированных граничных условиях прилипания на стенке, симметрии и сопряжения с учетом кинетики испарения. Показано повышение эффективности процесса за счет использования нестационарного режима орошения.
Работы [12, 13] посвящены построению модели и изучению взаимного влияния микро- и макромасштабов при конкурирующих процессах химической конденсации в мелкодисперсной смеси реагирующего газа с твердыми частицами. Данная модель позволяет оценить фазовую структуру, динамику роста либо испарения частиц. На основе численных расчетов получены поля концентрации, температур, распределения фракций частиц мелкодисперсной твердой фазы. Влияние термической ректификации на укрепление смеси на контактных ступенях с низко интенсивным массообменом и вопросы интенсификации ректификации за счет целенаправленного воздействия на процесс термическими эффектами, вызванными испарением и конденсацией исследованы в [14]. Работа [15] посвящена расчету коэффициента конденсации (отношение числа сконденсировавшихся на поверхности частиц к числу частиц, упавших на эту поверхность) с позиции молекулярно-кинетической теории и в ней показано преимущество этого подхода его определения.
В [1, 2, 4, 6] приведены обзор и результаты исследований, в которых рассматриваются различные виды граничных условий на поверхности конденсации, с учетом изменения вязкости конденсата от температуры, переохлаждения жидкости, инерционных сил в уравнениях сохранения импульса, влияние перегрева пара, влияние турбулентности в различных постановках задачи исследования.
Много сделано для развития теории расчета процессов конденсации Д.А. Лабунцовым и его учениками [16–19].
В настоящее время исследования процессов пленочной конденсации в различных условиях продолжаются как аналитическими, так и численными методами на основе уравнений сохранения массы, импульса и энергии для жидкой (конденсат) и газовой фаз (пар), и получены определенные положительные результаты, например, в работах [20–26].
Авторами работы [22] исследована теплоотдача при конденсации и кипении в трубчатом испарителе с гладкой и шероховатой поверхностью при гравитационном стекании пленки воды. Получены зависимости для расчета величины коэффициента теплоотдачи, выявлено влияние на процесс теплообмена винтовой шероховатости. В [23] аналогично работе [9] исследовано неизотермическое течение пленки жидкости при конденсации в микроканалах с учетом скольжения скорости на стенке канала. Установлено, что толщина жидкой пленки уменьшается с увеличением коэффициента скольжения. Работа [24] посвящена исследованию численным методом конечных объемов модели конденсации пленки из турбулентной газопаровой смеси в осесимметричном нисходящем потоке в вертикальной трубе на основе уравнений сохранения массы, импульса и энергии в жидкой пленке и области смеси. При этом использованы три модели турбулентности. Исследовано влияние изменения входного числа Рейнольдса, разности температур между входом и на стенке и массовой доли газообразного газа для паровоздушных смесей на процесс пленочной конденсации.
Несмотря на многочисленные теоретические и экспериментальные исследования процессов пленочной конденсации в различных постановках сопряженный тепломассообмен при пленочной конденсации с учетом неизотермического течения хладагента внутри конденсатора, пленки конденсата и газовой фазы (пара) исследован недостаточно полно.
Целью данной работы является математическое моделирование пленочной конденсации с совместным учетом термогидродинамической обстановки в хладагенте в ограниченной области стекающей пленки конденсата и газового потока при изменении их физических свойств, а также экспериментальное изучение процесса.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
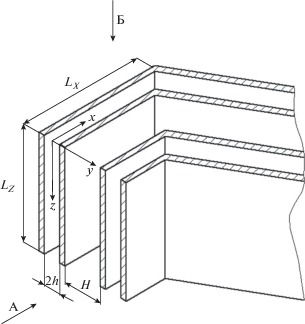
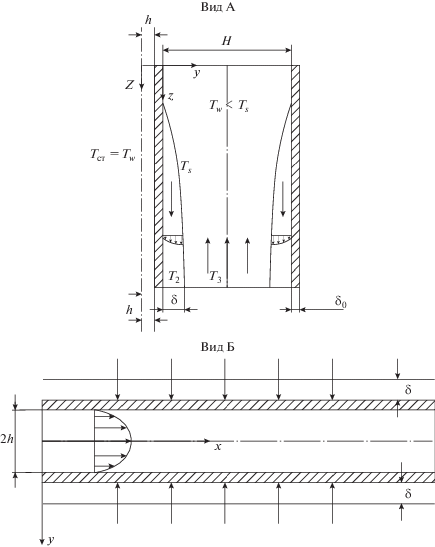
Рассматривается ламинарный установившийся режим пленочной конденсации, который может быть реализован, например, в конденсаторах, приведенных в [25]. Конденсатор (теплообменник) состоит из блоков, теплообменные элементы которых выполнены в форме прямой полой призмы из тонких металлических листов, с образованием внутреннего щелевого канала для теплоносителя (хладагента) (рис. 1, 2). Теплообменные элементы расположены друг к другу с образованием наружных вертикальных щелевых каналов для перемещения в аксиальном направлении теплоносителя – газа (пара).
При работе конденсатора хладагент течет внутри щелевого канала полой призмы. За счет охлаждения стенок канала и теплообмена через стенки канала с вертикально движущейся газовой фазой образуется пленка конденсата, которая стекает по поверхности канала (рис. 2).
В области течения хладагента и газа (рис. 2) выполняются соотношения ${{L}_{z}} \approx {{L}_{x}} \gg {\text{2}}h{\text{(}}H\,{\text{ > }}\,{\text{2}}h{\text{)}}$. Тогда исходная система уравнений, описывающая установившееся плоское ламинарное течение хладагента внутри призмы, пленки конденсата и газовой фазы (пара) в декартовой системе координат x, y, z записывается в виде
(1.1)
$\frac{{\partial {{V}_{{1x}}}}}{{\partial x}} + \frac{{\partial {{V}_{{1y}}}}}{{\partial y}} = 0,$(1.2)
$\begin{gathered} {{\rho }_{1}}\left( {{{V}_{{1x}}}\frac{{\partial {{V}_{{1x}}}}}{{\partial x}} + {{V}_{{1y}}}\frac{{\partial {{V}_{{1x}}}}}{{\partial y}}} \right) = \\ = - \frac{{\partial {{p}_{1}}}}{{\partial x}} + {{F}_{{1x}}} + \frac{\partial }{{\partial y}}\left( {{{\mu }_{1}}\frac{{\partial {{V}_{{1x}}}}}{{\partial y}}} \right), \\ \end{gathered} $(1.5)
${{\rho }_{1}}{{c}_{{1{{p}_{1}}}}}\left( {{{V}_{{1x}}}\frac{{\partial {{T}_{1}}}}{{\partial x}} + {{V}_{{1y}}}\frac{{\partial {{T}_{1}}}}{{\partial y}}} \right) = \frac{\partial }{{\partial y}}\left( {{{\lambda }_{1}}\frac{{\partial {{T}_{1}}}}{{\partial y}}} \right),$(2.1)
$\frac{{\partial {{V}_{{2y}}}}}{{\partial y}} + \frac{{\partial {{V}_{{2z}}}}}{{\partial z}} = 0,$(2.2)
$\begin{gathered} {{\rho }_{2}}\left( {{{V}_{{2y}}}\frac{{\partial {{V}_{{2z}}}}}{{\partial y}} + {{V}_{{2z}}}\frac{{\partial {{V}_{{2z}}}}}{{\partial z}}} \right) = \\ = - \frac{{\partial {{p}_{2}}}}{{\partial z}} + {{F}_{{2z}}} + \frac{\partial }{{\partial y}}\left( {{{\mu }_{2}}\frac{{\partial {{V}_{{2z}}}}}{{\partial y}}} \right), \\ \end{gathered} $(2.5)
${{\rho }_{2}}{{c}_{{2{{p}_{2}}}}}\left( {{{V}_{{2y}}}\frac{{\partial {{T}_{2}}}}{{\partial y}} + {{V}_{{2z}}}\frac{{\partial {{T}_{2}}}}{{\partial z}}} \right) = \frac{\partial }{{\partial y}}\left( {{{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial y}}} \right),$(3.1)
$\frac{{\partial {{V}_{{3y}}}}}{{\partial y}} + \frac{{\partial {{V}_{{3z}}}}}{{\partial z}} = 0,$(3.2)
$\begin{gathered} {{\rho }_{3}}\left( {{{V}_{{3y}}}\frac{{\partial {{V}_{{3z}}}}}{{\partial y}} + {{V}_{{3z}}}\frac{{\partial {{V}_{{3z}}}}}{{\partial z}}} \right) = \\ = - \frac{{\partial {{p}_{3}}}}{{\partial z}} + {{F}_{{3z}}} + \frac{\partial }{{\partial y}}\left( {{{\mu }_{3}}\frac{{\partial {{V}_{{3z}}}}}{{\partial y}}} \right), \\ \end{gathered} $(3.5)
${{\rho }_{3}}{{c}_{{3{{p}_{3}}}}}\left( {{{V}_{{3y}}}\frac{{\partial {{T}_{3}}}}{{\partial y}} + {{V}_{{3z}}}\frac{{\partial {{T}_{3}}}}{{\partial z}}} \right) = \frac{\partial }{{\partial y}}\left( {{{\lambda }_{3}}\frac{{\partial {{T}_{3}}}}{{\partial y}}} \right),$Здесь уравнения (1.1)–(1.5) описывают движение хладагента внутри полой прямой призмы, уравнения (2.1)–(2.5) течение стекающей пленки, а уравнения (3.1)–(3.5) движение газа (пара), а (3.6) – теплопередачу через стенку; ${{F}_{{1y}}} = {{F}_{{1x}}} = 0,$ ${{F}_{{1z}}} = {{\rho }_{1}}g;$ ${{F}_{{2y}}} = {{F}_{{2x}}} = 0,$ ${{F}_{{2z}}} = {{\rho }_{2}}g;$ ${{F}_{{3x}}} = {{F}_{{3y}}} = 0,$ ${{F}_{{3z}}} = {{\rho }_{3}}g;$ ${{\mu }_{i}} = {{\mu }_{i}}({{T}_{i}}),$ $i = \overline {1,3} $ (учитывается только изменение вязкости от температуры), индексы 1, 2, 3 соответственно относятся к хладагенту, пленке жидкости и газовой фазе.
Данная система уравнений решается при соответствующих граничных условиях, причем граничные условия на поверхности конденсации могут иметь разные формулировки в зависимости от реальных условий работы конденсаторов, которые имеют следующий вид:
(4.1)
$\frac{{\partial {{V}_{{1x}}}}}{{\partial y}} = 0,\,\,\,\frac{{\partial {{T}_{1}}}}{{\partial y}} = 0,\,\,\,{{V}_{{1y}}} = 0\,\,\,{\text{при}}\,\,\,y = 0;$(4.2)
$\begin{gathered} {{V}_{{1x}}} = {{V}_{{1y}}} = 0,\,\,\,{{\lambda }_{1}}\frac{{\partial {{T}_{1}}}}{{\partial y}} = {{\lambda }_{4}}\frac{{\partial {{T}_{4}}}}{{\partial y}}\,\,\,{\text{при}}\,\,\,y = \pm h; \\ {{T}_{4}} = {{T}_{2}},\,\,\,{{\lambda }_{4}}\frac{{\partial {{T}_{4}}}}{{\partial y}} = {{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial y}},\,\,\,{{V}_{{2y}}} = {{V}_{{2z}}} = 0, \\ \end{gathered} $(4.3)
$\begin{gathered} - {{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial y}} = \alpha ({{T}_{{10}}} - {{T}_{{{\text{cт}}}}}) \approx \alpha ({{T}_{{1{\text{ср}}}}} - {{T}_{{4{\text{ср}}}}}) \\ {\text{при}}\,\,\,y = h + {{\delta }_{0}}, \\ {{\mu }_{2}}\frac{{\partial {{V}_{{2z}}}}}{{\partial y}} = {{\mu }_{3}}\frac{{\partial {{V}_{{3z}}}}}{{\partial y}} + \frac{{d{{\sigma }_{2}}}}{{\partial z}},\,\,\,{{V}_{{2z}}} = {{V}_{{3z}}}, \\ {{T}_{2}} = {{T}_{3}} = {{T}_{{2S}}},\,\,\,{{p}_{2}} = {{p}_{3}} + {{\sigma }_{2}}\frac{{{{d}^{2}}\delta }}{{d{{z}^{2}}}} \\ \end{gathered} $при
(4.5)
$\begin{gathered} \frac{{\partial {{T}_{3}}}}{{\partial y}} = 0,\,\,\,\frac{{\partial {{V}_{{3z}}}}}{{\partial y}} = 0,{{V}_{{3y}}} = 0 \\ {\text{при}}\,\,\,y = {{\delta }_{1}} = h + {{\delta }_{0}} + \frac{H}{2}; \\ \end{gathered} $(5.1)
${{V}_{{1x}}} = {{V}_{{1xvх}}},\,\,\,{{T}_{1}} = {{T}_{{1vх}}},\,\,\,{{р}_{1}} = {{р}_{{1vх}}}\,\,\,{\text{при}}\,\,\,x = {{x}_{{vх}}};$(5.2)
${{V}_{{2z}}} = {{V}_{{2zvх}}},\,\,\,{{T}_{2}} = {{T}_{{2vх}}}\,\,\,{\text{при}}\,\,\,z = {{z}_{{vх}}} = {{z}_{0}};$(5.3)
$\begin{gathered} {{V}_{{3z}}} = {{V}_{{3zvх}}},\,\,\,{{T}_{3}} = {{T}_{{3vх}}},\,\,\,{{V}_{{3y}}} = 0, \\ {{р}_{3}} = {{р}_{{3{\text{v}}х}}}\,\,\,{\text{при}}\,\,\,z = {{L}_{z}}, \\ \end{gathered} $(5.4)
$\begin{gathered} {{T}_{{10}}} \approx {{T}_{{1{\text{ср}}}}} = \frac{1}{h}\int\limits_0^h {{{T}_{1}}dy = {{B}_{1}}\frac{{{{h}^{2}}}}{6}} + {{C}_{1}}, \\ {{T}_{{{\text{ст}}}}} \approx {{T}_{{4{\text{ср}}}}} = \frac{1}{{{{\delta }_{0}}}}\int\limits_h^{h + {{\delta }_{0}}} {{{T}_{4}}dy = {{C}_{4}}\left( {h + \frac{{{{\delta }_{0}}}}{2}} \right)} + {{C}_{5}}. \\ \end{gathered} $Решение краевой задачи (1.1)–(1.5), (2.1)–(2.5), (3.1)–(3.6), (4.1)–(4.5) и (5.1)–(5.3) представляет собой сложную математическую задачу. Поэтому рассмотрим решение этой задачи в некоторых конкретных частных случаях.
I. Конденсация при медленных режимах течения (Re $ \ll $ 1). В этом случае задача существенно упрощается и в уравнениях сохранения импульса можно пренебречь левыми частями (инерционными членами). Такие режимы течения выполняются во многих случаях пленочной конденсации и уравнения сохранения (1.1)–(1.5), (2.1)–(2.5), (3.1)–(3.6) удается проинтегрировать (решить) при граничных условиях (4.1)–(4.5) и (5.1)–(5.3).
Алгоритм решения уравнений (1.1)–(1.5), (2.1)–(2.5), (3.1)–(3.6):
1. Из уравнений (1.3)–(1.4), (2.3)–(2.4), (3.3)–(3.4) соответственно следует, что
(6)
${{р}_{1}}(x,z) = {{\rho }_{1}}gz + {{р}_{1}}(x),\,\,\,{{р}_{2}} = {{р}_{2}}(z),\,\,\,{{р}_{3}} = {{р}_{3}}(z),$2. Для интегрирования уравнений сохранения энергии (1.5), (2.5), (3.5) используем приближенный метод Слезкина [26], согласно которому соответственно вводятся функции
(7.1)
${{B}_{1}}(x,z) = \frac{{{{\rho }_{1}}{{c}_{{1{{p}_{1}}}}}}}{{{{\lambda }_{1}}h}}\int\limits_0^h {\left( {{{V}_{{1x}}}\frac{{\partial {{T}_{1}}}}{{\partial x}} + {{V}_{{1y}}}\frac{{\partial {{T}_{1}}}}{{\partial y}}} \right)} dy,$(7.2)
${{B}_{2}}(x,z) = \frac{{{{\rho }_{2}}{{c}_{{2{{p}_{2}}}}}}}{{{{\lambda }_{2}}\delta }}\int\limits_{h + {{\delta }_{0}}}^{h + {{\delta }_{0}} + \delta } {\left( {{{V}_{{2y}}}\frac{{\partial {{T}_{2}}}}{{\partial y}} + {{V}_{{2z}}}\frac{{\partial {{T}_{2}}}}{{\partial z}}} \right)} dy,$(7.3)
${{B}_{3}}(x,z) = \frac{{{{\rho }_{3}}{{c}_{{3{{p}_{3}}}}}}}{{{{\lambda }_{3}}\left( {\frac{H}{2} - \delta } \right)}}\int\limits_{h + {{\delta }_{0}} + \delta }^{h + {{\delta }_{0}} + \frac{H}{2}} {\left( {{{V}_{{3y}}}\frac{{\partial {{T}_{3}}}}{{\partial y}} + {{V}_{{3z}}}\frac{{\partial {{T}_{3}}}}{{\partial z}}} \right)} dy,$Тогда после интегрирования уравнений
${{B}_{1}}(x,z) = \frac{{{{\partial }^{2}}{{T}_{1}}^{2}}}{{\partial {{y}^{2}}}},$ ${{B}_{2}}(x,z) = \frac{{{{\partial }^{2}}{{T}_{2}}}}{{\partial {{y}^{2}}}},$ ${{B}_{3}}(x,z) = \frac{{{{\partial }^{2}}{{T}_{3}}}}{{\partial {{y}^{2}}}}$ и ${{\lambda }_{4}}\frac{{{{\partial }^{2}}{{T}_{4}}}}{{\partial {{y}^{2}}}} = 0$ при соответствующих граничных условиях получаются следующие выражения для температур ${{T}_{1}},{{T}_{2}}$ и ${{T}_{3}},{{T}_{4}}$:
(8.1)
$\begin{gathered} {{T}_{1}} = {{B}_{1}}(x,z)\frac{{{{y}^{2}}}}{2} + {{C}_{1}}, \\ {{T}_{2}} = {{B}_{2}}(x,z)\frac{{{{y}^{2}}}}{2} + {{C}_{2}}y + {{{\tilde {C}}}_{2}}, \\ {{T}_{3}} = {{B}_{3}}(x,z)\left( {\frac{{{{y}^{2}}}}{2} - {{\delta }_{1}}y} \right) + {{C}_{3}}, \\ {{T}_{4}} = {{C}_{4}}y + {{C}_{5}},\,\,\,{{\delta }_{1}} = h + {{\delta }_{0}} + \frac{H}{2}, \\ \end{gathered} $(8.2)
${{C}_{2}}(x,z) = \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}{{B}_{1}}h - {{B}_{2}}(h + {{\delta }_{0}}),$(8.4)
$\begin{gathered} {{{\tilde {С}}}_{2}}\left( {x,z} \right) = {{T}_{{2S}}} - \frac{{{{{(h + {{\delta }_{0}} + \delta (z))}}^{2}}}}{2} - \\ - \,\,{{C}_{2}}(h + {{\delta }_{0}} + \delta (z)), \\ \end{gathered} $(8.5)
$\begin{gathered} {{C}_{5}}(x,z) = \frac{{{{B}_{2}}}}{2}{{(h + {{\delta }_{0}})}^{2}} + \\ + \,\,{{C}_{2}}(h + {{\delta }_{0}}) - {{C}_{4}}(h + {{\delta }_{0}}) + {{{\tilde {С}}}_{2}}, \\ \end{gathered} $(8.6)
$\begin{gathered} {{C}_{1}}(x,z) = - \frac{{{{\lambda }_{2}}}}{\alpha }\left[ {{{B}_{2}}(h + {{\delta }_{0}}) + {{C}_{2}}} \right] + \\ + \,\,{{C}_{4}}\left( {h + \frac{{{{\delta }_{0}}}}{2}} \right) - {{B}_{1}}\frac{{{{h}^{2}}}}{6} - {{C}_{5}}, \\ \end{gathered} $(8.7)
$\begin{gathered} {{C}_{3}}\left( {x,z} \right) = {{T}_{{2S}}} - {{B}_{3}} \times \\ \times \,\,\left[ {\frac{{{{{\left( {h + {{\delta }_{0}} + \delta } \right)}}^{2}}}}{2} - {{\delta }_{1}}\left( {h + {{\delta }_{0}} + \delta } \right)} \right]. \\ \end{gathered} $3. Из уравнений (1.1)–(1.2), (2.1)–(2.2), (3.1)–(3.2) определяются поля скоростей ${{V}_{{1x}}},\,{{V}_{{1y}}},\,{{V}_{{2y}}},\,{{V}_{{2z}}},\,{{V}_{{3y}}},\,{{V}_{{3z}}}$ при известных зависимостях температуры ${{T}_{1}},{{T}_{2}},{{T}_{3}}$ (8.1). При этом были использованы полиномиальные зависимости вязкостей ${{\mu }_{i}}({{T}_{i}})$ от температуры
(9.1)
$\frac{{{{\mu }_{i}}({{T}_{{i0}}})}}{{{{\mu }_{i}}({{T}_{i}})}} = 1 + \sum\limits_{k = 1}^{{{n}_{i}}} {{{\alpha }_{{ik}}}\tilde {T}_{{ik}}^{k}} ,\,\,\,\left( {{{{\tilde {T}}}_{i}} = {{T}_{i}} - {{T}_{{i0}}}} \right).$3.1. Например, из уравнения (1.2) определяется ${{V}_{{1x}}}$ с учетом зависимости (9.1):
(9.2)
$\begin{gathered} {{V}_{{1x}}}(x,y) = \int\limits_h^y {\frac{{p_{1}^{'}(x)y}}{{{{\mu }_{1}}({{T}_{1}})}}dy} = \tilde {p}{{_{{}}^{'}}_{1}}(x)\left\{ {\frac{{\left( {{{y}^{2}} - {{h}^{2}}} \right)}}{2}} \right. + \\ + \,\,{{a}_{{11}}}\left[ {{{W}_{{11}}}\left( {x,y,z} \right) - {{W}_{{11}}}\left( {x,h,z} \right)} \right] + \\ \left. {\frac{{^{{^{{^{{}}}}}}}}{{_{{_{{}}}}}} + \,\,{{a}_{{12}}}\left[ {{{W}_{{12}}}\left( {x,y,z} \right) - {{W}_{{12}}}\left( {x,h,z} \right)} \right]} \right\}, \\ \end{gathered} $3.2. При известном ${{V}_{{1x}}}(x,y)$ из уравнения (1.1) после соответствующих операций дифференцирования и интегрирования с учетом граничного условия ${{V}_{{1y}}}(x,h) = 0$ определяется поперечная скорость ${{V}_{{1y}}}(x,y)$ в виде
где(10.2)
$\begin{gathered} {{{\tilde {W}}}_{{11}}}(x,y,z) = \left( {\frac{{{{h}^{2}}y}}{2} - \frac{{{{y}^{3}}}}{6}} \right) + \\ + \,\,{{a}_{{11}}}\left[ {{{B}_{1}}\left( {\frac{{{{h}^{4}}y}}{8} - \frac{{{{y}^{5}}}}{{40}}} \right) + \left( {{{C}_{1}} - {{T}_{{10}}}} \right)\left( {\frac{{{{y}^{3}}}}{6} - \frac{{{{h}^{2}}y}}{2}} \right)} \right] + \\ + \,\,{{a}_{{12}}}\left[ {B_{1}^{2}\left( {\frac{{{{y}^{7}}}}{{168}} - \frac{{{{h}^{6}}y}}{{24}}} \right) + 2{{B}_{1}}\left( {{{C}_{1}} - {{T}_{{10}}}} \right)} \right. \times \\ \times \,\,\left( {\frac{{{{y}^{5}}}}{{40}} - \frac{{{{h}^{4}}y}}{8}} \right) + \left. {{{{\left( {{{C}_{1}} - {{T}_{{10}}}} \right)}}^{2}}\left( {\frac{{{{y}^{3}}}}{6} - \frac{{{{h}^{2}}y}}{2}} \right)} \right], \\ \end{gathered} $(10.3)
$\begin{gathered} {{{\tilde {W}}}_{{12}}}(x,y,z) = \\ = \,\,{{a}_{{11}}}\left[ {B_{1}^{'}\left( {\frac{{{{h}^{4}}y}}{8} - \frac{{{{y}^{5}}}}{{40}}} \right) + C_{1}^{'}\left( {\frac{{{{y}^{3}}}}{6} - \frac{{{{h}^{2}}y}}{2}} \right)} \right] + \\ + \,\,{{a}_{{12}}}\left[ {2{{B}_{1}}B_{1}^{'}\left( {\frac{{{{y}^{7}}}}{{168}} - \frac{{{{h}^{6}}y}}{{24}}} \right) + 2B_{1}^{'}\left( {{{C}_{1}} - {{T}_{{10}}}} \right)} \right. \times \\ \times \,\,\left( {\frac{{{{y}^{5}}}}{{40}} - \frac{{{{h}^{4}}y}}{8}} \right) + 2{{B}_{1}}C_{1}^{'}\left( {\frac{{{{y}^{5}}}}{{40}} - \frac{{{{h}^{4}}y}}{8}} \right) + \\ \left. { + \,\,2C_{1}^{'}\left( {{{C}_{1}} - {{T}_{{10}}}} \right)\left( {\frac{{{{y}^{3}}}}{6} - \frac{{{{h}^{2}}y}}{2}} \right)} \right], \\ \end{gathered} $знак “ ' ” означает производную по x.
3.3. Аналогичным образом определяются поля скоростей ${{V}_{{2y}}},{{V}_{{2z}}},{{V}_{{3y}}},{{V}_{{3z}}}$ по уравнениям (2.1)–(2.2), (3.1)–(3.2) при соответствующих граничных условиях:
(11.1)
$\begin{gathered} {{V}_{{2z}}}(y,z) = \int\limits_{h + {{\delta }_{0}}}^y {\frac{{\left( {\rho _{2}^{'}(z) - {{F}_{{2z}}}} \right)y + {{C}_{6}}}}{{{{\mu }_{2}}({{T}_{2}})}}} dy = \\ = \tilde {p}_{2}^{'}(z)\left[ {{{W}_{{21}}}\left( {x,y,z} \right) - {{W}_{{21}}}\left( {x,h + {{\delta }_{0}},z} \right)} \right] + \\ + \,\,\frac{{{{C}_{6}}}}{{{{\mu }_{2}}({{T}_{{20}}})}}\left[ {{{W}_{{22}}}\left( {x,y,z} \right) - {{W}_{{22}}}\left( {x,h + {{\delta }_{0}},z} \right)} \right], \\ \end{gathered} $(11.2)
$\begin{gathered} {{W}_{{21}}}(x,y,z) = {{y}^{2}} + {{a}_{{21}}} \times \\ \times \,\,\left[ {{{B}_{2}}\left( z \right)\frac{{{{y}^{4}}}}{8} + {{C}_{2}}\frac{{{{y}^{3}}}}{3} + \left( {{{{\tilde {C}}}_{2}} - {{T}_{{10}}}} \right)\frac{{{{y}^{2}}}}{2}} \right] + \\ + \,\,{{a}_{{22}}}\left[ {B_{2}^{2}\left( z \right)\frac{{{{y}^{6}}}}{{24}} + C_{2}^{2}\frac{{{{y}^{4}}}}{3} + {{{\left( {{{{\tilde {C}}}_{2}} - {{T}_{{10}}}} \right)}}^{2}}\frac{{{{y}^{2}}}}{2} + } \right. \\ + \,{{B}_{2}}\left( z \right){\kern 1pt} {{C}_{2}}\frac{{{{y}^{5}}}}{5} + {{B}_{2}}\left( z \right) \times \\ \times \,\,\left( {{{{\tilde {C}}}_{2}} - {{T}_{{10}}}} \right)\frac{{{{y}^{4}}}}{4} + 2\left. {\left( {{{{\tilde {C}}}_{2}} - {{T}_{{10}}}} \right)\frac{{{{y}^{3}}}}{3}} \right], \\ \end{gathered} $(11.3)
$\begin{gathered} {{V}_{{2y}}}\left( {x,y,z} \right) = - \int\limits_{h + {{\delta }_{0}}}^y {\frac{{\partial {{V}_{{2z}}}}}{{\partial z}}} dy \\ {\text{с учетом граничного условия}} \\ {{V}_{{2z}}}\left( {x,y,z} \right) = 0\,\,\,\,{\text{при}}\,\,\,\,y = h + {{\delta }_{0}}; \\ \end{gathered} $(11.4)
$\begin{gathered} {{V}_{{3z}}}\left( {x,y,z} \right) = \int {\frac{{\left( {p_{3}^{'}(z) - {{F}_{{3z}}}} \right)}}{{{{\mu }_{3}}({{T}_{3}})}}} \left( {y - {{\delta }_{1}}} \right)dy + {{C}_{8}} = \\ = \frac{{\left( {p_{3}^{'}(z) - {{F}_{{3z}}}} \right)}}{{{{\mu }_{3}}({{T}_{{30}}})}}\left\{ {\left( {\frac{{{{y}^{2}}}}{2} - {{\delta }_{1}}y} \right)} \right. + \\ + \,\,{{a}_{{31}}}\left[ {{{B}_{3}}(z)\left( {\frac{{{{y}^{4}}}}{8} - \frac{{{{\delta }_{1}}{{y}^{3}}}}{2} + \frac{{\delta _{1}^{2}{{y}^{2}}}}{3}} \right)} \right. + \\ \left. { + \,\,\left( {{{C}_{3}} - {{T}_{{30}}}} \right)\left( {\frac{{{{y}^{2}}}}{2} - {{\delta }_{1}}y} \right)} \right] + \\ + \,\,{{a}_{{32}}}\left[ {B_{3}^{2}(z)\left( {\frac{{{{y}^{6}}}}{{24}} - \frac{{{{\delta }_{1}}{{y}^{5}}}}{4} + \frac{{\delta _{1}^{2}{{y}^{4}}}}{2} - \frac{{\delta _{1}^{3}{{y}^{3}}}}{3}} \right)} \right. + \\ + \,\,2B_{3}^{{}}(z)\left( {{{C}_{3}} - {{T}_{{30}}}} \right)\left( {\frac{{{{y}^{4}}}}{8} - \frac{{{{\delta }_{1}}{{y}^{3}}}}{2} + \frac{{\delta _{1}^{2}{{y}^{2}}}}{3}} \right) + \\ \left. {\left. { + \,\,{{{\left( {{{C}_{3}} - {{T}_{{30}}}} \right)}}^{2}}\left( {\frac{{{{y}^{2}}}}{2} - {{\delta }_{1}}y} \right)} \right]} \right\} + {{C}_{8}} = \\ = {{{\tilde {V}}}_{{3z}}}\left( {x,y,z} \right) + {{C}_{8}}, \\ \end{gathered} $(11.5)
$\begin{gathered} {{C}_{8}} = {{V}_{{2z}}}\left( {x,h + {{\delta }_{0}} + \delta (z),z} \right) - \\ - \,\,{{{\tilde {V}}}_{{3z}}}\left( {x,h + {{\delta }_{0}} + \delta (z),z} \right); \\ \end{gathered} $(11.6)
$\begin{gathered} {{V}_{{3y}}}\left( {x,y,z} \right) = - \int\limits_{{{\delta }_{1}}}^y {\frac{{\partial {{V}_{{3z}}}}}{{\partial z}}} dy\,\, \\ {\text{с учетом граничного условия}} \\ {{V}_{{3z}}}\left( {x,{{\delta }_{1}},z} \right) = 0. \\ \end{gathered} $4. Во всех полученных выражениях (8.1)–(8.7), (9.2)–(9.3), (10.1)–(10.3), (11.1)–(11.6) для определения полей температур и скоростей присутствуют пока неизвестные величины ${{B}_{1}}(x,z),$ ${{B}_{2}}(x,z),$ ${{B}_{3}}(x,z)$ и $\delta (x,z)$. Для их определения используются зависимости (7.1)–(7.3) и условие изменения расхода конденсата $Q$ по высоте конденсатора (теплообменника) z с учетом потока массы при конденсации ${{Q}_{g}}$ и равенства теплового потока к стенке с тепловым потоком при охлаждении пара (газа) и выделенного скрытой теплотой парообразования, освобождаемой во время конденсации пара (уравнение баланса энергии в пленке конденсата):
$\frac{{dQ}}{{dz}} = {{Q}_{g}}$ – массовая скорость конденсации,
$Q = {{\rho }_{2}}\int\limits_{h + {{\delta }_{0}}}^{h + {{\delta }_{0}} + \delta } {{{V}_{{2z}}}dy} $ – расход конденсата в пленке, где ${{Q}_{g}}$ определяется из соотношения
${{T}_{{2s}}},{{T}_{w}} = {{T}_{{{\text{ст}}}}}$ – температура пленки на межфазной поверхности пленки (температура насыщения) и стенки соответственно.
В результате получается система из четырех нелинейных дифференциальных уравнений, которая решается численными методами Рунге–Кутты (Гира) четвертого порядка с проверкой устойчивости и сходимости решения.
5. Неизвестные величины перепадов давлений $p_{1}^{'}(z),p_{2}^{'}(z),p_{3}^{'}(z)$, присутствующие в полученных решениях, пересчитываются на каждом шаге численных расчетов из условий баланса (сохранения) массы хладагента, конденсата и газовой фазы с учетом процесса конденсации.
ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ АЛГОРИТМА И СТРУКТУРА ПРОГРАММЫ ДЛЯ ПРОВЕДЕНИЯ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА
1. После подстановки полученных выражений для ${{V}_{{1x}}},{{V}_{{1y}}},{{V}_{{2z}}},$ ${{V}_{{2y}}},{{V}_{{3z}}},{{V}_{{3y}}},$ ${{T}_{1}},{{T}_{2}},{{T}_{3}}$ по алгоритму решения задачи (1.1)–(1.5), (2.1)–(2.5), (3.1)–(3.5), (3.6) при граничных условиях (4.1)–(4.5) и (5.1)–(5.3) в соотношения (7.1)–(7.3) и (11) для нахождения значений четырех пока неизвестных величин ${{B}_{1}}(x,z),\,\,{{B}_{2}}(x,z),$ ${{B}_{3}}(x,z)$ и $\delta (x,z)$ получаем следующую систему дифференциальных уравнений:
где зависимости ${{f}_{1}},{{f}_{2}},{{f}_{3}},{{f}_{4}}$ определяются по решениям (7)–(11).В системе дифференциальных уравнений (12.1)–(12.4) первое уравнение представляет собой дифференциальное уравнение первого порядка относительно производной функции ${{B}_{1}}(x,z)$ по переменной $x$. Три других уравнения представляют дифференциальные уравнения первого порядка относительной функций ${{B}_{2}}(x,z),$ ${{B}_{3}}(x,z),$ $\delta (x,z)$ по переменной $z$.
2. Порядок численного решения системы дифференциальных уравнений (12.1)–(12.4) следующий. Плоскость $\left( {x,z} \right)$ разбивается сеткой на узловые точки ${{x}_{i}}\left( {i = \overline {0,n} } \right)$, ${{z}_{j}}\left( {j = \overline {0,m} } \right)$. Узел $({{x}_{0}},{{z}_{0}})$ помещается в начало координат (0,0), а $({{x}_{n}},{{z}_{m}})$ в точку $({{L}_{x}},{{L}_{z}})$. Система дифференциальных уравнений (12.1)–(12.4) описывает двумерную задачу. Для ее решения применяется следующий подход: ее решение сводится к решению двух одномерных задач. Плоскость $\left( {x,z} \right)$ разбивается (прямоугольник $\left( {{{L}_{x}} \times {{L}_{z}}} \right)$) сеткой на узловые точки $({{x}_{i}},{{z}_{j}})\,\,i = \overline {0,n} ;\,\,j = \overline {0,m} $. Шаг между узловыми точками вдоль оси Ох – ${{h}_{x}} = {{{{L}_{x}}} \mathord{\left/ {\vphantom {{{{L}_{x}}} n}} \right. \kern-0em} n}$; шаг между узловыми точками вдоль оси Оz – ${{h}_{z}} = {{{{L}_{z}}} \mathord{\left/ {\vphantom {{{{L}_{z}}} m}} \right. \kern-0em} m}$. Фиксируется начальное сечение вдоль оси Ох – ${{x}_{0}} = {{x}_{{vх}}}$. Для ${{x}_{0}}$ и ${{z}_{0}}$ вычисляются значения ${{B}_{1}}({{x}_{0}},{{z}_{0}}),$ ${{B}_{3}}({{x}_{0}},{{z}_{0}})$. Поскольку в сечении ${{z}_{0}}$ для всех ${{x}_{i}}\,\,\delta \left( {{{x}_{i}},{{z}_{0}}} \right) = 0$, поэтому ${{B}_{2}}\left( {{{x}_{i}},{{z}_{0}}} \right) = 0$. В результате для нахождения значений ${{B}_{2}}\left( {{{x}_{{vх}}},{{z}_{j}}} \right),$ ${{B}_{3}}\left( {{{x}_{{vх}}},{{z}_{j}}} \right),$ $\delta \left( {{{x}_{{vх}}},{{z}_{j}}} \right),$ $\left( {j = \overline {1,m} } \right)$ получается задача Коши для системы из трех дифференциальных уравнений первого порядка.
Далее методом Рунге–Кутты решается задача Коши для системы (12.2)–(12.4) и определяются значения функций ${{B}_{2}}\left( {{{x}_{{vх}}},{{z}_{j}}} \right),$ ${{B}_{3}}\left( {{{x}_{{vх}}},{{z}_{j}}} \right),$ $\delta \left( {{{x}_{{vх}}},{{z}_{j}}} \right),$ $j = \overline {1,m} $.
После этого решается задача Коши для уравнения (12.1). В правую часть этого уравнения входят перепады давлений $P_{1}^{'}(z)$ и 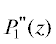 , которые вычисляются из условия постоянства расхода хладагента. В правую часть уравнения (12.1) также входит $\frac{{d{{B}_{2}}(x,z)}}{{dz}}$. Этот член уравнения определяет усредненный по толщине пленки конденсата конвективный
теплоперенос, так как в пленке течение в направлении оси х отсутствует, то конвективный перенос тепла также в направлении х будет отсутствовать и этим членом можно пренебречь. В результате решения задачи Коши
для уравнения (12.1) находим значение функции ${{B}_{1}}\left( {{{x}_{{vх}}} + {{h}_{x}},{{z}_{0}}} \right)$. После этого решается задача Коши для системы (12.2)–(12.4). Далее эта процедура
повторяется до тех пор, пока значение х в текущем сечении будет равно ${{L}_{x}}$.
, которые вычисляются из условия постоянства расхода хладагента. В правую часть уравнения (12.1) также входит $\frac{{d{{B}_{2}}(x,z)}}{{dz}}$. Этот член уравнения определяет усредненный по толщине пленки конденсата конвективный
теплоперенос, так как в пленке течение в направлении оси х отсутствует, то конвективный перенос тепла также в направлении х будет отсутствовать и этим членом можно пренебречь. В результате решения задачи Коши
для уравнения (12.1) находим значение функции ${{B}_{1}}\left( {{{x}_{{vх}}} + {{h}_{x}},{{z}_{0}}} \right)$. После этого решается задача Коши для системы (12.2)–(12.4). Далее эта процедура
повторяется до тех пор, пока значение х в текущем сечении будет равно ${{L}_{x}}$.
Программа расчетов состоит из блока для ввода исходных данных, блока решателя и блока вывода результатов расчетов, которая составлена на основе алгоритма решения уравнений (1.1)–(1.5), (2.1)–(2.5), (3.1)–(3.6) и вышеизложенного алгоритма. По составленной программе расчетов был реализован вычислительный эксперимент (ВЭ) по изучению процесса пленочной конденсации, некоторые результаты которого приведены на рис. 4.
Решение краевой задачи (1.1)–(1.5), (2.1)–(2.5), (3.1)–(3.6), (4.1)–(4.5), (5.1)–(5.4) при Re ≥ 1 может быть проведено только численными методами, например методом поверхностей равных расходов [4]. Это тема отдельных самостоятельных исследований.
ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ПЛЕНОЧНОЙ КОНДЕНСАЦИИ В ПЛАСТИНЧАТОМ ТЕПЛООБМЕННИКЕ
Физическое моделирование процесса пленочной конденсации в пластинчатых теплообменниках (ПТ) было проведено с целью выявить их качественные и количественные характеристики, оценить влияние расхода и входной температуры хладагента, их конструктивных особенностей на процесс конденсации парогазовой смеси на основе экспериментальных данных и сравнить результаты математического и физического моделирования.
Для проведения эксперимента были выбраны два вида сырья: пары воды и трет-бутилового спирта (ТБС). Для каждого вида сырья был сконструирован свой лабораторный экспериментальный стенд. Схематическое изображение экспериментального стенда для анализа процесса пленочной конденсации паров ТБС представлено на рис. 3а. Стенд состоит из испарителя Е-1 объемом 0.0075 м3, обвитого греющими кабелями мощностью 4 кВт, емкости Е-2 для хладагента и насоса Н-1 для его подачи, питательной емкости Е-3, насоса Н-2 для подачи ТБС из питательной емкости Е-3, пластинчатого теплообменника Т-1, емкости Е-4 для конденсата, электронного манометра РЕ для измерения давления, термопары ТЕ для измерения температуры, счетчика FE для измерения расходов хладагента и ТБС. Пластинчатый теплообменник Т-1 (рис. 3б) имеет полезную площадь теплообменника 0.23 м2. Внутри теплообменника на входе парообразного продукта установлен распределитель для равномерного распределения потока пара по всем пластинам, а также закрытая тарелка для сбора образующегося конденсата. Парообразный продукт подается в межтрубное пространство, а хладагент в трубное пространство. Эксперименты были проведены при различных значениях входной температуры хладагента ${{T}_{{vx.xl}}}$ и парообразного ТБС ${{T}_{{v.TBC}}}$, расходах хладагента ${{V}_{{xl}}}$ (рис. 4).
Рис. 3.
Схематическое изображение экспериментального стенда для анализа процесса пленочной конденсации паров ТБС (а) и пластинчатого теплообменника Т-1 (б): 1 – штуцер для ввода хладагента; 2 – штуцер для вывода хладагента; 3 – штуцер для слива конденсата; 4 – распределители; 5 – глухая тарелка; 6 – термопара для измерения температуры; 7 – штуцер для подачи пара; 8 – межтрубное пространство; 9 – теплообменные пластины (трубное пространство); 10 – термопара для измерения температуры.
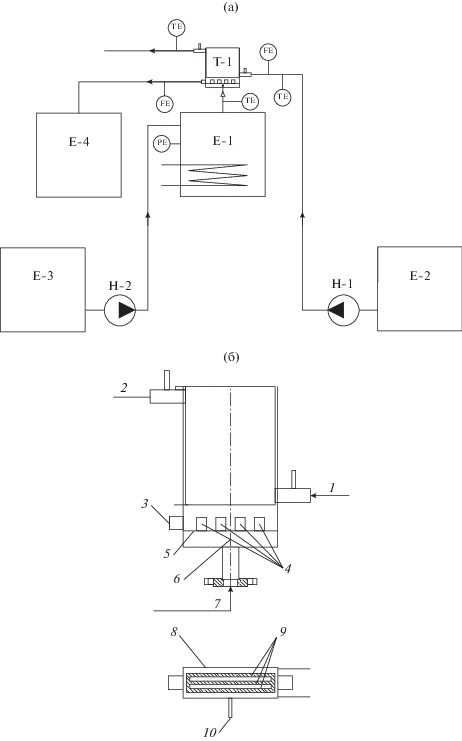
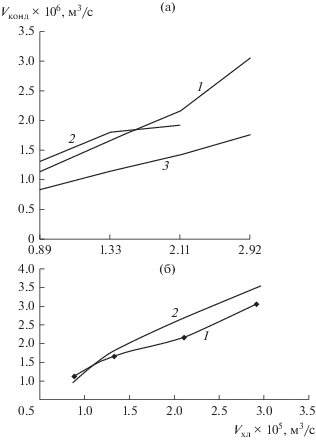
Рис. 4.
Зависимость расхода конденсата ТБС от расхода хладагента (а) и сравнение результатов вычислительного эксперимента с экспериментальными данными (б). Рис. 4а: 1 – входная температура ТБС ${{T}_{{Tvx}}} = 88^\circ {\text{C}}$; входная температура хладагента ${{T}_{{xvx}}} = 28.1^\circ {\text{C}}$; 2 – ${{T}_{{Tvx}}} = 90^\circ {\text{C}}$; ${{T}_{{xvx}}} = 30^\circ {\text{C}}$; 3 – ${{T}_{{Tvx}}} = 89^\circ {\text{C}}$; ${{T}_{{xvx}}} = 29^\circ {\text{C}}$; рис. 4б: 1 – эксперимент; 2 – расчет по математической модели (${{T}_{{Tvx}}} = 88^\circ {\text{C}}$; ${{T}_{{xvx}}} = 28^\circ {\text{C}}$).
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
На основании построенной математической модели процесса пленочной конденсации в пластинчатых теплообменниках и программы расчетов реализован физический эксперимент. Результаты расчетов показали, что процесс пленочной конденсации зависит от физико-механических свойств хладагента и паровой фазы, от их входных температур, расхода (скорости течения) хладагента.
Анализ результатов экспериментов и расчетов по математической модели показывает, что увеличение расхода хладагента повышает количество образующегося конденсата до определенного значения. При определенных расходах хладагента его скорость становится достаточно высокой и влияние термического сопротивления пластин становится определяющим, что приводит к стабилизации расхода конденсата. Входная температура ${{T}_{{vx.xl}}}$ также влияет на расход конденсата. Некоторые результаты экспериментов приведены на рис. 4. Сравнение результатов вычислительного эксперимента, полученных на основании построенной математической модели, с экспериментальными данными (рис. 4б) показало их приемлемое совпадение (относительная погрешность порядка 10–15%).
Решение задачи моделирования процесса пленочной конденсации и ее анализ показывают необходимость постановки и решения проблемы его оптимального аппаратурного оформления.
ЗАКЛЮЧЕНИЕ
Построенная математическая модель в конкретных частных случаях совпадает с результатами работы [9] и согласуется с ранее известными, приведенными в работах [1, 2] решениями. Например, если не рассматривать течение охлаждающей среды внутри полой призмы и взять ее температуру ${{T}_{1}} = {{T}_{0}}$ и стенки ${{T}_{4}} = {{T}_{{{\text{ст}}}}}$ и пренебречь конвективным переносом тепла в уравнении (2.5) $\left( {{{B}_{2}}(z) = 0} \right)$ и трением на границе раздела газ–жидкость при постоянных физических свойствах конденсата и газа и граничных условиях (4.3)–(4.4), то наше решение полностью совпадает с решением [9]. Кроме того, если принять распределение температуры конденсата в виде ${{T}_{2}} = {{T}_{{2S}}}$ – $\left( {{{T}_{{2S}}} - {{T}_{{{\text{ст}}}}}} \right)$${{\left( {\frac{{\delta - y + h + {{\delta }_{0}}}}{\delta }} \right)}^{n}}$, то наше решение при граничном условии (4.3) переходит в решение, приведенное в работе [2].
Разработанная математическая модель процесса пленочной конденсации позволяет определить все ее основные характеристики для аппаратов рассмотренного типа [25].
Был проведен вычислительный эксперимент при различных режимах работы аппарата и параметрах исходного сырья.
Численные расчеты и экспериментальные исследования показали зависимость процесса пленочной конденсации от многих параметров. Установлено их взаимовлияние на гидродинамическую обстановку в аппарате, анализ которой дает возможность поставить и решить вопросы оптимального аппаратурного оформления соответствующего процесса конденсации.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-43-160008).
ОБОЗНАЧЕНИЯ
| ${{C}_{{1{{\rho }_{1}}}}},{{C}_{{2{{\rho }_{1}}}}},{{C}_{{3{{\rho }_{1}}}}}$ | коэффициенты удельной теплоемкости хладагента, конденсата и газа соответственно, Дж/(кг К) |
| ${{F}_{{1{{x}_{j}}}}},{{F}_{{2{{x}_{j}}}}},{{F}_{{3{{x}_{j}}}}}$ | компоненты массовых сил в направлении координат ${{x}_{j}}$ |
| $2h,{{\delta }_{0}},\delta \left( z \right),H$ | соответственно ширина канала и толщина полой призмы, толщина пленки и ширина канала для газовой фазы, м |
| ${{h}_{2}}$ | теплота парообразования (фазового превращения пара в конденсат), Дж/кг |
| p1, p2, p3 | давления хладагента, конденсата и газа соответственно, Па |
| $Q,\;{{Q}_{g}}$ | соответственно массовый расход конденсата в пленке и массовая скорость конденсации, кг/с и кг/(м с) |
| T1, T2, T3 | температуры соответственно хладагента, конденсата и газа, °C |
| ${{T}_{{ст}}} = {{T}_{W}},{{T}_{{2S}}}$ | температуры стенки и насыщения, °С |
| ${{V}_{{1{{x}_{j}}}}},{{V}_{{2{{x}_{j}}}}},{{V}_{{3{{x}_{j}}}}}$ | компоненты скорости хладагента, пленки конденсата и газовой фазы соответственно по оси ${{x}_{j}}\left( {x,y,z} \right)$, м/с |
| α | коэффициент теплоотдачи, Вт/(м2 К) |
| λ1, λ2, λ3 | коэффициенты теплопроводности хладагента, конденсата и газа соответственно, Вт/(м К) |
| μ1, μ2, μ3 | динамические вязкости хладагента, конденсата и газа соответственно, (Н с)/м2 |
| ρ1, ρ2, ρ3 | плотности хладагента, конденсата и газа соответственно, кг/м3 |
| ${{\sigma }_{2}}$ | коэффициент поверхностного натяжения пленки, Н/м |
Список литературы
Теплопередача в двухфазном потоке / Под ред. Баттерворса Д., Хьюитта Г. М.: Энергия, 1980.
Михалевич А.А. Математическое моделирование массо- и теплопереноса при конденсации. Минск: Наука и техника, 1982.
Кутателадзе С.С. Теплопередача при конденсации и кипении. М.: Машгиз, 1952.
Холпанов Л.П. Шкадов В.Я. Гидродинамика и тепломассообмен с поверхностью раздела. М.: Наука, 1990.
Шервуд Т., Пигфорд Р., Уилки Ч. Массопередача. М.: Химия, 1982.
Справочник по теплообменникам. Т. 1 / Под ред. Петухова Б.С., Шикова В.К. М.: Энергоатомиздат, 1987.
Кинни Р.В., Спэрроу Е.М. Турбулентное течение, тепло- и массообмен в трубе с поверхностным отсосом // Теплопередача. 1970. Т. 92. № 2. С. 121.
Леонтьев А.И. Инженерные методы расчета трения и теплообмена на проницаемой поверхности // Теплоэнергетика. 1972. № 9. С. 12.
Nusselt W. Surface condensation of water vapours // Z. Ves. Dt. Ing. 1916. V. 60. № 26. P. 569.
Черный Г.Г. Ламинарное движение газа и жидкости в пограничном слое с поверхность разрыва // Изв. Акад. наук СССР. Отд. тех. наук. 1954. № 112. С. 38.
Dashkov G.V., Malenko G.L., Solodukhin A.D., Tyutyuma V.D. Modeling of the evaporative cooling of running-down liquid films in the slit channel of the spraying device of a cooling tower // J. Eng. Phys. Thermophys. 2014. V. 27. № 6. P. 1414. [Дашков Г.В., Маленко Г.Д., Солодухин А.Д., Тютюма В.Д. Моделирование испарительного охлаждения стекающих пленок жидкостей в щелевом канале оросительного устройства градирни // Инж.-физ. ж. 2014. Т. 27. № 6. С. 1356.]
Markov A.A. Model of micro- and macroscale chemical condensations in a gas mixture with solid particles flowing in a channel with a heated wall // Theor. Found. Chem. Eng. 2007. V. 41. № 4. P. 333. [Марков А.А. Модель химической конденсации на микро- и макроуровнях при течении смеси газа с твердыми частицами в канале с нагретой стенкой // Теор. осн. хим. технол. 2007. Т. 41. № 4. С. 355.]
Markov A.A., Filimonov I.A. Chemical condensation model for the flow of a reacting mixture in a tube // Theor. Found. Chem. Eng. 2008. V. 42. № 5. P. 333. [Марков А.А., Филимонов И.А. Модель химической конденсации для течения реагирующей смеси в трубе // Теор. осн. хим. технол. 2008. Т. 42. № 5. С. 494.]
Voinov N.A., Zemtsov D.A., Zhukova O.P. Study of thermal rectification in a column with low mass transfer on the steps // Theor. Found. Chem. Eng. 2017. V. 51. № 2. P. 191. [Войнов Н.А., Земцов Д.А., Жукова О.Г. Исследование термической ректификации в колонне с низким массообменном на ступенях // Теор. осн. хим. технол. 2017. Т. 51. № 2. С. 174.]
Kryukov A.P., Levashov V.Y., Pavlyukevich N.V. Condensation coefficient: definitions, estimations, modern experimental and calculation data // J. Eng. Phys. Thermophys. 2014. V. 27. № 1. P. 237. [Крюков А.П., Левашов В.Ю., Павлюхевич Н.В. Коэффициент конденсации: определения, современные экспериментальные и расчетные данные, оценки величины // Инж.-физ. ж. 2014. Т. 27. № 1. С. 229.]
Лабунцов Д.А. О влиянии на теплоотдачу при пленочной конденсации пара зависимости физических параметров конденсата от температуры // Теплоэнергетика. 1957. № 1. С. 49.
Лабунцов Д.А. О влиянии конвективного переноса тепла и сил инерции на теплообмен при ламинарном течении конденсатной пленки // Теплоэнергетика. 1957. № 2. С. 47.
Лабунцов Д.А., Ягов В.В. Механика двухфазных сред. М.: МЭИ, 2000.
Ягов В.В. Теплообмен в однофазных средах и при фазовых превращениях. М.: МЭИ, 2014.
Кукушкин С.А., Осипов А.В. Процессы конденсации тонких пленок // Усп. физ. наук. 1998. Т. 168. № 10. С. 1083.
Ганчев Б.Г., Никитин В.Н. Движение и теплообмен при свободном стекании пленок жидкостей по вертикальной поверхности. М.: МВТУ им. Н.Э. Баумана, 1970.
Voinov N.A., Zhukova O.P., Nikolaev A.N. Heat transfer in condensation and boiling in a tubular film evaporator // Theor. Found. Chem. Eng. 2012. V. 46. № 4. P. 359. [Войнов Н.А., Жукова О.П., Николаев Н.А. Теплоотдача при кипении и конденсация в пленочном трубчатом испарителе // Теор. осн. хим. технол. 2012. Т. 46. № 4. С. 432.]
Al-Jarrah J.A., Khadrawi A.F., Al-Nimr M.A. Film condensation on a vertical microchannel // Int. Commun. Heat Mass Transfer. 2008. V. 35. P. 1172.
Groff M.K., Ormisfon S.J., Soliman H.M. Numerical solution of film condensation from turbulent flow of vapor-gas mixtures in vertical tubes // Int. J. Heat Mass Transfer. 2007. V. 50. P. 3899.
Zhao T.S., Liao Q. Theoretical analyses of film condensation heat transfer inside vertical mini triangular channels // Int. J. Heat Mass Transfer. 2002. V. 45. P. 2829.
Hassaninejadafarahani F., Ormiston S. Numerical analyses of laminar reflux condensation from gas-vapour mixtures in vertical parallel plate channels // Int. J. Mech. Mechatronics Eng. 2015. V. 9. № 5. P. 794.
Фарахов М.И., Ахмитшин А.А., Кузнецов В.А. и др. Теплообменник радиально-спирального типа (варианты). Пат. 2583316 РФ. 2016.
Тарг С.М. Основные задачи теории ламинарных течений. М.: ГИТТЛ, 1951.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии