Теоретические основы химической технологии, 2020, T. 54, № 4, стр. 440-451
Стационарные состояния ферментативного процесса получения молочной кислоты по заданной концентрации основного субстрата
Е. Л. Гордеева a, Л. В. Равичев a, Ю. Л. Гордеева b, *
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
b Московская государственная академия ветеринарной медицины и биотехнологии им. К.И. Скрябина
Москва, Россия
* E-mail: l.s.gordeev@yandex.ru
Поступила в редакцию 13.01.2020
После доработки 21.01.2020
Принята к публикации 07.02.2020
Аннотация
Приведена расчетная схема, обобщающая теоретические представления технологии непрерывной ферментации молочной кислоты при заданной концентрации основного субстрата в потоке, поступающем в ферментер. Последовательность формирования расчетной схемы включает предварительный анализ и основной анализ. В предварительном анализе получены соотношения, формирующие область оценки граничных показателей, отвечающих заданному значению продуктивности процесса. Отмечены координаты точки максимальной продуктивности − величины \left[ {{{S}_{{{\text{opt}}}}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {{D}^{{{\text{opt}}}}}} \right]; координаты особых точек: для точки 1 − \left[ {{{S}_{1}}\left( {{{D}_{1}}} \right),{{D}_{1}}} \right]; для точки 2 − \left[ {{{S}_{2}}\left( {{{D}_{2}}} \right),{{D}_{2}}} \right]; для точки 3 − \left[ {{{S}_{3}}\left( {{{D}_{3}}} \right),{{D}_{3}}} \right] и для точки 4 − \left[ {{{S}_{4}}\left( {{{D}_{4}}} \right),{{D}_{4}}} \right]. Для точки максимальной продуктивности и особых точек даны соотношения для вычисления начальных значений концентраций основного субстрата S0 и соответствующих начальных концентраций компонента, воспроизводящего субстрат в процессе ферментации M0. Значения координат явились ограничениями в формировании соотношений основного анализа, определяющие множества для выбора значений M0 и D по заданному значению S0. Схема формирования множеств представлена тремя частями: I, II и III. Границы частей определены соотношениями (21), (22) и (23). Приведена последовательность формирования множеств для каждой части и показано, что для части I существует единственное множество Мн1; для части II − два множества Мн1* и Мн2*; для части III − три множества Мн1**, Мн2**, Мн3**. Приведены таблицы для вычисления элементов множеств при заданном значении S0. Полученные теоретические соотношения использованы для численного расчета по оценке показателей множественности стационарных состояний для каждого из множеств Мн. Показано, что диапазон задания S0 наиболее широк для части I, в то время как диапазон формирования величины протока D наибольший для части III. Численные оценки в сравнительном варианте для множеств частей II и III показали, что конечные концентрации компонентов при одинаковых начальных условиях отличаются по значениям M0, M и S. Последнее дает возможность получить сравнительные оценки для дальнейшей переработки полученных компонентов (выделение молочной кислоты, утилизация и использование непревращенных компонентов, выделение побочного продукта и т.п.).
ВВЕДЕНИЕ
В настоящей работе рассматриваются стационарные состояния технологического процесса непрерывной ферментации молочной кислоты. Технологическое обеспечение процесса определяется тремя входными показателями – величиной протока через ферментер (D, ч–1); величиной концентрации основного субстрата в поступающем потоке (S0, г/л) (под основным субстратом понимается субстрат, непосредственно потребляемый микроорганизмами; для многих микроорганизмов часто основным субстратом является глюкоза [1]); величиной концентрации компонента сырья, воспроизводящего основной субстрат в процессе ферментации (M0, г/л). Так, в [2] этим компонентом является мальтоза, при деградации которой воспроизводится основной субстрат. В работе [3] дополнительное количество субстрата образуется деградацией крахмала. Общее количество субстрата, потребляемого микроорганизмами, складывается из двух составляющих – часть от основного субстрата и часть от компонента, воспроизводящего субстрат. В последней части, если обозначить константу деградации как kM, ч–1, то количество образуемого субстрата будет равно kMM, где M – концентрация в ферментере, г/л. Таким образом, две величины S0 и M0 дополняют друг друга в практической реализации технологического процесса. Величина протока D является независимой величиной, имеющей ограниченное значение Dпред, при котором субстрат вымывается из ферментера, “не успев” вступить в процесс синтеза. Таким образом, в результате процесса синтеза в потоке, покидающем ферментер, остаются компоненты в следующих концентрациях: P, г/л – концентрация молочной кислоты; S, г/л – концентрация субстрата; X, г/л – концентрация биомассы; M, г/л – концентрация компонента, воспроизводящего субстрат; B, г/л – концентрация побочного продукта. Здесь B представляет продукт, который, возможно, образуется в процессе синтеза молочной кислоты. При использовании различных штаммов микроорганизмов побочные продукты (в совокупности) могут получаться в малых количествах и не иметь практической ценности. Однако в работе [4] в качестве побочного продукта приведено образование бактериоцина в виде низина или педиоцина, т.е. продуктов, имеющих самостоятельную ценность. В публикации [4] в качестве микроорганизмов использованы Lactococcus lactis и Pediococcus asidilactici.
Основы формирования обобщенной математической модели, учитывающей вышеизложенные положения, приведены в публикации [5]. Система уравнений имеет следующий вид:
(1)
\left\{ \begin{gathered} - DX + \mu X = 0 \hfill \\ \left( {\alpha \mu + \beta } \right)X - DP = 0 \hfill \\ \left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X - DB = 0 \hfill \\ D\left( {{{S}_{0}} - S} \right) - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\mu X + {{k}_{M}}M = 0 \hfill \\ D\left( {{{M}_{0}} - M} \right) - {{k}_{M}}M = 0 \hfill \\ \mu = {{\mu }_{{{\text{max}}}}}{{\left( {1 - \frac{X}{{{{X}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}} \hfill \\ \end{gathered} \right..Математическая модель содержит элементы, учитывающие возможность ингибирования, включенные в соотношение кинетики: ингибирование биомассой (Xmax, n1), продуктом (Pmax, n2), субстратом (Ki).
Использование уравнений математической модели требует иметь оценки констант, которые получают по экспериментальным данным для конкретного штамма микроорганизмов. Результаты преобразования системы (1) приведены в приложении (формулы (П.1)−(П.11)), которые необходимы для решения поставленной задачи.
Настоящая задача связана с определением множественности стационарных состояний по заданным значениям D, S0 и M0.
Результаты оценки множественности по заданной величине D приведены в работе [6].
Множественность по заданным значениям S0 и M0 целесообразно рассмотреть последовательно, т.е. первоначально необходимо получить показатели процесса, когда задается только значение S0. Именно этот анализ выполнен в настоящей публикации.
Последующий шаг определяется условием, когда задается только M0. В настоящей работе это вариант не рассматривается.
Для решения поставленной задачи требуется выполнение предварительных расчетов, суть которых заключается в возможности получения соотношений, обеспечивающих реальное осуществление процесса. Таким образом, дальнейший анализ базируется на уравнениях математической модели (1).
ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
Целью предварительного анализа является получение характеристики объекта, для которого будет оцениваться множественность.
Задачей технологического процесса является получение показателей, обеспечивающих заданное значение продуктивности по целевому продукту QP, г/(л ч) – молочной кислоте. При этом возможен вариант получения максимальной продуктивности maxQP или продуктивности меньше максимальной. В последнем случае возможна экономия сырьевых материалов или лучшие условия выделения целевого продукта и др.
Первая задача, которая решается при получении характеристик объекта, есть задача оценки maxQP и определение величины протока Dopt, обеспечивающего maxQP.
Максимальное значение QP вычисляется с использованием уравнений (П.8) и (П.2), т.е. вычисляется значение Dopt, обеспечивающее maxQP в уравнении
(2)
{{\left( {\frac{{{{K}_{i}}}}{2}} \right)}^{2}}{{\left[ {A\left( D \right)\frac{{{{\mu }_{{{\text{max}}}}}}}{D} - 1} \right]}^{2}} - {{K}_{m}}{{K}_{i}} = 0.Уравнение (2) решается численно. Получаем
Для maxQP и Dopt вычисляется {{S}_{{{\text{opt}}}}} по (П.6) или (П.7). Получаем
(4)
\begin{gathered} {{S}_{{{\text{opt}}}}} = S_{1}^{'}\left( {{{D}^{{{\text{opt}}}}}} \right) = S_{2}^{'}\left( {{{D}^{{{\text{opt}}}}}} \right) = \\ = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{\text{max}}{{Q}_{P}}}}{{\left( {\alpha {{D}^{{{\text{opt}}}}} + \beta } \right)}} + {{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered}Положение точки maxQP обозначено значениями
Следующая задача заключается в получении оценок при условии
Для QP по условию (6) также решается уравнение (П.8), используя (П.2). Получаем два значения D1 и D2 (значения D не могут быть меньше D1 и не могут быть больше D2 по условиям (П.6) и (П.7)).
Для D1 и D2 вычисляются значения S '(D1) и S '(D2) по (П.6):
(7)
\begin{gathered} {{S}_{1}} = S_{1}^{'}\left( {{{D}_{1}}} \right) = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha {{D}_{1}} + \beta } \right)}} + \\ + \,\,{{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = S_{2}^{'}\left( {{{D}_{1}}} \right), \\ \end{gathered}(8)
\begin{gathered} {{S}_{2}} = S_{1}^{'}\left( {{{D}_{2}}} \right) = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha {{D}_{2}} + \beta } \right)}} + \\ + \,\,{{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = S_{2}^{'}\left( {{{D}_{2}}} \right). \\ \end{gathered}В соотношениях (7) и (8) имеем следующее условие:
Точки с координатами \left[ {{{S}_{1}},\;{{D}_{1}}} \right] и \left[ {{{S}_{2}},\;{{D}_{2}}} \right] назовем особыми точками 1 и 2.
Координаты особых точек 1 и 2 определяют область значений величины протока D при QP < < maxQP:
Далее, для QP по (6) вычисляется D3 из значений D по (10), обеспечивающее максимальное значение S_{1}^{'} по (П.6). Для D3 вычисляется {{S}_{3}} = \max S_{1}^{'}\left( {{{D}_{3}}} \right). Координаты особой точки 3:
Для QP по (6) вычисляется D4 из (10), обеспечивающее минимум S_{2}^{'} по (П.7). Для D4 вычисляется {{S}_{4}} = \min S_{2}^{'}\left( {{{D}_{4}}} \right). Координаты особой точки 4:
Координаты точки maxQP и особых точек являются ограничительными характеристиками объекта для любого QP по условию (6).
Для каждой из этих точек имеется возможность вычислить множество значений S0 и M0 в потоке, поступающем в ферментер.
В табл. 1 представлены соотношения, формирующие множества S0 и M0 для точки экстремума и особых точек.
Таблица 1.
Соотношения для вычисления компонент множеств для S0 и M0 для точки оптимального условия и особых точек
| Оптимальная точка {{D}^{{{\text{opt}}}}}, ч–1; {{S}_{{{\text{opt}}}}}, г/л |
S_{0}^{i} = {{S}_{{{\text{opt}}}}}\frac{{{{n}_{0}} - i}}{{{{n}_{0}}}} (13) |
| M_{0}^{i} = \frac{i}{{{{n}_{0}}}}\frac{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}}{{{{k}_{M}}}}{{S}_{{{\text{opt}}}}} (14) | |
| {{D}_{k}}, ч–1; {{S}_{k}}, г/л k = 1.0. Особая точка 1: D{}_{1}; {{S}_{1}} |
S_{0}^{i} = {{S}_{k}}\frac{{{{n}_{k}} - i}}{{{{n}_{k}}}} (15) |
| k = 2.0. Особая точка 2: D{}_{2}; {{S}_{2}} | M_{0}^{i} = \frac{i}{{{{n}_{k}}}}\frac{{{{D}_{k}} + {{k}_{M}}}}{{{{k}_{M}}}}{{S}_{k}} (16) |
| k = 3.0. Особая точка 3: D{}_{3}; {{S}_{3}} k = 4.0. Особая точка 4: D{}_{4}; {{S}_{4}} |
Значения n0 и nk задает пользователь; i = 0–n0; i = 0–nk |
Условия вычисления S_{0}^{i} определяются следующими неравенствами:
для точки экстремума
для особых точек
Значения n0, nk пользователь задает произвольно в виде неотрицательного числа для каждого номера. Значения i = 0–n0 для точки экстремума, i = 0–nk для особых точек.
Ниже приведем численный расчет с использованием констант базового варианта для системы (1) (табл. 2).
Таблица 2.
Численные значения констант для базового варианта
| Km, г/л | Ki, г/л | µmax, ч–1 | Xmax, г/л | Pmax, г/л | n1 | n2 | YX/S, г/г | kM, ч–1 | α, г/г | β, ч–1 | αB, г/г | βB, ч–1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.2 | 164 | 0.48 | 30 | 98.0 | 0.5 | 0.5 | 0.4 | 0.035 | 2.2 | 0.02 | 1.1 | 0.01 |
По решению уравнения (2) получены следующие значения для оптимальной точки:
Для вычисления координат особых точек использовано следующее условие:
Значение n0 для оптимальной точки и nk для всех особых точек принято равным четырем (n0 = = 4, nk = 4), значение i использовано в расчетах по условию i = 0–n0 и i = 0–nk и было одинаковым: 0.0; 1.0; 2.0; 3.0; 4.0.
Вычисляются элементы множеств {{S}_{0}} и {{M}_{0}} для точки экстремума и особых точек с использованием исходных данных.
Исходные данные:
1) мощность множеств принята одинаковой для всех расчетов (n0 = 4, nk = 4) и равна 5 (i = 0.0; 1.0; 2.0; 3.0; 4.0);
2) координаты точки экстремума и особых точек для {{Q}_{P}} = 6.0 г/(л ч):
точка экстремума
особая точка 1
особая точка 2
особая точка 3
особая точка 4
По результатам предварительного анализа пользователь имеет возможность выбрать или задать значение {{S}_{0}}, отвечающее условиям точки экстремума или какой-либо из особых точек.
Формула вычисления M_{0}^{i} в табл. 1 получена для каждого принятого или заданного значения S_{0}^{i} по (П.4):
(19)
\begin{gathered} M_{0}^{i} = \frac{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {{{S}_{{{\text{opt}}}}} - S_{0}^{i}} \right] - \\ {\text{для}}\,\,{\text{точки}}\,\,{\text{экстремума}}, \\ \end{gathered}(20)
M_{0}^{i} = \frac{{{{D}_{k}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {{{S}_{k}} - S_{0}^{i}} \right] - {\text{для}}\,\,{\text{особых}}\,\,{\text{точек}},
В табл. 3 представлены результаты вычислений S_{0}^{i} и M_{0}^{i} по исходным данным, приведенным выше.
Таблица 3.
Результаты расчета множеств S0 (г/л) и M0 (г/л)
| № п/п | i | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|
| 1 | Точка экстремума | S_{0}^{0} = 57.4 M_{0}^{0} = 0.0 | S_{0}^{1} = 43.05M_{0}^{1} = 98.4 | S_{0}^{2} = 28.7M_{0}^{2} = 196.8 | S_{0}^{3} = 14.35M_{0}^{3} = 295.7 | S_{0}^{4} = 0.0M_{0}^{4} = 393.6 |
| 2 | Особая точка 1 | S_{0}^{0} = 77.6M_{0}^{0} = 0.0 | S_{0}^{1} = 58.2 M_{0}^{1} = 73.82 | S_{0}^{2} = 38.8 M_{0}^{2} = 147.64 | S_{0}^{3} = 19.4 M_{0}^{3} = 231.46 | S_{0}^{4} = 0.0 M_{0}^{4} = 295.28 |
| 3 | Особая точка 2 | S_{0}^{0} = 35.35M_{0}^{0} = 0.0 | S_{0}^{1} = 26.51M_{0}^{1} = 87.29 | S_{0}^{2} = 17.67M_{0}^{2} = 174.58 | S_{0}^{3} = 8.83 M_{0}^{3} = 261.87 | S_{0}^{4} = 0.0 M_{0}^{4} = 349.16 |
| 4 | Особая точка 3 | S_{0}^{0} = 143.28M_{0}^{0} = 0.0 | S_{0}^{1} = 107.46M_{0}^{1} = 177.05 | S_{0}^{2} = 71.64M_{0}^{2} = 354.11 | S_{0}^{3} = 35.82 M_{0}^{3} = 531.16 | S_{0}^{4} = 0.0 M_{0}^{4} = 708.06 |
| 5 | Особая точка 4 | S_{0}^{0} = 29.0M_{0}^{0} = 0.0 | S_{0}^{1} = 21.75 M_{0}^{1} = 65.25 | S_{0}^{2} = 14.5M_{0}^{2} = 13.05 | S_{0}^{3} = 7.25M_{0}^{3} = 195.75 | S_{0}^{4} = 0.0M_{0}^{4} = 261.0 |
Далее рассматривается более общая задача задания S0 для условий, отличных от рассмотренных выше.
ОСНОВНОЙ АНАЛИЗ
Целью основного анализа является получение соотношений для вычисления технологических показателей S0, M0, D и, соответственно, остальных показателей процесса ферментации P, X, S, M, B по заданному значению {{S}_{0}}.
В основном анализе используются данные предварительного анализа по координатам точки экстремума и особых точек.
Если значение S0 задается по значениям для точки экстремума или особых точек, т.е. {{S}_{0}} = {{S}_{{{\text{opt}}}}} или {{S}_{0}} = {{S}_{1}} или {{S}_{0}} = {{S}_{2}} или {{S}_{0}} = {{S}_{3}} или {{S}_{0}} = {{S}_{4}}, то для всех вышеприведенных условий значение M0 = 0. Показатели процесса вычисляются по (П.11).
В дальнейшем этот вариант не рассматривается, т.е. анализ выполняется исключая рассмотрение точки экстремума и особых точек.
Основываясь на предварительном анализе, область задания {{S}_{0}} разделяется на три части:
(21)
{\text{Часть}}\,\,{\text{I}}\,:{{S}_{1}}\left( {{{D}_{1}}} \right) \leqslant {{S}_{0}} \leqslant {{S}_{3}}\left( {{{D}_{3}}} \right);(22)
{\text{Часть}}\,\,{\text{II}}\,:{{S}_{2}}\left( {{{D}_{2}}} \right) \leqslant {{S}_{0}} \leqslant {{S}_{1}}\left( {{{D}_{1}}} \right);(23)
{\text{Часть}}\,\,{\text{III}}\,:{{S}_{4}}\left( {{{D}_{4}}} \right) \leqslant {{S}_{0}} \leqslant {{S}_{2}}\left( {{{D}_{2}}} \right).В соотношениях (21)–(23) указаны значения D, для которых вычисляются Sk.
При заданном S0 по любой из частей вычисляются по два значения величины протока, обеспечивающие это значение.
По части I: D_{1}^{1} и D_{1}^{2} вычисляются по (П.6), где S_{1}^{'} = {{S}_{0}}, D_{1}^{1} < {{D}_{3}}, D_{1}^{2} > {{D}_{3}}.
По части II: D_{2}^{1} вычисляется по (П.7), где S_{2}^{'} = {{S}_{0}}; D_{2}^{2} вычисляется по (П.6), где S_{1}^{'} = {{S}_{0}}; D_{2}^{1} < {{D}_{4}}, D_{2}^{2} > {{D}_{3}}.
По части III: D_{3}^{1} и D_{3}^{2} вычисляются по (П.7), где S_{2}^{'} = {{S}_{0}}, D_{3}^{1} < {{D}_{4}}, D_{3}^{2} > {{D}_{4}}.
Условия формирования множеств значений M0 и D при заданном значении S0 рассмотрим отдельно для каждой части.
Часть I.
1. По заданному (или выбранному) S0 по условию (21) вычисляются значения D_{1}^{1} и D_{1}^{2} по решению уравнения (П.6), используя (П.2) для QP по (6). Таким образом, область значений D ограничена следующим условием:
где S_{1}^{'} в (П.6) равно S0.
2. Вычисляется шаг h по D:
где n1 – произвольное положительное число.
3. Вычисляется значение {{D}^{i}}, используя шаг h:
где i = 0–n1.
4. Соотношение (26) преобразуем, используя (25):
При i = 0 {{D}^{i}} = D_{1}^{1}; при i = n1{{D}^{i}} = D_{1}^{2}.
5. Для каждого номера i имеется возможность вычислить S_{1}^{'}\left( {{{D}^{i}}} \right) по (П.6).
6. Вычисляется M_{0}^{i} по формуле
(28)
M_{0}^{i} = \frac{{{{D}^{i}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {S_{1}^{'}({{D}^{i}}) - {{S}_{0}}} \right].Получаем множество значений M0 и D в виде Мн1 для принятого S0:
Итоговые формулы приведены в табл. 4.
Таблица 4.
Соотношения для вычисления множества M0 и D при заданном значении S0
| Часть I | Часть II | |
|---|---|---|
| S{\kern 1pt} '\left( {{{D}_{1}}} \right) < {{S}_{0}} < S_{1}^{'}\left( {{{D}_{3}}} \right) | S{\kern 1pt} '\left( {{{D}_{2}}} \right) < {{S}_{0}} < S{\kern 1pt} '\left( {{{D}_{1}}} \right) | |
| D_{1}^{1} и D_{1}^{2} по (П.6); S_{1}^{'} = {{S}_{0}}, D_{1}^{1} < {{D}_{3}}, D_{1}^{2} > {{D}_{3}} |
D_{2}^{1} по (П.7); S_{2}^{'} = {{S}_{0}},D_{2}^{1} < {{D}_{4}} D_{2}^{2} по (П.6); S_{1}^{'} = {{S}_{0}}, D_{2}^{2} > {{D}_{3}} |
|
| {{D}^{i}} = D_{1}^{1} + \frac{i}{{{{n}_{1}}}}\left( {D_{1}^{2} - D_{1}^{1}} \right) {{n}_{1}} > 0; i = 0{\kern 1pt} - {\kern 1pt} {{n}_{1}} |
{{D}^{i}} = {{D}_{1}} + \frac{i}{{n_{2}^{1}}}\left( {D_{2}^{2} - {{D}_{1}}} \right) n_{2}^{1} > 0; i = 0{\kern 1pt} - {\kern 1pt} n_{2}^{1} |
{{D}^{i}} = {{D}_{1}} + \frac{i}{{n_{2}^{2}}}\left( {D_{2}^{1} - {{D}_{1}}} \right) n_{2}^{2} > 0; i = 0{\kern 1pt} - {\kern 1pt} n_{2}^{2} |
| {{S'}_{1}}\left( {{{D}^{i}}} \right) по (П.6) | S_{1}^{'}\left( {{{D}^{i}}} \right) по (П.6) | S_{2}^{'}\left( {{{D}^{i}}} \right) по (П.7) |
| M_{0}^{i} = \frac{{{{D}^{i}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {S_{1}^{'}({{D}^{i}}) - {{S}_{0}}} \right] | M_{0}^{i} = \frac{{{{D}^{i}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {S_{1}^{'}({{D}^{i}}) - {{S}_{0}}} \right] | M_{0}^{i} = \frac{{{{D}^{i}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {S_{2}^{'}({{D}^{i}}) - {{S}_{0}}} \right] |
| {\text{Мн1}}:\;\left\{ {M_{0}^{i},\;{{D}^{i}}} \right\} | {\text{Мн1}}*:\;\left\{ {M_{0}^{i},\;{{D}^{i}}} \right\} | {\text{Мн2}}*:\;\left\{ {M_{0}^{i},\;{{D}^{i}}} \right\} |
| Часть III | ||
| S_{2}^{'}\left( {{{D}_{4}}} \right) < {{S}_{0}} < S{\kern 1pt} '\left( {{{D}_{2}}} \right) | ||
| D_{3}^{1} и D_{3}^{2} по (П.7); S_{2}^{'} = {{S}_{0}}, D_{3}^{1} < {{D}_{4}}, D_{3}^{2} > {{D}_{4}} | ||
| {{D}^{i}} = {{D}_{1}} + \frac{i}{{n_{3}^{1}}}\left( {{{D}_{2}} - {{D}_{1}}} \right) n_{3}^{1} > 0; i = 0{\kern 1pt} - {\kern 1pt} n_{3}^{1} |
{{D}^{i}} = {{D}_{1}} + \frac{i}{{n_{3}^{2}}}\left( {D_{3}^{1} - {{D}_{1}}} \right) n_{3}^{2} > 0; i = 0{\kern 1pt} - {\kern 1pt} n_{3}^{2} |
{{D}^{i}} = D_{3}^{2} + \frac{i}{{n_{3}^{3}}}\left( {{{D}_{2}} - D_{3}^{2}} \right) n_{3}^{3} > 0; i = 0{\kern 1pt} - {\kern 1pt} n_{3}^{3} |
| S_{1}^{'}\left( {{{D}^{i}}} \right) по (П.6) | S_{2}^{'}\left( {{{D}^{i}}} \right) по (П.7) | S_{2}^{'}\left( {{{D}^{i}}} \right) по (П.7) |
| M_{0}^{i} = \frac{{{{D}^{i}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {S_{1}^{'}({{D}^{i}}) - {{S}_{0}}} \right] | M_{0}^{i} = \frac{{{{D}^{i}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {S_{2}^{'}({{D}^{i}}) - {{S}_{0}}} \right] | M_{0}^{i} = \frac{{{{D}^{i}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {S_{2}^{'}({{D}^{i}}) - {{S}_{0}}} \right] |
| {\text{Мн1}}**:\;\left\{ {M_{0}^{i},\;{{D}^{i}}} \right\} | {\text{Мн2}}**:\;\left\{ {M_{0}^{i},\;{{D}^{i}}} \right\} | {\text{Мн3}}**:\;\left\{ {M_{0}^{i},\;{{D}^{i}}} \right\} |
Для каждого номера из (29) и принятого S0 по (П.11) вычисляются остальные показатели процесса.
Часть II. Особенностью для части II является возможность формирования двух множеств Мн1* и Мн2* для задания M0 и D при принятом S0.
2.1. Для обоих множеств общим является вычисление D_{2}^{1} по решению (П.7), где S_{2}^{'} = {{S}_{0}}, и D_{2}^{2} по решению (П.6), где S_{1}^{'} = {{S}_{0}}, S0 по условию (22).
2.2. Последовательность формирования множеств аналогична последовательности для части I (здесь не приводится). Результирующие формулы даны в табл. 4 для множеств Мн1* и Мн2*.
Часть III. Особенностью для части III является возможность формирования трех множеств Мн1**, Мн2** и Мн3** для задания M0 и D при принятом S0.
3.1. Для трех множеств общим является вычисление D_{3}^{1} и D_{3}^{2} по решению уравнения (П.7), где S_{2}^{'} = {{S}_{0}}, S0 по условию (23).
3.2. Последовательность формирования множеств аналогична последовательности для части I (так же как и части II, и здесь не приводится). Результирующие формулы даны в табл. 4 для множеств Мн1**, Мн2** и Мн3**.
Ниже приведены результаты числового расчета показателей технологического процесса, полученные по соотношениям табл. 4 с использованием формул (П.11) для констант табл. 2. На рис. 1 показаны зависимости S{\kern 1pt} ' от D, полученные по условию QP < maxQP: QP = 6.0, 7.0 и 8.0 г/(л ч).
Рис. 1.
Зависимость S{\kern 1pt} ' от D для значений QP, г/(л ч): 6.0; 7.0; 8.0. Особые точки 1, 2, 3 и 4 – QP = 6 г/(л ч); точка 5 – maxQP.
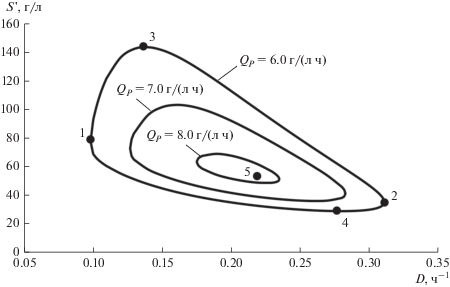
Зависимости получены по решению уравнений (П.6) и (П.7). На рисунке также обозначена точка 5 (maxQP). Нетрудно видеть, что область технологических показателей сужается с увеличением QP.
ЧИСЛЕННЫЙ РАСЧЕТ
Расчет выполняется для всех трех частей согласно табл. 4. В расчете использованы численные значения констант базового варианта (табл. 2) для системы (1). Во всех приведенных ниже расчетах использованы данные предварительного анализа для точки экстремума и особых точек, а также формулы табл. 4 с указанием вида множества.
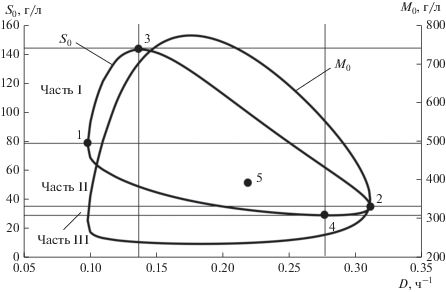
На рис. 2 показаны портреты для S0 и M0, ограничивающие их значения при QP = 6.0 г/(л ч).
Портрет S0 содержит значения в области величины протока D по координатам особых точек 1 и 2, т.е. значений от 0.09818 до 0.3107 ч–1. Все значения S0 при M0 = 0.
Портрет M0 содержит значения для той же области D для всех M0 при S0 = 0.
На рис. 2 отмечены границы частей I, II и III в соответствии с (21)–(23), по которым выполнен дальнейший расчет.
Часть I
1. Принимается значение S0 согласно неравенству (21):
Принято S0 = 91.932 г/л.
Вычисления по пп. 2–4 проводятся по формулам табл. 4 для множества Мн1.
2. Вычисляются D_{1}^{1} и D_{1}^{2} по (П.6) по следующему условию:
D_{1}^{1} < {{D}_{3}}, т.е. D_{1}^{1} < 0.138 ч–1; D_{1}^{2} > {{D}_{3}}, т.е. D_{1}^{2} > > 0.138 ч–1. S_{1}^{'} в (П.6) равно{{S}_{0}} = 91.932 г/л.
Получено D_{1}^{1} = 0.1 ч–1; D_{1}^{2} > 0.23045 ч–1.
3. Вычисляется Di.
Показатели n1 > 0 и i = 0.0–n1 выбраны следующим образом.
Записали \Delta = D_{1}^{2} - D_{1}^{1} = 0.23045 – 0.1 = 0.13045.
Значение n1 принято равным 6.552; значения i: 0.0; 1.0; 2.0; 3.0; 4.0; 5.0; 6.0; 6.552.
Полученные значения Di для соответствующих значений i приведены в табл. 5.
Таблица 5.
Результаты вычислений Di, S_{1}^{'}\left( {{{D}^{i}}} \right) и M_{0}^{i}
| i | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 6.552 |
| Di | 0.1 | 0.12 | 0.14 | 0.16 | 0.18 | 0.20 | 0.22 | 0.23045 |
| S_{1}^{'}\left( {{{D}^{i}}} \right) | 91.932 | 136.14 | 143.20 | 137.15 | 125.85 | 112.64 | 99.00 | 91.932 |
| M_{0}^{i} | 0.0 | 195.78 | 256.34 | 251.93 | 208.35 | 139.04 | 51.495 | 0.0 |
4. Вычисляем S_{1}^{'}({{D}^{i}}) и M_{0}^{i}.
Результаты вычислений по п. 4 также сведены в табл. 5.
Таким образом, для S0 = 91.932 г/л получили множество Мн1 из 8 пар значений (M_{0}^{i}, {{D}^{i}}). Количество пар может быть иным в зависимости от заданных значений i по условию i = 0–n1 и заданных значений n1.
В данном случае (в приведенном расчете) пользователь может сделать выбор из 8 вариантов. Остальные показатели процесса для каждого из вариантов вычисляются по (П.11).
Так, если принят вариант для i = 3.0, технологические показатели по (П.11) будут: S0 = 91.932 г/л; M0 = 251.93 г/л; D = 0.16 ч–1; P = 37.5 г/л; X = 16.13 г/л; S = 96.83 г/л; M = 206.71 г/л; B = 18.75 г/л.
Расчет по части I завершен.
Часть II. В части II формируются два множества Мн1* и Мн2* (см. табл. 4). В дальнейшем расчете пп. 1 и 2 являются общими для Мн1* и Мн2*.
1. Принимается значение S0 согласно неравенству (22):
Принято S0 = 53.54 г/л.
2. Вычисляется D_{2}^{1} по (П.7), где D_{2}^{1} < {{D}_{4}}, т.е. D_{2}^{1} < 0.28 ч–1. S_{2}^{'} в (П.7) равно S0 = 53.54 г/л. Получено D_{2}^{1} = 0.1237 ч–1.
Вычисляется D_{2}^{2} по (П.6), где D_{2}^{2} > {{D}_{4}}, т.е. D_{2}^{2} > > 0.28 ч–1. S_{2}^{'} в (П.6) равно S0 = 53.54 г/л. Получено D_{2}^{2} = 0.29 ч–1.
Формирование Мн1*
Вычисление по пп. 3–5 проводится по формулам табл. 4 для множества Мн1*.
3. Вычисляется Di.
Показатели n_{2}^{1} > 0и i = 0.0 - n_{2}^{1} выбраны следующим образом.
Записали \Delta = D_{2}^{2} - {{D}_{1}} = 0.29 – 0.09818 = 0.19182.
Значение n_{2}^{1} принято равным 19.18; значения i: 0.0; 1.0; 1.5; 2.0; 2.552; 3.0; …; 19.0; 19.18.
Полученные значения Di для соответствующих значений i приведены в табл. 6.
Таблица 6.
Результаты расчетов по пп. 4 и 5 для Мн1* и Мн2*
| Множество | i | 0.0 | 1.0 | 1.5 | 2.0 | 2.552 | 3.0 | … | 19.18 |
| Di | 0.09818 | 0.1082 | 0.1132 | 0.1182 | 0.1237 | 0.1282 | … | 0.29 | |
| Мн1* | {{S'}_{1}}\left( {{{D}^{i}}} \right) | 77.6 | 118.207 | 127.72 | 134.30 | 139.09 | 141.48 | … | 53.54 |
| M_{0}^{i} | 91.55 | 264.58 | 314.10 | 353.50 | 387.91 | 410.05 | … | 0.0 | |
| Мн2* | {{S'}_{2}}\left( {{{D}^{i}}} \right) | 77.6 | 61.42 | 58.49 | 56.01 | 53.54 | |||
| M_{0}^{i} | 91.55 | 32.24 | 20.960 | 10.811 | 0.0 |
4. Вычисляем {{S'}_{1}}\left( {{{D}^{i}}} \right).
5. Вычисляется M_{0}^{i}.
Результаты вычислений по пп. 4 и 5 также сведены в табл. 6.
Таким образом, для S0 = 53.54 г/л получили множество Мн1* из 22 пар значений (M_{0}^{i}, Di). Количество пар может быть иным в зависимости от заданных значений i по условию i = 0.0 - n_{2}^{1} и заданных значений n_{2}^{1}.
В данном расчете пользователь может сделать выбор из 22 вариантов. Остальные показатели процесса для каждого из вариантов вычисляются по (П.11).
Формирование Мн2*
Как уже отмечалось выше, пп. 1 и 2 в части II являются общими для Мн1* и Мн2*. Поэтому дальнейший расчет проводится с п. 3 (3а).
Вычисление по пп. 3а–5а проводится по формулам табл. 4 для множества Мн2*.
3а. Вычисляется Di.
Показатели n_{2}^{2} > 0 и i = 0.0 - n_{2}^{2} выбраны следующим образом.
Записали \Delta = D_{2}^{1} - {{D}_{1}} = 0.1237 – 0.09818 = 0.02552.
Значение n_{2}^{2} принято равным 2.552; значения i: 0.0; 1.0; 1.5; 2.0; 2.552.
Полученные значения Di для соответствующих значений i приведены в табл. 6.
4а. Вычисляем S_{2}^{'}({{D}^{i}}).
5а. Вычисляется M_{0}^{i}.
Результаты вычислений по пп. 4а и 5а сведены в табл. 6.
Таким образом, для S0 = 53.54 г/л получили множество Мн2* из 4 пар значений (M_{0}^{i}, Di). Количество пар может быть иным в зависимости от заданных значений i по условию i = 0.0 - n_{2}^{2} и заданных значений n_{2}^{2}.
В данном расчете пользователь может сделать выбор из 4 вариантов. Остальные показатели процесса для каждого из вариантов вычисляются по (П.11).
В заключении по приведенному расчету для части II отметим следующее.
Значение i для Мн1* и Мн2* подбиралось таким образом, чтобы для n_{2}^{1} = 19.18 в Мн1* и для n_{2}^{2} = 2.552 в Мн2* первые 4 значения в обоих множествах Di были одинаковыми (см. табл. 6). Это дало возможность сравнить показатели процесса по (П.11) для значения Di первых четырех компонентов Мн1* и Мн2*. Результаты расчета приведены в табл. 7.
Таблица 7.
Результаты оценок технологических показателей по (П.11) для i = 1.5 в Мн1* и Мн2*
| Множество | S0, г/л | D1.5, ч–1 | M_{0}^{{1.5}}, г/л | P, г/л | X, г/л | B, г/л | S, г/л | M, г/л |
|---|---|---|---|---|---|---|---|---|
| Мн1* | 53.54 | 0.1132 | 314.10 | 53.00 | 22.30 | 26.50 | 71.97 | 239.92 |
| Мн2* | 53.54 | 0.1132 | 20.96 | 53.00 | 22.30 | 26.50 | 2.736 | 16.00 |
Значение i для каждого из множеств для сравнения принято равным 1.5. В результате использованы следующие данные:
для Мн1*: S0 = 53.54 г/л; D1.5 = 0.1132 ч–1; M_{0}^{{1.5}} = 314.11 г/л; QP = 6.0 г/(л ч);
для Мн2*: S0 = 53.54 г/л; D1.5 = 0.1132 ч–1; M_{0}^{{1.5}} = 20.96 г/л; QP = 6.0 г/(л ч).
Часть III. В части III формируются три множества Мн1**, Мн2** и Мн3** (см. табл. 4). В дальнейшем расчете пп. 1 и 2 являются общими для Мн1**, Мн2** и Мн3**.
1. Принимается значение S0 согласно неравенству (23):
Принято S0 = 30 г/л.
2. Вычисляются D_{3}^{1} и D_{3}^{2} по (П.7), где D_{3}^{1} < {{D}_{4}}, т.е. D_{3}^{1} < 0.28 ч–1; D_{3}^{2} > {{D}_{4}}, т.е. D_{3}^{2} > 0.28 ч–1. S_{2}^{'} в (П.7) равно 30 г/л. Получено D_{3}^{1} = 0.25 ч–1; D_{3}^{2} = 0.30.
Формирование Мн1**
Вычисление показателей по пп. 3–5 проводится по формулам табл. 4 для множества Мн1**.
3. Вычисляется Di.
Показатели n_{3}^{1} > 0 и i = 0.0 - n_{3}^{1} выбраны следующим образом.
Записали \Delta = {{D}_{2}} - {{D}_{1}} = 0.3107 – 0.09818 = 0.2125.
Значение n_{3}^{1} принято равным 10.62; значения i: 0.0; 1.0; 2.0; 3.0; …; 7.59; …; 10.09; 10.216; 10.341; 10.466; 10.62.
Полученные значения Di для соответствующих значений i приведены в табл. 8.
Таблица 8.
Результаты расчетов по пп. 4 и 5 для Мн1**, Мн2** и Мн3**
| Мн1** | Мн2** | ||||
|---|---|---|---|---|---|
| i | {{D}^{i}} | S_{1}^{'} | M_{0}^{i} | S_{2}^{'} | M_{0}^{i} |
| 0.0 | 0.09818 | 77.6 | 181.12 | 77.6 | 181.12 |
| 1.0 | 0.1182 | 134.30 | 456.54 | 56.00 | 113.80 |
| 2.0 | 0.1382 | 143.28 | 560.57 | 48.33 | 90.71 |
| 3.0 | 0.1582 | 138.00 | 596.16 | 42.79 | 70.60 |
| … | … | … | … | … | … |
| 7.59 | 0.25 | 79.03 | 400.00 | 30.04 | 0.0 |
| … | … | … | … | Мн3** | |
| 10.09 | 0.30 | 46.78 | 160.61 | 30.02 | 0.0 |
| 10.216 | 0.3025 | 44.933 | 143.997 | 30.419 | 4.04 |
| 10.341 | 0.305 | 42.676 | 123.138 | 31.093 | 10.618 |
| 10.466 | 0.3075 | 40.695 | 104.65 | 31.808 | 17.693 |
| 10.62 | 0.3107 | 35.35 | 52.842 | 35.35 | 52.842 |
4. Вычисляем S_{1}^{'}({{D}^{i}}).
5. Вычисляется M_{0}^{i}.
Результаты вычислений по пп. 4 и 5 также сведены в табл. 8.
Формирование Мн2**
Вычисление показателей по пп. 3а–5а проводится по формулам табл. 4 для множества Мн2**.
3а. Вычисляется Di.
Показатели n_{3}^{2} > 0 и i = 0.0 - n_{3}^{2} выбраны следующим образом.
Записали \Delta = D_{3}^{1} - {{D}_{1}} = 0.25 - 0.09818 = 0.1518 .
Значение n_{3}^{2} принято равным 7.59; значения i: 0.0; 1.0; 2.0; 3.0; …; 7.59.
Полученные значения Di для соответствующих значений i приведены в табл. 8.
4а. Вычисляем S_{2}^{'}({{D}^{i}}).
5а. Вычисляется M_{0}^{i}.
Результаты вычислений по пп. 4а и 5а также сведены в табл. 8.
Формирование Мн3**
Вычисление по пп. 3б–5б проводится по формулам табл. 4 для множества Мн3**.
3б. Вычисляется Diи значения i в области значений Di: 0.3–0.3107.
Значения Di приняты равными 0.3; 0.3025; 0.305; 0.3075; 0.3107.
Соответствующие значения i по формуле расчета Diв табл. 4 по Мн3**: Di = 0.3 (i = 10.09); Di= 0.3025 (i = 10.216); Di= 0.305 (i = 10.341); Di= 0.3075 (i = 10.466); Di = 0.3107 (i = 10.62).
Значения D i представлены в табл. 8.
4б. Вычисляем S_{2}^{'}({{D}^{i}}).
5б. Вычисляем M_{0}^{i}.
Результаты вычислений по пп. 4б и 5б также сведены в табл. 8.
Сопоставление результатов оценок показателей процесса для множеств Мн1** и Мн2** для i = 2.0 (см. табл. 8) приведено в табл. 9.
Таблица 9.
Результаты оценок технологических показателей по (П.11) для i = 2.0 в Мн1** и Мн2** (табл. 8)
| Множество | S0, г/л | D2, ч–1 | M_{0}^{2}, г/л | P, г/л | X, г/л | B, г/л | S, г/л | M, г/л |
|---|---|---|---|---|---|---|---|---|
| Мн1** | 30 | 0.1382 | 560.57 | 43.415 | 18.516 | 21.707 | 96.99 | 447.29 |
| Мн2** | 30 | 0.1382 | 90.71 | 43.415 | 18.516 | 21.707 | 2.04 | 72.379 |
Сопоставление результатов оценок показателей процесса для множеств Мн1** и Мн3** для i = = 10.341 (см. табл. 8) приведено в табл. 10.
Таблица 10.
Результаты оценок технологических показателей по (П.11) для i = 10.341 в Мн1** и Мн3** (табл. 8)
| Множество | S0, г/л | D10.341, ч–1 | M_{0}^{{10.341}}, г/л | P, г/л | X, г/л | B, г/л | S, г/л | M, г/л |
|---|---|---|---|---|---|---|---|---|
| Мн1** | 30 | 0.305 | 123.138 | 19.672 | 8.683 | 9.836 | 20.968 | 110.462 |
| Мн3** | 30 | 0.305 | 10.618 | 19.672 | 8.683 | 9.836 | 9.386 | 9.525 |
ЗАКЛЮЧЕНИЕ
Разработанная методология оценки множеств и их наполнение для определения входных показателей процесса M0 и D по заданному значению S0 является универсальной, т.е. может быть использована для любых значений S0, определяемых в границах условия функционирования определенных штаммов микроорганизмов.
Диапазон возможных заданий S0 определяется для каждой из частей. Так, для части I этот диапазон самый широкий – от S0(D1) до maxS0(D3); для части II диапазон уже – от S0(D1) до S0(D2); и самый узкий для части III − от S0(D2) до minS0(D4).
Диапазон оценок по величине протока самый широкий от D1 до D2 по части III; меньший по части II и самый узкий по части I.
Сопоставление результатов расчета для одинаковых начальных условий (S0, D) по множеству 1* и 2* в части II и по 1** и 2** и 1** и 3** по части III показало следующее. Показатели процесса различаются по М0, M и S (см. табл. 7, 9, 10), причем различия существенные. Последнее очень важно, так как технология процесса получения молочной кислоты включает последующие стадии − выделение целевого продукта, побочных продуктов, остатков сырьевых компонентов S и M.
Таким образом, разработанная методология может служить теоретической основой для создания непрерывного технологического процесса ферментативного получения молочной кислоты по заданному значению S0 и выбору подходящих начальных значений M0 и D.
Исследование выполнено при финансовой поддержке РХТУ им. Д.И. Менделеева. The reported study was funded by Mendeleev University of Chemical Technology.
Инструменты
Теоретические основы химической технологии