1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 54, № 4, 2020

Теоретические основы химической технологии, 2020, T. 54, № 4, стр. 504-513

Моделирование термогазодинамических процессов при получении кремния из его галогенидов

Л. В. Шабарова a, *, А. Д. Плехович a, А. М. Кутьин a, П. Г. Сенников a, Р. А. Корнев a

a Институт химии высокочистых веществ им. Г.Г. Девятых РАН
Нижний Новгород, Россия

* E-mail: shabarova@ihps.nnov.ru

Поступила в редакцию 07.02.2019
После доработки 07.02.2020
Принята к публикации 14.02.2020

Полный текст (PDF)

Аннотация

Разработана методика моделирования газодинамических и тепловых условий получения порошкообразного кремния из тетрахлорида и тетрафторида кремния в высокочастотном индукционном плазмохимическом реакторе. Модель включает в себя описание турбулентного течения смеси идеальных вязких сжимаемых газов с учетом индуктивного нагрева газа посредством теплопроводности, конвекции и излучения, а также с учетом влияния силы электромагнитного поля на движение плазмы. Образование порошкообразных частиц реализуется в соответствии с результатами термодинамических расчетов, а распределение частиц в потоке описывается механизмом диффузии. Приведены результаты моделирования конверсии летучих хлорида и фторида кремния в высокочастотном индукционном плазмотроне с вихревой стабилизацией потока.

Ключевые слова: вычислительный эксперимент, идеальный газ, термодинамика, электромагнитное поле, диффузия, кремний

ВВЕДЕНИЕ

Галогениды кремния SiX4 (X = Cl, F) являются основными участниками различных технологических цепочек получения высокочистого кремния. Тетрахлорид кремния представляет собой основной побочный продукт при получении кремния водородным восстановлением трихлорсилана [1], силана при диспропорционировании трихлорсилана [2] и при синтезе гексахлордисилана [3]. Содержание примесей в тетрахлориде кремния находится на уровне чистоты исходного трихлорсилана. Поэтому важной задачей является перевод этого высокочистого побочного продукта как в хлорсиланы, так и собственно кремний [1]. Особенно перспективны для этой цели плазмохимические методы гидрирования тетрахлорида кремния. В ранних патентах [4, 5] гидрирование тетрахлорида кремния проводили в условиях ВЧ-разряда (13.56 МГц), а в [6] – в условиях дугового (12.5 кВт) разряда в водородной плазме. В [7] разработан метод получения трихлорсилана в разряде постоянного тока в аргоно-водородной плазме. В [8–10] исследовался процесс разложения тетрахлорида кремния с образованием элементарного кремния в СВЧ-разряде. В [11] изучалось применение низкочастотной плазмы (880 кГц) для осаждения тонких пленок кремния из SiCl4. Была достигнута высокая скорость роста и степень нанокристалличности. В целом, однако, несмотря на многочисленные исследования процесса восстановления тетрахлорида кремния в различных типах разрядов, плазмотрон с технологическими характеристиками, пригодными для промышленного применения, до сих пор не разработан.

Структурный аналог тетрахлорида кремния – тетрафторид кремния SiF4 – содержит в своем составе максимальное количество кремния (27%) и поэтому перспективен для его получения, тем более что он является отходом различных производств и доступен в промышленных количествах [12, 13]. Хорошо известна технология компании Ethyl Corporation, по которой тетрафторид кремния переводится в силан [14] с последующим выделением поликремния. Прямое восстановление фторида кремния или его термическое разложение до элементарного кремния практически невозможно из-за высокой энергии связи Si–F, равной 540 кДж/моль [15]. Альтернативой может быть вновь плазмохимический метод конверсии SiF4 в кремний. Известны многочисленные работы (см., например, [16–19]), посвященные получению тонких пленок аморфного и микрокристаллического кремния из низкотемпературной неравновесной плазмы как на основе чистого SiF4, так и его смеси с силаном, поддерживаемой разрядами различных типов. Необходимость использования этого производного кремния в данном случае обусловлена модификацией поверхности слоев кремния активными радикалами фтора. Однако для получения поликристаллического порошка кремния этот подход впервые был реализован только сравнительно недавно в работе [20]. В высокочастотном индукционном разряде при 13.56 МГц и введенной мощности 4 кВт при давлении газовой смеси SiF4/Н2/Ar от 0.1 до 30 торр получали мелкодисперсный порошок Si, причем процесс был организован таким образом, что частицы кремния укрупнялись в ходе процесса разложения фторида. Скорость осаждения составляла от 0.5 до 5 г/ч. Авторы патента [20] полагают, что с целью повышения производительности процесс осаждения можно проводить при мощности до 50 кВт, давлении 100–1000 торр и соотношении потоков фторида и водорода 1/1. К сожалению, в этой работе не приводятся количественные данные о реализации предложенной технологии и о степени чистоты получаемого кремния.

Перспективным методом одностадийного восстановления галогенидов до элементарного кремния может быть термическая аргоно-водородная плазма мощного высокочастотного индукционного (ВЧИ) плазмотрона [21, 22]. Данный тип плазмотронов успешно применяется для различных целей, например в процессах высокотемпературной обработки поверхностей [23], сфероидизации порошков [24], для получения материалов (например, нитрида бора [25]). Использование плазмы и плазмотронов данного типа позволяет получать локализованную внутри кварцевой трубы термическую плазму, не загрязненную конструкционными материалами реактора [26], что является важным фактором при получении высокочистых веществ и материалов.

На начальном этапе конструирования ВЧИ-плазмотрона целесообразно провести анализ эффективности газодинамических и тепловых условий получения кремния из его галогенидов в смеси с водородом и аргоном в термической плазме, поддерживаемой ВЧИ-разрядом. Такой анализ возможен с помощью методики моделирования термогазодинамических процессов, основанной на сочетании термодинамического расчета состава термической плазмы [27] и моделирования плазмохимического реактора методами вычислительной гидродинамики (CFD-моделирования) [28–32]. Термодинамические расчеты позволяют получить температурную зависимость концентрации веществ, образовывающихся в плазме. В свою очередь, с помощью CFD-моделирования можно получить газодинамическую картину движения в плазмохимическом реакторе как исходных компонентов газовой смеси, так и продуктов реакции. Совместное использование инструментов вычислительной гидродинамики и методик термодинамических расчетов позволяет предсказать оптимальные режимы работы и конструкцию ВЧИ-плазмотрона.

В работе [33] методами вычислительной гидродинамики исследовано течение аргоно-водородной плазмы в ВЧИ-плазмотроне мощностью до 50 кВт с вихревой подачей плазмообразующего газа, определены тепловые и кинетические условия индуктивного нагрева плазмы.

Цель настоящей работы – сравнительный теоретический анализ процессов водородного восстановления тетрахлорида кремния и тетрафторида кремния в ВЧИ-плазме при совместном использовании методов вычислительной газодинамики и термодинамики. Её применение определяет газодинамические, тепловые и термодинамические условия получения кремния из его летучих хлорида и фторида в ВЧИ-плазмотроне с вихревой стабилизацией потока аргоно-водородной плазмы.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

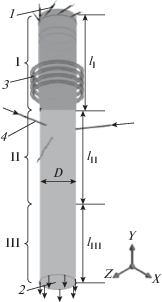
Математическая модель плазмохимического реактора. Вычислительные эксперименты проведены для модели плазмохимического реактора мощностью до 50 кВт с вихревой подачей плазмообразующего газа (рис. 1). Рассматривается течение в плазмотроне I, в котором реализуется формирование и индуктивный нагрев аргоно-водородной плазмы; в реакционной камере II, в которую осуществляется подача газа-носителя водорода и газа-реагента; а также в охлаждаемом канале III, в котором целевой продукт конверсии конденсируется.

Рис. 1.

Схема ВЧИ-плазмохимического реактора: 1 – входные трубки для подачи смеси Ar–Н2 (8 трубок); 2 – выход; 3 – индуктор; 4 – входные трубки для подачи газа-носителя и газа-реагента (3 трубки); I – зона индуктивного нагрева плазмы; II – реакционная зона; III – охлаждаемый канал; D = 0.1 м, lI = 0.3 м, lII = 0.4 м, lIII = 4 м.

Задачу моделирования газодинамики плазмохимического реактора целесообразно разбить на два этапа. На первом этапе решается задача течения в аргоно-водородной индуктивно связанной плазме в зоне плазмотрона I. Соответствующие методика и результаты моделирования приведены в [10]. Модель включает описание турбулентного течения вязкого сжимаемого газа в неоднородном температурном поле с учетом индуктивного нагрева газа посредством теплопроводности, конвекции и излучения, а также с учетом влияния силы электромагнитного поля на движение плазмы.

На втором этапе решается задача течения аргоно-водородной плазмообразующей смеси и поступающих из входных трубок 4 (рис. 1) газа-носителя и газов-реагентов в зонах II и III (рис. 1). Определенные в результате решения задачи в зоне I поля скоростей и температур аргоно-водородной смеси используются при задании граничного условия на границе плазмотрона и реакционной камеры при решении задачи в зонах II и III. Ниже изложена математическая постановка газодинамической и тепловой задачи в зонах II и III (рис. 1) с учетом образования целевого продукта на основании термодинамических расчетов.

Процесс рассматривается как задача о гомогенном движении вязких сжимаемых идеальных газов (аргоно-водородная смесь, газ-носитель водород и газ-реагент) в неоднородном температурном поле с учетом теплообмена посредством теплопроводности и конвекции. Режим течения газа полагается турбулентным. На основании [33] и предварительных расчетов по верификации модели образование порошкообразных частиц целевого продукта рассматривается в следующих допущениях.

1. На этапе развития и формирования плазмы в зоне I реактора еe химический состав считается близким к равновесному состоянию вследствие высокой температуры и существенно активированной электронной подсистемы. Совместное действие указанных факторов в значительной степени снимает кинетические ограничения на достижение термически и химически равновесных состояний, состав которых, соответствующий температурам по сечениям реактора, представлен на рис. 2. В неравновесном процессе термической и химической релаксации реакционной смеси, протекающем за зоной еe плазмохимической активации, превалирующий по концентрации водород связывает активный фтор или хлор с образованием HF или HCl и качественно обосновывает упрощающее допущение о диффузионном формировании фазы дисперсного кремния из газообразных атомов кремния. Отметим, что скорость достаточно быстрых безактивационных процессов релаксационной кинетики является диффузионно определяющей.

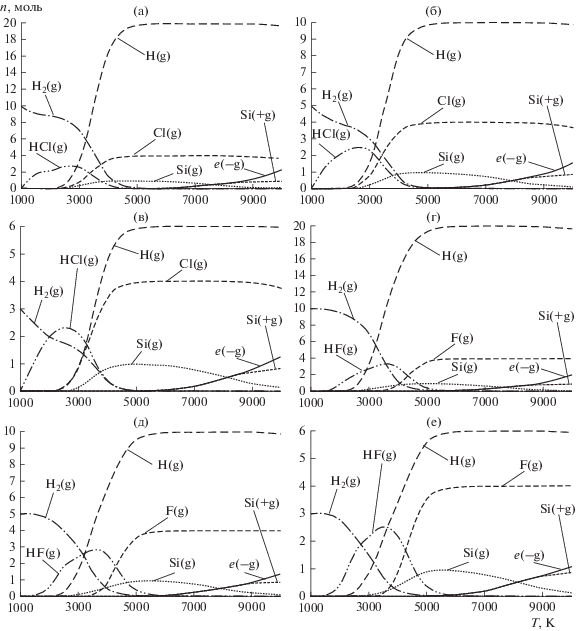
Рис. 2.

Температурная зависимость состава продуктов превращения при давлении 1 атм для следующих смесей: (а) – 1SiCl4 + 10H2 + 50Ar; (б) – 1SiCl4 + 5H2 + 25Ar; (в) – 1SiCl4 + 3H2 + 15Ar; (г) – 1SiF4 + 10H2 + 50Ar; (д) – 1SiF4 + 5H2 + + 25Ar; (е) – 1SiF4 + 3H2 + 15Ar.

2. Из всех возможных продуктов реакции в газодинамическую модель течения включается только целевой продукт (кремний). Его образование описывается температурным законом, полученным на основании соответствующего термодинамического расчета, в зависимости от концентрации в данной ячейке расчетной области газов-реагентов. Авторами были проведены физические эксперименты по водородному восстановлению фторида кремния при атмосферном давлении в ВЧИ-плазмотроне мощностью до 16 кВт, конструкция которого была аналогична исследуемому плазмохимическому реактору. В экспериментах наблюдалось осаждение конденсированного кремния на внутренней поверхности формирователя газового потока. На основании указанных результатов физических экспериментов полагается, что газообразный и ионизированный кремний в охлаждаемом канале III перейдет в конденсированную форму. Процесс конденсации в задаче не моделируется.

3. Радиус порошкообразных частиц кремния составляет около 100 нм, что позволяет отнести их к классу высокодисперсных коллоидных частиц. Определение размера частиц порошка проводили на анализаторе размера частиц SALD 2300 (Shimadzu) методом лазерной дифракции, а также методом сканирующей электронной микроскопии на электронных микроскопах SUPRA 50VP и NEON 40 (Carl Zeiss, Германия). Движение таких частиц в газообразной и жидкой средах имеет характер хаотического броуновского движения. Для описания распределения порошкообразных частиц целевого продукта в газовой смеси справедливо диффузионное представление и применимо уравнение диффузии.

Ввиду отсутствия физической симметрии течения задача решалась в трехмерной постановке. Расчетная область задачи включает в себя реакционную зону плазмохимического реактора (зона II, рис. 1) и охлаждаемый канал (зона III, рис. 1). Течение газов описывается следующей системой уравнений [34]:

(1)
${\text{div}}({{f}_{i}}{{\rho }_{i}}\bar {V}) - {{S}_{{{\text{reag}}}}} = 0,$
(2)
$\begin{gathered} {\text{div}}(\rho \bar {V} \times \bar {V}) = - {\text{gradp}} + \\ + \,\,{\text{div}}\left( {{{\mu }_{e}}\left( {{\text{grad}}\bar {V} + {{{({\text{grad}}\bar {V})}}^{T}} - \frac{2}{3}\delta {\text{div}}\bar {V}} \right)} \right), \\ \end{gathered} $
(3)
${\text{div}}(\rho {{c}_{p}}T \times \bar {V}) = {\text{div}}({{\lambda }_{e}}\nabla T) + \frac{{\partial p}}{{\partial t}}.$

В уравнениях неразрывности (1), движения (2) и энергии (3) индекс i = 1 соответствует аргоно-водородной плазмообразующей смеси, i = 2 – газу-носителю (водороду); i = 3 – газу-реагенту; fi, ρi – объемная доля и плотность соответствующей среды, при этом $\sum\limits_{i = 1}^3 {{{f}_{i}}} = 1;$ $\rho = \sum\limits_{i = 1}^3 {{{f}_{i}}{{\rho }_{i}}} $; V – скорость; p – давление, ${{c}_{p}}$ – удельная теплоемкость при постоянном давлении (${{c}_{p}} = \sum\limits_{i = 1}^3 {{{f}_{i}}{{c}_{p}}_{i}} $), Т – температура, ${{\mu }_{e}},{{\lambda }_{e}}$ – эффективные динамическая вязкость и теплопроводность, ${{\mu }_{e}} = \mu + {{\mu }_{t}}$, ${{\lambda }_{e}} = \lambda + {{\lambda }_{t}}$, $\mu ,\lambda $ – ламинарные вязкость и теплопроводность ($\mu = \sum\limits_{i = 1}^3 {{{f}_{i}}{{\mu }_{i}}} $, $\lambda = \sum\limits_{i = 1}^3 {{{f}_{i}}{{\lambda }_{i}}} $), ${{\mu }_{t}},{{\lambda }_{t}}$ – турбулентные (вихревые) вязкость и теплопроводность, Sreag – массовый источниковый член (сток) газа-реагента в единице объема. Система уравнений (1)–(3) замыкается SST-моделью (Shear Stress Transport) турбулентности Ментера [35].

Распределение целевого продукта описывается уравнением диффузии

(4)
${\text{div}}(\rho \bar {V}c) = {\text{div}}\left( {\sum\limits_{i = 1}^4 {{{\rho }_{i}}{{D}_{i}}} {\text{grad}}\,c} \right) + {{S}_{{{\text{reag}}}}},$
где с и Di – массовая концентрация и коэффициент диффузии в соответствующей среде порошкообразных частиц целевого продукта.

Величина источникового члена Sreag определяется в соответствии с результатами термодинамических расчетов состава термической плазмы:

(5)
${{S}_{{{\text{reag}}}}} = {{c}_{{M{\text{*}}}}}(T){{f}_{3}}{{\rho }_{3}}{{M{\text{*}}} \mathord{\left/ {\vphantom {{M{\text{*}}} {{{M}_{3}}}}} \right. \kern-0em} {{{M}_{3}}}},$
где ${{c}_{{M*}}}(T)$ – изменение мольной концентрации целевого продукта в единицу времени; M*, M3 – молярные массы соответственно целевого продукта и газа-реагента.

Коэффициенты диффузии порошкообразных частиц целевого продукта в расплавах оценивается по формуле Стокса–Эйнштейна [33]: Di = = $\frac{{kT}}{{6\pi {{\mu }_{i}}R}},$ где R – радиус частицы.

Система уравнений (1)–(3) дополняется граничными условиями, которые задаются в соответствии с экспериментальными условиями процесса конверсии в плазмохимическом реакторе с вихревой стабилизацией потока. На входы трубок 4 (рис. 1) подается смесь водорода и газа-реагента комнатной температуры с заданным объемным расходом и соотношением компонентов в смеси. На входную границу, отделяющую зоны плазмотрона I и реакционной камеры II, подается плазмообразующий газ с заданными на границе полями скоростей и температур, определенными из решения задачи в зоне плазмотрона I [33]. На выходной границе 2 задаeтся нулевое избыточное давление. На всех твердых стенках ставится условие прилипания, при этом в зоне реакционной камеры II температура боковой стенки составляет 1450 К, в зоне охлаждаемого канала III – 573 К; стенки входных трубок 4 полагаются адиабатическими.

Граничными условиями уравнения (4) являются нулевая концентрация с на входных границах 1, 4 и отсутствие потока целевого продукта через твердые стенки расчетной области.

В начальный момент времени в расчетной области находится покоящаяся смесь газа-носителя и газа-реагента комнатной температуры под нулевым избыточным давлением, концентрация целевого продукта равна нулю.

Значения плотности, вязкости, удельной теплоемкости и теплопроводности плазмообразующего газа и газа-носителя водорода в модели задаются функциями температуры [36–38].

Для исследованных газов-реагентов (SiF4, SiCl4,) удельная теплоемкость определяется по аддитивной схеме с использованием базы данных NIST, входные параметры для расчета – коэффициенты полиномиального эмпирического уравнения зависимости удельной теплоемкости газа от температуры. Вязкость рассчитывается по формуле Лихта и Штехерта [39], входные параметры для расчета – молярная масса, критическое давление и температура газа, средняя погрешность формулы по результатам экспериментов составляет 4.7% [39]. Теплопроводность рассчитывается по формуле Гильзенрата и Тулукяна, входные параметры для расчета – удельная теплоемкость и вязкость газа со средней погрешностью 8% [39].

Система уравнений (1)–(4) и дополнительные соотношения (5) с соответствующими граничными и начальными условиями представляют собой математическую модель термогазодинамики ВЧИ-плазмохимического реактора с завихрителем с учетом образования порошкообразных частиц целевого продукта. Проведено сеточное исследование задачи. Оптимальная сеточная модель содержит 800 000 элементов.

Термодинамическое моделирование многокомпонентной плазмохимической системы выполнено с помощью программного комплекса Chemical Thermodynamics Calculator [40], объединяющего компьютерную реализацию метода Гиббса [41] с его расширением на анализ так называемых условно-равновесных состояний вместе с банком термодинамических функций. В расчетах использован банк данных ИВТАН ТЕРМО [42].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Предложенная модель использована для сравнительного исследования конверсии тетрахлорида (SiCl4) и тетрафторида кремния (SiF4) в Si. Проведены вычислительные эксперименты для оценки производительности исследуемого плазмохимического реактора при образовании Si в зависимости от расхода газа-реагента (SiCl4 или SiF4). Расходы на входе в реактор соответствовали экспериментальным и составляли: 150 : 18 л/мин для плазмообразующей аргоно-водородной смеси Ar:Н2; 12 л/мин для газа-носителя водорода. Расход газа-реагента в расчетах являлся варьируемым параметром и составлял QГР = 3, 6 и 10 л/мин. Энерговыделение в плазме составляло 38 кВт. Радиус порошкообразных частиц Si задавался равным R = 100 нм.

На рис. 2 приведены термодинамически рассчитанные зависимости количества вещества основных продуктов реакции от температуры при соответствующих расходах газов и в соответствующем задаче температурном диапазоне. Данные, представленные на рис. 2, использованы при задании в математической модели источникового члена Sreag в уравнениях (1) и (4).

Ввиду малости концентраций продуктов реакции и, как следствие, незначительного влияния их на газодинамику плазмохимического реактора, из всех продуктов реакции, полученных по результатам термодинамического расчета, учитывались только целевые продукты – газообразный кремний и его ионизированная форма. При этом общее изменение молярной концентрации целевого продукта (Si) при расчете массового источника Sreag составляет

(6)
${{c}_{{M*}}} = {{c}_{{M{\text{Si}}g}}}(T) + {{c}_{{M{\text{Si}}g + }}}(T),$
где ${{c}_{{M{\text{Si}}g}}}(T),{{c}_{{M{\text{Si}}g + }}}(T)$ – изменения молярных концентраций соответственно газообразной и ионизированной форм кремния.

В газодинамической модели также не учитывалась диссоциация молекулярного водорода в атомарную форму на начальных этапах развития и формирования плазмы при температурах выше 3000 К (рис. 2), ввиду малости объема расчетной области (<7% от всего объема), температура в которой превышает 3000 К. Таким образом, образование кремния происходит согласно температурной зависимости концентрации (6), а его последующее диффузионное движение учитывается уравнениями модели (1)–(5).

Результаты моделирования тепловых и газодинамических условий в реакторе при конверсии SiCl4 в Si для случаев минимального и максимального расхода газа реагента ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{{\text{4}}}}}}}$ = 3 и 10 л/мин приведены на рис. 3.

Рис. 3.

(а) – поле температур в осевом сечении реактора; (б) – изоповерхность Т = 4000 К и линии тока в верхней части реактора; (в) – распределение объемной доли SiCl4 в осевом сечении.

Увеличение расхода ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{{\text{4}}}}}}}$ с 3 до 10 л/мин приводит к более резкому охлаждению плазмообразующего газа потоком, поступающим из трубок 4 (рис. 3а). Так, средняя температура газовой смеси в реакционной камере II падает на 8% (на 400 К), а в охлаждаемом канале III на 10% (на 130 К). Средняя осевая скорость потока при этом увеличивается незначительно. Отсутствие геометрической симметрии при вводе смеси H2 и SiCl4 приводит к нарушению осевой симметрии температурного поля (рис. 3а). Приведенные результаты свидетельствуют о завихренном течении газового потока, что обусловлено, в свою очередь, завихренностью потока, поступающего в плазмотрон из входных трубок 1. Поступающие из трубок 4 H2 и SiCl4 вовлекаются в общий вихревой поток (рис. 3б), в результате распределение SiCl4 в объеме реактора имеет спиральный характер (рис. 3в).

Результаты расчетов по массовой концентрации кремния в реакторе при конверсии SiСl4 в Si для различных расходов газа-реагента ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{{\text{4}}}}}}}$ приведены на рис. 4.

Рис. 4.

Распределение концентрации Si при его конверсии из SiCl4 в осевом (а) и поперечных сечениях реактора 1–5 (б–г) при ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{4}}}}}$ = 3 (б), 6 (в) и 10 (г) л/мин.

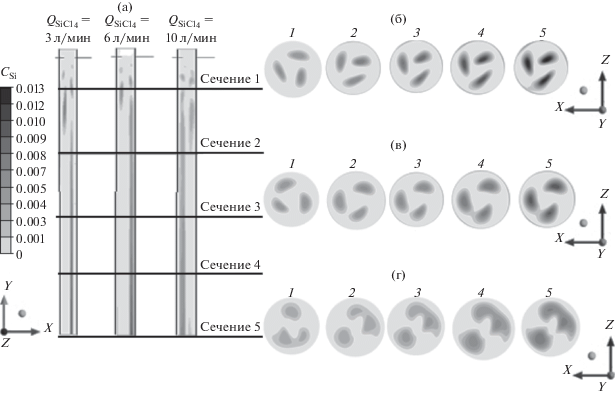
Производительность конверсии SiCl4 в Si, полученная по результатам вычислительного эксперимента, составляет 39 г/ч при степени конверсии γ = 18% для ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{{\text{4}}}}}}}$ = 3 л/мин, 46 г/ч при γ = 11% для ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{{\text{4}}}}}}}$ = 6 л/мин, 50 г/ч при γ = 7% для ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{{\text{4}}}}}}}$ = = 10 л/мин. Степень конверсии γ характеризует процентную долю газа-реагента, превратившуюся в ходе химической реакции в целевой продукт:

$\gamma = {{{{Q}_{M}}_{{{\text{Si - }}2}}M{\text{*}}} \mathord{\left/ {\vphantom {{{{Q}_{M}}_{{{\text{Si - }}2}}M{\text{*}}} {{{Q}_{M}}_{{{\text{ГР - }}4}}{{M}_{3}}}}} \right. \kern-0em} {{{Q}_{M}}_{{{\text{ГР - }}4}}{{M}_{3}}}} \times 100\% ,$
где QMSi-2 и QMГР-4 – массовые расходы соответственно кремния через выходную границу 2 и газа-реагента через входную границу 4.

При увеличении расхода SiCl4 выход целевого продукта несколько возрастает, но степень конверсии падает. Это связано с понижением температуры реактора (рис. 3а) и уменьшением объема высокотемпературной зоны (>3000 K), в которой, по результатам термодинамических расчетов, должно происходить образование Si (рис. 2). Вместе с тем термодинамические расчеты свидетельствуют, что чем выше соотношение H2 : SiCl4 в газовой смеси, тем больше образуется в ходе химической реакции целевого продукта Si (рис. 2). Данный результат объясняется необходимостью избытка водорода для эффективного протекания реакции водородного восстановления Si. При увеличении ${{Q}_{{{\text{SiC}}{{{\text{l}}}_{{\text{4}}}}}}}$ в CFD-расчетах соотношение H2 : SiCl4 уменьшается, что, наряду с уменьшением температуры, приводит к неэффективному расходованию газа-реагента в плазмохимическом реакторе. Таким образом, для увеличения выхода целевого продукта реакции вместе с повышением расхода газа-реагента необходимо и повышение расхода H2. При этом можно ожидать, что существует некий максимально допустимый для рассматриваемой конструкции реактора расход H2. Так, при увеличении доли H2 в плазмообразующей аргоно-водородной смеси температура плазмы и диаметр разряда уменьшаются [33], что, в конечном счете, может привести к необходимости увеличения нагрузки на генератор для повышения энерговыделения в плазме с целью обеспечения наличия стабильного плазменного разряда. В свою очередь, увеличение расхода водорода через трубки 4 может негативно сказаться как на завихренном характере течения потока, обеспечивающем охлаждение стенок реактора, так и на снижении температуры в реакционной камере II, что приведет к еще большему уменьшению высокотемпературной зоны, оптимальной для образования Si. Определение оптимального расхода H2 и газа-носителя целесообразно проводить средствами разработанной математической модели.

Расчеты по модели (1)–(5) показывают, что использование в качестве газа-реагента SiF4 вместо SiCl4 приводит к уменьшению средней температуры газовой смеси в реакционной камере II на 3% (на 150 К), а в охлаждаемом канале III на 5% (на 60 К). Средняя осевая скорость потока при этом увеличивается менее чем на 5% (менее 0.1 м/с). В целом газодинамические и тепловые условия в плазмохимическом реакторе при конверсии SiF4 аналогичны условиям для конверсии SiCl4 (рис. 3).

На рис. 5 приведены полученные по модели (1)–(5) массовые концентрации порошкообразного Si в реакторе при подаче в реактор в качестве газа-реагента SiF4. Производительность при конверсии SiF4 в Si составляет 6 г/ч при γ = 3% для ${{Q}_{{{\text{Si}}{{{\text{F}}}_{4}}}}}$ = 3 л/мин, 6 г/ч при γ   = 1.5% для ${{Q}_{{{\text{Si}}{{{\text{F}}}_{4}}}}}$ = 6 л/мин, 4 г/ч при γ = 0.5% для ${{Q}_{{{\text{Si}}{{{\text{F}}}_{4}}}}}$ = 10 л/мин.

Рис. 5.

Распределение концентрации Si при его конверсии из SiF4 в осевом (а) и поперечных сечениях реактора 1–5 (б–г) при ${{Q}_{{{\text{Si}}{{{\text{F}}}_{4}}}}}$ = 3 (б), 6 (в) и 10 (г) л/мин.

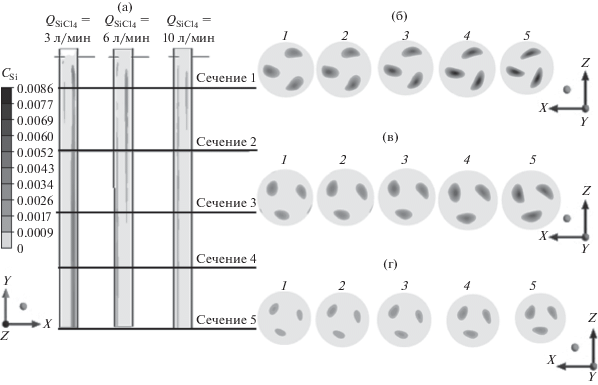
Таким образом, результаты расчетов для исследованной конструкции плазмохимического реактора свидетельствуют о низкой производительности при конверсии SiF4 в Si в условиях термической ВЧИ-плазмы. Для ее повышения необходимо изменение конструкции плазмотрона с целью обеспечения доставки летучего фторида в высокотемпературную область (>5000 K). Предложенная математическая модель будет полезна при проектировании новой конструкции плазмохимического реактора, отвечающей указанному критерию.

ЗАКЛЮЧЕНИЕ

С помощью математической модели газодинамических и тепловых условий получения материалов в ВЧИ-плазмохимическом реакторе с вихревой подачей газа, основанной на сочетании термодинамических расчетов термической плазмы и моделирования конструкции реактора средствами вычислительной гидродинамики, проведены сравнительные вычислительные эксперименты для конверсии кремния из его тетрахлорида и тетрафторида в элементарный кремний. Получены значения прогнозируемой производительности и степени конверсии для различных расходов газа-реагента. Установлено, что газодинамические условия в исследуемом плазмохимическом реакторе более эффективны для конверсии кремния из его тетрахлорида по сравнению с использованием в качестве газа-реагента тетрафторида кремния.

В дальнейшем планируется использование разработанной методики моделирования при проектировании конструкции плазмотрона для повышения производительности процесса конверсии тетрафторида кремния как в части определения оптимального расхода газа-носителя и газа-реагента, так и обеспечения доставки газа-реагента в высокотемпературную зону.

Работа выполнена при финансовой поддержке Министерства образования и науки (программы № 0095-2019-0008 и №0095-2019-0003).

ОБОЗНАЧЕНИЯ

с массовая концентрация порошкообразных частиц
${{c}_{p}}$ удельная теплоемкость при постоянном давлении, Дж/(кг К)
D коэффициент диффузии, м2/с
f объемная доля
M молярная масса, кг/моль
n количество вещества, моль
p давление, Па
Q расход газа, л/мин
Sreag массовый источниковый член (сток) газа-реагента в единице объема
Т абсолютная температура, К
V скорость, м/с
γ степень конверсии, %
λ теплопроводность, Вт/(м К)
μ динамическая вязкость, Па с
ρ плотность, кг/м3

ИНДЕКСЫ

1 аргоно-водородная плазмообразующая смесь
2 водород
3 газ-реагент
e ламинарный поток
i номер компонента
t турбулентный поток
ГР газ-реагент
* целевой продукт

Список литературы

  1. Сивошинская Т.И., Гранков И.В., Шабалин Ю.П., Иванов Л.С. Переработка тетрахлорида кремния, образующегося в производстве полупроводникового кремния // ЦНИИЭИ Цветмет. 1989. Вып. 2. С. 43.

  2. Taylor P.A. Purification Technigues and Analytical Methods for Gaseous and Metallic Impurities in High-purity Silane // J. Cryst. Growth. 1988. V. 89. P. 28.

  3. Nuss J.W., Urry G.J. // Inorg. Nucl. Chem. 1964. V. 26. P. 435.

  4. Sarma K.R., Ricejr M.J. High pressure plasma hydrogenation of silicon tetrachloride. Pat. 4309259 USA. 1982.

  5. Sarma K.R., Chanley C.S. Process for the hydrogenation of silicon tetrachloride. Pat. 4542004 USA. 1985.

  6. Lepage J.-L., Gerard S. Заявка 2530638 Франция. Получение трихлорсилана, используемого для получения высокочистого кремния. 1984.

  7. Громов Г.Н., Болгов М.В., Муравицкий С.А. и др. Способ получения трихлорсилана плазмохимическим гидрированием тетрахлорида кремния и устройство для его осуществления. Пат. 2350558 РФ. 2009.

  8. Lu Z., Zhang W. Hydrogenation of Silicon Tetrachloride in MicroWave Plasma // Chin. J. Chem. Eng. 2014. V. 22. № 2. P. 227.

  9. Wu L., Ma Z., He A., Wang J. Studies on destruction of silicon tetrachloride using microwave plasma jet // J. Hazard. Mater. 2010. V. 173. № 1–3. P. 305.

  10. Wu L., Ma Z., He A., Wang J. Decomposition of silicon tetrachloride by microwave plasma jet at atmospheric pressure // Inorg. Mater. 2009. V. 45. № 12. P. 1403.

  11. Deryzemlia A.M., Kryshtal P.G., Malykhin D.G., Radchenko V.I., Shirokov B.M. Deposition of nanocrystalline silicon films into low frequency induction RF discharge // Probl. At. Sci. Technol. 2014. № 1 (89). P. 147.

  12. Логинов А.В., Гарбар А.М. Тетрафторид кремния: свойства, получение и применение // Высокочист. вещества. 1989. № 5. С. 27.

  13. Туманов Ю.Н. Плазменные и высокочастотные процессы получения и обработки материалов в ядерном топливном цикле: настоящее и будущее. М.: ФИЗМАТЛИТ, 2003. С. 760.

  14. Boone J.E., Richards D.M., Bossier J.A. Процесс получения силана. Pat. 4309259 USA. 1991.

  15. Кутьин А.М., Поляков В.С., Сенников П.Г. // Тезисы докладов V Международной конференции “Кремний 2008". Черноголовка: Граница, 2008. С. 178.

  16. Djeridane Y., Abramov A., Roca i Cabarrocas P. // Thin Solid Films. 2007. V. 515. P. 7451.

  17. Kumar S., Brenot R., Kalache B., Tripathi V., Vanderhaghen R., Drevillon B., Roca i Cabarrocas P. // Solid State Phenom. 2001. V. 80–81. P. 237.

  18. Bruno G., Capezzuto P., Cicala G. RF glow discharge of SiF4-H2 mixtures: Diagnostics and modeling of the a-Si plasma deposition process // J. Appl. Phys. 1991. V. 69. № 10. P. 7256.

  19. Vodopyanov A.V., Golubev S.V., Mansfeld D.A., Sennikov P.G., Drozdov Yu.N. Experimental investigations of silicon tetrafluoride decomposition in ECR discharge plasma // Rev. Sci. Instrum. 2011. V. 82. Article number 063503.

  20. Nagano M., Mriya T. et al. Метод и аппаратура для получения высокочистого кремния. Pat. 0250764 USA. 2004.

  21. Корнев Р.А., Шабарова Л.В., Шишкин А.И. Газодинамические и тепловые процессы в высокочастотном индукционном плазмотроне с тангенциальной стабилизацией газового потока // Теор. осн. хим. технол. 2017. Т. 51. № 5. С. 589.

  22. Корнев Р.А., Сенников П.Г., Шабарова Л.В., Шишкин А.И., Дроздова Т.А., Синцов С.В. Восстановление BCl3 в аргоно-водородной ВЧИ плазме атмосферного давления // Хим. выс. энерг. 2019. Т. 53. № 3. С. 235.

  23. Matveev I., Matveyeva S., Zverev S. Experimental investigations of the APT-60 High-Pressure Inductively Coupled Plasma System on different Plasma Gases // IEEE Trans. Plasma Sci. 2014. V. 42. № 12. P. 3891. https://doi.org/10.1109/TPS.2014.2362414

  24. Bernardi D., Colombo V., Ghedini E., Mentrelli A. Three-dimensional modeling of inductively coupled plasma torches // Pure Appl. Chem. 2005. V. 77. № 2. P. 359.

  25. Fathalizadeh A., Pham T., Mickelson W., Zettl A. Scaled Synthesis of Boron Nitride Nanotubes, Nanoribbons, and Nanococoons Using Direct Feedstock Injection into an Extended-Pressure, Inductively-Coupled Thermal Plasma // Nano Lett. 2014. V. 14. P. 4881.

  26. Каренгин А.Г. Плазменные технологии переработки веществ (Часть 1). Томск: Томский политехнический университет, 2008.

  27. Mostaghimi J., Boulos M.I. Two-Dimensional Electromagnetic Field Effects in Induction Plasma Modelling // Plasma Chem. Plasma Process. 1989. V. 9. № 1. P. 25.

  28. Уэйлес С. Фазовые равновесия в химической технологии: в 2-х ч. Ч. 1. М.: Мир, 1989.

  29. Xue S., Proulx P., Boulos M.I. Extended-field electromagnetic model for inductively coupled plasma // J. Phys. D: Appl. Phys. 2001. V. 34. P. 1897.

  30. Гришин Ю.М., Мяо Л. Численное моделирование плазмодинамических процессов в технологическом ВЧИ-плазмотроне с газовым охлаждением // Наука образ. МГТУ им. Н.Э. Баумана. 2016. № 05. С. 104.

  31. Rehmet C., Cao T., Cheng Y. Numerical study of Si nanoparticles formation by SiCl4 hydrogenation in RF plasma // Plasma Sources Sci. Technol. 2016. V. 25. № 2. Article number 025011.

  32. Ivanov D.V., Zverev S.G. Mathematical simulation of processes in ICP/RF plasma torch for plasma chemical reactions // IEEE Trans. Plasma Sci. 2017. V. 45. № 12. P. 3125.

  33. Шабарова Л.В., Корнев Р.А., Сенников П.Г. Моделирование газодинамических и тепловых процессов в аргоно-водородной индуктивно-связанной плазме с вихревой стабилизацией // Хим. выс. энерг. 2018. Т. 52. № 5. С. 409.

  34. Андерсон Д., Таннехил Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен: в 2-х т. М.: Мир, 1990.

  35. Быстров Ю.А., Исаев С.А., Кудрявцев Н.А., Леонтьев А.И. Численное моделирование вихревой интенсификации теплообмена в пакетах труб. СПб.: Судостроение, 2005.

  36. Воробьев А.Х. Диффузионные задачи в химической кинетике. М.: Изд-во Московского университета, 2003.

  37. Murphy A.B. Transport Coefficients of Hydrogen and Argon–Hydrogen Plasmas // Plasma Chem. Plasma Process. 2000. V. 20. № 3. P. 279.

  38. Гамбург Д.Ю. Водород. Свойства, получение, хранение, транспортирование, применение. М.: Химия, 1989.

  39. Бретшнайдер С. Свойства газов и жидкостей. М.: Химия, 1966.

  40. Абрамов А.Н., Плехович А.Д., Кутьин А.М., Яшков М.В., Гурьянов А.Н. Анализ образования фазы муллита в стекле сердцевины алюмосиликатного волоконного световода, легированного хромом // Неорг. матер. 2018. Т. 54. № 9. С. 993.

  41. Kourkkari P., Pajarre R. A Gibbs energy minimization method for constrained and partial equilibria // Pure Appl. Chem. 2011. V. 83. P. 1243.

  42. Иориш В.С., Белов Г.В., Юнгман В.С. Программный комплекс ИВТАН ТЕРМО для Windows и его использование в прикладном термодинамическом анализе. Препринт № 8-415. М.: ОИВТАН, 1998.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал