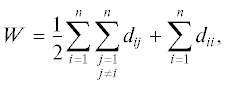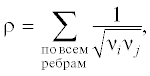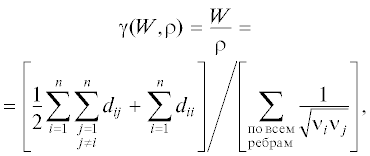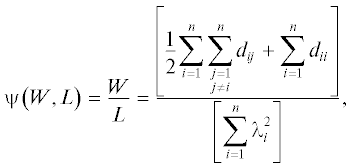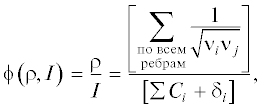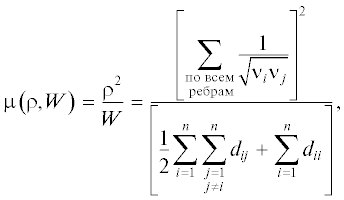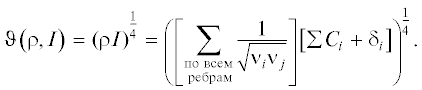Теоретические основы химической технологии, 2020, T. 54, № 4, стр. 496-503
Взаимосвязь теплоемкости и топологических характеристик молекул в рядах газообразных замещенных производных алкенов при давлении 100 кПа и в интервале температур от 298.15 до 1000 К
М. Ю. Доломатов a, b, Т. М. Аубекеров a, *, Э. В. Вагапова a, К. Р. Ахтямова a
a Уфимский государственный нефтяной технический университет
Уфа, Россия
b Башкирский государственный университет
Уфа, Россия
* E-mail: timur_1995@inbox.ru
Поступила в редакцию 28.01.2019
После доработки 13.02.2020
Принята к публикации 14.02.2020
Аннотация
Предложена многофакторная нелинейная модель структура–свойство для расчета изобарной молярной теплоемкости алкенов в газовой фазе. Особенностью модели является включение топологических дескрипторов, таких как индекс Винера, индекс Рандича, собственных значений топологической матрицы и др., а также индекса, учитывающего цис- и транс-изомерию алкенов. Полученная модель адекватно описывает теплоемкость для углеводородов с числом атомов углерода больше трех. Разработана соответствующая программа расчета молярной теплоемкости. Предложенная модель может быть использована в химико-технологических и проектных расчетах химических реакторов и установок нефтехимии.
ВВЕДЕНИЕ
Расчет термодинамических свойств углеводородов, в частности теплоемкости, является актуальной фундаментальной и прикладной задачей, связанной с расчетом термодинамических функций и направлений химических реакций. Теплоемкость необходима для оценки энтальпии и энтропии образования молекул и связанных с ними термодинамических потенциалов, так как расчет этих величин выражается известными формулами термодинамики. Поэтому теплоемкость является важной характеристикой органических соединений, которая востребована при проведении химико-технологических и теплофизических расчетов. Известны различные методики расчета этой величины, в том числе построенные на методе статистической термодинамики, структурных инкрементов, теории молекулярных графов в моделях типа структура–свойство. Несмотря на это, существующие методики расчета этой величины характеризуются сложностью и часто неадекватны экспериментальным данным.
Целью данной работы является разработка нелинейной топологической модели структура–свойство для более точного расчета молярной теплоемкости алкенов с различными типами молекулярной структуры. Точность модели подтверждается результатами статистической обработки данных. Приведено сравнение экспериментальных и расчетных значений теплоемкости, показывающее приемлемую адекватность предложенной регрессионной модели. Результаты исследования могут быть рекомендованы для проведения научных и инженерных расчетов.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для прямого расчета теплоемкости методом статистической термодинамики необходимо знать соответствующие статистические суммы, учитывающие вклады колебательного, вращательного и поступательного движений в свободной энергии молекул. Для сложных молекул этот подход не всегда дает адекватные эксперименту результаты, так как не учитываются ангармонические колебания и различные взаимодействия атомов. Для решения инженерных задач, возникающих в химической технологии, широко применяются эмпирические методы, которые учитывают вклады отдельных структурных групп в теплоемкость, и методы, которые включают различные связи между теплоемкостью и структурными параметрами углеводородов. Наиболее часто для расчетов используется эмпирическая форма, выраженная степенным рядом (1), который выражает температурную зависимость теплоемкости [1]:
Кроме того, известны способы расчета физико-химических свойств [2], в том числе теплоемкости, которые используют топологические параметры [3–5]. Недостатком этих работ является низкая точность расчетов: относительная ошибка в ряде случаев достигает 10 и более процентов.
Для решения задачи, поставленной в настоящей работе, использован подход, рассмотренный ранее для расчета критических свойств алканов [6]. В предлагаемых моделях в качестве топологических параметров использованы: индекс Винера (3), индекс Рандича (4), индекс, учитывающий геометрическую изомерию (5), а также индекс, который представляет собой сумму квадратов собственных значений топологической матрицы молекулярного графа (МГ) (2).
В соответствии с [7] в качестве параметра, характеризующего электронное строение молекул, использована сумма квадратов собственных значений МГ, которая косвенно отражает энергетический спектр электронных состояний молекул:
Для характеристики взаимного расположения атомов использован индекс Винера, который отражает степень связанности углеродных атомов в органических молекулах и определяется через полусумму топологических расстояний между всеми n атомами в молекулярном графе и рассчитывается по следующей формуле:
где ${{d}_{{ii}}} = 1 - {6 \mathord{\left/ {\vphantom {6 {{{Z}_{i}}}}} \right. \kern-0em} {{{Z}_{i}}}};$ ${{d}_{{ij}}} = {1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0em} k} - {{36} \mathord{\left/ {\vphantom {{36} {{{Z}_{i}}{{Z}_{j}}}}} \right. \kern-0em} {{{Z}_{i}}{{Z}_{j}}}}.$Для характеристики разветвленности молекул используется индекс Рандича [8], который характеризует разветвленность углеродного скелета и различается для изомеров углеводородов (индекс молекулярной связности):
где ${{{\nu }}_{i}}$ – число ребер графа, отходящих от i-й вершины;${{{\nu }}_{j}}$ – число ребер графа, отходящих от j-й вершины.Для определения степени или значения стерических эффектов, присутствующих в углероде, используется полуэмпирический топологический индекс [9], который зависит не только от первичного, вторичного, третичного или четвертичного положений углерода, но и от размера групп заместителей. Данный индекс рассчитывается по следующей формуле:
где Ci – значение, приписываемое каждому углеродному атому i в молекуле, а δi представляет собой сумму логарифма значения каждого смежного атома углерода: ${{\delta }_{i}} = \lg {{C}_{1}} + \lg {{C}_{2}}$ + $\lg {{C}_{3}} + \lg {{C}_{4}}.$В соответствии с подходом QSPR (quantitative structure–property relationship), принятым в изучении связи структура–свойство, будем искать полуэмпирические модели, связывающие молярную теплоемкость и вышеупомянутые топологические индексы, так называемые молекулярные дескрипторы.
Для этого выразим молярную теплоемкость в виде аддитивной функции, зависящей от температуры, структурно-химических характеристик и параметров, отражающих энергетический спектр молекулы. Таким образом, теплоемкость принимается зависящей от 5 переменных: L, W, ρ, I и температуры. Эта зависимость может быть представлена рядом следующего вида:
(6)
$\begin{gathered} C(L,W,\rho , I,T) = \\ = ({{a}_{0}} + {{a}_{1}}W + {{a}_{2}}\rho + {{a}_{3}}L + {{a}_{4}}I)C(T) + \varepsilon . \\ \end{gathered} $Коэффициенты a1–a4 в ряду (6) имеют следующий вид:
Смысл коэффициентов a1–a3 в ряду (6) заключается в характеристике возмущения свойств в гомологическом ряду молекул под влиянием структурных топологических факторов и энергии взаимодействия при заданной температуре. Как показывают исследования, различные топологические индексы могут быть связаны между собой, поэтому целесообразно ввести обобщенные топологические параметры, зависящие одновременно от двух индексов:
Поскольку формула (7) представляет собой отношение индекса Винера к индексу Рандича, то имеем новый параметр, химические свойства которого заключаются в отношении протяженности к разветвленности молекулярного графа. Индекс Винера входит в формулу (7) как компонент. Новый индекс (7) включает в себя не только расстояния, в отличие от индекса Винера этот обобщенный индекс включает число ребер, исходящих от каждой вершины графа.
Как известно, теплоемкость органических соединений сложным образом зависит от температуры, так как выражается через вклады колебательной, вращательной и поступательной энергии молекул. В большинстве случаев используются методы статистической термодинамики [10], дающие ошибки в расчете статистических сумм при переходе к сложным молекулам. Для представления теплоемкости как функции температуры представим теплоемкость как произведение двух независимых величин, зависящих от структуры молекул и от температуры среды.
Каждую составляющую этого произведения выразим через эмпирические зависимости:
(12)
$\begin{gathered} C(L,\rho ,I,\gamma ,\psi ,\phi ,\mu ,\vartheta ) = {{a}_{0}} + {{a}_{1}}L + {{a}_{2}}\rho + {{a}_{3}}I + \\ + \,\,{{a}_{4}}{{\rho }^{2}} + {{a}_{5}}\psi + {{a}_{6}}\gamma + {{a}_{7}}\phi + {{a}_{8}}\mu + {{a}_{9}}\vartheta . \\ \end{gathered} $В соответствии с современной скейлинговой теорией фазовых переходов теплоемкость как характеристика фазового перехода второго рода равна приведенной температуре в некоторой степени [11].
В данном случае предполагается, что теплоемкость связана с некоторыми характеристиками перехода, которые независимы друг от друга. Температурную составляющую представим в виде степенной зависимости
Составляющая (13) определяется двумя компонентами, которые характеризуют соответственно температурное изменение теплоемкости. Для удобства расчетов введем относительную температуру, которая равна отношению абсолютной к стандартной термодинамической температуре:
В формуле (13) коэффициент α характеризует увеличение теплоемкости с ростом температуры, коэффициент β характеризует релаксацию энергии за счет перераспределения колебательных степеней свободы и вращательных степеней свободы в протяженных молекулах.
В гомологических рядах предположим, что параметр β зависит от температуры, поэтому β = ζτ.
Таким образом представим молярную теплоемкость в гомологическом ряду алкенов в виде произведения, состоящего из двух сомножителей. Первый из этих сомножителей характеризует вклад топологических индексов в формировании теплоeмкости. Второй сомножитель характеризует зависимость теплоемкости от температуры:
В формуле (15) топологические характеристики не зависят от температуры. Поэтому модель примет следующий вид:
(16)
$\begin{gathered} C\left( {L,~\rho ,I,\gamma ,\psi ,\phi ,\mu ,\vartheta ,T} \right) = C\left( S \right)C\left( T \right) = \\ = ({{a}_{0}} + {{a}_{1}}L + {{a}_{2}}\rho + {{a}_{3}}I + {{a}_{4}}{{\rho }^{2}} + \\ + \,\,{{a}_{5}}\psi + {{a}_{6}}\gamma + {{a}_{7}}\phi + \\ + \,\,{{a}_{8}}\mu + {{a}_{9}}\vartheta )({{\tau }^{\alpha }}{{\tau }^{{ - \zeta \tau }}}). \\ \end{gathered} $РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В качестве объектов исследования использованы экспериментальные данные по молярной теплоемкости 52 производных углеводородов ряда алкенов, включая цис- и транс-изомеры и соединения, замещенные алкильными группами [12]. В табл. 1 приведены соответствующие топологические параметры, рассчитанные по специальной программе [13]. Коэффициенты зависимости (16) рассчитывали методом наименьших квадратов по алгоритму многофакторного регрессионного анализа. Соответствующие коэффициенты зависимости (16) приведены в табл. 2.
Таблица 1.
Значения топологических индексов алкенов
| № | Соединение | ρ | L | W | I | γ | ψ | ϕ | μ | ϑ |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Этилен | 0.500 | 2 | 0.5 | 1.701 | 0.250 | 0.250 | 1.000 | 0.294 | 0.500 |
| 2 | Пропилен | 0.986 | 4 | 3 | 2.654 | 0.972 | 0.750 | 3.043 | 0.372 | 0.324 |
| 3 | Бутилен-1 | 1.524 | 6 | 8.5 | 3.463 | 2.323 | 1.417 | 5.577 | 0.440 | 0.273 |
| 4 | Цис-бутилен-2 | 1.488 | 6 | 8 | 3.656 | 2.214 | 1.333 | 5.376 | 0.407 | 0.277 |
| 5 | Изобутен | 1.354 | 6 | 7.5 | 3.086 | 1.833 | 1.250 | 5.539 | 0.439 | 0.244 |
| 6 | Пентен-1 | 2.024 | 8 | 18 | 4.271 | 4.095 | 2.250 | 8.895 | 0.474 | 0.227 |
| 7 | 2-метилбутен-1 | 1.914 | 8 | 16 | 3.894 | 3.663 | 2.000 | 8.359 | 0.491 | 0.229 |
| 8 | 2-метилбутен-2 | 1.866 | 8 | 15 | 4.039 | 3.482 | 1.875 | 8.039 | 0.462 | 0.232 |
| 9 | Гексен-1 | 2.524 | 10 | 32.5 | 5.080 | 6.371 | 3.250 | 12.876 | 0.497 | 0.196 |
| 10 | Цис-гексен-2 | 2.526 | 10 | 31 | 5.273 | 6.381 | 3.100 | 12.272 | 0.479 | 0.206 |
| 11 | 2-метилпентен-1 | 2.414 | 10 | 29.5 | 4.703 | 5.827 | 2.950 | 12.220 | 0.513 | 0.198 |
| 12 | 4-метилпентен-1 | 2.379 | 10 | 29.5 | 4.972 | 5.660 | 2.950 | 12.400 | 0.478 | 0.192 |
| 13 | 2-метилпентен-2 | 2.404 | 10 | 27.5 | 4.847 | 5.779 | 2.750 | 11.439 | 0.496 | 0.210 |
| 14 | Цис-3-метилпентен-2 | 2.427 | 10 | 27 | 4.872 | 5.890 | 2.700 | 11.125 | 0.498 | 0.218 |
| 15 | 2-этилбутен-1 | 2.475 | 10 | 28.5 | 4.703 | 6.126 | 2.850 | 11.515 | 0.526 | 0.215 |
| 16 | 3,3-диметилбутен-1 | 2.197 | 10 | 25.5 | 4.735 | 4.827 | 2.550 | 11.607 | 0.464 | 0.189 |
| 17 | 2,3-диметилбутен-2 | 2.250 | 10 | 24.5 | 4.471 | 5.063 | 2.450 | 10.889 | 0.503 | 0.207 |
| 18 | Цис-гептен-2 | 3.026 | 12 | 51 | 6.082 | 9.157 | 4.250 | 16.854 | 0.498 | 0.180 |
| 19 | 2-метилгексен-1 | 2.914 | 12 | 49 | 5.511 | 8.491 | 4.083 | 16.815 | 0.529 | 0.173 |
| 20 | 2-метилгексен-2 | 2.904 | 12 | 46 | 5.656 | 8.433 | 3.833 | 15.840 | 0.513 | 0.183 |
| 21 | Цис-2-метилгексен-3 | 2.937 | 12 | 46 | 5.876 | 8.626 | 3.833 | 15.662 | 0.500 | 0.188 |
| 22 | Цис-5-метилгексен-2 | 2.882 | 12 | 47 | 5.974 | 8.306 | 3.917 | 16.308 | 0.482 | 0.177 |
| 23 | 5-метилгексен-1 | 2.879 | 12 | 49 | 5.780 | 8.289 | 4.083 | 17.020 | 0.498 | 0.169 |
| 24 | 3-метилгексен-1 | 2.934 | 12 | 47 | 5.780 | 8.608 | 3.917 | 16.019 | 0.508 | 0.183 |
| 25 | Цис-3-метилгексен-2 | 2.927 | 12 | 45 | 5.680 | 8.567 | 3.750 | 15.374 | 0.515 | 0.190 |
| 26 | Цис-3-метилгексен-3 | 2.965 | 12 | 44 | 5.631 | 8.791 | 3.667 | 14.840 | 0.527 | 0.200 |
| 27 | Цис-4-метилгексен-2 | 2.937 | 12 | 45 | 5.974 | 8.626 | 3.750 | 15.322 | 0.492 | 0.192 |
| 28 | 4-метилгексен-1 | 2.917 | 12 | 47 | 5.780 | 8.509 | 3.917 | 16.112 | 0.505 | 0.181 |
| 29 | 4,4-диметилпентен-1 | 2.670 | 12 | 43 | 5.543 | 7.129 | 3.583 | 16.105 | 0.482 | 0.166 |
| 30 | 2,3-диметилпентен-1 | 2.835 | 12 | 43 | 5.404 | 8.037 | 3.583 | 15.168 | 0.525 | 0.187 |
| 31 | 2,3-диметилпентен-2 | 2.811 | 12 | 40 | 5.279 | 7.902 | 3.333 | 14.230 | 0.532 | 0.198 |
| 32 | Цис-3,4-диметилпентен-2 | 2.809 | 12 | 41 | 5.573 | 7.890 | 3.417 | 14.596 | 0.504 | 0.192 |
| 33 | 3,4-диметилпентен-1 | 2.807 | 12 | 43 | 5.673 | 7.879 | 3.583 | 15.319 | 0.495 | 0.183 |
| 34 | 2,4-диметилпентен-1 | 2.770 | 12 | 45 | 5.404 | 7.673 | 3.750 | 16.245 | 0.513 | 0.171 |
| 35 | 2,4-диметилпентен-2 | 2.777 | 12 | 42 | 5.548 | 7.712 | 3.500 | 15.124 | 0.501 | 0.184 |
| 36 | 3,3-диметилпентен-1 | 2.758 | 12 | 41 | 5.543 | 7.607 | 3.417 | 14.866 | 0.498 | 0.186 |
| 37 | 2-этилпентен-1 | 2.975 | 12 | 47 | 5.511 | 8.851 | 3.917 | 15.798 | 0.540 | 0.188 |
| 38 | 3-этилпентен-1 | 2.972 | 12 | 45 | 5.780 | 8.833 | 3.750 | 15.141 | 0.514 | 0.196 |
| 39 | Транс-пентен-2 | 2.026 | 8 | 17 | 4.406 | 4.105 | 2.125 | 8.391 | 0.460 | 0.241 |
| 40 | Транс-гексен-2 | 2.526 | 10 | 31 | 5.214 | 6.381 | 3.100 | 12.272 | 0.484 | 0.206 |
| 41 | Транс-гексен-3 | 2.564 | 10 | 30.5 | 5.135 | 6.574 | 3.050 | 11.895 | 0.499 | 0.216 |
| 42 | Транс-гептен-2 | 3.026 | 12 | 51 | 6.023 | 9.157 | 4.250 | 16.854 | 0.502 | 0.180 |
| 43 | Транс-гептен-3 | 3.064 | 12 | 50 | 5.944 | 9.388 | 4.167 | 16.319 | 0.516 | 0.188 |
| 44 | Транс-2-метилгексен-3 | 2.937 | 12 | 46 | 5.836 | 8.626 | 3.833 | 15.662 | 0.503 | 0.188 |
| 45 | Транс-5-метилгексен-2 | 2.882 | 12 | 47 | 5.915 | 8.306 | 3.917 | 16.308 | 0.487 | 0.177 |
| 46 | Транс-3-метилгексен-2 | 2.927 | 12 | 45 | 5.651 | 8.567 | 3.750 | 15.374 | 0.518 | 0.190 |
| 47 | Транс-3-метилгексен-3 | 2.965 | 12 | 44 | 5.611 | 8.791 | 3.667 | 14.840 | 0.528 | 0.200 |
| 48 | Транс-4-метилгексен-2 | 2.937 | 12 | 45 | 5.915 | 8.626 | 3.750 | 15.322 | 0.497 | 0.192 |
| 49 | Транс-4,4-диметилпентен-2 | 2.699 | 21 | 41 | 5.678 | 7.285 | 1.952 | 15.191 | 0.475 | 0.178 |
| 50 | Транс-3,4-диметилпентен-2 | 2.809 | 12 | 41 | 5.543 | 7.890 | 3.417 | 14.596 | 0.507 | 0.192 |
| 51 | 4-метил-транс-2-гептен | 3.437 | 14 | 69 | 6.724 | 11.813 | 4.929 | 20.076 | 0.511 | 0.171 |
| 52 | 3-метил-цис-3-гептен | 3.465 | 14 | 68 | 6.440 | 12.006 | 4.857 | 19.625 | 0.538 | 0.177 |
Таблица 2.
Коэффициенты зависимости (16)
| Коэффициент | Численное значение | Размерность |
|---|---|---|
| a0 | 348.12 | Дж/(моль К) |
| a1 | –8.154 | Дж/(моль К) |
| a2 | 246.397 | Дж/(моль К) |
| a3 | 29.15 | Дж/(моль К) |
| a4 | –17.33 | Дж/(моль К) |
| a5 | –50.24 | Дж/(моль К) |
| a6 | 11.95 | Дж/(моль К) |
| a7 | 14.57 | Дж/(моль К) |
| a8 | –148.8 | Дж/(моль К) |
| a9 | –401.3 | Дж/(моль К) |
| α | 0.871 | Безразмерная величина |
| ζ | –0.0575 | Безразмерная величина |
Адекватность зависимости (16) оценивалась по статистическим характеристикам – конкордации, множественной корреляции и стандартной ошибке. В табл. 3 приведены сравнения справочных и расчетных значений молярной теплоемкости при постоянном давлении. Поскольку основными топологическими характеристиками модели являются протяженность и разветвлённость молекулы, то к небольшим молекулам ряда алкенов n = 2 и 3 данная модель не может быть применена, поэтому рекомендуем использовать данную модель для углеводородов с количеством атомов углерода 4 и более.
Таблица 3.
Сравнение справочных [12] и расчетных значений молярной теплоемкости
| Соединение | Справочное значение молярной теплоемкости, Дж/(моль К) | Расчетное значение молярной теплоемкости, Дж/(моль К) | Абсолютная погрешность, Дж/(моль К) |
Относительная погрешность, % |
|---|---|---|---|---|
| 298 К | ||||
| Этилен | 43.91 | 44.14 | 0.23 | 0.53 |
| Пропилен | 64.97 | 64.42 | 0.55 | 0.85 |
| Бутилен-1 | 88.38 | 88.38 | 0.00 | 0.00 |
| Цис-бутилен-2 | 82.13 | 83.15 | 1.02 | 1.24 |
| 2-этилбутен-1 | 137.39 | 136.21 | 1.18 | 0.86 |
| 3,3-диметилбутен-1 | 131.39 | 130.76 | 0.63 | 0.48 |
| Цис-гептен-2 | 147.25 | 151.70 | 4.45 | 3.02 |
| 2-метилгексен-1 | 157.40 | 156.12 | 1.28 | 0.81 |
| 2-метилгексен-2 | 151.76 | 153.55 | 1.79 | 1.18 |
| 5-метилгексен-1 | 155.30 | 154.29 | 1.01 | 0.65 |
| Цис-3-метилгексен-2 | 151.76 | 152.74 | 0.97 | 0.64 |
| Цис-3-метилгексен-3 | 151.76 | 152.50 | 0.74 | 0.49 |
| 4-метилгексен-1 | 151.63 | 153.04 | 1.41 | 0.93 |
| 2,3-диметилпентен-1 | 155.43 | 154.16 | 1.26 | 0.81 |
| 2,3-диметилпентен-2 | 151.55 | 153.15 | 1.60 | 1.05 |
| 2,4-диметилпентен-1 | 155.43 | 155.82 | 0.39 | 0.25 |
| 2,4-диметилпентен-2 | 151.55 | 152.40 | 0.85 | 0.56 |
| 2-этилпентен-1 | 155.96 | 154.91 | 1.05 | 0.67 |
| Транс-гексен-2 | 136.25 | 133.23 | 3.02 | 2.21 |
| Транс-гексен-3 | 137.95 | 133.79 | 4.16 | 3.02 |
| Транс-гептен-2 | 154.14 | 152.07 | 2.07 | 1.34 |
| Транс-гептен-3 | 151.58 | 152.03 | 0.45 | 0.30 |
| Транс-5-метилгексен-2 | 151.42 | 152.35 | 0.93 | 0.61 |
| Транс-3-метилгексен-2 | 151.76 | 152.97 | 1.21 | 0.79 |
| Транс-3-метилгексен-3 | 151.76 | 152.66 | 0.90 | 0.59 |
| 4-метил-транс-2-гептен | 174.30 | 166.51 | 7.80 | 4.47 |
| 3-метил-цис-3-гептен | 174.65 | 167.25 | 7.40 | 4.24 |
| 500 К | ||||
| Этилен | 61.16 | 65.91 | 4.75 | 7.77 |
| Пропилен | 93.19 | 96.18 | 3.00 | 3.22 |
| Бутилен-1 | 128.34 | 131.96 | 3.62 | 2.82 |
| Цис-бутилен-2 | 121.73 | 124.15 | 2.42 | 1.99 |
| 2-этилбутен-1 | 200.03 | 203.37 | 3.35 | 1.67 |
| 3,3-диметилбутен-1 | 193.56 | 195.23 | 1.67 | 0.86 |
| Цис-гептен-2 | 227.35 | 226.50 | 0.85 | 0.37 |
| 2-метилгексен-1 | 234.11 | 233.10 | 1.01 | 0.43 |
| 2-метилгексен-2 | 231.42 | 229.26 | 2.16 | 0.93 |
| 5-метилгексен-1 | 234.57 | 230.36 | 4.21 | 1.79 |
| Цис-3-метилгексен-2 | 231.42 | 228.04 | 3.38 | 1.46 |
| Цис-3-метилгексен-3 | 231.42 | 227.69 | 3.73 | 1.61 |
| 4-метилгексен-1 | 233.90 | 228.49 | 5.41 | 2.31 |
| 2,3-диметилпентен-1 | 234.49 | 230.17 | 4.32 | 1.84 |
| 2,3-диметилпентен-2 | 231.84 | 228.65 | 3.18 | 1.37 |
| 2,4-диметилпентен-1 | 234.49 | 232.65 | 1.84 | 0.79 |
| 2,4-диметилпентен-2 | 231.84 | 227.53 | 4.30 | 1.86 |
| 2-этилпентен-1 | 234.23 | 231.29 | 2.94 | 1.26 |
| Транс-гексен-2 | 195.34 | 198.92 | 3.58 | 1.83 |
| Транс-гексен-3 | 195.89 | 199.75 | 3.86 | 1.97 |
| Транс-гептен-2 | 229.89 | 227.05 | 2.83 | 1.23 |
| Транс-гептен-3 | 230.66 | 226.99 | 3.67 | 1.59 |
| Транс-5-метилгексен-2 | 231.92 | 227.46 | 4.45 | 1.92 |
| Транс-3-метилгексен-2 | 231.42 | 228.39 | 3.03 | 1.31 |
| Транс-3-метилгексен-3 | 231.42 | 227.94 | 3.48 | 1.51 |
| 4-метил-транс-2-гептен | 266.39 | 248.60 | 17.79 | 6.68 |
| 3-метил-цис-3-гептен | 265.90 | 249.71 | 16.19 | 6.09 |
| 800 К | ||||
| Этилен | 85.03 | 89.58 | 4.54 | 5.34 |
| Пропилен | 129.24 | 130.73 | 1.49 | 1.15 |
| Бутилен-1 | 175.11 | 179.34 | 4.23 | 2.42 |
| Цис-бутилен-2 | 171.12 | 168.74 | 2.38 | 1.39 |
| 2-этилбутен-1 | 269.96 | 276.41 | 6.44 | 2.39 |
| 3,3-диметилбутен-1 | 266.17 | 265.34 | 0.83 | 0.31 |
| Цис-гептен-2 | 311.89 | 307.83 | 4.05 | 1.30 |
| 2-метилгексен-1 | 316.06 | 316.81 | 0.75 | 0.24 |
| 2-метилгексен-2 | 312.18 | 311.59 | 0.59 | 0.19 |
| 5-метилгексен-1 | 316.03 | 313.09 | 2.94 | 0.93 |
| Цис-3-метилгексен-2 | 312.18 | 309.93 | 2.25 | 0.72 |
| Цис-3-метилгексен-3 | 312.18 | 309.46 | 2.72 | 0.87 |
| 4-метилгексен-1 | 316.28 | 310.54 | 5.74 | 1.82 |
| 2,3-диметилпентен-1 | 315.72 | 312.83 | 2.89 | 0.92 |
| 2,3-диметилпентен-2 | 312.93 | 310.77 | 2.17 | 0.69 |
| 2,4-диметилпентен-1 | 315.72 | 316.19 | 0.47 | 0.15 |
| 2,4-диметилпентен-2 | 312.93 | 309.24 | 3.69 | 1.18 |
| 2-этилпентен-1 | 316.89 | 314.34 | 2.54 | 0.80 |
| Транс-гексен-2 | 266.35 | 270.36 | 4.01 | 1.50 |
| Транс-гексен-3 | 268.20 | 271.48 | 3.29 | 1.23 |
| Транс-гептен-2 | 313.73 | 308.59 | 5.14 | 1.64 |
| Транс-гептен-3 | 314.38 | 308.51 | 5.87 | 1.87 |
| Транс-5-метилгексен-2 | 313.24 | 309.15 | 4.09 | 1.30 |
| Транс-3-метилгексен-2 | 312.18 | 310.41 | 1.77 | 0.57 |
| Транс-3-метилгексен-3 | 312.18 | 309.79 | 2.39 | 0.77 |
| 4-метил-транс-2-гептен | 359.60 | 337.88 | 21.73 | 6.04 |
| 3-метил-цис-3-гептен | 358.55 | 339.38 | 19.17 | 5.35 |
Для характеристики качества регрессионного уравнения был вычислен коэффициент множественной корреляции $R \approx 0.997$, подтверждающий сильную связь предложенных топологических характеристик молекулы углеводорода с ее молярной теплоемкостью. Для статистической достоверности была рассчитана корреляционная поправка: ${{S}_{r}} = \frac{{{\text{1}} - {{R}^{{\text{2}}}}}}{{\sqrt {n - {\text{1}}} }}$ (для $n > {\text{30}}$). Так как в нашем случае ${{S}_{r}} = {\text{0}}{\text{.00086}}$ и $\left| {\frac{R}{{S{}_{r}}}} \right|$ = $\left| {\frac{{{\text{0}}{\text{.997}}}}{{{\text{0}}{\text{.00086}}}}} \right|$ = $1159 \geqslant {\text{3}}$ для алкенов соответственно, то связь нельзя считать случайной и регрессионное уравнение проходит через центр облака исходных точек. Разработанная модель предназначена для проведения расчетов на ЭВМ. В настоящее время она реализована в виде программы на языке Maple. Проведенные численные эксперименты показывают, что уменьшение количества составляющих уравнения (16) значительно снижает адекватность модели для всех членов гомологического ряда. Основываясь на вышесказанном, можно сделать вывод об адекватности предлагаемой модели (16), которая удовлетворительно описывает молярную теплоемкость как функцию структурных параметров и температуры.
ЗАКЛЮЧЕНИЕ
В настоящей работе получена модель структура–свойство, которая адекватно передает зависимость молярной теплоемкости от топологических параметров молекул: индекса Винера, индекса Рандича, суммы квадратов собственных значений топологической матрицы и индекса, характеризующего расположение цис- и транс-алкенов в пространстве.
Полученная модель обеспечивает приемлемую адекватность, что подтверждается следующими критериями: коэффициент множественной корреляции 0.997, стандартная ошибка 2 и средняя относительная ошибка 1.9%. Следовательно, разработанная модель может быть использована при расчете термодинамических функций: энтальпий, энтропий и свободных энергий образования органических соединений и в термодинамике химических реакций.
Полученные результаты могут быть использованы в научных и инженерных приложениях.
ОБОЗНАЧЕНИЯ
| A, B, C, D, E | эмпирические постоянные коэффициенты, зависящие от природы вещества |
| а0, а1, a2, а3, а4 | коэффициенты, зависящие от температуры |
| С | теплоемкость, Дж/(моль К) |
| d | элементы матрицы расстояний |
| k | кратность связи между атомами |
| T | температура |
| Z | заряд ядра (числа всех электронов) |
| ε | остаточный член |
| λ | собственные значения МГ |
| ν | число ребер графа |
ИНДЕКСЫ
Список литературы
Жоров Ю.М. Термодинамика химических процессов. М.: Химия, 1985.
Баскин И.И., Маджидов Т.И., Варнек А.А. Введение в хемоинформатику: учебное пособие. Казань: Изд-во Казанского университета, 2016.
Урядов В.Г., Аристова Н.В., Курдюков А.И., Офицеров Е.Н. // Хим. компьют. модел. Бутлеровские сообщ. 2000. № 3. С. 67.
Урядов В.Г., Аристова Н.В., Курдюков А.И., Офицеров Е.Н. // Хим. компьют. модел. Бутлеровские сообщ. 2002. № 6. С. 31.
Офицеров Е.Н., Урядов В.Г., Аристова Н.В. // Журн. физ. хим. 2005. Т. 21. № 3. С. 15.
Доломатов М.Ю., Аубекеров Т.М., Коледин О.С., Ахтямова К.Р., Вагапова Э.В., Ковалева Э.А. // Журн. физ. хим. 2019. Т. 93. № 12. С. 1.
Доломатов М.Ю., Шамова Н.А., Трапезникова Е.Ф., Аубекеров Т.М., Стенькин А.В. // Хим. технол. 2016. № 1. С. 45.
Химические приложения топологии и теории графов / Под ред. Кинга Р. М.: Мир, 1987.
Heinzen V.E.F., Soares M.F., Yunes R.A. Semi-empirical topological method for the prediction of the chromatographic retention of cis- and trans-alkene isomers and alkanes // J. Chromatogr. A. 1999. V. 849. № 2. P. 495.
Ландау Л.Д., Лившиц Е.М. Курс теоретической физики. Т. 5. Статистическая физика. М.: Физматлит, 2002.
Анисимов М.А. Критические явления в жидкостях и жидких кристаллах. М.: Наука, 1987.
Доломатов М.Ю., Павлов Т.И., Аубекеров Т.М. База данных физико-химических свойств органических соединений. Пат. 2018620459 РФ. 2018.
Шамова Н.А., Доломатов М.Ю., Трапезникова Е.Ф., Аубекеров Т.М., Стенькин А.В. Программа расчета физико-химических свойств органических соединений с использованием двумерных топологических характеристик. Пат. 2015613203 РФ. 2015.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии