Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 531-543
Обеспечение стабильности работы этиленового региона химико-технологического комплекса по переработке газов крекинга и пиролиза за счет учета динамики протекания входящих в него процессов
А. М. Алиев a, А. Р. Сафаров a, *, И. И. Османова a, А. М. Гусейнова a, И. В. Балаев a
a Институт катализа и неорганической химии им. акад. М.Ф. Нагиева НАН Азербайджана
Баку, Азербайджан
* E-mail: agil_s@mail.ru
Поступила в редакцию 13.02.2019
После доработки 16.03.2020
Принята к публикации 15.05.2020
Аннотация
В работе изучаются динамика процессов этиленового региона химико-технологического комплекса, причины изменения активности катализаторов, выбираются функции, учитывающие нестационарность процессов, составляются их динамические кинетические модели и на основе полных математических описаний решаются задачи их оптимального управления, что в итоге позволило выполнить поставленную цель – сохранить оптимальные производительности целевых продуктов, найденных при оптимизации процессов химико-технологического комплекса для стационарных условий их протекания.
ВВЕДЕНИЕ
Процессы нефтеперерабатывающей и нефтехимической отраслей промышленности в основном – каталитические, характерной чертой которых является их протекание в условиях нестационарной активности катализатора. Дезактивация катализаторов – одна из главных проблем химической промышленности. Эта проблема является не только сложной, но и наименее изученной в промышленном катализе.
Классификация процессов дезактивации катализаторов проводится в работах [1–3]. Закоксовывание, как наиболее распространенный случай отравления катализаторов дегидрирования, изучалось в [1–5]. А.М. Алиевым с сотрудниками проведена большая работа по выявлению причин и характера изменения активности разного типа катализаторов для разных промышленных каталитических процессов [3].
Вопросам моделирования нестационарных химических процессов посвящено значительное количество работ [5–8]. Рядом исследователей Томского политехнического университета [9–11] предложен подход к разработке кинетических моделей промышленного процесса риформинга бензинов на платиновых катализаторах и на полиметаллическом катализаторе КР-108 У. Показано, что в условиях процесса риформинга интенсивно протекает процесс образования кокса, учет которого на активной поверхности даст возможность моделировать нестационарный процесс риформинга бензинов при подборе катализаторов.
В [11] приведена классификация моделей и кинетические факторы, влияющие на увеличение эффективности протекания процесса при нестационарном состоянии катализатора.
Разработке кинетических моделей нестационарных каталитических процессов с учетом характерных особенностей изменения активности катализаторов посвящена работа [12]. В ней, в частности, показаны и объяснены часто встречающиеся кривые зависимости активности катализатора от времени его работы с характерными периодами изменения активности: ее возрастание, период стационарной активности и период падения активности.
Анализ преимуществ проведения гетерогенно-каталитических химико-технологических процессов в нестационарных условиях и способы их оптимизации проведен в работе [8].
Однако работы, посвященные анализу кинетических моделей и направленные на формирование активного состояния катализатора, крайне немногочисленны, что иногда связано с отсутствием нестационарных кинетических моделей реакций.
В связи с этим не вызывает сомнений актуальность выявления характера и причин изменения активности катализатора со временем, необходимости разработки динамических кинетических моделей процессов для математического их описания.
ПОСТАНОВКА ЗАДАЧИ
Для удовлетворения потребности Азербайджана в олефинах, получаемых из газов крекинга и пиролиза с БНЗ им. Г. Алиева и установки ЭП-300 Сумгаитского завода “Этилен-Полиэтилен”, и их рационального использования в Институте катализа и неорганической химии им. акад. М.Ф. Нагиева НАН Азербайджана был разработан химико-технологический комплекс (ХТК) по совместной переработке этих газов. Работа такого ХТК позволит достичь требуемой производительности ХТК по нужным Азербайджану целевым продуктам с минимальными затратами. В работах [13–15] произведен полный расчет всего химико-технологического комплекса по переработке газов крекинга и пиролиза. Расчет всех процессов, входящих в ХТК, проводился по математическим моделям, составленным для стационарных условий их протекания. Однако рассмотренные в ХТК процессы, как каталитические, так и некаталитические, часто протекают в условиях нестационарности, вызванной разными причинами [3]. В зависимости от условий проведения процессов изменение их активности во времени происходит по-разному, снижая производительность реактора, срок службы катализатора, селективность процесса.
Наша цель заключается в том, чтобы данные по оптимальным производительностям целевых продуктов, полученных при оптимизации всего ХТК и удовлетворяющих потребностям в них Азербайджана, не были бы нарушены из-за возможной нестационарности процессов.
В работе [13] для сокращения размерности задачи весь химико-технологический комплекс был разбит на пять регионов, самым большим из которых по количеству процессов (девять процессов) является этиленовый регион. Для всех процессов приведены данные по условиям их проведения, а также стехиометрические и кинетические модели со значениями кинетических констант. В рассматриваемой статье для получения полного математического описания процессов кинетические модели дополнялись уравнениями теплового баланса и гидродинамики, а также факторами нестационарности процессов, после чего стало возможным перейти к их управлению.
Рассмотрим конкретные процессы этиленового региона в порядке расположения их по схеме ХТК [13].
1. Пиролиз этана. К стехиометрической и стационарной кинетической моделям [13] добавлены:
– уравнение теплового баланса [16]:
(1)
$\frac{{dT}}{{dL}} = \frac{{\pi {{d}_{H}}q - \sum\limits_j {{{r}_{j}}\Delta {{H}_{{Rj}}}} }}{{\sum\limits_i {\left( {\frac{{g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{0}}}{{\bar {M}}}\sum\limits_i {\alpha _{i}^{'}} + \sum\limits_i {\Delta {{n}_{i}}} } \right){{C}_{{pi}}}} }}$– уравнение скорости образования кокса [17]:
(2)
${{r}_{{\text{C}}}} = {{k}_{{\text{1}}}}{\text{C}}_{{\text{4}}}^{ + } = {{k}_{{{\text{01}}}}}{\text{exp}}\left( { - \frac{{{{E}_{{\text{1}}}}}}{{RT}}} \right){\text{C}}_{{\text{4}}}^{ + }$– выражение изменения диаметра трубы в результате коксоотложения [18]:
(3)
${\Delta }{{d}_{{\text{в}}}} = 2\frac{{{{r}_{{\text{C}}}}{\Delta \tau }}}{{{{{\rho }}_{{\text{C}}}}}}.$С учетом значений исходных данных для расчета промышленного реактора [13] и зависимости ${\Delta }{{d}_{{\text{в}}}}$ от времени (3) уравнение Дарси–Вейсбаха, представленное в [16] для стационарной модели, примет следующий вид:
(4)
$\frac{{dP}}{{dl}} = - {\text{2160}}{\text{.4}} \times {\text{1}}{{{\text{0}}}^{{ - 1{\text{3}}}}}\left( {{\text{1}} + \frac{{{\text{30}}{{d}_{{\text{в}}}}\left( {\tau } \right)}}{{{{L}_{{\text{0}}}}}}} \right)\frac{{g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{\text{0}}}}}{{{{P}_{{\text{0}}}}d_{{\text{в}}}^{{\text{5}}}\left( {\tau } \right)}}.$Некаталитический процесс пиролиза этана протекает в нестационарных условиях, вызванных отложениями кокса на стенках трубчатого змеевика. Откладывающийся кокс с течением времени уменьшает диаметр реактора, из-за чего происходит увеличение перепада давления между входом и выходом из реактора. А так как для промышленного реактора пиролиза этана существует ограничение на конечное давление (Pk ≥ 1.95 атм – в целях преодоления гидравлического сопротивления в последующей аппаратуре), то для сохранения его необходимо по мере увеличения перепада давления со временем увеличивать давление на входе. Кроме того, уменьшение диаметра трубы изменяет гидродинамическую картину в реакторе, что снижает интенсивность процесса и приводит к уменьшению производительности по этилену. Чтобы этого избежать, нужно постепенно повышать загрузку реактора, но так, чтобы выход этилена оказывался в пределах значения, полученного при расчете процесса по стационарной модели (900 кг/ч). Для того чтобы в любой момент времени можно было бы точно определить, насколько необходимо увеличить загрузку этана и одновременно входное давление реактора при соблюдении указанных условий, на основании полученных после статистической обработки промышленных данных за 700 часов работы реактора предложено регрессионное уравнение зависимости выхода этилена ${{g}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}}\left( Y \right)$ от управляющих параметров: времени работы печи (X1), загрузки реактора (X2) и перепада давления в нем (X3):
Коэффициенты вычислены по программе Matlab [19].
Уравнения кинетики [13], теплового баланса (1) и уравнений (2)–(4), учитывающих динамику процесса из-за коксоотложения, совместно с регрессионным уравнением (5) составят математическое описание процесса для нестационарных условий его протекания. В табл. 1 приведены ход и результаты расчета процесса пиролиза этана с применением функции управления (5).
Таблица 1.
Ход и результаты расчета нестационарного процесса пиролиза
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Время τ, ч X1 |
Загрузка реактора ${\text{g}}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{\text{0}}}$, кг/ч X2 |
Перепад давления ΔP, атм X3 |
Уменьшение внутреннего диаметра Δdв, м | Конечный диаметр dвк, м | Толщина коксоотложения Δtc, мм | Давление на входе в реактор P0, атм | Давление на выходе из реактора Pk, атм | Выход этилена $g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{эксп}}}}$Yэксп |
Выход этилена $g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{расч}}}}$$Y_{{{\text{расч}}}}^{{\left( {\text{5}} \right)}}$ |
Относительная погрешность $\frac{{\left( {{{Y}_{{{\text{эксп}}}}} - Y_{{{\text{расч}}}}^{{\left( {\text{5}} \right)}}} \right)}}{{{{Y}_{{{\text{эксп}}}}}}} \times 100\% $ |
Выход этилена ${\text{g}}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{расч}}}}$$\overline {\text{Y}} _{{{\text{расч}}}}^{{\left( 6 \right)}}$ |
Относительная погрешность $\frac{{\left( {{{{\text{Y}}}_{{{\text{эксп}}}}}{\text{ - }}\overline {\text{Y}} _{{{\text{расч}}}}^{{\left( 6 \right)}}} \right)}}{{{{{\text{Y}}}_{{{\text{эксп}}}}}}} \times 100\% $ |
| 100 | 2504 | 0.904 | 0.00424 | 0.1280 | 2.12 | 3.245 | 2.341 | 900.14 | 940.35 | –4.46 | 898.3 | 0.2044 |
| 200 | 2510 | 1.088 | 0.00898 | 0.1232 | 4.50 | 3.253 | 2.165 | 901.1 | 896.04 | 0.56 | 899.1 | 0.2224 |
| 300 | 2526.8 | 1.252 | 0.01274 | 0.1195 | 6.40 | 3.274 | 2.022 | 899.5 | 863.28 | 4.02 | 898.1 | 0.1556 |
| 400 | 2619.3 | 1.438 | 0.01605 | 0.1162 | 8.02 | 3.395 | 1.958 | 900 | 860.31 | 4.41 | 897.9 | 0.2333 |
| 500 | 2993.8 | 1.922 | 0.02030 | 0.1119 | 10.20 | 3.878 | 1.956 | 901.13 | 899.99 | 0.12 | 899.1 | 0.2253 |
| 600 | 3057.6 | 2.018 | 0.02410 | 0.1081 | 12.05 | 3.970 | 1.952 | 900.46 | 911.55 | –1.23 | 899 | 0.1624 |
| 700 | 3086.4 | 2.05 | 0.02950 | 0.1027 | 14.75 | 4.000 | 1.950 | 900.61 | 926.35 | –2.86 | 898.6 | 0.2232 |
| Δср = 0.58% | Δср = 0.2038% | |||||||||||
Как видим, сопоставление значений выходов этилена $g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{расч}}}}$ вычисленных по зависимости (5), с экспериментальными их значениями $g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{эксп}}}}$, дало значительные погрешности (столбцы 9, 10, 11 табл. 1). Поэтому, проведя полиномиальную аппроксимацию между $g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{расч}}}}$ и $g_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{эксп}}}}$, получили уточненное регрессионное уравнение:
(6)
$\begin{gathered} {{\overline Y }_{{{\text{расч}}}}} = - 5646 + 21.24{{Y}_{{{\text{расч}}}}} - \\ - \,\,0.02295Y_{{{\text{расч}}}}^{{\text{2}}} + 8.256 \times {{10}^{{ - 6}}}Y_{{{\text{расч}}}}^{{\text{3}}}, \\ \end{gathered} $расчет по которому привел к более точному по сравнению с регрессионным уравнением (5) приближению к экспериментальным значениям (столбцы 12, 13 табл. 1).
Использование предложенной функции управления процессом пиролиза в нестационарных условиях (6) дает возможность сохранить выход этилена на требуемом уровне и не нарушить ограничение, налагаемое на конечное давление.
2. Полимеризация этилена. Полимеризация этилена при высоком давлении представляет собой цепной процесс, протекающий по свободно-радикальному механизму в присутствии инициатора – кислорода в трубчатом реакторе при температуре (200–280°С), постоянном давлении (120–300 МПа). Суммарная степень превращения (95–98%). Математическое описание процесса в стационарных условиях [20]:
Стехиометрическая схема: $n{\text{A}} \to {{\left( {\text{A}} \right)}_{n}}$.
Кинетические уравнения для мономера и инициатора:
(7)
$\frac{{dx}}{{dl}} = - {{A}_{{\text{R}}}}{{\left[ M \right]}_{{\text{0}}}}{\text{exp}}\left( { - \frac{{{{b}_{{\text{1}}}}}}{T}} \right)T{{y}^{{\frac{{\text{1}}}{{\text{2}}}}}},$(8)
$\frac{{dy}}{{dl}} = - {{A}_{{\text{I}}}}{{\left[ M \right]}_{{\text{0}}}}{\text{exp}}\left( { - \frac{{{{b}_{{\text{2}}}}}}{T}} \right)y{\text{,}}$Уравнение теплового баланса:
(9)
$\frac{{dT}}{{dl}} = - {{a}_{{\text{3}}}}{\text{exp}}\left( { - \frac{{{{b}_{{\text{1}}}}}}{T}} \right)x{{y}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {{a}_{{\text{4}}}}\left( {T - {{T}_{{\text{0}}}}} \right){\text{,}}$(10)
${{a}_{{\text{3}}}} = {{A}_{{\text{R}}}}{{\left[ M \right]}_{0}}{{Q}_{{\text{R}}}};\,\,\,\,{{a}_{{\text{4}}}} = - {\text{4}}{K \mathord{\left/ {\vphantom {K {{\pi }d_{{{\text{вн}}}}^{{\text{2}}}{{С}_{{\text{p}}}}{\rho }}}} \right. \kern-0em} {{\pi }d_{{{\text{вн}}}}^{{\text{2}}}{{С}_{{\text{p}}}}{\rho }}}.$Однако в промышленности процесс протекает в нестационарных условиях из-за образованного при пиролизе этана ацетилена, являющегося ядом для инициатора и приводящего к снижению качества и производительности полиэтилена. Чтобы приостановить распад инициатора и сохранить плотность полимера, предложена функция нестационарности, учитывающая отравляющее воздействие на него ацетилена:
(11)
${\theta } = {{{\text{e}}}^{{ - \left( {A{{{\text{e}}}^{{ - \frac{{{{E}_{{{\text{in}}}}}}}{{RT}}}}}} \right){{t}_{{\text{R}}}}b{{F}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}}}}}{\text{,}}$считая при этом, что концентрация ядов пропорциональна количеству поступающего на полимеризацию этилена $\left( {b \times {{F}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}}} \right)$.
Эту функцию, учитывающую изменение активности инициатора также от времени реакции tR, вводим в уравнение скорости расходования мономера в стационарных условиях:
(12)
$\frac{{dx}}{{dl}} = \left[ { - {{A}_{{\text{R}}}}{{{\left[ M \right]}}_{{\text{0}}}}{\text{exp}}\left( { - \frac{{{{b}_{{\text{1}}}}}}{T}} \right)T{{y}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]{\theta }{\text{.}}$Уравнения (8), (9), (12) совместно с выражением (11) составляют полную математическую модель процесса полимеризации этилена в нестационарных условиях, с помощью которой определяется истинное распределение мономера по длине реактора и более точный выход полимера. В случае изменения производительности полиэтилена по сравнению с его количеством, получаемым в стационарных условиях, изменением значения θ можно будет регулировать процесс, сохраняя выход полиэтилена на нужном для региона уровне. Новое значение θ получится либо за счет изменения количеств подаваемых в полимеризатор этилена, либо инициатора.
3. Прямая гидратация этилена. Режимные условия процесса и математическая модель приведены в [13, 21]. К ним добавлены:
уравнение теплового баланса
(13)
$\frac{4}{{{{{\rho }}_{{{\text{кат}}}}}{\pi }{{D}^{{\text{2}}}}}}\frac{{dT}}{{dl}} = - \frac{{\sum r {\Delta }{{H}_{{\text{R}}}}}}{{\sum\limits_{i = {\text{1}}}^{\text{3}} {{{n}_{i}}{{{\text{C}}}_{{{\text{p}}i}}}} }} - {{Q}_{{{\text{наг}}}}}$и уравнение перепада давления по длине реактора
(14)
$\begin{gathered} \frac{{dP}}{{dl}} = - \left( {\frac{{{\text{150}}\left( {{\text{1}} - {\varepsilon }} \right)}}{{{\text{Re}}}} + {\text{1}}{\text{.75}}} \right) \times \\ \times \,\,\frac{{{{{\rho }}_{{{\text{газ}}}}}u_{{\text{0}}}^{{\text{2}}}\left( {{\text{1}} - {\varepsilon }} \right)}}{{{{d}_{{\text{p}}}}g{{{\varepsilon }}^{{\text{3}}}}}} \times {\text{0}}{\text{.987}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{5}}}}}. \\ \end{gathered} $Катализатором процесса является фосфорная кислота. Активность катализатора в процессе работы снижается вследствие уноса кислоты. В промышленности предлагается для возмещения количества фосфорной кислоты непрерывно добавлять ее в парогазовую смесь на входе в реактор, что приводит к большому ее расходу [23]. Мы предлагаем более целесообразный способ – способ периодической подачи кислоты. Для наблюдения за ходом процесса предложена функция управления θ, равная отношению текущего и исходного значений фосфорной кислоты: θ = Gтек/Gисх, фактически означающую долю ее активных центров, изменяющуюся в процессе работы катализатора из-за частичного уноса кислоты.
Значения θ в пусковом периоде (50–100 ч), когда достигается стабильная активность катализатора, близки к единице. С течением времени они уменьшаются. Поэтому для сохранения стабильной работы катализатора за критериальное значение функции управления приняли θ = 0.98, когда разница между исходным и текущим значениями фосфорной кислоты еще мала.
В табл. 2 приведено сравнение результатов расчета процесса при промышленном и предлагаемом способах его осуществления, из которого видно, что при промышленном способе принятое значение θ = 0.98 нарушается сразу после пускового периода катализатора и с течением времени продолжает снижаться из-за уменьшения количества катализатора. Аналогичная ситуация за оставшиеся 400 ч работы катализатора наблюдалась еще три раза. При этом уносится, а значит, и вносится в реактор за 500 ч работы 697.5 кг фосфорной кислоты (при непрерывной ее подаче). Во избежание большого расхода катализатора предлагается каждый раз при отклонении θ от принятого значения 0.98 добавлять к оставшемуся количеству фосфорной кислоты такое дополнительное ее количество, которое приводило бы катализатор к стабильному состоянию. При этом функция управления примет следующий вид: ${\theta }{\kern 1pt} {\text{'}} = \frac{{{{G}_{{{\text{тек}}}}} + {{G}_{{{\text{доб}}}}}}}{{G_{{{\text{исх}}}}^{{\text{'}}}}} = \frac{{G_{{{\text{тек}}}}^{{\text{'}}}}}{{G_{{{\text{исх}}}}^{{\text{'}}}}}$, когда полученное на данном временном интервале значение $G_{{{\text{тек}}}}^{{\text{'}}}$ становилось исходным $G_{{{\text{исх}}}}^{{\text{'}}}$ для следующих интервалов. Как видим из таблицы, периодические добавки фосфорной кислоты (в сумме 291.6 кг) вместо непрерывной ее подачи позволяют сохранять стабильную работу реактора в течение всего срока его работы, а также значительно сократить расходы фосфорной кислоты (291.6 кг вместо 697.5 кг).
Таблица 2.
Сравнение результатов расчета процесса гидратации при промышленном и предлагаемом способах его осуществления
| Промышленный способ | Предлагаемый способ | ||||||
|---|---|---|---|---|---|---|---|
| Временные интервалы работы каталзатора, ч | Скорость уноса фосф. кислоты, кг/ч (по интервалам) |
Количество унесенной фосф. кислоты за каждые 50 ч, Gунес, кг | Текущее количество фосфорной кислоты, Gтек, кг | Функция управления
θ = Gтек/Gисх (без добавок) |
Добавки фосфорной кислоты, Gдоб, кг | Текущее количество
фосфорной кислоты, кг $G_{{{\text{тек}}}}^{{\text{'}}} = {{G}_{{{\text{тек}}}}} + {{G}_{{{\text{доб}}}}}$ |
Функция управления ${\theta }{\kern 1pt} {\text{'}} = \frac{{{{G}_{{{\text{тек}}}}} + {{G}_{{{\text{доб}}}}}}}{{G_{{{\text{исх}}}}^{{\text{'}}}}}$ (с добавками) |
| 0 | 0 | 0 | 6534 | 1 | – | – | – |
| 0–50 | 2.00 | 100 | 6434 | 0.9847 | – | – | 0.985 |
| 50–100 | 1.95 | 97.5 | 6336.5 | 0.9698 | 66.8 | 6403.3 | 0.98 |
| 100–150 | 1.9 | 95.0 | 6241.5 | 0.9552 | – | – | 0.98 |
| 150–200 | 1.8 | 90 | 6151.5 | 0.9415 | 58.3 | 6209.8 | 0.961 |
| 200–250 | 1.7 | 85 | 6066.5 | 0.9285 | – | – | 0.98 |
| 250–300 | 1.4 | 70 | 5996.5 | 0.9177 | 89.1 | 6085.6 | 0.966 |
| 300–350 | 1.2 | 60 | 5936.5 | 0.9086 | – | – | 0.98 |
| 350–400 | 1.0 | 50 | 5886.5 | 0.9009 | 77.4 | 5963.9 | 0.967 |
| 400–450 | 0.8 | 40 | 5846.5 | 0.8947 | – | – | 0.98 |
| 450–500 | 0.2 | 10 | 5836.5 | 0.8932 | – | – | 0.98 |
| ∑697.5 | ∑291.6 | ||||||
Используя промышленные данные, для контроля за процессом гидратации определили регрессионную зависимость
по которой можно в любой момент времени найти текущее значение фосфорной кислоты и соответствующее ему значение θ, а значит, в случае несоответствия ее принятому критерию определить нужную на данном этапе добавку катализатора. Введя выбранную функцию управления θ в стационарную кинетическую модель процесса [13], получили динамическую кинетическую модель:
(16)
$\begin{gathered} \frac{{dn}}{{dt}} = \frac{{k{\kern 1pt} '{\theta }}}{{{{{\left( {\frac{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{\text{0}}} - n}}{{n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{\text{0}}} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{\text{0}}} - n}}P} \right)}}^{{\frac{{\text{1}}}{{\text{2}}}}}}}} \times \\ \times \,\,\left( {\frac{{n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{\text{0}}} - n}}{{n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{\text{0}}} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{\text{0}}} - n}}P - K_{{\text{p}}}^{{ - {\text{1}}}}\frac{n}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{\text{0}}} - n}}} \right) \times \\ \times \,\,\frac{{{{{\left( {n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{\text{0}}} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{\text{0}}} - n} \right)}}^{{\text{2}}}}}}{{P\left( {n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}^{{\text{0}}} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{\text{0}}}} \right)}}. \\ \end{gathered} $Уравнение (16) совместно с уравнениями теплового баланса (13), потери напора (14) и регрессионном уравнением (15) составляют полную математическую модель процесса с учетом нестационарности его протекания. Использование этой модели позволяет поддерживать производительность этилового спирта на нужном (стационарном) уровне с наименьшими затратами на расход фосфорной кислоты.
Так как процессы окислительного превращения этилового спирта в уксусную кислоту и этерификации уксусной кислоты этиловым спиртом (под номерами 4 и 5 соответственно) в течение 500 ч работы катализаторов проявляют стабильную активность, то при расчете региона пользовались математическими моделями, приведенными в [13] для стационарных условий.
6. Деалкилирование толуола. На основании расчетов процесса деалкилирования толуола с водяным паром, проводимого на катализаторе [Ni–Co–Cr/Al2O3/Al] под действием сверхвысокочастотного излучения (СВЧ), по математической модели, представленной в [13], получены оптимальные условия реакции: объемная скорость подачи реакционной массы – 1800 ч–1; мольные соотношения толуол:водяной пар – (1 : 4), температура – 500°С; степень превращения толуола – 58.8%; избирательность по бензолу – 76.6%; по ксилолам – 7.5% [24]. При найденных оптимальных условиях проведено исследование процесса в пилотной установке в течение 1000 ч работы катализатора. Замечено, что с течением времени активность катализатора медленно снижается из-за накопления по реакции диспропорционирования толуола нежелательных ксилолов, блокирующих и отравляющих активные центры катализатора, вследствие чего избирательность по бензолу падает. Для учета влияния изменения активности катализатора со временем τ на производительность процесса предложена следующая функция дезактивации катализатора:
Включая θ в уравнение скорости образования бензола, получили совместно с остальными уравнениями стационарной модели [13] динамическую кинетическую модель процесса:
(18)
$\begin{gathered} {{W}_{{{\text{БЕНЗ}}}}} = \left[ {\frac{{k_{{{\text{ЭФФ}}}}^{{\text{1}}}{{P}_{{{\text{ТОЛ}}}}}}}{{{\text{1}} + {{K}_{{{\text{ТОЛ}}}}}{{P}_{{{\text{ТОЛ}}}}}}} + \frac{{k_{{{\text{ЭФФ}}}}^{{\text{2}}}{{P}_{{{\text{ТОЛ}}}}}}}{{{\text{1}} + {{K}_{{{\text{ТОЛ}}}}}{{P}_{{{\text{ТОЛ}}}}}}}} \right. + \\ \left. { + \,\,\frac{{k_{{{\text{ЭФФ}}}}^{{\text{3}}}{{P}_{{{\text{ТОЛ}}}}}{{P}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{{\text{1}} + {{K}_{{{\text{ТОЛ}}}}}{{P}_{{{\text{ТОЛ}}}}} + {{K}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{P}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}} \right]{\theta }{\text{.}} \\ \end{gathered} $Для сохранения избирательности по бензолу на оптимальном уровне (76.6%), полученном при использовании СВЧ в стационарных условиях, предложено разбавлять реакционную смесь (толуол + водяной пар) на входе в реактор водородом. Разбивая весь интервал работы катализатора (1000 ч) на временные участки по 200 ч, на каждом из них с учетом добавок водорода в интервале [0.1–1.75] на единицу массы толуола определяли соответствующие им избирательности по бензолу SБ и ксилолам Sксил. На основании полученных данных составлены регрессионные зависимости избирательностей (SБ и Sксил) от управляющих параметров – добавок водорода M и времени работы катализатора τ:
Система уравнений стационарной модели [13] с учетом (17) и (18), а также регрессионных уравнений (19), (20) составляет математическое описание процесса в условиях нестационарности.
Расчеты по полученной модели за 1000 ч работы катализатора представлены в табл. 3, из которой видно, что наиболее близкие к оптимальным значения избирательностей по бензолу и ксилолам (представлены в первой строке таблицы) соответствуют добавкам водорода к смеси (Т + Н2О) в интервале [0.2–1.5].
Таблица 3.
Наилучшие выходы бензола при указанных добавках водорода к реакционной смеси на входе в реактор
| Объемная скорость подачи Т + Н2О + Н2, ч–1 |
Соотношения | Избирательность по бензолу, % | Избирательность по ксилолам, % | ||
|---|---|---|---|---|---|
| Т | Н2О | Н2 | |||
| 1800опт | 1 | 4 | – | 76.6опт | 7.5опт |
| 1835 | 1 | 4 | 0.1 | 75.6 | 7.5 |
| 1872 | 1 | 4 | 0.2 | 76.0 | 7.4 |
| 1980 | 1 | 4 | 0.5 | 76.2 | 7.1 |
| 2070 | 1 | 4 | 0.75 | 76.5 | 6.9 |
| 2160 | 1 | 4 | 1 | 77.0 | 6.6 |
| 2250 | 1 | 4 | 1.25 | 77.1 | 6.5 |
| 2340 | 1 | 4 | 1.50 | 77.3 | 6.3 |
| 2430 | 1 | 4 | 1.75 | 75.5 | 8.4 |
Добавки водорода в найденном интервале их изменения способствуют снижению интенсивности реакции образования ксилолов и, следовательно, увеличению избирательности по бензолу, что становится ясным при сравнении со случаем проведения процесса без добавок водорода: при τ = 1000 ч избирательности по бензолу и ксилолам составляют 73.2 и 11.2% соответственно (табл. 4).
Таблица 4.
Результаты работы катализатора в течение 1000 ч (без добавок водорода)
| Время работы катализатора, ч | 200 | 400 | 600 | 800 | 1000 |
| Избирательность по бензолу, % | 76.6 | 75.8 | 75.0 | 74.4 | 73.2 |
| Избирательность по ксилолам, % | 1.2 | 2.3 | 8.4 | 9.9 | 11.2 |
Таким образом, используя при расчетах процесса нестационарную математическую модель с учетом функции управления θ, а также предлагаемый метод добавок водорода к реакционной смеси (Т + Н2О) в найденном интервале их изменения, сможем сохранить производительность по бензолу на нужном, оптимальном, уровне.
7. Алкилирование бензола этиленом. Изотермический барботажный реактор; катализатор – хлористый алюминий; температура – 130°С; давление – 0.4 МПа. На основании экспериментальных данных, взятых с установки Сумгаитского завода СК, в [25] представлены стехиометрическая схема и соответствующие ей уравнения скорости образования этилбензола ЭБ (целевого продукта) и полиалкилбензолов ПАБ (побочных продуктов):
(21)
$\begin{gathered} {\text{Б}} + {\text{Э}}\xrightarrow{{{{k}_{1}}}}{\text{ЭБ,}} \\ {\text{ЭБ}} + {\text{Э}}\xrightarrow{{{{k}_{2}}}}{\text{ПАБ,}} \\ {\text{ПАБ}} + {\text{Б}}\xrightarrow{{{{k}_{3}}}}{\text{2ЭБ,}} \\ {\text{2ЭБ}} + {\text{Б}}\xrightarrow{{{{k}_{4}}}}{\text{ПАБ,}} \\ \end{gathered} $(22)
$\begin{gathered} \frac{{d{{X}_{{{\text{ЭБ}}}}}}}{{dl}} = \frac{{\left( {{\gamma }P - A} \right)\left( {{{K}_{{\text{1}}}}{{C}_{{\text{k}}}}{{X}_{{\text{Б}}}} - {{K}_{{\text{2}}}}{{C}_{{\text{k}}}}{{X}_{{{\text{ЭБ}}}}}} \right)}}{{{{W}_{{\text{Ж}}}}\left( {{\text{1}} + B} \right)}} + \\ + \,\,\frac{{{{K}_{{\text{3}}}}{{C}_{{\text{k}}}}{{С}_{{\text{Б}}}}{{X}_{{{\text{ПАБ}}}}} - {{K}_{{\text{4}}}}{{C}_{{\text{k}}}}{{С}_{{\text{Б}}}}X_{{{\text{ЭБ}}}}^{{\text{2}}}}}{{{{W}_{{\text{Ж}}}}}}, \\ \end{gathered} $(23)
$\begin{gathered} \frac{{{\text{d}}{{X}_{{{\text{ПАБ}}}}}}}{{dl}} = \frac{{{{K}_{{\text{D}}}}C_{{{\text{ЭТ}}}}^{{\text{2}}}T\left( {{\gamma }P - A} \right){{K}_{{\text{2}}}}{{C}_{{\text{k}}}}{{X}_{{{\text{ЭБ}}}}}}}{{{\text{273}}{{M}_{{\text{г}}}}{{{\gamma }}_{{\text{г}}}}FP{{W}_{{\text{Ж}}}}}} + \\ + \,\,\frac{{{{K}_{{\text{4}}}}{{C}_{{\text{k}}}}{{X}_{{\text{Б}}}}X_{{{\text{ЭБ}}}}^{{\text{2}}} - {{K}_{{\text{3}}}}{{C}_{{\text{k}}}}{{С}_{{\text{Б}}}}{{X}_{{{\text{ПАБ}}}}}}}{{{{W}_{{\text{Ж}}}}}}{\text{,}} \\ \end{gathered} $(24)
$\begin{gathered} {\text{где}}\,\,A = \frac{{\left( {{{K}_{{\text{3}}}}{{X}_{{\text{Б}}}}{{X}_{{{\text{ПАБ}}}}} - {{K}_{{\text{4}}}}X_{{{\text{ЭБ}}}}^{{\text{2}}}} \right){{C}_{{\text{k}}}}n_{{\text{Б}}}^{{\text{2}}}{{{\gamma }}_{{\text{ж}}}}}}{{{{K}_{{\text{D}}}}{{W}_{{\text{г}}}}}}, \\ B = \frac{{\left( {{{K}_{{\text{1}}}}{{X}_{{\text{Б}}}} + {{K}_{{\text{2}}}}{{X}_{{{\text{ЭБ}}}}}} \right){{C}_{{\text{k}}}}{{n}_{{\text{Б}}}}}}{{{{K}_{{\text{D}}}}{{W}_{{\text{г}}}}}}. \\ \end{gathered} $Полиалкилбензолы (ПАБ), образующиеся в процессе одновременно с целевым продуктом (этилбензолом), являются побочными продуктами, блокирующими с течением времени поверхность катализаторного комплекса (КК), снижающими скорость образования, а значит, и выход этилбензола. Для сохранения значения уже полученной при оптимизации ХТК стационарной производительности этилбензола выбрана функция управления θ, учитывающая соотношение непрореагировавших этилена и бензола в продуктах реакции θ = GЭТ/GБ. Каждому такому значению θ в любой момент времени соответствует определенная концентрация этилбензола. Своевременное обнаружение непрореагировавших этилена и бензола, расчет их соотношения θ, сравнение с заданным (проектным) значением $\overline {\theta } $, определяемым по предлагаемой формуле ${\bar {\theta }} = 0.3{{e}^{{ - 0.2\tau }}},$ и внесение необходимых изменений в зависимости от отклонения способствуют повышению селективности процесса. Введение функции θ в правую часть стационарного уравнения скорости образования этилбензола позволило скорректировать количества этилена и бензола на входе в алкилатор и получить на выходе из него требуемое по проекту количество этилбензола, найденное для стационарных условий протекания процесса:
(25)
$\begin{gathered} \frac{{d{{X}_{{{\text{ЭБ}}}}}}}{{dl}} = \left[ {\frac{{\left( {{\gamma }P - A} \right)\left( {{{K}_{{\text{1}}}}{{C}_{{\text{k}}}}{{X}_{{\text{Б}}}} - {{K}_{{\text{2}}}}{{C}_{{\text{k}}}}{{X}_{{{\text{ЭБ}}}}}} \right)}}{{{{W}_{{\text{Ж}}}}\left( {{\text{1}} + B} \right)}}} \right. + \\ \left. { + \,\,\frac{{{{K}_{{\text{3}}}}{{C}_{{\text{k}}}}{{С}_{{\text{Б}}}}{{X}_{{{\text{ПАБ}}}}} - {{K}_{{\text{4}}}}{{C}_{{\text{k}}}}{{С}_{{\text{Б}}}}X_{{_{{{\text{ЭБ}}}}}}^{{\text{2}}}}}{{{{W}_{{\text{Ж}}}}}}} \right]{\theta }{\text{.}} \\ \end{gathered} $В табл. 5 приводится сравнение показателей процесса, полученных при осуществлении его по известному промышленному способу, с оптимальными значениями, рассчитанными по предлагаемому способу управления.
Таблица 5.
Сравнение известного и предлагаемого способов проведения процесса
| № | Промышленный способ | Предлагаемый способ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Вход в алкилатор | Выход | Вход в алкилатор | Выход | |||||||
| ${\text{G}}_{{\text{K}}}^{{св}},$ кг/ч |
${{{\text{G}}}_{{{\text{ЭТ}}}}},$ кг/ч |
${{{\text{G}}}_{{\text{Б}}}},$ кг/ч |
${{{\text{G}}}_{{{\text{ПАБ}}}}},$ кг/ч |
${{{\text{G}}}_{{{\text{ЭБ}}}}},$ кг/ч |
${\text{G}}_{{\text{K}}}^{{св}},$ кг/ч |
${{{\text{G}}}_{{{\text{ЭТ}}}}},$ кг/ч |
${{{\text{G}}}_{{\text{Б}}}},$ кг/ч |
${{{\text{G}}}_{{{\text{ПАБ}}}}},$ кг/ч | ${{{\text{G}}}_{{{\text{ЭБ}}}}},$ кг/ч |
|
| 1 | 420 | 5348.12 | 51 477.17 | 4517.20 | 20 976.56 | 420 | 5183.20 | 51 134.52 | 4416 | 21 071.91 |
| 2 | 420 | 5253.88 | 51 178.45 | 4452.80 | 20 803.20 | 420 | 5183.20 | 51 134.52 | 4416 | 21 106.58 |
| 3 | 420 | 5654.40 | 54 473.20 | 4554.00 | 21 063.24 | 420 | 5183.20 | 51 134.52 | 4416 | 21 063.24 |
| 4 | 420 | 4829.80 | 46 477.94 | 4517.20 | 20 629.84 | 420 | 5183.20 | 51 134.52 | 4416 | 21 071.91 |
| 5 | 420 | 5583.72 | 53 858.18 | 4259.60 | 21 037.24 | 420 | 5183.20 | 51 134.52 | 4416 | 21 149.92 |
| 6 | 420 | 5501.26 | 53 067.44 | 4121.60 | 20 993.90 | 420 | 5183.20 | 51 134.52 | 4416 | 21 167.26 |
| 7 | 420 | 5030.06 | 46 978.74 | 4664.40 | 20 673.18 | 420 | 4924.04 | 48 577.79 | 4195.2 | 20 954.89 |
| 8 | 420 | 5124.30 | 48 481.15 | 4728.80 | 20 716.52 | 420 | 3592.90 | 35 495.44 | 3054.4 | 20 868.21 |
| 9 | 420 | 5242.10 | 50 677.65 | 4084.80 | 20 794.53 | 420 | 3592.90 | 35 495.44 | 3054.4 | 20 846.54 |
Как видно из этой таблицы, использование предлагаемого способа управления позволяет увеличить выходы этилбензола в среднем на 1%, уменьшить количество полиалкилбензолов на выходе из алкилатора на 8–10%, что, в свою очередь, способствует уменьшению затрат на процесс разделения этилбензола на 2–3%.
8. Дегидрирование этилбензола. К режимным параметрам процесса, его стехиометрической и кинетической моделям [13, 26] добавлено уравнение теплового баланса:
(26)
$\frac{{dT}}{{dl}} = \frac{{{{N}_{{\text{0}}}}}}{{{{C}_{{{\text{p}}\,{\text{ср}}}}}{{N}_{{\text{Т}}}}}}{{Q}_{{\text{2}}}}\frac{{d{{x}_{2}}}}{{dl}}.$Представленная в [13] система уравнений совместно с уравнением (26) описывает процесс, протекающий в стационарных условиях.
Однако в промышленной практике осуществление процесса в неподвижном слое окисного катализатора Р-2 сопровождается медленным падением активности катализатора на всем протяжении процесса из-за адсорбции на поверхности катализатора малых количеств примесей (ядов), содержащихся в потоке исходных реагентов или продуктов реакции, что приводит к уменьшению производительности реактора. Для учета влияния степени отравления катализатора на его активность и в предположении адсорбционного характера процесса отравления ядами предложена следующая функция дезактивации:
(27)
${\theta } = {\text{1}} - {{\left[ {\left( {{\text{1}} - n} \right)A{{{\text{e}}}^{{ - \frac{{{{{\text{E}}}_{{\text{A}}}}}}{{{\text{RT}}}}}}}\left( {{{N}_{{\text{0}}}}M} \right)\left( {{\tau } - {{{\tau }}_{{\text{0}}}}} \right)} \right]}^{{\frac{{\text{1}}}{{{\text{1}} - n}}}}}.$Включая (27) в уравнение стационарной кинетической модели [13], получим динамическую кинетическую модель с учетом дезактивации катализатора:
(28)
$\frac{{d{{x}_{{\text{2}}}}}}{{dl}} = {{{\lambda }}_{{\text{2}}}}\frac{{{\text{1}} - {{x}_{{\text{2}}}} - {{x}_{{\text{5}}}}}}{{{\text{1}} + {{x}_{{\text{2}}}}}}{\theta }{\text{.}}$В промышленных условиях падения выхода целевого продукта избегают либо с помощью постепенного увеличения температуры на входе в реактор при неизменной степени разбавления сырья водяным паром, либо за счет работы на максимальной степени разбавления сырья водяным паром при неизменной входной температуре. С целью выявления одновременного влияния обоих указанных параметров на конверсию этилбензола в стирол и селективность процесса в условиях нестационарности проведена статистическая обработка промышленных данных с установки ПО “Оргсинтез” за 5000 часов работы катализатора Р-2, в результате которой получены регрессионные уравнения зависимостей управляемых параметров: конверсии этилбензола в стирол х2 и селективности процесса S от управляющих: степени разбавления сырья водяным паром М, температуры паросырьевой смеси на входе в реактор t0 и времени работы установки τ:
(29)
$\begin{gathered} {{x}_{2}} = 1.257042166 + 0.002389131M - \\ - \,\,0.001472064{{t}_{0}} - 0.00000426802\tau , \\ \end{gathered} $(30)
$\begin{gathered} S = 0.791438979 + 0.003849415M - \\ - \,\,0.000108156{{t}_{0}} - 0.00000528188\tau , \\ \end{gathered} $которые совместно с уравнением скорости образования толуола и бензола [13] и уравнениями (26)–(28) составили математическое описание процесса с учетом нестационарности его протекания. По нестационарной модели для каждого временного интервала (по 500 ч при сроке работы катализатора 5000 ч) находили температуру паросырьевой смеси на входе в реактор и степень разбавления сырья водяным паром. За критерий оптимальности принимался расход водяного пара. Из всех полученных траекторий в табл. 6 представлен оптимальный с точки зрения расхода водяного пара вариант, из которого видно, что для поддержания постоянными для всего периода работы катализатора оптимальных значений выхода стирола 41% и селективности процесса 92% температуру смеси на входе в реактор целесообразно снижать от 597.6 в начале до 592.1°С в конце периода работы катализатора, а степень разбавления сырья водяным паром одновременно повышать с 16.7 до 21.3.
Таблица 6.
Оптимальный вариант управления процессом
| Конверсия этилбен-зола в сти-рол х2 Селектив-ность S, мол. % |
Параметры | Время работы катализатора τ, ч | Среднее значение расхода водяного пара за 5000 ч работы катализатора | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 | 45 000 | 5000 | ${{\bar {N}}_{\Pi }}$ = = 3826.62 кмоль/ч | ||
| х2 = 41 S = 92 |
M | 16.7 | 16.9 | 17.1 | 17.4 | 17.7 | 18.2 | 18.7 | 19.4 | 20.2 | 21.3 | ${{\bar {G}}_{\Pi }}$ = = 68879.16 кг/ч |
| t0 | 597.6 | 597.3 | 597.1 | 596.4 | 595.7 | 594.9 | 594.1 | 593.3 | 592.6 | 592.1 | ||
| NП | 3483.62 | 3525.34 | 3567.06 | 3629.64 | 3692.22 | 3763.76 | 3900.82 | 4046.84 | 4213.72 | 4443.18 | ||
При этом затраты на водяной пар снижаются по сравнению с заводскими на 25%.
Дальнейшее использование катализатора приводит к ускорению коксоотложения и соответственно к снижению выхода стирола по сравнению с оптимальным вариантом. Чтобы сохранить выход примерно на постоянном уровне, нами предложено незначительно повышать входную температуру паросырьевой смеси при сохранении степени разбавления сырья водяным паром неизменной. Результаты этого предложения представлены в табл. 7, из которой видно, что повышение температуры примерно на 4°С в течение следующих 2000 ч позволяет немного повысить выход, сохраняя его в пределах оптимального, и хотя селективность процесса с увеличением температуры немного снижается, однако до 7000 ч результаты работы катализатора могут считаться удовлетворительными.
Таблица 7.
Результаты работы катализатора после 5000 ч
| Время работы катализатора τ, ч | Температура паросырьевой смеси на входе в реактор t0, °C | Степень разбавления сырья водяным паром М, моль/моль | Конверсия этилбензола в стирол x2, мол. % | Селективность процесса S, мол. % |
|---|---|---|---|---|
| 5000 | 592.1 | 21.3 | 41.0 | 92 |
| 5500 | 593.0 | 21.3 | 41.2 | 91.9 |
| 6000 | 594.0 | 21.3 | 41.3 | 91.85 |
| 6500 | 595.0 | 21.3 | 41.35 | 91.70 |
| 7000 | 596.0 | 21.3 | 41.3 | 91.60 |
| 7500 | 597.0 | 21.3 | 41.28 | 91.40 |
Дальнейшее повышение температуры приводит уже к падению выхода стирола из-за ускорения процесса коксоотложения.
Таким образом, совершенно отличный от промышленного способ управления процессом обоими управляющими параметрами позволяет не только снизить затраты на водяной пар, но и продлить на 2000 ч срок службы катализатора, т.е. получить ощутимую экономическую выгоду.
9. Полимеризация стирола. К кинетической модели [13] добавлено уравнение теплового баланса [27]:
(31)
${\rho }V{{C}_{{\text{p}}}}\frac{{dT}}{{dt}} = {{M}_{{{\text{st}}}}}{\Delta }H\frac{{d{{x}_{{\text{m}}}}}}{{dt}} - {{q}_{{{\text{pot}}}}},$которые в совокупности составляют математическую модель процесса, протекающего в стационарных условиях.
Однако при дегидрировании этилбензола образуются, кроме стирола, толуола и бензола, еще и побочные продукты, содержащие небольшое количество фенилацетилена. Поэтому на полимеризацию поступает не чистый стирол, а с добавкой ~5 млн–1 фенилацетилена, который быстро и необратимо адсорбируется на инициаторе, отравляя его и вызывая его распад. Принимая, что активность инициатора падает линейно с количеством поступающего с исходным стиролом фенилацетилена, предложена следующая зависимость изменения активности инициатора со временем реакции t:
Для сохранения скорости полимеризации и получения полистирола той же молекулярной массы и качества, что и в стационарных условиях, функция нестационарности θ введена в уравнение скорости расходования мономера:
(33)
$\frac{{d{{x}_{{\text{m}}}}}}{{dt}} = \left[ {{{k}_{{{\text{EFF}}}}}\left( {{\text{1}} - {{x}_{{\text{m}}}}} \right)\sqrt {\frac{{{{I}_{{\text{0}}}}\left( {{\text{1}} - {{x}_{{\text{I}}}}} \right)}}{{\left( {{\text{1}} + {\varepsilon }{\kern 1pt} {{x}_{{\text{m}}}}} \right)F\left( {{{x}_{{\text{m}}}}} \right)}}} } \right]{\theta ,}$т.е. получена динамическая кинетическая модель процесса.
При отличии производительности полистирола от ее стационарного значения, изменяя величину θ за счет увеличения чистоты подаваемого в реактор стирола или количества инициатора, можно отрегулировать процесс и получить требуемый выход целевого продукта.
Так как процессы этиленового региона работают не синхронно и периоды изменения активности катализаторов по времени не совпадают, кроме того, причины нарушения стационарности в каждом процессе разные, то общую функцию управления всем регионом составить невозможно. Однако математические модели процессов, разработанные с учетом нестационарной активности катализаторов, имеют гибкую структуру, т.е. с течением времени идет процесс самонастройки этих моделей. Подстройка математической модели производится либо периодически через определенные промежутки времени, либо после того как несоответствие между расчетными и экспериментальными значениями превосходит определенную, заранее заданную, величину.
При таком подходе регион становится гибкой химико-технологической системой, сохраняющей свою работоспособность даже при возможных изменениях внешних и внутренних воздействий.
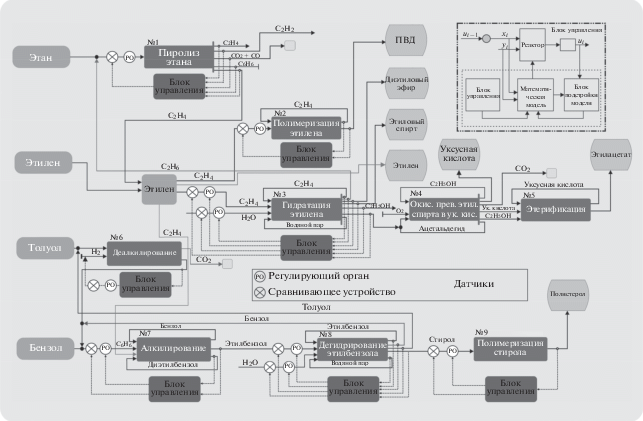
Общая схема управления этиленовым регионом ХТК представлена на рис. 1, на котором каждому процессу, протекающему в нестационарных условиях, соответствует свой блок управления с использованием подобранной для этого процесса функции нестационарности.
ЗАКЛЮЧЕНИЕ
Использование функций нестационарности в каждом конкретном процессе позволило поддерживать производительности целевых продуктов на выходе из этиленового региона на оптимальном уровне, найденном при оптимизации всего химико-технологического комплекса в стационарных условиях.
ОБОЗНАЧЕНИЯ
| Процесс № 1 | |
| ${{С}_{{{{{\text{p}}}_{i}}}}}$ | теплоемкость i-компонента, кДж/(кмоль К) |
| $C_{{\text{4}}}^{ + }$ | сумма концентраций всех компонентов выше, чем С3Н8 |
| dн | наружный диаметр трубы, м |
| dв | внутренний диаметр трубы, м |
| Δdв | изменение диаметра трубы, м |
| E1 | энергия активации, кДж/кмоль |
| ${\text{g}}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{\text{0}}}$ | загрузка этана, кг/ч |
| ΔHRj | тепловой эффект j-й реакции, кДж/кмоль |
| k01 | предэкспоненциальный множитель константы скорости реакции образования кокса |
| L0 | длина прямолинейного участка трубы, м |
| l | текущая длина реактора, м |
| $\overline M $ | средняя молекулярная масса пирогаза, кг/кмоль |
| Δni | измененное в результате реакции число молей i-го компонента, кмоль/ч |
| P | текущее давление в реакторе, Па |
| P0 | давление на входе в реактор, Па |
| q | теплонапряженность радиантных труб, кДж/(м2 ч) |
| R | газовая постоянная, (Па м3)/(кмоль К) |
| rc | скорость образования кокса |
| rj | скорость j-й реакции, кмоль/(ч м) |
| T | текущая температура, К |
| Δtc | увеличение толщины кокса, мм |
| ${\alpha }_{{\text{i}}}^{'}$ | начальная доля i-го компонента в поступающей на пиролиз смеси |
| ρC | плотность кокса, кг/м3 |
| Δτ | интервал времени, ч |
| Процесс № 2 | |
| A | предэкспоненциальный множитель |
| AI, AR | предэкспоненциальные множители для реакций инициирования и роста цепи, м3/(моль с) |
| b | коэффициент, учитывающий эффективность процесса гидрирования ацетилена |
| CP | удельная теплоемкость реакционной смеси, ккал/(кг град) |
| dвн | внутренний диаметр труб реактора, м |
| Еин | энергия активации разложения инициатора под воздействием ацетилена, кДж/моль |
| EI, ER | энергии активации реакций инициирования и роста цепи, кДж/моль |
| ${{F}_{{{{{\text{C}}}_{2}}{{{\text{H}}}_{4}}}}}$ | расход этилена, кмоль/ч |
| [I] | концентрация инициатора, моль/м3 |
| K | коэффициент теплопередачи, ккал/(м2 г град) |
| l | текущая координата длины реактора, м |
| [M]0, [M] | входная и текущая концентрации мономера, моль/м3 |
| QR | тепловой эффект реакции, кДж/моль |
| R | газовая постоянная, кДж/(моль К) |
| Т, T0 | начальная и текущая температуры, К |
| tR | время реакции, ч |
| x = [M]/[M]0 | безразмерная концентрация мономера |
| y = [I]/[M]0 | безразмерная концентрация инициатора |
| ρ | плотность реакционной смеси, кг/м3 |
| Процесс № 3 | |
| ${{С}_{{{{{\text{p}}}_{i}}}}}$ | теплоемкость i-го компонента, ккал/(моль град) |
| D | диаметр реактора, м |
| dp | эквивалентный диаметр частиц, м |
| Gисх, Gтек, Gдоб | исходное, текущее, добавленное значения фосфорной кислоты, кг |
| $G_{{{\text{тек}}}}^{{\text{'}}}$, $G_{{{\text{исх}}}}^{{\text{'}}}$ | текущее и исходное количества фосфорной кислоты в предлагаемом способе, кг |
| g | ускорение свободного падения, м/с2 |
| ΔHR | теплота реакции, ккал/моль |
| Kp | константа равновесия, атм–1 |
| $k{\kern 1pt} '$ | константа скорости реакции, атм0.5/с |
| l | длина реактора, м |
| ni | текущее число молей i-го компонента, моль/ч |
| $n,{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}},{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ | текущие значения этилового спирта, этилена и воды, моль/с |
| P | общее давление системы, атм |
| Qнаг | теплота, идущая на нагрев этилена, ккал/моль |
| r | скорость реакции, моль/(кгкат ч) |
| T | температура реакции, К |
| tR | условное время реакции, с |
| u0 | линейная скорость, м/с |
| ε | порозность |
| μ | вязкость газа, кг/(м с) |
| ρгаз | плотность газа, кг/м3 |
| ρкат | плотность катализатора, кг/м3 |
| Re | число Рейнольдса |
| Процесс № 6 | |
| кА | константа скорости адсорбции ядов, ч–1 |
| M | добавка водорода |
| SБ | избирательность по бензолу |
| Sксил | избирательность по ксилолам |
| α | мольная доля ксилолов в реакторе |
| θ | доля свободной поверхности катализатора |
| τ | время работы катализатора, ч |
| Процесс № 7 | |
| CЭТ, Ск, СБ | концентрации этилена, КК и бензола, моль/м3 |
| ${{d{{X}_{{{\text{ЭБ}}}}}} \mathord{\left/ {\vphantom {{d{{X}_{{{\text{ЭБ}}}}}} {dl}}} \right. \kern-0em} {dl}}$, ${{d{{X}_{{{\text{ПАБ}}}}}} \mathord{\left/ {\vphantom {{d{{X}_{{{\text{ПАБ}}}}}} {dl}}} \right. \kern-0em} {dl}}$ | соответственно скорости накопления этилбензола и полиалкилбензолов |
| F | площадь поперечного сечения алкилатора, м2 |
| GЭТ, GБ, $G_{{\text{К}}}^{{{\text{св}}}}$ | текущие значения расходов этилена, бензола и свежего КК, кг/ч |
| K1–K4 | константы скоростей реакций |
| КD | константа диффузионного обмена, м2/с |
| МГ | молекулярная масса этилена, кг/моль |
| nБ | мольная скорость бензола, моль/с |
| P | текущее давление, Па |
| Т | текущая температура, К |
| WГ, WЖ | линейные скорости газового и жидкого потоков, моль/(м3 с) |
| ХБ, ХЭБ, ХПАБ | мольные доли бензола, этилбензола и ПАБ |
| γ | коэффициент, учитывающий растворимость этилена в жидкой фазе |
| γж, γг | удельные веса жидкой фазы и этилена, кг/м3 |
| θ | функция управления |
| $\overline {\theta } $ | проектное значение θ |
| τ | время контакта реагирующих веществ, ч |
| Процесс № 8 | |
| А | предэкспонента константы скорости адсорбции ядов на поверхности катализатора |
| Cpcp | средняя теплоемкость участвующих в основной реакции (получения стирола) компонентов, ккал/(кмоль град) |
| EA | энергия активации процесса адсорбции, кДж/кмоль |
| l | длина реактора, м |
| М = NП/N0 | соотношение водяной пар : этилбензол |
| N0 | поступающий на дегидрирование этилбензол, кмоль/ч |
| NТ | текущее количество этилбензола, кмоль/ч |
| NП | количество водяного пара, кмоль/ч |
| n | показатель степени |
| R | газовая постоянная, кДж/(моль К) |
| Т | текущая температура процесса, К |
| x2 | степень превращения этилбензола в стирол |
| x5 | степень превращения этилбензола в бензол и толуол |
| τ | текущее время, ч |
| τ0 | время разработки катализатора, ч |
| Процесс № 9 | |
| Cp | теплоемкость среды, Дж/(кг К) |
| ΔH | энтальпия процесса, Дж/кг |
| I0 | начальная концентрация инициатора, моль/м3 |
| k | константа скорости распада инициатора, моль–1 |
| Mst | масса стирола, кг |
| Nst | количество поступающего в полимеризатор стирола, кмоль/ч |
| qpot | тепловой поток потерь в окружающую среду, Вт |
| t | время контакта, ч |
| V | объем реакционной среды, м3 |
| xI | конверсия инициатора |
| xm | конверсия мономера |
| α | мольная доля фенилацетилена в исходном сырье |
| ε | коэффициент изменения объема в ходе реакции полимеризации |
| ρ | плотность реакционной среды, кг/м3 |
Список литературы
Боресков Г.К. Влияние изменений состава катализатора на кинетику реакций гетерогенного катализа // Кинет. катал. 1972. Т. 13. № 3. С. 543.
Хьюз Р. Дезактивация катализаторов. М.: Химия, 1989.
Алиев А.М. Моделирование нестационарных каталитических процессов. Дис. … докт. техн. наук. Баку: ИТПХТ АН Азерб. ССР, 1984.
Буянов Р.А. Закоксование катализаторов. Новосибирск: Наука, 1983.
Гынгазова М.С. Моделирование работы реакторов процесса риформинга бензинов с непрерывной регенерацией катализатора с учетом коксообразования. Автореф. дис. … канд. техн. наук. Томск: Томск. нац. политехн. ун-т, 2011.
Галушин С.А. Моделирование нестационарных процессов на поверхности платиносодержащих катализаторов в промышленных реакторах установок риформинга бензинов. Автореф. дис. … канд. техн. наук. Томск: Нац. исслед. Томск. политехн. ун-т, 2004.
Кузнецов Ю.Ш., Слинько М.Г. Моделирование процессов при изменяющейся активности катализатора // Хим. пром-сть. 1981. № 11. С. 3.
Островский А.С. Математические методы и моделирование при исследовании гетерогенно-каталитических химико-технологических процессов. Автореф. дис. … канд. техн. наук. Пермь: Пермский государственный техн. ун-т, 2000.
Костенко А.В., Кравцов А.В., Иванчина Э.Д., Абрамин А.Л. Использование нестационарной кинетической модели для оценки и прогнозирования активности и стабильности платиновых катализаторов в промышленном процессе риформинга бензинов // Изв. Томск. политех. унив. 2004. Т. 307. № 5. С. 103.
Ярмухаметов Р.Р., Кравцов А.В., Иванчина Э.Д., Галушин С.А., Мельник Д.И. Использование нестационарной кинетической модели для оценки условий реформирования бензиновой фракции на полиметаллическом катализаторе КР-108У // Изв. Томск. политех. унив. 2004. Т. 307. № 2. С. 113.
Решетников С.И. Использование нестационарного состояния катализатора для управления скоростью и селективностью реакций. Автореф дис. … докт. хим. наук. Новосибирск: Институт катализа им. Г.К. Борескова СО РАН, 2008.
Алиев А.М., Османова И.И., Мамедов Э.М., Сафаров А.Р., Гусейнова А.М. Разработка кинетических моделей нестационарных каталитических процессов с учетом характерных особенностей изменения активности катализаторов // Хим. пром-сть. 2018. Т. 95. № 2. С. 64.
Aliyev A.M., Safarov A.R., Guseynova A.M. Calculation of ethylene region of chemical technological complex for processing of cracking and pyrolysis gases // Theor. Found. Chem. Eng. 2017. V. 51. № 4. P. 404. [Алиев А.М., Сафаров А.Р., Гусейнова А.М. Расчет этиленового региона химико-технологического комплекса по переработке газов крекинга и пиролиза // Теор. осн. хим. технол. 2017. Т. 51. № 4. С. 397.]
Aliyev A.M., Safarov A.R., Guseynova A.M. Full calculation of a chemical-technological complex for processing of cracking and pyrolysis gases based on the kinetic models of the processes // Theor. Found. Chem. Eng. 2017. V. 51. № 5. P. 716. [Алиев А.М., Сафаров А.Р., Гусейнова А.М. Расчет химико-технологического комплекса по переработке газов крекинга и пиролиза на основе кинетических моделей процессов // Теор. осн. хим. технол. 2017. Т. 51. № 5. С. 569.]
Aliyev A.M., Safarov A.R., Osmanova I.I., Guseynova A.M., Mamedov Z.A. Optimal design of a chemical technological complex for coprocessing cracking and pyrolysis gases // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 956. [Алиев А.М., Сафаров А.Р., Османова И.И., Гусейнова А.М., Мамедов З.А. Оптимальное проектирование химико-технологического комплекса по совместной переработке газов крекинга и пиролиза // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 628.]
Бабаев А.И., Алиев А.М., Таиров А.З., Гусейнова А.М., Исмаилов Н.Р. Моделирование и оптимизация процесса пиролиза этана с обратной связью. Часть I. Моделирование и исследование процесса // Азерб. хим. ж. 2008. № 3. С.16.
Ramirez Hernandez A.Y. A model for the prediction of olefin production and coke deposition during thermal cracking of light hydrocarbons. MS Thesis in Chemical Engineering. Medellin: Universidad Nacional de Colombia, 2012.
Yan M. Simulation and optimization of an ethylene plant. MS Thesis in Chemical Engineering. Texas Tech Univ., 2000.
Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. Matlab 7. СПб.: БХВ-Петербург, 2005.
Поляков А.В., Дунтов Ф.И., Софиев А.Э. Полиэтилен высокого давления. Научно-технические основы промышленного синтеза. Л.: Химия, 1988.
Гельбштейн А.И., Бакши Ю.М., Темкин М.И. Кинетика парофазной гидратации этилена на фосфорно-кислотном катализаторе // Докл. Акад. наук СССР. 1960. Т. 132. С. 384.
Белоглазов И.Н., Голубев В.О. Основы расчета фильтрационных процессов. М.: Руда и Металлы, 2002.
Технологический регламент для проектирования производства изопропилового спирта мощностью 100 тыс. т/год в составе Сумгаитского ПО “Синтезкаучук”, 1989.
Мурадова П.А., Литвишков Ю.Н. Кинетические закономерности стимулированной микроволновым излучением реакции деалкилирования толуола с водяным паром в присутствии Ni–Co–Cr/Al2O3/Al-катализатора // Сборник материалов международной научной конференции. М., 2015. С. 27.
Алиев А.М., Таиров А.З., Гусейнова А.М., Зайцева З.А., Юсифов Р.Ю. Оптимальное управления процессом алкилирования бензола этиленом в присутствии катализатора AlCl3 // Азерб. Хим. Журн. 2006. № 2. С. 87.
Научно-технический отчет лаборатории химико-технологических процессов. Баку: Институт теоретических проблем химической технологии, 1985.
Сафин М.А. Разработка системы автоматического управления реактором синтеза суспензионной полимеризации стирола с учетом кинетики процесса. Дис. … канд. техн. наук. М.: РХТУ им. Д.И. Менделеева, 2014.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии