1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 54, № 5, 2020

Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 544-553

Гомология и изомерия структур фазовых диаграмм и технологических схем ректификации

А. В. Фролкова a, А. К. Фролкова a, *, В. И. Жучков a, Е. Г. Махнарылова a

a МИРЭА – Российский технологический университет (Институт тонких химических технологий им. М.В. Ломоносова)
Москва, Россия

* E-mail: frolkova@gmail.com

Поступила в редакцию 18.11.2019
После доработки 03.12.2019
Принята к публикации 25.12.2019

Полный текст (PDF)

Аннотация

Рассмотрены приложения понятий гомологии и изомерии к структурам фазовых диаграмм и схем ректификации многокомпонентных смесей. Исследованы три гомологических ряда схем разделения трех-, четырех- и пятикомпонентных смесей вода–ароматические углеводороды (бензол, толуол, этилбензол, пропилбензол), построенных на сочетании ректификации и расслаивания. В каждом из рядов наблюдается ранжирование схем по возрастанию энергозатрат: предварительное расслаивание–второе заданное разделение–первое заданное разделение исходной смеси. Показана линейная зависимость энергозатрат от числа компонентов–гомологов в смеси и возможность предсказания энергозатрат в схемах (на примере системы с бутилбензолом). Сравнение схем–изомеров, характеризующихся одинаковым числом аппаратов, но разной последовательностью выделения продуктов, показало энергетическое преимущество второго заданного разделения при условии выделения продуктовых потоков воды и бензола из флорентийского сосуда в виде равновесных жидких фаз.

Ключевые слова: структура, фазовая диаграмма, схема разделения, гомологический ряд, изомерия схем, математическое моделирование

ВВЕДЕНИЕ

Явления гомологии и изомерии в настоящее время рассматриваются не только в химии, но и в физике, термодинамике гетерогенных систем, химической технологии, биологии и др. [1]. Наиболее полно эти два понятия разработаны в химии и связаны со строением химических соединений. Изомерами называют вещества, имеющие одинаковый качественный и количественный состав, но различающиеся стехиометрической конфигурацией молекул. Гомология относится к определенному классу органических соединений, когда ряд веществ имеют сходные строение и свойства, но отличаются между собой по составу молекул на одну или несколько групп CH2 (гомологическая разность).

Изучение структурных изомеров и гомологических рядов позволяет установить и использовать в дальнейшем общие закономерности изменения их свойств для корреляции данных, планирования натурного эксперимента, решения прогностических задач методами экстра(интер)поляции, т.е. для распространения выводов, сделанных для ограниченного числа объектов, на всю их совокупность или какую-либо часть.

Такая постановка задачи представляется целесообразной и для исследования технологических объектов, подпадающих по определенным признакам под приведенные выше понятия. Более того возможно установление новых или новая интерпретация существующих закономерностей во взаимосвязанных множествах, к которым, в частности, относятся множества структур диаграмм парожидкостного равновесия (ПЖР) и множества структур технологических схем разделения смесей [2]. По существу речь может идти о создании нетривиальных подходов к синтезу и дискриминации схем ректификационного разделения многокомпонентных смесей с использованием общенаучных понятий “гомология” и “изомерия”.

Исследования свойств смесей, содержащих компоненты–гомологи, компоненты, варьируемые по гомологическому ряду, ведутся с разной интенсивностью достаточно длительное время. В научной литературе представлено изучение свойств растворов и фазовых диаграмм преимущественно бинарных [3–9] и тройных [9–14], в меньшей степени – четырехкомпонентных [15–17] систем, в которых один или два компонента варьируются по гомологическим рядам. При этом число компонентов в системе остается неизменным. Такие системы в общем случае не образуют гомологический ряд структур фазовых диаграмм, за исключением случая одинакового фазового поведения в составляющих с варьируемым компонентом-гомологом (например, ацетон–хлороформ–бензол, ацетон–хлороформ–толуол, ацетон–хлороформ–этилбензол). Тем не менее такой подход оказался весьма плодотворным при исследовании и прогнозе биазеотропии в системах карбоновые кислоты – бутиловые эфиры одноименных кислот [7], эволюции области расслаивания в тройных системах [10]. С другой стороны, в тройных системах предельный углеводород (С6–С8)–вода–фурфурол [12] и четверных системах предельный углеводород (С6–С8)–вода–фурфурол–циклогексан [16] одинаковые структуры диаграмм и схем реализуются только для ближайших по числу атомов углерода алканов. А при значительном различии молекулярных весов алканов структура фазовой диаграммы изменяется кардинально, что влечет за собой и изменение структуры схемы, т.е. указанные выше системы, как уже отмечалось, не образуют гомологические ряды.

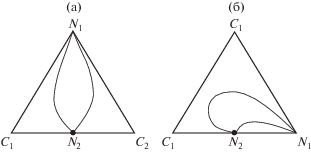
К системам с постоянным числом компонентов применимо понятие изомерии, которое в работе [1] было использовано при рассмотрении структур диаграмм парожидкостного равновесия трехкомпонентных систем. Диаграммы–изомеры характеризуются одним набором особых точек определенного типа, но отличаются их взаимным расположением (т.е. такие диаграммы относятся к одному классу и типу [18]). Пример диаграмм–изомеров приведен на рис. 1.

Рис. 1.

Пример диаграмм–изомеров (класс и тип 3.1–01): а – подтип 1а; б – подтип 1b [18]; N, С – особые точки типа узел, седло.

Диаграммы систем, содержащих разное число компонентов, относятся к гомологическому ряду, если последовательным стягиванием в точку ряда вершин структуры диаграмм переводимы друг в друга [2]. Любой элемент симплекса независимо от его размерности может быть стянут в точку, если он не имеет никаких особых точек, кроме своих вершин. На рис. 2 приведен гомологический ряд фазовых диаграмм, характерным признаком которых является наличие одного седловидного бинарного азеотропа С2 и двух областей дистилляции [19–21].

Рис. 2.

Пример диаграмм–гомологов, содержащих один бинарный седловидный азеотроп и сепаратрическое многообразие (заштриховано) в концентрационном симплексе: а – трех-; б – четырех-; в – пятикомпонентной систем [20].

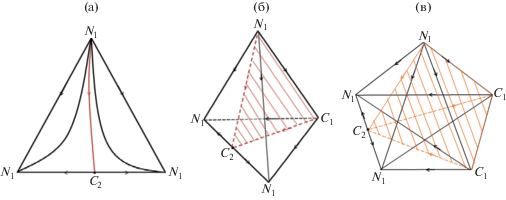
Чтобы получить диаграмму–гомолог размерности n – 1, где n – число компонентов в системе, к исходной тройной системе необходимо добавить n – 3 компонента (особые точки типа С1). Число седловидных азеотропов, порождающих сепаратрические многообразия (седла первого или n – 2 порядка), при синтезе диаграмм–гомологов измениться не может (т.е. конкретное число областей дистилляции является постоянным признаком диаграмм–гомологов). Структуры сепаратрических поверхностей в этом случае так же образуют гомологический ряд.

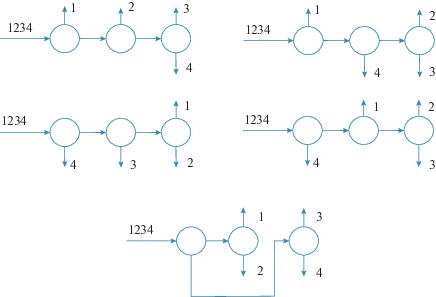
Понятие изомерии и гомологии можно применить и к структуре технологических схем. Представление схем в виде ориентированных графов [2, 21, 22], где вершинами являются аппараты и потоки, а ребрами – связи между аппаратами, наиболее наглядно иллюстрирует скелетную изомерию. Для n-компонентной зеотропной смеси все множество схем–изомеров определяется по формуле С.В. Львова [23]. На рис. 3 приведены ориентированные графы схем ректификации четырехкомпонентной зеотропной смеси.

Рис. 3.

Ориентированные графы схем–изомеров разделения четырехкомпонентной зеотропной смеси.

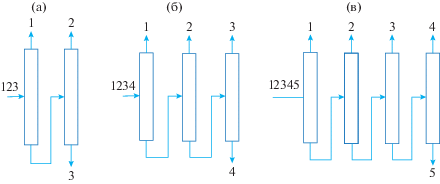
Все пять схем являются схемами–изомерами, поскольку число разделяемых компонентов и число колонн остается постоянным, однако каждый вариант отличается порядком выделения продуктовых потоков в дистилляте или кубе. Если рассматривать гомологический ряд диаграмм ПЖР зеотропных систем с числом компонентов 3, 4, 5 и т.д., то схемы их разделения будут представлять собой схемы–гомологи (рис. 4), причем здесь наблюдается увеличение на единицу числа колонн, т.е. ректификационная колонна является постоянной структурной единицей или гомологической разностью.

Рис. 4.

Пример гомологического ряда схем, ориентированных на первое заданное разделение зеотропных смесей: а – трех-; б – четырех-; в – пятикомпонентной.

Характеристическим признаком гомологических рядов схем могут выступать разделительные комплексы различного функционального действия. Так, выше приведен пример гомологических рядов, в которых используется комплекс, основанный на кривизне сепаратрического многообразия. В работе [20] рассмотрены системы этилацетат-н.спирты (С2–С4), структуры диаграмм ПЖР которых образуют гомологический ряд. Ему соответствует гомологический ряд схем, в которых присутствует последовательность линейно соединенных колонн и комплекс колонн, работающих под разными давлениями.

Важной задачей на этапе предпроектной разработки схем является выбор энергетически более эффективного варианта разделения смеси конкретного состава и возможность предварительной оценки энергозатрат на разделение смесей с большим числом компонентов. В первом случае исследуются схемы–изомеры, во втором – схемы–гомологи.

Настоящая работа посвящена исследованию закономерностей изменения энергозатрат на разделение в гомологических рядах схем и в схемах–изомерах, а также оценке прогностических возможностей выявленных закономерностей. Объектом исследования выступают модельные системы, содержащие воду (В), бензол (Б) и его гомологи: толуол (Т), этилбензол (ЭБ), пропилбензол (ПБ), диаграммы ПЖР которых являются представителями одного гомологического ряда. Стоит задача синтеза и анализа схем–гомологов и схем–изомеров, используемых для разделения смесей разного состава. В качестве метода исследования выбран вычислительный эксперимент с использованием программного комплекса AspenPlus V.10.0.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ФАЗОВОГО РАВНОВЕСИЯ

Расчет фазового равновесия проводился на основе уравнения локальных составов NRTL:

(1)
$\begin{gathered} \ln {{\gamma }_{i}} = \frac{{\sum\limits_j {{{x}_{i}}{{\tau }_{{ji}}}{{G}_{{ji}}}} }}{{\sum\limits_k {{{x}_{k}}{{G}_{{ki}}}} }} + \\ + \,\,\sum\limits_j {\frac{{{{x}_{j}}{{G}_{{ij}}}}}{{\sum\limits_k {{{x}_{k}}{{G}_{{kj}}}} }}} \left( {{{\tau }_{{ij}}} - \frac{{\sum\limits_m {{{x}_{m}}{{\tau }_{{mj}}}{{G}_{{mj}}}} }}{{\sum\limits_k {{{x}_{k}}{{G}_{{kj}}}} }}} \right), \\ \end{gathered} $
где ${{G}_{{ij}}} = \exp ( - {{\alpha }_{{ij}}}{{\tau }_{{il}}});$ ${{\tau }_{{ij}}} = {{\alpha }_{{ij}}} + \frac{{{{b}_{{ij}}}}}{T} + {{e}_{{ij}}}\ln T + {{f}_{{ij}}}T;$ ${{\alpha }_{{ij}}} = {{c}_{{ij}}} + {{d}_{{ij}}}(T - 273.15\,{\text{К}});$ ${{\tau }_{{ii}}} = 0;$ ${{G}_{{ii}}} = 1.$

Параметры модели и относительные ошибки описания температуры кипения, состава равновесного пара и составов равновесных жидких фаз приведены в табл. 1.

Таблица 1.  

Параметры уравнения NRTL для пятикомпонентной системы вода (В)–бензол (Б)–толуол (Т)– этилбензол (ЭБ)–пропилбензол (ПБ) и ошибки описания фазового равновесия

Система aij aji bij bji сij   Δy (Δx'), %   ΔT (Δx''), %
В–Б 140.087 45.1905 –5954.31 591.368 0.2   1.56   0.04
В–Т 627.053 –247.879 –27 269.4 14 759.8 0.2   3.08   0.07
В–ЭБ 1.00584 –10.505 2260.01 4458.59 0.2   0.07   0.02
В–ПБ 0 0 2970.26 2970.26 0.2   –   –
Б–Т –2.8852 2.1911 1123.95 –863.731 0.3   1.05   0.17
Б–ЭБ –1.4701 1.1017 642.112 –515.27 0.3   3.18   0.09
Б–ПБ 0 0 30.073 –81.082 0.3   2.40   0.16
Т–ЭБ 0 0 –369.59 549.95 0.3   4.88   0.38
ЭБ–ПБ 0 0 33.64 –34.1094 0.3   –   –

Для систем с водой указаны относительные ошибки описания составов равновесных жидких слоев (Δx', Δx") при температуре 20°С.

В табл. 2 показаны ошибки описания азеотропных характеристик (состав, температура кипения).

Таблица 2.  

Сравнение экспериментальных [24, 25] и расчетных данных по азеотропии в бинарных составляющих при Р = 760 мм рт. ст.

Азеотроп $x_{1}^{{{\text{эксп}}}}$, мол. % $x_{1}^{{{\text{расч}}}}$, мол. % ∆х1, % Т  эксп, °С Т  расч, °С ∆Т, %
В–Б 29.99 29.90 0.30 69.80 69.35 0.64
В–Т 55.42 55.68 0.47 85.00 84.39 0.72
В–ЭБ 75.42 75.07 0.46 92.00 92.18 0.20
В–ПБ 85.69 85.93 0.28 95.35 95.82 0.49

Сравнение экспериментальных [24, 25] и расчетных данных свидетельствует об адекватности математического моделирования фазового равновесия системы жидкость–пар и жидкость–жидкость имеющимся набором параметров.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

На рис. 5 приведены структуры фазовых диаграмм трех систем: В–Б–Т, В–Б–Т–ЭБ, В–Б–Т–ЭБ–ПБ, образующие гомологический ряд.

Рис. 5.

Структуры диаграмм фазового равновесия систем, содержащих воду и гомологи бензола; а – трех-; б – четырех-; в – пятикомпонентной; темно-серым цветом показаны сепаратрические многообразия; светло-серым – бинодальные многообразия.

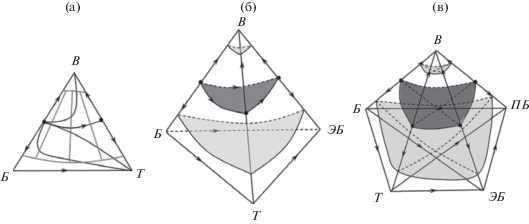
На всех диаграммах азеотроп вода–бензол представляет собой точку типа неустойчивый узел; азеотроп, образованный водой с тяжелокипящим компонентом (толуол, этилбензол, пропилбензол), – седло. Последний порождает сепаратрическое многообразие, соответственно, первой, второй и третьей размерности. Данные поверхности обладают простейшей структурой и представляют собой гомологичные симплексы (линия, криволинейный треугольник и криволинейная пирамида). Диаграммы ПЖР характеризуются наличием двух областей дистилляции, но разным числом подобластей ректификации: три, четыре, пять для трех-, четырех- и пятикомпонентных систем. В табл. 3 приведены обозначения подобластей ректификации и перечень наборов продуктов, соответствующих конкретной подобласти.

Таблица 3.  

Обозначение подобластей ректификации и соответствующие им наборы продуктовых потоков при разделении трех-, четырех- и пятикомпонентных смесей

n Обозна-чение подо-бласти Набор продуктовых потоков
3 А3 В + AzВ–Б + AzВ–Т
С3 Т + AzВ–Б + AzВ–Т
K3 Т + Б + AzВ–Б
4 А4 В + AzВ–Б + AzВ–Т + AzВ–ЭБ
С4 ЭБ + Т+AzВ–Б + AzВ–Т
K4 ЭБ + Т + Б + AzВ–Б
Е4 ЭБ + AzВ–Б + AzВ–Т + AzВ–ЭБ
5 А5 В + AzВ–Б + AzВ–Т + AzВ–ЭБ + AzВ–ПБ
С5 ПБ + ЭБ + Т + AzВ–Б + AzВ–Т
K5 ПБ + ЭБ + Т + Б + AzВ–Б
Е5 ПБ + ЭБ + AzВ–Б + AzВ–Т + AzВ–ПБ
G5 ПБ + AzВ–Б + AzВ–Т + AzВ–ПБ + AzВ–ЭБ

Az – обозначение азеотропной точки.

Вода характеризуется ограниченной взаимной растворимостью со всеми ароматическими соединениями и диаграммы расслаивания также представляют собой ряд диаграмм–гомологов: содержат одну область двухфазного расслаивания открытого типа (границы области расслаивания – бинодальные многообразия первой, второй, третьей размерности для трех-, четырех- и пятикомпонентных систем). Сепаратрическое многообразие во всех случаях принадлежит области двухфазного расслаивания, что позволяет использовать сочетание ректификации и расслаивания для разделения данных смесей [26, 27].

Для составов смеси, принадлежащих разным подобластям ректификации, проведен синтез схем разделения, основанных на сочетании ректификации и расслаивания. Рассматриваются схемы с минимальным числом аппаратов: один флорентийский сосуд и число ректификационных колонн, не превышающее число компонентов в смеси. На рис. 6 приведены возможные схемы разделения с указанием принадлежности исходного состава смеси конкретной подобласти ректификации.

Рис. 6.

Схемы разделения смесей вода–бензол–толуол, вода–бензол–толуол–этилбензол и вода–бензол–толуол–этилбензол–пропилбензол разного состава (пояснения в тексте).

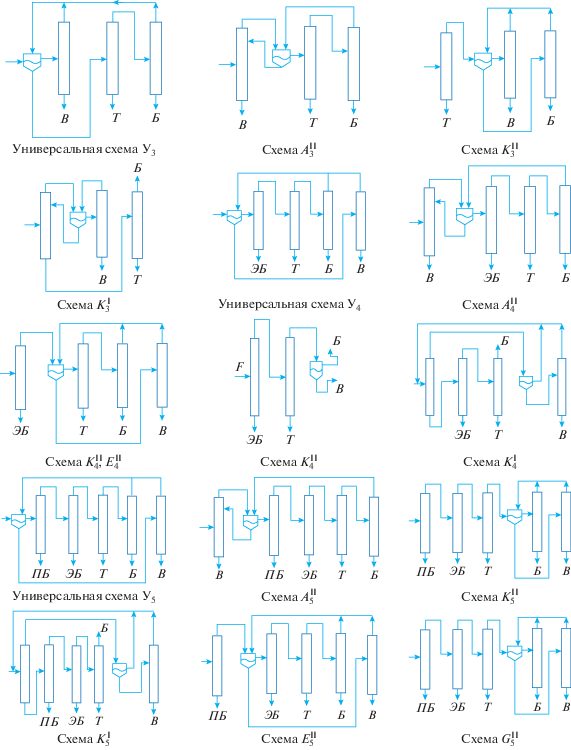
Универсальными У3, 4, 5 названы схемы, которые разделяют расслаивающиеся смеси, принадлежащие любой подобласти ректификации. Для составов, входящих в подобласть “С”, схемы содержат большее число аппаратов и на рис. 6 не приводятся. Таким образом, к схемам–гомологам относятся схемы разделения трех-, четырех- и пятикомпонентных смесей, составы которых принадлежат конкретной подобласти ректификации: (У3, У4, У5); (${\text{K}}_{3}^{{\text{I}}}$, ${\text{K}}_{4}^{{\text{I}}}$, ${\text{K}}_{5}^{{\text{I}}}$); (${\text{K}}_{3}^{{{\text{II}}}}$, ${\text{K}}_{4}^{{{\text{II}}}}$, ${\text{K}}_{5}^{{{\text{II}}}}$); (${\text{A}}_{3}^{{{\text{II}}}}$, ${\text{A}}_{4}^{{{\text{II}}}}$, ${\text{A}}_{5}^{{{\text{II}}}}$). Верхний индекс I (II) означает, соответственно, режим первого (второго) заданного разделения в первой колонне схем.

К схемам–изомерам относятся схемы разделения смесей, принадлежащих конкретной подобласти ректификации и содержащих одинаковое число аппаратов: (У3, ${\text{K}}_{3}^{{\text{I}}}$, ${\text{K}}_{3}^{{{\text{II}}}}$); (У3, ${\text{A}}_{3}^{{{\text{II}}}}$); (У4, ${\text{K}}_{4}^{{\text{I}}}$, ${\text{K}}_{4}^{{{\text{II}}}}$); (У5, ${\text{K}}_{5}^{{{\text{II}}}}$); (У5, ${\text{A}}_{5}^{{{\text{II}}}}$); (У5, ${\text{G}}_{5}^{{{\text{II}}}}$); (У5, ${\text{E}}_{5}^{{{\text{II}}}}$). Следует иметь в виду, что при выходе на составляющую, содержащую три и более компонентов–гомологов (Б–Т–ЭБ и Б–Т–ЭБ–ПБ), число схем–изомеров возрастет. Последнее связано с тем, что указанные зеотропные составляющие можно делить с использованием изомерных модулей за счет организации в колоннах разных заданных разделений: второго (как показано на рис. 6), первого (для n = 4 и n = 5) и промежуточного (для n = 5). Число таких модулей определяется по формуле С.В. Львова [23].

РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА

Для дальнейшего проведения вычислительного эксперимента выбран исходный состав, принадлежащий подобласти ректификации “К” и обогащенный бензолом (70 мол. %, концентрации остальных компонентов равны). Данный выбор обусловлен большей вариантностью структур сравниваемых схем. Количество исходной смеси 100 кмоль/ч. Таким образом, для разделения трех-, четырех- и пятикомпонентной смесей будут рассматриваться следующие схемы: универсальные схемы У3(4, 5), схемы ${\text{K}}_{{3(4,5)}}^{{\text{I}}}$ (с учетом изомерных модулей “а”, “б”, “в”) и ${\text{K}}_{{3(4,5)}}^{{{\text{II}}}}$ (без учета изомерных модулей). При расчете ректификации варьировались следующие параметры: эффективность колонны (N, т.т.), уровень подачи (NF) исходной смеси F, флегмовое число (R). Исходная смесь подавалась при температуре кипения. Давление по всех колоннах 760 мм рт. ст. Критерием выбора режима служили минимальные энергозатраты при достижении заданного качества продуктовых потоков (Qсумм, кВт).

Следует отметить, что потоки, покидающие флорентийский сосуд, дальнейшей очистки не требуют, поскольку содержание основного вещества (веществ) в водном (органическом) слое отвечает ГОСТ (ароматические соединения и вода практически нерастворимы друг в друге). По этой причине при расчете схем колонны разделения водного или бензольного слоя не рассматривались. Кроме того, концентрация воды в органическом слое, содержащем несколько компонентов-гомологов, настолько мала, что ею можно пренебречь в дальнейших расчетах (примесь воды не снижает качество получаемых продуктов), т.е. часть колонн исключается из расчета.

В табл. 4 приведены статические параметры работы ректификационных колонн и суммарные энергозатраты на разделение.

Таблица 4.  

Параметры работы колонн схем разделения и энергозатраты

№ колонны N, т.т. NF R Qкол, кВт Qсумм, кВт
Универсальная схема У3
1 30 15 3 24.41 24.41
Схема $K_{3}^{{\text{I}}}$
1 10 5 0.1 9.14 33.55
2 28 14 3 24.41
Схема $K_{3}^{{{\text{II}}}}$
1 26 13 1.1 17.71 17.71
Универсальная схема У4
1 20 10 0.5 13.37 37.70
2 34 17 3 24.33
Схема $K_{4}^{{{\text{Ia}}}}$
1 10 5 (2) 0.1 5.33 42.61
2 30 15 2 18.13
3 40 20 3 19.15
Схема $K_{4}^{{{\text{Ia}}}}$K4Iб
1 10 5 (2) 0.1 5.33 47.29
2 28 14 1.5 17.63
3 32 16 3 24.33
Схема $K_{4}^{{{\text{II}}}}$
1 26 13 0.5 13.50 31.78
2 24 12 1.4 18.28
Универсальная схема У5
1 30 15 0.4 13.84 51.80
2 22 12 1 13.58
3 28 14 1.1 24.38
Схема $K_{5}^{{{\text{Ia}}}}$
1 10 5 (2) 0.5 4.67 69.59
2 30 15 2 17.72
3 40 20 3 22.58
4 38 19 3.5 24.62
Схема $K_{5}^{{{\text{Iб}}}}$
1 10 5 (2) 0.5 4.67 79.46
2 32 16 1.8 21.65
3 42 21 3.5 29.87
4 40 20 3 23.27
Схема $K_{5}^{{{\text{Iв}}}}$K5Iв
1 10 5 (2) 0.5 4.67 71.78
2 20 10 2 20.17
3 38 19 2.8 22.97
4 38 19 3.5 23.97
Схема $K_{5}^{{{\text{II}}}}$
1 34 17 0.5 14.56 45.93
2 36 18 0.7 14.19
3 30 15 1.3 16.68

Схемы a, б, в отличаются использованием первого, второго или промежуточного заданного разделения при разделении смесей Б–Т–ЭБ и Б–Т–ЭБ–ПБ.

Анализ полученных данных показывает, что в гомологических рядах с предварительным расслаиванием исходной смеси (У3, У4, У5) и организацией второго заданного разделения (${\text{K}}_{3}^{{{\text{II}}}}$, ${\text{K}}_{4}^{{{\text{II}}}}$, ${\text{K}}_{5}^{{{\text{II}}}}$) наблюдается практически линейная зависимость суммарных энергозатрат от числа компонентов–гомологов в смеси (Б–Т, Б–Т–ЭБ, Б–Т–ЭБ–ПБ, соответственно). Увеличение числа колонн на единицу повышает энергозатраты на 14 кВт в ряду (${\text{K}}_{3}^{{{\text{II}}}}$, ${\text{K}}_{4}^{{{\text{II}}}}$, ${\text{K}}_{5}^{{{\text{II}}}}$) и на 13.3–14.1 кВт в ряду (У3, У4, У5). Данный факт объясняется и фазовым поведением смесей–гомологов, близким к идеальному. Таким образом, можно ожидать, что при разделении шестикомпонентной смеси, содержащей бутилбензол, энергозатраты составят около 60 кВт в схеме K 6II и около 65 кВт в схеме У6. Проведенные расчеты двух указанных схем (при заданном исходном составе и принятых допущениях) подтвердили прогноз: энергозатраты составили соответственно 63 и 66 кВт.

Наиболее энергоэффективной из числа схем–изомеров при разделении смеси с закрепленным числом компонентов является схема K II. Ее преимущества наиболее заметны для схем разделения тройной смеси (на 27.5% по сравнению с универсальной схемой). Для n = 4, 5, 6 снижение энергозатрат составляет 15.7, 11.3, 4.5%, что связано отчасти с увеличением количеств дистиллатных потоков за счет снижения концентрации (и количеств кубовых потоков) всех гомологов, кроме бензола, в закрепленном количестве исходной смеси. Схемы, ориентированные на режим первого заданного разделения, имеют большее число колонн и, соответственно, характеризуются большими энергозатратами. Их можно сравнивать как схемы, содержащие изомерные модули (например, схемы ${\text{K}}_{5}^{{{\text{Iа}}}}$, ${\text{K}}_{5}^{{{\text{Iв}}}}$, ${\text{K}}_{5}^{{{\text{Iб}}}}$), причем здесь подтверждается тенденция повышения энергозатрат в ряду режимов первого (69.59 кВт), промежуточного (71.78 кВт), второго (79.46 кВт) заданных разделений.

ЗАКЛЮЧЕНИЕ

Исследованы закономерности изменения энергозатрат в схемах–гомологах и схемах–изомерах при разделении смесей, содержащих воду и гомологи бензола (толуол, этилбензол, пропилбензол). При заданных условиях синтеза схем (постоянное содержание в исходной смеси одного из компонентов, возможность отбора в качестве продуктов равновесных слоев во флорентийском сосуде) показана возможность экстраполяции величин энергозатрат в схемах–гомологах, что подтверждено вычислительным экспериментом при разделении шестикомпонентной смеси (с бутилбензолом) с использованием предварительного расслаивания исходной смеси и режима второго заданного разделения. Расчет схем–изомеров выявил в качестве энергоэффективной для всех рассмотренных смесей схему, ориентированную на второе заданное разделение.

Результаты исследования позволяют дополнить типовой план синтеза принципиальных схем ректификации [2] процедурами, которые связаны с возможностью распространения накопленного в научно-технической литературе опыта и выявленных нами закономерностей на схемы разделения многокомпонентных смесей-гомологов.

Работа выполнена в рамках государственного задания Минобрнауки РФ (проект № 10.8454.2017/БЧ).

ОБОЗНАЧЕНИЯ

F поток исходной смеси, кмоль/ч
N эффективность колонны, теоретические тарелки
NF номер тарелки подачи исходной смеси
n число компонентов
Р давление, мм рт. ст.
Qкол энергозатраты в кипятильнике колонны, кВт
Qсумм суммарные энергозатраты по схеме, кВт
R флегмовое число
Т температура кипения, °С
xi концентрация компонента i в жидкой фазе, мол. %
yi концентрация компонента i в паровой фазе, мол. %

ИНДЕКСЫ

I (II) первое (второе) заданное разделение
i номер компонента
3, 4, 5 компонентность системы

Список литературы

  1. Серафимов Л.А., Фролкова А.К., Раева В.М. Изомерия как общенаучное понятие // Вестн. МИТХТ. 2011. Т. 6. № 6. С. 54.

  2. Жаров В.Т., Серафимов Л.А. Физико-химические основы дистилляции и ректификации. Л.: Химия, 1975.

  3. Dymond J.H. Vapour–liquid equilibria in alkan–1–ol + + n–alkane mixtures // Pure Appl. Chem. 1994. № 3. P. 553.

  4. Suntsov Yu. New Method of Predicting the Thermodynamic Properties of Solutions // J. Chem. Chem. Eng. 2014. № 8. P. 306.

  5. Das G., dos Ramos M.C., McCabe C. Accurately modeling benzene and alkylbenzenes using a groupcontribution based SAFT approach // Fluid Phase Equilib. 2014. V. 362. P. 242.

  6. Кушнер Т.М., Файнбург Г.Д., Витман Т.А., Серафимов Л.А. Получение надежных данных по парожидкостному равновесию в гомологичных системах н.спирты–н.парафины // Теор. осн. хим. технол. 1991. Т. 25. № 2. С. 175.

  7. Шутова Г.В. Физико-химические закономерности биазеотропии в бинарных системах. Дис. … канд. техн. наук. М.: МИТХТ, 1992.

  8. Gonzalez J.A., Carmona F.J., Riesco N. Thermodynamics of mixtures containing ethers characterization of systems of MTBE, TAME or ETBE with n–alkanes, cyclohexane, benzene, alkan–1–ols or alkan–2–ols // Chem. Phys. 2000. № 2. P. 102.

  9. Rao M.R., Rao C.V. Measurement and correlation of liquid–liquid equilibria of binary and ternary systems containing methanol and hydrocarbons // J. Sci. Ind. Res. 1955. № 14B. P. 204.

  10. Береговых В.В. Исследования в области физико-химических основ ректификации тройных расслаивающихся смесей. Дис. … канд. техн. наук. М.: МИТХТ, 1971.

  11. Колючкина Г.Я. Исследования в области разделения гетероазеотропных смесей. Автореф. дис. … канд. техн. наук. М.: МИТХТ, 1972.

  12. Колючкина Г.Я., Пономарев В.Н., Тимофеев В.С. Фазовые равновесия жидкость–жидкость в системах предельные углеводороды–вода–фурфурол // Труды института (МИТХТ им. М.В. Ломоносова). 1973. Т. 3. Вып. I. С. 98.

  13. Иванова Г.Г., Теличко Т.Н, Тимофеев В.С., Серафимов Л.А. Исследование фазовых равновесий в ряду систем н.углеводороды–вода–бензиловый спирт // Труды института (МИТХТ им. М.В. Ломоносова). 1974. Т. 4. Вып. I. С. 101.

  14. Frolkova A.V., Akishina A.A., Illarionova Ye., Frolkova A.K. Diagrams of phase equilibria of ternary systems containing aniline, water and saturated hydrocarbons // XX International Conference of Chemical Thermodynamics in Russia (RCCT-2015). Nizhniy Novgorod, 2015. P. 230.

  15. Shashkova Yu., Stoyakina I., Frolkova A.V., Frolkova A.K. Phase diagrams of quaternary homologous systems of complex physico-chemical nature // XXI International Conference on Chemical Thermodynamics in Russia (RCCT-2017). Novosibirsk, 2017. P. 298.

  16. Себякин А.Ю. Особенности ректификационного разделения многокомпонентных многофазных смесей органических веществ. Дис. … канд. техн. наук. М.: Московский технологический университет, 2017.

  17. Бедретдинов Ф.Н., Челюскина Т.В. Исследование различных изомногообразий в четырехкомпонентных системах, содержащих биазеотропные бинарные составляющие // Тонкие хим. технол. 2018. Т. 13. № 1. С. 45. https://doi.org/10.32362/2410-6593-2018-13-1-45-54

  18. Serafimov L.A. Thermodynamic and Topological Analysis of Liquid–Vapor Phase Equilibrium Diagrams and Problems of Rectification of Multicomponent Mixtures // Mathematical Methods in Contemporary Chemistry. Amsterdam: Gordon and Breach, 1996. P. 557.

  19. Крупинова О.Н., Фролкова А.К., Серафимов Л.А. Исследование гомологических рядов разделительных комплексов, основанных на кривизне разделяющего многообразия // Хим. пром-сть. 1999. № 7. С. 33.

  20. Фролкова А.К. Теоретические основы разделения многокомпонентных многофазных систем с использованием функциональных комплексов. Дис. … докт. техн. наук. М.: МИТХТ, 2000.

  21. Фролкова А.К. Разделение азеотропных смесей. Физико-химические основы и технологические приемы. М.: ВЛАДОС, 2010.

  22. Тимошенко А.В. Серафимов Л.А. Графометрия как метод системного анализа поливариантности организации технологических схем ректификационного разделения // Теор. осн. хим. технол. 1997. Т. 31. № 5. С. 527.

  23. Львов С.В. Некоторые вопросы ректификации бинарных и многокомпонентных смесей. М.: АН СССР, 1960.

  24. Огородников С.К., Лестева Т.М., Коган В.Б. Азеотропные смеси. Л.: Химия, 1971.

  25. Хорсли Л. Таблицы азеотропных смесей. М.: Изд-во иностранной литературы, 1951.

  26. Фролкова А.В., Меркульева А.Д., Гаганов И.С. Синтез схем разделения расслаивающихся смесей: современное состояние проблемы // Тонкие хим. технол. 2018. Т. 13. № 3. С. 5.

  27. Frolkova A.V., Frolkova A.K., Podtyagina A.V., Spiryakova V.V. Energy Savings in Flowsheets based on Combination of Distillation and Splitting Processes // Theor. Found. Chem. Eng. 2018. V. 52. № 5. P. 771.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал