Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 649-660
Самоподдерживающиеся процессы умягчения–опреснения воды. Простые двухкомпонентные системы
Р. Х. Хамизов a, *, И. В. Комарова a, Н. К. Галкина a, А. Г. Прудковский a
a Институт геохимии и аналитической химии им. В.И. Вернадского РАН
Москва, Россия
* E-mail: khamiz@mail.ru
Поступила в редакцию 02.11.2019
После доработки 20.01.2020
Принята к публикации 31.01.2020
Аннотация
Методом численного эксперимента исследована возможность организации стационарных самоподдерживающихся процессов умягчения–опреснения соленых вод на примере двухкомпонентных модельных растворов, содержащих ионы кальция и натрия. В таких процессах умягченная с помощью катионита вода подвергается опреснению, а образующийся при этом рассол, без каких-либо дополнительных химических реагентов, используется для регенерации катионита в повторяющихся циклах сорбции–десорбции. Интерес к самоподдерживающимся процессам связан с новыми технологическими возможностями создания систем водоподготовки нового поколения, например мобильных автономных установок или систем с высокой степенью извлечения пресной воды и концентрирования рассола. Рассмотрены фундаментальные основы самоподдерживающихся процессов. Проведены расчеты динамики ионного обмена для многих десятков последовательных циклов умягчения–опреснения при изменении варьируемых параметров: соотношения компонентов в исходном растворе, минерализации таких растворов, степени концентрирования рассолов, состава опресненной воды. Показаны условия, при которых формируются или не достигаются стационарные режимы.
ВВЕДЕНИЕ
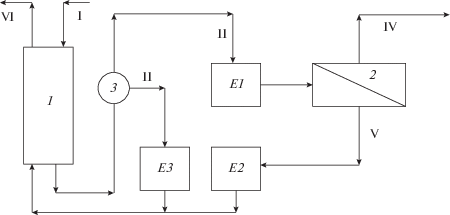
Идея самоподдерживающихся (СМП) процессов умягчения–опреснения возникла в 1970-х годах в лаборатории конверсии морской воды Калифорнийского университета [1, 2] и была связана с быстро растущей индустрией опреснения и исследованием возможности создания не потребляющих привозных химических реагентов замкнутых систем для решения специальных технологических задач. Эта идея проиллюстрирована далее на рис. 1 и заключается в следующем: в повторяющемся циклическом процессе через колонну с катионитом в Na-форме пропускается морская вода, и ионы жесткости сорбируются в результате реакции ионного обмена, умягченная вода подвергается глубокому опреснению без опасности образования отложений слаборастворимых веществ, рассол, содержащий только соли натрия, накапливается и возвращается на регенерацию катионита после его отработки для вытеснения катионов жесткости и обратного перевода катионита Na-форму. Экономически целесообразная реализация такой идеи позволила бы произвести существенные преобразования в технологии опреснения морской воды, в частности, позволила бы преодолеть так называемый гипсовый барьер, ограничивающий степень извлечения пресной воды, а также улучшить условия эксплуатации дистилляционных и мембранных опреснительных систем. При использовании двух колонн, работающих в противофазе, можно было бы организовать процесс, в котором непрерывно осуществляются умягчение и регенерация. На первый взгляд, кажется, что такая система с “саморегенерацией”, показанная на рисунке, невозможна, однако есть фундаментальная причина ее принципиальной реализуемости, а именно, известный в ионном обмене “эффект электроселективности” или “концентрационно-валентностный эффект” [3]. Суть эффекта можно сформулировать следующим образом: при одном и том же соотношении эквивалентных концентраций разнозарядных катионов в растворе, селективность катионита к ионам с меньшим зарядом повышается с увеличением суммарной концентрации катионов. Покажем это. Пусть в соответствии с законом действующих масс коэффициент равновесия (концентрационная константа) обмена ионов ${{A}^{{{{z}_{A}}}}}$ и ${{В}^{{{{z}_{B}}}}}~$ (с зарядами ${{z}_{A}}$ и ${{z}_{B}}$), выраженный в молях (или моль-эквивалентах) имеет вид
(1)
$K_{B}^{A} = {{\left( {\frac{{{{{\bar {c}}}_{A}}}}{{{{c}_{A}}}}} \right)}^{{{{z}_{B}}}}}{{\left( {\frac{{{{c}_{B}}}}{{{{{\bar {c}}}_{B}}}}} \right)}^{{{{z}_{A}}}}}~,$Рис. 1.
Схема СМП-процесса: 1 – колонна с катионитом, 2 – опреснитель, 3 – переключающее устройство потоков со стадии вытеснения электролита на стадию умягчения, Е1 – емкость для умягченной воды, Е2 – емкость для регенерационного рассола, Е3 – емкость для электролита, вытесненного из межзернового пространства слоя катионита, I – поток исходной воды, II – поток электролита, вытесненного из межзернового пространства слоя катионита, III – поток умягченной воды, IV – поток опресненной воды, V – поток регенерирующего рассола, VI – сброс.
Для простоты возьмем случай, когда коэффициент равновесия – постоянная величина. Если теперь выразить концентрации компонентов в эквивалентных долях (например, YA = = ${{{{z}_{A}}{{c}_{A}}} \mathord{\left/ {\vphantom {{{{z}_{A}}{{c}_{A}}} {\left( {{{z}_{A}}{{c}_{A}} + {{z}_{B}}{{c}_{B}}} \right)}}} \right. \kern-0em} {\left( {{{z}_{A}}{{c}_{A}} + {{z}_{B}}{{c}_{B}}} \right)}}$ = ${{{{z}_{A}}{{c}_{A}}} \mathord{\left/ {\vphantom {{{{z}_{A}}{{c}_{A}}} {{{с}_{{\Sigma }}}}}} \right. \kern-0em} {{{с}_{{\Sigma }}}}}$), то из (1) нетрудно вывести математическое выражение для эффекта электроселективности:
(2)
${{{{{\left. {\frac{{\bar {Y}_{A}^{{{{{{z}_{B}}} \mathord{\left/ {\vphantom {{{{z}_{B}}} {{{z}_{A}}}}} \right. \kern-0em} {{{z}_{A}}}}}}}}{{1 - \overline {{{Y}_{A}}} }}} \right|}}_{{{{с}_{{{\Sigma }1}}}}}}} \mathord{\left/ {\vphantom {{{{{\left. {\frac{{\bar {Y}_{A}^{{{{{{z}_{B}}} \mathord{\left/ {\vphantom {{{{z}_{B}}} {{{z}_{A}}}}} \right. \kern-0em} {{{z}_{A}}}}}}}}{{1 - \overline {{{Y}_{A}}} }}} \right|}}_{{{{с}_{{{\Sigma }1}}}}}}} {{{{\left. {\frac{{\bar {Y}_{A}^{{{{{{z}_{B}}} \mathord{\left/ {\vphantom {{{{z}_{B}}} {{{z}_{A}}}}} \right. \kern-0em} {{{z}_{A}}}}}}}}{{1 - \overline {{{Y}_{A}}} }}} \right|}}_{{{{с}_{{{\Sigma }2}}}}}}}}} \right. \kern-0em} {{{{\left. {\frac{{\bar {Y}_{A}^{{{{{{z}_{B}}} \mathord{\left/ {\vphantom {{{{z}_{B}}} {{{z}_{A}}}}} \right. \kern-0em} {{{z}_{A}}}}}}}}{{1 - \overline {{{Y}_{A}}} }}} \right|}}_{{{{с}_{{{\Sigma }2}}}}}}}} = {{\left( {\frac{{{{c}_{{{{{\Sigma }}_{1}}}}}}}{{{{c}_{{{{{\Sigma }}_{2}}}}}}}} \right)}^{{{{{{z}_{B}}} \mathord{\left/ {\vphantom {{{{z}_{B}}} {{{z}_{A}} - 1}}} \right. \kern-0em} {{{z}_{A}} - 1}}}}}~.$Легко показать для ${{z}_{A}} = 2$ и ${{z}_{B}} = 1$, например для ионов кальция и натрия соответственно, что эквивалентная доля двухзарядного иона в сорбенте будет уменьшаться с увеличением суммарной концентрации. Эффект влияния суммарной концентрации в такой же степени проявляется и для случая, когда коэффициент равновесия, в отличие от термодинамической константы, не является постоянной величиной. Дело в том, что возможные изменения в селективности многократно больше изменений концентрационных констант и могут составить несколько порядков. С точки зрения баланса сорбции–десорбции катионов в циклическом процессе эффект электроселективности означает, что если привести в равновесие слой ионита в колонне с разбавленным раствором смеси ионов кальция и натрия, а затем с более концентрированным раствором с тем же соотношением компонентов, например, с помощью схемы на рис. 1, концентрированный раствор будет всегда десорбировать из ионита часть ионов кальция за счет обменной сорбции ионов натрия. Однако следует иметь в виду, что СМП-процесс является динамическим и его реализуемость определяется различными факторами, включая так называемое равновесное сжатие или кинетическое размытие концентрационных фронтов в слое катионита, т. е. изменение формы этих фронтов. В связи с этим можно указать еще на одну закономерность, которая также создает возможность осуществления самоподдерживающегося процесса: при одной и той же суммарной концентрации раствора (${{с}_{{\Sigma }}} = {\text{const}}$) селективность сорбента к иону с большим зарядом, как правило, повышается с уменьшением его эквивалентной доли в растворе (или сорбенте). Это также следует из анализа соотношения (1) при его выражении через эквивалентные доли. Следствием этого является разная скорость движения изоконцентрационных точек фронта распределения компонентов вдоль слоя сорбента в условиях равновесной динамики обмена одно- и двухзарядного ионов в зависимости от их соотношения в этих точках [4]:
(3)
${{\left( {\frac{{\partial X}}{{\partial t}}} \right)}_{{\bar {Y}}}} = \frac{v}{{\varepsilon + {{\partial{ \bar {Y}}} \mathord{\left/ {\vphantom {{\partial{ \bar {Y}}} {\partial Y}}} \right. \kern-0em} {\partial Y}}}},$Несмотря на перечисленные фундаментальные обоснования принципиальной возможности осуществления СМП-процесса, его не удавалось реализовать для морской воды. Теоретические расчеты с использованием равновесной модели динамики, проведенные авторами [5], позволили сформулировать требования к характеристикам катионита, который можно было использовать для эффективного умягчения перед опреснением морской воды. Оказалось, что требуется весьма высокая селективность к кальцию по отношению к ионам магния, которой не обладают промышленно выпускаемые иониты, в частности, сильнокислотные сульфокатиониты или слабокислотные иониты с карбоксильными функциональными группами. В работе [6] изложены результаты апробации модели динамики ионного обмена более общего характера с проведением расчетов десятков последовательных циклов сорбции–регенерации при изменении варьируемых условий. Были более четко сформулированы количественные требования (в виде набора значений равновесных констант парного обмена и кинетических характеристик) к катионитам для осуществления СМП-процесса для морской воды. В этой же работе были описаны свойства предложенного нами ранее ионообменного материала на основе химически модифицированного цеолита типа А (МЦА) с искаженной кристаллической структурой. Анализ, сделанный в работе [6], позволил сделать некоторые обобщения, связанные с организацией самоподдерживающихся процессов: 1) процесс реализуем только в противоточном варианте, при этом желательно, чтобы на стадиях сорбции и регенерации более плотный раствор всегда находился в слое катионита ниже менее плотного раствора; 2) в самоподдерживающемся процессе, вышедшем на стационарный режим, эффективно работает только некоторая часть емкости сорбционного слоя, требования к катиониту связаны с тем, чтобы эта часть составляла какую-то существенную долю от полной обменной емкости всего слоя; 3) СМП-процесс умягчения–опреснения морской воды можно построить только для декальцинирования с использованием катионитов, неселективных к магнию. Были проведены исследования возможности переноса анализа, сделанного в [6] на другие типы соленых вод, однако рассмотрение было ограничено неорганическим сорбентом типа МЦА [7]. В связи с новыми возможностями, которые открывает создание самоподдерживающихся процессов, или просто процессов умягчения–опреснения с рециркуляцией рассолов для частичной или полной регенерации катионита, исследования в этой области проводились весьма активно и продолжаются в настоящее время [8–11]. Весьма интересные результаты были получены авторами из университета Технион, которые предлагают комбинированные сорбционно-мембранные процессы переработки вод разной минерализации с использованием нанофильтрационных методов [10, 11]. В этих процессах вместе с пресной водой выделяются ценные компоненты, в частности сульфат магния из морской воды [10], или получаемая из слабосоленых источников пресная вода (для орошения) обогащается полезными компонентами, например, солями калия вместо солей натрия [11]. Процессы такого же типа были предложены для переработки природных подземных вод [12]. В настоящее время переработка таких солоноватых или соленых подземных вод, представляющих важный ресурс многих стран, а также ряда российских регионов (Крыма, Калмыкии, Ставрополья и др.) не менее актуальна, чем опреснение морской воды. Однако научные и технологические основы возможности организации СМП-процессов для таких вод в применении к широко доступным промышленно выпускаемым катионообменникам не были до сих пор разработаны. Для изучения закономерностей влияния варьируемых условий на процессы умягчения–опреснения представляется целесообразным исследование простейших модельных систем с помощью численных экспериментов. Обычные эксперименты здесь практически бесполезны, так как потребуется изучение динамики большого количества последовательных циклов сорбции–регенерации. Настоящая работа посвящена решению этих проблем.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Математическое моделирование динамики ионного обмена в циклических процессах. В работе [7] для проведения динамических расчетов в циклических процессах на МЦА была использована общая модель многокомпонентного ионного обмена с линейными кинетическими уравнениями разностного типа. Авторы [13] предложили более сложную модель расчета катионирования на цеолитах, учитывающую конвективные процессы продольной дисперсии. В данной работе мы используем так называемую послойную (тарельчатую) модель динамики ионного обмена, которая, с одной стороны, лучше всего апробирована для процессов ионообменной сорбции и регенерации в поточном и противоточном режимах на сильнокислотном катионите [14], с другой стороны, она обеспечивает быстрый счет большого количества последовательных циклов с изменяющимися характеристиками (до выхода на стационарный режим).
Решается задача о прохождении элюента через сорбционную колонну заданной длины L и сечения S, равномерно наполненной сорбентом. Предполагается, что раствор движется по колонне с постоянной скоростью v. Обозначим через ${{\bar {c}}_{i}}(x,t)$ концентрации (моль-экв/л) веществ в сорбенте, традиционно рассчитывающиеся на единицу объема колонны, а через ${{c}_{i}}(x,t)$ концентрации веществ в растворе, движение которых описываемые уравнениями переноса:
(4)
$\frac{{\partial {{c}_{i}}}}{{\partial t}} + v\frac{{\partial {{c}_{i}}}}{{\partial x}} + \frac{1}{\varepsilon }\frac{{\partial {{{\bar {c}}}_{i}}}}{{\partial t}} = {{D}_{{{\text{Li}}}}}\frac{{{{\partial }^{2}}{{c}_{i}}}}{{\partial {{x}^{2}}}}$с граничными условиями первого рода на входе ${{c}_{i}}(0,t) = {{f}_{i}}(t)$, условиями второго рода на выходе из колонки $\frac{{\partial {{c}_{i}}(L,t)}}{{\partial x}} = 0$ и некоторыми начальными условиями при t = 0: ci(x, 0) = ci0(x); ${{\bar {c}}_{i}}(x,0) = {{\bar {c}}_{{i0}}}(x)$. Обмен ионов между раствором и неподвижным сорбентом описывается в приближении квазистационарности:
(5)
$\frac{{{{{\bar {c}}}_{i}}}}{{{{c}_{i}}}} = K_{{\text{H}}}^{{{\text{Cat}},\,i}}{{\left( {\frac{{{{{\bar {c}}}_{{\text{H}}}}}}{{{{c}_{{\text{H}}}}}}} \right)}^{{{{z}_{i}}}}},$(6)
${{c}_{{{\text{OH}}}}} + \sum\limits_{j = 1}^m {{{c}_{j}}} = {{c}_{{\text{H}}}} + \sum\limits_{i = 1}^n {{{c}_{i}}} ,$Моделирование ионообменных процессов проведено нами с помощью созданной нами программы Createscheme [14], основанной на моделировании решений дифференциальных уравнений, описывающих эти процессы в приближении квазистационарности.
Послойная модель. Уравнения переноса моделируются разностной схемой
пространственные и временные шаги которой Δx, Δt выбираются удовлетворяющими условию квазистационарности процесса, а именно: $\Delta x = v\Delta t$, а величина шага Δt задается в соответствии с характерными временами процессов: $\Delta t > \Delta {{t}_{1}}$ – характерное время внутренней диффузии; $\Delta t > \Delta {{t}_{2}}$ – характерное время внешней диффузии; $\Delta t \geqslant \frac{{{{D}_{{{\text{Li}}}}}}}{{{{v}^{2}}}}$ – характерное время продольной диффузии.
После каждого шага по длине колонны состояние неподвижной фазы слоя с концентрациями ионов ${{\bar {c}}_{i}}$ приводится в равновесие с концентрациями ионов в жидкой фазе ${{c}_{i}}$. Для расчета равновесия ионов в катионном обмене используем следующую систему уравнений, полученную из соотношений (5)–(8):
(10)
$\begin{gathered} F(x,y) = x + \\ + \,\,\sum\limits_{i = 1}^n {\frac{{{{{\hat {c}}}_{i}}}}{{\varepsilon + K_{{\text{H}}}^{{{\text{Cat}},\,i}}{{{\left( {\frac{y}{x}} \right)}}^{{{{z}_{i}}}}}}}} - \frac{{{{{10}}^{{ - 14}}}}}{x} - \sum\limits_{j = 1}^m {{{c}_{j}}} = 0, \\ \end{gathered} $(11)
$G(x,y) = y + \sum\limits_{i = 1}^n {\frac{{{{{\hat {c}}}_{i}}K_{{\text{H}}}^{{{\text{Cat}},\,i}}{{{\left( {\frac{y}{x}} \right)}}^{{{{z}_{i}}}}}}}{{\varepsilon + K_{{\text{H}}}^{{{\text{Cat}},\,i}}{{{\left( {\frac{y}{x}} \right)}}^{{{{z}_{i}}}}}}} - {{{\bar {c}}}_{\Sigma }} = 0} .$Система двух уравнений (10), (11) с двумя неизвестными $x = {{c}_{{\text{H}}}},$ $y = {{\bar {c}}_{{\text{H}}}}$ решается на каждом шаге для всех слоев колонны специальной подпрограммой, учитывающей все особенности выписанных уравнений.
Описанный здесь послойный метод моделирования был успешно проверен сравнением с экспериментальными данными [14].
Условия проведения численных экспериментов. Для расчетов выбраны следующие параметры: диаметр слоя катионита в колонне – 0.5 м (площадь сечения – 0.196 м2); Высота слоя – 1 м; объем слоя сорбента – 0.196 м3; скорость пропускания растворов на стадиях сорбции – 5 колоночных объемов (0.980 м3/ч); скорость пропускания растворов на стадиях регенерации – 1 колоночный объем в час (0.196 м3/ч).
Предполагается, что катионит загружен в колонну так, что отсутствует жидкость вне слоя. Свободный объем жидкости определяется только порозностью (межзерновым пространством) стационарного слоя. Циклический процесс осуществляется в соответствии со схемой, показанной на рис. 1, на которой принципиально наличие емкостей Е1–Е3.
В каждом цикле стадия сорбции начинается с вытеснения рассола, который остался в межзерновом пространстве слоя катионита после предыдущего цикла регенерации. Также в каждом цикле стадия регенерации начинается с так называемой частичной регенерации с использованием рассола, полученного после указанной выше операции вытеснения. Циклы удобнее описывать по цепочке: вытеснение (и частичная сорбция)–основная сорбция–частичная регенерация–основная регенерация.
Нулевой цикл. Катионит находится в исходной Na-форме. Исходная вода заданного состава (${{c}_{{\Sigma }}} = {{c}_{o}}$) поступает сверху вниз на катионит и собирается в емкость Е1. Стадия умягчения заканчивается в момент заданного проскока кальция на выходе из фильтра. Весь объем воды ${{V}_{S}}$ из Е1 подается на опреснение. Задается концентрация регенерационного раствора ${{c}_{R}}$. Определяется коэффициент концентрирования рассола $~{{k}_{R}} = {{{{c}_{R}}} \mathord{\left/ {\vphantom {{{{c}_{R}}} {{{c}_{o}}}}} \right. \kern-0em} {{{c}_{o}}}}.$ Объем раствора на регенерацию ${{V}_{R}} = \,\,~{{{{V}_{S}}} \mathord{\left/ {\vphantom {{{{V}_{S}}} {{{k}_{R}}}}} \right. \kern-0em} {{{k}_{R}}}}$. Концентрированный раствор после выпаривания поступает в емкость Е2. Весь раствор из емкости Е2 подается на регенерацию снизу вверх в колонну.
Первый и последующие циклы. Вытеснение и частичная сорбция. Исходная вода подается на колонну сверху вниз с целью вытеснения использованного на предыдущей стадии регенерационного раствора из межзернового пространства слоя катионита. Раствор собирается в емкость Е3.
Основная сорбция на первом и всех последующих циклах. По достижению заданной концентрации ионов натрия завершается процесс вытеснения, и поток умягченной воды собирается в Е1, откуда подается в опреснитель для получения пресной воды и рассола для регенерации, собираемого, в свою очередь, в емкость Е2. Во всех циклах частичная регенерация проводится вытесненным рассолом из Е3, а основная – рассолом после опреснения из Е2.
В табл. 1 представлены составы модельных растворов, использованные в численных экспериментах.
Таблица 1.
Состав исходной воды
| Модельные растворы | СNa, моль-экв/л | СCa, моль-экв/л | C0, моль-экв/л |
|---|---|---|---|
| 1 | 0.025 | 0.025 | 0.05 |
| 2 | 0.02 | 0.03 | |
| 3 | 0.015 | 0.035 | |
| 4 | 0.01 | 0.040 | |
| 5 | 0.05 | 0.05 | 0.1 |
| 6 | 0.15 | 0.15 | 0.3 |
| 7 | 0.25 | 0.25 | 0.5 |
В модели были использованы следующие равновесные параметры – характеристики сульфокатионита КУ-2 (полученные экспериментально и апробированные ранее в расчетах [14]), а также критерии “проскока” компонентов на различных стадиях: полная обменная емкость (ПОЕ): ${{\bar {c}}_{{\Sigma }}} = 2{\text{\;}}$ моль-экв/л. Константы равновесия ионного обмена: $K_{{\text{H}}}^{{{\text{Na}}}} = 1.2;\,\,K_{{\text{H}}}^{{{\text{Ca}}}} = 5.3.$
Критерий завершения стадии сорбции: проскок ионов Ca2+ до ${{c}_{{{\text{Ca}}}}}~$= 0.005 моль-экв/л.
Критерий завершения процесса вытеснения: проскок ионов Na+ до ${{c}_{{{\text{Na}}}}}$ = 0.15 моль-экв/л.
Завершением стадии регенерации считалось пропускание всего объема рассола из емкости Е2 через колонну снизу вверх. Накопление полученного концентрата и дальнейшая его переработка не рассматривались в рамках настоящих численных экспериментов.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
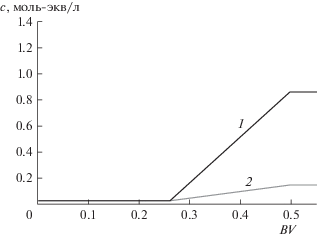
В начале изложения на одном примере совокупных значений всех варьируемых параметров, а именно: на примере модельного раствора № 1 из таблицы, степени концентрирования регенерирующего рассола, полученного после опреснения: $~{{k}_{R}} = 30$ (${{c}_{{\text{R}}}} = 1.5~\,\,{\text{моль - }}{\kern 1pt} {{{\text{экв}}} \mathord{\left/ {\vphantom {{{\text{экв}}} {\text{л}}}} \right. \kern-0em} {\text{л}}}$), а также нулевых потерь соли натрия с опресненной водой, покажем вид выходных кривых на стадиях сорбции и регенерации, а также распределение компонентов в колонне после соответствующих стадий. На рис. 2 представлены выходные кривые Ca2+ в различных циклах до заданного проскока 10% от содержания суммы компонентов в исходном растворе.
Рис. 2.
Выходные кривые сорбции Ca2+ на катионите из раствора Ca2+ 0.025 + Na+ 0.025 моль-экв/л: а – нулевой цикл; б – первый цикл; в – 6–10-й циклы.
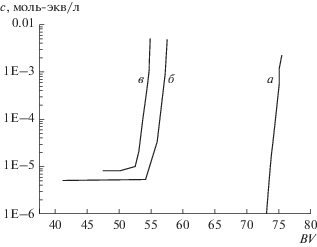
Как видно из этих кривых, сорбционная емкость слоя катионита, начиная с 1-го цикла, существенно уменьшается по сравнению с емкостью Na-формы катионита в нулевом цикле. После шестого цикла процесс выходит на стационарный режим. При этом емкость слоя по кальцию остается на уровне 2/3 от исходной емкости (54 вместо 76 колоночных объемов пропущенного раствора). Кривые на рисунке даны не с начала процесса: в самом его начале, в первом и дальнейших циклах, имеет место вытеснение рассола, оставшегося в межзерновом пространстве слоя после регенерации катионита в предыдущем цикле. Выходные кривые вытеснения компонентов показаны на рис. 3.
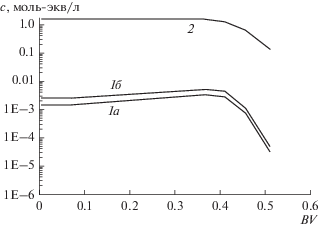
Рис. 3.
Выходные кривые вытеснения рассола в начале сорбционного процесса: 1 – Са2+; 2 – Na+; а – первый цикл; б – 6–10-й циклы.
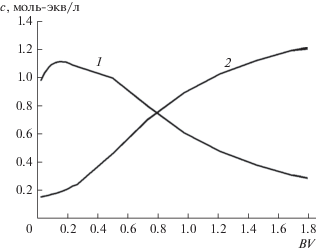
Противоточная регенерация в каждом цикле начинается с пропускания вытесненного при сорбции рассола. Полученные при этом результаты частичной регенерации показаны на рис. 4.
На рис. 5 представлены выходные кривые компонентов в процессе основной регенерации катионита рассолом, полученным после опреснения умягченного фильтрата.
Выходные кривые регенерации совпадают для всех циклов. Можно проверить, что в самоподдерживающемся процессе сохраняется баланс: а) объемы растворов, используемых на стадиях, иллюстрируемых на рис. 3 и 4, компенсируют друг друга и совпадают с постоянным объемом межзернового пространства; б) объем раствора, пропущенного на стадии сорбции, деленный на коэффициент концентрирования рассола при опреснении (${{k}_{R}} = 30~$ для данного случая), равен объему рассола, прошедшего через слой на стадии основной регенерации (в колоночных объемах: 54/30 = 1.8).
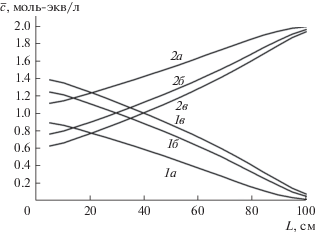
На рис. 6 показаны кривые распределения компонентов по слою катионита в фазе сорбента после стадии основной регенерации. Правый край рисунка соответствует низу колонны.
Рис. 6.
Концентрационные профили распределения компонентов по слою катионита после основной регенерации: 1 – Са2+; 2 – Na+; а – первый цикл; б – 6–10-й циклы.
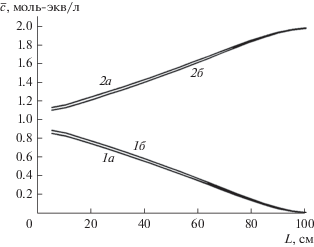
Представленные кривые незначительно отличаются друг от друга и только в головной части колонны. Видно, что существенная часть колонны всегда занята двухзарядным компонентом: после каждой стадии регенерации не менее трети емкости катионита остается в Ca-форме. Однако за счет эффекта электроселективности и изменения форм концентрационных профилей компонентов в колоннах при пропускании существенного объема исходного раствора через колонну с таким распределением компонентов не происходит “загрязнения” умягченного раствора ионом жесткости. Становится возможным стабильный самоподдерживающийся процесс умягчения-опреснения, в котором в циклах сорбции–десорбции не требуются дополнительные реагенты для регенерации катионита.
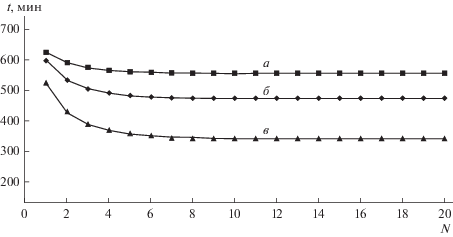
Влияние на СМП-процесс потерь соли Na+ с опресненной водой. На практике опреснительные установки позволяют получать воду с ненулевым солесодержанием. Для самоподдерживающегося процесса это означает, что часть соли натрия, используемой для регенерации в циклических процессах, будет “уноситься” с пресной водой. Тем не менее численные эксперименты показывают возможность осуществления СМП-процесса с реальными опреснительными системами. На рис. 7 показано, как в зависимости от номера цикла меняется время сорбции кальция до заданного проскока из того же модельного раствора № 1 для трех значений концентрации соли натрия в опресненной воде (при всех прочих равных условиях).
Рис. 7.
Зависимость времени сорбции Ca2+ до заданного проскока от номера цикла при трех значениях содержания соли натрия (моль-экв/л) в опресненной воде: а – Na+ = 0; б – Na+ = 0.01; в – Na+ = 0.015. Исходный раствор: Ca2+ 0.025 моль-экв/л + Na+ 0.025 моль-экв/л. Регенерация 1.5 моль-экв/л рассолом после опреснения.
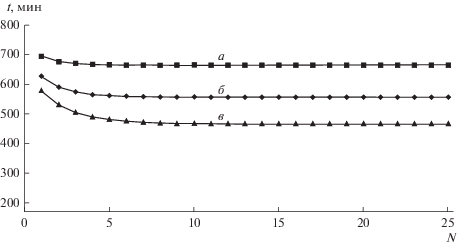
Видно, что для всех случаев после 10-го цикла происходит стабилизация процесса. При этом с повышением солесодержания в опресненной воде уменьшается работающая часть емкости катионита, пропорциональная времени сорбции. Для концентрации 0.015 моль-экв/л (0.878 мг/л), что практически соответствует верхнему уровню солесодержания воды питьевого качества после опреснительных установок, время уменьшается до 450 мин, что соответствует уменьшению емкости в два раза по сравнению с натриевой формой катионита (время сорбции на нулевом цикле 912 мин). На рис. 8 показаны соответствующие выходные кривые сорбции компонентов после стабилизации, где также видно уменьшение емкости слоя катионита в два раза (38 вместо 76 колоночных объемов в нулевом цикле).
Рис. 8.
Выходные кривые сорбции Ca2+, соответствующие данным на рис. 7: а – Na+ = 0; б – Na+ = 0.01; в – Na+ = 0.015 моль-экв/л.
На рис. 9 представлены концентрационные кривые распределения компонентов по слою катионита после его регенерации в различных циклах. Видно, что концентрационные профили существенно меняются в зависимости от увеличения солесодержания опресненной воды, и все большая часть емкости катионита оказывается “блокированной” ионами кальция и не участвующей в процессе умягчения.
Рис. 9.
Концентрационные профили распределения компонентов (1 – Са2+; 2 – Na+) по слою катионита для различных значений солесодержания в опресненной воде: а – Na+ = 0; б – Na+ = 0.01; в – Na+ = = 0.015 моль-экв/л.
Возможность использования самоподдерживающихся процессов с потерей значительной части емкости катионита определяется не технологическими, а экономическими соображениями, связанными с капитальными затратами на соответствующие установки. Предварительные оценки показывают, что процесс, соответствующий кривым в на рис. 7 и 8, вполне целесообразен. Очевидно также, что дальнейшее увеличение солесодержания в опресненной воде (что вполне допускалось бы требованиями к воде для орошения) не имеет смысла, так как существует возможность осуществления рассмотренных выше процессов со смешением пресной воды с исходной солоноватой водой.
Влияние степени концентрирования рассола. Степень концентрирования рассола, получаемого при опреснении умягченной воды, является важным фактором, так как в соответствии с формулой (1) определяет эффект электроселективности. На рис. 10 показано изменение зависимости времени сорбции кальция до заданного проскока от номера цикла при изменении концентрации регенерирующего рассола. Выбран практически важный и наиболее типичный случай, когда концентрация соли в опресненной воде примерно наполовину меньше значения, определяемого требованиями к питьевой воде.
Рис. 10.
Зависимость времени сорбции Ca2+ до заданного проскока от номера цикла при трех значениях концентрации соли натрия (моль-экв/л) в рассоле для регенерации: а – 1.5; б – 1.0; в – 0.5. Исходный раствор Ca2+ 0.025 моль-экв/л + Na+ 0.025 моль-экв/л. Солесодержание в опресненной воде 0.01 моль-экв/л.
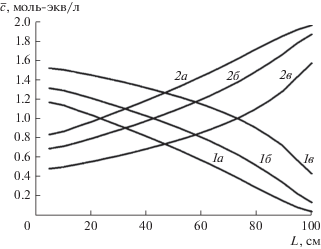
Видно, что СМП-процесс может быть реализован во всех случаях, но с уменьшением степени концентрирования рассола для регенерации существенно уменьшается полезная емкость катионита (рис. 11), используемая в каждом цикле после выхода на стационарный режим. В частности, при использовании 0.5 моль-экв/л рассола (со степенью концентрирования k = 10) полезная емкость катионита по кальцию и, соответственно, время сорбции падает почти в 3 раза (341 мин по сравнению с 912 мин).
Рис. 11.
Концентрационные профили распределения компонентов по слою катионита (1 – Са2+; 2 – Na+) после регенерации в 10-м цикле для различных значений степени концентрирования регенерирующего рассола: а – 1.5; б – 1.0; в – 0.5 моль-экв/л.
Влияние соотношения компонентов в исходном растворе. Соотношение концентраций компонентов, в нашем случае Na+ и Ca2+, определяет, какой резерв однозарядных ионов имеется в системе, чтобы можно было организовать самоподдерживающийся процесс.
Численные эксперименты проведены для солесодержания в опресненной воде 0.01 моль-экв/л и концентрации регенерирующего рассола 1.5 моль-экв/л для разных соотношений кальция и натрия в исходной воде:
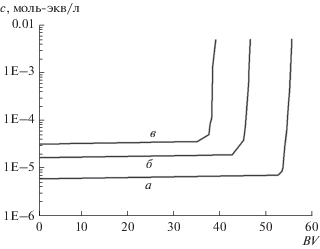
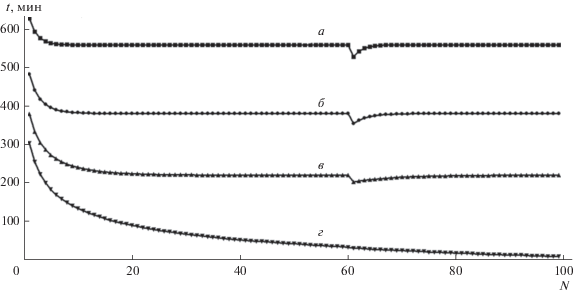
Для проверки возможности формирования стационарного самоподдерживающегося процесса в этом случае пришлось сделать численный эксперимент с 99 последовательными циклами сорбции–регенерации. Дополнительная проверка возможности стационарного процесса была сделана с помощью внесения в счет искусственного дефекта на 60-м цикле, а именно удаления на одном из циклов десятой доли регенерирующего раствора. Как видно из результатов счета (рис. 12), все кривые сорбции, кроме кривой г восстанавливаются после внесения дефекта и опять выходят на стационарный режим, а кривая г свидетельствует о том, что для ${{c}_{{{\text{Na}}}}}:{{c}_{{{\text{Ca}}}}}$ = 0.01 : 0.04 самоподдерживающийся режим не формируется.
Рис. 12.
Зависимость времени сорбции Ca2+ до заданного проскока от номера цикла при четырех эквивалентных соотношениях компонентов в исходном растворе с суммарной концентрацией 0.05 моль-экв/л: а – Na+ = 0.025 + Ca2+ = = 0.025; б – Na+ = 0.02 + Ca2+ = 0.03; в – Na+ = 0.015 + Ca2+ = 0.035; г – Na+ = 0.01+ Ca2+ = 0.04. Концентрация натрия в очищенной воде 0.01 моль-экв/л.
Влияние суммарной концентрации исходного раствора. На первый взгляд вопросы, рассматриваемые в данном разделе, кажутся полностью аналогичными предыдущим. На самом деле они взаимосвязаны, но между ними есть отличия, которые обусловлены следующим: при одной и той же степени концентрирования регенерирующих рассолов по сравнению с исходной водой, например, при kR = 20, результаты двух случаев: сорбции из 0.05 моль-экв/л раствора и регенерации с помощью 1 моль-экв/л раствора, а также сорбции из 0.1 моль-экв/л раствора и регенерации с помощью 2 моль-экв/л раствора не совпадают друг с другом и, как показывают расчеты, эффективная емкость катионита во втором случае более чем в 1.5 раза меньше емкости для случая с исходным более разбавленным раствором.
На рис. 13 и 14 представлены зависимости продолжительности времени сорбции кальция при заданном проскоке и нескольких концентрациях регенерирующего рассола для двух значений суммарных концентраций исходной воды (с0 = 0.1 и 0.5 моль-экв/л) при эквивалентном соотношении концентрации компонентов 1 : 1 и потере соли натрия с опресненной водой на уровне 0.01 моль-экв/л.
Рис. 13.
Зависимость времени сорбции Ca2+ от номера цикла для исходной суммарной концентрации раствора 0.1 моль-экв/л (Ca2+ = 0.05, Na+ = 0.05) при различных концентрациях регенерирующего раствора (моль-экв/л): а – 2.0; б – 1.5; в – 1.0; г – 0.5.
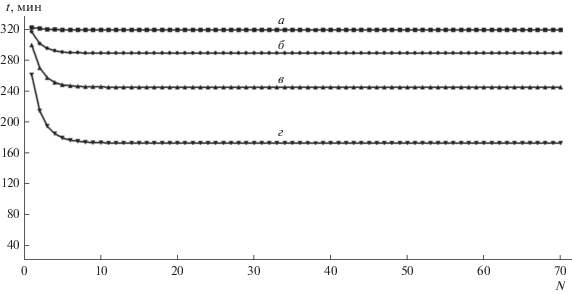
Рис. 14.
Зависимость времени сорбции Ca2+ от номера цикла для исходной суммарной концентрации раствора 0.5 моль-экв/л (Ca2+ = 0.25, Na+ = 0.25) при различных концентрациях регенерирующего раствора (моль-экв/л): а – 2.0; б – 1.5; в – 1.0; г – 0.5.
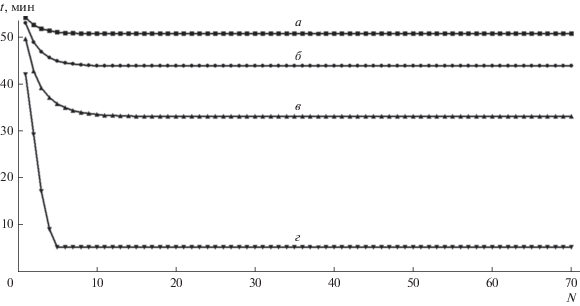
В этих случаях, несмотря на возможность формирования СМП-процесса, его целесообразность определяется не технологическими, а экономическими соображениями, связанными в основном с капитальными затратами. Например, для исходной суммарной концентрации перерабатываемой воды ${{c}_{0}} = ~$ 0.5 моль-экв/л, в самом лучшем случае, когда проводится регенерация получаемым в процессе 2 моль-экв/л раствором соли натрия, время сорбции в стационарном режиме составляет всего 52 мин (по сравнению с 912 мин для Na-формы катионита). Таким образом, работающая емкость катионита уменьшается в 17.5 раз, т.е. только 5.7% емкости является обратимо обменной в таких условиях. Более 94% ПОЕ остается блокированной ионами кальция.
Расчеты для реальной морской воды не были проведены в этой работе, такие расчеты проводились ранее [5, 7] с использованием других программ. Наши расчеты согласуются с ними, и из проведенного анализа понятно, почему самоподдерживающийся процесс не может быть рациональным для морской воды при использовании сильнокислотных катионитов.
ЗАКЛЮЧЕНИЕ
Проведенные численные эксперименты на примере модельных растворов кальция и натрия и анализ полученных результатов показывает осуществимость на практике стационарных циклических самоподдерживающихся процессов умягчения–опреснения с использованием сильнокислотного катионита, в которых регенерация катионита в каждом цикле осуществляется только за счет возвратного рассола, получаемого при опреснении умягченной воды. Это дает возможность создания автономных стационарных и передвижных систем водоподготовки при использовании СМП-процесса для переработки соленых и солоноватых вод, не требующих привозных реагентов и, соответственно, вспомогательных устройств хранения реагентов и приготовления регенерационных растворов.
На характеристики самоподдерживающихся процессов, а именно количество циклов до выхода на стационарный режим, а также продолжительность этих циклов на стадиях сорбции и регенерации, оказывают влияние: соотношение концентраций двух- и однозарядных ионов в исходном растворе, суммарная концентрация этих растворов, степень концентрирования возвратных рассолов по сравнению с исходными растворами, относительные потери однозарядных ионов, “уносимые” с опресненной водой. Наиболее сильное влияние на возможность осуществления СМП-процессов оказывают два взаимосвязанных фактора: суммарная концентрация и степень концентрирования рассола.
В стационарном самоподдерживающемся процессе реализуется лишь часть ионообменной емкости слоя умягчительной колонны; реализуемость самоподдерживающегося процесса определяется критической величиной отношения работающей емкости к ПОЕ, или продолжительности сорбционного цикла в стационарном состоянии к продолжительности такого цикла на Na-форме катионита при прочих равных условиях. Значение указанной критической величины определяется не технологическими, а экономическими факторами (кроме случаев, когда СМП-процесс не может быть реализован из-за нулевой продолжительности цикла).
Проведенный анализ показывает методологию расчетов рациональных условий организации СМП-процессов в реальных условиях переработки природных и техногенных вод.
ОБОЗНАЧЕНИЯ
| BV | колоночный объем |
| $c$ | концентрация в растворе, моль-экв/л |
| $\bar {c}$ | концентрация в фазе ионита, моль-экв/л (на объем слоя) или моль-экв/л |
| ${{\hat {c}}_{i}}$ | средняя концентрация i-го компонента в сечении слоя катионита, моль-экв/л (с учетом жидкой и твердой фазы) |
| $D$ | коэффициент диффузии, см2/с |
| $F,f,G$ | функции |
| K | концентрационная константа (коэффициент) равновесия ионного обмена |
| k | степень концентрирования |
| L | высота слоя катионита, см или м |
| m | количество анионных компонентов |
| N | номер сорбционного цикла |
| n | количество катионных компонентов в системе |
| S | площадь сечения слоя катионита, см2 |
| t | время, мин |
| V | объем, л |
| $v$ | линейная скорость, см/с |
| W | объемная скорость раствора, л/мин |
| $X$ | координата точки концентрационного фронта вдоль слоя катионита |
| x | координата по высоте колонны, отсчитываемая от точки входа раствора |
| $Y$ | эквивалентная доля компонента в растворе |
| $\bar {Y}$ | эквивалентная доля компонента в слое сорбента |
| z | заряд иона |
| $\varepsilon $ | порозность (доля межзеренного пространства в слое катионита) |
ИНДЕКСЫ
Список литературы
Klein G., Vermeulen T. Cyclic performance of layered beds for binary ion exchange // AIChE Symp. Ser. 1975. V. 71. № 152. P. 69.
Klein G. Design and development of cyclic operations // NATO ASI Ser. E. 1981. V. 33. P. 427.
Гельферих Ф. Иониты. М.: Изд-во иностранной литературы, 1962.
Khamizov R.Kh., Ivanov V.I., Madani A.A. Dual temperature ion exchange // React. Funct. Polym. 2010. V. 70. P. 521.
Barba D., Brandani V., Foscolo P.U. A method based on equilibrium theory for a current choice of cationic resin in sea water softening // Desalination. 1983. V. 48. № 2. P. 133.
Muraviev D.N., Khamizov R.Kh., Tikhonov N.A., Morales J.G. Clean (“Green”) Ion Exchange Technologies. IV. High-Ca-selectivity ion-exchange material for self-sustaining decalcification of mineralized waters process // Ind. Eng. Chem. Res. 2004. V. 43. № 8. P. 1868.
Tokmachev M.G., Tikhonov N.A., Khamizov R.Kh. Investigation of cyclic self-sustaining ion exchange process for softening water solutions on the basis of mathematical modeling // React. Funct. Polym. 2008. V. 68. P. 1245.
Boodo F. Method for purifying water by cyclic ionic exchange. US Patent 2011/0278225. 2011.
Flodman H.R., Dvorak B.I. Brine reuse in ion-exchange softening: salt discharge, hardness leakage, and capacity tradeoffs // Water Environ. Res. 2012. V. 84. № 6. P. 535.
Tang S., Brinchak L., Cohen Y., Lahav O. Selective separation of divalent ions from seawater using an integrated ion-exchange/nanofiltration approach // Chem. Eng. Process. 2018. V. 126. P. 8.
Brinchak L., Keller O., Tang S., Fridman-Bishop N., Lahav O. A membrane-based recycling process for minimizing environmental effects inflicted by ion-exchange softening applications // Sep. Purif. Technol. 2019. V. 223. P. 23.
Хамизов Р.Х., Хамизов С.Х. Способ переработки природных солоноватых вод на ионитах с получением растворов сложных минеральных удобрений и установка для его осуществления (варианты). Патент 2686147 РФ // Бюлл. изобрет. 2019. № 12.
Safonyk A., Prysiazhniuk I., Prysiazhniuk O., Naumchuk O. Mathematical modeling singularly perturbed processes of water softening on sodium-cationite filters // IAPGOS. 2019. № 1. P. 37.
Комарова И.В., Галкина Н.К., Прудковский А.Г. Вычислительный эксперимент как способ оценки эффективности работы водоподготовительных установок при поточной и противоточной регенерации ионообменных фильтров // Сорбционные хроматогр. процессы. 2018. Т. 18. № 5. С. 776.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии