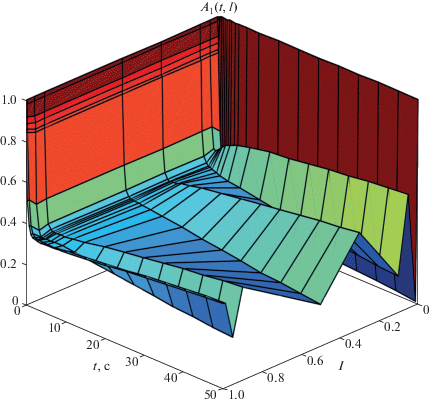
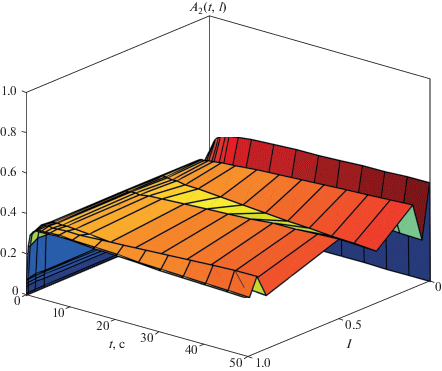
Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 643-648

Квазиинварианты химических реакций в реакторе идеального вытеснения

Н. И. Кольцов^*

Чувашский государственный университет им. И.Н. Ульянова
Чебоксары, Россия

Поступила в редакцию 22.07.2019
После доработки 13.11.2019
Принята к публикации 20.11.2019

DOI: 10.31857/S0040357120040089

Аннотация

Математические модели неравновесных процессов в распределенных системах описываются дифференциальными уравнениями в частных производных с заданными краевыми условиями и, как правило, не могут быть решены аналитически. Отсутствие точных решений таких моделей не позволяет найти точные инварианты, т.е. функции строго постоянные на этих решениях. В данной статье разработан метод определения приближенных пространственно-временных кинетических инвариантов (квазиинвариантов) химических реакций, не учитывающих диффузию, в условиях реактора идеального вытеснения. Пространственно-временные квазиинварианты представляют собой явные алгебраические выражения, связывающие неравновесные значения концентраций реагентов и/или температур, измеренных в двух или более экспериментах с различными специально подобранными начальными и входными условиями (мультиэкспериментах). Подбор подходящих начальных условий позволяет найти такие функции от решений, которые слабо зависят от времени и длины реактора, т.е. остаются практически постоянными в течение всей реакции во всем объеме реактора. Показано, что число квазиинвариантов определяется числом независимых переменных модели (концентраций реагентов и температуры). Применение метода проиллюстрировано на примере одностадийной реакции, протекающей в реакторе идеального вытеснения. Найденные для этой реакции квазиинвариантные 3D-поверхности сопоставлены с 3D-графиками изменения концентраций и температуры в ходе реакции. Показано, что квазиинварианты изменяются в меньшем диапазоне (по оси ординат), чем соответствующие им концентрации и температуры в разных экспериментах, т.е. являются пространственно-временными приближенными инвариантами. Такого рода квазиинварианты можно “наблюдать” на зависимостях переменных модели (концентраций, температур) от времени и длины реактора в виде различных сплющенных трехмерных структур (“лежачих” волн). Метод расширяет инструментарий анализа нестационарной кинетики химических реакций в распределенных системах идеального вытеснения.

Ключевые слова: химическая кинетика, распределенные системы без диффузии, реактор идеального вытеснения, мультиэксперименты, квазиинварианты

ВВЕДЕНИЕ

Реальные физико-химические и биологические системы, как правило, неоднородны (распределены во времени и пространстве). Различные подходы к моделированию распределенных и сосредоточенных систем для анализа процессов в химических реакторах изложены в ставших классическими монографиях Д.А. Франк-Каменецкого, Р. Ариса, М.Г. Слинько, Д. Перлмуттера, Б.В. Вольтера, И.Е. Сальникова, В.С. Бескова, Ю.Ш. Матроса, Г.М. Островского, Г.С. Яблонского, В.И. Быкова и др. (см., например, [1–12]). В этих работах показано, что при описании таких моделей дифференциальными уравнениями в частных производных могут воспроизводиться различные нестационарные эффекты (стоячие, бегущие, квазистохастические волны, синхронные автоколебания и др.) и стационарные неоднородные распределения (диссипативные структуры). Одной из недавно обнаруженных нестационарных характеристик химических систем являются концентрационные инварианты, которые представляют собой комбинации неравновесных концентраций реагентов, остающиеся строго постоянными в течение всей реакции. Впервые на них обратили внимание Г.С. Яблонский с соавторами [13–20], предложившие и развившие метод граничных дуал-экспериментов (МДЭ) для нахождения точных концентрационных инвариантов линейных и некоторых нелинейных реакций. Недавно получено и экспериментальное подтверждение существования таких инвариантов в нелинейной реакции [21]. Однако результаты этих работ применимы только в закрытых системах при использовании граничных взаимно-обратных (термодинамических) экспериментов, проводимых при полном отсутствии продукта или полном отсутствии исходного реагента. В общем случае, т.е. для произвольных нелинейных реакций, эти результаты не применимы и точные инварианты найти не возможно, но можно найти приближенные концентрационные и температурные инварианты (квазиинварианты), т.е. комбинации неравновесных концентраций реагентов или температур, остающиеся практически постоянными в течение всей реакции. Обнаружить их можно методом мультиэкспериментов (ММЭ), применимым для сложных реакций и любых (не только граничных) экспериментов в сосредоточенных системах в условиях реактора идеального смешения (РИС) [22–24]. Целью данной работы является обобщение ММЭ на нелинейные реакции, протекающие в распределенных системах в условиях реактора идеального вытеснения (РИВ). Обобщенный ММЭ позволяет рассчитать две новые характеристики распределенных систем – пространственно-временные концентрационные и температурные квазиинварианты.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Пусть реакция с участием веществ A_j протекает через стадии

(1)

$\begin{gathered} {{a}_{i}}_{1}{{{\mathbf{A}}}_{1}} + {{a}_{i}}_{2}{{{\mathbf{A}}}_{2}} + \ldots + {{a}_{{ij}}}{{{\mathbf{A}}}_{j}} = \\ = \,\,{{b}_{i}}_{1}{{{\mathbf{A}}}_{1}} + {{b}_{i}}_{2}{{{\mathbf{A}}}_{2}} + \ldots + {{b}_{{ij}}}{{{\mathbf{A}}}_{i}}, \\ \end{gathered} $

где a_ij ≥ 0, b_ij ≥ 0 – стехиометрические коэффициенты; i = 1,…, s – номер стадии; j = 1,…, n – номер реагента. Динамика реакции (1) в РИВ, с учетом изменений концентраций реагентов и температуры во времени и по длине реактора, при отсутствии диффузии описывается уравнениями [1–12]

(2)

${{\partial {{A}_{j}}} \mathord{\left/ {\vphantom {{\partial {{A}_{j}}} {\partial t}}} \right. \kern-0em} {\partial t}} + q{{\partial {{A}_{j}}} \mathord{\left/ {\vphantom {{\partial {{A}_{j}}} {\partial l}}} \right. \kern-0em} {\partial l}} = {{\Sigma }_{i}}({{b}_{{ij}}} - {{a}_{{ij}}}){{r}_{i}},$

(3)

${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial t}}} \right. \kern-0em} {\partial t}} + q{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial l}}} \right. \kern-0em} {\partial l}} = b{{\Sigma }_{i}}{{r}_{i}}{{Q}_{{i~}}} + \,\gamma \left( {{{T}_{x}}--T} \right),$

где A_j – текущие концентрации реагентов, мол. д.; t – время, с; q – линейная скорость потока, м/c; r_i = ${{k}_{{ + i}}}\prod A_{j}^{{aij}} - {{k}_{{ - i}}}\prod A_{j}^{{bij}}$ − скорости стадий по закону действующих масс, 1/с; k_±i = k_±i0exp(−E_±i/RT) − константы скоростей стадий, 1/с; k_±i0 и E_±i − предэкспоненты и энергии активации стадий; R − газовая постоянная; l и L – безразмерные текущая и общая длины реактора; T – текущая температура, К; T_x − температура стенки реактора, К; Q_i − тепловые эффекты стадий, Дж; β ≡ 1/(SρC_p), (К с²)/(кг м); γ ≡ αβF/L, 1/с; S – площадь поперечного сечения потока, м²; ρ – плотность теплоносителя, кг/м³; С_р – удельная теплоемкость теплоносителя, Дж/(кг К); α – коэффициент теплопередачи, Вт/(м² К); F – площадь поверхности теплообмена, м². Зададим следующие начальные и входные условия (НУ):

(4)

$\begin{gathered} {{A}_{j}}(0,l) = {{A}_{j}}_{0}(l),\,\,T(0,l) = {{T}_{0}}(l), \\ {{A}_{j}}(t,0) = {{A}_{j}}_{0}(t),\,\,T(t,0) = {{T}_{0}}(t), \\ \end{gathered} $

(5)

${{\partial {{A}_{j}}(0,l)} \mathord{\left/ {\vphantom {{\partial {{A}_{j}}(0,l)} {\partial l}}} \right. \kern-0em} {\partial l}} = 0,\,\,{{\partial T(0,l)} \mathord{\left/ {\vphantom {{\partial T(0,l)} {\partial l}}} \right. \kern-0em} {\partial l}} = 0,$

где A_j0(l), T₀(l), A_j0(t), T₀(t) − заданные функции. Система (2)–(5) не решается аналитически и ее точные инварианты не известны. Найдем для этой системы временные и пространственные квазиинварианты.

Временные квазиинварианты. Разложим неизвестные решения системы (2)–(5) в ряд по двум переменным t и l:

(6)

$\begin{gathered} {{A}_{j}}\left( {t,l} \right) \approx {{A}_{j}}\left( {0,0} \right) + \\ + \,\,t\partial {{A}_{j}}{{\left( {0,0} \right)} \mathord{\left/ {\vphantom {{\left( {0,0} \right)} {\partial t}}} \right. \kern-0em} {\partial t}} + l\partial {{A}_{j}}{{\left( {0,0} \right)} \mathord{\left/ {\vphantom {{\left( {0,0} \right)} {\partial l}}} \right. \kern-0em} {\partial l}}, \\ \end{gathered} $

(7)

$T\left( {t,l} \right) \approx T\left( {0,0} \right) + t\partial T{{\left( {0,0} \right)} \mathord{\left/ {\vphantom {{\left( {0,0} \right)} {\partial t}}} \right. \kern-0em} {\partial t}} + l\partial T{{\left( {0,0} \right)} \mathord{\left/ {\vphantom {{\left( {0,0} \right)} {\partial l}}} \right. \kern-0em} {\partial l}}.$

Перепишем эти соотношения с учетом (2)–(5):

(8)

${{A}_{j}} \approx {{A}_{j}}_{0} + t{{\Sigma }_{i}}({{b}_{{ij}}} - {{a}_{{ij}}}){{r}_{i}},$

(9)

$T \approx {{T}_{0}} + t\left[ {\beta {{\Sigma }_{i}}{{r}_{i}}{{Q}_{i}} + \gamma \left( {{{T}_{x}}--T} \right)} \right].$

Вычислим эти выражения для двух неравновесных НУ A_j01, T₀₁ и A_j02, T₀₂:

(10)

$\begin{gathered} {{A}_{{j1}}} - {{A}_{{j01}}} \approx t{{\Sigma }_{i}}({{b}_{{ij}}} - {{a}_{{ij}}}){{r}_{{i01}}}, \\ {{A}_{j}}_{2} - {{A}_{j}}_{{02}} \approx t{{\Sigma }_{i}}({{b}_{{ij}}} - {{a}_{{ij}}}){{r}_{{i02}}}, \\ \end{gathered} $

(11)

$\begin{gathered} {{T}_{1}} - {{T}_{{01}}} \approx \gamma ({{T}_{x}}--{{T}_{{01}}})t + t\beta {{\Sigma }_{i}}{{Q}_{i}}{{r}_{{i01}}}, \\ {{T}_{2}} - {{T}_{{02}}} \approx \gamma ({{T}_{x}}--{{T}_{{02}}})t + t\beta {{\Sigma }_{i}}{{Q}_{i}}{{r}_{{i02}}}, \\ \end{gathered} $

где r_i01= ${{k}_{i}}\prod A_{{j01}}^{{aij}} - {{k}_{{ - i}}}\prod A_{{j01}}^{{bij}}$, r_i02= ${{k}_{i}}\prod A_{{j02}}^{{aij}}$ – ‒ ${{k}_{{ - i}}}\prod A_{{j02}}^{{bij}}$. Исключим t из каждой пары (10)–(11) и найдем n + 1 основных временных квазиинвариантов

(12)

${{I}_{j}} \equiv {{A}_{{j1}}} - {{A}_{{j2}}}{{R}_{{j0}}} \approx {{A}_{{j01}}} - {{A}_{{j02}}}{{R}_{{j0}}} \equiv {{K}_{{j0}}},$

(13)

$T \equiv {{T}_{1}} - {{T}_{2}}{{R}_{{T0}}} \approx {{T}_{{01}}} - {{T}_{{02}}}{{R}_{{T0}}} \equiv {{K}_{{T0}}},$

где R_j0 ≡ ∑_i(b_ij − a_ij)r_i01/r_i02, R_T0 ≡ [γ(T_x – T₀₁) + + βΣ_iQ_ir_i01]/[γ(T_x –T₀₂) + βΣ_iQ_ir_i02]. Очевидно, что линейные комбинации выражений (12)–(13) также являются квазиинвариантами. Квазиинварианты (12)–(13) можно “улучшить” с помощью критерия улитки [22], т.е. требований

(14)

$\begin{gathered} {{K}_{{j\infty }}} \equiv {{A}_{{j\infty }}}(1 - {{R}_{{j0}}}) \approx {{K}_{{j0}}}, \\ {{K}_{{T\infty }}} \equiv {{T}_{\infty }}(1 - {{R}_{{T0}}}) \approx {{K}_{{T0}}}, \\ \end{gathered} $

где A_j∞ = A_j1∞ = A_j2∞ и T_∞= T_1∞ = T_2∞ − равновесные значения при ∂A_j/∂t + q∂A_j/∂l = ∂T/∂t + q∂T/∂l = = 0. Нетривиальные решения уравнений (14) определяют НУ для возможного дополнительного сжатия поверхностей квазиинвариантов.

Пространственные квазиинварианты. Выберем вместо (5) другие входные условия ∂A_j(t,0)/∂t = 0, ∂T(t,0)/∂t = 0 и подставим их в (6)–(7), тогда соотношения (8)–(9) примут вид

(15)

$\begin{gathered} {{A}_{j}} \approx {{A}_{{j0}}} + ({l \mathord{\left/ {\vphantom {l q}} \right. \kern-0em} q}){{\Sigma }_{i}}({{b}_{{ij}}} - {{a}_{{ij}}}){{r}_{i}}, \\ T \approx {{T}_{0}} + ({l \mathord{\left/ {\vphantom {l q}} \right. \kern-0em} q})[\beta {{\Sigma }_{i}}{{r}_{i}}{{Q}_{i}} + \gamma ({{T}_{x}}--T)]. \\ \end{gathered} $

Вычислим эти выражения для тех же НУ (4), исключим из них l и получим n+1 основных пространственных квазиинвариантов, которые совпадают по форме с (12)–(13), но получены из других уравнений. Таким образом, выражения (12)–(13) являются пространственными и временными квазиинвариантами.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Применим полученные соотношения к реакции

(1.1)

${\text{А}} = {\text{B}}.$

Для этой реакции система (2)–(3) примет вид

(1.2)

${{\partial A} \mathord{\left/ {\vphantom {{\partial A} {\partial t}}} \right. \kern-0em} {\partial t}} + q{{\partial A} \mathord{\left/ {\vphantom {{\partial A} {\partial l}}} \right. \kern-0em} {\partial l}} = - {{r}_{1}},\,\,{{\partial B} \mathord{\left/ {\vphantom {{\partial B} {\partial t}}} \right. \kern-0em} {\partial t}} + q{{\partial B} \mathord{\left/ {\vphantom {{\partial B} {\partial l}}} \right. \kern-0em} {\partial l}} = {{r}_{1}},$

(1.3)

${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial t}}} \right. \kern-0em} {\partial t}} + q{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial l}}} \right. \kern-0em} {\partial l}} = \beta {{Q}_{1}}{{r}_{1}} + \gamma \left( {{{T}_{x}}--T} \right),$

где A и B – концентрация исходного вещества А и продукта B; r₁ = k₁A − k₋₁B; k_±1 = k_±10exp(−E_±1/RT). Функции НУ A_j0(l), T₀(l), A_j0(t), T₀(t) в (4)–(5) примем постоянными. Из (1.2) следуют два неравновесных закона сохранения (ЗС) для реакции (1): A + B = exp(l−qt) и A + B = exp(qt−l), которые следует учитывать при планировании экспериментов. Пространственно-временные квазиинварианты (12)–(13) для системы (1.2)–(1.3) запишутся как

(1.4)

${{I}_{A}} \equiv {{A}_{1}} - {{A}_{2}}{{R}_{{A0}}} \approx {{A}_{{01}}} - {{A}_{{02}}}{{R}_{A}} \equiv {{K}_{{A0}}},$

(1.5)

${{I}_{B}} \equiv {{B}_{1}} - {{B}_{2}}{{R}_{{B0}}} \approx {{B}_{{01}}} - {{B}_{{02}}}{{R}_{B}} \equiv {{K}_{{B0}}},$

(1.6)

${{I}_{T}} \equiv {{T}_{1}} - {{T}_{2}}{{R}_{{T0}}} \approx {{T}_{{01}}} - {{T}_{{02}}}{{R}_{T}} \equiv {{K}_{{T0}}},$

где R_A0 = r₁₀₁/r₁₀₂, R_B0 = r₁₀₁/r₁₀₂, R_T0 = [γ(T_x–T₀₁) + + βQ₁r₁₀₁]/[γ(T_x–T₀₂) + βQ₁r₁₀₂)], r₁₀₁ = k₁₀₁A₀₁ − ‒ k₋₁₀₁B₀₁, r₁₀₂ = k₁₀₁A₀₂ − k₋₁₀₁B₀₂, k_±101 = = k_±10exp(−E₁/RT₀₁), k_±102 = k_±10 exp(−E₁/RT₀₂). Критерий улитки (14) соответственно примет вид

(1.7)

$\begin{gathered} {{K}_{{A\infty }}} \equiv {{A}_{\infty }}(1 - {{R}_{{A0}}}) \approx {{A}_{{01}}} - {{A}_{{02}}}{{R}_{{A0}}}, \\ {{K}_{{B\infty }}} \equiv {{B}_{{j\infty }}}(1 - {{R}_{{B0}}}) \approx {{B}_{{01}}} - {{B}_{{02}}}{{R}_{{B0}}}, \\ \end{gathered} $

(1.8)

${{K}_{{T\infty }}} \equiv {{T}_{\infty }}(1 - {{R}_{{T0}}}) \approx {{T}_{{01}}} - {{T}_{{02}}}{{R}_{{T0}}}.$

Линейные комбинации выражений (1.4)–(1.6) тоже являются квазиинвариантами.

Рассчитаем условия экспериментов для “наблюдения” квазиинвариантов. Пусть константы скоростей и энергии активации стадий k₁₀ = 2, k₋₁₀ = 1 и E₁= E₋₁= 2, температуры T₀= 300, T_x = 200 и R = 2, β = γ = 1, q = 1; Q₁ = 1, A₀ = 1, B₀ = 0. Выберем, с учетом ЗС, для пары экспериментов НУ, например: A₀₁ = 1, B₀₁ = 0, T₀₁ = 300 и A₀₂ = 0, B₀₂ = 1, T₀₂ = 310, тогда K_A0 = 1, K_B0 = 2, K_T0 ≈ 26 и K_A∞ = 1, K_B∞ = 2, K_T∞ ≈ 36, $I_{A}^{*}$ ≈ $I_{B}^{*}$ ≈ $I_{T}^{*}$ ≈ 2. Зависимости концентраций реагента А от времени и длины реактора для этих экспериментов приведены на рис. 1 и 2 .

Рис. 1.

Зависимость A₁(t, l) для первого эксперимента с НУ A₀₁ = 1, B₀₁ = 0, T₀₁ = 300.

Рис. 2.

Зависимость A₂(t, l) для второго эксперимента с НУ A₀₂ = 0, B₀₂ = 1, T₀₂ = 310.

Пространственно-временные квазиинварианты для реагента A (1.4) и температуры (1.6) для этой пары экспериментов показаны на рис. 3 и 4 .

Рис. 3.

Концентрационный пространственно-временной квазиинвариант I_A(t, l) для двух экспериментов с НУ A₀₁ = 1, B₀₁ = 0, T₀₁ = 300 и A₀₂ = 0, B₀₂ = 1, T₀₂ = 310.

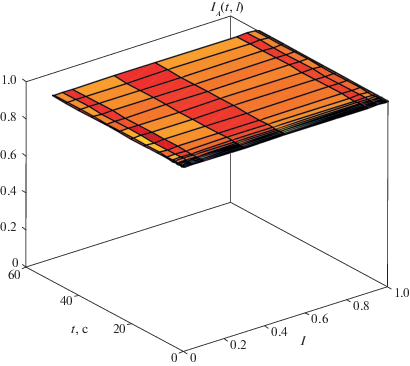
Рис. 4.

Температурный пространственно-временной квазиинвариант I_T(t, l) для двух экспериментов с НУ A₀₁ = 1, B₀₁ = 0, T₀₁ = 300 и A₀₂ = 0, B₀₂ = 1, T₀₂ = 310.

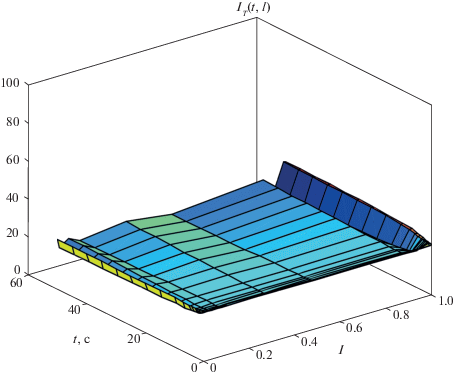
Из этих рисунков видно, что пространственно-временные квазиинвариантные зависимости практически постоянны во времени и по длине реактора и изменяются значительно меньше, чем соответствующие неравновесные концентрации реагента или температуры. Визуально подобные квазиинварианты могут представлять собой и более сложные сплющенные трехмерные структуры (“лежачие” волны, улитки, подушки и т.д.).

ЗАКЛЮЧЕНИЕ

Разработано обобщение ММЭ для химических реакций, протекающих в распределенных неизотермических системах, в условиях РИВ с кинетикой закона действующих масс. Метод не требует знания точных решений дифференциальных уравнений в частных производных, а основан на анализе приближенных решений этих уравнений, соответствующих любым начальным условиям (необязательно граничным как в МДЭ). Метод позволяет обнаруживать два типа пространственно-временных квазиинвариантов (концентрационные и температурные) для химических реакций в РИВ и рассчитать условия проведения соответствующих экспериментов. На графиках зависимости от времени и длины реактора пространственно-временные квазиинварианты напоминают “лежачие” волны, дополняя список известных ранее нестационарных эффектов (стоячие, бегущие и другие волны). Теоретическая и практическая значимость метода состоит в следующем: улучшение понимания закономерностей неравновесных химических процессов в реакторах идеального вытеснения; возможность обнаруживать множество (по числу реагентов) новых неравновесных квазиинвариантных характеристик химических процессов; возможность априори предсказывать, обнаруживать и исследовать неизвестные кинетические закономерности в реакциях, протекающих в распределенных системах без учета диффузии; появление новых инструментов идентификации механизмов химических реакций; возможность поиска новых путей повышения эффективности режимов работы химических реакторов.

Автор выражает благодарность В.Х. Федотову за внимательные и полезные обсуждения результатов работы.

ОБОЗНАЧЕНИЯ

A_j	концентрации реагентов, мол. д.
a_ij, b_ij	безразмерные стехиометрические коэффициенты
С_р	удельная теплоемкость, Дж/(кг К)
E_±i	энергии активации стадий
F	площадь поверхности теплообмена, м²
k_±i	константы скоростей стадий, 1/с
k_±i0	предэкспоненты скоростей стадий, 1/с
L	безразмерная общая длина реактора
l	безразмерная текущая длина реактора
Q_i	тепловые эффекты стадий, Дж
q	линейная скорость потока, м/c
R	газовая постоянная
r_i	скорости стадий, 1/с
S	площадь поперечного сечения, м²
T	текущая температура, К
T_x	температура стенки реактора, К
t	время, с
α	коэффициент теплопередачи, Вт/(м² К)
ρ	плотность теплоносителя, кг/м³

ИНДЕКСЫ

0	начальное значение
i	номер стадии
j	номер реагента

Список литературы

Франк-Каменецкий Д.А. Основы макрокинетики. Диффузия и теплопередача в химической кинетике. М.: Интеллект, 2008.
Арис Р. Анализ процессов в химических реакторах. Л.: Химия, 1967.
Слинько М.Г. Моделирование химических реакторов. Новосибирск: Наука, 1968.
Перлмуттер Д. Устойчивость химических реакторов. Л.: Химия, 1976.
Вольтер Б.В., Сальников И.Е. Устойчивость режимов работы химических реакторов. М.: Химия, 1981.
Матрос Ю.Ш. Нестационарные процессы в каталитических реакторах. Новосибирск: Наука, 1982.
Яблонский Г.С., Быков В.И., Горбань А.Н. Кинетические модели каталитических реакций. Новосибирск: Наука, 1983.
Бесков В.С. Общая химическая технология. М.: Академкнига, 2005.
Быков В.И., Цыбенова С.Б. Нелинейные модели химической кинетики. М.: URSS, 2011.
Островский Г.М., Волин Ю.М., Зиятдинов Н.Н. Оптимизация в химической технологии. Казань: Фэн, 2005.
Ziyatdinov N.N. Modeling and Optimization of Chemical-Technological Processes and Systems // Theor. Found. Chem. Eng. 2017. V. 51. № 5. P. 889. [Зиятдинов Н.Н. Моделирование и оптимизация химико-технологических процессов и систем // Теор. осн. хим. технол. 2017. Т. 51. № 5. С. 546.]
Bykov V.I., Tsybenova S.B., Yablonsky G.S. Chemical Complexity via Simple Models. Berlin: De Gruyter, 2018.
Yablonsky G.S., Constales D., Marin G.B. Equilibrium relationships for non-equilibrium chemical dependences // Chem. Eng. Sci. 2011. V. 66. P. 111.
Constales D., Yablonsky G.S., Marin G.B. Thermodynamic time invariances for dual kinetic experiments: Nonlinear single reactions and more // Chem. Eng. Sci. 2012. V. 73. P. 20.
Constales D., Yablonsky G.S., Marin G.B. Intersections and coincidences in chemical kinetics: linear two-step reversible-irreversible reaction mechanism // Comput. Math. Appl. 2013. V. 65. № 10. P. 1614.
Yablonsky G.S. Decoding Complexity of Chemical Reactions // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 608. [Yablonsky G.S. Decoding Complexity of Chemical Reactions // Теор. осн. хим. технол. 2014. Т. 48. № 5. С. 551.]
Branco P.D., Yablonsky G.S., Marin G.B., Constales D. New Patterns in Steady-State Chemical Kinetics: Intersections, Coincidences, Map of Events (Two-Step Mechanism) // Entropy. 2015. V. 17. № 10. P. 6783.
Branco P.D., Yablonsky G.S., Marin G.B., Constales D. Gateway analysis for complex reaction mechanisms: Kinetic informative detachable (KID) sub-mechanisms // Chem. Eng. Sci. 2018. V. 178. P. 183.
Branco P.D., Yablonsky G.S., Marin G.B., Constales D. New invariances of chemical reactions from Scaled Incremental Conversion (SIC) // Chem. Eng. Sci. 2018. V. 184. P. 25.
Yablonsky G.S., Branco P.D., Marin G.B., Constales D. Conservatively perturbed equilibrium in chemical kinetics // Chem. Eng. Sci. 2019. V. 196. P. 384.
Peng B., Yablonsky G.S., Constales D., Marin G.B. Experimental confirmation of a new invariant for a non-linear chemical reaction // Chem. Eng. Sci. 2018. V. 191. P. 262.
Федотов В.Х., Кольцов Н.И. Метод определения квазиинвариантов в кинетике химических реакций // Изв. высш. учебн. завед. Хим. хим. технол. 2016. Т. 59. № 5. С. 72.
Федотов В.Х., Кольцов Н.И. Кинетические квазиинварианты химических реакций в открытых системах // Изв. высш. учебн. завед. Хим. хим. технол. 2019. Т. 62. № 8. С. 76.
Fedotov V.Kh., Kol’tsov N.I. Quasi-Invariants of Chemical Reactions with Nonideal Kinetics // Russ. J. Phys. Chem. В. 2019. V. 13. № 2. P. 262. [Федотов В.Х., Кольцов Н.И. Квазиинварианты химических реакций с неидеальной кинетикой // Хим. физ. 2019. Т. 38. № 4. С. 23.]

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал