Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 608-614
Расчет и свойства функции неоднородности при фазовом превращении многокомпонентных систем
М. А. Носырев a, *, Д. М. Попов a, Л. В. Равичев a, Р. Б. Комляшев a
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: vnissok@list.ru
Поступила в редакцию 23.03.2020
После доработки 08.04.2020
Принята к публикации 15.05.2020
Аннотация
Приводится вывод уравнения для расчета функции неоднородности в процессах равновесного фазового превращения жидкость–пар. В полученных уравнениях отсутствуют производные от коэффициентов активности по степени фазового превращения. Для расчетов используются данные о равновесных составах фаз и о теплоте фазового превращения. Исследовано изменение функции неоднородности в зависимости от относительной летучести и степени фазового превращения. На примере испарения реальной азеотропной смеси показано, что пренебрежение теплотами смешения в жидкой фазе приводит к незначительным погрешностям.
ВВЕДЕНИЕ
В настоящее время большое внимание уделяется расчетным методам определения парожидкостного равновесия [1–4]. В технике широко используются процессы превращения массы, основанные на ее качественных изменениях. Так, в ходе разнообразных химических превращений изменяется структура молекул. В результате фазового превращения изменяется агрегатное состояние. При коагуляции и диспергировании изменяются размеры частиц. Примеры подобного рода можно продолжить. В статье [5] приведен обобщенный количественный метод описания различных процессов превращения вещества, основанный на феноменологической общности этих процессов, вследствие чего любой процесс превращения может быть описан динамической системой уравнений
где ni – масса вещества, соответствующая данному признаку (например, структура атомов, молекул, размер частиц, агрегатное состояние). Параметр ξ есть отношение превращенной массы к максимально возможной превращенной массе и не зависит от индекса i. Выражение (1) определяет фазовую скорость изменения массы. Отношение этих изменений равно отношению соответствующих параметров νi, что позволяет считать их стехиометрическими коэффициентами и использовать уравнение (1) для их определения.Выражения (1) обычно использовали только для химических реакций (особенно в связи с методом де Донде [6, 7]. Указывалось также, что возможно использование их и для фазовых превращений [6]. Однако практические примеры ограничивались переходом одного компонента в бинарной системе.
В настоящей статье рассматриваются процессы фазового превращения жидкость–пар в многокомпонентных системах. Такие процессы широко применяются в химической технологии для разделения смесей методами перегонки или ректификации. Характерной особенностью этих процессов является то, что траектории их фигуральных точек располагаются на равновесных гиперповерхностях (или весьма близко к ним). Это позволяет использовать равновесную термодинамику для решения прикладных задач.
ФУНКЦИЯ НЕОДНОРОДНОСТИ ДЛЯ РЕАЛЬНЫХ СИСТЕМ
Рассмотрим процесс смещения равновесного состояния при внешнем тепловом воздействии на закрытую двухфазную многокомпонентную систему. Термодинамический анализ такого процесса выполнен в работе [8]. Установлено, что термодинамические свойства такой системы изменяются в ходе процесса в зависимости от функции неоднородности αТ,р, которая является безразмерной величиной и связана с функцией де Донде выражением
(2)
$\begin{gathered} {{\alpha }_{{T,p}}} = \frac{{{{a}_{{T,p}}}}}{{RT}} = \frac{1}{{RT}}{{\left( {\frac{{\partial A}}{{\partial \xi }}} \right)}_{{T,p}}} = \\ = \,\,\frac{1}{{RT}}\sum\limits_j {\sum\limits_i {{{\nu }_{j}}{{\nu }_{i}}{{{\left( {\frac{{\partial {{\mu }_{i}}}}{{\partial {{n}_{j}}}}} \right)}}_{{T,p}}}} } , \\ \end{gathered} $Способ расчета производной от сродства по степени превращения впервые дан де Донде [6]. В основе метода лежит дифференцирование известного выражения для химического потенциала и получение явных функций для смешанных частных производных (∂μi/∂nj)Т, р. В результате функция де Донде выражается суммой двух слагаемых: первое определяется составом и стехиометрическими коэффициентами в данной точке процесса и не включает никаких производных, а второе представляет собой сумму, включающую частные производные от коэффициентов активности компонентов в виде ∑νi(∂lnγi/∂ξ)T, p, расчет которых не приведен. Поэтому авторы [7] ограничивают этот метод только идеальными растворами.
В настоящей работе мы попытаемся устранить это ограничение и получить выражение для расчета функции неоднородности для любых реальных смесей. В основе предлагаемого метода лежит замена частных производных при постоянных р, Т частными производными при постоянных р, ξ. Такой прием позволяет выразить частные производные от коэффициентов активности через теплоты смешения и избежать вычисления производных (∂lnγi/∂ξ)T, p.
Для любой многокомпонентной системы, превращения в которой описывается одним стехиометрическим уравнением, изменения состояния описываются тремя переменными. Для технических целей это обычно давление, температура и степень фазового превращения. При равновесном превращении в изобарных условиях имеется взаимосвязь между частными производными:
(3)
${{\left( {\frac{{\partial A}}{{\partial \xi }}} \right)}_{{T,p}}} = - {{\left( {\frac{{\partial A}}{{\partial T}}} \right)}_{{\xi ,p}}}{{\left( {\frac{{\partial T}}{{\partial \xi }}} \right)}_{p}}.$Для индексации частных производных используется система обозначений, принятая в [7]. Используя известное выражение [7]
и учитывая уравнение (2), получим
(5)
${{\alpha }_{{T,p}}} = \frac{{{{h}_{{T,p}}}}}{R}{{\left( {\frac{{\partial \left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}} \right)}}{{\partial \xi }}} \right)}_{p}},$Выразим производную в правой части этого уравнения через составы фаз в данной точке процесса. Для этого найдем взаимосвязь ее с коэффициентом фазового распределения компонента Ki, равным отношению концентраций компонента в равновесных фазах. Если система состоит из действительных (по Гиббсу [10]) компонентов, то для каждого из них выполняется условие равенства химических потенциалов в фазах x и y, что приводит к соотношению
где $p_{i}^{0}$ – упругость паров чистого компонента i при температуре системы.Найдем частную производную (∂lnKi/∂ξ)p, используя известные соотношения [7]:
(7)
${{\left( {\frac{{\partial \ln A}}{{\partial T}}} \right)}_{p}} = \frac{{{{h}_{i}}_{{T,p}}}}{{R{{T}^{2}}}},$Умножая выражение (7) на стехиометрический коэффициент компонента νi и суммируя для всех компонентов смеси, получим
(9)
$\sum {{\nu }_{i}}{{\left( {\frac{{\partial \ln {{K}_{i}}}}{{\partial T}}} \right)}_{p}} = \sum \frac{{{{v}_{i}}{{h}_{{iT,p}}}}}{{R{{T}^{2}}}} = \frac{{{{h}_{{T,p}}}}}{{R{{T}^{2}}}}.$Сравнивая это выражение с уравнением (5), можно записать
(10)
${{\alpha }_{{T,p}}} = - \sum {{v}_{i}}{{\left( {\frac{{\partial \ln {{K}_{i}}}}{{\partial \xi }}} \right)}_{p}}.$Производная по степени фазового превращения определяется с помощью уравнений материального баланса для превращения в закрытой системе, которые выведены в [9]:
(11)
$\frac{{d{{x}_{i}}}}{{d\xi }} = - \frac{{{{v}_{i}} - {{x}_{i}}}}{{{\text{1}} - {{\varphi }_{y}}}},\,\,\,\,\frac{{d{{y}_{i}}}}{{d\xi }} = - \frac{{{{v}_{i}} - {{y}_{i}}}}{{{\text{1}} - {{\varphi }_{y}}}},$(12)
$\begin{gathered} {{\left( {\frac{{d\ln {{K}_{i}}}}{{d\xi }}} \right)}_{p}} = \frac{{d{{y}_{i}}}}{{{{y}_{i}}d\xi }} - \frac{{d{{x}_{i}}}}{{{{x}_{i}}d\xi }} = \frac{{\left( {{{\nu }_{i}} - {{y}_{i}}} \right)}}{{{{y}_{i}}{{\varphi }_{y}}}} + \\ + \,\,\frac{{\left( {{{\nu }_{i}} - {{x}_{i}}} \right)}}{{{{x}_{i}}{{\varphi }_{x}}}} = \frac{1}{{{{\varphi }_{x}}{{\varphi }_{y}}}}\left( {\frac{{{{\nu }_{i}}{{z}_{i}}}}{{{{x}_{i}}{{y}_{i}}}} - 1} \right). \\ \end{gathered} $В уравнении (12) величина zi = φxxi + φyyi представляет собой брутто-концентрацию компонента i в двухфазной системе. В закрытой системе в любой точке процесса эта величина остается постоянной.
Подставляя (12) в уравнение (10), получим выражение для расчета функции неоднородности при равновесном фазовом превращении многокомпонентной смеси в изобарных условиях:
(13)
${{\alpha }_{{T,p}}} = \frac{{\text{1}}}{{{{\varphi }_{x}}{{\varphi }_{y}}}}\left( {\sum {\frac{{v_{i}^{2}{{z}_{i}}}}{{{{x}_{i}}{{y}_{i}}}}} - {\text{1}}} \right).$Стехиометрический коэффициент для процесса фазового превращения в соответствии с [9] можно представить в виде
(14)
${{\nu }_{i}} = \frac{{{{\Phi }_{i}}\left( {1 - {{\beta }_{i}}} \right)}}{{\sum {{\Phi }_{j}}\left( {1 - {{\beta }_{j}}} \right)}},$Если коэффициенты распределения компонентов смеси в ходе процесса изменяются одинаково (например, имеют одинаковые теплоты фазового превращения в идеальной смеси), то значения βi одинаковы и уравнение (14) упрощается и принимает следующий вид:
Это уравнение с определенной точностью может быть использовано и для различающихся значений βi. Возникающая при этом погрешность δi определяется соотношением
Для оценки величины погрешности определим порядок значений величины. Произведение φxφy максимально может иметь значение 0.25 в точке φx = φy = 0,5 и приближается к нулю в точках исчезновения одной из фаз. Производная (dlnKi/dξ)p приближенно определяется соотношением коэффициентов распределения в конце (ξ = 1) и начале (ξ = 0) процесса в виде ln(Ki1/Ki0). В свою очередь, это выражение по известному уравнению можно записать в виде
Для большинства органических соединений мольные теплоты испарения близки между собой и имеют порядок 104 Дж/моль. Разность температур насыщения жидкости и пара одинакового состава максимальна в области средних концентраций и уменьшается до нуля для фаз одинакового состава (чистые компоненты и азеотропы). Для систем даже с большей относительной летучестью максимальная разность обратных температур не превышает 10–4 К–1. Поэтому величина βi имеет порядок 10–1–10–2. Разность величин βi – βj определяется различиями в теплотах испарения компонентов i и j. Обычно эти различия на порядок меньше самих теплот испарения. Поэтому можно считать, что βi – βj имеет порядок 10–2–10–3. Используя полученные оценки, определим максимальную погрешность от замены уравнения (14) на уравнение (15) как величину не более 10–2, т.е. несколько процентов.
В качестве примера приведем результаты расчета стехиометрического коэффициента для метанола в его смеси с н-амиловым спиртом. Система характеризуется высокой относительной летучестью компонентов, равной 16. Равновесные концентрации метанола в фазах х = 0.34, y = 0.89. Брутто-концентрация метанола принята равной z = 0.5. Для этих условий расчет νi по уравнению (14) дал величину 0.795, а по уравнению (15) – величину 0.806. Различие составляет 1.4%. Очевидно, что с уменьшением относительной летучести различие в результатах расчета будет еще меньше.
При подстановке уравнения (15) в уравнение (13) получим приближенное уравнение для расчета функции неоднородности:
(16)
${{\alpha }_{{T,p}}} = \frac{1}{{{{\varphi }_{x}}{{\varphi }_{y}}}}\left( {\frac{1}{{\sum {{\Phi }_{i}}}} - 1} \right).$Для фаз одинакового состава все концентрации компонента одинаковы xi = yi = zi, при этом ∑Фi = 1 и функция неоднородности равна нулю. В общем случае эти концентрации не равны между собой, сумма ∑Фi < 1 и функция неоднородности, оставаясь в отрицательной области, по абсолютной величине становится отличной от нуля, причем это отличие тем больше, чем большие различия в составах контактирующих фаз. В табл. 1 приведены абсолютные значения функции неоднородности для различных бинарных систем.
Таблица 1.
Влияние относительной летучести на величину функции неоднородности
| № | Система | х | у | Относительная летучесть | Функция неоднородности (абсолютные значения) |
|---|---|---|---|---|---|
| 1 | Гептан–метилциклогексан | 0.495 | 0.505 | 1.04 | 4 × 10–4 |
| 2 | Пропанол– н-амиловый спирт |
0.33 | 0.67 | 5.9 | 0.536 |
| 3 | Метанол– н-амиловый спирт |
0.20 | 0.80 | 16.0 | 2.25 |
| 4 | Бензол–дифенил | 0.09 | 0.91 | 102.0 | 8.21 |
Расчет проведен для условий φx = φy = 0.5 и z1 = z2= 0.5. Здесь и далее равновесные данные взяты из справочника [11]. Для системы гептан–метилциклогексан линии жидкости и пара настолько близки, что составы фаз практически одинаковы во всей области концентраций. Функция неоднородности по абсолютной величине мало отличается от нуля. По мере увеличения относительной летучести и связанного с этим увеличения различий в составах фаз функция неоднородности быстро возрастает по абсолютной величине. В пределе функция неоднородности может иметь бесконечно большую отрицательную величину. Согласно уравнению (16) это соответствует условию ∑Фi = 0. При этом двухфазная система состоит из взаимно нераспределяющихся компонентов, так что каждый из них присутствует лишь в одной фазе.
В точках исчезновения одной из фаз расчет по уравнению (16) приводит к неопределенности, которую раскроем следующим образом. Пусть фаза y находится в дифференциально малом количестве, т.е. φy → 0. При этом очевидно, что доля жидкой фазы стремится к единице, т.е. φx → 1, состав жидкой фазы близок к брутто-составу xi → zi, а стехиометрический коэффициент согласно уравнению (15) близок к равновесному составу паровой фазы νi → yi. Из уравнений (10) и (12) следует, что в этом случае
(17)
${{\alpha }_{{T,p}}} = - \sum {{{\nu }_{i}}\left( {\frac{1}{{{{y}_{i}}}}\frac{{d{{y}_{i}}}}{{d\xi }} - \frac{1}{{{{x}_{i}}}}\frac{{d{{x}_{i}}}}{{d{{y}_{i}}}}} \right) = \sum {{{K}_{i}}_{x}\frac{{d{{x}_{i}}}}{{d\xi }}} } .$Из соответствующего уравнения изменения концентраций (11) найдем, что
Подставляя это выражение в (17), получим
где нижний индекс x означает, что функция неоднородности относится к состоянию начала кипения исходной жидкости состава xi = yi. Аналогично можно получить второе предельное выражение функции неоднородности для случая, когда фаза x находится в очень малом количестве φx → 0. При этом выполняется условие φy → 1, yi → zi, νi → xi и уравнение имеет следующий вид:где нижний индекс y относится к состоянию начала конденсации пара состава yi = zi. Очевидно, что уравнение (19) можно отнести также и к точке конца конденсации пара исходного состава zi. Коэффициенты распределения Kix и Kiy относятся к температурам и составам в этих предельных точках.
Для бинарных систем уравнение (19) может быть преобразовано следующим образом:
(21)
${{\alpha }_{{T,p,}}}_{x} = \frac{{{{{\left[ {{{y}_{i}}({{z}_{i}}) - {{z}_{i}}} \right]}}^{2}}}}{{{{z}_{i}}\left( {1 - {{z}_{i}}} \right)}}.$Аналогично преобразуется уравнение (20):
(22)
${{\alpha }_{{T,p,}}}_{y} = \frac{{{{{\left[ {{{z}_{i}} - {{x}_{i}}({{z}_{i}})} \right]}}^{2}}}}{{{{z}_{i}}\left( {1 - {{z}_{i}}} \right)}}.$Уравнения (21) и (22) относятся к состояниям, соответствующим точкам пересечения вертикали z = const с равновесными линиями жидкости и пара на диаграмме T–x, y. В области, промежуточной между этими двумя точками, функция неоднородности рассчитывается по уравнению (16). На рис. 1 представлены результаты расчета функции неоднородности для смеси пропанол–н-амиловый спирт в виде зависимости абсолютных значений αT,p от степени испарения φy. Каждая кривая соответствует принятому брутто-составу.
Рис. 1.
Зависимость функции неоднородности от степени превращения смеси пропанол–н-амиловый спирт для различных брутто-составов.
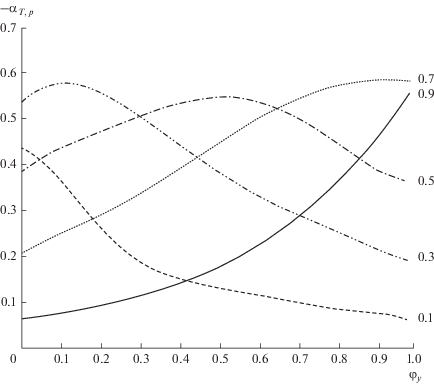
В начале процесса (φy = 0) значение αT,p определяется уравнением (21), а в конце процесса (φy = 1) – уравнением (22). Видно, что в ходе процесса функция неоднородности изменяется существенно нелинейным образом. Обычно на этой зависимости наблюдается максимум абсолютной величины (соответственно, минимум в отрицательной области определения αT,p), соответствующий условиям максимального различия в составах контактирующих фаз.
Величина функции неоднородности αT,p позволяет прогнозировать ход изменения температуры в процессе превращения. Для этого следует уравнение (5) записать в интегральном виде:
(23)
$\frac{1}{T} = \frac{1}{{{{T}_{0}}}} + \int\limits_0^\xi {\frac{R}{{{{h}_{{T,p}}}}}{\kern 1pt} } {{\alpha }_{{T,p}}}d\xi .$Пределы интегрирования определяются условиями задачи. Так, если известна температура начала кипения смеси заданного состава T0 = Tx, то по уравнению (23) можно определить температуру при любой промежуточной степени испарения ξ, которая совпадает с долей вновь образованной фазы, т.е. ξ = φy. Алгоритм расчета базируется на уравнениях (16), (15) и (11). В качестве исходной информации используются экспериментальные данные по составу равновесных фаз при постоянном давлении, а также данные по теплотам испарения и теплотам смешения. При отсутствии экспериментальных данных о равновесных составах фаз следует использовать расчетные методы, изложенные, например, в [12] или [13].
При расчете по уравнению (23) следует учитывать, что тепловой эффект превращения смеси определяется уравнением
(24)
${{h}_{{T,p}}} = \sum {{v}_{i}}{{h}_{i}}_{{T,p}}^{\theta } + \sum {{v}_{i}}{{h}_{i}}_{x}^{M} - \sum {{v}_{i}}{{h}_{i}}_{y}^{M}$и изменяется в ходе процесса. В расчетной практике это выражение можно упростить. Известно, что эффекты смешения в паровой фазе пренебрежимо малы. Теплоты смешения в жидкой фазе обобщены и представлены в [14]. Из этих данных следует, что максимально теплоты смешения составляют величину не более 400 кал/моль, в исключительных случаях доходящую до 800 кал/моль. Поэтому применительно к фазовым превращениям жидкость–пар пренебрежение тепловым эффектом смешения в жидкой фазе приведет к ошибке не более чем 3–5%.
Для иллюстрации вышеизложенного был выполнен расчет изменения температуры при испарении реальной смеси метилэтилкетон–циклогексан. Смесь имеет ярко выраженный минимальный азеотроп в точке x = 0.48. Теплота смешения в жидкой фазе достигает 300 кал/моль, теплоты испарения индивидуальных компонентов равны соответственно 7240 и 7420 кал/моль. Результаты расчета представлены на рис. 2. Сплошные линии показывают зависимость температуры от степени испарения и построены следующим образом. Для каждой равновесной ноды, определяющей набор равновесных значений x, y и T, с учетом принятого брутто-состава z определялась соответствующая степень испарения:
Рис. 2.
Изменение температуры при испарении смеси метилэтилкетон–циклогексан для различных брутто-составов. Точки – расчет по уравнению (26).
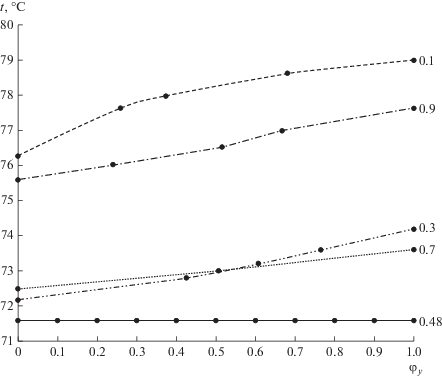
Видно, что линии изменения температуры в зависимости от степени испарения имеют различный характер, обусловленный структурой диаграммы равновесия. Так, линия для z = 0.9 имеет точку перегиба, линии z = 0.3 и z = 0.7 монотонны и достаточно близки между собой. Линия для z = 0.48 соответствует азеотропному составу и является горизонтальной, что указывает на отсутствие изменения температуры в этом случае. Отметим, что такое построение линий T = f(φy) возможно лишь для бинарных смесей, поскольку при постоянном давлении равновесные кривые единственны. Для многокомпонентных систем необходимо определять траекторию изменения состава путем интегрирования уравнений (11).
Точками на рис. 2 показаны результаты расчета по уравнению (26), записанному в предположении постоянства теплоты испарения на участке интегрирования:
(26)
$\frac{1}{T} = \frac{1}{{{{T}_{x}}}} + \frac{R}{{{{h}_{{T,p}}}}}\int\limits_0^{{{\varphi }_{y}}} {\kern 1pt} {{\alpha }_{{T,p}}}d{{\varphi }_{y}}.$При расчетах по этому уравнению температура Tx определялась по равновесным данным для выбранного z. Тепловой эффект процесса hT,p рассчитывался по теплотам испарения чистых компонентов без учета эффектов смешения по уравнению (24). Функция неоднородности определялась по уравнению (16). Видно, что результаты практически совпадают.
Из этого следует, что предложенный в данной работе метод расчета функции неоднородности совместим с данными по фазовому равновесию и является термодинамически корректным. Этот метод применим не только к идеальным, но и к реальным системам. Поэтому указанное в начале данной статьи ограничение на использование функции де Донде можно считать преодоленным.
Расчет функции неоднородности по предложенному методу может быть использован не только для определения хода изменения температуры, но и для расчета конфигуративной теплоемкости двухфазных систем по методу [8], а также при решении вопросов модерации и устойчивости двухфазных систем [7].
ЗАКЛЮЧЕНИЕ
Разработан метод и получена формула для расчета функции неоднородности при фазовых превращениях жидкость–пар в многокомпонентных системах. Изучены основные свойства этой функции и показано, что она является обобщенной характеристикой степени различия составов равновесных фаз. Метод с точностью не хуже чем 3–5% может быть применен для реальных систем.
ОБОЗНАЧЕНИЯ
| А | сродство |
| hT,p | тепловой эффект фазового превращения |
| Ki | коэффициент распределения |
| nj | масса компонента j |
| р | давление |
| $p_{i}^{0}$ | упругость паров чистого компонента |
| R | газовая постоянная |
| Т | температура |
| хi, уi | мольная доля компонента i |
| αT,p | функция неоднородности |
| μi | химический потенциал компонента i |
| νi | стехиометрический коэффициент фазового превращения |
| ξ | степень превращения |
| φх, φу | доля жидкой и паровой фазы в общей массе двухфазной системы |
ИНДЕКСЫ
Список литературы
Desideri A., Gusev S., van den Broek M., Lemort V., Quoilin S. Experimental comparison of organic fluids for low temperature ORC (organic Rankine cycle) systems for waste heat recovery applications // Energy. 2016. V. 97. P. 460.
Wang J., Zhao L., Wang X. An experimental study on the recuperative low temperature solar Rankine cycle using R245fa // Appl. Energy. 2012. V. 94. P. 34.
Mavrou P., Papadopoulos A.I., Seferlis P., Linke P., Voutetakis S. Selection of working fluid mixtures for flexible Organic Rankine Cycles under operating variability through a systematic nonlinear sensitivity analysis approach // Appl. Therm. Eng. 2015. V. 89. P. 1054.
Abudour A.M., Mohammad S.A., Robinson R.L.Jr., Gasem K.A.M. Generalized binary interaction parameters for the Peng–Robinson equation of state // Fluid Phase Equilib. 2014. V. 383. P. 156.
Попов Д.М. Изменение массы и состава вещества в процессах превращения // Журн. физ. хим. 1992. Т. 65. № 10. С. 2221.
Де Донде Т., Ван Риссельберг П. Термодинамическая теория сродства. Книга принципов. М.: Металлургия, 1984.
Пригожин И., Дефэй Р. Химическая термодинамика. Новосибирск: Наука, 1968.
Попов Д.М. Изменение температуры и теплоемкости двухфазной многокомпонентной системы в процессах фазового превращения жидкость–пар // Журн. физ. хим. 1998. Т. 72. № 10. С. 1776.
Попов Д.М. Расчет изменения состава фаз при дистилляции (конденсации) многокомпонентных систем // Теор. осн. хим. технол. 1989. Т. 23. № 2. С. 171.
Гиббс Д.В. Термодинамика. М.: Наука, 1982.
Коган В.В., Фридман В.М., Кафаров В.В. Равновесие между жидкостью и паром. Справочное пособие. Кн. 1, 2. М.: Наука, 1966.
Морачевский А.Г. Термодинамика равновесия жидкость–пар. Л.: Химия, 1989.
Уэйлес С. Фазовые равновесия в химической технологии. Т. 2. М.: Мир, 1989.
Белоусов В.П., Морачевский А.Г. Теплоты смешения жидкостей. Л.: Химия, 1970.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


