Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 615-622
Реакторная динамика процесса суспензионной полимеризации стирола
Д. П. Вент a, А. Г. Лопатин a, *, Б. А. Брыков a, В. П. Савельянов a
a Новомосковский институт Российского химико-технологического университета им. Д.И. Менделеева
Новомосковск, Россия
* E-mail: a_lopatin@mail.ru
Поступила в редакцию 27.11.2019
После доработки 14.04.2020
Принята к публикации 15.05.2020
Аннотация
На специально созданной установке, управляемой персональным компьютером, изучена реакторная динамика суспензионной полимеризации стирола. Установлено, что изменения в ходе процесса управляющих воздействий (мер мощности нагрева и мощности на валу мешалки) закономерно отражают изменения физического (релаксационного) состояния полимерно-мономерных частиц. Предложено использовать это явление для управления процессом.
ВВЕДЕНИЕ
Суспензионная полимеризация стирола является примером сложного нелинейного динамического процесса. Отличительной особенностью его является то, что полимер растворим в своем мономере, что приводит к сильному изменению не только эффективной вязкости полимерно-мономерных частиц (ПМЧ), но также и самого механизма подвижности макромолекул в них. Результатом является диффузионное торможение всех элементарных стадий самой реакции полимеризации. Может быть, поэтому этот процесс интенсивно изучался на всех иерархических уровнях его математического описания по [1].
На атомно-молекулярном уровне четко описана его термодинамика. Сложнее обстоит дело с описанием его кинетики [2, 3]. Обычная кинетическая схема радикальной полимеризации с квадратичным обрывом цепи путем рекомбинации осложняется заметным диффузионным торможением всех элементарных стадий реакции [4].
На стадии инициирования вследствие увеличения вязкости ПМЧ только примерно половина инициатора расходуется на зарождение цепей из-за так называемого эффекта клетки (cage effect). На стадии роста цепи, начиная с некоторой конверсии, наблюдается ускорение реакции вследствие диффузионного торможения реакции обрыва цепи (так называемый гель-эффект). Наконец, на стадии завершения процесса происходит стеклование ПМЧ (glass effect) [5] и остановка реакции до достижения 100% конверсии мономера в полимер вследствие “замуровывания” активных центров в жесткой матрице твердого полимера. Это создает затруднения в экспериментальном определении конверсии мономера в полимер [2, 3, 6]. Следствием является одновременное существование множества кинетических моделей этого процесса с существенно различающимися константами скоростей элементарных стадий реакции и большим числом эмпирических параметров [2, 3, 7].
Несколько лучше дело обстоит с описанием на втором уровне – уровне частицы в окружающей ее среде. Из-за сильного нарастания вязкости в принципе возможно затруднение отвода тепла реакции из ПМЧ и неконтролируемое повышение температуры в них. Однако, по данным [8], такой “тепловой взрыв” в данном случае не наблюдается.
Не вызывает затруднений и описание этого процесса на следующем, третьем уровне. Реакционная смесь представляет собой совокупность ПМЧ, являющихся практически периодическими микрореакторами, в которых и происходит реакция полимеризации. Реакционная смесь в них является раствором инициатора в растворе полимера в мономере вплоть до завершения реакции. Для ее протекания не требуется перенос массы, энергии и импульса через границу раздела фаз.
Наибольшие затруднения возникают при описании следующего, четвертого иерархического уровня – уровня совокупности (ансамбля) ПМЧ. Здесь прежде всего надо отметить явную ее стадийность, отмечаемую рядом исследователей [1, 9].
ПМЧ под действием напряжений сдвига, создаваемых лопастями мешалки, могут распадаться на более мелкие частицы, которые в свою очередь способны сливаться. Примерно до 40% конверсии наблюдается равновесие этих процессов диспергирования и коалесценции. Однако при ее увеличении диспергирование ПМЧ высокой и неньютоновской вязкости постепенно отключается, и процесс входит в так называемую липкую стадию [1], в которой интенсивно увеличивается средний диаметр ПМЧ за счет нарастающего превалирования коалесценции над диспергированием. Более того, обнаружено [10], что на этой стадии происходит не только слияние ПМЧ, но и их слипание без слияния в одну каплю. Это приводит к изменениям внутренней структуры ПМЧ: они представляют собой уже не “плотные” частицы, а частицы фрактальной структуры. Естественно, это оказывает существенное влияние на распределение частиц по размерам и, по-видимому, затрудняет его прогнозирование и расчет – например, методами популяционного баланса [11].
В этот же период возникает возможность выхода процесса из-под контроля. Если скорость слияния (слипания) ПМЧ превосходит скорость их “твердения” вследствие реакции полимеризации, то возможно их слияние в одну большую “каплю” полимера. Это неприятное явление наблюдалось даже в промышленных условиях. Устойчивость процесса, естественно, определяется начальными условиями его проведения: температурой синтеза, количеством инициатора и концентрацией стабилизатора. Наблюдения показали [12], что динамическая устойчивость обеспечивается главным образом достаточной концентрацией стабилизатора. Интенсивная турбулизация реакционной смеси явно дестабилизирует процесс.
Наконец, на пятом иерархическом уровне определяются конструктивные особенности реактора, обеспечивающие поддержание в нем определенной тепловой и гидродинамической обстановки с учетом их влияния на качество получаемой продукции: тип и конструкция мешалки и теплообменных поверхностей и т.п. Технологически наиболее важным является поддержание в реакторе устойчивой суспензии ПМЧ. Такая суспензия термодинамически неустойчива и ее метастабильность обеспечивается регулируемым перемешиванием [13, 14] и введением так называемых стабилизаторов – веществ, препятствующих слиянию и слипанию ПМЧ. С точки зрения конструкции реактора важным оказывается тип и расположение в реакторе мешалки. Перемешивание определяет и качество получаемого продукта, гранулометрический состав полимерного бисера. Существует обширная литература по этому вопросу [1, 15, 16].
Определенный интерес, с нашей точки зрения, представляет и рассмотрение реактора как объекта в окружающей его среде. Речь идет как о состоянии самого реактора (его реакционной среды), так и об управляющих воздействиях, обеспечивающих необходимые условия в нем в их взаимосвязи и взаимозависимости. Настоящая работа и относится к относительно слабо изученной динамике этих связей.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Опыты проводились на специально разработанной для этих целей установке, управляемой персональным компьютером, на базе стандартного металлического реактора объемом 350 мл [2, 3].
Перемешивание реакционной смеси осуществлялось двухлопастной мешалкой, число ее оборотов поддерживалось постоянным с помощью частотно-регулируемого привода электродвигателя. Обогрев реактора осуществлялся через его стенку нагревательной спиралью из нихрома. Заданная температура поддерживалась с помощью программируемого логического контроллера ПЛК 150 фирмы OWEN. Особенностью установки было то, что измерялись и регистрировались не только текущие значения управляемых параметров внутри реактора (температура и число оборотов мешалки), но также и величины, которые их обеспечивали (частота, подаваемая с частотно-регулируемого привода, и напряжение, подаваемое на нагреватель). Все эти данные записывались в память компьютера с интервалом в 1 с для дальнейшей обработки.
Методика проведения опытов была следующей [23]. В реактор загружались рецептурные количества дистиллированной воды (130 мл), стирола (75 мл) и раствора стабилизатора (поливиниловый спирт, 24 мл). Суммарно объем реакционной массы составлял 230 мл. Температурный режим процесса 75°С.
С помощью системы управления реактор выводился на заданную температуру. После выхода реактора на температурный стационар в реактор вводился инициатор – пероксид бензоила (1.12 г) в виде его раствора в мономере.
Момент ввода инициатора принимался за начало процесса, хотя температура в реакторе несколько падала с последующим выходом обратно на уставку. Дальнейший ход процесса полностью контролировался системой управления, причем за ходом снимаемых кривых можно было следить по графикам на экране монитора. Записанные в память компьютера данные обрабатывались с помощью известных методов. Предварительными опытами было установлено, что форма кривых не зависела от соотношений мономер–вода, мономер–стабилизатор, концентрации инициатора и температуры.
Получаемый в результате проведения полимеризации на лабораторном реакторе полистирол имеет набор физико-химических свойств, полностью соответствующий свойствам суспензионного полистирола, получаемого на АО “Пластик” [24].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
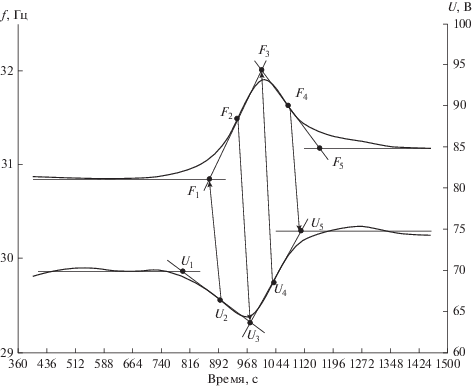
На рис. 1 представлены типичные кривые изменения во времени регистрируемых мер мощностей, затрачиваемых на поддержание в реакторе неизменными температуры реакционной смеси и числа оборотов мешалки и их сглаживание. В качестве таких мер использовались величины напряжения U, подаваемого на нагревательную спираль реактора, и частоты f, подаваемой с частотно-регулируемого привода на электропривод мешалки. Хорошо видно, что соответствующие кривые в определенный период процесса обнаруживают согласованные изменения: наблюдается уменьшение потребления энергии на нагрев и увеличение – на перемешивание. Эти изменения закономерно связаны с начальными условиями процесса [17].
На этом же рисунке представлены и наблюдающиеся связи между характеристическими точками разных кривых, обозначенных нижними индексами. Выделенные ими области, по-видимому, характеризуют изменение физического состояния ПМЧ. Хорошо также видно некоторое отставание кривой напряжения U от кривой частоты f, которое логично объясняется тепловой инерционностью системы обогрева реактора с помощью нагревательной спирали через стенку реактора. Как было замечено нами, это временное отставание примерно совпадает с длиной волны регулирования температуры.
То, что мы имеем дело именно с изменениями физического (релаксационного) состояния ПМЧ, видно из анализа изменений во времени вязкости растворов полистирола в стироле при температуре синтеза. Она рассчитывалась по формуле Спенсера и Уильямса [17]. Единственной особенностью кривой зависимости вязкости этих растворов от степени превращения является четко выраженный перегиб при примерно 10% концентрации полистирола в стироле, который, по-видимому, имеет место при образовании системы динамических зацеплений макромолекул. При более высоких концентрациях наблюдается гладкая кривая, максимальный и минимальный угловые коэффициенты которой позволяют выделить еще одну точку при примерно 45% концентрации полистирола в стироле. Эта концентрация, вероятно, соответствует отключению диспергирования ПМЧ, что и наблюдалось нами [11].
Таким образом, изменение вязкости собственно ПМЧ не объясняет происхождения обнаруженных нами изменений динамических переменных. Согласованное поведение напряжения U и частоты f является свидетельством характерных изменений свойств реакционной среды, которая представляет собой суспензию ПМЧ в водной фазе. Эта фаза является раствором стабилизатора в воде, и, очевидно, не изменяется в ходе процесса. Поэтому наблюдаемые изменения можно отнести к изменениям самих ПМЧ.
С этой точки зрения особый интерес вызывает кривая U, отражающая изменение во времени потребности в нагреве реакционной смеси. Заметим, что, в отличие от промышленных реакторов, в данном случае требуется нагрев реакционной смеси из-за больших потерь тепла через неизолированные поверхности реактора.
Дифференциальный тепловой баланс реактора [18] в условиях теплового и механического стационара с учетом кинетической модели [25] процесса суспензионной полимеризации стирола имеет следующий вид (температура реакционной смеси и число оборотов мешалки поддерживаются постоянными):
(1)
$\left\{ \begin{gathered} {{V}_{p}}{{\rho }_{x}}{{c}_{{{{p}_{x}}}}}\frac{{d{{T}_{x}}}}{{dt}} = {{G}_{x}}{{c}_{p}}_{x}\left( {{{T}_{{{{x}_{0}}}}} - {{Т}_{х}}} \right) + {{\alpha }_{x}}{{S}_{{{\text{внеш}}}}}({{Т}_{{{\text{ст}}}}} - {{Т}_{х}}), \hfill \\ {{m}_{{{\text{ст}}}}}{{с}_{р}}_{{{\text{ст}}}}\frac{{d{{Т}_{{{\text{ст}}}}}}}{{dt}} = {{\alpha }_{{{\text{ст}}}}}{{S}_{{{\text{внутр}}}}}({{Т}_{{{\text{р}}{\text{.с}}{\text{.}}}}} - {{Т}_{{{\text{ст}}}}}) - \hfill \\ - \,\,{{\alpha }_{x}}{{S}_{{{\text{внеш}}}}}({{Т}_{{{\text{ст}}}}} - {{Т}_{х}}), \hfill \\ {{V}_{{{\text{p}}{\text{.с}}{\text{.}}}}}{{\rho }_{{{\text{р}}{\text{.с}}{\text{.}}}}}{{c}_{{{{p}_{{{\text{р}}{\text{.с}}{\text{.}}}}}}}}\frac{{d{{T}_{{{\text{р}}{\text{.с}}{\text{.}}}}}}}{{dt}} = ( - \Delta Н){{k}_{p}}{{\lambda }_{0}}M{{V}_{{{\text{стирол}}}}} - \hfill \\ - \,\,{{K}_{P}}{{\rho }_{{{\text{p}}{\text{.c}}{\text{.}}}}}{{N}^{3}}d_{{\text{м}}}^{5} - {{\alpha }_{{{\text{ст}}}}}{{S}_{{{\text{внутр}}}}}({{Т}_{{{\text{р}}{\text{.с}}{\text{.}}}}} - {{Т}_{{{\text{ст}}}}}), \hfill \\ \frac{{d{{x}_{m}}}}{{dt}} = \frac{{{{k}_{{p0}}}\varphi ({{x}_{m}})}}{{\varphi ({{x}_{m}}) + {{\theta }_{p}}{{\lambda }_{0}}{{k}_{{p0}}}}}{{\lambda }_{0}}\left( {1 - {{x}_{m}}} \right), \hfill \\ \frac{{d{{x}_{I}}}}{{dt}} = \left( {{{k}_{d}} + \varepsilon \frac{{{{k}_{{p0}}}\varphi ({{x}_{m}})}}{{\varphi ({{x}_{m}}) + {{\theta }_{p}}{{\lambda }_{0}}{{k}_{{p0}}}}}\frac{{1 - {{x}_{m}}}}{{1 + \varepsilon {{x}_{m}}}}{{\lambda }_{0}}} \right)\left( {1 - {{x}_{I}}} \right), \hfill \\ \frac{{d{{\lambda }_{0}}}}{{dt}} = 2f{{k}_{d}}\left( {1 - {{x}_{I}}} \right){{I}_{0}} - \hfill \\ - \,\,\left( {\frac{{{{k}_{{tc0}}}\varphi ({{x}_{m}})}}{{\varphi ({{x}_{m}}) + {{\theta }_{{tc}}}{{\lambda }_{0}}{{k}_{{tc0}}}}} + \varepsilon \frac{{{{k}_{{p0}}}\varphi ({{x}_{m}})}}{{\varphi ({{x}_{m}}) + {{\theta }_{p}}{{\lambda }_{0}}{{k}_{{p0}}}}}\frac{{1 - {{x}_{m}}}}{{1 + \varepsilon {{x}_{m}}}}} \right)\lambda _{0}^{2}. \hfill \\ \end{gathered} \right.$Начальные условия интегрирования уравнений модели (1): температура процесса 75°С, начальная концентрация инициатора 61.65 моль/м3. Численные значения констант модели приведены в [25].
Потери тепла в окружающую среду различны для изолированной (стенки и днище реактора) и неизолированной поверхностей (крышка). Потери от последней можно считать постоянными, поскольку температура крышки реактора равна температуре в реакторе, которая поддерживается постоянной. Потери через изолированную поверхность в принципе переменны и связаны с величиной напряжения U, подаваемого на нагреватель реактора. Интервал его изменения, однако, составляет величину порядка 14%. Это позволяет в первом приближении считать потери величиной постоянной.
Наибольшую сложность представляет оценка роли диссипации механической энергии мешалки в тепловую. Величина энергии диссипации для несжимаемой жидкости может быть оценена по соотношению [19]
(2)
${{\dot {E}}_{{{\text{кин}}}}} = - \frac{\eta }{2}\int\limits_V {{{{\left( {\frac{{\partial {{v}_{i}}}}{{\partial {{x}_{k}}}} + \frac{{\partial {{v}_{k}}}}{{\partial {{x}_{i}}}}} \right)}}^{2}}dV} .$Выражение (2) с помощью анализа размерностей приводится к виду
(3)
${{\dot {E}}_{{{\text{кин}}}}} = - \frac{\eta }{2}\dot {V}f\,\,\,\,{\text{или}}\,\,\,\,{{\dot {E}}_{{{\text{кин}}}}} = - \frac{\eta }{2}V\dot {f}.$Верхней точкой обозначены производные по времени.
В нашем случае f величина постоянная. С учетом этого применимо только первое из выражений (3).
Изменение объема реакционной смеси во времени обусловлено только уменьшением объема дисперсной фазы из-за различия плотностей полистирола и стирола и в приближении аддитивности выражается известным соотношением
Поскольку объем дисперсионной среды (воды) величина постоянная, изменение общего объема реакционной смеси в реакторе есть
т.е. оно полностью определяется кинетикой реакции полимеризации.
Отсюда для оценки вклада кинетической энергии диссипации получаем
(6)
${{\dot {E}}_{{{\text{кин}}}}} = - \frac{{\eta {{V}_{0}}\varepsilon f}}{2}\frac{{d{{x}_{M}}}}{{d\iota }}.$Однако вязкость η в этой формуле относится к реакционной смеси в целом, т.е. к дисперсии ПМЧ в воде. Ее оценка также возможна.
Для дисперсий жидкость–жидкость в [20] предложена формула, учитывающая сфероидальные колебания капель при сдвиговых колебаниях среды, создаваемых у нас лопастями вращающейся мешалки:
(7)
$\frac{{\eta {\text{*}}}}{{{{\eta }_{2}}}} = 1 + \frac{5}{2}\varphi \left[ {\frac{{{{\eta }_{1}} + {{{{\eta }_{2}}} \mathord{\left/ {\vphantom {{{{\eta }_{2}}} 5}} \right. \kern-0em} 5}}}{{{{\eta }_{1}} + {{\eta }_{2}}}} + \frac{{a{{\eta }_{1}}}}{{3({{\delta }_{1}}{{\eta }_{2}} + {{\delta }_{2}}{{\eta }_{1}})}}} \right].$Разумно предполагается, что толщина пограничного слоя с обеих сторон поверхности раздела фаз значительно меньше радиуса капли.
Величину δ2 – толщину вязкого слоя со стороны дисперсионной среды в этом уравнении можно считать неизменной во времени, поскольку окружная скорость лопастей мешалки поддерживается постоянной, а постоянная температура обеспечивает неизменность свойств водной фазы. Вязкость сплошной (водной) фазы η2, которая определяется концентрацией стабилизатора (ПВС), также можно считать величиной постоянной. Тогда эффективная вязкость дисперсии в целом будет определяться только вязкостью ПМЧ η1. Имеющиеся в литературе [1] оценки свидетельствуют о том, что в самый важный период процесса – вход в липкую стадию – раствор полимера в мономере находится в состоянии, переходном от вязкотекучей к вязкоупругой жидкости. По данным [1], эта стадия начинается при примерно 65% превращении мономера в полимер и заканчивается при 80%, что хорошо соответствует нашим данным. Значения вязкости растворов полистирола в стироле имеют величину порядка сотен–тысяч Па с, т.е. на 5–6 порядков превышают значения вязкости непрерывной фазы. Поэтому представляется вполне приемлемым предположение η1 $ \gg $ η2. Тогда уравнение (7) переходит в известную формулу Эйнштейна для суспензии твердых частиц:
(8)
$\frac{{\eta {\text{*}}}}{{{{\eta }_{2}}}} = 1 + \frac{5}{2}\varphi \left( {1 + \frac{a}{{3{{\delta }_{2}}}}} \right).$Объемная доля органической массы в реакторе является функцией конверсии мономера. В приближении аддитивности зависимость имеет следующий вид:
(9)
$\varphi = \frac{{{{\varphi }_{0}}}}{{{{\varphi }_{0}} + {{{\left( {1 + \varepsilon {{x}_{M}}} \right)}}^{{ - 1}}}}},$Подстановкой (8) в (6) с учетом (9) получаем оценку вклада энергии диссипации:
(10)
$\begin{gathered} {{{\dot {E}}}_{{{\text{кин}}}}} = - \frac{{{{\eta }_{2}}{{V}_{0}}\varepsilon f}}{2} \times \\ \times \,\,\left[ {1 + \frac{5}{2}\left( {\frac{{{{\varphi }_{0}}}}{{{{\varphi }_{0}} + {{{\left( {1 - \varepsilon {{x}_{M}}} \right)}}^{{ - 1}}}}}} \right)\left( {1 + \frac{a}{{3{{\delta }_{2}}}}} \right)} \right]\frac{{d{{x}_{M}}}}{{d\iota }}. \\ \end{gathered} $В этом выражении появляется величина, характеризующая динамические свойства системы, а именно средний радиус ПМЧ а.
Таким образом, энергия диссипации оказывается сложной нелинейной функцией конверсии, скорости ее изменения во времени и среднего диаметра ПМЧ. Это обусловливает дополнительное выделение тепла в реакторе и, как следствие, некоторое уменьшение потребности в нагреве реакционной смеси, наблюдаемое в эксперименте.
Из-за экспериментальных сложностей измерения среднего диаметра ПМЧ во времени, аналитический вид функции а(t) неизвестен. Известно только [8, 11], что она имеет вид логистической кривой, верхним пределом которой является средний диаметр конечного полимерного бисера. Отсюда следует, что наблюдаемые экстремумы на кривых частоты f являются результатом рассеяния энергии перемешивания в сложном сочетании изменения физического состояния ПМЧ в результате протекания реакции полимеризации.
Изложенное выше позволяет систематически проанализировать динамическое поведение системы во времени.
В начальный период процесса, до точки U1, мы наблюдаем практически неизменные затраты мощности как на нагрев, так и на перемешивание. Это позволяет отнести эту область к стадии равновесия процессов коалесценции и редиспергирования [1], которая имеет место при небольших степенях превращения мономера в полимер, обусловливающих практически ньютоновское поведение раствора. Этой стадии соответствует также слабый рост среднего диаметра ПМЧ [8, 21]. По-видимому, вязкотекучее состояние ПМЧ сохраняется довольно долго, вплоть до 35% превращения мономера [1].
Однако после этой точки, на отрезке {U1, U2} происходит заметное падение требуемой мощности нагрева (кривая U). Это обусловлено нарастанием скорости выделения тепла вследствие влияния гель-эффекта. Одновременно постепенно нарастает мощность, необходимая для поддержания постоянного числа оборотов мешалки (кривая f до точки f1). Физически это означает, что начинаются изменения реологических свойств ПМЧ, связанные с увеличением в них концентрации полимера. Они начинают приобретать высокоэластические свойства. Соответствующим образом и изменяется их реакция на действующие на них напряжения деформации. Часть энергии деформации идет уже не на дробление капель, а на нагрев самих ПМЧ. Заметим, что в общем тепловом балансе влияние это невелико и составляет около 3–5% общей тепловой нагрузки. Для этого периода характерным является также увеличение скорости роста среднего диаметра ПМЧ вследствие уменьшения возможности их диспергирования [1, 8].
Точка U2 определяет наибольшую скорость падения потребности в нагреве. Из рис. 1 видно, что ее можно сопоставить с точкой f1, характеризующей начало интенсивного роста потребности в энергии перемешивания. Физически это означает прогрессирующую потерю ПМЧ способности к диспергированию при сохранении способности к слипанию (слиянию) и начало так называемой липкой стадии процесса по [1]. Макромолекулы в ПМЧ уже не способны к перемещению, и подводимые напряжения деформации изменяют положение только их сегментов, которые после снятия деформации релаксируют в прежнее состояние. Энергия релаксации выделяется в виде тепла. Поэтому потребность в нагреве несколько уменьшается (отрезок {U2, U3}). Этот период характеризуется также интенсивным ростом среднего диаметра ПМЧ.
Минимум напряжения нагрева наблюдается в точке U3, которой можно сопоставить точку f2 на кривой частоты как меры мощности, затрачиваемой на перемешивание реакционной смеси. Это соответствует максимальной скорости роста этой частоты на отрезке {f1, f2}. После нее начинается постепенное ее уменьшение на отрезке {f2, f3}. Физически это означает начало процесса “твердения” ПМЧ вследствие постепенного их стеклования. Заметим, что стеклование имеет место при температуре синтеза, что обусловлено известным [5] снижением температуры стеклования в присутствии растворителя. Поэтому использование в кинетических моделях ее величины для полимера является ошибочным. Мы получали твердые гранулы полистирола даже при 60°С.
Таблица 1.
Связь управляющих воздействий между собой и с физическим состоянием ПМЧ в стадиях суспензионной полимеризации стирола
| Напряжение нагрева | Частота с частотно-регулируемого привода | Физическое состояние ПМЧ |
|---|---|---|
| U1 – начало гель-эффекта, рост тепловыделения | Не изменяется | Равновесие коалесценции–редиспергирования |
| U2 – максимум скорости тепловыделения | f1 – начало диссипации энергии перемешивания на вязкоупругих ПМЧ | ПМЧ приобретают вязкоупругие свойства |
| U3 – конец гель-эффекта, включается нагрев |
f2 – максимум роста скорости диссипации | Усиление вязкоупругих свойств ПМЧ |
| U4 – максимум скорости нагрева | f3 – максимум диссипации на ПМЧ | Начало процесса стеклования ПМЧ |
| U5 – тепловой стационар | f4 – максимум скорости падения диссипации | Продолжение стеклования ПМЧ |
| Не изменяется | f5 – механический стационар | “Твердые” ПМЧ |
Начинающийся процесс перехода ПМЧ из вязкоупругого в стеклообразное состояние постепенно уменьшает выделение энергии диссипации, что мы и наблюдаем на кривой напряжения компенсирующего нагрева на отрезке {U3, U4} – оно начинает расти. Однако потребность в энергии перемешивания на участке {f2, f3} продолжает увеличиваться, хотя и с постепенным уменьшением скорости. Это обусловлено изменением физического состояния. Прилагаемые к ПМЧ напряжения деформации затрагивают все меньшую часть их объема из-за роста их “твердости”. Максимум энергии перемешивания достигается в точке f3, соответствующей максимуму скорости нарастания напряжения на отрезке {U3, U4}, необходимого для поддержания постоянной температуры реакционной смеси, в точке U4. Реакционная смесь в этот период представляет собой суспензию “почти твердых” ПМЧ в водной фазе, причем их средний диаметр практически не изменяется. Затухает в них и процесс полимеризации из-за “замуровывания” активных центров в жесткой системе теряющих подвижность сегментов макромолекул и высокой вязкости. В соответствии с этим процессом наблюдается постепенное уменьшение скорости нарастания напряжения на отрезке {U4, U5}.
Точка U5 соответствует достижению конечного теплового плато, устанавливается напряжение нагрева, просто компенсирующее потери тепла в окружающую среду. Эта точка соответствует максимуму скорости падения потребности в энергии перемешивания f4. Процесс стеклования имеет кинетическую природу [5, 22] и ПМЧ “твердеют” постепенно, поэтому даже после достижения теплового стационара по напряжению нагрева мы наблюдаем некоторое время снижение в потребности в энергии перемешивания на отрезке {f4, f5}. Стационарное состояние по энергии перемешивания достигается только в точке f5. После этого момента реакционная смесь представляет собой суспензию твердых (стеклообразных) ПМЧ в водной фазе при температуре синтеза.
ЗАКЛЮЧЕНИЕ
Динамические изменения регулирующих воздействий на реактор содержат в себе информацию о характере протекающих в нем физико-химических процессов и изменениях свойств реакционной среды. Об этом наглядно свидетельствует сводка полученных данных, приведенная в табл. 1.
Особо интересной представляется обнаруженная закономерная связь между мерами тепловыделения в ходе полимеризации и мощности на валу мешалки. Определение теплового потока, связанного с протеканием экзотермической реакции полимеризации, возможно по конверсии мономера. Однако последняя задача оказывается сложной и в настоящее время надежная методика отсутствует. Кроме того, такое определение обязательно будет давать запаздывающие результаты из-за тепловой инерции в цепи “измеритель температуры–реакционная масса–теплообменная поверхность”.
Мера мощности на валу мешалки однозначно характеризует изменения физического (релаксационного) состояния полимерно-мономерных частиц в момент измерения и свободна от какого-либо запаздывания. Это позволяет считать ее удобным параметром оперативного слежения за ходом процесса и использовать для организации системы его регулирования.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 17-07-01368).
ОБОЗНАЧЕНИЯ
| $a$ | радиус капли ПМЧ, м |
| ${{c}_{p}}$ | теплоемкость, Дж/(кг К) |
| d | диаметр, м |
| f | фактор эффективности инициатора |
| G | массовый расход, кг/с |
| $\Delta H$ | тепловой эффект реакции, Дж/моль |
| I | концентрация инициатора, моль/м3 |
| КР | коэффициент мощности, зависящий от типа применяемого перемешивающего устройства и от значения центробежного критерия Рейнольдса, (Дж с2)/(кг м2) |
| k | константа скорости, м3/(моль с) |
| kp | константа скорости роста цепи, м3/(моль с) |
| М | концентрация стирола, моль/м3 |
| m | масса, кг |
| N | скорость вращения мешалки, с–1 |
| q | тепловой поток, Вт |
| S | площадь поверхности теплопередачи, м2 |
| Т | температура, К |
| V | объем, м3 |
| x | степень конверсии |
| α | коэффициент теплоотдачи, Вт/(м2 К) |
| δ | толщина слоев фаз, м |
| ε | коэффициент изменения объема в ходе реакции полимеризации |
| η | вязкость, Па с |
| η* | эффективная вязкость суспензии, Па с |
| θ | время “миграции”, с |
| λ0 | нулевой момент живой полимерной цепи, моль/м3 |
| ρ | плотность, кг/м3 |
| φ | объемная доля дисперсной фазы в суспензии |
| φ(хm) | функция, определяющая влияние степени конверсии мономера на изменение констант скоростей роста и обрыва цепей в период гель-эффекта |
ИНДЕКСЫ
Список литературы
Кафаров В.В., Дорохов И.Н., Дранишников Л.В. Системный анализ процессов химической технологии. Процессы полимеризации. М.: Наука, 1991.
Вент Д.П., Сафин М.А., Лопатин А.Г., Савельянов В.П. Прикладная кинетика суспензионной полимеризации стирола // Теор. осн. хим. технол. 2014. Т. 48. № 3. С. 356. [Vent D.P., Safin M.A., Lopatin A.G., Savelyanov V.P. Applied kinetics of styrene suspension polymerization // Theor. Found. Chem. Eng. 2014. V. 48. № 3. P. 332.]
Вент Д.П., Лопатин А.Г., Савельянов В.П., Брыков Б.А. Факторный анализ кинетики радикальной полимеризации метилметакрилата // Теор. осн. хим. технол. 2018. Т. 52. № 5. С. 555. [Vent D.P., Lopatin A.G., Savelyanov V.P., Brykov B.A. Factorial analysis of the kinetics of radical polymerization of methyl methacrylate // Theor. Found. Chem. Eng. 2018. V. 52. № 5. P. 825.]
Байзенбергер Дж.А., Себастиан Д.Х. Инженерные проблемы синтеза полимеров. М.: Химия, 1988.
Тагер А.А. Физико-химия полимеров. М.: Химия, 1968.
Santos J.C., Lopes C.N., Reis M.M., Giudici R., Sayer C., Machado R.A.F., Araújo P.H.H. Comparison of techniques for the determination of conversion during suspension polymerization reactions // Braz. J. Chem. Eng. 2008. V. 25. № 2. https://doi.org/10.1590/S0104-66322008000200017
Tefera N., Weikert G., Westerterp K.R. Modeling of Free Radical Polymerization up to High Conversion. Development of a Mathematical Model // J. Appl. Polym. Sci. 1997. V. 63. P. 1663.
Киреев В.В., Шаршакова Ю.В., Клочков А.Н., Савельянов В.П. О механизме формирования распределения частиц по размерам при суспензионной полимеризации стирола // Высокомол. соедин. Сер. Б. 2004. Т. 46. № 8. С. 1449.
Jahanzad F., Sajjadi S., Brooks B.W. Characteristic intervals in suspension polymerization reactor: An experiment and modeling study // Chem. Eng. Sci. 2005. V. 60. № 20. P. 5574.
Киреев В.В., Шаршакова Ю.В., Клочков А.Н., Савельянов В.П. Динамика формирования распределения частиц по размерам в суспензионной полимеризации стирола // Высокомол. соедин. Сер. Б. 2006. Т. 48. № 5. С. 874.
Kotoulas C., Kiparissides C. A generalized population balance model for the prediction of particle size distribution in suspension polymerization reactors // Chem. Eng. Sci. 2006. V. 61. № 2. P. 332.
Неустроева Т.В., Савельянов В.П. Порог коагуляции как динамическая характеристика суспензионной полимеризации // Пласт. массы. 2008. № 8. С. 38.
Лопатин А.Г., Вент Д.П., Брыков Б.А., Стекольников А.Ю. Способ автоматического управления реактором суспензионной полимеризации. Пат. 2669791 РФ. 2018.
Лопатин А.Г., Вент Д.П., Брыков Б.А., Стекольников А.Ю. Способ автоматического управления реактором суспензионной полимеризации. Пат. 2679221 РФ. 2019.
Казанская В.П., Виноградский В.Ф., Николаев А.Ф. Влияние перемешивания на гранулометрические характеристики // Пласт. массы. 1982. № 5. С. 8.
Tanaka M., O’Shima E. Effect of Location of Submerged Impeller on Particle Size in Suspension Polymerization of Styrene // Kagaku Kogaku Ronbunshu. 1985. V. 11. № 4. P. 376. https://doi.org/10.1252/kakoronbunshu.11.376
Лопатин А.Г., Сафин М.А., Вент Д.П., Савельянов В.П. Влияние перемешивания на динамику реактора полимеризации стирола // Изв. Тул. гос. унив. Естеств. науки. 2012. № 2. С. 212.
Вент Д.П., Лопатин А.Г., Брыков Б.А., Богатиков В.Н., Пророков А.Е. Диагностика состояний и управление динамическими процессами в слабоструктурированных и плохоформализуемых средах. Монография. Новомосковск: РХТУ им. Д.И. Менделеева, Новомосковский институт (филиал), 2018.
Савельянов В.П. Общая химическая технология полимеров. Учебное пособие для вузов. М.: Академкнига, 2007.
Верещагина Т.Н. Динамические свойства гетерогенных сред и колебательно-волновые процессы в теплообменных аппаратах. Автореф. дис. … докт. техн. наук. Обнинск: ГНЦ РФ-ФЭП, 2007.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Учебное пособие. В 10 т. Т. VI. Гидродинамика. М.: Наука, 1988.
Привалко В.П. Молекулярное строение и свойства полимеров. Л.: Химия, 1986.
Сафин М.А. Разработка системы автоматического управления реактором синтеза суспензионной полимеризации стирола с учетом кинетики процесса. Дис. … канд. техн. наук. М.: РХТУ им. Д.И. Менделеева, 2014.
АО “Пластик” (2020) Полистирол. http://oaoplastic.ru/products/polistirol. Дата обращения: 03.04.2020.
Curteanu S. Modeling and simulation of free radical polymerization of styrene under semibatch reactor conditions // Cent. Eur. J. Chem. 2003. V. 40. P. 69. https://doi.org/10.2478/BF02479259
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии