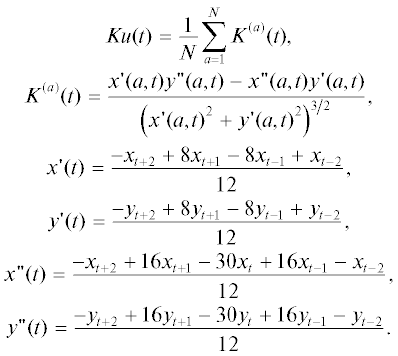Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 720-725
Потенциально-интегрально-индексный алгоритм анализа пульсаций давления газовых потоков в сложных трубопроводах
Р. Р. Кантюков a, В. П. Мешалкин a, b, О. Б. Бутусов a, c, *
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
b Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
c Московский международный университет
Москва, Россия
* E-mail: butusov-1@mail.ru
Поступила в редакцию 10.07.2020
После доработки 13.07.2020
Принята к публикации 14.07.2020
Аннотация
Предложен потенциально-интегрально-индексный алгоритм анализа пульсаций давления газовых потоков в сложных трубопроводах. Пульсации давления характеризуют турбулентную структуру газовых потоков, оказывающих ударные воздействия на стенки трубопроводов, что является одной из важнейших причин опасного механического явления – вибрации, приводящей к механическим разрушениям трубопровода. В каждой точке газового потока упорядоченные последовательности пульсаций давления образуют временные ряды, анализ которых можно выполнить с использованием статистического метода одномерной и двухмерной временной развертки пульсаций давления, образующейся при изменении размеров скользящего окна, охватывающего различные области стохастических пульсаций. Показано, что предложенный алгоритм позволяет находить особые точки временного ряда, которые не обнаруживаются с помощью традиционного непрерывного вейвлет-преобразования, что играет важную роль в оценке динамической стохастической структуры пульсаций давления потоков в трубопроводе.
ВВЕДЕНИЕ
Разрывы трубопроводов являются опасными явлениями техногенного характера и должны учитываться как причина технологических рисков. Одной из важных гидродинамических причин разрывов трубопроводов являются турбулентные пульсации нестационарных газовых потоков. В работах [1, 2] проведен системный анализ экологических и технологических рисков полиэтиленовых и стальных трубопроводов, в результате которого с помощью интегральных индексов пульсации газовых потоков получена гидродинамическая оценка причин возникновения разрывов трубопроводов. В работах [2, 3] временные ряды пульсаций давления газового потока и результаты их воздействия на стенки трубопровода изучались как с помощью фрактально-текстурного анализа, так и с помощью непрерывных вейвлет-преобразований.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Для оценки воздействия пульсаций давления турбулентных газовых потоков на стенки трубопроводов можно использовать временные ряды следующих интегральных показателей (индексов), характеризующих особенности стохастических пульсаций газовых потоков:
1. “Относительная гистограмма пульсаций давления”, показатель вычисляемый по уравнениям
(1)
$\eta _{{ij}}^{{(k)}} = \sum\limits_{\mu = 1}^M {\delta \left( {\left[ {\frac{{P_{{ij}}^{{(\mu )}}}}{\Delta }} \right] - k} \right)} ,\,\,\,\,q_{{ij}}^{{(k)}} = \frac{{\eta _{{ij}}^{{(k)}}}}{{\sum\limits_k {\eta _{{ij}}^{{(k)}}} }},$Как следует из (1), пульсации давления нормализованы и масштабированы с помощью специального параметра – ширина интервала квантования.
2. “Пульсации среднего давления” на заданном участке трубопровода:
(2)
$\left\langle {{{P}^{{(M)}}}} \right\rangle = \sum\limits_k {k\Delta } \left\langle {{{q}^{{(k)}}}} \right\rangle ,$3. “Стандартное отклонение пульсаций среднего давления” на заданном участке трубопровода:
(3)
$\left\langle {{{S}^{{(M)}}}} \right\rangle = \sqrt {\sum\limits_\mu {\sum\limits_k {{{{(P_{{ij}}^{{(\mu )}} - k\Delta )}}^{2}}\left\langle {{{q}^{{(k)}}}} \right\rangle } } } .$4. “Потеря скорости потока” для заданного участка трубопровода, которая рассчитывается по уравнениям
(4)
$\begin{gathered} u_{k}^{{(i1)}} = \frac{1}{{{{N}_{{y1}}}}}\sum\limits_{j = j1}^{j2} {{{u}_{{i1,j}}},} \\ u_{k}^{{(i2)}} = \frac{1}{{{{N}_{{y2}}}}}\sum\limits_{j = j3}^{j4} {{{u}_{{i2,j}}},} \\ \delta {{u}_{k}}(M) = u_{k}^{{(i1)}} - u_{k}^{{(i2)}}, \\ \end{gathered} $5. “Средняя кривизна траектории частиц”, вычисляемая по уравнениям
Методические предпосылки разработки интегрально-индексного алгоритма. В работе [3] разработаны алгоритмы метода “частицы в ячейках”, использованные для расчета турбулентных двухмерных нестационарных газовых потоков и интегральных показателей воздействия турбулентных пульсаций на стенки трубопроводов. Отметим, что в настоящее время метод гидродинамического моделирования “частицы в ячейках” широко применяется для решения сложных задач газовой динамики, таких как моделирование плазмы и динамика разреженного газа [4–7]. На рис. 1 представлены временные ряды интегральных показателей: “Потеря скорости потока” и “Средняя кривизна траекторий частиц”, рассчитанных методом “частицы в ячейках” [2, 3].
Рис. 1.
Графики временных рядов интегральных показателей для узла трубопровода типа “конфузор”: (а) – интегральный показатель “Потеря средней скорости”; (б) – интегральный показатель “Средняя кривизна траектории” частиц-маркеров.
Представленные на рис. 1 временные ряды интегральных показателей, характеризуют интенсивность воздействия пульсаций турбулентных газовых потоков на стенки трубопровода. В настоящее время существует достаточно обширный набор методов статистического анализа одномерных и многомерных временных рядов [8]. Одним из наиболее эффективных методов является непрерывный вейвлет-анализ, зарекомендовавший себя множеством удачных решений практических задач как визуального, так и количественного анализа временных рядов [9].
Непрерывный вейвлет-анализ является мощным инструментом для изучения временных рядов одномерных показателей [2, 3]. Мощность непрерывного вейвлет-преобразования обусловлена тем, что в результате преобразования одномерного сигнала в двухмерный сигнал проявляются некоторые структурные свойства исходного временного ряда, не определяемые классическими статистическими методами анализа временных рядов.
По существу метод непрерывного вейвлет-преобразования является сверткой следующего вида [9]:
(6)
$W(s,c) = \frac{1}{{\sqrt s }}\int\limits_{ - \infty }^\infty {f(t)\varphi \left( {\frac{{t - c}}{s}} \right)dt} .$Параметр s определяет ширину вейвлета, параметр c – положение центра вейвлета на временной оси. Таким образом, вейвлет представляет собой произвольную, но локализованную функцию, удовлетворяющую условию обобщенного нулевого среднего
Если φ(t) удовлетворяет условию (2), то вейвлет называется вейвлетом m-го порядка.
Для получения двухмерного преобразования одномерного временного ряда строки двухмерного изображения непрерывного вейвлет-преобразования вычисляются по формулам (1) с использованием вейвлетов разной степени сжатия или растяжения. В результате формируется двухмерное изображение, которое называется спектром непрерывного вейвлет-преобразования. Аналогичные 1D–2D преобразования могут быть получены также другими методами.
В разработанном авторами оригинальном потенциально-интегрально-индексном алгоритме анализа пульсаций давления также используется масштабирование вдоль временной оси, но в качестве масштаба предложено использовать ширину скользящего окна, в чем предложенный алгоритм существенно отличается от алгоритма непрерывного вейвлет-преобразования. Основу предложенного алгоритма составляет, так называемое потенциальное преобразование, идея которого аналогична “Преобразованию расстояний (Distance transform)”, предложенное и использованное в работах [10–12] для анализа структурных особенностей мозаики пикселей изображения. Сущность “Преобразования расстояний” заключается в замене пикселей изображения расстояниями между ними. При этом для расчета расстояний между пикселями могут быть использованы различные критерии и метрики.
В отличие от “Преобразования расстояний” в предлагаемом нами алгоритме используются не расстояния, а псевдопотенциалы, описывающие виртуальное взаимодействие пикселей бинарного изображения. Фактически псевдопотенциалы можно рассматривать как некоторые новые дополнительные метрики. Следует отметить, что метрики с дополнительными свойствами можно построить и без использования аналогий с виртуальными частицами, но использование понятия временного ряда расширяет физический смысл предлагаемого алгоритма.
Сущность и основные этапы потенциально-интегрально-индексного алгоритма. Сущность предложенного алгоритма заключается в преобразовании одномерного временного ряда в двухмерное изображение с использованием только двух псевдопотенциалов: потенциала Изинга и Кулоновского потенциала.
Предлагаемый алгоритм состоит из следующих этапов.
Этап 1. Предварительное преобразование временного ряда стохастических пульсаций давления.
Шаг 1.1. Очистка временного ряда от трендов.
Шаг 1.2. Очистка временного ряда от выбросов.
Шаг 1.3. Нормализация временного ряда.
Этап 2. Бинаризация временного ряда.
Шаг 2.1. Выбор вида бинаризации (с одним или с двумя порогами).
При бинаризации с одним порогом расчет выполняется по формуле (8а), с двумя порогами –по формуле (8б):
(8a)
${{b}_{j}} = \left\{ \begin{gathered} 1,\,\,\,\,{{x}_{j}} \geqslant T, \hfill \\ 0,\,\,\,{{x}_{j}} < T, \hfill \\ \end{gathered} \right.$(8б)
${{b}_{j}} = \left\{ \begin{gathered} 1,\,\,\,\,{{x}_{j}} \in \left[ {{{T}_{1}},{{T}_{2}}} \right], \hfill \\ 0,\,\,\,{{x}_{j}} \notin \left[ {{{T}_{1}},{{T}_{2}}} \right]. \hfill \\ \end{gathered} \right.$Шаг 2.2. Выбор величины порогов бинаризации.
Этап 3. Потенциальное преобразование бинарных точек.
Назовем точки, для которых ${{b}_{j}} = 1$, “белыми” точками, а точки, для которых ${{b}_{j}} = 0$, “черными” точками.
Шаг 3.1. Выбор вида потенциального преобразования (взаимодействие только между “белыми” точками; взаимодействие только между “черными” точками; взаимодействие только между “белыми” и черными точками).
Шаг 3.2. Расчет потенциалов взаимодействия бинарных точек с помощью скользящего окна.
Потенциальное преобразование Изинга вычисляется по формуле [13]
(9)
${{U}_{{I{\text{sin }}g}}}\left( C \right) = \left\{ \begin{gathered} J\sum\limits_{\left( {u,v \in W} \right)} {{{S}_{u}}{{S}_{v}}} = \sum\limits_{\left( {u,v \in W} \right)} {\left( {2{{b}_{u}} - 1} \right)\left( {2{{b}_{v}} - 1} \right)} , \hfill \\ {{r}_{{u,v}}} \leqslant R, \hfill \\ 0,\,\,\,\,{{r}_{{u,v}}} > R. \hfill \\ \end{gathered} \right.$Потенциальное преобразование рассчитывается только для точек, расположенных внутри скользящего окна.
Этап 4. Вычисление и анализ двухмерной спектрограммы потенциального преобразования. Двухмерная спектрограмма получается в результате объединения строк, каждая из которых является графиком потенциала, вычисленного на этапе 3 при использовании различных размеров скользящего окна.
Шаг 4.1. Повышение контрастности спектрограммы с помощью нормализация.
Шаг 4.2. Выбор цветовой гаммы, наилучшим образом представляющей при визуальном анализе характерные особенности спектрограммы.
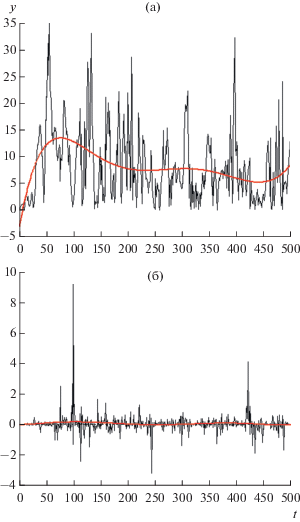
Основные результаты анализа воздействия пульсаций газовых потоков на стенки трубопроводов, полученные при использовании потенциального преобразования Изинга. Результаты предварительного преобразования на этапе 1 (очистка тренда и нормализация представлены на рис. 2.
Рис. 2.
Очищенные от тренда и нормализованные временные ряды (узел типа “конфузор”): (а) – потеря средней скорости; (б) – средняя кривизна траекторий.
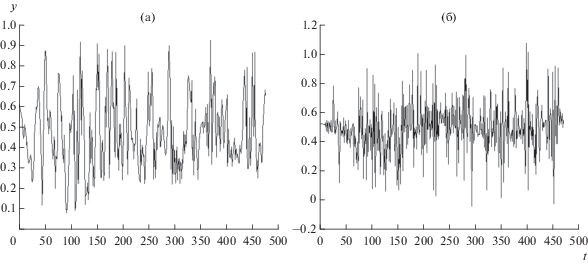
На втором этапе выполняется бинаризация временного ряда. На третьем этапе вычисляется потенциал для каждого положения скользящего по временному ряду окна. Полученные в результате графики потенциала представлены на рис. 3. На четвертом этапе вычисляются двухмерные спектрограммы потенциального преобразования. Полученные спектрограммы представлены на рис. 4. Для сравнения на рис. 5 представлены спектрограммы, рассчитанные с помощью классического непрерывного вейвлет-преобразования.
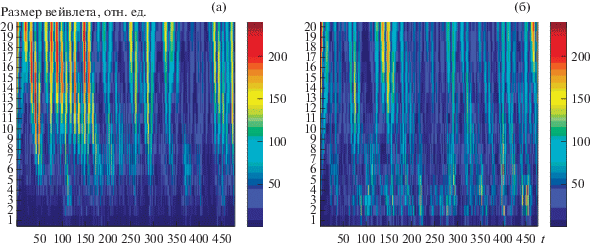
Рис. 3.
Графики потенциала Изинга, полученные с помощью скользящего окна (узел типа “конфузор”): (а) – потеря средней скорости; (б) – средняя кривизна траекторий.
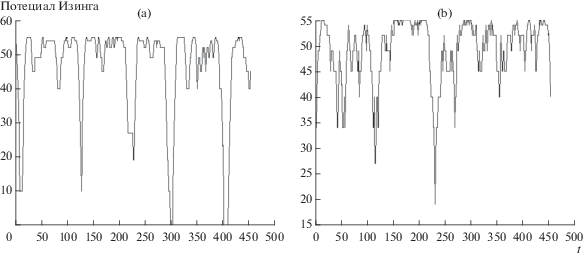
Рис. 4.
Двухмерные спектрограммы потенциального преобразования Изинга для типового узла сложного трубопровода типа “конфузор”: (а) – потеря средней скорости; (б) – средняя кривизна траекторий.
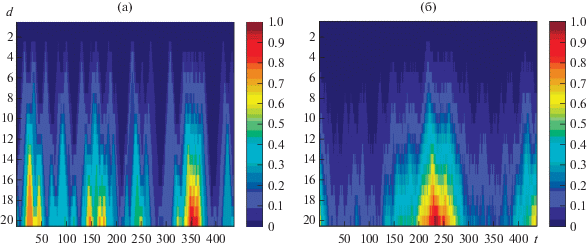
Рис. 5.
Спектрограммы непрерывного вейвлет-преобразования для типового узла сложного трубопровода типа “конфузор”: (а) – потеря средней скорости; (б) – средняя кривизна траекторий.
Как следует из сравнения рис. 4 и 5, спектрограммы потенциального преобразования временных рядов пульсаций давления газовых потоков дают более полное представление об особых точках временного ряда по сравнению с классическим непрерывным вейвлет-преобразованием (рис. 5). Следует отметить, что найденные особые точки временного ряда пульсаций давления газовых потоков абсолютно не заметны на графиках исходных временных рядов и плохо проявляются на спектрограммах классического непрерывного вейвлет-преобразования.
ЗАКЛЮЧЕНИЕ
Потенциальное преобразование временных рядов интегральных индексов газовых потоков является эффективным инструментом анализа стохастической пульсационной структуры газовых потоков в трубопроводах. На спектрограммах классического непрерывного вейвлет-преобразования особые точки временных рядов пульсаций давления выделяются менее четко, что обуславливает объективную необходимость использования потенциального преобразования временных рядов в качестве эффективного дополнения классического непрерывного вейвлет-преобразования. Пульсационная стохастическая структура турбулентных пульсаций газовых потоков в трубопроводах может отображаться с использованием различных интегральных показателей (“Относительная гистограмма пульсаций давления”; “Пульсации среднего давления”; “Стандартное отклонение пульсаций среднего давления”; “Потеря скорости потока”; “Средняя кривизна траектории частиц”).
Таким образом, применение предлагаемого потенциально-интегрально-индексного алгоритма стохастических пульсаций позволяет получать более полный результат анализа пульсационной структуры газовых потоков в результате использования нескольких интегральных показателей, характеризующих пульсационные характеристики газовых потоков с разных сторон, что позволяет прогнозировать причины возникновения вибраций.
ОБОЗНАЧЕНИЯ
| a | номер частицы-маркера |
| ${{b}_{j}} \in \left\{ {0,\;1} \right\}$ | бинарные точки (результат бинаризации временного ряда) |
| C | центральная точка скользящего окна |
| c | величина смещения вейвлета на безразмерной временной оси |
| f(t) | функция, описывающая временной ряд |
| i, j | безразмерные координаты ячейки расчетной сетки |
| J | безразмерный параметр модели (в расчетах принято J = 1) |
| М | общее число шагов моделирования |
| m | порядок вейвлета |
| N | количество частиц-маркеров, использованных для вычисления средней кривизны на шаге t временного ряда |
| NG | общее число ячеек в заданной области газопровода |
| $P_{{ij}}^{{(\mu )}}$ | давление в ячейке с координатами i и j на μ-м шаге моделирования, Па |
| $q_{{ij}}^{{(k)}}$ | безразмерные относительные частоты пульсаций давления на k-м уровне квантования |
| R | максимально возможное расстояние между точками |
| ${{r}_{{u,v}}} \leqslant R$ | расстояние между точками с номерами u и $v$ |
| ${{S}_{u}},\;{{S}_{v}}$ | величины, принимающие значения +1 для белых точек и –1 для черных точек |
| $s \in {{R}^{ + }}$ | масштаб непрерывного вейвлет-преобразования |
| $T,{{T}_{1}},{{T}_{2}}$ | пороги бинаризации |
| t | номер шага временного ряда |
| $u,v$ | координаты точек внутри скользящего окна |
| W | скользящее окно |
| ${{x}_{t}},{{y}_{t}}$ | временные ряды координат частиц-маркеров, м |
| Δ | ширина интервала квантования, Па |
| $\eta _{{ij}}^{{(k)}}$ | безразмерные абсолютные частоты пульсаций давления на k-м уровне квантования |
| μ | номер шага моделирования |
| $\varphi (x)$ | вейвлетная функция (вейвлет) |
| ΩG | безразмерная заданная область газопровода |
Список литературы
Бутусов О.Б., Гимранов Р.К., Казанский Г.М., Кантюков Р.А., Кантюков Р.Р., Мешалкин В.П., Модин В.К., Мустафин Ф.М., Попов А.Г. Компьютерный анализ экологических рисков газопроводных систем // Изв. высш. учебн. завед. Хим. хим. технол. 2015. Т. 58. № 3. С. 87.
Гимранов Р.К., Кантюков Р.А., Бутусов О.Б., Мешалкин В.П., Попов А.Г., Кантюков Р.Р. Компьютерный анализ интегральных показателей и индексов комплексной оценки воздействия пульсаций газовых потоков на стенки сложных трубопроводов // Изв. высш. учебн. завед. Хим. хим. технол. 2015. Т. 58. № 6. С. 82.
Бутусов О.Б., Мешалкин В.П. Компьютерное моделирование нестационарных газовых потоков в сложных трубопроводах. М.: Физматлит, 2005.
Григорьев Ю.Н., Вшивков В.А., Федорук М.П. Численное моделирование методами частиц-в-ячейках. Новосибирск: СО РАН, 2004.
Хокни Р., Иствуд Дж. Численное моделирование методом частиц. М.: Мир, 1987.
Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. М.: Наука, 1982.
Березин Ю.А., Вшивков В.А. Метод частиц в динамике разреженной плазмы. Новосибирск: Наука, 1980.
Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. М.: Финансы и статистика, 1998.
Короновский А.А., Храмов А.Е. Непрерывный вейвлетный анализ и его приложения. М.: Физматлит, 2003.
Danielsson P.-E. Euclidean distance mapping // Comput. Graphics Image Process.1980. V. 14. P. 227.
Borgefors G. Distance transform in digital image // Comput. Vision, Graphics Image Process. 1986. V. 34. P. 344.
Strand R. Sparse object representations by digital distance functions // Discrete Geometry for Computer Imagery (Lecture Notes in Computer Science. V. 6607). Berlin: Springer, 2011. P. 211.
Биндер К., Хеерман Д.В. Моделирование методом Монте-Карло в статистической физике: введение. М.: Наука. Физматлит, 1995.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии