Теоретические основы химической технологии, 2021, T. 55, № 2, стр. 154-187
Современное состояние в области анализа, синтеза и оптимального функционирования многоассортиментных цифровых химических производств: аналитический обзор
А. Ф. Егоров a, *, Т. В. Савицкая a, **, П. Г. Михайлова a, ***
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: egorov@muctr.ru
** E-mail: savitsk@muctr.ru
*** E-mail: mikhaylova_pavla@muctr.ru
Поступила в редакцию 14.09.2020
После доработки 02.10.2020
Принята к публикации 05.10.2020
Аннотация
Предложен аналитический обзор современного состояния в области многоассортиментных химических производств. Представлен всесторонний анализ трудов зарубежных и отечественных ученых по проблеме гибкости при проектировании многоассортиментных химико-технологических систем в условиях неопределенности. Рассмотрены работы по планированию и составлению расписания работы многоассортиментных химических производств. Рассмотрены формулировки задач смешанно-целочисленного линейного и нелинейного программирования, методы их решения и комплексы программных средств для их решения. Приведен краткий анализ отечественных информационных систем, баз данных по технологиям, оборудованию, производителям, потребителям, ассортименту мало- и среднетоннажной химической продукции. Представлен обзор современных направлений в области создания интеллектуальных систем проектирования и оптимального функционирования гибких автоматизированных многоассортиментных химических производств на основе базовых положений Индустрии 4.0.
ВВЕДЕНИЕ
В 2017 г. Правительство РФ утвердило план мероприятий “дорожной карты” по развитию малотоннажной химии в РФ до 2030 г. [1].
“Дорожная карта” разработана в соответствии с Планом мероприятий по реализации Стратегии развития химического и нефтехимического комплекса на период до 2030 года, утвержденного распоряжением Правительства Российской Федерации от 18.05.2016 № 954-р. К реализации данной стратегии, наряду с Минпромторгом России, подключены другие министерства и ведомства РФ, в том числе Министерство науки и высшего образования РФ (Минобрнауки).
Основная цель развития производств малотоннажной химической продукции на современном этапе – импортозамещение.
Информация о классификации химических производств по объемам выпуска продукции представлена в табл. 1 [2].
Таблица 1.
Классификация химических производств по объемам выпуска продукции
| Объёмы производства | Размер рынка, млрд долл. | Единичная мощность, тыс. т | Количество продуктов | Цена, долл./кг |
|---|---|---|---|---|
| Малотоннажая химия (fine chemicals) | ~100 | <50 | ~100 000 | 5–10 |
| Среднетоннажная химия (speciality chemicals) | ~1100 | <150 | ~10000 | 1.5–5 |
| Крупнотоннажная химия (commodity chemicals) | ~1400 | >150 | 100–200 | 0.5–1.5 |
В России к малотоннажной химии зачастую относят продукцию, которая в остальном мире считается среднетоннажной. Кроме того, российское потребление отдельных химических продуктов исчисляется не тоннами, а десятками и сотнями килограммов, что выводит производство подобных продуктов в область лабораторных технологий производства [2].
В [1] отмечается, что наиболее крупными сегментами в малотоннажной химии (МТХ) и среднетоннажной химии (СТХ) являются: полимеры, строительные добавки, поверхностно-активные вещества, вещества для электроники, на их долю должно приходиться 35% мирового потребления.
Мировые лидеры – производители МТХ и СТХ – компании BASF, DOW, Henkel, AkzoNobel, DuPont, Huntsman, Hexion, Spolcheme.
Наибольшее потребление продукции МТХ в России в период 2013–2015 гг. наблюдалось в нефтегазовом секторе, сельском хозяйстве, товарах повседневного спроса [1].
Сравнительный анализ проблемы становления и развития малотоннажной химии в России и за рубежом за период 40 лет, включая современное состояние, в рамках реализации Мероприятий “Дорожной карты” [1] представлен в работах [3, 4]. В [5] проведен анализ зарубежного рынка производства и потребления высокотехнологичными отраслями промышленности химических реактивов и особо чистых веществ.
В соответствии со стратегией развития химической и нефтехимической промышленности России на период до 2030 г. в РФ предусмотрена модернизация действующих химических заводов и строительство новых [6, 7].
Периодические процессы, такие как производство лаков, красок, различных добавок и т.д., широко используются в малотоннажной химической промышленности. Они во многом определяют качество продукции других отраслей промышленности: текстильной, автомобильной, резиновой, радиотехнической и т.д.
Однако большинство направлений деятельности в области малотоннажной химии связано с развитием технологий, и не получил пока должного развития вопрос создания гибких многоассортиментных малотоннажных производств химической продукции. Создание именно таких производств является перспективным направлением реализации принципов энерго- и ресурсоэффективных химических производств [8].
За рубежом исследования в области создания гибких химических производств относятся к середине 70-х–началу 80-х гг. 20 в. [9–21]. Наиболее известными зарубежными учеными в этой области являются Гроссман И.Е. [10, 11, 16, 18–20], Риппин Д.В.Т. [12, 13, 17], Реклайтис Ж.В. [15], Сухами И. и Мах Р.С.Х. [14], Карими Л.А. [15] и другие. В России с середины 1980-х гг. были начаты активные работы по созданию методологии проектирования гибких, легко перенастраиваемых производств [22], нашедшие свое воплощение в трудах Кафарова В.В. [22–28] и учеников его школы Мешалкина В.П. [25, 28], Перова В.Л. [29–31], Макарова В.В. [27, 32], Бодрова В.И. [33, 34], Дворецкого С.И. [33–35], Малыгина Е.Н. [36–38], Бессарабова А.М. [39, 40], Егорова А.Ф. [29, 30, 41], Островского Г.М. [42, 43] и других российских ученых. В те годы перед отраслями химического профиля стояла задача создания высокоэффективных ресурсо- и энергосберегающих технологических процессов, производств и аппаратов.
Актуальность создания гибких автоматизированных производственных систем (ГАПС) в химической и смежных отраслях промышленности связана, прежде всего, с необходимостью сокращения сроков проходящих от разработки способа получения химического продукта до его промышленной реализации.
Большое значение при проектировании гибких многоассортиментных химических производств имеет создание модульных установок и анализ гибкости модулей и химико-технологических систем [31, 44–48]. Эти вопросы также будут раскрыты в настоящей обзорной статье.
В первом разделе настоящего обзора представлен всесторонний анализ исследований проблемы гибкости при проектировании многоассортиментных химико-технологических систем (ХТС) в условиях неопределенности на основе трудов зарубежных [65, 69–81] и отечественных ученых [62, 66, 68, 83].
Следующим направлением исследований, рассмотренным во втором разделе данной статьи, является анализ планирования и составления расписания работы (функционирования) многоассортиментных химических производств. Эти проблемы базируются на фундаментальных постановках задач смешанно-целочисленного (дискретно-целочисленного) линейного или нелинейного программирования [86–95, 101–105].
В обзоре будут рассмотрены формулировки (постановки) задач смешанно-целочисленного линейного и нелинейного программирования, методы их решения и комплексы программных средств для решения данного класса задач (разделы 2 и 3) [109–157 ].
В обзоре дается краткий анализ отечественных информационных систем, баз данных по технологиям, оборудованию, производителям, потребителям, ассортименту мало- и среднетоннажной химической продукции (раздел 4) [158–172].
В заключительной части статьи представлен обзор современных направлений в области создания интеллектуальных систем проектирования и оптимального функционирования гибких автоматизированных многоассортиментных химических производств на основе базовых положений Индустрии 4.0 – создания цифровой экосреды “Умного предприятия” (цифровых двойников, фабрик будущего, интернета вещей, обработки больших массивов данных и др.) (раздел 5) [71, 109, 173–184].
Таким образом, в настоящей статье представлен научно-аналитический обзор современного состояния в области анализа, синтеза и оптимального функционирования многоассортиментных гибких автоматизированных и цифровых химических производств.
АНАЛИЗ, СИНТЕЗ И ОПТИМИЗАЦИЯ РАБОТЫ ОБОРУДОВАНИЯ И ВЫПУСКА ПРОДУКЦИИ В УСЛОВИЯХ НЕЧЕТКОЙ НЕОПРЕДЕЛЕННОСТИ МНОГОАССОРТИМЕНТНЫХ ПРОИЗВОДСТВ ХИМИЧЕСКОЙ ПРОДУКЦИИ
Модульный принцип организации гибких автоматизированных производственных систем. Модульный принцип организации гибких автоматизированных производств является одним из наиболее перспективных направлений проектирования многоассортиментных производств в химических и смежных отраслях промышленности [44–56].
Модульность – это возможность использования многофункционального оборудования для реализации в нем множества типовых одностадийных химико-технологических процессов (ХТП) [44–47]. Организация гибкой ХТС по модульному принципу заключается в использовании унифицированного технологического оборудования многофункционального назначения [44], а также типовых конфигураций систем управления на базе ЭВМ. Многофункциональность оборудования заключается в возможности реализации на едином технологическом оборудовании разнообразных, технологически подобных процессов, а также возможность их совмещения в одном аппарате (перемешивание, нагрев, химическая реакция, массообмен, теплоотвод и т.п.).
Вопросы создания блочно-модульных гибких автоматизированных производственных систем в химической и смежных отраслях промышленности рассмотрены в работах [44–52]. Известно применение модульного принципа для проектирования многофункционального оборудования и для проектирования модульных производств в условиях неопределенности ассортимента и поступления сырья [44, 45]. Предложено использование универсальных технологических модулей для реализации на их основе множества химико-технологических процессов для выпуска на единой перенастраиваемой схеме широкого ассортимента вяжущих материалов [49] и исследованы вопросы анализа и оценки их экологической безопасности. В [50] рассмотрены основы создания гибких блочно-модульных установок и схем для очистки сточных вод и регенерации растворителей. В [51] описана современная концепция организации модульного производства специализированных полимеров, организуемых на основе аппаратурных модулей со стандартизированными интерфейсами. Модульное производство реализуется на базе транспортных контейнеров и отвечает высокой степени индивидуализации и настройки на выпуск конкретного продукта ассортимента.
В [47, 48] дано определение модуля, согласно которому под модулем понимается относительно самостоятельная технологическая или аппаратурная единица, предназначенная для реализации одного или нескольких одностадийных химико-технологических процессов, включающая основное и вспомогательное оборудование, систему коммуникаций и средства оперативного управления.
Реализация множества ХТП в одном модуле, как правило, предполагает наличие многовариантности размеров оборудования, что соответствует гибкому аппаратурному модулю. Конструктивно гибкий аппаратурный модуль представляет собой относительно самостоятельную аппаратурную единицу, обладающую определенной функциональной избыточностью, позволяющей без изменения структуры реализовывать разные одностадийные ХТП.
Гибкий аппаратурный модуль отличается унифицированным характером функционирования за счет включения в него нескольких единиц основного однотипного или разнотипного оборудования одинакового или разного размера, согласующих емкостей, системы гибких коммуникаций, средств управления, позволяющих быстро и с минимальными затратами изменять его структуру при переходе с одного продукта на другой.
Множество аппаратурных модулей различного целевого назначения образуют аппаратурный блок, предназначенный для реализации одного или нескольких многостадийных ХТП. Совокупность аппаратурных блоков формирует технологическую структуру гибкой или совмещенной ХТС.
В [44] рассмотрены три основных направления реализации блочно-модульного подхода. Первое предполагает анализ возможности совмещения в группы выпуска многоассортиментной продукции по физико-химическим свойствам, технологическому и аппаратурному оформлению. Для больших групп продуктов разрабатываются аппаратурно-технологические комплексы жесткой нетрансформируемой структуры. Основная трудность его использования заключается в необходимости очистки при смене номенклатуры выпускаемой продукции.
Второе направление заключается в разработке единого многофункционального нетрансформируемого модульного блока с максимальной функциональной избыточностью оборудования, обеспечивающей возможность проведения различных последовательностей технологических операций за счет переключения аппаратов посредством коммуникационных линий.
Третье направление связано с созданием легко трансформируемых установок минимальной функциональной избыточности из аппаратов или их частей. Данный подход позволяет обеспечить выпуск заданной номенклатуры продукции при минимальных капитальных затратах; эффективное использование оборудования при минимальных его размерах, а также наибольшее соответствие аппаратурного оформления требованиям технологии.
В работе [45] рассматривается гибкое экспериментальное модульное производство химических реактивов с периодическим способом организации процессов. Проводится автоматизированный выбор оборудования при синтезе оптимальных гибких производств, в основу которого положен анализ сопоставления элементов подмножества физико-химических свойств процесса с элементами подмножества конструкционных параметров аппарата.
В [46] предложен модульный способ организации ХТС, базирующийся на перемещении оборудования, позволяющий изменять не только структуру производства при переходе с продукта на продукт, но и аппаратурный состав. В работе изложены принципы формирования оптимального парка аппаратурных модулей для организации многоассортиментного производства перспективного ассортимента продукции фиксированной структуры при минимальных затратах на его создание. Синтез модульных производств предложено выполнять в виде итеративной двухэтапной процедуры, включающей формирование оптимального парка аппаратурных модулей и последующий синтез из них модульного производства для выпуска продуктов фиксированного ассортимента.
В работах [32, 46, 47] рассмотрен процесс формирования аппаратурных модулей (стационарных или мобильных), из которых формируется аппаратурное оформление гибкого многоассортиментного производства.
Важные аспекты, связанные с исследованием возможности перенастройки модульных производств в режиме реального времени рассмотрены в работе [52].
Модульное системное проектирование рассматривается как метод для реализации различных функциональных требований с минимальным количеством ресурсов [53], а также возможностью оптимизировать операционную емкость всей системы, добавляя модули для лимитирующих стадий производства [54]. Современные модульные производственные системы не предназначены для реконфигурации в режиме реального времени. Для быстрого реагирования на новые продукты, которые имеют меньший размер партии, из-за более короткого жизненного цикла продукта, быстрая и экономичная реконфигурация, а также добавление функциональности имеют огромное значение [52].
Гибкая модульная производственная система является ключевым фактором для компаний-производителей реагирования на тенденцию производства отдельных продуктов, которые необходимы потребителям [55, 56]. Примеры создания блочно-модульных установок в производствах реактивов и особо чистых веществ представлены далее в настоящем обзоре [164–168].
Создание гибких блочно-модульных производств неразрывно связано с исследованием проблемы гибкости.
Гибкость как мера неопределенности. Гибкость, определяемая в широком смысле слова [23] – есть способность системы к быстрой ресурсосберегающей переориентации как отдельных подсистем, так и всего производства на выпуск другой продукции или переработку других видов сырья.
В гибкой ХТС различают три вида гибкости.
Технологическая гибкость – это способность технологической системы использовать различные виды многофункционального оборудования, при перенастройке этой системы с выпуска одной номенклатуры продукции на другую.
Технологическая гибкость [24] ХТС обеспечивается аппаратурным подобием технологических стадий, периодическим способом организации процессов и гибкими коммуникациями между аппаратами.
Аппаратурная гибкость – это способность быстро и с минимальными затратами перестраивать аппаратурное оформление в системе (как заменой отдельных конструктивных элементов, так и подключением отдельных единиц вспомогательного оборудования). Аппаратурная гибкость должна быть обеспечена при перенастройке на выпуск другой номенклатуры продукции.
Структурная гибкость – это возможность изменения структуры гибкой схемы в процессе ее функционирования при переходе от одной номенклатуры продукции к другой.
Различным аспектам проблемы гибкости посвящены публикации [9, 11, 23, 24, 48, 57–81].
В [9] введено понятие статической гибкости или перестраиваемости процесса, характеризующее возможности заложенные в процессе и позволяющие перестроить его на выпуск других продуктов или использование других видов сырья и энергии. Кроме того, введено понятие динамической гибкости, характеризующей возможности технологической системы устойчиво работать при действии различного рода возмущений по составу сырья, параметрам используемой энергии, в условиях изменения спроса и т.п. В соответствии с этим подходом гибкость – это способность проектируемой системы сохранять работоспособность при изменении внешних и внутренних параметров системы [22, 57]. В этом заключается отличие понятия гибкости от понятия надежности, под которой понимается способность системы сохранять работоспособность во времени. Для того, чтобы производство обладало гибкостью необходимо на самых ранних стадиях проектирования учитывать эти особенности.
Вопросам оценки гибкости оборудования и ХТС в целом посвящены работы [9, 11, 23, 24, 42, 43, 48, 57–81]. Исследования [42, 43] посвящены теоретическим вопросам определения гибкости простых единиц оборудования. В работе [43] раскрыты смысловые аспекты анализа гибкости при создании модульных производств; предложено определять технологическую и конструкционную гибкость. Вопросам моделирования и проектирования ХТС с учетом гибкости посвящены работы [47, 48, 57–70].
В [71] проведен обзор трансформации подходов к гибкости.
В последние десятилетия многочисленные исследования были посвящены изучению гибкости производства и производственных систем [72–75].
Де Мейер и др. [72] определили четыре аспекта: качество, надежность, рентабельность и гибкость как конкурентные приоритеты в производстве, в то время как гибкость рассматривается как наивысший аспект. Авторы исследовали производственную стратегию крупных производителей Европы, Северной Америки и Японии в 1986 г. Чтобы справиться с сокращением жизненного цикла продукции и увеличением колебаний рынка/спроса, производство должно было обеспечить широкий спектр продуктов, конструкций и колебаний объема. Японские производители стремились повысить конструктивную гибкость и гибкость объема (производительности) и сосредоточились на решении традиционного конфликта между рентабельностью и гибкостью.
В работе [73] представлен обзор различных видов гибкости и их взаимосвязей. Классифицируются одиннадцать аспектов гибкости в производстве. Это гибкость машины, обработки материалов, эксплуатации, процесса, продукта, маршрутизации, объема, расширения, программ, производства и рынка. Эта классификация считается одной из наиболее основательных классификационных систем [74]. Гервин и Тарондо [75] рассматривали гибкость продукта, процесса и объема как гибкость, ориентированную на рынок.
Многочисленные исследования были посвящены изучению гибкости с помощью сетей Петри, которые представлены в [71]. Аланш и др. [76] представил симулятор на основе сети Петри для проектирования и внедрения гибких производственных систем (ГПС) (Flexible Manufacturing Systems (FMS)). Нарахари и др. [77] построили модель сети Петри для анализа различных аспектов поведения FMS. Эль-Сайед и др. [78] разработали имитационную модель для изучения производительности гибкой производственной системы с переменными производственными коэффициентами. Буалем и др. [79] использовали сеть массового обслуживания для моделирования гибкой производственной системы для анализа ее эффективности. В ходе их исследования была изучена модель очередей, состоящая из двух станций и трех классов. Сарен и Тибериу [80] рассмотрели литературу об использовании средств моделирования и их методологии для решения задач проектирования и эксплуатации в гибкой производственной системе в период с 1982 по 2015 г. Их исследования показывают, что инструменты Visual SLAM AweSim и (Colored Petri Nets) CPN в основном используются для решения FMS и других систем дискретных событий.
В работе [81] отмечается, что гибкость, присущая многоцелевым установкам, создает сложности при проектировании и синтезе таких установок. Чтобы гарантировать, что любой ресурс, включенный в проект, может использоваться максимально эффективно, на этапе проектирования должны учтены подробные соображения о планировании производства. Поэтому важно учитывать проектирование, синтез и планирование одновременно.
Проблема проектирования и эксплуатации периодических установок в условиях неопределенности актуальна в настоящее время. Существующие в литературе подходы к решению этой проблемы делятся на 2 группы.
1. Динамическое планирование. Данный подход регулирует неопределенность путем корректировки графика, сгенерированного детерминированной моделью, при реализации неопределенных параметров.
2. Стохастическое планирование. Этот подход учитывает информацию о неопределенности на первоначальном этапе планирования, и его целью является создание оптимальных и надежных графиков при наличии неопределенности.
Синтез многономенклатурных производств химической продукции. В работе [82] на основе отечественных и зарубежных публикаций приведена систематизация основных проблем оптимальной организации многономенклатурных производств химической продукции.
К этим проблемам относятся: автоматизированное моделирование; структурный и параметрический синтез; распределение ресурсов; календарное планирование; оперативное управление; организация работы технологического оборудования и производства в целом; моделирование технологических аппаратов, работающих в периодическом и полупериодическом режимах; логическое управление дискретными исполнительными механизмами.
Все перечисленные проблемы исследуются учеными с начала 1960-х годов и актуальны в настоящее время.
В соответствии с системным подходом [23–28] стратегия исследования гибких ХТС представляет собой многоэтапную задачу [47, 83].
1. Формирование ассортимента, предполагающее его классификацию на основной и дополнительный, и решение задачи синтеза оптимальной ХТС и возможности выпуска на ней дополнительного ассортимента.
2. Анализ возможности совместного выпуска ассортимента и определение минимального количества типов модулей для реализации совмещенной или гибкой ХТС в случае, если ассортимент совместим, или рекомендаций по их выпуску по индивидуальным технологиям в случае не совмещаемого ассортимента.
3. Формирование типовых модулей и построение принципиальной структуры гибкой ХТС в модульном исполнении.
4. Оценка степени гибкости модулей и производства в целом [9, 11, 23, 24, 42, 43, 48, 57–70].
5. Оптимизация выпуска ассортимента (группировка продуктов, маршруты и организация их выпуска) [82, 84, 85].
6. Структурно-параметрический синтез и многокритериальная оптимизация с использованием различных критериев: минимум капитальных или приведенных затрат, минимум времени выпуска ассортимента и/или простоев оборудования, максимум гибкости, – с целью определения оптимальной структуры и размеров оборудования.
В общем случае задача синтеза оптимальных ХТС представляет собой смешанно-целочисленную задачу линейного (Mixed-Integer Linear Programming (MILP)) [86–91] или нелинейного (Mixed-Integer Nonlinear Programming (MINLP)) программирования [92–95, 101–105]. Для решения данной задачи применяются алгоритмы [10, 17, 101–105]: эвристического, направленного перебора, анализа и отсеивания вариантов, ветвей и границ, целочисленного программирования, динамического программирования, геометрического программирования, обобщенного дизъюнктивного программирования [103, 104], внешней аппроксимации [105] и другие.
7. Оценка гибкости синтезируемой схемы и определение ее оптимального значения [47, 48, 61, 68, 83].
8. Разработка оптимального календарного плана с учетом реальной производственной ситуации [82, 90, 91, 115, 116, 118, 119].
9. Определение степени негативных воздействий основного производства, связанных со сбросами и выбросами в окружающую среду, и выработка рекомендаций по их уменьшению. Организация гибких схем очистки стоков и выбросов, регенерации растворителей и ценных компонентов, утилизации твердых отходов [49, 50].
10. Разработка технико-экономического обоснования целесообразности и эффективности действующего или проектируемого производства. Составление бизнес-плана [83].
11. Проектирование гибкой информационно-управляющей подсистемы – автоматизированной системы управления технологическими процессами и производством в целом [22, 29, 30, 101].
Каждый этап представляет самостоятельную задачу исследования с соответствующими теоретическими и практическими проработками. Предлагаемый подход применим для исследования индивидуальных, совмещенных и гибких ХТС в модульном исполнении. Относительная независимость этапов друг от друга позволяет решать некоторые из них в любой последовательности, а при необходимости, исключать этапы, не характерные для рассматриваемых производств.
Некоторые из перечисленных выше задач анализа и синтеза ХТС рассмотрены далее в настоящем обзоре.
Основным этапом технологического проектирования гибких ХТС является синтез химико-технологической системы. Синтез ХТС осуществляется на основе предварительно разработанных математических моделей [25, 28, 100, 108], конкретный вид которых зависит от количества производимых продуктов, числа и типов стадий, а также способа соединения аппаратурных стадий между собой.
Целью синтеза химико-технологических систем является определение наилучшей структуры и оптимальных размеров оборудования, обеспечивающих достижение желаемой цели (заданной производительности, сроков выпуска и т.п.) на основе исходной информации о технологических процессах.
Вопросы синтеза решаются для индивидуальных, совмещенных и гибких химико-технологических систем фиксированного и переменного ассортимента.
Прежде, чем синтезировать совмещенную или гибкую ХТС, формируют оптимальный ассортимент продукции с учетом взаимозаменяемости ее отдельных видов. Задача формирования ассортимента является внешней по отношению к задаче синтеза совмещенной или гибкой ХТС. Но именно мобильность ассортимента служит основной причиной организации гибкого легко перенастраиваемого производства. Так как для каждого класса многоассортиментной продукции задача формирования ее оптимального ассортимента имеет свою специфику, то в дальнейшем будем считать, что ГАПС создается для оптимального ассортимента продукции.
Следует выделить два направления синтеза ХТС: структурный и структурно-параметрический.
В результате структурного синтеза формируется структура индивидуальной, совмещенной или гибкой химико-технологической системы, реализуемая на выбранных типах оборудования [26, 32, 36, 37, 96].
В результате реализации структурного синтеза определяется аппаратурный состав и связи многоассортиментной (гибкой) ХТС. Это направление применимо для фиксированного ассортимента и схем с неполным совмещением стадий (с элементами гибкости). Однако структурный синтез не решает проблему синтеза полностью, так как не позволяет определить размеры оборудования синтезируемой ХТС. Эти вопросы решаются при структурно-параметрическом синтезе [26, 32, 47, 66, 83, 96–98].
Моделирование, синтез, организация дискретных и дискретно-непрерывных многоассортиментных химических производств. Моделирование дискретных интерактивных и конкурентных процессов в ХТС с периодическим режимом работы аппаратов представлено в работе [99].
При моделировании ХТС, включающей аппараты, работающие в периодическом режиме, появляются проблемы моделирования дискретных процессов: смена функциональных состояний технологических аппаратов; начало/окончание взаимодействия аппаратов при транспортных операциях; конфликты из-за общего ресурса и т.д.
В качестве примера рассмотрено моделирование простых и сложных взаимодействий подающих и принимающих аппаратов, соединенных общим коллектором. В роли моделей вышеупомянутых процессов использованы сети Петри. Синхронизация времени начала разгрузки подающего и загрузки принимающего аппаратов в асинхронной модели совершается по правилу редукции. Моделирование конфликта из-за общего ресурса отображается фрагментом сети Петри в виде общей позиции у нескольких переходов.
В работе [96] рассмотрен выбор оборудования, который основывается на методе трехуровневой иерархии задач:
на верхнем уровне в рассмотрение берется задача поиска параметров ХТС, которые будут обеспечивать эффективную эксплуатацию на производстве;
на среднем уровне задача выбора определяется для поиска размеров и требуемого количества оборудования. А также рассматривается задача поиска вариантов переработки партий продуктов для всех стадий ХТС;
на нижнем уровне процесс изучается как задача технологического и механического расчета оборудования на каждой стадии.
Автором предложен метод, который предусматривает декомпозицию основной задачи на задачу нелинейного программирования и на задачи дискретного программирования. К задаче нелинейного программирования относят поиск оптимальных параметров режима функционирования технологической системы. К задачам дискретного программирования относят оптимальный выбор оборудования для отдельно взятой стадии процесса. Декомпозируя так задачу, сначала совершается прогноз значений параметров. Затем параметры итеративно уточняются.
Авторами [98] представлен параллельный гибридный метаэвристический подход к оптимальному выбору производственного оборудования. Задача проектирования заключается в определении количества и производительности основного технологического оборудования, коммунальных услуг и резервуаров для хранения, таких, чтобы конструкционные и производственные цели достигались при минимальных капитальных и эксплуатационных затратах.
Задача оптимального проектирования многоцелевых периодических установок формулируется как смешанная задача целочисленного нелинейного программирования (MINLP). Многие нелинейные модели для периодических производств могут быть переформулированы, как смешанные целочисленные задачи линейного программирования (MILP), при условии, что размеры ограничены дискретными значениями. Поиск оптимального решения таких задач может стать проблемой, так как количество рассматриваемых операций растет экспоненциально, так что даже самые быстрые компьютеры требуют огромного количества времени для анализа.
В статье предлагается подход к оптимальному проектированию многоцелевых периодических установок, который основан на двух метаэвристиках: имитация отжига и оптимизация муравьиной колонии. Имитация отжига широко используется для решения оптимизационных задач. Кроме этого, в работе приводится алгоритм реализации гибридного подхода муравьиной колонии и имитации отжига.
Системы поддержки принятия решений при проектировании многоассортиментных производств. Дальнейшим развитием предложенных задач выбора оборудования является разработка систем поддержки принятия решений для проектирования химико-технологического оборудования для периодического производства [6, 7].
Авторы [6] на основе исследования этапов жизненного цикла, которые проходит технологическое оборудование показали, что около 80% затрат на технологическое оборудование формируется на стадии его проектирования.
В современных условиях цифровизации экономики разработка технологического оборудования должна осуществляться с использованием информационных технологий, в том числе систем поддержки принятия решений (СППР) на всех этапах разработки, вплоть до формирования технической документации [6]. Авторы проводят обзор современного состояния развития систем поддержки принятия решений по автоматизированному проектированию технологического оборудования для химического периодического производства.
Также в статье [6] представлены методы и направления развития автоматизированных систем поддержки принятия решений, основные тенденции развития систем с элементами искусственного интеллекта.
В настоящее время для решения различных задач активно разрабатывают информационные системы на основе онтологии [6].
Для разработки объектно-независимых компонентных систем с искусственным интеллектом было проведено большое количество исследований, а также показано, что использование знаний является перспективным направлением развития автоматизированных информационных систем, и его следует использовать для решения задач разработки технологического оборудования.
Совместное рассмотрение знаний о разработке технологического оборудования и проблемы создания системы информационного обеспечения принятия решений предложено в работе [7]. Для выполнения ряда функций должна быть создана информационная система поддержки принятия решений.
Представлены информационные модели для решения задач расчета определяющих размеров аппаратов ХТС и разработки отдельного технологического аппарата. Предложены различные типы графов для формального описания структуры разрабатываемых ХТС и технологических аппаратов.
Основой системы информационной СППР для решения этих задач являются информационные модели, которые представляют собой формализованную совокупность фактов, понятий, инструкций, предназначенных для удовлетворения информационных потребностей решаемых задач. Информационные модели и результаты решения указанных задач должны храниться и обрабатываться в выбранном информационном хранилище, которое чаще всего используется в качестве базы данных.
Авторы подробно рассматривают задачу определения количества и размеров аппаратов на каждом этапе проектирования технологической системы [7]. Задача ставится как задача оптимизации, критерием оптимизации являются капитальные и эксплуатационные затраты.
Проектирование ХТС в условиях неопределенности. Проектирование ХТС при учете вероятностных ограничений. В работе [66] отмечается, что даже при известных исходных данных при проектировании оптимальных химико-технологических систем имеется неопределенность из-за внешних и внутренних воздействий на ХТС. Причины неопределенности могут быть следующие: непостоянность состава поступающего сырья; изменение массообменных, теплообменных характеристик оборудования; неточности коэффициентов математических моделей и др. Изменения условий функционирования ХТС влияют на эффективность работы системы. При решении задач проектирования оптимальных ХТС прогнозируемые изменения условий функционирования создаваемой ХТС формализуются в виде сведений о неопределенных параметрах.
Для решения задач оптимизации с учетом неопределенности существуют разные подходы: стохастическое программирование; робастная оптимизация; аппроксимирующее динамическое программирование; оптимизация с учетом мягких ограничений [62–66, 92–95, 101–107, 118, 119].
Для решения задач проектирования с учетом неопределенности в исходной информации используют одноэтапную (ОЭЗО) или двухэтапную (ДЭЗО) постановки задач оптимизации. ОЭЗО используется, если изменение управляющих воздействий на этапе функционирования ХТС не предполагается. ДЭЗО используется, если на этапе функционирования ХТС будут возможны уточнение экспериментальных данных и подстройка управления под изменения условий функционирования. Автор статьи [66] рассматривает ОЭЗО с отдельными вероятностными ограничениями (ОЭЗОВО) и неопределенные параметры с известными параметрами закона распределения.
Основная трудность при использовании известных методов нелинейного программирования для решения задач проектирования заключается в объеме вычислений многомерных интегралов. Существует три группы методов снижения этих сложностей: модификации квадратур; методы статистических испытаний Монте-Карло; методы сведения вероятностных ограничений к детерминированному виду.
Автор предлагает подход к решению ОЭЗОВО, базирующийся на преобразовании отдельных вероятностных ограничений. Этот подход включает в себя следующие основные операции: 1) аппроксимация критерия с целью исключения на каждом шаге оптимизационной процедуры многомерного интегрирования; 2) аппроксимация областей совокупностями многомерных прямоугольников в пространстве неопределенных параметров; 3) уточнение используемых аппроксимаций за счет разбиения области неопределенности на подобласти.
Для демонстрации эффективности предложенного метода автор решает ОЭЗО с вероятностными и жесткими ограничениями для разных уровней вероятности и разных размеров области неопределенности предложенным способом (метод 1) и способом, описанным в [62] (метод 2), для двух ХТС.
В первом примере автор рассматривает технологическую систему, состоящую из реактора и теплообменника [63] с рециклом. Во втором примере рассматривается задача проектирования системы реакторов [64], которых протекают реакции превращения вещества А в вещество В и, далее, в вещество С.
При рассмотрении вышеупомянутых примеров автор доказывает, что без учета статистической зависимости неопределенных параметров решение ОЭЗОВО, полученное обоими методами, дает значение критерия, меньшее на 3–18%, чем в [64]. При этом время решения, затраченное при использовании первого метода, меньше, чем время, затраченное при использовании второго метода.
Предложенный в статье способ решения опирается на построение задач, дающих верхнюю оценку критерия ОЭЗОВО. Вычисление верхней оценки критерия ОЭЗОВО сводится к решению последовательности задач нелинейного программирования, размерность которых не изменяется от итерации к итерации.
На этапе формулирования задачи оптимизации решается задача выбора между подходом робастной оптимизации и стохастическим программированием [65]. При использовании робастной оптимизации (оптимизация с мягкими ограничениями, предпочтительнее для случая с небольшим временным интервалом учета неопределенности) основной задачей является обеспечение работоспособности или гибкости ХТС. Использование стохастического программирования применимо для задач с длительным периодом учета неопределенности, в течение которого возможна реконструкция ХТС. Существует 2 типа неопределенности – экзогенная (не зависит от получаемого решения) и эндогенная (на ее поведение влияет решение задачи оптимизации). Экзогенную неопределенность в химической технологии относят к неопределенности на рынке, например, ценам на нефть. Эндогенная неопределенность может быть оценена только после того, как решение было получено. Большинство задач включает оба типа неопределенности, но оптимизация с учетом обоих типов практически не изучалась. Автор работы [65] предлагает формулировку задачи многостадийной оптимизации в виде задачи смешанного дискретно-непрерывного линейного дизъюнктивного программирования. Кроме того, автор показывает, что учет экзогенной и эндогенной неопределенности приводит к резкому увеличению размерности решаемой задачи.
Авторы работы [66] формулируют задачу проектирования оптимальных ХТС, как задачу стохастического программирования в виде одноэтапной задачи оптимизации с вероятностными ограничениями. Предполагается, что оптимальный режим работы ХТС определяется на этапе проектирования и далее не изменяется. Сложность решения задач стохастического программирования заключается в огромных объемах вычисления на каждой итерации оптимизационной процедуры для определения значений левых частей ограничений и критерия задачи. Авторы [66] получают оценку искомого критерия в виде задачи нелинейного детерминированного программирования. Уточнение аппроксимаций в ходе итерационной процедуры проводится авторами за счет разбиения области неопределенности на подобласти. В отличие от ранее предложенных, этот метод не приводит к экспоненциальному увеличению размерности решаемых задач.
В [69] приведено использование методов стохастического программирования при решении задач проектирования многоассортиментных производств в условиях неопределенности.
При разработке технологической схемы важно учитывать неопределенность в поставках и ценах на сырье, а также в спросе на готовую продукцию.
Для решения таких задач используются методы стохастического программирования. В стохастическом программировании предполагается, что распределение вероятностей неопределенных параметров известны заранее.
Частным случаем стохастического программирования является двухэтапное стохастическое программирование.
Разработан и приведен улучшенный L-образный метод двухэтапного стохастического программирования [69] и приведены примеры решения задач.
Оптимальноe проектированиe многопродуктовых многосерийных (многостадийных) производств в детерминированных условиях. Рассматривается многопродуктовое (многоассортиментное) многостадийное производство (задача Гроссмана и Сарджента) [18]. Задача формируется как двухэтапная задача стохастического программирования. На первом этапе рассчитывается количество и объем единиц оборудования. На втором этапе рассчитываются: размер партии каждого продукта; количество аппаратов на каждой стадии цикла; время выпуска (всех партий для каждого продукта). Приведена математическая постановка задачи.
Рассматривается пример многоассортиментного производства по выпуску 5 продуктов, включающего 6 стадий. На каждой стадии максимальное время обработки составляет 4 временных единицы. Предполагается существование трех сценариев выпуска продукции, для которых спрос на каждый продукт может быть высоким, средним или низким. Вероятность среднего спроса 25 или 50%. Высокий и низкий спрос +10 и –10% от среднего.
В детерминированной постановке задачи число оптимизируемых переменных составляет: 96 двоичных переменных, 64 непрерывных переменных, 316 ограничений.
Решена задача планирования в условиях неопределенности спроса на продукцию. Число оптимизируемых переменных в этом случае составляет: 84 – двоичных переменных; 2158 – непрерывных переменных; 2167 – ограничений.
Решение осуществлялось с использованием методов параллельных вычислений на 12 процессорном персональном компьютере.
В работе [102] авторами показана эволюция стратегий динамической оптимизации и ее влияние на оптимальное проектирование и управление ХТП и ХТС. Авторы приводят разностные схемы для численного решения двойственной задачи динамической оптимизации на основе предложенной математической формулировки задачи оптимизации, как задачи нелинейного программирования, учитывающей ограничения типа равенств и неравенств. На ряде реальных примеров из химической технологии авторы [102] продемонстрировали значительные достижения для эффективного и надежного решения задач динамической оптимизации. Примеры также показывают важность применения более гибких формулировок задач, усовершенствованных платформ для моделирования и эффективных программных инструментов для решения задач нелинейного программирования большой размерности. В работе [102] также сформулированы перспективы дальнейшего развития данного направления. Делается упор на необходимость учета неопределенности и многокритериальности при формулировке решений задач оптимального управления.
Проектирование химических производств с учетом гибкости. При проектировании химических производств с учетом гибкости следует выделить два направления [83].
1. Проектирование с заданной степенью гибкости, т.е. определение допустимых диапазонов изменения значений параметров, которые в процессе проектирования должны обеспечивать заданную степень гибкости. Необходимым является удовлетворение экономическим критериям и обеспечение заданных производительностей.
2. Определение оптимальной степени гибкости, т.е. установление зависимости между затратами на повышение степени гибкости при проектировании или функционировании ХТС и его прибылью от использования гибкой ХТС (от реализации выпущенной продукции при ее эксплуатации), обеспечивающими оптимальную степень гибкости.
В [83] приведены постановки задач оптимального проектирования многоассортиментных периодических производств в условиях определенности исходной информации как задачи нелинейного программирования и проектирования с учетом неопределенных параметров, в качестве которых могут быть: коэффициенты переноса, константы скоростей химических реакций, стоимости выпускаемой продукции. Кроме того, во время эксплуатации производства случайным образом могут изменять внешние параметры (температуры, скорости, составы потоков сырья и др.).
Приводятся математические постановки задач определения теста гибкости – т.е. допустимого диапазона изменения технологических параметров, обеспечивающих функционирование системы и количественной оценки индекса гибкости системы для найденного допустимого диапазона изменения технологических параметров.
В работах [31, 47] рассмотрена проблема количественной оценки гибкости формируемых модулей многоассортиментных производств. Авторы приводят математическую постановку задачи оценки гибкости, алгоритмы решения смешанной дискретно-целочисленной оптимизационной задачи. На основе стратегии активных состояний в работах определяются выражения, которые являются необходимыми и достаточными для получения решения.
В [48, 61] рассмотрены вопросы создания многоассортиментных модульных химических производств с учетом гибкости. Предложен двухуровневый подход к оценке гибкости многоассортиментных модульных ХТС. На первом уровне оценивается гибкость модулей, на втором – ХТС в целом. Проводится классификация типовых структур модульных схем и приводятся математические постановки задач определения гибкости совмещенных ХТС с промежуточными емкостями и ХТС с неполным совмещением стадий с промежуточными емкостями и параллельными аппаратами разных типов и объемов. Предложена стратегия решения задач оценки гибкости многоассортиментных ХТС с использованием только активных состояний, сформулированы эвристические правила идентификации этих активных состояний и предложена методика их использования. В [61] приведены примеры практического использования разработанных в [48] методов и алгоритмов для проектирования многоассортиментного производства по выпуску двух продуктов на трех модулях, одном –типовом и двух – индивидуальных. В [61] предложена математическая постановка задачи синтеза многоассортиментных химических производств с учетом гибкости и предложен алгоритм ее решения.
В статье [69] содержится историческая перспектива и обзор новаторской работы, разработанной М. Морари [9] в области устойчивости к химическим процессам. Представлен обзор ранних математических формулировок и методов решения, разработанных И.Е. Гроссманом и его коллегами для количественной оценки статической устойчивости (гибкости). Дан краткий обзор некоторых основополагающих идей М. Морари и его коллег в области динамической устойчивости.
В статье [69] рассматриваются математические формулировки для анализа гибкости, разработанные И.Е. Гроссманом с соавторами в период 1983–1991 гг. [19, 57, 60, 63, 67], получившие развитие в последующих работах [65, 69, 70].
Приведены словесные и математические постановки задач анализа теста гибкости и индекса гибкости, а также методы их решения для случаев с независимыми и коррелированными неопределенными параметрами. Формулируется двухэтапная задача проектирования технологических процессов.
В работе [68] рассмотрена проблема оценки способности ХТС удовлетворять проектным ограничениям на этапе функционирования, возникающая при оптимальном проектировании.
Рассмотрена задача оценки гибкости ХТС для двух стадий: проектирования и функционирования.
На формулировку условий гибкости влияет ряд факторов. Формулировка условий гибкости, приведенная в работе, зависит от уровня неопределенности параметров на этапе функционирования. Неопределенные параметры делятся на 2 группы:
1) параметры, которые можно корректировать на этапе функционирования;
2) параметры, которые нельзя уточнить на этапе функционирования.
Существует 4 варианта условий гибкости для следующих случаев.
Вариант 1: рассматривают все неопределенные параметры первой группы. В этом случае ХТС при фиксированных значениях конструктивных переменных будет гибкой, если для любого значения неопределенного параметра, принадлежащего области значений, можно подобрать такие значения вектора управляющих переменных, что все ограничения будут выполняться.
Вариант 2: ХТС при фиксированных значениях конструктивных переменных будет гибкой, если для любых значений неопределенных параметров первой группы можно подобрать такие значения вектора управляющих переменных, что для всех значений неопределенных параметров второй группы все ограничения будут выполняться.
Вариант 3: вектор неопределенных параметров состоит из 2 подвекторов неопределенных параметров первой и второй групп. На этапе функционирования ХТС значения компонентов вектора неопределенных параметров первой группы могут быть определены с некоторой ошибкой, зависящей от неточности датчиков. При этом компоненты вектора неопределенных параметров второй группы не могут быть уточнены.
Вариант 4: вектор неопределенных параметров второй группы имеет недостаток, что он не учитывает дополнительную экспериментальную информацию, которая имеется на этапе функционирования. В данном случае ХТС при фиксированных значениях конструктивных переменных будет гибкой, если для любого значения вектора неопределенных параметров первой группы можно подобрать такие значения вектора управляющих переменных, что для всех значений неопределенных параметров второй группы все ограничения будут выполняться.
В статье авторы рассматривают 2 подхода к вычислению значений функции гибкости.
1. Метод “ветвей и границ”. Вычисление значения функции гибкости сводится к задаче максимизации функции, зависящей от вектора конструктивных переменных и неопределенных параметров. Данный метод является итерационной процедурой, которая позволяет определить положение максимума решаемой задачи.
2. Метод “разбиений и границ”. Данный метод представляет собой двухуровневую процедуру, которая основана на разбиении области неопределенных параметров на подобласти. На нижнем уровне вычисляют верхнюю и нижнюю границы функции гибкости для всей области неопределенных параметров. Верхний уровень используют для разбиения некоторых подобластей, полученных на предыдущих итерациях.
В работе [106] предлагается многоцелевое линейное программирование для моделирования компромисса сложности и гибкости системы многоассортиментного периодического производства. Рассмотрены переменные стратегического, тактического и оперативного принятия решений.
В [107] авторами представлен обзор литературы, посвященной методологиям реализации “бережливого” производства. Обзор показывает, что принцип “бережливого” производства и инструменты для его реализации становятся довольно популярными для развития производственных систем путем сокращения расходования ресурсов, которые не вносят непосредственного вклада в создание ценности, воспринимаемой заказчиком. Области применения “бережливого” производства довольно разнообразны, начиная от промышленных секторов, таких как автомобилестроение, самолетостроение и заканчивая переработкой отходов [107, 117, 125, 173, 176].
Корректные методологии для реализации “бережливого” производства все еще обсуждаются в практических и научных сообществах, и целостные, единые подходы встречаются крайне редко.
В работе отмечается, что для дальнейшего расширения “бережливого” производства необходимы целостные подходы и совместные усилия между взаимосвязанными сторонами проектирования производственных систем.
Общий диагноз текущего состояния производственной системы может привести к более детальному плану и помочь сэкономить время, избегая повторяющихся процессов сбора информации [107].
Авторы работы представляют целостный методологический подход (на основе “бережливого” производства) к проектированию гибких производственных систем, интегрирующий все соответствующие компоненты, в том числе управление производственными ресурсами, планирование операций, а также внутреннюю логистику [107].
В статье описывается методология для комплексного проектирования производственных систем. Акцент делается на описании основных этапов методики и набора инструментов, которые могут быть использованы для поддержки каждого этапа. Также в работе описано применение данного методологического подхода к перепроектированию производственных систем.
В итоге, авторы делают вывод, что комплексный методологический подход, предложенный в работе, рассматривает все составляющие системы производства, включая планирование операций, определяющих компоновку производственного оборудования, а также размеры логистической инфраструктуры. Этот подход и разработанные инструменты подходят для проектирования и оценки новых гибких производственных систем охвата заказных продуктов, которые производятся в небольшом объеме, и продуктов с высоким уровнем адаптации под индивидуальные требования заказчика.
ПЛАНИРОВАНИЕ И СОСТАВЛЕНИЕ РАСПИСАНИЙ РАБОТЫ МНОГОАССОРТИМЕНТНЫХ ХИМИЧЕСКИХ ПРОИЗВОДСТВ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ ИНФОРМАЦИИ
Для обеспечения оптимального функционирования многоассортиментных химических производств (МАХП) известны традиционные подходы, на основе которых разработаны математические модели и алгоритмы: управления отдельными технологическими процессами; технико-экономического и календарного планирования [109–138 ].
В последние годы активно развиваются научные исследования в области решения следующих задач:
планирования МАХП с учетом их последующего функционирования;
планирования и составления расписаний в условиях неопределенности информации;
интеграции методов планирования и составления расписаний;
интеграции методов планирования, составления расписаний и управления в режиме реального времени.
Планирование технического обслуживания оборудования рассматривается отдельно от технологических решений, но связанно с ними. Действия по техническому обслуживанию направлены на сохранение или восстановление производительности процесса. Профилактическое обслуживание планируется проводить регулярно, чтобы сохранить состояние оборудования, в то время как корректирующие действия по техническому обслуживанию необходимы, когда оборудование выходит из строя. Планирование процедур технического обслуживания является сложной задачей, так как операторы должны учитывать компромиссы между затратами на само техническое обслуживание, поддержание высокой готовности оборудования и причины производственных сбоев, которые создают помехи в реализации и исполнении плановых решений по планированию производственных процессов [109].
По сути, планирование технического обслуживания должно соединять временную шкалу планирования/планирования производственных процессов с более длительным временным горизонтом, учитывающим влияние (отсутствие) технического обслуживания на долгосрочные технологические операции [110]. На самом простом уровне решения по техническому обслуживанию оборудования могут быть встроены в планирование производства с помощью параметризации ухудшения состояния оборудования. Например, можно предположить, что изменение состояния оборудования зависит только от количества времени, прошедшего с момента последнего события технического обслуживания [111], используя параметр скорости изменения, выведенный из архивных данных.
Более сложные модели снижения работоспособности могут быть построены на основе мониторинга производительности оборудования. Для этого могут быть использованы данные, например, о потреблении энергии, выходе процесса [112, 113], а полученные модели могут быть встроены в плановые расчеты. Последние разработки в области мониторинга состояния оборудования, которые опираются на потоки данных по конкретному оборудованию, такие как вибрация машины, температура, звук и видеозаписи для получения более точной информации о состоянии оборудования, также были включены в планирование производства [114–116].
В статье [117] приводится формулировка задач краткосрочного планирования и технического обслуживания для многоассортиментных периодических производств с учетом загрязнения технологического оборудования.
Рассмотрено многоассортиментное периодическое производство, включающее емкость для приготовления исходного сырья мономера, гомогенизатора для приготовления мономерной эмульсии и реактора периодического действия, в котором после загрузки эмульсии осуществляется процесс полимеризации с подачей инициатора. После завершения процесса полимеризации продукт перегружается в один из множества резервуаров.
Рассматривается описанный выше процесс для случая не более 20 заказов и не более трех уникальных рецептур (продуктов).
Сначала решались задачи без учета технического обслуживания, связанного с загрязнением оборудования – реакторов и теплообменников. Затем решалась задача с учетом технического обслуживания в зависимости от последовательности выпускаемых продуктов. Под техническим обслуживанием понимается очистка реакторов и теплообменников от загрязнения.
В работе составлены математические модели с учетом того, что отсутствуют емкости между стадиями производства и/или имеются емкости (резервуары) для хранения конечных продуктов бесконечного размера.
Рассмотрены различные постановки задач по техническому обслуживанию с целью устранения загрязнений:
модели по техническому обслуживанию, выполняемому независимо от производственных заказов;
модели технического обслуживания, выполняемого перед каждым производственным заказом.
Обзор составления расписаний и планирования в условиях неопределенности был предложен в статье [118], которая является первой работой, пытающейся дать всестороннее описание достижений и будущих направлений составления расписаний и планирования в условиях неопределенности информации.
Петков и Маранас рассмотрели планирование и составление расписаний для многопродуктовых серийных производств в условиях неопределенности спроса [119].
Баласубраманян и Гроссман рассмотрели проблему планирования в условиях неопределенности спроса для многоассортиментной периодической установки [120], и эти неопределенности были подчинены стандартному нормальному распределению. Проблема оперативного планирования крупномасштабных промышленных периодических производств в условиях неопределенности сроков и объемов спроса была решена Вердерем и Флоудас с использованием различных методов, которые представляли собой робастную оптимизацию [121] и условную систему оценки риска [122].
В работе [123] рассмотрены вопросы проектирования и составления расписания для периодических химических производств. Приводятся результаты разработки и решения стохастической оптимизационной модели.
В работе [124] изложен алгоритм аналитического решения задач смешанно-целочисленного линейного программирования MILM (mp-MILP) для случая неопределенных значений коэффициентов левой и правой частей системы неравенств (ограничений) и коэффициентов целевой функции (данная неопределенность названа авторами глобальной неопределенностью).
В частности, рассматриваются решения задачи составления расписания в условиях глобальной неопределенности.
Рассмотрен ряд примеров решения задач составления расписаний. Рассмотрено двухстадийное производство трех продуктов (A, B и C). Предполагается, что время обработки продукта B на второй стадии является неопределенной величиной, равномерно распределенной на интервале 4–8 ч.
Также рассмотрен пример двухстадийного выпуска пяти продуктов. Были получены две альтернативные последовательности выпуска продуктов: D–E–C–A–B и D–A–C–E–B.
Рассмотрена задача составления расписания для трехстадийного выпуска четырех продуктов, включающего стадию смешения, два параллельно работающих реактора и стадию сепарации.
Показана эффективность предложенных алгоритмов MILP-задач в условиях глобальной неопределенности на гипотетических примерах и при решении задач составления расписаний для многоассортиментных производств.
В статье [125] рассматривается интеграция тактических и оперативных решений, при которых известно прогнозируемое значение спроса на продукцию на определенный горизонт планирования (3–6 мес.). Необходимо принять решение о распределении выпуска продукции между отдельными ее производителями. Для каждого производителя необходимо решить задачи краткосрочного планирования производства продукции и выполнения заказов ее поставки различным потребителям на 2–3 нед. При этом задача планирования решается каждый месяц, а задача выполнения заказов ее поставки различным потребителям расписаний – еженедельно. Эти периоды называются в статье “горизонты принятия решений”.
В качестве критериев оптимизации решения задач используется прибыль от реализуемой продукции (удовлетворяющей определенному спросу) при ограничениях на производственные, складские и транспортные расходы.
Представлена интегрированная модель планирования и составления расписаний (Integrated Planning and Scheduling Models (IPSM)), которая состоит из модели планирования и модели составления расписания, объединенными уравнениями связи (связующими ограничениями) [125].
Эта задача фактически является задачей составления оптимальной производственной программы.
Для моделирования в работе [125] используется агентное моделирование. Агентами, включенными в разработанную “платформу” для моделирования интегрированных процессов, являются: “планировщик” спроса, “планировщик” логистики, “планировщик” интегрированного планирования.
В статье [126] представлен краткий обзор проблемы многомасштабного временного моделирования, а также интеграции различных моделей для уровней принятия решений планирования, составления расписаний и контроля.
Оптимизация в масштабах всего предприятия (Enterprise-Wide Optimization (EWO)) стала основной целью в связи с растущим давлением для сохранения конкурентоспособности на мировом рынке. Она предполагает оптимизацию поставок, производственную и сбытовую деятельность компании для снижения затрат, материальных запасов и воздействия на окружающую среду и максимизацию прибыли.
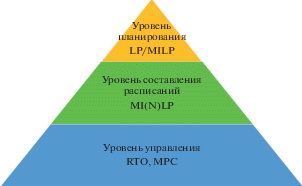
Основные задачи оптимизации в масштабах всего предприятия включают в себя, прежде всего, интеграцию нескольких масштабов по шкале времени от нескольких лет, месяцев до минут для решения задач планирования, составления расписаний и контроля. Вторая серьезная проблема, которая является следствием характера трех основных уровней принятия решений – необходимо координировать различные типы моделей, как показано на рис. 1. Как правило, уровень планирования включает линейное программирование (Linear Program (LP)) и модели MILP, модели MILP/MINLP используются на уровне составления расписания и планирования, а модели прогнозирующего управления (Model Predictive Control (MPC) и оптимизации в реальном времени (Real Time Optimization (RTO)) – на уровне управления.
Рис. 1.
Иерархическая структура моделей оптимизации в масштабах всего предприятия: MILP – Mixed Integer Linear Programming (смешанное целочисленное линейное программирование), MINLP – Mixed Integer Nonlinear Programming (смешанное целочисленное нелинейное программирование), RTO – Real Time Optimization (оптимизация в реальном времени), MPC – Model Predictive Control (модель прогнозирующего управления).
Известны три основных подхода составления расписаний:
1) агрегация модели подробного планирования;
2) проекция модели планирования на решения уровня составления расписаний;
3) итеративная декомпозиция моделей планирования и составления расписаний.
Первый подход рассмотрен в работах Эрдирик–Доган и Гроссмана [127, 128]. Второй подход – в работе Сунга и Маравелиаса [129]. Третий подход – в работе Терразас и Гроссман [130] и Кальфа [131].
Авторы [127, 128] рассмотрели вопросы планирования и составления расписаний как задач смешанно-целочисленного линейного программирования (MILP). Эта модель основана на непрерывном представлении во временной области на основе временных интервалов.
Для обеспечения интеграции планирования и составления расписаний проблема разбивается на два основных уровня:
Верхний уровень соответствует модели планирования на заданном временном горизонте – упрощенная MILP, в которой влияние изменений отражается через ограничения [131]. Эта модель дает нижнюю границу общей стоимости.
На нижнем уровне модель планирования MILP для каждого объекта может быть решена независимо.
В работе [132] рассматриваются вопросы интеграции задач планирования, составления расписаний и многопараметрического нелинейного управления.
Изменчивая глобальная рыночная среда, растущая конкуренция и необходимость снижения затрат и воздействия на окружающую среду – некоторые из причин, которые привели обрабатывающие отрасли к поиску более оперативных и интегрированных производственных процессов. Оптимизация в масштабах предприятия направлена на решение вышеупомянутых задач.
В рамках EWO авторы стремятся к более интегрированному принятию решений посредством скоординированной оптимизации функциональных возможностей цепочки поставок, чтобы в целом гарантировать эффективный обмен информацией и оптимальные операции на разных уровнях принятия решений. Концептуальное представление оптимизации в масштабах предприятия объединяет различные уровни принятия решения, ключевые решения и временные шкалы – от планирования цепей поставок, составления расписания, календарного планирования до оптимизации (оперативного планирования) в режиме реального времени и управления [133].
Традиционно проблемы планирования, составления расписаний и управления моделировались и решались последовательно. В последнее время ряд исследовательских работ был посвящен их интеграции [132].
Естественно следует, что интеграция планирования, диспетчеризации (составления расписания, календарного планирования) и управления (Integrated Planning Scheduling and Control (iPSC)) может привести к более эффективному производству, поскольку синергетический эффект между отдельными проблемами может улучшить операции процесса.
В работе предложена структура для iPSC с обратной связью при динамических возмущениях и показано, как учет неопределенных условий работы вызывает необходимость интеграции среди разных уровней принятия решений.
Интеграция контроля и составления расписаний привлекла значительное внимание со стороны исследовательского сообщества из-за потенциальной выгоды, вытекающей из использования лежащих в их основе синергетических эффектов [134, 135].
В ходе ряда тематических исследований авторы продемонстрировали, как замкнутый контур интегрированного составления расписаний и управления (Integrated Scheduling and Control (iSC)) может справиться с отклонением помех в течение производственного и переходного периодов. Альтернативная методология для замкнутого цикла iSC была представлена в [136]. В автономном режиме авторы создали несколько PI-контроллеров для каждого возможного перехода и изучили интегрированную задачу как оптимальное одновременное планирование и выбор контроллера.
Стремясь сократить время, необходимое для решения этой задачи, Чжугэ и Иерапетритоу [137] предложили использовать многопараметрическую модель прогностического управления в контексте iSC. Сначала была линеаризована исходная нелинейная модель системы, а затем был разработан контроллер. Затем полученные решения были включены в модель планирования в виде набора ограничений, а общий замкнутый контур интегрированного составления расписаний и управления смоделирован как MILP. Позже те же авторы предложили использовать быструю модель прогнозирующего управления [138].
Для уровня управления представлена новая концепция контроллеров с несколькими заданными значениями для специального класса нелинейных динамических систем. Исследования показывают, что использование контроллеров с несколькими заданными значениями в рамках замкнутого цикла позволяет в реальном времени реализовывать решения, принятые интегрированной системой в условиях динамических сбоев.
ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ СПЕЦИАЛИЗИРОВАННОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧ МОДЕЛИРОВАНИЯ, СИНТЕЗА, ПРОЕКТИРОВАНИЯ И УПРАВЛЕНИЯ МНОГОАССОРТИМЕНТНЫМИ ХИМИЧЕСКИМИ ПРОИЗВОДСТВАМИ
Для решения задач смешанного целочисленного линейного программирования, смешанного целочисленного нелинейного программирования, обобщенного дизъюнктивного программирования (Generalized Disjunctive Programming (GDP)) широко используется программный продукт GAMS (General Algebraic Modeling System).
GAMS – это высокоуровневая система моделирования для математического программирования и оптимизации. Он состоит из компилятора языка и ряда связанных с ним так называемых решателей, которые представляют собой либо автономные исполняемые файлы, либо библиотеки, доступные из программы [139].
Язык моделирования GAMS позволяет быстро переводить задачи оптимизации в компьютерный код. Компилятор языка GAMS затем переводит этот код в формат, который решатели могут интерпретировать и выполнить. Такая архитектура обеспечивает большую гибкость, позволяя изменять используемые решатели без изменения формулировки модели.
GAMS создает задачи оптимизации из пользовательских моделей и данных, а также извлекает результаты для анализа и обработки, но не решает задачу оптимизации. Вместо этого в GAMS используются вышеупомянутые решатели (в настоящее время – 53 шт.). На сайте [139] представлено их краткое описание, типы моделей (табл. 2) и поддерживаемые платформы.
Таблица 2.
Типы моделей GAMS
| Тип модели GAMS | Описание типа модели | |
|---|---|---|
| LP | Linear Program | Линейное программирование |
| NLP | Nonlinear Program | Нелинейное программирование |
| QCP | Quadratically Constrained Program | Программирование с квадратичными ограничениями |
| DNLP | Discontinuous Nonlinear Program | Дискретное нелинейное программирование |
| MIP | Mixed Integer Program | Частично-целочисленное программирование |
| RMIP | Relaxed Mixed Integer Program | Мягкое смешанное целочисленное программирование |
| MINLP | Mixed Integer Nonlinear Program | Частично-целочисленное нелинейное программирование |
| RMINLP | Relaxed Mixed Integer Nonlinear Program | Мягкое частично-целочисленное нелинейное программирование |
| MIQCP | Mixed Integer Quadratically Constrained Program | Частично-целочисленное программирование с квадратичными ограничениями |
| RMIQCP | Relaxed Mixed Integer Quadratically Constrained Program | Мягкое частично-целочисленное программирование с квадратичными ограничениями |
Базовый модуль GAMS включает в себя все решатели с открытым исходным кодом, некоторые бесплатные решатели и ссылки (около 20), а также все другие решатели в ограниченных по размеру версиях. Хотя все они включены в систему GAMS, некоторые из них требуют коммерческой лицензии, а использование регулируется лицензионным соглашением. Есть бесплатная ознакомительная лицензия.
В обзоре [140] представлен широкий спектр зарубежного коммерческого и свободно распространяемого программного обеспечения для решения задач MINLP, в том числе и языка MINOPT (Mixed Integer Nonlinear Optimizer – смешанный целочисленный нелинейный оптимизатор), который был разработан К.А. Швайгером и К.А. Флудасом (кафедра химического машиностроения, Принстонский университет) в качестве языка моделирования для широкого круга оптимизационных задач. Для задач MINLP в MINOPT предложено несколько алгоритмов, таких как варианты внешней аппроксимации (Outer Approximation (ОА)), общего разложения по Бендерсу (General Benders Decomposition (GBD)) и обобщенная перекрестная декомпозиция (Generalized Cross Decomposition (GCD)) [140].
Дистрибутив языка свободно доступен на сайте http://titan.princeton.edu/MINOPT.
MINOPT – это язык моделирования для решения широкого спектра оптимизационных задач, сформулированных в виде математических программ. Это комплексная система, которая может решать задачи линейного программирования, смешанного целочисленного линейного программирования, нелинейного программирования, нелинейного программирования с дифференциальными и алгебраическими ограничениями, задачи смешанного целочисленного нелинейного программирования с дифференциальными и алгебраическими ограничениями, задачи оптимального управления и смешанные целочисленные задачи оптимального управления. MINOPT имеет также интерфейсы к коммерческому программному обеспечению для задач оптимизации [141].
Авторами [140] представлены для ознакомления широкодоступные решатели MINLP и описания их основных свойств. Большинство решателей не основаны на “чистом” алгоритме, но они объединяют несколько методов и идей для повышения своей производительности. Среди решателей MILP наиболее известными коммерческими являются CPLEX, Gurobi и XPRESS. Решатели GLPK и Cbc, последний является частью инициативы COIN-OR (Computational Infrastructure for Operations Research – вычислительная инфраструктура для исследования операций) и является одним из наиболее признанных решателей с открытым исходным кодом для MILP. Все эти решатели реализуют арсенал методов в рамках структуры ветвей и границ. В случае нелинейного программирования (НЛП) такие решатели, как CONOPT, Knitro, Mosek и SNOPT, являются хорошо известными коммерческими продуктами, а IPOPT (Interior Point Optimizer – оптимизатор внутренней точки) – хорошо известным решателем с открытым исходным кодом (также частью инициативы COIN-OR). Существует большая вариативность алгоритмов, лежащих в основе решателей НЛП. Например, CONOPT реализует обобщенный метод редуцированного градиента (Generalized Reduced Gradient (GRG)), в то время как IPOPT, Knitro и Mosek используют метод внутренней точки. А SNOPT использует подход последовательного квадратичного программирования (Sequential Quadratic Programming (SQP)) [142].
В обзоре [140] приводятся только основные характеристики решателей. Краткое изложение решателей и программное обеспечение для решения проблем MINLP ранее также было предоставлено [143]. Решатели реализованы на различных языках программирования либо в виде автономных исполняемых файлов, либо в виде библиотек, доступных из программ алгебраического моделирования, таких как GAMS, AMPL (A Mathematical Programming Language – язык математического программирования) и AIMMS (Advanced Interactive Multimedia Modeling System – усовершенствованная интерактивная мультимедийная система моделирования). Другие решатели реализованы непосредственно на тех же языках программирования, что и их моделирующие системы, например MATLAB, Python-Pyomo, Julia-JuMP. Решатели, используемые при численном моделировании, представлены в табл. 3.
Таблица 3.
Обзор и сравнение решателей для выпуклой MINLP [140]
| № п/п |
Решатель | Разработчик(и), страна, сайт | Реализованные алгоритмы, методы | В каких пакетах прикладных программ может использоваться | Тип лицензии |
|---|---|---|---|---|---|
| 1. | AlphaECP (Alpha Extended Cutting Plane – альфа-расширенный метод секущих плоскостей) | Исследовательская группа T. Вестерлунда в университете Або Академи, Финляндия, www.gams.com/latest/docs/ S_ALPHAECP.html | ECP (Extended Cutting Plane – расширенный метод секущих плоскостей), GAECP (Generalized Alpha Extended Cutting Plane – обобщенный альфа-расширенный метод секущих плоскостей) | GAMS, NEOS (Network-Enabled Optimization System – сетевая система оптимизации) | Kоммерческая |
| 2. | ANTIGONE (Algorithms for coNTinuous/Integer Global Optimization of Nonlinear Equations – алгоритмы непрерывной/целочисленной глобальной оптимизации нелинейных уравнений) |
Майзенер (R. Misener) и Флоудас (C.A. Floudas), Принстонский университет, США, www.gams.com/latest/docs/S_ANTIGONE.html | Метод ветвей и границ, локальные решатели CONOPT или SNOPT для поиска возможных решений и CPLEX для ослабления ограничений MILP | GAMS, NEOS | Kоммерческая |
| 3. | AOA (AIMMS Outer Approximation) | AIMMS, Нидерланды, www.aimms.com/english/developers/resources/solvers/aoa | Основан на методах внешней Аппроксимации и реализует как обычные методы OA, так и
линейные и нелинейные методы ветвей
и границ LP/NLP-BB. CPLEX и Gurobi доступны в качестве линейных подпрограмм. Для решения задач НЛП можно использовать CONOPT, IPOPT, Knitro, Minos и SNOPT |
AIMMS | Kоммерческая (исходный код доступен) |
| 4. | BARON (Branch and Reduce Optimization Navigator – навигатор оптимизации ветвей и границ) | Исследовательская группа Н.В. Сахинидиса, США, www.minlp.com/baron | Метод многогранных ветвей и границ решает линейные задачи программирования-релаксации в узлах BB. Включает IPOPT, FilterSD или FilterSQP для решения подзадач NLP, а также может использовать любой доступный решатель NLP в GAMS. Cbc, CPLEX или Xpress могут использоваться как подпрограммы LP и MILP | автономно; AIMMS, AMPL, GAMS, JuMP, MATLAB, NEOS, Pyomo, YALMIP | Kоммерческая |
| 5. | BONMIN (Basic Open-source Nonlinear Mixed Integer Programming – базовое нелинейное смешанное целочисленное программирование с открытым исходным кодом) | П. Бонами в сотрудничестве между Университетом Карнеги-Меллона (США) и IBM Research в рамках инициативы COIN-OR (Computational Infrastructure for Operations Research – вычислительная инфраструктура для исследования операций), projects.coin-or.org/Bonmin | NLP-BB, LP/NLP-BB, OA, алгоритм технико-экономического планирования, метод ветвей и границ на основе OA, гибридный подход. В качестве подпрограмм BONMIN использует IPOPT для NLP и Cbc или CPLEX для проблем MILP | автономно; AMPL, C++, GAMS, JuMP, MATLAB, NEOS, OS, Pyomo, YALMIP | Открытый исходный код (EPL (Eclipse Public License) 1.0) |
| 6. | Couenne (Convex Over and Under Envelopes for Nonlinear Estimation – выпуклые над и под огибающими для нелинейной оценки) | Разработан П. Белотти в рамках инициативы COIN-OR в сотрудничестве между Университетом
Карнеги-Меллона (США) и IBM Research projects.coin-or.org/Couenne |
Реализует основанный на LP метод пространственных ветвей и границ в качестве своего
основного алгоритма в дополнение к методам сокращения границ и первичной эвристике. Использует IPOPT как подпрограмму NLP, CBC или CPLEX как подпрограмму MILP и CLP, CPLEX, Gurobi, SoPlex или Xpress как подпрограмму LP |
автономно; AMPL, C++, GAMS, JuMP, NEOS, OS, Pyomo. В настоящее время это единственный глобальный решатель MINLP, доступный в пакете оптимизации COIN-OR |
Открытый исходный код (EPL 1.0) |
| 7. | DICOPT (Discrete Continuous Optimizer – дискретный непрерывный оптимизатор) | Разработан исследовательской группой И.Е. Гроссмана в Университете Карнеги-Меллона (США), www.gams.com/latest/docs/ S_DICOPT.html | Методы ослабления равенства и расширенного штрафа в сочетании с внешней аппроксимацией
OA. DICOPT может использовать любые доступные подпрограммы MILP и NLP, имеющиеся в GAMS |
GAMS, NEOS | Kоммерческая |
| 8. | Knitro (Nonlinear Interior point Trust Region Optimization – нелинейная внутренняя точечная оптимизация доверительной области) | Artelys (США), www.artelys.com/knitro |
Первый метод использует алгоритм NLP-BB, и второй метод основан на алгоритме LP/NLP-BB. Третий метод, основанный на подходе последовательного квадратичного программирования, в основном предназначен для задач со стоимостными функциями и может обрабатывать задачи MINLP, где дискретные переменные не могут быть ослаблены, например, функции, заданные симуляторами черного ящика | AIMMS, AMPL, C++, C#, Fortran, Java, JuMP, GAMS, NEOS, Pyomo, Python, YALMIP | коммерческая |
| 9. | LINDO (Linear, Interactive, and Discrete Optimizer – линейный, интерактивный и дискретный оптимизатор) | LINDO Systems Inc., www.lindo.com | Включает специальные алгоритмы для решения линейного, квадратичного программирования (QP), конического программирования, полуопределенного программирования (Semidefinite Programming (SDP) и общих задач нелинейного программирования. Для задач со смешанными целыми числами LINDO использует подход ветвей и границ. Для решения общих нелинейных задач LINDO требуется решатель NLP CONOPT. Кроме того, если доступен решатель Mosek, он используется для эффективного решения конических и SDP-задач | C, C++, Delphi, Excel/What’s Best!, Fortran, Java, JuMP, GAMS, LINGO, MATLAB, NEOS, .NET, Ox, Python, R |
коммерческая |
| 10. | SCIP (Solving Constraint Integer Programs – решение целочисленных программ с ограничениями) | Разработан Т. Ахтербергом в Берлинском институте Цузе в сотрудничестве с Техническим университетом Дармштадта, Рейнско-Вестфальским техническим университетом Ахена и университетом Эрлангена-Нюрнберга. Дополнен Вигерске и Глейкснер, scip.zib.de | Основан на ветвлении для целочисленного программирования с ограничениями и смешанного целочисленного программирования. Для решения выпуклой и невыпуклой задачи MINLP с использованием многогранных внешних аппроксимаций и метода пространственных ветвей и границ. В решателе также используются различные первичные эвристические методы и методы сжатия границ | автономно; AMPL, C, GAMS, JuMP, MATLAB, NEOS, Java, Pyomo, Python | Свободно распространяемое для академического использования (ZIB academic license); коммерческая |
Таким образом, в зарубежной практике для решения смешанно-целочисленных задач нелинейного программирования широко используются специализированные системы моделирования и оптимизации.
Кроме перечисленных выше программных комплексов для моделирования химико-технологических процессов и систем широко используются следующие программные комплексы.
Aspen HYSYS (https://www.aspentech.com/en/ products/engineering/aspen-hysys). Программа позволяет производить динамическое моделирование отдельных процессов и всей технологической цепочки, а также разрабатывать и отлаживать схемы регулирования процессов. Имеется возможность выполнять расчеты основных конструктивных характеристик сепарационного оборудования, емкостей, теплообменной аппаратуры, тарельчатых и насадочных ректификационных колонн и оценку стоимости оборудования. Программа имеет развитый графический интерфейс и хорошо интегрирована с офисными приложениями Microsoft. Программа платная, но доступна пробная версия [144].
Aspen Plus (https://www.aspentech.com/en/products/engineering/aspen-plus). Продукт американской компании Aspen Technologies Inc. Программа Aspen Plus разработана для Unix-платформ DEC-alpha и Solaris. Aspen Plus – система для статического моделирование процессов, основанных на химическом и фазовом превращении. Имеет широкий набор алгоритмов, который постоянно расширяется. Система имеет развитый графический интерфейс. Имеется возможность выполнять расчеты основных конструктивных характеристик и оценку стоимости оборудования. Программа платная, пробной версии нет [145].
ChemCad (https://www.chemstations.com/ CHEMCAD). Продукт американской компании ChemStations Inc. ChemCad – пакет программ для моделирования и расчета технологических схем с рециклическими потоками органических и неорганических веществ и смесей (например, нефтяных фракций), а также энергетических потоков. ChemCad позволяет создавать, анализировать и оптимизировать различные варианты технологического оформления производственных процессов, оценивать их эффективность и выбирать наилучший из них [146].
ChemCad предназначен для выполнения следующих задач:
подготовки оптимальных исходных данных по единицам оборудования и трубопроводным системам для рабочего инженерно-технического проектирования при создании новых, а также реконструкции и диверсификации действующих химических и нефтехимических производств;
исследования и оптимизации работы систем автоматического регулирования химико-технологических процессов, в том числе и в составе систем автоматизированного управления технологическими процессами;
разработки динамических моделей действующих технологических процессов, так называемых “виртуальных производств” при создании тренажеров для операторов и инженеров химических производств.
Пакет программ платный, но доступна демоверсия.
В работе [147] продемонстрированы возможности универсальной моделирующей программы ChemCad [148] для решения задач системного анализа и оптимизации ХТС.
В статье [80] приведено программное обеспечение для моделирования гибких производственных систем (табл. 4).
Таблица 4.
Программы для разработки и моделирования гибких производственных систем
| № п/п | Название программы | Описание, функциональные возможности |
|---|---|---|
| 1. | ARENA | Моделирование дискретных событий. Создает модель процесса, размещая модули (элементы), которые отображают последовательные процессы или логику событий |
| 2. | Auto Mod | Моделирование производственных и логистических систем. Графическое моделирование для анализа сложных производственных систем и систем обработки материалов. Предназначена для детального анализа операций и потоков |
| 3. | Visual SLAM AweSim | Создание сети или блок-схемы для моделирования дискретных событий и непрерывных моделей |
| 4. | MATLAB Petri Net Toolbox | Моделирование, анализ и проектирование дискретных систем событий на основе моделей сети Петри |
| 5. | CPN tools | Графическое моделирование и анализ раскрашенных сетей Петри |
| 6. | TINA | Набор инструментов для создания временных сетей Петри |
| 7. | CPN-AMI | Набор инструментов для моделирования и верификации сетей Петри |
| 8. | GreatSPN | Качественный и количественный анализ сетей Петри (в том числе, стохастических) |
| 9. | Romeo | Набор инструментов для временных сетей Петри T-Time |
| 10. | Snoopy | Создавание и анимация иерархических графов, среди прочего, сетей Петри (стохастических, непрерывных, временных, гибридных/расширенных) |
| 11. | SimHPN | Моделирование, анализ и синтез систем, смоделированных с помощью гибридных сетей Петри |
| 12. | Delphi simulation software | Моделирование гибкой производственной системы. Объектно-ориентированные функциональные сети в гибкой производственной системе |
| 13. | Artifex PN software tool | Среда моделирования и симуляции поддерживает проектирование систем дискретных событий (в том числе сетей Петри) |
| 14. | QUEST | Инструменты моделирования и симуляции для производственной системы. Объектно-ориентированное моделирование. Системный анализ и возможность вывода результатов для системы дискретных событий |
| 15. | SIM PROCESS | Инструмент иерархического моделирования, сочетающий в себе отображение процессов, объектно-ориентированное моделирование, моделирование дискретных событий и калькуляцию затрат. Разработка графических моделей, оптимизация процессов, оценки деятельности, ресурсов и производственных затрат, визуализация динамики процессов и узких мест |
Для исследований авторами рекомендуется использовать CPNtools (графическое моделирование раскрашенных сетей Петри) и MATLAB Petri Net Toolbox, поскольку они подходят для академических целей и могут быть связаны с другими модулями, такими как, например, нечеткая логика или нейронные сети, что удовлетворяет исследовательским требованиям. А инструменты Visual SLAM AweSim (сетевые или поточные диаграммы) и CPN Tools в основном используются для решения задач моделирования гибких производственных систем и других систем дискретных событий.
Решение производственных задач с использованием специализированного программного обеспечения представлено в работах [132, 149–151].
Работа [149] посвящена конкретному практическому применению метода “ветвей и границ” (Branch and Bound (B&B)) на графических процессорах – оптимальному подбору химического оборудования для многопродуктовых периодических установок.
Наиболее распространенный подход, используемый для решения этой проблемы, формулируется как модель смешанного целочисленного нелинейного программирования (MINLP). Вариант, гарантирующий глобальную оптимальность в решении задачи периодического проектирования, основывается на разработке линейных моделей. Многие нелинейные модели для периодического проектирования можно переформулировать, как задачи линейного программирования (MILP), в которых размеры ограничены дискретными значениями. С помощью подхода B&B уменьшаются объемы вычислений.
Современные компьютеры все чаще становятся гетерогенными, с различными типами вычислительных единиц. Например, многоядерные системы повышают производительность не только за счет добавления ядер, но также и путем включения специализированных возможностей обработки (графические процессоры (Graphics Processing Units (GPUs)), цифровые процессоры (Digital Signal Processors (DSPs)), и т.д.) для обработки конкретных задач. Графические процессоры (GPUs) в настоящее время являются самым мощным вычислительным оборудованием, при этом доступным по цене. С помощью центрального процессора (Central Processing Unit (CPU)) графические процессоры могут не только создавать 3D-графики, но и выполнять высокопроизводительные универсальные расчеты.
В данной статье авторы исследуют реализацию метода B&B на CPU-GPU системе с использованием среды программирования CUDA. Чтобы облегчить структурированное исследование пространства поиска, оно рассматривается как дерево. Автор подробно описывает структуру дерева, а также как им пользоваться.
Далее перечислены некоторые примеры использования системы GAMS.
Оптимизация планирования предприятия в условиях изменяющейся во времени неопределенности: на примере исследования производства поливинилхлорида [150].
Решение задачи краткосрочного (оперативного) планирования параллельного процесса крекинга с несколькими типами сырья [151].
Моделирование интегрированной задачи планирования, составления расписаний и управления производством продукта в непрерывном реакторе с мешалкой [132].
В результате проведенного анализа можно сказать, что основными ограничениями массового использования зарубежного программного обеспечения являются: дороговизна; англоязычные интерфейсы; решение в основном задач оптимизации, и в меньшей степени задач моделирования гибких ХТС и организации выпуска ассортимента.
Кафедра компьютерно-интегрированных систем в химической технологии (КИС ХТ) РХТУ им. Д.И. Менделеева на протяжении долгих лет занимается разработкой программного обеспечения решения задач синтеза гибких и индивидуальных ХТС.
Далее представлены разработки кафедры КИС ХТ РХТУ им. Д.И. Менделеева [152–157].
1. Программное обеспечение для расчета длительностей технологических операций Duration.
Предназначено для решения задач синтеза гибких и индивидуальных ХТС по критерию капитальных затрат на оборудование.
Для работы программного модуля разработаны и интегрированы множество разнообразных алгоритмов, наиболее важные из них: обобщенный алгоритм расчета; алгоритмы расчета постадийного материального индекса, подходящего размера аппарата, определения общего аппарата, проверки коэффициентов заполнения аппарата, определения подходящего размера емкости и другие. Заполнение исходных данных разделено на этапы, которые включают: плановый срок выпуска продукции, количество продуктов, размеры партий продуктов, плотности входящего и дополнительного потоков, коэффициенты заполнения аппаратов, стандартные ряды аппаратов (их размеры и стоимость), длительности стадий и другие данные для расчета. В результате осуществляется подбор оборудования и определяется время, необходимое для проведения типовых технологических операций (нагревание/охлаждение, загрузка/выгрузка) в выбранном оборудовании [152, 153].
2. Программный модуль SoF CES (Synthesis of Flexible Chemical Engineering Systems – синтез гибких химико-технологических систем) предназначен для синтеза гибких и индивидуальных химико-технологических систем [154, 155].
Для реализации программного модуля разработаны и интегрированы следующие алгоритмы: формирования принципиальной структуры многоассортиментной ХТС и расчета материальных балансов, расчета постадийных объемов потоков, определения подходящих размеров аппаратов периодического или полунепрерывного действия и емкостей, расчета стоимости оборудования. Ввод исходных данных разделен на 9 шагов, которые включают плановый срок выпуска продукции, количество продуктов, количество стадий, производительность схемы, коэффициенты заполнения аппаратов, стандартные ряды аппаратов (их размеры и стоимость), длительности стадий и др.
В процессе вычисления программный модуль выводит на экран не только конечные результаты (капитальные затраты на схему, количество партий продуктов, время выпуска продукции), но и промежуточные результаты, такие как коэффициенты заполнения аппаратов, таблицы материальных потоков и другие.
3. Программный модуль I2S предназначен для задач моделирования многоассортиментных химико-технологических систем [156, 157], а именно – для определения лучшей последовательности выпуска многоассортиментной продукции гибкой или совмещенной ХТС.
Программа по заданным временам производства продуктов и длительностям переналадок рассчитывает время, необходимое для производства всех вариантов последовательностей выпуска продукции. Работа программы основана на следующих алгоритмах: определения начального и конечного времени производства продукта в последовательности, обработки заданных значений, вывода графических зависимостей и создания текстового отчета о произведенных расчетах. Исходными данными являются: матрица времени производства и матрица переналадок. Результаты расчета – времена выпуска, вычисленные для каждой последовательности продуктов. На выходе программа выдает полную информацию о рассчитанной последовательности в виде графиков и текстового отчета.
Перечисленные программные модули написаны на языке Delphi в интегрированной среде разработки приложений – Delphi версий XE8 и 10.2.
На все разработки кафедры КИС ХТ имеются свидетельства о государственной регистрации программ для ЭВМ [152, 154, 156].
Разработанные программные средства широко используются для учебных и научно-исследовательских задач моделирования и синтеза многоассортиментных ХТС и организации выпуска ассортимента.
АНАЛИЗ ИНФОРМАЦИОННЫХ РЕСУРСОВ: БАЗ ДАННЫХ И ИНФОРМАЦИОННЫХ СИСТЕМ ПО ТЕХНОЛОГИЯМ, ОБОРУДОВАНИЮ, ПРОИЗВОДИТЕЛЯМ, ПОТРЕБИТЕЛЯМ, АССОРТИМЕНТУ МАЛО- И СРЕДНЕТОННАЖНОЙ ХИМИЧЕСКОЙ ПРОДУКЦИИ
При решении задач проектирования, планирования, составления расписания работы многоассортиментных химических производств с использованием специализированного программного обеспечения необходимо использовать информационные ресурсы.
В рамках “дорожной карты” по развитию производства малотоннажной химии в Российской Федерации на период до 2030 г. было предложено рассмотреть возможность создания на базе государственной информационной системы промышленности (ГИСП) [158] информационно-справочного раздела по малотоннажной химической продукции, выпускаемой на территории Российской Федерации.
Информационно-справочный раздел по малотоннажной химической продукции, выпускаемой на территории Российской Федерации, должен охватывать вопросы технического регулирования малотоннажной и среднетоннажной химической продукции в России и за рубежом, отслеживать мировые новости, способствовать координации науки и бизнеса в данной области, освещать вопросы сырьевого обеспечения, создавать систему горизонтальных связей между производством и потреблением [1].
В государственной информационной системе промышленности имеется раздел Каталог продукции, который представляет собой полный унифицированный перечень промышленной продукции и услуг, выпускаемой предприятиями РФ: формируется производителями содержит карточки промышленной продукции с указанием технических характеристик, сертификатов, стандартов и т.д., предоставляет статистические данные по запросу: региональные, отраслевые, направления импортозамещения и т.д. включает возможность быстрого поиска продукции.
Для химической продукции в настоящее время в каталоге доступно 3173 наименования, для фармацевтической – 1611.
При поддержке Минпромторга России, НТЦ “Химвест”, Российского союза химиков и РХТУ им. Д.И. Менделеева реализуется информационный ресурс “Химический комплекс России”, в котором имеется раздел по развитию малотоннажной химии в России [2].
В данном разделе представлена информация о классификации химических производств по объемам выпуска продукции (табл. 1), рассмотрены основные направления использования малотоннажной химии, перечислены научные центры и предприятия по выпуску продукции малотоннажной химии.
Важным информационным ресурсом является также Бюро наилучших доступных технологий (НДТ) [159].
На сайте Бюро НДТ [160] для зарегистрированных пользователей доступна база данных “Бюро НДТ” – система, предназначенная для сбора и обработки данных, необходимых для определения технологии в качестве наилучшей доступной технологии, а также разработки и актуализации информационно-технических справочников по наилучшим доступным технологиям. Позволяет обработать исходные данные предприятий с целью получения обобщенных данных по отраслям промышленности или областям применения наилучших доступных технологий [161].
В соответствии с Постановлением Правительства Российской Федерации № 1508 от 28 декабря 2016 г. функции Бюро НДТ переданы в созданный в рамках проведения в России Года Экологии Центр экологической промышленной политики (ЦЭПП) [161].
Для разработки нормативно-методической базы в области НДТ приказом Росстандарта от 1 августа 2014 г. № 1236 создан Технический комитет ТК 113 “Наилучшие доступные технологии”.
Полноправными членами ТК 113 в настоящее время являются 40 организаций и компаний [162], среди них: ОАО “РОСНАНО”, ПАО “Газпром”, РХТУ им. Д.И. Менделеева, ООО “Сибур” (управляющая компания), АО “МХК "ЕвроХим”, Минприроды России, Минэнерго России, РГУ нефти и газа им. И.М. Губкина, Минпромторг России.
Примером зарубежных баз данных по наилучшим доступным технологиям является перечень справочных документов, представленный на сайте Европейской комиссии в разделе Европейское бюро по комплексному предотвращению и контролю загрязнения (European Integrated Pollution Prevention and Control (IPPC) Bureau (EIPPCB)) [163].
Наряду с поиском информации по предприятиям и технологиям, при проектировании многоассортиментных химических производств важными являются информационные ресурсы по оборудованию. При решении задач выбора оборудования для моделирования и синтеза многоассортиментных ХТС рекомендуется использовать актуальную информацию, представленную на сайтах предприятий-производителей и компаний-дистрибьютеров лабораторного и промышленного оборудования.
В качестве примеров можно отметить следующие:
каталог оборудования группы компаний ТЭФОС, ООО ТД “Нефтехиммаш КО” (Нижний Новгород) www.tefos.ru;
лабораторное оборудование компании “БИОХИМПРО” www.biohimpro.ru;
официальный дистрибьютор высокотехнологичного оборудования химических процессов от ведущих производителей Китая компания AKIKO www.akiko.ru.
Для разработки гибких технологий производств химических реактивов, особо чистых веществ, защитных пропиточных композиций для дорожных покрытий и др. Научным центром “Малотоннажная химия” давно и активно используются CALS-технологии (Continuous Acquisition and Life cycle Support (CALS) – непрерывная информационная поддержка жизненного цикла продукта) [164–168].
В работах [164–168] представлены основные направления использования CALS-технологий для информационной поддержки, создания и сопровождения блочно-модульных производств химических реактивов и особо чистых веществ.
Авторами научного центра разработана методология синтеза и практической реализации гибких технологий получения химических реактивов и особо чистых веществ на базе концепции CALS. В статье [164] разработаны типовые CALS-проекты универсальных модульных установок на примере ассортимента алифатических углеводородов и петролейных эфиров реактивной квалификации. При создании многоассортиментных производств химических реактивов и особо чистых веществ рассматриваются четыре иерархических уровня: номенклатурный, производственно-технологический, организационно-технологический и организационно-производственный. Созданной иерархической структуре соответствуют три вида гибкости: технологическая, структурная и организационная.
Сотрудниками Научного центра “Малотоннажная химия” разработаны информационные модели на базе CALS-технологии для производства ортофосфорной кислоты особой чистоты, используемой в методе высокоэффективной жидкостной хроматографии. Разработаны информационный CALS-проект исходных данных на проектирование и CALS-система компьютерного менеджмента качества, содержащая иерархическую базу данных об анализируемых веществах, составе их примесей и аналитических методах [166].
Использование CALS-концепции в проекте ортофосфорной кислоты особой чистоты позволяет сделать серьезный шаг к разработке базы для внедрения автоматизированных систем менеджмента качества, сократить время аналитических исследований и повысить достоверность результатов научных исследований [166].
Концепция CALS максимально упрощает многие процедуры подготовки документов. Так, данные для лабораторной аккредитации по оборудованию в форме таблицы готовятся в автоматическом режиме по базе данных измерительных средств с необходимыми характеристиками. Кроме того, можно автоматизированно решать такие задачи, как заказ материалов и запасных частей, планирование и учет работ, предусмотренных регламентом, диагностика и поиск неисправностей оборудования и многое другое [166].
В [165] представлены результаты разработки модульного производства защитных пропиточных композиций для дорожных асфальтобетонных покрытий, а именно технологического регламента, в основе информационной структуры которого лежит “Положение о технологических регламентах производства продукции на предприятиях химического комплекса” с использованием системы компьютерной поддержки – CALS-технологии. Для этого использованы реализованные ранее авторами базы данных, в которые заложены основные типы нормативно-технической документации: технические условия, технологический регламент, лабораторный регламент, исходные данные на проектирование.
На основе информационных CALS-технологий в [167] проведена разработка аппаратурных модулей многоассортиментных производств на примере ассортимента алифатических углеводородов особой чистоты. Созданы CALS-проекты технологических регламентов модулей адсорбционной очистки, химической очистки, предварительной ректификации, точной ректификации и финишной ректификации.
Кроме разработки гибких модульных производств химических реактивов и особо чистых веществ в Научном центре “Малотоннажная химия” проведен анализ зарубежного рынка малотоннажной химии для обеспечения высокотехнологичных отраслей промышленности указанными продуктами, представленный в [5].
В настоящее время разработан ряд баз данных и информационных систем для решения задач проектирования оборудования многоассортиментных химических производств и химических продуктов [169].
На кафедре “Компьютерно-интегрированные системы в машиностроении” Тамбовского государственного технического университета разработана методика и создана система автоматизированного выбора и расчета фильтров для разделения суспензий. Система реализована в среде Visual Basic [170]. Промышленная версия данной системы была принята конструкторским отделом ОАО “Пигмент”.
В работе [171] описывается модуль подбора оборудования, который является частью интеллектуальной системы информационной поддержки по выбору технологических схем производства твердых лекарственных форм Pharmsystem.
В статье [172] рассматриваются автоматизированные методы и инструменты для разработки продуктов на основе химических веществ.
ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ ПРОЕКТИРОВАНИЯ И ОПТИМАЛЬНОГО ФУНКЦИОНИРОВАНИЯ ГИБКИХ АВТОМАТИЗИРОВАННЫХ МНОГОАССОРТИМЕНТНЫХ ХИМИЧЕСКИХ ПРОИЗВОДСТВ НА ОСНОВЕ БАЗОВЫХ ПОЛОЖЕНИЙ ИНДУСТРИИ 4.0
Индустрия 4.0 – четвертая промышленная революция [173–184] – создание цифровой экосреды “Умного предприятия” (цифровых двойников, фабрик будущего, интернета вещей, обработки больших массивов данных и др.).
Четвертая промышленная революция представляет собой объединение промышленности и цифровых технологий, приводящее к созданию цифровых производств или умных заводов и фабрик, где все устройства, машины, продукция и люди общаются между собой посредством цифровых технологий и интернета.
Индустрия 4.0 охватывает всевозможные направления и технологии: аддитивные технологии, 3D-печать; моделирование и визуализация; интеграция систем; интернет вещей; кибербезопасность; облачные сервисы; дополненная реальность; виртуальная реальность; планирование и анализ в режиме реального времени; искусственный интеллект; большие данные и аналитика.
Наиболее известные проекты по внедрению новых цифровых технологий в промышленности, которые заявили о себе, можно привести в качестве примера Индустрии 4.0.
1. Модуль моделирования и визуализации. При проектировании различных химических аппаратов с использованием систем автоматизированного проектирования разработчик может произвести симуляцию с использованием 3D-графики.
2. Программное обеспечение, позволяющее объединить отдельные технологические процессы, информация от которых собирается в нем, которое систематизирует данные, а также сигнализирует о различных событиях (времени работы, простое, перегреве, вибрации, износе узлов и т.д.).
3. Самовосстанавливающееся оборудование. При достижении некоторого износа оборудования, информация об этом поступает механику и в службу снабжения предприятия. Эта операция реализуется с помощью специальных датчиков на оборудовании.
4. Цифровой двойник оборудования и производственной системы.
5. Единое цифровое пространство производства продукции.
6. Удаленная настройка оборудования для производства умной продукции.
7. Мониторинг всех производственных, технологических и других процессов.
Химические предприятия являются источниками больших массивов данных. На большинстве производственных объектов базы данных хранят показания датчиков и управляющих воздействий (часто записанные с частотой (шагом) 1 мин или менее), и во многих случаях имеются архивы за десять или более лет. Таким образом, наука о данных может оказать значительное влияние на анализ и совершенствование функционирования химических процессов.
В работе [109] авторы полагают, что данные могут предоставить еще один класс ценных сведений, помимо обнаружения неисправностей, в работе химических процессов. Рассматривается роль данных как “моста”, соединяющего различные временные/пространственные шкалы химических процессов в математическом моделировании и многокритериальном, интегрированном принятии решений. Анализ “больших данных” находит применение в химической промышленности, включающей сложные физико-химические системы. Исторические (имевшие место, архивные) эксплуатационные данные (которые являются многочисленными и доступны при небольших затратах) могут быть преобразованы в полезную информацию для многомасштабного математического моделирования химических процессов.
На современных производственных объектах предпринимаются большие усилия по использованию текущих достижений в области информационно-коммуникационных технологий с целью повышения эффективности и экономии энергии и затрат. Технологическое оборудование оснащается все большим количеством датчиков и обладает более совершенными коммуникационными и вычислительными возможностями, что делает их кибер-физическими системами, способными взаимодействовать с окружающей средой не только физически, но и посредством цифровой связи. Они собирают, хранят и обмениваются информацией, обеспечивая потенциал для улучшения производственного процесса. Для систематического использования имеющейся информации широко принята концепция создания цифрового двойника физического объекта [176]. Цифровой двойник хранит исторические данные и текущее состояние физического объекта, которые могут быть использованы для прогнозирования его будущего поведения. Экономическая цель этих разработок состоит в том, чтобы всегда поддерживать оптимальное состояние производства, имея возможность адаптироваться к изменениям спроса и получать запросы на индивидуализированную продукцию.
В статье [177] авторами показано, как использовать возможности, которые предлагает структура моделирования на основе сети Петри, предложенная в работе [178], для планирования гибких производственных систем. Основанная на базовой информации о производственной системе, которая, как ожидается, будет элементарной частью цифрового двойника, предложенная структура моделирования позволяет генерировать сетевую модель системы Петри. В работе [177] предложена методика использования математического описания модели [178] для определения гибкого производственного графика, минимизирующего себестоимость продукции, с помощью модели прогнозирующего (упреждающего) управления (MPC).
Существует большое количество литературы по управлению с использованием сетей Петри (например, [179]), которые в основном могут быть классифицированы на проблемы запрещенных состояний и проблемы запрещенной последовательности. В отличие от этих двух классов проблем, авторами [177] рассмотрены специально разработанные сети Петри с желаемыми степенями свободы.
Индустрия 4.0 характеризуется сильной индивидуализацией выпускаемой продукции в условиях высоко гибкого производства. Ориентированное на клиента производство ведет непосредственно к сложным гибким производственным системам, для функционирования которых необходимы моделирование и оптимизация. Анализ наличия гибких производственных систем в Индустрии 4.0 направлен на снижение рисков непредвиденных отказов оборудования и связанных с ними потерь, а также поддержку оптимизации производственных систем. В работе [71] используются расширенные цветные стохастические сети Петри для построения модели гибкой производственной системы с тремя единицами оборудования.
Индивидуализация является одним из восьми наиболее важных современных глобальных мегатрендов, которые оказывают непосредственное влияние на производство [180]. В их работе описаны пять концепций фабрик будущего. Это адаптируемое производство, сетевое производство, цифровое производство, обучающее производство и устойчивое на протяжении жизненного цикла производство. Эти концепции фабрик будущего указывают на направление развития производственных систем в Индустрии 4.0.
С ростом насыщения рынка эти рынки трансформировались в рынки покупателей, что вынудило производителей к дифференциации продукции [181]. Растущие требования к индивидуальным продуктам для конкретного клиента, не только постепенно привлекают внимание производителей, но и незаметно влияют на их производственную стратегию. В связи с растущей глобальной конкуренцией многие компании ориентируются на продукты под заказ и быстрое время выхода на рынок [181]. Для производителя необходимо эффективно изготавливать различные варианты продукции в разных размерах партии.
В отличие от рассмотренных выше, в работе [71] построена модель расширенных цветных стохастических сетей Петри для моделирования гибкости производственных систем с тремя независимыми линиями (единицами оборудования). По сравнению с моделями системы с фиксированной структурой, она может моделировать гибкие структуры и, следовательно, гибкие производственные процессы. Рассмотрены различные комбинации единиц оборудования (линий) для моделирования производства различных вариантов с различными процессами.
В последнее время было предложено множество решений для отслеживания цепочки поставок, основанных на блокчейне [182].
В работе [183] отмечается, что получение адекватной и своевременной информации о жизненном цикле продукта и процессах его производства является трудоемкой и дорогостоящей процедурой. Эта проблема может быть в некоторой степени облегчена с помощью Интернета вещей (Internet of Things (IoT)), который отслеживает данные в режиме реального времени. Чтобы управлять жизненным циклом продукта, необходимо оценить множество альтернативных сценариев, которые невозможно выполнить вручную. Поэтому в исследовании [183] авторами разработан инструмент поддержки принятия базовых решений интернета вещей для управления жизненным циклом.
Управление жизненным циклом не является постепенным односторонним процессом, поскольку в течение жизненного цикла могут происходить определенные изменения в течение срока службы продукта. Поэтому необходимо время от времени учитывать переоценку жизненного цикла продукта, когда продукт доступен на рынке, по различным причинам, таким как изменения в сырье или поставок, изменение технологии, изменение источника энергии и др. Таким образом, управление жизненным циклом продукта играет ведущую роль.
За последние несколько лет технологии отслеживания (сбора, мониторинга) информации через Интернет вещей стали широко использоваться в различных областях, поскольку IoT работает с разнообразным оборудованием и системами считывания информации, таким как сенсорные сети, устройство считывания радиочастотной идентификации (Radio Frequency Identification (RFID)), штрих-код и оборудование для двумерного кода, а также имеет множество глобальных средств, влияющих на различные промышленные разработки [184]. Поэтому необходимо интегрировать надлежащий механизм сбора данных, чтобы упростить управление жизненным циклом продукта и повысить экологические характеристики продукта в течение срока его службы на рынке.
В этой связи “зеленая маркировка” (Green Label) требует от производителей проводить анализ и учет влияния производимых продуктов на окружающую среду на каждом этапе жизненного цикла продукта или процесса, от подготовки к производству до утилизации [183]. Следовательно, объединенная методика переоценки жизненного цикла продукта, которая связана с получением данных в реальном времени, экологическим дизайном и поддержкой принятия решений на основе облачных вычислений в единую модель, является перспективным направлением создания экологически чистых производств в будущем.
ЗАКЛЮЧЕНИЕ
В настоящей обзорной статье представлено всестороннее системно-аналитическое исследование современного состояния и развития теоретических основ в области анализа, синтеза и оптимального функционирования малотоннажных многоассортиментных химических производств, подготовленное по материалам публикаций ведущих ученых и научных школ в периодических изданиях, рецензируемых в международных и отечественных базах данных, монографий и диссертаций. Проведенное исследование показало, что теоретические основы, заложенные более 40 лет назад ведущими зарубежными и отечественными учеными, не потеряли свою актуальность и находят практическое применение при создании высокотехнологичных цифровизированных наукоемких производств в химической и смежных отраслях промышленности на основе базовых положений Индустрии 4.0.
Настоящий обзор будет полезен специалистам, занимающимся вопросами проектирования, реконструкции, модернизации предприятий химического комплекса в отраслевых сегментах, где намечены приоритетные и прорывные направления импортозамещения мало- и среднетоннажной химии, а также ученым, преподавателям, аспирантам и студентам вузов.
Исследование выполнено при финансовой поддержке РХТУ им. Д.И. Менделеева.
Список литературы
Правительство России: официальный сайт (2020) План мероприятий (“дорожная карта”) по развитию производства малотоннажной химии в Российской Федерации на период до 2030 г. Утвержден распоряжением Правительства Российской Федерации от 15 декабря 2017 г. № 2834-р. http://static.government.ru/media/files/BXMyJhAEHhaR9pbRmu4rQxY2ZAz7P7GF.pdf. Дата обращения: 27.07.2020.
Химический комплекс России (2020) Развитие малотоннажной химии в России. http://chemcomplex.ru/мало. Дата обращения: 28.07.2020.
Калюжный С.В. Мал золотник да дорог // Хим. жизнь. 2018. № 6.
Клепиков Д.Н., Выголов Н.В., Ильиных Л.В. Приоритетные направления развития малотоннажной химии в Российской Федерации // Вестн. хим. пром-сти. 2016. № 5(92). С. 18.
Клевцов А.А., Трохин В.Е., Бессарабов А.М., Стоянов О.В. Разработка стратегии координирующего органа для эффективного управления производством продукции малотоннажной химии в РФ // Вестн. технол. унив. 2019. Т. 22. № 11. С. 141.
Mokrozub V.G., Malygin E.N. Development of decision-making support systems to design chemical process equipment for batch production // Adv. Mater. Technol. 2019. № 2. P. 48.
Mokrozub V., Malygin E., Nemtinov V. Information models for problems solving of hardware design of multi-range chemical industries // MATEC Web Conf. 2018. V. 224. Article number 02060. https://doi.org/10.1051/matecconf/201822402060
Bogomolov B.B., Zubarev A.M., Meshalkin V.P., Men’shikov V.P., Boldyrev V.S. Intelligent logical information algorithm for choosing energy- and resource-efficient chemical technologies // Theor. Found. Chem. Eng. 2019. V. 53. № 5. P. 709. [Богомолов Б.Б., Болдырев В.С., Зубарев А.М., Мешалкин В.П., Меньшиков В.В. Интеллектуальный логико-информационный алгоритм выбора энергоресурсоэффективной химической технологии // Теор. осн. хим. технол. 2019. Т. 53. № 5. С. 483.]
Morary M. Flexibility and resiliency of process systems // Comput. Chem. Eng. 1983. V. 7. № 4. P. 423.
Grossmann I.E. Mixed-integer programming approach for the synthesis of integrated process flowsheets // Comput. Chem. Eng. 1985. V. 9. P. 463.
Grossmann I.E., Floudas C.A. Active constraint strategy for flexibility analysis in chemical processes // Comput. Chem. Eng. 1987. V. 11. P. 675.
Rippin D.W.T. Design and operation of multiproduct and multipurpose batch chemical plants an analysis of problem structure // Comput. Chem. Eng. 1983. V. 7. P. 463.
Rippin D.W.T. Simulation of single and multiproduct batch chemical plants for optimal design and operation // Comput. Chem. Eng. 1983. V. 7. № 3. P. 137.
Suhami I., Mah R.S.H. Optimal design of multipurpose batch plants // Ind. Eng. Chem. Process Des. Dev. 1982. V. 21. № 1. P. 94.
Karimi I.A., Reklaitis G.V. Intermediate storage in noncontinuous processes involving stage of parallel units // AIChE J. 1985. V. 31. № 1. P. 44.
Swaney R.E., Grossmann I.E. An index for operational flexibility in chemical process design. Part II: Computational algorithms // AIChE J. 1985. V. 31. № 4. P. 631.
Sparrow R.E., Forder G.J., Rippin D.W.T. The choice of equipment sizes for multiproduct batch plants. Heuristics vs. branch and bound // Ind. Eng. Chem. Process Des. Dev. 1975. V. 14. № 3. P. 197.
Grossmann I.E., Sargent R.W. Optimum design of multipurpose chemical plants // Ind. Eng. Chem. Process Des. Dev. 1979. V. 18. № 2. P. 343.
Grossmann I.E., Halemane K.P., Swaney R.E. Optimization strategies for flexible chemical processes // Comput. Chem. Eng. 1983. V. 7. № 4. P. 439.
Grossmann I.E., Halemann K.P. A decomposition strategy for designing flexible chemical plants // AIChE J. 1982. V. 28. № 4. P. 686.
Floudas C.A., Grossmann I.E. Synthesis of flexible heat exchanger networks with uncertain flowrates and temperatures // Comput. Chem. Eng. 1987. V. 11. № 4. P. 319.
Специальный выпуск, посвященный гибким автоматизированным системам в малотоннажной химии // Журн. Всес. хим. о-ва им. Д.И. Менделеева. 1987. Т. 32. № 3.
Кафаров В.В., Макаров В.В., Егоров А.Ф. Гибкие автоматизированные производственные системы химической и смежных отраслей промышленности // Итоги науки и техники. Процессы и аппараты химической технологии. Т. 16. М.: ВИНИТИ, 1988. С. 92.
Кафаров В.В. Гибкие автоматизированные производственные системы химической промышленности // Журн. Всес. хим. о-ва им. Д.И. Менделеева. 1987. Т. 32. № 3. С. 252.
Кафаров В.В., Перов В.Л., Мешалкин В.П. Принципы математического моделирования химико-технологических систем. М.: Химия, 1974.
Кафаров В.В., Мешалкин В.П., Перов В.Л. Математические основы автоматизированного проектирования химических производств. М.: Химия, 1979.
Кафаров В.В., Макаров В.В. Гибкие автоматизированные производственные системы в химической промышленности. М.: Химия, 1990.
Кафаров В.В., Мешалкин В.П. Анализ и синтез ХТС. Учебник для вузов. М.: Химия, 1991.
Перов В.Л., Егоров А.Ф. Использование принципов адаптации при построении гибких автоматизированных производственных систем // Журн. Всес. хим. о-ва им. Д.И. Менделеева. 1987. Т. 32. № 3. С. 322.
Перов В.Л., Егоров А.Ф. Стратегия гибкого управления многоассортиментными химическими производствами в условиях неопределенности // Теор. осн. хим. технол. 1994. Т. 28. № 5. С. 519.
Перов В.Л., Бельков В.П., Савицкая Т.В. Теоретические и практические аспекты гибкости многоассортиментных производств // Изв. высш. учебн. завед. Хим. хим. технол. 1991. № 12. С. 98.
Макаров В.В., Тарасова Е.C. Модель и алгоритм синтеза гибкой ХТС многоассортиментного производства // Принципы кибернетической организации химических производств. Труды МХТИ. 1988. Вып. 152. С. 81.
Кафаров В.В., Бодров В.И., Дворецкий С.И. и др. Новое поколение гибких автоматизированных химических производств // Теор. осн. хим. технол. 1993. Т. 27. № 2. С. 254.
Бодров В.И., Дворецкий С.И., Матвейкин В.Г. Проблемы управления в многоассортиментных ГАПС нового поколения // Теор. осн. хим. технол. 1994. Т. 28. № 5. С. 537.
Дворецкий С.И. Синтез гибких автоматизированных малотоннажных химических производств. Дис. … докт. техн. наук. Тамбов: ТИХМ, 1991.
Малыгин Е.Н., Мищенко С.В. Проектирование гибких производственных систем в химической технологии // Журн. Всес. хим. о-ва им. Д.И. Менделеева. 1987. Т. 32. № 3. С. 280.
Малыгин А.Н. Методы автоматизированного синтеза многоассортиментных химических производств. Дис. … докт. техн. наук. Тамбов: ТИХМ, 1986.
Малыгин Е.Н., Фролова Т.А. Задача оптимального календарного планирования гибких химико-технологических схем // Хим. пром-сть. 1992. № 6. С. 55.
Рябенко Е.А., Малышев Р.М., Бессарабов А.М. Гибкие многоассортиментные химико-технологические системы в технологии химических реактивов и особо чистых веществ // Теор. осн. хим. технол. 1996. Т. 30. № 1. С. 104.
Бессарабов А.М. Синтез оптимальных химико-технологических систем получения особо чистых оксидных материалов. Дис. … докт. техн. наук. М.: РХТУ им. Д.И. Менделеева, 1991.
Егоров А.Ф. Принципы и стратегия гибкого управления многоассортиментными химическими производствами в условиях неопределенности. Дис. … докт. техн. наук. М.: РХТУ им. Д.И. Менделеева, 1996.
Ostrovsky G.M., Volin Y.M., Senyavin M.M. About one approach solving two stage optimization problem under uncertainty // Comput. Chem. Eng. 1997. V. 21. № 3. P. 317.
Островский Г.М., Волин Ю.М., Сенявин М.М., Бережинский Т.А. О гибкости химико-технологических процессов // Теор. осн. хим. технол. 1994. Т. 28. № 1. С. 54.
Задорский В.М., Русалин С.М., Фокин А.П., Жиденко В.Ф. Аппаратурно-технологическое обеспечение гибкости ХТС // Журн. Всес. хим. о-ва им. Д.И. Менделеева. 1987. Т. 32. № 3. С. 273.
Лысенко А.Ю. Моделирование и оптимизация при реконструкции действующих многоассортиментных производств. Дис. … канд. техн. наук. М.: МХТИ им. Д.И. Менделеева, 1988.
Кадосова Е.С. Синтез модульных ХТС в промышленности синтетических красителей. Дис. … канд. техн. наук. М.: МХТИ им. Д.И. Менделеева, 1990.
Савицкая Т.В. Использование модульного принципа при построении гибких производственных систем медицинской промышленности. Дис. … докт. техн. наук. М.: РХТУ им. Д.И. Менделеева, 1992.
Перов В.Л., Бельков В.П., Савицкая Т.В. Проектирование многоассортиментных химико-технологических систем с учетом гибкости. Ч. 1. Теоретические основы оценки гибкости // Изв. высш. учебн. завед. Хим. хим. технол. 2000. Т. 43. Вып. 6. С. 81.
Вердиян М.А., Егоров А.Ф., Савицкая Т.В., Тюрина Н.С. Гибкие малоотходные технологии функциональных порошковых материалов // Хим. технол. 2003. № 11. С. 38.
Егоров А.Ф., Савицкая Т.В., Пугачева В.С. Проектирование гибких схем производства лекарственных препаратов и очистки сточных вод // Сборник научных статей “Математическое моделирование, ресурсосбережение и экологическая безопасность технологий”. М.: МГУИЭ, 1998. С. 49.
Becker T., Lier S., Werners B. Value of modular production concepts in future chemical industry production networks // Eur. J. Oper. Res. 2019. V. 276. № 3. P. 957.
Friedrich J., Scheifele S., Verl A., Lechler A. Flexible and modular control and manufacturing system // Procedia CIRP. 2015. V. 33. P. 115.
Reuter A., Kircher C., Verl A. Manufacturer-independent mechatronic information model for control systems // Prod. Eng. 2010. V. 4. P. 165.
Wang W., Koren Y. Scalability planning for reconfigurable manufacturing systems // J. Manuf. Syst. 2012. V. 31. № 2. P. 83.
Mass Customization und Kundenintegration. Neue Wege zum innovativen Produkt / Ed. Piller F.T., Stotko C.M. Düsseldorf: Symposion, 2003.
Business-wissen.de – Werkzeuge für Organisation und Management (2020) Mass Customization – Mit individualisierten Standardprodukten zum Erfolg. http://www.business-wissen.de/artikel/mass-customization-mit-individualisierten-standardprodukten-zum-erfolg. Cited 24 July 2020.
Pistikopoulos E.N., Grossmann I.E. Optimal design of flexibility in linear systems // Comput. Chem. Eng. 1988. V. 12. № 5. P. 383.
Straub D.A., Grossmann I.E. Evaluation and optimization of stochastic flexibility in multiproduct batch plants // Comput. Chem. Eng. 1992. V. 16. № 2. P. 69.
Pistikopoulos E.N., Grossmann I.E. Evaluation and redesign for improving flexibility in linear system with infeasible nominal parameters // Comput. Chem. Eng. 1988. V. 12. № 12. P. 841.
Pistikopoulos E.N., Grossmann I.E. Optimal retrofit design for improving process flexibility in nonlinear systems. Part I: Fixed degree of flexibility. Part II: Optimal degree of flexibility // Comput. Chem. Eng. 1988. V. 12. № 12. P. 719.
Перов В.Л., Бельков В.П., Савицкая Т.В. Проектирование многоассортиментных химико-технологических систем с учетом гибкости. Ч. 2. Практическое использование критерия гибкости // Изв. высш. учебн. завед. Хим. хим. технол. 2001. Т. 44. № 4. С. 93.
Ostrovsky G.M., Lapteva T.V., Ziyatdinov N.N. Optimal design of chemical processes under uncertainty // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 583. [Островский Г.М., Лаптева Т.В., Зиятдинов Н.Н. Проектирование оптимальных химико-технологических систем в условиях неопределенности // Теор. осн. хим. технол. 2014. Т. 48. № 5. С. 527.]
Halemane K.P., Grossmann I.E. Optimal process design under uncertainty // AIChE J. 1983. V. 29. P. 425.
Wendt M., Li P., Wozny G. Nonlinear chance-constrained process optimization under uncertainty // Ind. Eng. Chem. Res. 2002. V. 41. P. 3621.
Grossmann I.E., Apap R.M., Calfa B.A., Garcia-Herreros P., Zhang Q. Mathematical programming techniques for optimization under uncertainty and their application in process systems engineering // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 893.
Ostrovsky G.M., Lapteva T.V., Ziyatdinov N.N., Silvestrova A.S. Chemical process design with chance constraints // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 961. [Островский Г.М., Лаптева Т.В., Зиятдинов Н.Н., Сильвестрова А.С. Проектирование химико-технологических систем при учете вероятностных ограничений // Теор. основы хим. технологии. 2017. Т. 51. № 6. С. 618.]
Grossmann I.E., Straub D.A. Recent developments in the evaluation and optimization of flexible chemical processes // Proceedings of COPE-91 / Eds. Puigjaner L., Espuna A. Barcelona, 1991. P. 49.
Ostrovskii G.M., Ziyatdinov N.N., Lapteva T.V., Pervukhin I.D. Flexibility analysis of chemical technology systems // Theor. Found. Chem. Eng. 2007. V. 41. № 3. P. 235. [Островский Г.М., Зиятдинов Н.Н., Лаптева Т.В., Первухин И.Д. Оценка гибкости химико-технологических систем // Теор. осн. хим. технол. 2007. Т. 41. № 3. С. 249.]
Li C., Grossmann I.E. An improved L-shaped method for two-stage convex 0-1 mixed integer nonlinear stochastic programs // Comput. Chem. Eng. 2018. V. 112. P. 165.
Grossmann I.E., Calfa B.A., Garcia-Herreros P. Evolution of concepts and models for quantifying resiliency and flexibility of chemical processes // Comput. Chem. Eng. 2014. V. 70. P. 22.
Long F., Zeiler P., Bertsche B. Modelling the flexibility of production systems in Industry 4.0 for analysing their productivity and availability with high-level Petri nets // IFAC-PapersOnLine. 2017. V. 50. № 1. P. 5680.
De Meyer A., Nakane J., Miller J.G., Ferdows K. Flexibility: The next competitive battle the manufacturing futures survey // Strategic Manage. J. 1989. V. 10. № 2. P. 135.
Sethi A.K., Sethi S.P. Flexibility in manufacturing: a survey // Int. J. Flexible Manuf. Syst. 1990. V. 2. № 4. P. 289.
Gupta Y.P., Somers T.M. The measurement of manufacturing flexibility // Eur. J. Oper. Res. 1992. V. 60. № 2. P. 166.
Gerwin D., Tarondeau J.C. Consequences of Programmable Automation for French and American Automobile Factories: An International Case Study // Production Management: Methods and Studies / Ed. Lev B. Amsterdam: North-Holland, 1986. P. 85.
Alanche P., Benzakour K., Dolle F., Gillet P., Rodrigues P., Valette R. PSI: A Petri net based simulator for flexible manufacturing systems // Advances in Petri Nets 1984 / Ed. Rosenberg G. Berlin: Springer, 1985. V. 188. P. 1.
Narahari Y., Viswanadham N. A Petri net approach to the modelling and analysis of flexible manufacturing systems // Ann. Oper. Res. 1985. V. 3. № 8. P. 449.
El-Sayed H.M., Younis M.A., Mahmoud M.S. Modelling and simulation of a flexible manufacturing system with variable production ratios // Appl. Math. Modell. 1989. V. 13. № 7. P. 397.
Boualem M., Cherfaou M., Bouchentouf A.A., Aïssani D. Modeling, Simulation and Performance Analysis of a Flexible Production System // Eur. J. Pure Appl. Math. 2015. V. 8. № 1. P. 26.
Saren S.K., Tiberiu V. Review of flexible manufacturing system based on modeling and simulation // Ann. Univ. Oradea, Fasc. Manage. Technol. Eng. 2016. V. 25 (15). № 1. P. 113.
Floudas C.A., Lin X. Continuous-time versus discrete-time approaches for scheduling of chemical processes: a review // Comput. Chem. Eng. 2004. V. 28. № 11. P. 2109.
Макаров В.В. Оптимальная организация производств многономенклатурной химической продукции // Хим. пром-сть сегодня. 2008. № 1. С. 29.
Бельков В.П. Разработка методов анализа и синтеза гибких многоассортиментных химических производств периодического действия. Дис. … докт. техн. наук. М.: РХТУ им. Д.И. Менделеева, 2004.
Vaselenak A., Grossmann I.E., Westeberg W. An embedding formulation for the optimal scheduling and design of multipurpose batch plants // Ind. Eng. Chem. Res. 1987. V. 26. № 1. P. 139.
Егоров А.Ф., Бельков В.П., Комиссаров Ю.А., Савицкая Т.В. Одновременный синтез и составление расписания выпуска продукции многоассортиментных химических производств // Изв. высш. учебн. завед. Хим. хим. технол. 2004. Т. 47. № 10. С. 93.
Bansal V., Sakizlis V., Ross R., Perkins J.D., Pistikopoulos E.N. New algorithms for mixed-integer dynamic optimization // Comput. Chem. Eng. 2003. V. 27. № 5. P. 647.
Shimizu Y., Takamatsy T. Application of mixed-integer linear programming in multiterm expansion planning under multi-objectives // Comput. Chem. Eng. 1985. V. 9. № 4. P. 367.
Birewar D.B., Grossmann I.E. Efficient optimization algorithms for zero-wait scheduling of multiproduct batch plants // Ind. Eng. Chem. Res. 1989. V. 28. № 9. P. 1333.
Roman R., Grossmann I.E. Relation between MILP modelling and logical inference for chemical process synthesis // Comput. Chem. Eng. 1991. V. 15. № 2. P. 73.
Sahinidis N.V., Grossmann I.E. Reformulation of multi-period MILP model for planning and scheduling of chemical processes // Comput. Chem. Eng. 1991. V. 15. № 3. P. 255.
Orçun S., Altinel I.K., Hortaçsu Ö. General continuous time models for production planning and scheduling of batch processing plants: mixed integer linear program formulations and computational issues // Comput. Chem. Eng. 2001. V. 25. № 2–3. P. 371.
Kocis G.R., Grossmann I.E. Global optimization of noncovex mixed-integer nonlinear programming (MINLP) problems in process synthesis // Ind. Eng. Chem. Res. 1988. V. 27. № 8. P. 1407.
Viswanathan J., Grossmann I.E. A combined penalty function and outes-approximation method for MINLP optimization // Comput. Chem. Eng. 1991. V. 15. № 11. P. 769.
Türkay M., Grossmann I.E. Logic-based MINLP algorithms for the optimal synthesis of process networks // Comput. Chem. Eng. 1996. V. 20. № 8. P. 959.
Su L.J., Tang L.X., Grossmann I.E. Computational strategies for improved MINLP algorithms // Comput. Chem. Eng. 2015. V. 75. P. 40.
Карпушкин С.В. Методология аппаратурного оформления многоассортиментных химических производств. Автореф. дис. … докт. техн. наук. Тамбов: ТГТУ, 2007.
Егоров А.Ф., Бельков В.П., Тюрина Н.С. Оптимальный выбор типового оборудования при проектировании многоассортиментных химических производств // Хим. пром-сть. 2001. № 2. С. 40.
Borisenko A.B., Gorlatch S. Parallel hybrid methaheuristics approach for optimal selection of production equipment // Вестн. ТГТУ. 2018. Т. 24. № 2. С. 228.
Голубчиков М.А., Макаров В.В. Моделирование дискретных интерактивных и конкурентных процессов в ХТС с периодическим режимом работы аппаратов // Усп. хим. хим. технол. 2012. Т. 26. № 1(130). С. 18.
Ziyatdinov N.N. Modeling and optimization of chemical engineering processes and systems // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P.889. [Зиятдинов Н.Н. Моделирование и оптимизация химико-технологических процессов и систем // Теор. осн. хим. технол. 2017. Т. 51. № 6. С. 613.]
Dvoretsky D.S., Dvoretsky S.I. Integrated design of flexible chemical process, devices, and control systems // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 614. [Дворецкий Д.С., Дворецкий С.И. Интегрированное проектирование гибких химико-технологических процессов, аппаратов и систем управления // Теор. осн. хим. технол. 2014. Т. 48. № 5. С. 557.]
Biegler L.T. Integrated optimization strategies for dynamic process operations // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 910.
Trespalacios F., Grossmann I.E. Review of mixed-integer nonlinear and generalized disjunctive programming methods programming models // Chem. Ing. Tech. 2014. V. 86. № 7. P. 1.
Lee S., Grossmann I.E. New algorithms for nonlinear generalized disjunctive programming // Comput. Chem. Eng. 2000. V. 24. P. 2125.
Floudas C.A. Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications. Oxford: Oxford Univ. Press, 1995.
Javid N., Khalili-Damghani K., Makui A., Abdi F. Multi-objective flexibility-complexity trade-off problem in batch production systems using fuzzy goal programming // Expert Syst. Appl. 2020. V. 148. P. 113266.
Marques A.F., Alves A.C., Sousa J.P. An approach for integrated design of flexible production systems // Procedia CIRP. 2013. V. 7. P. 586.
Meshalkin V.P., Panchenko S.V., Dli M.I., Panchenko D.S. Analysis of the thermophysical processes and operating modes of electrothermic reactor using a computer model // Theor. Found. Chem. Eng. 2018. V. 52. № 2. P. 166. [Мешалкин В.П., Панченко С.В., Дли М.И., Панченко Д.С. Анализ теплофизических процессов и режимов работы электротермического реактора с использованием компьютерной модели // Теор. осн. хим. технол. 2018. Т. 52. № 2. С. 141.]
Tsay C., Baldea M. 110th Anniversary: Using Data to Bridge the Time and Length Scales of Process Systems // Ind. Eng. Chem. Res. 2019. V. 58. № 36. P. 16696.
Hadidi L.A., Al-Turki U.M., Rahim A. et al. Integrated models in production planning and scheduling, maintenance and quality: a review // Int. J. Ind. Syst. Eng. 2012. V. 10. № 1. P. 21.
Pistikopoulos E.N., Vassiliadis C.G., Arvela J., Papageorgiou L.G. Interactions of maintenance and production planning for multipurpose process plants a system effectiveness approach // Ind. Eng. Chem. Res. 2001. V. 40. P. 3195.
Yildirim M.B., Nezami F.G. Integrated maintenance and production planning with energy consumption and minimal repair // Int. J. Adv. Manuf. Technol. 2014. V. 74. P. 1419.
Liu S., Yahia A., Papageorgiou L.G. Optimal production and maintenance planning of biopharmaceutical manufacturing under performance decay // Ind. Eng. Chem. Res. 2014. V. 53. P. 17075.
Meeker W.Q., Hong Y. Reliability meets big data: opportunities and challenges // Qual. Eng. 2014. V. 26. P. 102.
Yildirim M., Sun X.A., Gebraeel N.Z. Sensor-driven condition-based generator maintenance scheduling—Part I: Maintenance problem // IEEE Trans. Power Syst. 2016. V. 31. № 6. P. 4253.
Yildirim M., Sun X.A., Gebraeel N.Z. Sensor-driven condition-based generator maintenance scheduling – Part II: Incorporating operations // IEEE Trans. Power Syst. 2016. V. 31. № 6. P. 4263.
Wu O., Ave G.D., Harjunkoski I., Bouaswaig A., Schneider S.M., Roth M., Imsland L. Optimal production and maintenance scheduling for a multiproduct batch plant considering degradation // Comput. Chem. Eng. 2020. V. 135. P. 106734.
Verderame P.M., Elia J.A., Li J. et al. Planning and scheduling under uncertainty: A review across multiple sectors // Ind. Eng. Chem. Res. 2010. V. 49. № 9. P. 3993.
Petkov S.B., Maranas C.D. Multiperiod Planning and Scheduling of Multiproduct Batch Plants under Demand Uncertainty // Ind. Eng. Chem. Res. 1997. V. 36. № 11. P. 4864.
Balasubramanian J., Grossmann I.E. Approximation to Multistage Stochastic Optimization in Multiperiod Batch Plant Scheduling under Demand Uncertainty // Ind. Eng. Chem. Res. 2004. V. 43. № 14. P. 3695.
Verderame P.M., Floudas C.A. Operational Planning of Large-Scale Industrial Batch Plants under Demand Due Date and Amount Uncertainty. I. Robust Optimization Framework // Ind. Eng. Chem. Res. 2009. V. 48. № 15. P. 7214.
Verderame P.M., Floudas C.A. Operational Planning of Large-Scale Industrial Batch Plants under Demand Due Date and Amount Uncertainty: II. Conditional Value-at-Risk Framework // Ind. Eng. Chem. Res. 2014. V. 48. № 15. P. 7214.
De Mirandaa J.L., Casquilhob M. Design and Scheduling of Chemical Batch Processes: Generalizing a Deterministic to a Stochastic Model // Theor. Appl. Math. Comput. Sci. 2011. V. 1. № 2. P. 71.
Charitopoulos V.M., Papageorgiou L.G., Dua V. Multi-parametric mixed integer linear programming under global uncertainty // Comput. Chem. Eng. 2018. V. 116. P. 279.
Brunaud B., Amaran S., Bury S., Wassick J. Grossmann I.E. Novel Approaches for the Integration of Planning and Scheduling // Ind. Eng. Chem. Res. 2019. V. 58. № 43. P. 19973.
Castro P.M., Grossmann I.E., Zhang Q. Expanding Scope and Computational Challenges in Process Scheduling // Comput. Chem. Eng. 2018. V. 114. P. 14.
Erdirik-Dogan M., Grossmann I.E. Planning Models for Parallel Batch Reactors with Sequence-Dependent Changeovers // AIChE J. 2007. V. 53. P. 2284.
Erdirik-Dogan M., Grossmann I.E. Slot-Based Formulation for the Short-Term Scheduling of Multistage, Multiproduct Batch Plants with Sequence-Dependent Changeovers // Ind. Eng. Chem. Res. 2008. V. 47. P. 1159.
Sung C., Maravelias C.T. A Projection-Based Method for Production Planning of Multiproduct Facilities // AIChE J. 2009. V. 55. P. 2614.
Terrazas-Moreno S., Grossmann I.E. A multiscale decomposition method for the optimal planning and scheduling of multisite continuous multiproduct plants // Chem. Eng. Sci. 2011. V. 66. P. 4307.
Calfa B.A., Agarwal A., Grossmann I.E., Wassick J.M. Hybrid Bilevel-Lagrangean Decomposition Scheme for the Integration of Planning and Scheduling of a Network of Batch Plants // Ind. Eng. Chem. Res. 2013. V. 52. P. 2152.
Charitopoulos V.M., Papageorgiou L.G., Dua V. Closed-loop integration of planning, scheduling and multi-parametric nonlinear control // Comput. Chem. Eng. 2019. V. 122. P. 172.
Grossmann I.E. Advances in mathematical programming models for enterprise-wide optimization // Comput. Chem. Eng. 2012. V. 47. P. 2.
Chu Y., You F. Model-based integration of control and operations: Overview, challenges, advances, and opportunities // Comput. Chem. Eng. 2015. V. 83. P. 2.
Dias L.S., Ierapetritou M.G. Integration of scheduling and control under uncertainties: Review and challenges // Chem. Eng. Res. Des. 2016. V. 116. P. 98.
Chu Y., You F. Integration of scheduling and control with online closed-loop implementation: Fast computational strategy and large-scale global optimization algorithm // Comput. Chem. Eng. 2012. V. 47. P. 248.
Zhuge J., Ierapetritou M.G. Integration of scheduling and control for batch processes using multi-parametric model predictive control // AIChE J. 2014. V. 60. № 9. P. 3169.
Zhuge J., Ierapetritou M.G. An integrated framework for scheduling and control using fast model predictive control // AIChE J. 2015. V. 61. № 10. P. 3304.
GAMS Development Corp. and GAMS Software GmbH (2020) System Overview. https://www.gams.com/products/gams/gams-language. Cited 25 July 2020.
Kronqvist J., Bernal D.E., Lundell A., Grossmann I.E. A review and comparison of solvers for convex MINLP // Optim. Eng. 2019. V. 20. P. 397.
Schweiger C., Floudas C.A. The MINOPT Modeling Language // Modeling Languages in Mathematical Optimization (Series in Applied Optimization. V. 88) / Ed. Kallrath J. Boston: Springer, 2004. P. 185.
Biegler L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes (MOS-SIAM Series on Optimization). Philadelphia: SIAM, 2010.
Bussieck M.R., Vigerske S. MINLP solver software // Wiley Encyclopedia of Operations Research and Management Science / Eds. Cochran J.J., Cox L.A.Jr., Keskinocak P., Kharoufeh J.P., Smith J.C. New York: Wiley, 2010.
Aspen Technology Inc (2020) Aspen HYSYS. https://www.aspentech.com/en/products/engineering/aspen-hysys. Cited 19 June 2020.
Aspen Technology Inc (2020) Aspen Plus. https://www.aspentech.com/en/products/engineering/aspen-plus. Cited 19 June 2020.
Chemstations Inc. (2020) CHEMCAD: Chemical Engineering Simulation Software. https://www.chemstations.com/CHEMCAD. Cited 19 June 2020.
Latypov R.M., Osipov E.V., Telyakov E.Sh. Systems Analysis of Equipment and Technology for Production of Glycols // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 980. [Латыйпов Р.М., Осипов Э.В., Теляков Э.Ш. Системный анализ аппаратурно-технологического оформления производств гликолей // Теор. осн. хим. технол. 2017. Т. 51. № 6. С. 637.]
Зиятдинов Н.Н., Лаптева Т.В., Рыжов Д.А. Математическое моделирование химико-технологических систем с использованием программы CHEMCAD: учебно-методическое пособие. Казань: Казанский гос. технол. ун-т, 2008.
Borisenko A.B., Haidl M., Gorlatch S. Using parallel Branch-and-Bound algorithm on GPUs for optimal design of multi-product batch plants // Вестн. ТГТУ. 2015. Т. 21. № 3. С. 406.
Gao X., Wang Y., Feng Z., Huang D., Chen T. Plant Planning Optimization under Time-Varying Uncertainty: Case Study on a Poly(vinyl chloride) // Ind. Eng. Chem. Res. 2018. V. 57. № 36. P. 12182.
Su1 L., Tang L., Grossmann I.E. Scheduling of cracking production process with feedstocks and energy constraints // Comput. Chem. Eng. 2016. V. 94. P. 92.
Сальников Е.Д., Савицкая Т.В. Программа для ЭВМ. Программное обеспечение для выбора оборудования периодического действия и расчета длительностей технологических операций “Duration”. Свидетельство о государственной регистрации программы для ЭВМ № 2017662859 РФ. 2017.
Savitskaya T.V., Egorov A.F., Mikhaylova P.G., Dementienko A.V. Multilevel training of chemists and technologists in the interdisciplinary training system using distance educational technologies // Proс. 4th International Conference on Information Technologies in Engineering Education (Inforino 2018). Moscow, 2018. https://doi.org/10.1109/INFORINO.2018.8581753 [Савицкая Т.В., Егоров А.Ф., Михайлова П.Г., Дементиенко А.В. Многоуровневая подготовка химиков-технологов в междисциплинарной системе обучения с использованием дистанционных образовательных технологий // Сб. тр. Информатизация инженерного образования. Междунар. науч.-практ. конф. – ИНФОРИНО-2018. М.: Национальный исследовательский ун-т “МЭИ”, 2018. С. 515.]
Сальников Е.Д., Савицкая Т.В. Программа для ЭВМ. Программное обеспечение для синтеза химико-технологических систем “SoF CES”. Свидетельство о государственной регистрации программы для ЭВМ № 2017662858 РФ. 2017.
Сальников Е.Д., Савицкая Т.В. Программный модуль для решения задач синтеза многоассортиментных химико-технологических систем // Сб. тр. Информатизация инженерного образования. Междунар. науч.-практ. конф. – ИНФОРИНО-2016. М.: МЭИ, 2016. С. 429.
Чернухин А.В., Сверчков А.М., Савицкая Т.В. Программное приложение для задач моделирования многоассортиментных химико-технологических систем. Свидетельство о государственной регистрации программы для ЭВМ № 2019665460 РФ. 2019.
Chernukhin A.V., Savitskaya T.V., Sverchkov A.M., Egorov A.F. Software Application for Research on the Organization of Cyclic Production of Multi-assorted Products // Proc. 5th International Conference on Information Technologies in Engineering Education (Inforino 2020). Moscow, 2020. https://doi.org/10.1109/Inforino48376.2020.9111749
Минпромторг России (2020) Государственная информационная система промышленности. https:// gisp.gov.ru/gisplk. Дата обращения: 03.08.2020.
Бюро наилучших доступных технологий (2020) О нас. http://burondt.ru/index/o-nas.html. Дата обращения: 01.08.2020.
Бюро наилучших доступных технологий (2020) База данных “Бюро НДТ”. http://burondt.ru/ lpage/#base-buro. Дата обращения: 01.08.2020.
Научно-исследовательский институт “Центр экологической промышленной политики” (2020) Наилучшие доступные технологии. https://eipc.center/ndt. Дата обращения: 01.08.2020.
Бюро наилучших доступных технологий (2020) ТК113. http://burondt.ru/informacziya/tk113/ tk113.html. Дата обращения: 01.08.2020.
European Commission (2020) Reference Documents. European IPPC Bureau. https://eippcb.jrc.ec.europa.eu/reference. Cited 1 August 2020.
Бессарабов А.М., Казаков А.А., Трохин В.Е., Стоянов О.В. Проблемно-ориентированные гибкие CALS-системы многоассортиментных производств химических реактивов и особо чистых веществ // Вестн. Казан. технол. унив. 2014. Т. 17. № 3. С. 292.
Разинов А.Л., Глушко А.Н., Бессарабов А.М., Чигорина Е.А., Приоров Г.Г., Стоянов О.В. Разработка информационной CALS-технологии модульного производства дорожных пропиток // Вестн. технол. унив. 2017. Т. 20. № 14. С. 94.
Бессарабов А.М., Трохин В.Е., Филатова Л.Н., Малышев Р.М., Стоянов О.В., Абзальдинов Х.С. Разработка информационной CALS-технологии процесса получения и аналитического мониторинга ортофосфорной кислоты особой чистоты // Вестн. технол. унив. 2019. Т. 22. № 11. С. 111.
Казаков А.А., Трохин В.Е., Вендило А.Г., Бессарабов А.М. Информационные CALS-проекты аппаратурных модулей в технологии особой чистоты // Усп. хим. хим. технол. 2012. Т. 26. № 1(130). С. 93.
Трохин В.Е., Бессарабов А.М., Вендило А.Г., Стоянов О.В. Разработка на основе концепции CALS модульной технологии получения ассортимента триметилалкоксисиланов особой чистоты // Вестн. технол. унив. 2016. Т. 19. № 2. С. 94.
Егоров С.Я., Шаронин К.А., Андреев Г.И., Немтинов К.В. Методика разработки электронно-графических каталогов технологического оборудования многоцелевого назначения // Инф. технол. проект. производ. 2011. № 2. С. 67.
Тамбовский государственный технический университет (2020) Кафедра “Компьютерно-интегрированные системы в машиностроении”. http:// www.apto.tstu.ru. Дата обращения: 31.08.2020.
Таптунов В.Н. Интеллектуальная система информационной поддержки выбора технологических схем производства твердых лекарственных препаратов. Автореф. дис. … канд. техн. наук. Иваново: Ивановский государственный химико-технологический университет, 2012.
Zhang L., Mao H., Liu Q., Gani R. Chemical product design – recent advances and perspectives // Curr. Opin. Chem. Eng. 2020. V. 27. P. 22.
Monostori L., Kádár B., Bauernhansl T. et al. Cyber-physical systems in manufacturing // CIRP Ann. 2016.V. 65. № 2. P. 621.
Bashir M., Muhammad B.B., Li Z. Minimal supervisory structure for flexible manufacturing systems using Petri nets // Proceedings of the 2nd International Conference on Control, Automation and Robotics (ICCAR). 2016. P. 291.
Hernández-Martínez E.G., Puga-Velazquez E.S., FoyoValdés S.A., Campaña J.M. Task-based Coordination of Flexible Manufacturing Cells using Petri Nets and ISA standards // IFAC-PapersOnLine. 2016. V. 49. № 12. P. 1008.
Negri E., Fumagalli L., Macchi M.A. Review of the Roles of Digital Twin in CPS-based Production Systems // Procedia Manuf. 2017. V. 11. P. 939.
Wenzelburger P., Allgöwer F. A Novel Optimal Online Scheduling Scheme for Flexible Manufacturing Systems // IFAC-PapersOnLine. 2019. V. 52. № 10. P. 1.
Wenzelburger P., Allgöwer F. A Petri Net Modeling Framework for the Control of Flexible Manufacturing Systems // IFAC-PapersOnLine. 2019. V. 52. № 13. P. 492.
Holloway L.E., Krogh B.H., Giua A. A Survey of Petri Net Methods for Controlled Discrete Event Systems // Discrete Event Dyn. Syst. 1997. V. 7. № 2. P. 151.
Westkämper E., Löffler C. Strategien der Produktion. Technologien, Konzepte und Wege in die Praxis. Berlin: Springer, 2016.
Brettel M., Friederichsen N., Keller M., Rosenberg M. How virtualization, decentralization and network building change the manufacturing landscape: An industry 4.0 perspective // Int. J. Mech. Ind. Sci. Eng. 2014. V. 8. № 1. P. 37.
Westerkamp M., Friedhelm V., Küpper A. Tracing manufacturing processes using blockchain-based token compositions // Digital Commun. Networks. 2020. V. 6. № 2. P. 167.
Kamalakkannan S., Kulatunga A.K., Bandara L.A.D.A.D. The conceptual framework of IoT based decision support system for life cycle management // Procedia Manuf. 2020. V. 43. P. 423.
Liu Y., Zhou G. Key Technologies and Applications of Internet of Things // Proc. 2012 Fifth International Conference on Intelligent Computation Technology and Automation. Zhangjiajie, 2012. P. 197.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


