Теоретические основы химической технологии, 2021, T. 55, № 2, стр. 188-194
Термодинамическая эффективность использования разделяющего агента в процессах ректификации
И. А. Сукин a, *, А. И. Балунов b, А. М. Цирлин a
a Институт программных систем им. А.К. Айламазяна РАН
Ярославская область, Веськово, Россия
b Ярославский государственный технический университет
Ярославль, Россия
* E-mail: ivsukin@gmail.com
Поступила в редакцию 07.12.2018
После доработки 25.12.2019
Принята к публикации 14.02.2020
Аннотация
Получена граница производительности колонны бинарной ректификации в зависимости от затрат теплоты. Показано, что затраты теплоты на моль разделяемой смеси в обратимом процессе для многокомпонентных смесей зависят от порядка разделения, а необратимые затраты монотонно с ними связаны. Это позволяет для выбора порядка разделения применять обратимые показатели. Рассмотрена задача о целесообразности использования разделяющего агента для повышения экономичности разделения смесей с близкими температурами кипения компонентов.
ВВЕДЕНИЕ
Анализу процессов разделения жидких смесей в колоннах ректификации посвящена обширная литература (см. [1–7] и др.). При этом одним из центральных вопросов является оценка минимальных затрат теплоты, необходимых для процесса разделения. Эти затраты определяют сложность разделения смеси при той или иной границе между фракциями, отделяемыми в куб и в дефлегматор. Затраты теплоты состоят из двух составляющих: затраты в обратимом процессе и дополнительные затраты, связанные с необратимостью процессов теплообмена в кубе и дефлегматоре и массообмена по высоте колонны. Когда размеры колонны, а вместе с ними и коэффициенты тепло- и массопереноса растут, необратимая составляющая затрат стремится к нулю.
На первый взгляд, в рамках обратимых процессов связь теплоты с производительностью установить невозможно, так как молярная работа разделения Гиббса зависит только от состава разделяемой смеси и не отражает таких ее свойств, как температуры кипения компонентов. Но это не так для процессов, использующих теплоту. Здесь требуется учесть коэффициент превращения теплоты в работу, а этот коэффициент для колонны ректификации зависит от температур в кубе и в дефлегматоре и уменьшается при сближении этих температур. Поэтому в процессах ректификации компоненты смеси с близкими температурами кипения можно разделить лишь при значительных затратах энергии.
Мы рассмотрим необратимые оценки затрат энергии на разделение смеси в процессе бинарной ректификации, покажем, что эти оценки хотя и больше, чем обратимые, но монотонно от них зависят. Выясним, в каком случае добавление в исходную смесь дополнительного компонента (разделяющего агента) позволяет получить экономию энергии.
СВЯЗЬ ПАРАМЕТРОВ СИСТЕМЫ С ЗАТРАТАМИ ТЕПЛОТЫ
Процесс разделения многокомпонентной смеси на две фракции в колонне ректификации характеризуется следующими параметрами.
1. Свойства разделяемой смеси: мольные доли компонентов в разделяемом потоке ${{x}_{{Fi}}},$ температуры кипения $T_{i}^{0}$ и мольные теплоты парообразования компонентов ${{r}_{i}},$ $i = 1, \ldots ,n$ при атмосферном давлении. Ниже предполагаем, что индексы $i$ возрастают по мере роста температуры кипения.
2. Состав продуктов: мольные доли компонентов в дефлегматоре (легкая фракция) ${{x}_{{Di}}}$ и в кубе (тяжелая фракция) ${{x}_{{Bi}}}.$
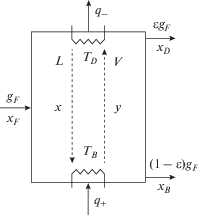
3. Технологические параметры колонны: давление, поддерживаемое в колонне $\bar {P},$ температура в кубе ${{T}_{B}},$ температура в дефлегматоре ${{T}_{D}}$ (см. рис. 1).
В условиях фиксированных составов потоков на входе и выходе колонны эти потоки пропорциональны друг другу и в качестве целевого может быть выбран любой из них, в частности поток ${{g}_{F}}$ разделяемой смеси. В этом случае под коэффициентом полезного действия (КПД) колонны будем понимать отношение числа молей разделяемой смеси на единицу затраченного тепла ${{q}_{ + }}$, подводимого в куб колонны.
Запишем уравнения термодинамических балансов колонны – энергетического, материального и энтропийного [8, 9]:
(1)
${{g}_{F}}{{x}_{F}} - {{g}_{F}}\varepsilon {{x}_{D}} - {{g}_{F}}(1 - \varepsilon ){{x}_{B}} = 0,$(2)
${{q}_{ + }} - {{q}_{ - }} + {{g}_{F}}{{h}_{F}} - {{g}_{F}}\varepsilon {{h}_{D}} - {{g}_{F}}(1 - \varepsilon ){{h}_{B}} = 0,$(3)
${{g}_{F}}\varepsilon {{s}_{D}} + {{g}_{F}}(1 - \varepsilon ){{s}_{B}} + \frac{{{{q}_{ - }}}}{{{{T}_{D}}}} - {{g}_{F}}{{s}_{F}} - \frac{{{{q}_{ + }}}}{{{{T}_{B}}}} = \sigma \geqslant {{\sigma }_{{{\text{min}}}}}.$Здесь $\sigma > 0$ – производство энтропии в колонне, $h$ – мольные энтальпии потоков, $s$ – мольные энтропии потоков, $\varepsilon = \frac{{{{x}_{F}} - {{x}_{B}}}}{{{{x}_{D}} - {{x}_{B}}}}$ – доля отбора верхнего продукта, ${{x}_{F}},$ ${{x}_{D}},$ ${{x}_{B}}$ – мольная доля легкой фракции, т.е. компонентов, чьи температуры кипения ниже выбранной границы разделения, в соответствующем потоке.
Предполагая, что колонна теплоизолирована и потери теплоты в окружающую среду значительно меньше, чем поток теплоты, затрачиваемый на разделение, можно считать, что ${{q}_{ + }} = {{q}_{ - }} = q.$
После исключения из этих соотношений всех переменных кроме потока разделяемой смеси, потока теплоты и производства энтропии получим неравенство, связывающее производительность и затраты теплоты с величиной производства энтропии:
(4)
$q \geqslant {{g}_{F}}\frac{{{{T}_{B}}}}{{{{T}_{B}} - {{T}_{D}}}}{{A}_{G}} + {{\sigma }_{{{\text{min}}}}}\frac{{{{T}_{B}}{{T}_{D}}}}{{{{T}_{B}} - {{T}_{D}}}},$(5)
$\begin{gathered} {{A}_{G}} = - R{{T}_{D}}\left[ {\sum\limits_i {{{x}_{{Fi}}}} \ln {{x}_{{Fi}}} - } \right. \\ \left. { - \,\,\varepsilon \sum\limits_i {{{x}_{{Di}}}} \ln {{x}_{{Di}}} - (1 - \varepsilon )\sum\limits_i {{{x}_{{Bi}}}} \ln {{x}_{{Bi}}}} \right]. \\ \end{gathered} $Здесь $\varepsilon $ – доля отбора верхнего продукта.
Как правило, давление в колонне выбирают таким образом, чтобы для охлаждения дефлегматора можно было использовать наружную воду, т.е. величина ${{T}_{D}}$ была несколько выше температуры окружающей среды.
СВЯЗЬ МЕЖДУ ЗАТРАТАМИ ТЕПЛОТЫ В ОБРАТИМОМ И В НЕОБРАТИМОМ ПРОЦЕССАХ
Как следует из (4), соотношение между затратами теплоты и работой разделения в обратимом процессе таково же как между мощностью и затратами тепла в обратимой тепловой машине с КПД Карно, равным
Пусть законы теплопереноса в кубе и в дефлегматоре имеют форму
где ${{T}_{ + }}$ и ${{T}_{ - }}$ – температуры греющего пара и охлаждающей жидкости, ${{\beta }_{B}}$ и ${{\beta }_{D}}$ – коэффициенты теплопереноса в кубе и дефлегматоре соответственно, а кинетика массообмена между потоком пара и жидкости в каждом сечении колонны характеризуется выражением где $y$ – концентрация компонента, соответствующая рабочей линии, ${{y}^{0}}$ – равновесная концентрация, $\mu $ – химические потенциалы, $k$ – коэффициент массопереноса. Концентрации и температура меняются от сечения к сечению.Для такой кинетики минимальная диссипация зависит от потока теплоты как [9]
(8)
${{\sigma }_{{{\text{min}}}}} = {{q}^{2}}\left( {\left[ {\frac{1}{{{{\beta }_{B}}{{T}_{B}}{{T}_{ + }}}} + \frac{1}{{{{\beta }_{D}}{{T}_{D}}{{T}_{ - }}}}} \right] + \left[ {\frac{{2({{x}_{D}} - {{x}_{B}})}}{{k{{r}^{2}}}}} \right]} \right).$После подстановки этого выражения в (4) можно привести это неравенство, определяющее границу области реализуемых режимов колонны, к следующему виду:
где $b$ и $a$ – характеристические параметры, связанные с параметрами колонны как(10)
$a = \left[ {\frac{1}{{{{\beta }_{B}}{{T}_{B}}{{T}_{ + }}}} + \frac{1}{{{{\beta }_{D}}{{T}_{D}}{{T}_{ - }}}} + \frac{{2({{x}_{D}} - {{x}_{B}})}}{{k{{r}^{2}}}}} \right]\frac{{{{T}_{D}}}}{{{{A}_{G}}}},$Здесь ${{K}_{T}}$ – температурный коэффициент:
КПД колонны (затраты теплоты на моль разделяемой смеси), соответствующий границе области реализуемости, выраженный через характеристические параметры, примет следующий вид:
Из (13) следует, что КПД достигает максимума, равного $b$ в обратимом процессе, когда ${{g}_{F}}$ и $q$ стремятся к нулю.
Рабочий участок границы области реализуемости соответствует тем значениям $q,$ при которых производительность с ростом затрат тепла не убывает. Он ограничен значением $q* = \frac{b}{{2a}}.$ КПД на рабочем участке линейно уменьшается от $b$ до $b{\text{/}}2.$
Введем относительный поток теплоты q0 = = q/q*. На рабочем участке ${{q}^{0}}$ изменяется от нуля до единицы. КПД колонны как функция ${{q}^{0}}$ равен
Так что, если величина обратимого КПД $b$ у одной колонны больше чем у другой, то это неравенство сохраняется и для КПД колонны в классе необратимых процессов во всей рабочей области.
РАСЧЕТ ТЕМПЕРАТУР В КУБЕ И В ДЕФЛЕГМАТОРЕ
Температуру в дефлегматоре на практике, как правило, задают приблизительно равной ${{T}_{D}} = 323\;{\text{K,}}$ чтобы в качестве охлаждающей жидкости можно было использовать воду при температуре окружающей среды, равной примерно 300 К.
Составы паровой фазы ${{y}_{D}}$ и жидкой фазы ${{x}_{D}}$ в дефлегматоре связаны друг с другом через константы фазового равновесия ${{K}_{{iD}}},$ зависящие от свойств $i$-го компонента, температуры ${{T}_{D}}$ и давления $\bar {P}$ в дефлегматоре:
Так как мольная доля каждого из компонентов в паре в равновесии равна отношению парциального давления этого компонента ${{P}_{{iD}}}$ к общему давлению $\bar {P},$ то
Парциальное давление ${{P}_{{iD}}}({{T}_{D}})$ – произведение давления паров чистого компонента $P_{{iD}}^{0}({{T}_{D}})$ на мольную долю этого компонента в жидкости.
Рассмотрим равновесие парожидкостной смеси в верхней части колонны. Состав потока, выходящего из дефлегматора, определен составом пара $y$ парожидкостной смеси. Состав жидкости в верхней части колонны зависит от $y,$ давления $\bar {P}$ и температуры ${{T}_{D}}$ как
Поскольку $\sum\limits_i {{{x}_{{Di}}}} = 1$, то из (15), (16) можно выразить $\bar {P}$ через ${{x}_{D}}{\text{:}}$
(17)
$\bar {P} = \frac{1}{{\sum\limits_{i = 1}^n {\frac{{{{x}_{{Di}}}}}{{P_{i}^{0}({{T}_{D}})}}} }}.$Аналогичным образом, зная давление в колонне $\bar {P},$ состав и свойства компонентов в кубе, можно найти температуру ${{T}_{B}}$ в кубе из уравнения парожидкостного равновесия для кубового продукта:
Полученное уравнение в подавляющем большинстве случаев может быть разрешено относительно ${{T}_{B}}$ только численно, но в силу того, что его правая часть монотонно растет с ростом ${{T}_{B}},$ оно имеет единственный действительный корень.
Если фракции представляют собой идеальные растворы, то для расчета давлений пара каждого из компонентов можно воспользоваться уравнением Антуана [11]:
где ${{A}_{i}},$ ${{B}_{i}}$ и ${{C}_{i}}$ – эмпирические коэффициенты, таблицы для которых имеются для большинства веществ. В случае неидеальности фракций необходимо использовать более сложные зависимости давления насыщенного пара компонента от температуры и его мольной доли в жидкости [7].Таким образом, алгоритм для расчета температур в кубе и в дефлегматоре состоит в следующем.
1. Задают температуру в дефлегматоре колонны ${{T}_{D}},$ составы потоков ${{x}_{F}},$ ${{x}_{D}},$ ${{x}_{B}}$ и соответствующие коэффициенты уравнения Антуана ${{A}_{i}},$ ${{B}_{i}},$ ${{C}_{i}}$ для каждого компонента.
2. Рассчитывают давление, которое необходимо поддерживать в колонне, чтобы при заданном составе температура ${{T}_{D}}$ принимала нужное значение, используя уравнение парожидкостного равновесия в дефлегматоре колонны (17). Необходимые значения давлений пара для каждого из компонентов находят из уравнения Антуана (19).
3. Решают численно относительно температуры кипения в кубе ${{T}_{B}}$ уравнение парожидкостного равновесия (18).
Пример 1. Двухкомпонентная смесь. Рассмотрим разделение смеси, данные о которой приведены в табл. 1 [7, 12].
Таблица 1.
Данные о смеси и продуктах разделения для примера 1
| Компонент | ${{x}_{F}}$ | ${{x}_{D}}$ | ${{x}_{B}}$ | A | B | C | r, кДж/моль |
|---|---|---|---|---|---|---|---|
| Бензол | 0.4 | 0.95 | 0.1 | 4.01814 | 1203.835 | –53.226 | 33.9 |
| Толуол | 0.6 | 0.05 | 0.9 | 4.07827 | 1343.943 | –53.773 | 37 |
1. Температура в дефлегматоре задана и равна ${{T}_{D}} = 323\;{\text{K}}{\text{.}}$ Свойства разделяемой смеси и продуктов разделения представлены в табл. 1.
2. Найдем парциальные давления чистых компонентов, воспользовавшись выражением (19):
По формуле (17) общее давление в колонне равно
3. Составим уравнение парожидкостного равновесия для куба колонны (см. (18)) и определим температуру в кубе:
Решив это уравнение численно, получим величину ${{T}_{B}} = 351\;{\text{K}}{\text{.}}$
4. Значение обратимого КПД ${{\eta }_{c}}$ равно
Таким образом, обратимый КПД колонны ректификации очень мал, а в режиме максимальной производительности он составит 4%.
Пример 2. Многокомпонентная смесь. Рассмотрим процесс разделения смеси, данные о котором приведены в табл. 2 [7, 12]. Граница разделения проходит между пропаном и н-бутаном. Найдем температурный коэффициент для выбранного варианта разделения, воспользовавшись вышеописанным алгоритмом.
Таблица 2.
Данные о смеси и продуктах разделения для примера 2
| Компонент | ${{x}_{F}}$ | ${{x}_{D}}$ | ${{x}_{B}}$ | A | B | C | r | ${{T}_{0}}$, K |
|---|---|---|---|---|---|---|---|---|
| Метан | 0.26 | 0.435 | 0 | 3.9895 | 443.028 | –0.49 | 8.5 | 111.65 |
| Этан | 0.09 | 0.15 | 0 | 4.50706 | 791.3 | –6.422 | 9.76 | 184 |
| Пропан | 0.25 | 0.41 | 0.01 | 4.53678 | 1149.36 | 24.906 | 16.25 | 231 |
| Н-бутан | 0.17 | 0.005 | 0.417 | 4.35576 | 1175.581 | –2.071 | 22.4 | 272 |
| Н-пентан | 0.11 | 0 | 0.274 | 3.9892 | 1070.617 | –40.454 | 26.5 | 309 |
| Н-гексан | 0.12 | 0 | 0.299 | 3.45604 | 1044.038 | –53.893 | 31 | 341 |
1. Температура в дефлегматоре задана и равна ${{T}_{D}} = 323\;{\text{K}}{\text{.}}$ Свойства разделяемой смеси и продуктов разделения представлены в табл. 2.
2. Давление, которое необходимо установить в колонне, находим из уравнения (17):
3. Из (18) после его численного решения аналогично примеру 1 найдем температуру в кубе:
4. Обратимый КПД равен
ЦЕЛЕСООБРАЗНОСТЬ ИСПОЛЬЗОВАНИЯ РАЗДЕЛЯЮЩЕГО АГЕНТА
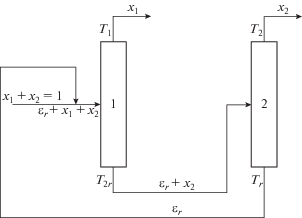
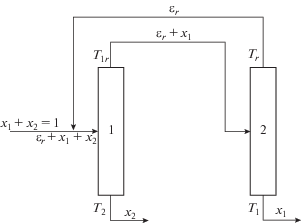
В процессах ректификации для разделения веществ с близкими температурами кипения или азеотропов используют схемы с разделяющим агентом (РА) [14]. При этом к разделяемой смеси добавляют РА, имеющий температуру кипения более низкую, чем компоненты разделяемой смеси (азеотропная ректификация) или более высокую (экстрактивная ректификация). Получившуюся трехкомпонентную смесь разделяют в каскаде из двух колонн. В первой из них отделяют смесь РА с компонентом, близким к нему по температуре кипения, а во второй разделяют эту смесь, возвращая РА на вход системы. На рис. 2 и 3 представлены схемы экстрактивной и азеотропной ректификации.
Термодинамический анализ таких систем [14] позволяет на качественном уровне выяснить, при каких условиях добавление РА снижает затраты теплоты на разделение 1 моля смеси.
Использование РА может оказаться целесообразным не только для азеотропных смесей, но и для трудноразделяемых веществ с близкими физико-химическими свойствами. При этом необходимо сопоставить затраты теплоты в системе с РА из двух колонн и смесителя с затратами теплоты в одной колонне с близкокипящими компонентами. Используя приведенные выше соотношения, вытекающие из термодинамических балансов, выясним, при каких условиях использование РА приведет к экономии тепловой энергии на 1 моль разделяемой смеси в обратимом приближении. В силу монотонной зависимости затрат тепла в необратимом процессе от его затрат в обратимом процессе это условие позволит оценить целесообразность использования РА и при заданной ненулевой производительности.
Подробнее рассмотрим экстрактивную ректификацию, а аналогичные соотношения для азеотропной ректификации приведем без вывода.
Сравнение обратимых затрат теплоты для экстрактивной ректификации. Обозначим через $\varepsilon $ число молей РА, добавляемое на один моль исходной смеси (степень разбавления), через ${{\eta }_{{c0}}},$ ${{\eta }_{{c1}}},$ ${{\eta }_{{c2}}}$ – обратимые КПД колонны, разделяющей исходную смесь, смесь трех компонентов с РА в первой колонне каскада и смесь РА с компонентом, ближайшим к нему по температуре кипения, во второй колонне.
Условие целесообразности использования РА в этих обозначениях примет следующую форму:
(20)
$\frac{{({{x}_{1}} + \varepsilon ){{A}_{{G1}}}}}{{{{\eta }_{{c1}}}}} + \frac{{({{x}_{2}} + \varepsilon ){{A}_{{G2}}}}}{{{{\eta }_{{c2}}}}} < \frac{{{{A}_{{G0}}}}}{{{{\eta }_{{c0}}}}}.$Здесь ${{x}_{1}}$ – мольная доля низкокипящего компонента в исходной смеси, ${{x}_{2}}$ – мольная доля высококипящего компонента, ${{x}_{2}} = 1 - {{x}_{1}}.$ В левой и в правой части этого неравенства фигурируют обратимые затраты теплоты, отнесенные к 1 молю исходной смеси. Мольная работа разделения равна
(21)
${{A}_{{G1}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{1}}}}{{1 + \varepsilon }}\ln \frac{{{{x}_{1}}}}{{1 + \varepsilon }} + \frac{{{{x}_{2}} + \varepsilon }}{{1 + \varepsilon }}\ln \frac{{{{x}_{2}} + \varepsilon }}{{1 + \varepsilon }}} \right).$Аналогично
(22)
${{A}_{{G2}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{2}}}}{{{{x}_{2}} + \varepsilon }}\ln \frac{{{{x}_{2}}}}{{{{x}_{2}} + \varepsilon }} + \frac{\varepsilon }{{{{x}_{2}} + \varepsilon }}\ln \frac{\varepsilon }{{{{x}_{2}} + \varepsilon }}} \right),$Нетрудно видеть, что подстановка этих выражений в неравенство (20) после сокращения левой и правой части неравенства на $R{{T}_{D}}$ приводит его к виду
(24)
$\begin{gathered} - \frac{{{{x}_{1}}\ln {{x}_{1}} + ({{x}_{2}} + \varepsilon )\ln ({{x}_{2}} + \varepsilon ) - (1 + \varepsilon )\ln (1 + \varepsilon )}}{{{{\eta }_{{c1}}}}} - \\ - \,\,\frac{{{{x}_{2}}\ln {{x}_{2}} + \varepsilon \ln \varepsilon - ({{x}_{2}} + \varepsilon )\ln ({{x}_{2}} + \varepsilon )}}{{{{\eta }_{{c2}}}}} < \\ < - \frac{{{{x}_{1}}\ln {{x}_{1}} + {{x}_{2}}\ln {{x}_{2}}}}{{{{\eta }_{{c0}}}}}. \\ \end{gathered} $С учетом независимости отношения температур кипения от давления в колонне термические обратимые КПД равны
(25)
${{\eta }_{{c0}}} = 1 - \frac{{{{T}_{1}}}}{{{{T}_{2}}}},\,\,\,\,{{\eta }_{{c1}}} = 1 - \frac{{{{T}_{1}}}}{{{{T}_{{2s}}}(\varepsilon )}},\,\,\,{{\eta }_{{c2}}} = 1 - \frac{{{{T}_{2}}}}{{{{T}_{s}}}}.$Здесь ${{T}_{s}}$ – температура кипения РА, ${{T}_{{2s}}}$ – температура кипения смеси второго компонента и РА, ${{T}_{2}}$ – температура кипения второго компонента при атмосферном давлении.
Справедливы следующие неравенства:
Сумма выражений, стоящих в числителях дробей в левой части неравенства (24), больше чем ${{A}_{{G0}}},$ так как схема с РА содержит смеситель и на разделение смешивающихся в нем потоков необходима дополнительная работа разделения.
Сравнение обратимых затрат теплоты для азеотропной ректификации. Для данного типа ректификации имеем ${{T}_{s}} < {{T}_{{1s}}} < {{T}_{1}} < {{T}_{2}},$ а выражения для обратимых работ разделения (21), (22) перепишутся в следующем виде:
(26)
${{A}_{{G1}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{1}} + \varepsilon }}{{1 + \varepsilon }}\ln \frac{{{{x}_{1}} + \varepsilon }}{{1 + \varepsilon }} + \frac{{{{x}_{2}}}}{{1 + \varepsilon }}\ln \frac{{{{x}_{2}}}}{{1 + \varepsilon }}} \right),$(27)
${{A}_{{G2}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{1}}}}{{{{x}_{1}} + \varepsilon }}\ln \frac{{{{x}_{1}}}}{{{{x}_{1}} + \varepsilon }} + \frac{\varepsilon }{{{{x}_{1}} + \varepsilon }}\ln \frac{\varepsilon }{{{{x}_{1}} + \varepsilon }}} \right).$Условие целесообразности использования РА, подобное (24), для азеотропной ректификации примет форму
(28)
$\begin{gathered} - \frac{{{{x}_{2}}\ln {{x}_{2}} + ({{x}_{1}} + \varepsilon )\ln ({{x}_{1}} + \varepsilon ) - (1 + \varepsilon )\ln (1 + \varepsilon )}}{{{{\eta }_{{c1}}}}} - \\ - \,\,\frac{{{{x}_{1}}\ln {{x}_{1}} + \varepsilon \ln \varepsilon - ({{x}_{1}} + \varepsilon )\ln ({{x}_{1}} + \varepsilon )}}{{{{\eta }_{{c2}}}}} < \\ < - \frac{{{{x}_{1}}\ln {{x}_{1}} + {{x}_{2}}\ln {{x}_{2}}}}{{{{\eta }_{{c0}}}}}. \\ \end{gathered} $Здесь
В силу того что отношение температур кипения мало зависит от давления, в выражениях для $\eta $ можно использовать отношения температур кипения при атмосферном давлении, тогда
(29)
${{\eta }_{{c0}}} = 1 - \frac{{{{T}_{1}}}}{{{{T}_{2}}}},\,\,\,\,{{\eta }_{{c1}}} = 1 - \frac{{{{T}_{{1s}}}(\varepsilon )}}{{{{T}_{2}}}},\,\,\,\,{{\eta }_{{c2}}} = 1 - \frac{{{{T}_{s}}}}{{{{T}_{1}}}}.$Пример 3. Рассмотрим азеотропное разделение смеси вода–пиридин [15] с концентрациями 0.51 и 0.49 соответственно. Температуры кипения компонентов: вода – ${{T}_{1}} = 373\;{\text{K,}}$ пиридин – ${{T}_{2}} = 388\;{\text{K}}{\text{.}}$ В качестве разделяющего агента используем метанол с ${{T}_{s}} = 338\;{\text{K,}}$ который образует с водой смесь, кипящую при температуре ${{T}_{{1s}}} = 353\;{\text{K}}$ при соотношении молей 14 : 86 [16]. Таким образом, к одному молю смеси вода–пиридин с мольными долями воды ${{x}_{1}}$ и пиридина ${{x}_{2}}$ нужно добавить $\varepsilon = 0.16{{x}_{1}} = 0.082$ моль метанола.
Рассчитаем термические КПД по формулам (29):
и подставим в неравенство (28). Получим
Левая часть этого неравенства равна 15, а правая 17.8. Относительная экономия Е составила 16%.
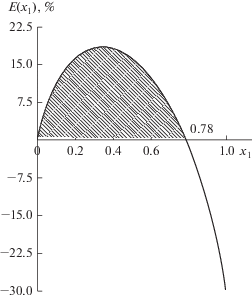
В предположении, что степень разбавления РА и все термические КПД фиксированы, построим зависимость процента экономии энергии от состава исходной смеси. График этой функции изображен на рис. 4. Видно, что добавление метанола в мольном соотношении 14 : 86 (массовое соотношение приблизительно 5 : 18) к воде целесообразно при мольной доле воды в исходной смеси ${{x}_{1}} < 0.78.$
ЗАКЛЮЧЕНИЕ
Получены уравнения, определяющие границу области возможных режимов колонны бинарной ректификации с заданной производительностью. Обратимые затраты теплоты зависят от порядка разделения в силу того, что от них зависит термический КПД колонны. Показано, что затраты теплоты на 1 моль разделяемой смеси с учетом необратимости монотонно зависят от обратимых затрат, что позволяет использовать обратимые показатели для выбора порядка разделения. Приведены условия, при которых использование РА позволяет получить экономию затрат энергии.
ОБОЗНАЧЕНИЯ
| ${{A}_{G}}$ | мольная работа разделения, Дж/моль |
| $a$ | коэффициент необратимости |
| $b$ | обратимый КПД |
| ${{g}_{F}}$ | поток разделяемой смеси, моль/с |
| ${{h}_{F}},$${{h}_{D}},$${{h}_{B}}$ | мольные энтальпии потоков, Дж/моль |
| ${{K}_{D}}$ | константа фазового равновесия |
| ${{K}_{T}}$ | температурный коэффициент |
| $k$ | коэффициент массопереноса |
| $P$ | парциальное давление, Па |
| ${{P}^{0}}$ | давление паров чистого компонента, Па |
| $\bar {P}$ | давление в колонне, Па |
| ${{q}_{ + }},$${{q}_{ - }},$$q$ | потоки теплоты, Вт |
| ${{r}_{i}}$ | мольная теплота парообразования i-го компонента, кДж/моль |
| ${{s}_{F}},$${{s}_{D}},$${{s}_{B}}$ | мольные энтропии потоков, Дж/(моль К) |
| ${{T}_{B}}$ | температура в кубе, K |
| ${{T}_{D}}$ | температура в дефлегматоре, K |
| ${{T}_{i}}$ | температура кипения i-го компонента, K |
| ${{x}_{{Bi}}}$ | мольная доля i-го компонента в кубе (тяжелая фракция) |
| ${{x}_{{Di}}}$ | мольная доля i-го компонента в дефлегматоре (легкая фракция) |
| ${{x}_{{Fi}}}$ | мольная доля i-го компонента в разделяемой смеси |
| ${{y}^{0}}$ | равновесная концентрация |
| $\alpha $ | относительная летучесть |
| ${{\beta }_{D}},$${{\beta }_{B}}$ | коэффициенты теплообмена в дефлегматоре и кубе, Вт/К |
| $\varepsilon $ | степень разбавления РА |
| $\eta $ | термический КПД |
| $\sigma $ | производство энтропии, Вт/К |
Список литературы
Александров И.А. Ректификационные и абсорбционные аппараты. М.: Химия, 1978.
Гельперин Н.И. Основные процессы и аппараты химической технологии. М.: Химия, 1981.
Павлов К.Ф. Примеры и задачи по курсу процессов и аппаратов химической технологии. Л.: Химия, 1987.
Петлюк Ф.Б. Многокомпонентная ректификация. Теория и расчет. М.: Химия, 1983.
Плановский А.Н. Процессы и аппараты химической и нефтехимической технологии. Учебник для вузов. М.: Химия, 1987.
Holland C.D. Fundamentals of Multicomponent Distillation. N.Y.: McGraw-Hill, 1981.
Kister H.Z. Distillation Design. N.Y.: McGraw-Hill, 1992.
Цирлин А.М. Необратимые оценки предельных возможностей термодинамических и микроэкономических систем. М.: Наука, 2003.
Sukin I.A., Balunov A.I., Schwalbe K. The Rule of Temperature Coefficients for Selection of Optimal Separation Sequence for Multicomponent Mixtures in Thermal Systems // J. Non-Equilib. Thermodyn. 2017. V. 42. № 4. P. 359.
Tsirlin A.M., Sukin I.A., Balunov A.I. Estimates of Energy Consumption and Selection of Optimal Distillation Sequence for Multicomponent Distillation // Theor. Found. Chem. Eng. 2016. V. 50. № 3. P. 250. [Цирлин А.М., Сукин И.А., Балунов А.И. Оценки затрат энергии на разделение многокомпонентных смесей в термических системах. Выбор последовательности разделения // Теор. осн. хим. технол. 2016. Т. 50. № 3. С. 258.]
Poling B.E., Prausnitz J.M., O’Connell J.P. Properties of Gases and Liquids. N.Y.: McGraw-Hill, 2004.
NIST Chemistry WebBook, NIST Standard Reference Database Number 69 / Eds. Linstrom P.J., Mallard W.G. Gaithersburg: National Institute of Standards and Technology (NIST), 2018.
Prigogine I., Kondepudi D. Modern Thermodynamics: From Heat Engines to Dissipative Structures. N.Y.: Wiley, 2014.
Коган В.Б. Азеотропная и экстрактивная ректификация. М.: Химия, 1971.
Крель Э. Руководство по лабораторной перегонке. М.: Химия, 1980.
Berg L., Zuyin Y. Separation of Pyridine from Water by Extractive Distillation. Pat. 5100514 USA. 1992.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии