Теоретические основы химической технологии, 2021, T. 55, № 3, стр. 319-331
Моделирование паровой конверсии метана в мембранном реакторе с никелевым катализатором и фольгой из палладиевого сплава
В. Н. Бабак a, *, Л. П. Диденко a, Ю. П. Квурт a, Л. А. Семенцова a, С. Е. Закиев a
a Институт проблем химической физики РАН
Черноголовка, Россия
* E-mail: tabor47@mail.ru
Поступила в редакцию 06.05.2020
После доработки 17.12.2020
Принята к публикации 14.01.2021
Аннотация
Разработана модель парового риформинга метана в каталитическом реакторе, рабочей частью которого являются две цилиндрические камеры, разделенные мембранной перегородкой. Верхняя камера вакуумируется, в нижней поддерживается атмосферное давление. При равномерной подаче сырья по внешнему периметру нижней камеры, проблема сведена к нахождению средних потоков СН4, Н2О, СО2, СО и Н2 из решения системы пяти нелинейных обыкновенных дифференциальных уравнений первого порядка. Расчеты проводили для мембраны Pd–6% Ru в интервале температур 673 K < T < 973 K при отношении входных потоков пар/метан, равном 3, и скорости подачи сырья 1800–9600 1/ч. В результате сравнения расчетов с экспериментальными данными получено теоретическое обоснование основных закономерностей процесса, наблюдаемых на практике.
ВВЕДЕНИЕ
Актуальная задача водородной энергетики – получение Н2 высокой чистоты. Водород широко используется в химической промышленности, в частности, для получения аммиака, соляной кислоты, метанола и т.д. [1]. Он необходим для работы низкотемпературных топливных элементов при производстве электроэнергии [2].
В настоящее время основным методом получения чистого Н2 является паровой риформинг природного газа, содержащего помимо СН4 до 3–10% более высоких гомологов (С2+-алканов). Процесс проводится обычно в традиционных каталитических реакторах (трубы, всевозможные полости) различных конструкций, размеров и способов нагрева [3–5]. Расчет подобных реакторов базируется на решении уравнений гидродинамики, конвективной диффузии и теплопередачи. Однако необходимые коэффициенты переноса для каталитических систем, как правило, неизвестны, а корреляции для потоков массы и тела являются эмпирическими. Для достижения высокой конверсии метана необходимы температуры ∼1000 K. Процесс является капитало- и энергоемким. Дополнительных затрат требует стадия очистки получаемых на выходе водородных смесей. Кроме того, при температурах риформинга из С2+ углеводородов образуются углеродные отложения (УО), дезактивирующие катализатор. Поэтому их предварительно удаляют из сырья в стадии предриформинга при “низких” температурах ≤700 K. Снижения капитальных и энергетических затрат можно достичь, используя мембранную технологию, объединяющую реакционный процесс и отвод Н2 из получаемых продуктов через мембраны. Впервые идеи каталитических мембранных процессов сформулированы в работах [6, 7]. Работы в этом направлении активно проводятся в настоящее время [8–13]. Особое внимание уделяется реакторам небольших размеров, простой геометрии, процессы в которых удается проводить при постоянных давлениях и температурах [14, 15].
В технологическом отделе Института проблем химической физики РАН проводятся исследования по получению чистого водорода методом паровой конверсии метана в мембранном реакторе, описание которого приведено в публикациях [16, 17].
В качестве материала мембран для увеличения производительности реактора использовали сплавы Pd–6% In, Pd–6% In–0.5% Ru, Pd–23% Ag, Pd–6% Ru, Pd–10% Ru, полученные в виде фольги методом холодного проката с промежуточным отжигом в инертной среде в Институте металлургии и материаловедения им. А.А. Байкова (ИМЕТ РАН) [18, 19].
Минимальная толщина бездефектной фольги, полученной таким способом, составляет ∼10 мкм, что необходимо для поддержания механической прочности мембраны.
Более тонкие палладиевые слои (менее 10 мкм) получают с помощью нанесения палладия на пористые подложки (пористые стекло, керамика и металлы) электрохимическими методами, химическим осаждением из паровой фазы, магнетронным напылением и т.д. [20–27]. Такие композиционные мембраны имеют высокую водородную проводимость, однако они недостаточно водородоселективны, достаточно сложны в изготовлении и не могут сохранять термическую и химическую стабильности продолжительное время. В отличие от них, фольговые мембраны имеют практически 100%-ную селективность по водороду, и для их изготовления не нужно применять сложную технологию. К преимуществам палладиевой фольги следует отнести простоту ее соединений с конструктивными элементами реактора, а также простоту утилизации.
В настоящей работе в качестве примера исследован паровой риформинг чистого метана в каталитическом реакторе с фольговой мембраной Pd–6% Re.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
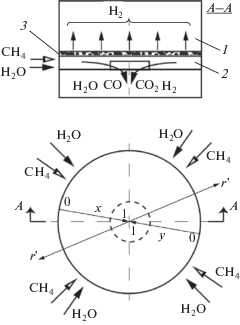
Схематическое изображение реакторе представлено на рис. 1. В нижнюю камеру засыпают частички промышленного никелевого катализатора (марка НИАП-03-01 с зернистой фракцией 0.2–0.4 мм и массовой долей Ni порядка 10%). Цилиндрические камеры (радиус $r_{{\max }}^{'} = 2.8$ см, высота $h = 4$ мм) разделены мембраной (толщина 30 мкм) из сплава Pd–6% Ru, избирательно пропускающей только молекулы Н2. Фольга имела форму диска (эффективная площадь $S$ = 15.2 см2), ее помещали между сетками тонкого плетения из нержавеющей стали для механической прочности. В нижней камере (отделение ретантата) поддерживали атмосферное давление. Верхнюю камеру (отделение пермиата) вакуумировали (∼2–4 мм рт. ст.). В отделение ретантата помещали 2 см3 (3.35 г) катализатора. Метан смешивают с водяным паром в отношении m = 2–7 и подают через отверстия, расположенные по периферии отделения ретантата, а продукты отводили через центральное отверстие ($r_{{\min }}^{'} \cong 1$ мм) и пропускали через холодильник для конденсирования непрореагировавшей воды. Объемную скорость “сухих” газов (СН4, Н2, СО, СО2) после холодильника измеряли пенным расходомером при T = 300 K и подавали в хроматограф (“Кристалл-5000” с ПИД и детектором по теплопроводности). Содержание Н2 в продуктах реакции определяли на колонке с молекулярными ситами 13Х (2 мм × 2 м, газ-носитель – аргон). Углеводородный состав (СН4) продуктов определяли на колонке НР-Al/KCl (0.5 мм × × 30 м, газ-носитель – гелий). Содержание СО и СО2 определяли на колонке с активированным углем (2 мм × 2 м, газ-носитель – гелий). Расходы газовых потоков контролировали регуляторами расхода РРГ-12 (“Электроприбор”, г. Зеленоград). Нагрев реактора осуществляли электропечью. Для контроля за температурой в реакторе и в печи использовали хромель-алюмелевые термопары.
ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ПАРОВОГО РИФОРМИНГА МЕТАНА В МЕМБРАННОМ РЕАКТОРЕ
При температурах $T \geqslant 400$ K на поверхности никеля между метаном и водяным паром протекают обратимые химические реакции [28–31]:
(1)
${\text{С}}{{{\text{H}}}_{4}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}} = {\text{CO}} + 3{{{\text{H}}}_{2}}~\,\,\,({{K}_{1}}),$(2)
${\text{СO}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}} = {\text{C}}{{{\text{O}}}_{2}} + {{{\text{H}}}_{2}}\,\,\,\,({{K}_{2}}).$При равномерной подаче Н2О и СН4 по периметру реактора можно предположить, что изменение концентраций $c_{i}^{'}$ в нижней камере происходит только в радиальном направлении r' (рис. 1). Пренебрегая диффузией по оси r' и интегрируя уравнения переноса по вертикальной координате z' от нуля до h, для расчета интегральных мольных потоков ${{N}_{i}}$ получаем следующие уравнения:
(3)
$\frac{{d{{N}_{i}}}}{{dr{\kern 1pt} '}} = (2\pi r{\kern 1pt} 'h){{\rho }_{{{\text{cat}}}}}{{\varphi }_{i}} - (2\pi r{\kern 1pt} '){{I}_{{i,S}}},$здесь ${{I}_{{i,S}}}$ – потоки частиц на поверхности мембраны, $N_{i}^{'}$ – мольные потоки в радиальном направлении, ${{N}_{i}}$ – интегральные потоки при фиксированном r', индекс “s” относится к поверхности мембраны, i = 1 относится к концентрации СН4, 2 – Н2О, 3 – СО, 4 – СО2, 5 – Н2; ${{\varphi }_{i}}$ – источник (сток) i-го компонента.
Введем безразмерные координаты ($r$ и $y$), отсчитываемые в радиальном направлении от центра фольги и от внешнего радиуса (рис. 1):
Уравнения для расчета интегральных потоков принимают вид:
(5)
$\begin{gathered} \frac{\partial }{{\partial y}}( - {{N}_{i}}) = 2{{w}_{{{\text{cat}}}}}(1 - y){{\varphi }_{i}} - 2S(1 - y){{I}_{{i,S}}} \\ {\text{или}}\,\,\,\frac{{\partial ( - {{N}_{i}})}}{{\partial x}} = {{w}_{{{\text{cat}}}}}{{\phi }_{i}} - S{{I}_{{i,S}}}. \\ \end{gathered} $Здесь введена безразмерная продольная координата $x = 2y - {{y}^{2}},$ отсчитываемая от внешней границы камеры ($0 \leqslant x \leqslant 1$).
Предполагается, что ${{I}_{{i,S}}} = 0$ для всех частиц, кроме водорода. Для потока водорода на поверхности мембраны выполняется закон Сивертса:
Для рассматриваемой мембраны Q0 = 6.1 × × 10–8 моль/м1/2 кг1/2, $E = 13.9$ кДж/моль [14].
Функции источников ${{\phi }_{i}}$ для частиц в соответствии с реакциями (1, 2) представим в виде
Экспериментальные значения ${{\tilde {k}}_{i}},$ ${{K}_{i}}$ известны из литературы [29, 30]:
(6)
$\begin{gathered} {{{\tilde {k}}}_{1}} = (1.17 - 2.68) \times {{10}^{{15}}}\exp [{{ - 28867} \mathord{\left/ {\vphantom {{ - 28867} T}} \right. \kern-0em} T}], \\ {{{\text{моль}}\,\,{\text{а}}{{{\text{т}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{\text{моль}}\,\,{\text{а}}{{{\text{т}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {{\text{к}}{{{\text{г}}}_{{{\text{cat}}}}}с}}} \right. \kern-0em} {{\text{к}}{{{\text{г}}}_{{{\text{cat}}}}}с}}, \\ {{{\tilde {k}}}_{2}} = (0.54 - 1.22) \times {{10}^{6}}\exp [{{ - 8074.3} \mathord{\left/ {\vphantom {{ - 8074.3} T}} \right. \kern-0em} T}], \\ {{{\text{моль}}\,\,{\text{ат}}} \mathord{\left/ {\vphantom {{{\text{моль}}\,\,{\text{ат}}} {{\text{к}}{{{\text{г}}}_{{{\text{cat}}}}}с}}} \right. \kern-0em} {{\text{к}}{{{\text{г}}}_{{{\text{cat}}}}}с}} \\ {{K}_{1}} = (7.85 - 12.24) \times {{10}^{{12}}}\exp [{{ - 220000} \mathord{\left/ {\vphantom {{ - 220000} {RT}}} \right. \kern-0em} {RT}}],\,\,{\text{а}}{{{\text{т}}}^{{\text{2}}}}, \\ {{K}_{2}} = (1.41 - 1.77) \times {{10}^{{ - 2}}}\exp [{{37720} \mathord{\left/ {\vphantom {{37720} {RT}}} \right. \kern-0em} {RT}}]. \\ \end{gathered} $Наименьшие значения взяты из [29], наибольшие – из [30]. Ниже будет показано, что эти расхождения не повлияют на полученные результаты.
Соответствующие коэффициенты Ленгмюра равны [29, 30]:
(7)
$\begin{gathered} {{k}_{{{\text{CO}}}}} = 8.23 \times {{10}^{{ - 5}}}\exp ({{70650} \mathord{\left/ {\vphantom {{70650} {RT}}} \right. \kern-0em} {RT}}),\,\,{\text{а}}{{{\text{т}}}^{{--{\text{1}}}}}; \\ {{k}_{{{\text{C}}{{{\text{Н}}}_{{\text{4}}}}}}} = 6.65 \times {{10}^{{ - 4}}}\exp ({{38280} \mathord{\left/ {\vphantom {{38280} {RT}}} \right. \kern-0em} {RT}}),\,\,{\text{а}}{{{\text{т}}}^{{--{\text{1}}}}}; \\ {{k}_{{{{{\text{Н}}}_{{\text{2}}}}}}} = 6.12 \times {{10}^{{ - 9}}}\exp ({{82900} \mathord{\left/ {\vphantom {{82900} {RT}}} \right. \kern-0em} {RT}}),\,\,{\text{а}}{{{\text{т}}}^{{--{\text{1}}}}}; \\ {{k}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{O}}}}} = 1.77 \times {{10}^{5}}\exp ({{ - 89680} \mathord{\left/ {\vphantom {{ - 89680} {RT}}} \right. \kern-0em} {RT}}). \\ \end{gathered} $Для нахождения потоков частиц в нижней камере получаем систему из пяти обыкновенных дифференциальных уравнений первого порядка:
(8)
$\begin{gathered} \frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = - {{b}_{1}}\left( {\frac{{{{w}_{{{\text{cat}}}}}}}{{{{N}_{{{\text{ВХ}}}}}}}} \right),\,\,\,\,\frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{\partial x}} = - ({{b}_{1}} + {{b}_{2}})\left( {\frac{{{{w}_{{{\text{cat}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right), \\ \frac{{d{{n}_{{{\text{CO}}}}}}}{{dx}} = ({{b}_{1}} - {{b}_{2}})\left( {\frac{{{{w}_{{{\text{cat}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right),\,\,\,\,\frac{{\partial {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}}}{{\partial x}} = {{b}_{2}}\left( {\frac{{{{w}_{{{\text{cat}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right), \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dx}} = (3{{b}_{1}} + {{b}_{2}})\left( {\frac{{{{w}_{{{\text{cat}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right) - S{{{{I}_{{{{{\text{H}}}_{2}},S}}}} \mathord{\left/ {\vphantom {{{{I}_{{{{{\text{H}}}_{2}},S}}}} {{{N}_{{{\text{BX}}}}}}}} \right. \kern-0em} {{{N}_{{{\text{BX}}}}}}}, \\ \end{gathered} $с граничными условиями на входе ($x = 0$):
(9)
${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 1,\,\,\,\,{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = m,\,\,\,\,{{n}_{{{\text{CO}}}}} = {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} = {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 0,$Безразмерные потоки ${{n}_{{{\text{CO}}}}}$ и ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ можно выразить через потоки ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}.$
Умножая первое уравнение (8) на 2, второе на (–1) и суммируя результат с третьим уравнением, получим равенства:
Используя граничные условия (9), выразим поток ${{n}_{{{\text{CO}}}}}$ как функцию ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ и ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$ при любом x:
(10)
${{n}_{{{\text{CO}}}}} = 2(1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}) - (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}).$Аналогично, умножая первое уравнение (8) на (–1), второе на (+1) и складывая полученный результат с четвертым уравнением, можно выразить потоки ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ как функцию ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ и ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}{\text{:}}$
(11)
${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} = (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) - (1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}).$Проводя подобные действия с первым, вторым и пятым уравнениями системы (8), последнюю можно заменить системой из следующих трех уравнений:
(12)
$\begin{gathered} \frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = - {{\alpha }_{1}}{{F}_{1}},\,\,\,\,\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dx}} = - {{\alpha }_{1}}{{F}_{1}} - {{\alpha }_{2}}{{F}_{2}}, \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dx}} + \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dx}} + 2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = - \beta \sqrt {{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}} . \\ \end{gathered} $С граничными условиями на входе ($x = 0$): ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 1,$ ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = m,$ ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 0.$
Выше введены безразмерные функции ${{F}_{1}}$ и ${{F}_{2}}{\text{:}}$
Безразмерные параметры ${{\alpha }_{1}},$ ${{\alpha }_{2}},$ $\beta $ равны
(13)
$\begin{gathered} {{\alpha }_{1}} = \frac{{{{{\tilde {k}}}_{1}}}}{{k_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}\left( {\frac{{{{w}_{{{\text{cat}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right)\frac{1}{{p_{{{\text{AT}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}},\,\,\,\,{{\alpha }_{2}} = \frac{{{{{\tilde {k}}}_{2}}}}{{k_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}\left( {\frac{{{{w}_{{{\text{cat}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right){{p}_{{{\text{AT}}}}}, \\ \beta = S\left[ {\frac{{{{Q}_{0}}\exp ({{ - E} \mathord{\left/ {\vphantom {{ - E} {RT)}}} \right. \kern-0em} {RT)}}}}{\delta }} \right] \times {{10}^{2}}\sqrt {10} {{p_{{{\text{AT}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} {{{N}_{{{\text{BX}}}}}}}} \right. \kern-0em} {{{N}_{{{\text{BX}}}}}}}. \\ \end{gathered} $Квадратная скобка в знаменателях функций ${{F}_{1}}$ и ${{F}_{2}}$ равна
Мольные доли частиц газовой смеси ${{X}_{i}}$ выражаются через потоки ${{n}_{i}}{\text{:}}$
(14)
$\begin{gathered} {{X}_{i}} = {{{{n}_{i}}} \mathord{\left/ {\vphantom {{{{n}_{i}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}},\,\,\,\,{{n}_{\sum }} = {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} + {{n}_{{{\text{CO}}}}} + {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + \\ + \,\,{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = 1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}. \\ \end{gathered} $В табл. 1 представлены значения некоторых кинетических параметров при различных температурах для мембранного модуля (${{w}_{{{\text{cat}}}}} = 3.5$ г, $S = 15.2$ см2, $\delta = 30$ мкм). Необходимые константы рассчитывали по формулам (6), (7). Все они будут использованы в дальнейшем.
Таблица 1.
Расчет безразмерных параметров для системы (12)
| T, K | 673 | 773 | 823 | 873 | 973 |
|---|---|---|---|---|---|
| ${{{{\alpha }_{1}}{{N}_{{{\text{BX}}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}{{N}_{{{\text{BX}}}}}} {p_{{{\text{AT}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {p_{{{\text{AT}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}$ | 1.95 ×10–3 | 7.13 × 10–3 | 1.35 × 10–2 | 2.27 × 10–2 | 5.27 × 10–2 |
| ${{{{\alpha }_{2}}{{N}_{{BX}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}{{N}_{{BX}}}} {{{p}_{{{\text{AT}}}}}}}} \right. \kern-0em} {{{p}_{{{\text{AT}}}}}}}$ | 20.46 | 1.61 | 0.58 | 0.22 | 0.047 |
| $({{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})p_{{{\text{AT}}}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}$ | 1.05 × 104 | 2.4 × 102 | 46.3 | 10.44 | 0.895 |
| ${{(\beta {{N}_{{{\text{BX}}}}})} \mathord{\left/ {\vphantom {{(\beta {{N}_{{{\text{BX}}}}})} {p_{{{\text{AT}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {p_{{{\text{AT}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}$ | 0.8 × 10–4 | 1.15 × 10–4 | 1.3 × 10–4 | 1.5 × 10–4 | 1.3 × 10–4 |
| ${{({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})} \mathord{\left/ {\vphantom {{({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})} {{{p}_{{{\text{AT}}}}}}}} \right. \kern-0em} {{{p}_{{{\text{AT}}}}}}}$ | 0.46 × 10–1 | 0.14 × 10–1 | 0.05 × 10–1 | 0.64 × 10–2 | 0.32 × 10–2 |
Система (12) решается численно методом Рунге–Кутты четвертого порядка. При атмосферном давлении в нижней камере (${{p}_{{{\text{AT}}}}} = 1$) параметрами, от которых зависят распределения потоков ${{n}_{i}}$ в нижней камере, являются температура ($T$), поток метана на входе ${{N}_{{{\text{BX}}}}}$ и отношение m.
Для эффективной работы ММ необходимо обеспечить контакт газа в нижней камере с катализатором по всему объему. На практике катализатор обычно засыпают приблизительно на 1/3–1/2 объема камеры (в наших экспериментах объем засыпки катализатора ∼2 см3, объем камеры ∼5.3 см3). Это необходимо, чтобы процесс протекал в режиме хаотического движения частичек катализатора в потоке газа для поддержания постоянной температуры в камере и выравнивания концентраций по высоте при фиксированном r'. Объемные скорости подачи сырья на входе ($G$) определяются следующим образом [32]:
(15)
$G \cong {{{{{\dot {V}}}_{\sum }}} \mathord{\left/ {\vphantom {{{{{\dot {V}}}_{\sum }}} {{{V}_{{{\text{cat}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{cat}}}}}}} = 30{{\dot {V}}_{\sum }}\,\,\left[ {{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{ч}}}} \right. \kern-0em} {\text{ч}}}} \right],\,\,\,\,{{\dot {V}}_{\sum }} = (1 + m)\dot {V},$Устойчивая работа реактора наблюдается в ограниченном интервале средних скоростей среды $\bar {u}{\kern 1pt} '{\text{:}}$ $\bar {u}_{{{\text{KP}}}}^{'} \leqslant \bar {u}{\kern 1pt} ' \leqslant 10\bar {u}_{{{\text{KP}}}}^{'}$ [32], где критическая скорость $\bar {u}_{{{\text{KP}}}}^{'}$ для катализатора с размером фракций ~0.3 мм по порядку величины равна $\bar {u}_{{{\text{KP}}}}^{'}$ ~ ~ $\sqrt {{{d}_{{{\text{cat}}}}}} = 0.1$ см/с.
Учитывая, что $\dot {V} = 2\pi r_{{\max }}^{'}h\bar {u}{\kern 1pt} '$ [см3/с], G = (1800) × × $(1800) \times \left( {2\pi r_{{\max }}^{'}h\bar {u}{\kern 1pt} '} \right)$ (1/ч), где $r_{{\max }}^{'}$ = 2.2 см, $h$ = = 0.35 см, ${{d}_{{{\text{cat}}}}}$ ≅ 0.03 см, можно показать, что допустимый интервал объемной скорости подачи сырья $G$ равен
(16)
${\text{1}}{{0}^{{\text{3}}}}\,\,\left( {{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{ч}}}} \right. \kern-0em} {\text{ч}}}} \right) \leqslant G \leqslant {{10}^{4}}\,\,\left( {{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{ч}}}} \right. \kern-0em} {\text{ч}}}} \right).$При “малой” скорости подачи ($G \leqslant {{10}^{3}}$ 1/ч) катализатор остается неподвижен и занимает ∼1/3 объема камеры. При большой скорости ($G \geqslant {{10}^{4}}$ 1/ч) происходит уплотнение катализатора в выходной области и перегрев реактора. В обоих случаях равномерный контакт газа и катализатора нарушается и предложенный ниже механизм взаимодействия перестает быть верным и наблюдаются заметные отклонения экспериментальных значений потока Н2 на выходе верхней камеры от теоретических.
Предполагая, что газовые смеси являются идеальными, используя закон Клапейрона–Менделеева, нетрудно показать, что мольный поток метана на входе ${{N}_{{{\text{BX}}}}}$ и объемная скорость подачи сырья $G$ связаны соотношением ($T$ ≅ 300 K):
(17)
${{N}_{{{\text{BX}}}}} = \left[ {{{{{p}_{{{\text{AT}}}}}G} \mathord{\left/ {\vphantom {{{{p}_{{{\text{AT}}}}}G} {450(1 + m)}}} \right. \kern-0em} {450(1 + m)}}} \right] \times {{10}^{{ - 5}}},\,\,{{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}.$Последнее означает, что по порядку величины допустимые значения потока СН4 на входе ${{N}_{{{\text{BX}}}}}$ ~ ~ 10–5–10–4 моль/с. Распределение потоков ${{n}_{i}}(x)$ внутри камеры зависит от величины кинематических параметров ${{\alpha }_{1}},$ ${{\alpha }_{2}}$ и $\beta .$
В рассматриваемой области температур кинетические константы ${{\alpha }_{1}},$ ${{\alpha }_{2}}$ удовлетворяют неравенствам ${{\alpha }_{2}} > {{\alpha }_{1}} \gg 1.$ Это означает, что безразмерные потоки ${{n}_{i}}$ должны заметно изменяться в узкой области $x \leqslant {1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}} \ll 1$ на входе газовой смеси в нижнюю камеру. Ниже будет показано, что существуют два несоизмеримых участка изменения потоков: начальный (короткий) и основной.
Численное решение системы уравнений (12) на начальном участке. Разделив уравнения системы (12) на ${{\alpha }_{1}}$ и вводя безразмерную продольную координату $z = {{\alpha }_{1}}x,$ преобразуем эту систему следующим образом:
(18)
$\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dz}} = - {{F}_{1}},\,\,\,\,\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dz}} = - {{F}_{1}} - \left( {\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}}}}} \right){{F}_{2}},$(19)
$\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dz}} + \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dz}} + 2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dz}} = - \left( {\frac{\beta }{{{{\alpha }_{1}}}}} \right)\sqrt {{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}} .$Граничные условия равны
Как видно (табл. 1), коэффициенты системы (18), (19) зависят только от температуры (${{p}_{{{\text{AT}}}}} = 1$).
Следовательно, безразмерные потоки ${{n}_{i}}(z)$ как функции координаты $z$ также зависят только от T. Расчет ${{n}_{i}}(z)$ для СН4, Н2О и Н2 представлен на рис. 2 ($m = 3$). Как видно, при увеличении $z$ потоки СН4 и Н2О отклоняются от соответствующих входных значений, причем эти отклонения увеличиваются при увеличении температуры. В частности, при $T \cong 1000$ K метан практически полностью расходуется на расстоянии от входа $z = {{z}_{{{\text{нач}}}}} \cong 10$ (${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 0$ при $z \geqslant 10$). В дальнейшем короткий участок $x \leqslant {{x}_{{{\text{нач}}}}} = {{10} \mathord{\left/ {\vphantom {{10} {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}}$ будем называть начальным участком. В отличие от потоков метана и воды поток водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(z)$ на этом участке монотонно увеличивается. Потоки СО и СО2 можно найти по общим формулам (10), (11). Нетрудно показать, что с ростом $z$ эти потоки монотонно увеличиваются. При $T \leqslant 800$ K углекислый газ можно не учитывать (${{n}_{{{\text{CO}}}}} \ll {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$). При $T \cong 1000$ K потоки СО и СО2 на выходе начального участка одного порядка (${{n}_{{{\text{CO}}}}} \cong {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} \cong 0.5$). Расчеты показали, что на начальном участке мембрана практически не влияет на потоки ${{n}_{i}}(z).$ Последнее, очевидно, является следствием того, что коэффициенты (${\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}}$) малы (табл. 1), и функцией $({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} $ в правой части уравнения (19) можно пренебречь по сравнению с производными в левой части. Последнее означает, что на начальном участке поток водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(z)$ можно выразить через потоки ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}(z)$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}(z),$ так как в этом случае уравнение (19) эквивалентно равенству:
(20)
${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) + 2(1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}),\,\,\,\,x \leqslant {{x}_{{{\text{нач}}}}}.$Рис. 2.
Расчет безразмерных потоков на начальном участке как функции координаты $z{\text{:}}$ 1 – $T$ = 973 K, 2 – 823, 3 – 773, 4 – 673 К. Сплошные линии – поток Н2 (${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$), штриховые линии – поток водяного пара (${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$), штрих-пунктирные линии – поток метана (${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$).
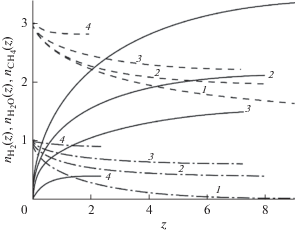
Из рис. 2 видно, что все производные ${{d{{n}_{i}}} \mathord{\left/ {\vphantom {{d{{n}_{i}}} {dz}}} \right. \kern-0em} {dz}}$ на выходе начального участка малы, следовательно, функции ${{F}_{1}}$ и ${{F}_{2}}$ (см. (18)) стремятся к нулю. Это означает, что обе реакции (1) и (2) достигают равновесного состояния, при котором скорости прямых и обратных реакций практически равны.
Безразмерные потоки ${{n}_{i}}(z)$ на выходе начального участка (${{x}_{{{\text{нач}}}}} = {{10} \mathord{\left/ {\vphantom {{10} {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}}$) можно получить и не решая систему (18), (19), а использовать только условия равновесия реакций (1) и (2) (равенства ${{F}_{1}} = {{F}_{2}} = 0$) и уравнение (20).
В результате получим нелинейную систему из трех алгебраических уравнений (21). Решение этой системы обозначим $n_{i}^{*}.$ Физический смысл потоков $n_{i}^{*}$ будет объяснен позднее.
(21)
$\begin{gathered} n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} - {{n}^{{*3}}} \times \\ \times \,\,{{{{\left[ {2(1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}) - (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})} \right]\left( {{1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left[ {2(1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}) - (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})} \right]\left( {{1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}} \right)} {\left( {1 + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}} \right)}}} \right. \kern-0em} {\left( {1 + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}} \right)}}}^{2}} = 0, \\ \left[ {2\left( {1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}} \right) - \left( {m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}} \right)} \right]n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} - n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}\left[ {\left( {m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}} \right) - \left( {1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}} \right)]} \right]\left( {{1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}} \right) = 0, \\ {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 2\left( {\left( {1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}} \right) + \left( {m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}} \right)} \right.. \\ \end{gathered} $Из второго уравнения системы (21) находим
(22)
$\frac{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}{{1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}} = 1 + \frac{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}.$В результате несложных преобразований получим эквивалентную систему (23)–(25):
(23)
$\frac{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}} = \frac{{2n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}{{4n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}},$(24)
$\begin{gathered} n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*} = \\ = \,\,\frac{{({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{{\left( {n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} \right)}}^{5}}}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}\left[ {4n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + 3({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} \right]{{{\left( {1 + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}} \right)}}^{2}}}}, \\ \end{gathered} $(25)
$\frac{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}{{1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}} = \frac{{4n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + 3({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}.$Из уравнения (23) получаем аналитическую зависимость равновесного потока пара $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$ от потока водорода $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}{\text{:}}$
(26)
$n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} = \frac{{\left( {m - \frac{3}{4}\left( {\frac{1}{{{{K}_{2}}}}} \right)n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} - \frac{1}{2}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} \right)}}{2} + \,\,\sqrt {\frac{{{{{\left( {m - \frac{3}{4}\left( {\frac{1}{{{{K}_{2}}}}} \right) - \frac{1}{2}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} \right)}}^{2}}}}{4} + \frac{3}{4}\left[ {m\left( {\frac{1}{{{{K}_{2}}}}} \right)n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} - \frac{1}{4}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*2}}\left( {\frac{1}{{{{K}_{2}}}}} \right)} \right]} .$Знак (+) перед радикалом в последнем выражении выбран по той простой причине, что выполняется неравенство $\frac{3}{4}n_{{{\text{H}}{}_{{\text{2}}}}}^{*}\left( {\frac{1}{{{{K}_{2}}}}} \right)\left( {m - \frac{{n_{{{\text{H}}{}_{{\text{2}}}}}^{*}}}{4}} \right) > 0,$ так как $n_{{{\text{H}}{}_{{\text{2}}}}}^{*} < 4$ (рис. 2) и $m \geqslant 2.$
Явную зависимость потока $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$ от $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ находим из уравнения (24), используя (26). Поток водорода $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ находится из уравнения системы (25), где $n_{{{\text{CH}}{}_{{\text{4}}}}}^{*}\left( {n_{{{\text{H}}{}_{{\text{2}}}}}^{*}} \right)$ и $n_{{{\text{H}}{}_{{\text{2}}}{\text{O}}}}^{*}\left( {n_{{{\text{H}}{}_{{\text{2}}}}}^{*}} \right)$ были найдены выше.
Уравнение (25) решали численно методом последовательных приближений, задавая нулевое значение $n_{{{\text{H}}{}_{{\text{2}}}}}^{{*(0)}},$ и добивались равенства левой и правой частей с заданной степенью точности [34]. Потоки $n_{{{\text{CO}}}}^{*}$ и $n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*}$ находим по общим формулам (10), (11).
В результате численных расчетов было показано, что решение системы (21), то есть потоки $n_{i}^{*}$ (i = СН4, Н2О, Н2, СО, СО2) равны соответствующим потокам на выходе начального участка при ${{x}_{{{\text{нач}}}}} = {{10} \mathord{\left/ {\vphantom {{10} {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}}$ (см. рис. 2). Если палладиевую фольгу заменить на непроницаемую для Н2 перегородку (например, на стальной диск, для которого параметр $\beta = 0$), то третье уравнение системы (12) становится эквивалентным равенству (20) при любом x, следовательно, в таком немембранном процессе за пределами начального участка потоки всех частиц остаются постоянными и равны $n_{i}^{*}.$ По физическому смыслу последние являются равновесными потоками немембранного процесса на основном участке ($x \geqslant {{x}_{{{\text{нач}}}}}$), так как получены из условия равенства скоростей прямых и обратных реакций (1) и (2) в этой области.
Ниже будет показано, что в мембранном процессе на основном участке из-за проникновения Н2 в верхнюю камеру через мембрану потоки ${{n}_{i}}(x)$ будут монотонно отклоняться от равновесных значений $n{\text{*}}{\text{.}}$ В частности, поток водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ при $x = {{x}_{{{\text{нач}}}}}$ проходит через максимум (${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}({{x}_{{{\text{нач}}}}}) = n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$) и в дальнейшем по мере удаления от входа монотонно уменьшается.
Решение проблемы за пределами начального участка (x > xнач). Учитывая, что допустимые значения потока водорода на входе нижней камеры принадлежат интервалу ${{10}^{{ - 5}}} \leqslant {{N}_{{BX}}} \leqslant {{10}^{{ - 4}}}$ [моль/с] (см. (17)), нетрудно показать, что безразмерные параметры ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ намного больше единицы (см. табл. 1). Если предположить, что на основном участке производные ${{\partial {{n}_{i}}} \mathord{\left/ {\vphantom {{\partial {{n}_{i}}} {\partial x}}} \right. \kern-0em} {\partial x}}$ ограничены (это будет показано в дальнейшем), то несмотря на отток водорода через мембрану в этой области условия равновесия реакций (1) и (2) не нарушаются, так как обе функции ${{F}_{1}}$ и ${{F}_{2}}$ практически равняются нулю (${{F}_{1}}$ ∼ ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}} \ll 1,$ ${{F}_{2}}$ ∼ ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{2}}}}} \right. \kern-0em} {{{\alpha }_{2}}}} \ll 1,$ см. (12)). Условия ${{F}_{1}} = {{F}_{2}} = 0$ позволяют найти потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ как функции ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ за пределами начального участка, где выполняется неравенство ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \leqslant n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}.$ Зная зависимости ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}),$ можно решить третье уравнение системы (18) и найти распределение потока водорода в нижней камере ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x).$ Представим это уравнение в следующем виде:
(28)
$\left( {2\frac{{\partial {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + \frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)\frac{{\partial n}}{{\partial x}} = - \beta \sqrt {\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{{{n}_{\sum }}}}} .$Решение этого уравнения нетрудно найти в квадратурах:
(29)
$\begin{gathered} \int\limits_{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}^{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {\frac{{\left( {2\frac{{\partial {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + \frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)\sqrt {\left( {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \right)} }}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} = \\ = - \beta (x - {{x}_{{{\text{нач}}}}}), \\ \end{gathered} $(30)
$\begin{gathered} \left( {\frac{{m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}} \right) = \\ = \frac{{{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + 2({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{n}^{3}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + 2({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{n}^{3}}} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}} \right. \kern-0em} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}}}{{{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} {(m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) + {{({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}} \mathord{\left/ {\vphantom {{({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}} \right. \kern-0em} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}}}} \right. \kern-0em} {(m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) + {{({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}} \mathord{\left/ {\vphantom {{({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}} \right. \kern-0em} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}}}}}. \\ \end{gathered} $Соответственно из второго уравнения системы (21) получим
(31)
$\left( {\frac{{m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}} \right) = \frac{{2{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}.$Приравнивая левые части соотношений (30) и (31), для нахождения зависимости ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ получаем нелинейное уравнение
(32)
$\begin{gathered} \frac{{(m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})[{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}]}}{{2{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} = \\ = \frac{{{{({{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}){1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{n}^{3}}} \mathord{\left/ {\vphantom {{({{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}){1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{n}^{3}}} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}} \right. \kern-0em} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}}}{{{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + 2({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{n}^{3}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + 2({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{n}^{3}}} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}} \right. \kern-0em} {{{{(1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}^{2}}}}}}. \\ \end{gathered} $Решение последнего при любом фиксированном ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ ($0 < {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} < n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$) находится методом последовательных приближений [34]. Задавая нулевое значение $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{(0)}},$ добивались равенства левой и правой частей уравнения (32) с заданной степенью точности. После нахождения функции ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ зависимость ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ определяли из уравнения (31):
(33)
$1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = \frac{{(m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})[{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}]}}{{2{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}.$Расчеты функций ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ для ряда температур (673, 773, 823, 873 и 973 K) представлены на рис. 3 ($m = 3$).
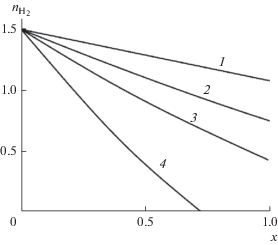
Рис. 3.
Расчеты функций ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ для ряда температур: 1 –$T$ = 673 K, 2 – 773, 3 – 823, 4 – 973 K. Сплошные кривые – поток водяного пара, штриховые линии – поток метана.
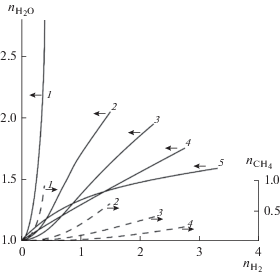
Как видно, при уменьшении ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ в результате перехода Н2 через мембрану потоки Н2О и СН4 также уменьшаются. Первые при ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \to 0$ стремятся к единице, вторые – к нулю. Численно продифференцировав функции ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ по переменной ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}},$ из уравнения (29) получаем распределение потоков Н2 внутри нижней камеры ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x).$ Соответствующие расчеты представлены на рис. 4–6 для трех температур (773, 823 и 973 K) и ряда значений объемных потоков $G$ (1800, 3600, 5400 и 9600 1/ч).
Рис. 4.
Распределение потока Н2 внутри нижней камеры при $T$ = 973 K: 1 – $G = 9600$ 1/ч, 2 – 5400, 3 – 3600, 4 – 1800 1/ч.
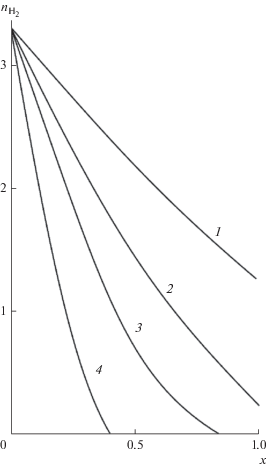
Рис. 5.
Распределение потока Н2 внутри нижней камеры при $T$ = 823 K: 1 –$G = 9600$ 1/ч, 2 – 5400, 3 – 3600, 4 – 1800 1/ч.
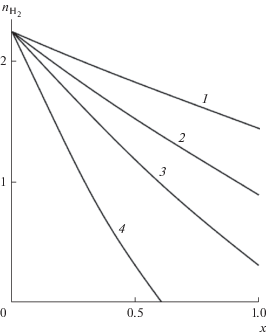
Рис. 6.
Распределение потока Н2 внутри нижней камеры при $T$ = 773 K: 1 –$G = 9600$ 1/ч, 2 – 5400, 3 – 3600, 4 – 1800 1/ч.
При достаточно “малых” $G$ ($G \leqslant 1800$ 1/ч) потоки водорода обращаются в нуль уже внутри нижней камеры. При увеличении $G$ потоки Н2 даже на выходе камеры при $x = 1$ отличны от нуля.
В качестве характеристики работы реактора, по которой можно судить о его эффективности, часто используют конверсию метана α:
(34)
$\alpha = \frac{{{{N}_{{{\text{BX}}}}} - {{N}_{{{\text{ВЫХ}}}}}}}{{{{N}_{{{\text{BX}}}}}}} = 1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}(1),$С помощью мембранной технологии можно добиться высокой конверсии СН4 ($\alpha \to 1$) даже при температурах менее 1000 K, если объемные потоки сырья $G$ достаточно “малы” ($G \leqslant 1800$ или ${{N}_{{{\text{BX}}}}} \leqslant {{10}^{{ - 5}}}$). В этих случаях потоки СН4 стремятся к нулю на выходе нижней камеры, как впрочем и потоки Н2 (рис. 3).
Другой важной характеристикой реактора является отвод водорода $\varphi $ – отношение интегрального потока Н2 через мембрану к суммарному его потоку на выходе из верхней (${{I}_{S}}$) и нижней камер (${{N}_{{{\text{BX}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)$):
(35)
$\begin{gathered} \varphi = \frac{{2\pi \int\limits_0^{r_{{\max }}^{'}} {r{\kern 1pt} '{{I}_{{{{{\text{H}}}_{{\text{2}}}}}}}dr{\kern 1pt} '} }}{{2\pi \int\limits_0^{r_{{\max }}^{'}} {r{\kern 1pt} '{{I}_{{{{{\text{H}}}_{{\text{2}}}}}}}dr{\kern 1pt} '} + {{N}_{{{\text{BX}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)}} = \\ = \frac{{\beta {{N}_{{{\text{BX}}}}}\int\limits_0^1 {\sqrt {{n \mathord{\left/ {\vphantom {n {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} dx} }}{{\beta {{N}_{{{\text{BX}}}}}\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} dx + {{N}_{{{\text{BX}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)} }}, \\ \end{gathered} $При $\varphi \to 1$ водород, полученный в результате протекания реакций (1) и (2), полностью удаляется через мембрану, а учитывая, что верхняя камера вакуумируется, мы получаем на выходе из нее практически чистый водород.
Расчеты безразмерных потоков частиц на выходе нижней камеры ${{n}_{i}}(1)$ приведены в табл. 2. В отличие от распределений ${{n}_{i}}(z)$ на начальном участке, потоки ${{n}_{i}}(x)$ на основном зависят не только от температуры, но и от объемной скорости подачи сырья $G$ (см., например, распределение потоков Н2 на рис. 4–6). Распределение потоков СН4 и Н2О на основном участке можно найти с помощью рис. 3 и 4–6, а потоков СО и СО2 – используя общие формулы (10), (11). Сравнивая рис. 2 и 4–6, видим, что поток водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x),$ достигая максимальной величины $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ на выходе начального участка, в дальнейшем монотонно уменьшается до соответствующего значения на выходе камеры ($x = 1$). Потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ при $x \geqslant {{x}_{{{\text{нач}}}}}$ также монотонно отклоняются от равновесных значений $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$ в сторону уменьшения, причем эти отклонения тем больше, чем меньше объемная скорость G. При высоких температурах метан полностью удаляется из реактора независимо от значений объемного потока G, при этом $\alpha \to 1.$ При более низких температурах $\alpha \cong 1$ при достаточно “малых” $G \leqslant 2000$ 1/ч. При “малых” $G$ на выходе нижней камеры в смеси присутствуют только пары воды и СО2. Для удаления воды газовую смесь после выхода из нижней камеры пропускают через холодильник, где она охлаждается до ∼300 K. Расчеты состава “сухой смеси после холодильника также представлены в табл. 2. В этом случае мольный состав ${{X}_{i}}$ вычисляется по общим формулам (14), где ${{n}_{\sum }} = 1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}.$ Таким образом при достаточно “малых” $G$ на выходе нижней камеры можно получить чистый углекислый газ.
Таблица 2.
Потоки частиц на выходе нижней камеры ${{n}_{i}}(1),$ состав смеси газов после холодильника ${{X}_{i}};$ поток Н2 на выходе верхней камеры $I_{S}^{{}}$ и отвод водорода $\varphi $ при различных $T$ и $G$
| T | G, 1/ч | ${{N}_{0}}$, $\frac{{{\text{моль}}}}{{\text{с}}}$ | ${{x}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ | ${{x}_{{{\text{CO}}}}}$ | ${{x}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ | ${{x}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$ | ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ | ${{n}_{{{\text{CO}}}}}$ | ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ | ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$ | ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ | ${{I}_{S}} \times {{10}^{4}}$, $\frac{{{\text{моль}}}}{{\text{с}}}$ | $\phi $ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 973 K | 1800 | 10–5 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0.40 (0.33) |
1.0 (0.82) |
| 3600 | 2 × 10–5 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0.77 (0.62) |
1.0 (0.81) |
|
| 5400 | 3 × 10–5 | 0.2 | 0.11 | 0.69 | 0 | 0.25 | 0.14 | 0.86 | 0 | 1.14 | 0.90 (0.7) |
0.92 (0.8) |
|
| 9600 | 5.5 × 10–5 | 0.56 (0.46) | 0.17 (0.23) | 0.27 (0.28) | 0 (0.03) |
1.26 | 0.38 | 0.62 | 0 | 1.38 | 1.20 (0.95) |
0.65 (0.76) |
|
| 823 K | 1800 | 10–5 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0.40 (0.33) |
1.0 (0.77) |
| 3600 | 2 × 10–5 | 0.23 (0.29) | 0.04 (0.10) | 0.73 (0.60) |
0 (0.01) |
0.3 | 0.05 | 0.95 | 0 | 1.05 | 0.70 (0.56) |
0.92 (0.72) |
|
| 5400 | 3 × 10–5 | 0.47 | 0.06 | 0.41 | 0.05 | 0.88 | 0.12 | 0.78 | 0.1 | 1.32 | 0.79 | 0.75 | |
| 9600 | 5.5 × 10–5 | 0.59 | 0.10 | 0.22 | 0.08 | 1.46 | 0.25 | 0.55 | 0.2 | 1.65 | 0.84 | 0.52 | |
| 773 K | 1800 | 10–5 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0.35 (0.30) |
1.0 (0.79) |
| 3600 | 2 × 10–5 | 0.31 (0.31) |
0.04 (0.06) | 0.60 (0.56) |
0.06 (0.07) |
0.44 | 0.05 | 0.87 | 0.08 | 1.21 | 0.57 (0.46) |
0.87 (0.68) |
|
| 5400 | 3 × 10–5 | 0.43 | 0.06 | 0.41 | 0.10 | 0.74 | 0.10 | 0.72 | 0.18 | 1.46 | 0.6 | 0.73 | |
| 9600 | 5.5 × 10–5 | 0.51 | 0.07 | 0.27 | 0.15 | 1.06 | 0.14 | 0.56 | 0.30 | 1.74 | 0.63 | 0.54 |
Наряду с указанными выше величинами в табл. 2 приведен расчет интегрального потока водорода через мембрану ${{I}_{S}}$ (или на выходе верхней камеры) и выход водорода $\varphi $ при различных условиях проведения процесса. Как видно, при фиксированной температуре с увеличением скорости подачи сырья $G$ поток Н2 через мембрану возрастает, однако при этом возрастает его поток ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)$ на выходе нижней камеры, что приводит к ухудшению эффективности реактора, то есть уменьшению $\varphi .$ Последнее означает, что с ростом $G$ мембрана не справляется с растущим потоком водорода.
На основании изложенного выше можно сделать вывод, что процесс парового риформинга метана выгоднее всего проводить при как можно меньших значениях $G$ (в исследованном интервале температур $G \leqslant 2000$ 1/ч). В этом случае (несмотря на некоторое уменьшение потока Н2 на выходе верхней камеры) достигаются: максимальная конверсия СН4 ($\alpha \Rightarrow 1$); коэффициент полезного действия реактора приближается к 100% ($\varphi \Rightarrow 1$); а также отпадает необходимость в разделении газовой смеси на выходе нижней камеры на компоненты, так как после холодильника мы получаем практически чистый углекислый газ. Отметим, что в результате вакуумирования верхней камеры на выходе ее присутствует практически чистый водород.
Для проверки применимости предложенной теории результаты расчетов сравнивали с экспериментальными данными (они приведены в скобках в табл. 2). Как видно, экспериментальные значения потоков Н2 через мембрану (${{I}_{S}}$) всегда занижены по сравнению с теоретическими (ошибка может достигать ∼20%). Основная причина, по-видимому, связана с дезактивацией мембраны метаном, окислами углерода и особенно водяными парами, как это было отмечено в работе [17]. Не исключена возможность утечки Н2 из реактора, так как процесс проводится при высоких температурах. Эти побочные эффекты нами не учитывались. Однако, несмотря на некоторые расхождения теории и эксперимента, основные закономерности процесса, наблюдаемые на практике, получили теоретическое обоснование, что подтверждает основные предположения, сделанные при построении теоретической модели.
ЗАКЛЮЧЕНИЕ
Предложена модель парового риформинга метана в каталитическом реакторе, рабочая часть которого – цилиндрические камеры, разделенные палладиевой мембраной. В нижней камере поддерживается атмосферное давление, а верхняя вакуумируется. Для расчета потоков Н2, водяного пара, СО, СО2 и СН4 в нижней камере получена система обыкновенных дифференциальных уравнений первого порядка.
Показано, что при реальных значениях кинетических констант существуют два несоизмеримых участка изменения локальных потоков. На первом, коротком, влиянием мембраны можно пренебречь, причем на выходе этого участка реакции достигают равновесия. Влияние мембраны становится заметным на втором участке, где, несмотря на проникновение водорода через мембрану в верхнюю камеру, условия равновесия реакций сохраняются.
Расчет парового риформинга СН4 проведен для мембраны Pd–6% Ru и никелевого катализатора в интервале температур 673–973 K при объемных скоростях подачи сырья $G \cong {{10}^{3}} - {{10}^{4}}$ 1/ч. Доказано, что процесс наиболее целесообразно проводить при значениях объемной скорости подачи сырья менее 2000 1/ч. В этом случае достигается максимальная конверсия СН4, коэффициент полезного действия реактора приближается к 100% и отпадает необходимость в последующем разделении газовой смеси, так как после прохождения ее через холодильник мы получаем практически чистый углекислый газ. Из-за вакуумирования в верхней камере присутствует чистый водород. Адекватность модели реальному процессу была проверена в результате сравнения расчетов с экспериментальными данными.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 13-03-12419).
ОБОЗНАЧЕНИЯ
| ${{b}_{1}},$${{b}_{2}}$ | скорости реакций (1) и (2), моль/(кгcat с) |
| $с_{i}^{'}$ | концентрация частиц, моль/м3 |
| $D$ | коэффициент диффузии, м2/с |
| ${{d}_{{{\text{cat}}}}}$ | диаметр частиц катализатора, м |
| $E$ | энергия активации, Дж/моль |
| $G$ | объемная скорость подачи сырья, 1/ч |
| $h$ | высота камер, м |
| ${{I}_{{{{{\text{H}}}_{{\text{2}}}},S}}}$ | локальный поток Н2 через мембрану, моль/(м2 с) |
| ${{I}_{S}}$ | интегральный поток Н2 через мембрану, моль/с |
| ${{K}_{1}}$ | константа равновесия реакции (1), ат2 |
| ${{K}_{2}}$ | константа равновесия реакции (2) |
| ${{k}_{i}}$ | константы равновесия Ленгмюра для СО, СН4, Н2, ат–1 |
| ${{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ | константа равновесия Ленгмюра для пара Н2О |
| ${{\tilde {k}}_{1}}$ | константа скорости прямой реакции (1), моль ат1/2/(кгcat с) |
| ${{\tilde {k}}_{2}}$ | константа скорости прямой реакции (2), моль/(ат кгcat с) |
| $m$ | отношение входных интегральных потоков пара и СН4 |
| $N_{i}^{'}$ | локальный мольный поток частиц, моль/(с м2) |
| ${{N}_{i}}$ | интегральный мольный поток частиц, моль/с |
| ${{N}_{{{\text{BX}}}}}$ | интегральный поток СН4 на входе в нижнюю камеру, моль/с |
| ${{n}_{i}}$ | безразмерный локальный поток компонента |
| ${{n}_{\sum }}$ | поток газовой смеси |
| ${{p}_{{{\text{AT}}}}}$ | давление в атмосферах, ат |
| ${{p}_{i}}$ | парциальное давление частиц, ат |
| ${{Q}_{0}}$ | предэкспоненциальный множитель в законе Сивертса, моль/(м1/2 кг1/2) |
| $r{\kern 1pt} '$ | радиальная координата, м |
| $r_{{\max }}^{'}$ | радиус камер, м |
| $r_{{\min }}^{'}$ | радиус выходного отверстия в нижней камере, м |
| $R$ | универсальная газовая постоянная, Дж/(моль град) |
| $r{\kern 1pt} ',$$z{\kern 1pt} '$ | цилиндрическая система координат, м |
| $r$ | безразмерные координаты, отсчитываемые от центра фольги |
| $S$ | площадь фольги, м2 |
| $T$ | температура, K |
| $u{\kern 1pt} ',$$\nu {\kern 1pt} '$ | компоненты скорости смеси газов, м/с |
| ${{w}_{{{\text{cat}}}}}$ | масса засыпки катализатора, кг |
| $x,$$y$ | безразмерные координаты, отсчитываемые от периферии фольги |
| ${{X}_{i}}$ | мольные доли i-го компонента смеси |
| $z$ | безразмерная координата на начальном участке |
| $\alpha $ | конверсия метана |
| ${{\alpha }_{1}},$${{\alpha }_{2}}$ | безразмерные скорости прямых реакций (1) и (2) |
| $\beta $ | безразмерный параметр, учитывающий поток Н2 через мембрану |
| $\varepsilon $ | порозность |
| ${{\rho }_{{{\text{cat}}}}}$ | плотность катализатора в нижней камере, кг/м3 |
| $\varphi $ | отвод водорода из ММ |
| ${{\phi }_{i}}$ | источник (сток) компонента i, моль/(кгcat с) |
Список литературы
Ramachandran R., Menon R.K. An overview of industrial uses of hydrogen // Int. J. Hydrogen Energy. 1998. V. 23. P. 593.
Kirillov V.A., Meshcheryakov V.D., Brizitskii O.F., Terent’ev V.Ya. Analysis of a power system based on low-temperature fuel cells and a fuel processor with a membrane hydrogen separator // Theor. Found. Chem. Eng. 2010. V. 44. № 3. P. 227.
Schädel B.T., Duisberg M., Deutschmann O. Steam reforming of methane, ethane, propane, butane, and natural gas over a rhodium-based catalyst // Catal. Today. 2009. V. 142. P. 42.
Butcher H., Quenzel C.J.E., Breziner L., Mettes J., Wilhite B.A., Bassard P. Design of an annular microchannel reactor (AMR) for hydrogen and/or syngas production via steam reforming // Int. J. Hydrogen Energy. 2014. V. 39. № 31. P. 18046.
Shigarov A.B., Meshcheryakov V.D., Kirillov V.A. Use of Pd membranes in catalytic reactors for steam methane reforming for pure hydrogen production // Theor. Found. Chem. Eng. 2011. V. 45. № 5. P. 595.
Грязнов В.М. Катализ на мембранах с избирательной проницаемостью // Докл. АН СССР. 1969. Т. 189. С. 794.
Gryaznov V.M. Hydrogen permeable palladium membrane catalyst. An aid to the efficient production of ultra pure chemicals and pharmaceuticals // Platinum Met. Rev. 1986. V. 36. P. 68.
Yuna S., Ted Oyama S. Correlations in palladium membranes for hydrogen separation: A review // J. Membr. Sci. 2011. V. 375. P. 28.
Орехов Н.В., Кустов Л.М., Кучеров А.В., Финашина Е.Д., Ермилова М.М., Ярославцев А.Б. Мембранные каталитические системы для конверсии алканов С2–С4 // Росс. технол. 2012. Т. 17. № 11. С. 21.
Takao K., Yoichi I., Takaya I., Hisataka Y., Hiroyuki T., Hideaki H., Yasuhiro T., Masaya I. Performance evaluation of membrane on catalyst module for hydrogen production from natural gas // Int. J. Hydrogen Energy. 2013. V. 38. P. 6079.
Li P., Wang Zh., Qiao Zh., Liu Y., Cao X., Li W., Wang I., Wang Sh. Recent developments in membranes for efficient hydrogen purification // J. Membr. Sci. 2015. V. 495. P. 130.
Anzelmo B., Wilcox I., Liguori S. Hydrogen production via natural gas steam reforming in Pd–Au membrane reactor. Comparison between methane and natural gas steam reactions // J. Membr. Sci. 2018. V. 568. P. 113.
Didenko L.P., Sementsova L.A., Chizhov P.E., Dorofeeva T.V. Influence of the propane content in methane on the parameters of steam reforming of a mixture in a membrane reactor with the industrial nickel catalyst and Pd–Ru alloy foil // Int. J. Hydrogen Energy. 2019. V. 44. P. 26396.
Babak V.N., Didenko L.P., Zakiev S.E. Hydrogen transport through a membrane module based on a palladium foil // Theor. Found. Chem. Eng. 2013. V. 47. P. 719.
Boeltken T., Wunsch A., Gietzelt T., Pfeifer P., Dittmeyer R. Ultra-compact microstructured methane steam reforming with integrated palladium membrane for on-site production of pure hydrogen: Experimental demonstration // Int. J. Hydrogen Energy. 2014. V. 30. P. 18058.
Didenko L.P., Savchenko V.I., Sementsova L.A., Bikov L.A. Hydrogen flux through the membrane based on the Pd–In–Ru foil // Int. J. Hydrogen Energy. 2016. V. 41. P. 307.
Babak V.N., Didenko L.P., Kvurt Yu.P., Sementsova L.A. Studying of operation of membrane module based on palladium foil at high temperatures // Theor. Found. Chem. Eng. 2018. V. 52. № 2. P. 181.
Slovetskii D.I., Chistov E.M. Patent 2416460, 2011.
Burkhanov G.S., Gorina N.B., Kolchugina N.B., Roshan N.R., Slovetsky D.I., Christov E.M. Palladium-based alloy membranes for separation of high purity hydrogen from hydrogen-containing gas mixtures // Platinum Met. Rev. 2011. V. 55. № 1. P. 3.
Tong H.D., Berenschot I.W.E., de Boer M.I., Gardeniers I.G.E., Wensink M., Jansen H.V., Nijdam W., Elwenspoek M.C., Gielens F.C., van Rijn C.I.M. Microfabrication of palladium–silver alloy membranes for hydrogen separation // J. Microelectromech. Syst. 2003. V. 12. № 5. P. 622.
Tong I., Shirai R., Kashina Y., Matsumura Y. Preparation of a pinhole-free Pd–Ag membrane on a porous metal support for pure hydrogen separation // J. Membr. Sci. 2005. V. 260. № 1. P. 84.
Mazali I.O., Filho A.G.S., Viana B.C., Filho I.M., Alves O.L. Size-controllable synthesis of nanozized-TiO2 anatase using porous Vycor glass as template // J. Nanopart. Res. 2006. V. 8. P. 141.
Huang Y., Dittmeyer R. Preparation of thin palladium membranes on a porous support with rough surface // J. Membr. Sci. 2007. V. 32. № 1. P. 160.
Pizzi D., Worth R., Baschatti M.G., Sarti G.C., Noda K. Hydrogen permeability of 2.5 μm palladium–silver membranes deposited on ceramic supports // J. Membr. Sci. 2008. V. 325. № 1. P. 446.
Gade S.K., Thoen P.M., Way I.D. Upsupported palladium alloy foil membranes fabricated by electroless plating // J. Membr. Sci. 2008. V. 316. № 1. P. 112.
Zhang X., Xiong G., Yang W.A. Modified electroless plating technique for thin dense palladium composite membranes with enhances stability // J. Membr. Sci. 2008. V. 314. P. 226.
Bayati B., Bayat Y., Charachi N., Ejtemaei M., Babalio A.A., Haghighi M., Drioli E. Preparation of crack-free nanocomposite ceramic membrane intermediate layers on α-alumina tubular supports // Sep. Sci. Technol. 2013. V. 48. P. 1930.
Calles I., Sanz R., Aligue D., Furones L., Murin P., Ordoñez S. Influence of the selective layer morphology on the permeation properties for Pd–PSS composite membranes prepared by electroless pore-plating: Experimental and modeling study // Sep. Purif. Technol. 2018. V. 194. P. 10.
Xu I., Froment G.F. Methane steam reforming. Methanation and water-gas shift, intrinsic kinetics // AIChE J. 1989. V. 35. № 1. P. 88.
Lin Y.M., Liu Sh.I., Chuang Ch.H., Chu Y.T. Effect of incipient removal of hydrogen through palladium membrane on the conversion of methane steam reforming: Experimental and modeling // Catal. Today. 2003. V. 82. № 1. P. 127.
Falko M., Marrelli P.L. Heat transfer and hydrogen permeability in modelling industrial membrane reactors for methane steam reforming // Int. J. Hydrogen Energy. 2007. V. 32. P. 2094.
Крылов О.В. Гетерогенный катализ. М.: Академкнига, 2004.
Oliveria E.L.G., Grande C.A., Rodrignes A.E. Steam methane reforming in a Ni/Al2O3 catalyst: Kinetics and diffusional limitations in extrudates // Can. J. Chem. Eng. 2009. V. 87. P. 945.
Демидович Б.П., Марон И.А., Шувалов Э.З. Численные методы анализа. М.: ГИФМЛ, 1963.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии