1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 55, № 3, 2021

Теоретические основы химической технологии, 2021, T. 55, № 3, стр. 332-338

Об анализе данных о равновесии жидкость–пар в многокомпонентных системах с применением искусственных нейронных сетей

А. М. Тойкка a, *, Г. Х. Мисиков a, А. В. Петров a

a Санкт-Петербургский государственный университет, Институт химии
Санкт-Петербург, Россия

* E-mail: a.toikka@spbu.ru

Поступила в редакцию 26.11.2020
После доработки 04.02.2021
Принята к публикации 04.02.2021

Полный текст (PDF)

Аннотация

Представлен краткий анализ возможностей применения метода искусственных нейронных сетей (ИНС) для оценки и корреляции данных о равновесии жидкость–пар. Рассмотрены преимущества метода Фокке в случае ограниченного объема данных, в данном случае – параметров парожидкостного равновесия. Рассмотрены шесть бинарных и четыре тройные системы с применением модифицированной методики Аргатова–Кочербитова. Оценка корректности применения метода ИНС представлена для значений избыточной энергии Гиббса, рассчитанных из данных о равновесии жидкость–пар.

Ключевые слова: искусственные нейронные сети, равновесие жидкость–пар, энергия Гиббса, моделирование, бинарные системы, тройные системы

ВВЕДЕНИЕ

Развитие методов термодинамического моделирования в последние десятилетия позволило достичь значительных научных результатов, позволивших, в том числе, расширить применение термодинамических подходов для решения прикладных задач. Действительно, применение моделей локальных составов (модель Вильсона, NRTL, UNIQUAC и другие), групповых моделей (UNIFAC и модификации), современных уравнений состояния, а также других моделей (например, PC SAFT) дает возможность упростить и оптимизировать организацию процессов химической технологии, существенно сократить затраты, связанные с экспериментальным определением термодинамических параметров [1–5]. Не менее важные результаты в этом отношении связаны с применением термодинамико-топологических подходов [6–8] для оптимизации технологий разделения, включая реакционно-массообменные процессы. Методы термодинамического моделирования и термодинамико-топологического анализа оказались особенно эффективными применительно к оценке и расчетам фазовых равновесий, являющихся научной основой процессов разделения. В то же время, для решения ряда практических задач в последние годы успешно применяется метод искусственных нейронных сетей (ИНС), являющийся эффективным аппаратом для оценки и расчета параметров сложных систем. Выигрышные стороны ИНС, интерес к развитию качественно новых подходов определил появление ряда работ, связанных с применением ИНС к расчету фазовых равновесий, включая равновесие жидкость–пар [9–11]. В то же время, следует иметь в виду, что анализ и аппроксимация, основанные на ИНС, при их относительной простоте, оставляют открытым вопрос о физической обоснованности результатов, надежности модели и её предсказательной способности.

Отметим также, что целесообразность развития методов анализа фазовых равновесий, включая равновесия жидкость–пар с применением ИНС может представляться спорной, так как ИНС обычно строится на основе больших баз данных. Например, при оценке и расчете параметров скорости звука и других свойств смесей природных газов обучение системы ИНС проводилось на основе 20 000–30 000 данных о поведении газов различных месторождений [12, 13]. Действительно, результаты аппроксимации с использованием таких распространенных методик, как многослойный перцептрон, прямо зависят от числа скрытых нейронов [14]. В случае фазовых равновесий, когда число экспериментальных данных, как правило, не столь велико, это может оказаться существенной проблемой, так как обучение подобной ИНС требует большого массива экспериментальных данных.

Недавно в работе [15] было предложено решить указанную проблему привлечения ограниченных массивов данных с использованием метода Фокке [16]. Объектом исследования являлись данные о равновесии жидкость–пар в тройных и бинарных системах. В работе Фокке [16] задача развития метода ИНС была также направлена на анализ и корреляцию данных о смесях веществ. Предложенные варианты позволяют ограничить число скрытых нейронов числом компонентов. Авторы [15] указывают, что подобный подход должен снизить аппроксимационную способность ИНС, но дает возможность привлечения существенно меньшего массива данных. Отметим, что хотя снижение точности расчетов могло бы быть основанием для отказа от метода Фокке, авторы [15] далее показывают, что модель Фокке, при определенном выборе функции активации, может быть сведена к уравнению Вильсона, то есть к уравнению популярной модели локальных составов [1]. Аналогичные выводы были сделаны ранее и Фокке [16], также указавшем, что его подход приводит к аналитическим зависимостям, соответствующим модели Вильсона в ее форме для избыточной энергии Гиббса. Более того, среди трех рассмотренных в [15] схем, две (одно- и двухуровневые ИНС) могут соответствовать модели NRTL, также при определенном выборе функции активации. Приводимые в статье [15] примеры для ряда бинарных и трехкомпонентных систем показывают, что предложенный подход дает результаты, существенно отличающиеся по точности, что, по-видимому, связано не только с особенностями метода ИНС, но и различиями в природе рассмотренных систем. Таким образом, перспективы применения метода ИНС для анализа равновесия жидкость–пар и данных о величинах избыточной энергии Гиббса достаточно обоснованы, но требуют дальнейшего обсуждения, в том числе, в связи с отмеченной предполагаемой чувствительностью метода при его применении к системам, существенно отличающимся своими физико-химическими свойствами.

В настоящей работе представлены некоторые результаты проведенного нами анализа возможностей применения метода, предложенного в [15], для описания равновесий жидкость–пар в системах с различным типом и степенью отклонений от идеальности и, соответственно, характером межмолекулярного взаимодействия компонентов.

РАСЧЕТНАЯ ЧАСТЬ

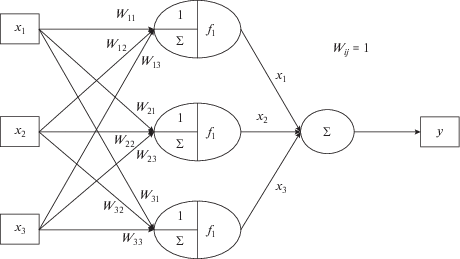
Проведенные расчеты и последующий анализ результатов проводились для избыточной энергии Гиббса (gE), величины которой рассчитывались по данным о равновесии жидкость–пар. Это дает возможность сопоставить наши результаты с выводами, приводимыми в работе [15] также для величин gE. Для аппроксимации данных о равновесиях жидкость–пар применяли одноуровневую ИНС, которая в общем виде, в соответствии с методом Фокке [16], представлена на рис. 1 и отвечает формуле

(1)
$y = ~{{f}^{{ - 1}}}\left( {\mathop \sum \limits_{i~ = ~1}^m {{x}_{i}}f\left( {\mathop \sum \limits_{j~ = ~1}^m {{a}_{{ij}}}{{x}_{j}}} \right)} \right),$
где f – функция активации, величины x (мольные доли компонентов) отвечают входным значениям, y – выходным значениям (gE/RT). При выборе в качестве функции активации логарифмической зависимости f(u) = ln(u) модель Фокке преобразуется к виду, соответствующему экспоненциальной форме уравнения модели Вильсона [1]:
(2)
$y~\, = \,~\mathop \prod \limits_{i~ = ~1}^m {{\left( {\mathop \sum \limits_{j~ = ~1~}^m {{a}_{{ij}}}{{x}_{j}}} \right)}^{{{{x}_{i}}}}},$
где aij – настраиваемые параметры модели. Подробный анализ преобразования представлен в работе [15]. Схема расчетов, предложенная в статье [15], приведена на рис. 1 для трехкомпонентных систем.

Рис. 1.

Схема расчетов по ИНС, предложенная в статье [15], для случая трехкомпонентных систем.

Таким образом, избыточная энергия Гиббса может быть выражена формулой, адаптированной для применения метода ИНС и одновременно отвечающей модели Вильсона:

(3)
$\frac{{{{g}^{E}}}}{{RT}}~\, = \,~\mathop \sum \limits_{i~ = 1}^m {{x}_{i}}{{f}_{1}}\left( {\frac{{\sum\limits_{j~ = 1}^m {{{x}_{j}}} }}{{\sum\limits_{j~ = 1}^m {{{W}_{{ij}}}{{x}_{j}}} }}} \right),$
где W – коэффициенты, соответствующие весам мольных долей в ИНС.

Для бинарной и тройной систем уравнение (3) принимает соответственно следующий вид:

(4)
$\begin{gathered} \frac{{{{g}^{E}}}}{{RT}}~\, = ~\,{{x}_{1}}{{f}_{1}}\left( {\frac{{{{x}_{1}}~ + {{x}_{2}}}}{{{{W}_{{11}}}{{x}_{1}}~ + ~{{W}_{{12}}}{{x}_{2}}}}} \right) + ~ \\ + \,\,{{x}_{2}}{{f}_{1}}\left( {\frac{{{{x}_{1}}~ + {{x}_{2}}}}{{{{W}_{{21}}}{{x}_{1}}~ + ~{{W}_{{22}}}{{x}_{2}}}}} \right), \\ \end{gathered} $
(5)
$\begin{gathered} \frac{{{{g}^{E}}}}{{RT}}\,~ = ~\,{{x}_{1}}{{f}_{1}}\left( {\frac{{{{x}_{1}}~ + {{x}_{2}}~ + ~{{x}_{3}}}}{{{{W}_{{11}}}{{x}_{1}}~ + ~{{W}_{{12}}}{{x}_{2}}~ + ~{{W}_{{13}}}{{x}_{3}}~}}} \right) + \\ + ~\,\,{{x}_{2}}{{f}_{1}}\left( {\frac{{{{x}_{1}}~ + {{x}_{2}}~ + ~{{x}_{3}}}}{{{{W}_{{21}}}{{x}_{1}}~ + ~{{W}_{{22}}}{{x}_{2}}~ + ~{{W}_{{23}}}{{x}_{3}}~}}} \right)~ + \\ + \,\,~{{x}_{3}}{{f}_{1}}\left( {\frac{{{{x}_{1}}~ + {{x}_{2}}~ + ~{{x}_{3}}}}{{{{W}_{{31}}}{{x}_{1}}~ + ~{{W}_{{32}}}{{x}_{2}}~ + ~{{W}_{{33}}}{{x}_{3}}~}}} \right). \\ \end{gathered} $

Расчеты для бинарных и тройных систем проводились по уравнениям (4) и (5), соответственно, с использованием функции активации f1(u) = = tanh(u – 1). Процедура аппроксимации проводилась на основе минимизации среднего квадратичного отклонения в программе Excel. Корректность выполнения данного алгоритма была предварительно проверена для систем, рассмотренных в статье [15]. В качестве новых объектов нами были выбраны бинарные и тройные подсистемы четырехкомпонентной системы ацетон–этанол–хлороформ–гексан. Выбор определялся сравнительно сложной топологической структурой диаграмм фазового равновесия: различный характер отклонений от идеальности, наличие различных типов азеотропов (положительные, отрицательный, седловой). Это соответствовало поставленной задаче изучения возможностей применения метода ИНС в варианте Фокке–Аргатова–Кочербитова для систем с различным характером межмолекулярного взаимодействия в растворе.

В качестве критерия оценки результатов расчетов использовали среднеквадратичное отклонение (СКО) и среднее относительное отклонение (СОО), которые определялись по следующим формулам:

(6)
${\text{СКО}}~\,\, = \,\,~\sqrt {\frac{{\sum\limits_{i~ = ~1}^n {{{{\left( {y_{i}^{{th}}~ - ~y_{i}^{{ex}}~} \right)}}^{2}}} }}{{n - 1}}} ,$
(7)
${\text{СОО}}~\, = ~\,\frac{1}{n}\mathop \sum \limits_{i~ = ~1}^n \left( {\left| {\frac{{y_{i}^{{th}}~ - ~y_{i}^{{ex}}}}{{y_{i}^{{ex}}}}} \right|} \right),$
где n – число составов, на основе которых проводился расчет, $y_{i}^{{th}}$ – значение величины для данного состава по результатам расчета, $y_{i}^{{ex}}$ – экспериментальное значение величины для этого же состава. Округление величин подбираемых параметров проводили с точностью, не превышающей ошибку аппроксимации. Для каждого значения погрешности расчета gE (разницы между экспериментальным и определенным значением) находили соответствующее отклонение для величин W. Далее результат для всех составов усреднялся.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Бинарные системы. Экспериментальные данные для бинарных систем опубликованы в работах [17–21]. Результаты расчетов при 328.15 K приведены в табл. 1. Значения СОО показывают, что погрешность расчетов gE для разных систем может существенно отличаться (СОО от 1 до 10), но вполне достаточна для практических целей. Детальный анализ данных показывает, что значительный вклад в СОО, значительно увеличивающий эти значения, вносят расчетные данные о gE для крайних составов концентрационных диапазонов. Очевидно, что это достаточно обычная для статистических оценок проблема, когда общий анализ данных включает величины, рассчитанные для малых концентраций. В данном случае, например, варьирование составов в пределах 0.01–0.05 мол. д. и энергий Гиббса в пределах 40 Дж позволяет снизить ошибку до величин, даже меньших усредненного значения.

Таблица 1.  

Результаты расчетов gE по методу ИНС для бинарных систем, T = 328.15 K

Система и источник данных W12 W21 СОО, % СКО
Ацетон–хлороформ [17] 1.313 1.681 1.1 0.0024
Ацетон–этанол [18] 0.48 1.01 8.0 0.009
Ацетон–гексан [19] 0.472 0.368 2.0 0.005
Хлороформ–гексан [17] 1.065 0.593 1.7 0.0018
Этанол–гексан [19] 0.32 0.12 9.0 0.04
Этанол–хлороформ [20] 0.30 0.93 10.0 0.013

Трехкомпонентные системы. Результаты расчетов для трехкомпонентных систем этанол–хлороформ–гексан (с тройным положительным азеотропом [22]), ацетон–хлороформ–гексан (с тройным седловым азеотропом [23]), ацетон–этанол–хлороформ (с тройным седловым азеотропом [21, 24]), и ацетон–этанол–гексан (без тройного азеотропа [18]) при 328.15 K приведены в табл. 2. Погрешность расчетов несколько превышает величины, приведенные для бинарных систем, но в целом и результаты и ошибки можно считать вполне приемлемыми для практических задач, или хотя бы качественной оценки параметров равновесия жидкость–пар (избыточных энергий Гиббса). Отметим также, что величины отклонений от экспериментальных величин имеют тот же порядок, что и соответствующие значения, приведенные для других трехкомпонентных систем в статье [15]. Кроме того, значения СОО показывают, что расчеты для трехкомпонентных систем имеют большую погрешность в сравнении с бинарными смесями. Анализ результатов позволяет сделать некоторые общие выводы.

Таблица 2.  

Результаты моделирования для тройных систем с помощью ИНС с постоянными коэффициентами аппроксимации Wik, T = 328.15 K: значения СОО и СКО для рассчитанных величин gE

Система и источник данных W12 W13 W21 W23 W31 W32 СОО, % СКО
Этанол–хлороформ-гексан [22] 0.28 0.60 1.03 0.58 –0.10 0.77 3 0.015
Ацетон–хлороформ–гексан [23] 1.22 0.43 1.71 0.81 0.38 0.77 14 0.007
Ацетон–этанол–хлороформ [24] 0.27 1.35 1.32 0.31 1.43 0.91 19 0.009
Ацетон–этанол–гексан [18] 0.25 0.39 1.10 0.10 0.50 0.27 7 0.040

1. Как и в случае бинарных систем, на краях концентрационного диапазона (малые концентрации веществ) погрешность расчетов, точнее, величины отклонений от экспериментальных данных, увеличивается (рис. 2 и 3).

Рис. 2.

Распределение погрешностей в системе ацетон–хлороформ–гексан: δ – относительное отклонение смоделированного значения gE от экспериментального; x1 – мольная доля ацетона; x2 – мольная доля хлороформа.

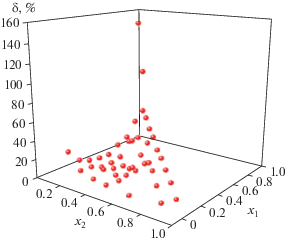
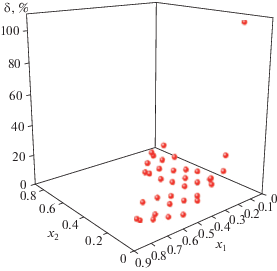
Рис. 3.

Распределение погрешностей в системе этанол–хлороформ–гексан: δ – относительное отклонение смоделированного значения gE от экспериментального; x1 – мольная доля этанола; x2 – мольная доля хлороформа.

2. Отмечается различие в результатах расчетов для систем, в которых отклонения от идеальности имеют один характер. Действительно, для систем этанол–хлороформ–гексан и ацетон–этанол–гексан, в которых трехкомпонентные и бинарные смеси проявляют только положительные отклонения от закона Рауля, получены лучшие результаты по сравнению с другими двумя тройными системами. Одним из путей решения проблемы описания равновесий в системах с разными по характеру отклонениями от идеальности, включая системы с седловым азеотропом, может быть поиск других функций активации для ИНС.

3. Совместное рассмотрение тройных систем и бинарных подсистем приводит к ухудшению аппроксимации в целом. Действительно, соответствующие коэффициенты аппроксимации wij для тройной и бинарных систем существенно различаются. Включение бинарных составов в банк данных о тройной системе ухудшает общую погрешность, в том числе и погрешность в расчетах gE для бинарных систем. Наилучшая корреляция с экспериментальными данными достигается при раздельном моделировании бинарных и тройных составов.

Первые два из приведенных выше пунктов не представляют большой проблемы. Например, более точная аппроксимация может быть достигнута в результате поиска лучшей, оптимальной функции активации. Приведенная третья проблема совместного описания трехкомпонентной системы и ее бинарных подсистем представляется, отчасти, неожиданной, так как бинарные подсистемы являются частью трехкомпонентной. В связи с этим нами была исследована возможность модернизации методики для оптимального совместного рассмотрения всей совокупности данных о тройной системе, в том числе, о бинарных подсистемах.

В результате проведенного нами анализа, включающего различные варианты концентрационного изменения коэффициентов Wij, было установлено, что линейное приближение для данной зависимости не вносит существенной ошибки в результаты расчетов. Предлагаемый вариант, обеспечивающий согласованность расчетов для тройных систем и бинарных подсистем, может быть представлен формулой, позволяющей характеризовать изменение бинарного коэффициента при введении третьего компонента:

(8)
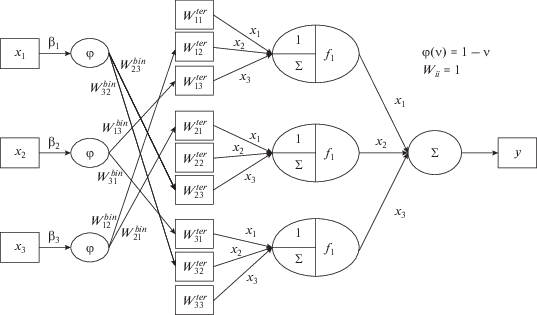
$W_{{ij}}^{{ter}}\left( {{{x}_{k}}} \right) = \,~W_{{ij}}^{{bin}}~\left( {1 - ~{{\beta }_{k}}~{{x}_{k}}} \right),$
где $W_{{ij}}^{{ter}}$ – значение коэффициента в тройной системе, $W_{{ij}}^{{bin}}$– значение коэффициента в бинарной системе i–j, βk – коэффициент корреляции, связывающий параметры бинарной и тройной системы; xk – концентрация третьего компонента (k).

В соответствии с формулой (8) переход от бинарной системы к трехкомпонентной описывается линейной зависимостью: это условие, с некоторым приближением, действительно выполняется для рассмотренных в работе систем. Схема, иллюстрирующая данную модификацию ИНС, представлена на рис. 4. Хотя в данном случае ИНС включает не 6, а 3 коэффициента, результаты проведенных расчетов практически не уступают точности, полученной по первой схеме (рис. 1). Вместе с тем для предлагаемой модификации ИНС также характерно увеличение относительного отклонения расчетных значений gE от экспериментальных на краях концентрационных диапазонов (при малых концентрациях одного из веществ). В то же время новая схема включает не шесть, а три параметра, что является вполне определенным преимуществом при расчетах.

Рис. 4.

Схема предложенной модификации ИНС.

Результаты расчетов по модифицированной схеме представлены в табл. 3.

Таблица 3.  

Значения коэффициентов корреляции, связывающих бинарные параметры (табл. 1) и тройные параметры (формула (8)), величины отклонений от экспериментальных значений gE и сравнение с результатами вычислений значений gE при постоянных коэффициентах для тройных систем (табл. 2)

Система/коэффициенты и отклонения Этанол– хлороформ–гексан Ацетон– хлороформ–гексан Ацетон– этанол–хлороформ Ацетон– этанол–гексан
β3 –3 0 0 2.4
β2 0 0.7 –0.5 0
β1 2.4 –0.52 1.1 –7.5
СОО (коэффициенты зависят от состава), % 6 5 8 4
СКО (коэффициенты зависят от состава) 0.022 0.007 0.012 0.040
СОО (постоянные коэффициенты), % 3 14 18 6
СКО (постоянные коэффициенты) 0.015 0.007 0.009 0.040

ЗАКЛЮЧЕНИЕ

Показано, что метод ИНС в варианте Фокке–Аргатова–Кочербитова может быть применен для анализа, расчета и аппроксимации данных о фазовых равновесиях жидкость–пар. Предложенная в настоящей работе модификация данного метода учитывает в явном виде связь данных о равновесии жидкость–пар в бинарных и тройных системах и, соответственно, позволяет проводить их анализ в рамках одной нейронной сети при уменьшенном количестве параметров. Кроме того, предложенный нами подход позволяет проводить анализ тройных систем на основе параметров, полученных для бинарных подсистем. При этом погрешность расчетов имеет в среднем тот же порядок, что и моделирование по методике [15]. В то же время расчеты по примененной методике ИНС для систем с различным характером отклонений от идеальности (положительные или отрицательные), топологическими особенностями поверхности давления, приводят к результатам, в разной степени согласующимися с экспериментальными данными (погрешность от 3 до 10%). Так, для тройной системы с седловой поверхностью давления ацетон–хлороформ–гексан, т.е. для системы с положительными и отрицательными отклонениями от идеального поведения, средняя ошибка имеет несколько большее значение в сравнении с системой с только положительными отклонениями (этанол–хлороформ–гексан). Поэтому перспективы развития методики, как и метода [15], в большой степени связаны с поиском оптимальных и более гибких функций активации при расчетах по методу ИНС.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-03-00375). Авторы благодарны В. Кочербитову (Университет Мальмо, Швеция) за полезные консультации. Исследования проведены с использованием вычислительных ресурсов Ресурсного центра “Вычислительный центр СПбГУ”.

ОБОЗНАЧЕНИЯ

a коэффициенты аппроксимации в модели Фокке
f функция активации
gE молярная избыточная энергия Гиббса, Дж/моль
m число компонентов в системе
n число экспериментальных составов
R универсальная газовая постоянная, Дж/(моль K)
T абсолютная температура, K
W коэффициенты аппроксимации в модели Фокке–Аргатова–Кочербитова
x мольная доля компонента в смеси (входные значения ИНС)
y выходные значения моделируемой величины (gE/RT)
β коэффициент корреляции

ИНДЕКСЫ

bin индекс бинарной системы
ex экспериментальное значение
i, j, k нумерация компонентов системы
ter индекс тройной системы
th теоретическое значение, полученное в ходе аппроксимации

Список литературы

  1. Wilson G. Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing // J. Am. Chem. Soc. 1964. V. 86. № 2. P. 127.

  2. Renon H., Prausnitz J.M. Local compositions in thermodynamic excess functions for liquid mixtures // AIChE J. 1968. V. 14. № 1. P. 135.

  3. Fredenslund A., Jones R.L., Prausnitz J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures // AIChE J. 1975. V. 21. P. 1086.

  4. Abrams D.S., Prausnitz J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems // AIChE J. 1975. V. 21. № 1. P. 116.

  5. Gross J., Sadowski G. Perturbed-Chain SAFT: an equation of state based on a perturbation theory for chain molecules // Ind. Eng. Chem. Res. 2001. V. 40. P. 1244.

  6. Serafimov L. State of the art in the thermodynamic and topological analysis of phase diagrams // Theor. Found. Chem. Eng. 2009. V. 43. № 3. P. 268.

  7. Serafimov L.A., Pisarenko Y.A., Kulov N.N. Coupling chemical reaction with distillation: Thermodynamic analysis and practical applications // Chem. Eng. Sci. 1999. V. 54. № 10. P. 1383.

  8. Serafimov L.A., Frolkova A.K. Local regularities of phase diagrams of multiphase systems // Theor. Found. Chem. Eng. 1998. V. 32. № 4. P. 347.

  9. Nguyen V., Tan R., Brondial Y., Fuchino T. Prediction of vaporeliquid equilibrium data for ternary systems using artificial neural networks // Fluid Phase Equilib. 2007. V. 254. № 1–2. P. 188.

  10. Moghadam M. Asgharzadeh S. On the application of artificial neural network for modeling liquid-liquid equilibrium // J. Mol. Liq. 2016. V. 220. P. 339.

  11. Roosta A., Hekayati J., Javanmardi J. Application of artificial neural networks and genetic programming in vapor–liquid equilibrium of C1 to C7 alkane binary mixtures // Neural Comput. Appl. 2019. V. 31. P. 1165.

  12. Farzaneh-Gord M., Mohseni-Gharyehsafa B., Ebrahimi-Moghadam A., Jabari-Moghadam A., Toikka A., Zvereva I. Precise Calculation of Natural Gas Sound Speed Using Neural Networks: An Application in Flow Meter Calibration // Flow Meas. Instrum. 2018. V. 64. P. 90.

  13. Farzaneh-Gord M., Rahbari H.R., Mohseni-Gharyehsafa B., Toikka A., Zvereva I. Machine learning methods for precise calculation of temperature drop during a throttling process // J. Therm. Anal. Calorim. 2020. V. 140. № 6. P. 2765.

  14. Haykin S. Neural Networks: A Comprehensive Foundation. Englewood Cliffs, N.J.: Prentice-Hall, 1999.

  15. Argatov I., Kocherbitov V. A note on artificial neural network modeling of vapor-liquid equilibrium in multicomponent mixtures // Fluid Phase Equilib. 2019. V. 502. P. 112282.

  16. Focke W. Mixture models based on neural network averaging // Neural Comput. 2006. V. 18. № 1. P. 1.

  17. Кудрявцева Л.С., Сусарев М.П. Равновесие жидкость–пар в системах хлороформ–гексан и ацетон–хлороформ // Журн. прикл. хим. 1963. Т. 36. № 6. С. 1231.

  18. Виниченко И.Г, Сусарев М.П. Исследование и расчет равновесия жидкость–пар в системе ацетон–этанол–н.-гексан // Журн. прикл. хим. 1966. Т. 39. С. 1583.

  19. Кудрявцева Л.С., Сусарев М.П. Равновесие жидкость–пар в системах ацетон–гексан и гексан–этиловый спирт при 35, 45, 55° и 760 мм рт. ст // Журн. прикл. хим. 1963. Т. 36. № 7. С. 1471.

  20. Scatchard G., Raymond C.L. Vapor–Liquid Equilibrium. II. Chloroform–Ethanol Mixtures at 35, 45 and 55° // J. Am. Chem. Soc. 1938. V. 60. P. 1278.

  21. Фролкова А.В., Фролкова А.К., Челюскина Т.В. Разделение четырехкомпонентной системы ацетон–хлороформ–этанол–вода автоэкстрактивногетероазеотропной ректификацией // Вестн. МИТХТ. 2010. Т. 5. № 6. С. 27.

  22. Кудрявцева Л.С., Сусарев М.П. Равновесие жидкость–пар в системе этиловый спирт–хлороформ–гексан при температурах 35, 45, 55° и давлении 760 мм рт. ст. // Журн. прикл. хим. 1963. Т. 36. № 9. С. 2025.

  23. Кудрявцева Л.С., Сусарев М.П. Равновесие жидкость–пар в системе ацетон–хлороформ–гексан при температурах 35, 45, 55° и давлении 760 мм рт. ст. // Журн. прикл. хим. 1963. Т. 36. № 8. С. 1710.

  24. Виниченко И.Г. Исследование, расчет равновесия между жидкостью и паром в четверной системе этанол–хлороформ–ацетон–гексан. Дис. … канд. хим. наук. Л.: ЛГУ, 1966.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал