Теоретические основы химической технологии, 2021, T. 55, № 4, стр. 529-538
Математическая модель оптимального управления процессом производства нефтяного кокса в трубчатых вращающихся печах
Ю. В. Шариков a, *, Ф. Ю. Шариков a, К. А. Крылов a
a Санкт-Петербургский горный университет
Санкт-Петербург, Россия
* E-mail: yvshar@mail.ru
Поступила в редакцию 21.10.2020
После доработки 17.12.2020
Принята к публикации 22.01.2021
Аннотация
Представлены методика и результаты исследования температурной стабильности сырого и модифицированного товарного нефтяного кокса. Метод TG/DSC был использован для экспериментального исследования процесса прокаливания нефтяного кокса и последующего описания характеристик улучшенного кокса в результате протекания реакции окисления. Было обнаружено, что товарный кокс все еще содержит в своем составе остаточные летучие вещества в заметных количествах. Высокотемпературная стабильность такого товарного, используемого для производства электродов, кокса (например, в печах производства кремния) или в карботермических процессах, может быть улучшена путем дополнительного обжига кокса при определенных условиях в трубчатой печи или электрокальцинаторе. Представлено моделирование реакции прокаливания кокса с использованием результатов термического анализа и аппарата формальной кинетики. Предложен подход для определения критического размера частицы данного кокса с учетом пространственной неоднородности за счет теплопроводности, при котором обеспечивается равномерное прокаливание по объему частицы для обеспечения однородного протекания процесса обжига по всему объему материала в печи, что делает возможным использовать квазигомогенную модель. С использованием кинетической модели реакции и информации о максимально допустимом размере частиц кокса проведено моделирование работы трубчатой вращающейся печи для определения оптимальных условий ее функционирования при получении кокса с заданными характеристиками – определен оптимальный температурный профиль материала по длине печи и скорость движения материала в трубчатой вращающейся печи. Количество золы в исследованном коксе было оценено как близкое к нулю, что делает его особенно ценным для металлургического производства.
ВВЕДЕНИЕ
Прокаливание различных углеродсодержащих материалов в инертной среде обычно проводят для улучшения их свойств и подготовки к дальнейшему использованию – получению углеродных или графитовых электродов, восстановлению оксидов металлов или кремния в карботермических процессах и др. Некоторые вредные примеси (например, сера) также могут быть частично удалены при прокаливании в определенных условиях. В результате получается пористый материал с более высоким содержанием углерода, значительно меньшим содержанием летучих веществ и примесей, более активный в твердофазных реакциях, а также с лучшими электрофизическими характеристиками [1, 2]. Дальнейшая термическая обработка позволяет получить менее пористый материал с высокой проводимостью, который устойчив к окислительным реакциям. Прокаливание кокса обычно проводят в специальных печах различного типа. Для этого процесса используют три вида печей – трубчатые вращающиеся печи, электрические кальцинаторы и ретортные печи. Вращающиеся печи более распространены в промышленности, также они имеют более высокую производительность, однако качество продукта после электрокальцинаторов, как правило, лучше [2–4]. В любом случае исходные характеристики сырья и особенности его прокаливания являются ключевыми параметрами для выбора оптимальных условий функционирования промышленного аппарата.
Антрацит долгое время был основным природным источником кокса для металлургии и производства различных электродов. В настоящее время нефтяной кокс успешно конкурирует с угольным коксом, так как обладает рядом принципиальных преимуществ (прежде всего, очень малой зольностью). Несмотря на это, он заметно дороже, так как технология его производства сложна, а качество сырья очень важно для получения конечного нефтяного кокса. В России не хватает высококачественного нефтяного кокса, а угольный кокс до сих пор широко используется для различных целей, в том числе для формирования электродов. Нефтяной кокс должен быть правильно подготовлен и, при необходимости, дополнительно модифицирован, если мы хотим получить продукт заданного качества. Данная работа посвящена методике определения характеристик товарного нефтяного кокса и дальнейшей модификации его свойств для карбо-металлургического применения и производства электродов. Было установлено, что определенный товарный нефтяной кокс не может быть использован непосредственно для формирования электродов из-за заметного количества остаточных летучих веществ. Исследования с применением методики TG/DSC является наилучшим способом проведения экспресс-анализа и позволяет охарактеризовать устойчивость к окислению и содержание летучих веществ в углях и коксах [5, 6, 7]. Эта же методика может быть применена и для непосредственного изучения кинетики промышленного процесса с разработкой соответствующей математической модели этого технологического процесса [8]. Очевидно, что это универсальный и мощный инструмент, позволяющий получить всю необходимую информации о скорости реакций для большинства исследуемых химических процессов, поскольку они обычно сопровождаются изменением массы твердой фазы с сопутствующим выделением или потреблением тепловой энергии [7–12]. Кривая TG или DSC обычно представляет собой не специфический, а обобщенный отклик на протекание сложного процесса. Кроме того, эти кривые очень информативны, так как содержат большое количество экспериментальных данных и позволяют выбрать характерные точки для проведения дополнительного анализа продукта в выбранных точках. Моделирование с применением формально-кинетического подхода позволяет представить сложный физико-химический процесс в виде системы дифференциальных уравнений и перейти к разработке математической модели промышленного аппарата [8–10, 13, 14].
МАТЕРИАЛЫ И МЕТОДЫ
Метод TG/DSC и кинетическое моделирование были применены для исследования реакции прокаливания и разработки математической модели вращающейся печи для определения оптимального режима прокаливания. Конечный продукт дополнительно характеризовался стабильностью к окислительным процессам.
Реагенты. Исходный нефтяной кокс был получен на Волгоградском нефтеперерабатывающем заводе (Волгоград, Россия).
Термический анализ. Кинетические измерения проводили с использованием термоанализатора Labsys evo (SETARAM Instrumentation). Применяли линейный режим нагрева со скоростью нагрева β = 10.0°C мин–1. Для исследования процесса прокаливания применяли проточную атмосферу азота (расход 20 мл мин–1). Для исследования окислительной стабильности коксов применяли статическую воздушную атмосферу.
Сбор и первичная обработка данных. Для проведения эксперимента, сбора данных и первичной обработки использовался программный пакет Calisto (v 1.086, AKTS AG). Для подготовки данных для кинетического анализа использовался программный пакет “Эксперимент” (v 4.31, CISP Ltd).
Кинетический анализ экспериментальных данных и моделирование. Программный пакет ReactOp Cascade (v 3.20, CISP Ltd) использовался для кинетического анализа данных, синтеза математической модели трубчатой печи и поиска оптимальных условий процесса прокаливания.
ЛИТЕРАТУРНЫЙ ОБЗОР
Вращающиеся печи широко используются в промышленности для таких процессов, как производство кокса, производство цементного клинкера, производство глинозема и др. [2–4]. Основные уравнения, касающиеся поведения твердого материала и газовой фазы внутри печи, были подробно изучены и обсуждены во многих работах, например [2–4, 10]. Тем не менее необходимо обозначить основные уравнения, для того чтобы объяснить возможность применения модели идеального вытеснения для описания движения как твердой, так и газовой фаз при прокаливании нефтяного кокса.
Движение твердого материала во вращающейся печи. Особенности транспортировки твердого порошкообразного материала внутри вращающейся печи влияют на все важные физико-химические процессы внутри барабана. Движение пересыпающегося слоя обычно принимается как для исходного сырья, так и для готового продукта. В результате вращения барабана вокруг своей оси под действием силы тяжести возникают два силовых момента. Эти моменты принимают участие в формировании этого пересыпающегося слоя. Следовательно, можно предположить модель перемешивания в радиальном направлении. Согласно модели движения, предложенной Н.Г. Срибнером [3], перемещение частиц вдоль оси барабана происходит только в пересыпающемся слое и зависит от свойств твердой фазы и конструктивных особенностей печи. Анализ полученных зависимостей позволил получить соотношение для расчета скорости движения материала во вращающейся печи в следующем виде:
Ввиду относительно малого размера частиц твердой фазы и небольшой скорости движения сыпучего материала – для описания его движения в трубчатой вращающейся печи может быть использована модель идеального вытеснения в продольном направлении и модель идеального перемешивания в поперечном сечении аппарата.
Горение газа и движение газовой фазы во вращающейся печи. Сжигание топлива, движущегося в турбулентном режиме внутри печи, обычно описывается сложной системой уравнений. Эта система включает уравнения протекания и непрерывности для потока вязкого сжимаемого газа, уравнения энергии и диффузии для компонентов горючей смеси и продуктов реакции с нелинейными источниками тепла и массы.
Интенсивность этих источников является функцией уравнений химической кинетики горения газа. Как правило, следует учитывать изменение молекулярной массы реагентов, разницу между теплоемкостью исходных продуктов и продуктов сгорания, тепловые потери, обусловленные выбросом пламени, а также явления диссоциации и ионизации. Эффекты от диффузии тепла, давления и теплопроводности также должны быть рассмотрены, если это возможно.
Расчеты, связанные с горением газа в турбулентном режиме, как правило, осложняются традиционными гидродинамическими трудностями, связанными с незамкнутой системой уравнений для среднего турбулентного движения Рейнольдса. Для замыкания системы уравнений следует использовать некоторые феноменологические модели среднего течения и уравнения, связывающие коэффициенты эффективности переноса (турбулентности) со средними значениями переменных и их производными. Таким образом, для аналитического представления процесса горения газа в турбулентном потоке необходимо ввести некоторые эмпирические коэффициенты и функции [3, 10].
Существенное упрощение математической постановки задачи абсолютно необходимо. Полная система уравнений Навье–Стокса относительно пограничного слоя должна быть заменена. Также можно пренебречь изменением давления в поле течения свободной струи. Теплопередача между газовой фазой, твердым материалом и барабаном печи обеспечивается за счет излучения в соответствии с уравнением Стефана–Больцмана. Теплопередача переходит в конвективную теплопередачу по закону Ньютона в случае течения газа после снижения температуры газовой фазы [10].
Основным параметром горящей газовой струи принимается длина пламени. Этот параметр непосредственно влияет на эффективность всего происходящего внутри вращающейся печи технологического процесса. Процедура оценки длины пламени горящего газа обсуждается в ряде статей (см., например, [15, 16]).
Пылеулавливание и возвращение пыли – основное уравнение. В самом начале прокаливания измельченного кокса в результате испарения воды и летучих веществ шихта претерпевает ряд изменений. Сначала сыпучий материал даже может потерять свою первоначальную подвижность, но после этого у него в новом гранулированном состоянии начинает проявляться подвижность несколько другого рода. Поскольку мы имеем дело с уже предварительно нагретым нефтяным коксом – эта стадия может иметь меньшее значение, но ею не следует полностью пренебрегать.
В результате удаления мелких частиц в процессе движения твердого материала, состав коксовой шихты меняется. Коксовая пыль, перешедшая во взвешенное состояние, практически полностью сгорает, благодаря чему можно снизить потребление природного газа. Эмпирическая формула для расчета массовой концентрации µ (кг/кг) пыли, сжигаемой в потоке газа внутри вращающейся печи, выглядит следующим образом [15, 16]:
(2)
$\mu = 2 \times {{10}^{{11}}}{{\left( {\mathop W\nolimits_g^2 \sqrt {\frac{{\mathop \rho \nolimits_g }}{{\mathop \rho \nolimits_M }}} } \right)}^{m}}\frac{{{{D}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{\left( {dr_{f}^{3}} \right)}}{{\frac{n}{\psi }}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Детали кинетического исследования. Нефтяные коксы обычно получают из высокоароматических вторичных газойлей каталитического крекинга или остатков газойля и тяжелых остатков пиролиза в полупериодическом режиме в специальных больших реакторах. После этого “зеленый” нефтяной кокс прокаливают при высокой температуре (свыше 1000°С) в трубчатых печах, электрокальцинаторах или ретортных печах. Электрические кальцинаторы и ретортные печи встречаются реже, но качество кокса, полученного в результате обработки в аппаратах данного типа, обычно выше. Можно сделать вывод, что правильный режим прокаливания является ключевым параметром, отвечающим за конечные характеристики кокса. Поиск оптимального температурного режима и скорости движения для конкретного “зеленого” или предварительно прокаленного кокса, а также обеспечение равномерного прокаливания материалов с различными гранулометрическими характеристиками в промышленной вращающейся печи является непростой задачей. Наша задача состояла в том, чтобы изучить товарный нефтяной кокс (который уже прошел процедуру прокалки) и предложить методику тестирования и улучшения его специфических характеристик, если это будет необходимо.
Сначала образец товарного кокса был испытан на устойчивость к окислению на воздухе в сопоставимых условиях, с применением методики TG/DTG/DSC. Были найдены температурные интервалы окисления и проведена оценка количества золы. Доказано, что количество золы в пределах погрешности определения близко к нулю (0 ± 0.25%). На рис. 1 показана экспериментальная кривая скорости изменения массы (TG) во времени, а на рис. 2 приведены кривые изменения массы (TG) и скорости изменения массы (DTG) в зависимости от температуры в процессе прокаливания в термоанализаторе.
Рис. 1.
Прокалка в инертной атмосфере. Скорость потери массы (DTG, мин–1 × 105) как функция температуры Т(°C) для товарного нефтяного кокса. Линейный нагрев, β = 10°C мин–1, поток азота N2 (20 мл мин–1).
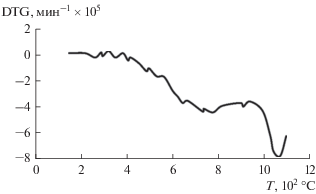
Рис. 2.
Окисление на воздухе. Изменение массы (1) и скорости потери массы (2) в зависимости от T (°C) для исходного нефтяного кокса. Начальная масса: 3.09 мг статический режим в атмосфере воздуха. Линейный нагрев, β = 10°C min–1, аппарат: Labsys Evo.
Было установлено, что при нагревании до 1100°C общая потеря массы составляла около 15%, что является довольно значительной величиной для уже прокаленного нефтяного кокса. Можно сделать вывод, что данный товарный нефтяной кокс может быть улучшен путем дополнительного прокаливания.
Дополнительное прокаливание до потери веса 10% делает этот кокс более активным в химических реакциях (например, для использования в пирометаллургических процессах) за счет улучшения его пористой структуры, а более глубокое прокаливание делает кокс стойким к окислению по сравнению с исходным коксом. Следовательно, основные свойства товарного кокса могут быть существенно улучшены в зависимости от его конкретного применения.
Следующая задача заключается в нахождении оптимального технологического режима трубчатой вращающейся печи для проведения дополнительного прокаливания кокса. Оптимальный технологический режим применительно к конкретной трубчатой печи подразумевает выбор гранулометрических характеристик сыпучего материала, температурного профиля в материале по длине печи и скорости его движения, через которую задается время пребывания кокса в горячей зоне данной печи. Для решения этой задачи, прежде всего, необходима кинетическая модель реакций, протекающих при прокаливании кокса.
Для решения этой задачи на основании экспериментальных данных по кинетике процесса прокаливания был использован программный пакет ReactOp Cascade v 3.20 для разработки структуры кинетической модели и решения обратной кинетической задачи по массивам экспериментальных данных. Для кинетического моделирования реакции прокаливания была применена формальная трехстадийная модель N-го порядка. Исходный кокс при прокаливании образует два вида коксового газа (Gas1 и Gas2), а остаточная твердая фаза в результате превращается в модифицированный кокс (‘COKE”).
Эта модель выглядит следующим образом:
гдеCraw – исходный товарный (“сырой”) кокс, подлежащий модификации;
Gas1 – газ коксования (1), в основном содержащий водород (H2);
Gas2 – газ коксования (2), содержащий метан и другие легкие углеводороды.
COKE – модифицированный кокс с улучшенными характеристиками.
Процедура решения обратной кинетической задачи заключалась в определении кинетических параметров по экспериментальным данным в результате минимизации суммы квадратов отклонений между экспериментальными и расчетными (т.е. сформированными за счет решения по выбранной кинетической модели) данными. Эта величина является комплексной функцией набора всех кинетических параметров, поэтому задача его определения состоит в нахождении минимального значения функции многих переменных [13, 14]. В результате решения задачи нахождения минимума функции рассогласования была получена хорошая корреляция между экспериментальными и расчетными кинетическими кривыми (см. рис. 3).
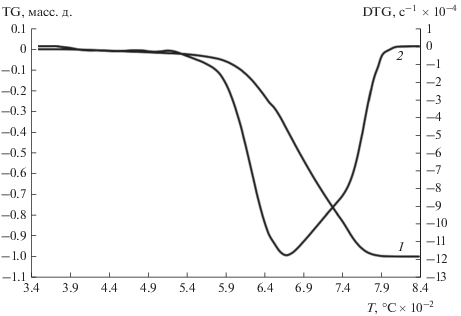
Рис. 3.
Результаты кинетического анализа реакции дополнительного прокаливания товарного нефтяного кокса в инертной атмосфере. Экспериментальная (точки) и расчетная (линии) потери веса (TG) (а) и скорость потери веса (DTG) (б). Трехступенчатая формальная модель N-го порядка.
Поиск оптимального температурного профиля внутри трубчатой вращающейся печи. Разность температур между пламенем горения топлива и твердым материалом является движущей силой теплопередачи в трубчатой печи. В зоне прокаливания температура должна быть строго определенной. Любой чрезмерный перегрев может вызвать ненужное скопление и агрегацию мелких частиц в сыпучем материале. Анализ результатов моделирования показал, что поведение температурных профилей для газовой фазы и твердого материала в процессе прокаливания кокса соответствует этим основным ограничениям, описанным в литературе.
Математическая модель процесса прокаливания позволяет определить оптимальный температурный профиль путем решения соответствующей оптимизационной задачи. В качестве критерия оптимизации процесса прокаливания может быть выбрана потеря массы исходного товарного нефтяного кокса (“сырого кокса”) на выходе из вращающейся печи. Это значение было определено в ходе термоаналитического исследования. Потеря массы на выходе должна составлять 10%, если нужен активный материал для проведения карботермических процессов, или 15%, если необходим материал для изготовления электродов. Задание температурного профиля по длине печи осуществляется следующим образом:
Критерий оптимизации выражается через потерю массы твердой шихты вдоль печи. Таким образом, управляющей переменной является управляющая функция T(l). Как правило, эта задача сводится к вариационному исчислению. Если представить искомый оптимальный температурный профиль в виде кусочно-линейной аппроксимации управляющей функции по длине печи, то можно перейти от вариационной задачи к задаче поиска экстремума функции нескольких переменных в допустимой области изменения температур:
Управляющие переменные (т.е. температура в определенных точках и координаты этих точек) должны быть найдены из заданной области управления. Для каждого шага ограничения температурного профиля устанавливаются отдельно. Это типичная задача поиска экстремума с ограничениями, заданными в виде неравенств. Для решения такого рода задач может быть использован метод нелинейного программирования. Решение таких задач реализовано в программном пакете ReactOp. Температурный профиль твердой фазы – это управляющая переменная, которую нужно найти путем решения оптимизационной задачи. В модель трубчатой печи была введена кинетическая модель реакций прокаливания и установлены оптимальные условия протекания процесса прокаливания нефтяного кокса. Последовательно применялись две модели вращающихся печей:
1) Стандартная модель реактора идеального вытеснения (без теплообмена и с температурным режимом T given) – для оценки длины печи, скорости движения материала, толщины слоя и диапазона режимов нагрева.
2) Модифицированная модель реактора идеального вытеснения с теплообменом для определения точного температурного режима материала при заданной скорости его движения, потери массы исходного кокса на выходе и выхода улучшенного кокса.
Задача поиска оптимального температурного профиля T(l) была успешно решена. Найденный оптимальный температурный профиль T(l) был введен в математическую модель процесса в печи и далее были определены расходы природного газа и воздуха на поддержание этого режима. Данная методика позволила найти необходимые значения управляющих переменных для промышленной вращающейся печи с заданными характеристиками (длина 20 м, диаметр 1 м, эффективный диаметр твердой шихты 0.2 м, линейная скорость движения шихты 0.20–0.50 м мин–1). Результаты решения оптимизационной задачи приведены в табл. 1 и на рис. 4.
Таблица 1.
Основные технологические параметры прокаливания нефтяного кокса
| Параметр | 10% потери массы | 15% потери массы |
|---|---|---|
| Температурный интервал, K | 1000–1150 | 1100–1250 |
| Скорость перемещения кокса, м мин–1 | 0.52 | 0.30 |
| Массовые доли продукции на выходе: | ||
| Кокс | 0.90 | 0.851 |
| Газ1 | 0.003 | 0.028 |
| Газ2 | 0.097 | 0.121 |
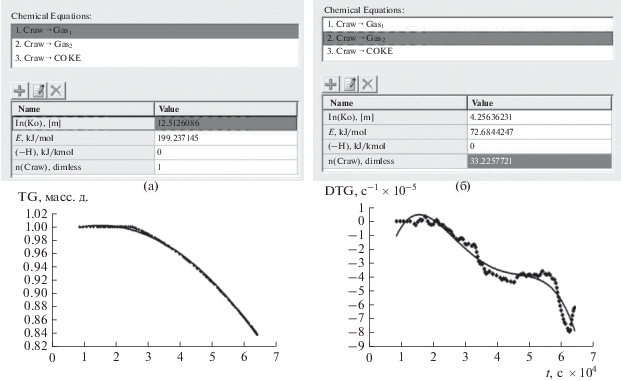
Рис. 4.
Оптимальный температурный профиль твердой фазы для процесса начального прокаливания кокса позволяет достичь конечной потери массы шихты на 15% от исходного значения. Длина печи – 20 м; расчетное значение линейной скорости заряда – 0.30 м мин–1.
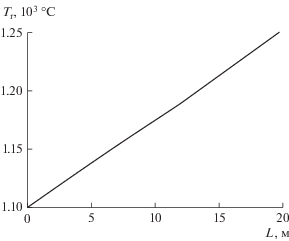
На рис. 5 приведены результаты моделирования при найденном оптимальном температурном профиле.
Рис. 5.
Конверсионные профили компонентов вдоль печи: 1 – общая потеря массы при прокаливании; 2 – потеря массы по реакции 1; 3 – потеря массы по реакции 2.
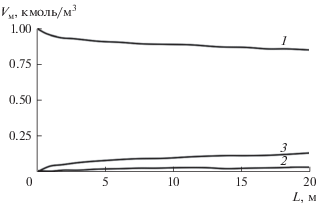
Для достижения конечной потери массы шихты на 15% от исходного значения расчетное значение линейной скорости движения сыпучего материала в печи должно составлять 0.30 м мин–1.
Обоснование возможности применения квазигомогенной модели процесса обжига в трубчатой вращающейся печи. Возможность использования квазигомогенной модели может быть обоснована только при доказательстве равномерного протекания процесса во всем объеме каждой гранулы петкокса.
Для этого необходимо создать математическую модель процесса в грануле с учетом теплового потока из окружающей среды внутрь частицы кокса с учетом кинетики химической реакции и теплового эффекта реакции, а также теплопроводности кокса.
Математическая модель такого этого процесса может быть описана следующей системой дифференциальных уравнений в частных производных [13, 14]:
(5)
$\frac{{\partial T}}{{\partial t}} = \frac{\lambda }{{{{\rho }_{M}}{{c}_{p}}}}\left( {\frac{{{{\partial }^{2}}T}}{{\partial {{r}^{2}}}} + \frac{\Gamma }{r}\frac{{\partial T}}{{\partial r}}} \right) \pm \sum\limits_{i,J}^{I,M} {{{w}_{{r,i,j}}}{{Q}_{j}}} ,$(6)
$\frac{{\partial {{c}_{i}}}}{{\partial t}} = {{D}_{i}}\left( {\frac{{{{\partial }^{2}}{{c}_{i}}}}{{\partial {{r}^{2}}}} + \frac{\Gamma }{r}\frac{{\partial {{c}_{i}}}}{{\partial r}}} \right) \pm \sum\limits_{i,J}^{I,M} {{{w}_{{r,i,j}}}} .$Со следующими начальными условиями:
и с граничными условиями 1, 2 или 3-го рода, либо в обобщенном виде с учетом лучистого теплообмена, теплового потока и условиями теплообмена по закону Ньютона – в зависимости от условий тепломассообмена между частицами кокса и окружающей средой [13, 14].
Для решения этой системы уравнений при различных значениях размера частицы и при обжиге с известной кинетикой превращений был использован программный пакет ThermEx, разработанный в РНЦ “Прикладная химия” и ЗАО CISP Ltd. Пакет позволяет задавать форму реакционной зоны, граничные и начальные условия тепломассообмена в реакторе, физико-химические свойства реакционной системы, кинетику и тепловой эффект химической реакции. Кинетические уравнения выбираются и задаются из банка данных формально-кинетических реакций, система также позволяет вводить в модели дополнительные стадии для модификации формальных моделей при необходимости [17, 18].
Расчеты проводили при последовательном уменьшении радиуса частиц от 0.100 до 0.0125 м. Было найдено, что при радиусе частицы 0.0125 м наблюдается очень незначительная неравномерность по конверсии внутри частицы в начальный момент времени. В дальнейшем процесс внутри частицы протекает уже достаточно равномерно, и реакция заканчивается практически одновременно по всему объему частицы. На рис. 6 и 7 приведены результаты моделирования в программном пакете ThermEx.
Рис. 6.
Результаты моделирования процесса прокалки в частице кокса с учетом пространственной неоднородности при решении системы уравнений (14), (15). Оптимальный температурный профиль задан в виде граничных условий 1-го рода. (а) – изменение температуры на поверхности частиц (1) и средней температуры внутри частицы (2) в зависимости от времени пребывания (от длины печи); (б) – изменение средней конверсии по реакции 1 (1) и по реакции 2 (2).
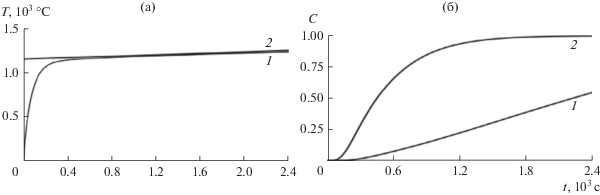
Рис. 7.
Радиальные профили изменения температур (а) и конверсий (б) в различные моменты текущего времени контакта ti, t1 < t2 < t3 < t4 < t5 < t6 < t7 в ТВП при оптимальном режиме.
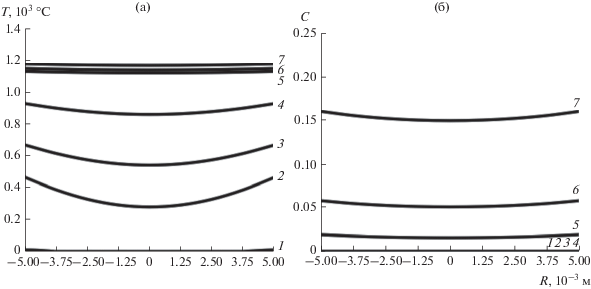
Из приведенных результатов следует, что при полученных данных о кинетике процесса обжига кокса при заданных условиях и при размере частиц радиусом не более 0.0125 м, процесс протекает равномерно во всем объеме гранулы, поэтому можно использовать квазигомогенную модель для моделирования процесса обжига в печи. В недавней работе [19], посвященной исследованию процесса обжига кокса с использованием метода TG/DSC, было показано, что гранулометрические характеристики кокса оказывают влияние на протекание процесса и качество получаемого кокса, но не было приведено объяснения полученному результату. Было высказано предложение проводить TG/DSC исследование для каждого образца кокса для точного определения оптимального температурного режима процесса обжига. Полученные в нашем исследовании результаты дают количественную методику оценки обнаруженного явления и позволяют создать методику экспериментально-расчетного определения параметров оптимального управления процессом обжига для каждого конкретного сорта петкокса.
ЗАКЛЮЧЕНИЕ
Полученные в ходе исследования результаты свидетельствуют об эффективности применения методики термического анализа совместно с математическим моделированием к задаче определения характеристик нефтяных коксов и их дальнейшей модификации в трубчатых вращающихся печах. Для разработки математической модели промышленной печи с известным химическим превращением была изучена кинетика соответствующей химической реакции с использованием метода TG-DTG или TG-DSC. В ходе кинетического моделирования была эффективно использована формальная модель для описания сложного гетерогенного процесса в промышленном аппарате. Следует подчеркнуть, что численные значения найденных кинетических параметров являются функцией дисперсности твердой фазы и способа приготовления шихты.
Разработанная математическая модель прокаливания нефтяного кокса адекватно описывает химические превращения через потерю массы шихты в выбранной вращающейся трубчатой печи.
На основании полученных результатов можно предложить следующий алгоритм определения оптимальных условий обжига кокса:
1. Для конкретного сорта кокса проводятся кинетические исследования с использованием термоанализатора типа Labsys evo (SETARAM Instrumentation).
2. С помощью программного комплекса ReactOp проводится решение обратной кинетической задачи, и определяются кинетические параметры модели, характеризующие процесс обжига данного сорта кокса.
3. С помощью программного комплекса ReactOp определяется оптимальный температурный профиль для выбранного размера и производительности реактора. Определяется максимально горячая точка в реакторе.
4. С помощью программного комплекса ThermEx определяется критический размер частиц для данного сорта кокса. Найденный оптимальный температурный режим задается в виде граничного условия 1-го рода на поверхности частицы кокса.
5. Создается система регулирования для поддержания необходимой температуры в максимально горячей точке реактора.
Таким образом, определяются оптимальные условия для обжига каждого конкретного сорта кокса.
Работа выполнена в рамках государственного задания по проекту № 075-00314-20-02. Кинетические измерения и моделирование проводили в Санкт-Петербургском горном университете с использованием оборудования и программного обеспечения, полученного при реализации Программы развития “Национальный исследовательский университет”.
Авторы выражают благодарность руководству Горного университета за создание условий, поддержку и внимание к работе.
ОБОЗНАЧЕНИЯ
| a | тангенс угла наклона барабанной печи |
| cp | теплоемкость, кДж кг–1 К–1 |
| ci | концентрация i-го компонента, кмоль м–3 |
| D | диаметр барабана печи, м |
| Di | коэффициент диффузии i-го компонента, м2 с–1 |
| d | средний диаметр частицы, м |
| n | число оборотов вращающейся печи, об мин–1 |
| Qj | тепловой эффект j-й реакции, кДж моль–1 |
| r | радиус частицы, м |
| rf | критерий многофракционной характеристики материала |
| T | температура, К |
| t | время, с |
| $v$ | кинематическая вязкость газов, м2 с–1 |
| Wg | расход газа, м с–1 |
| WM | линейная скорость движения материала, м мин–1 |
| wi,j | скорость превращения i-го компонента в j-й реакции, кмоль м–3 с–1 |
| αм | угол наклона свободной поверхности материала к оси печи, град |
| αp | угол наклона печи, град |
| β | скоростью нагрева, °C мин–1 |
| βс | экспериментально определяемый угол, град |
| Γ | фактор геометрической формы |
| λ | теплопроводность реакционной смеси, кДж м–1 К с–1 |
| µ | массовая концентрация пыли, кг/кг |
| v | кинематическая вязкость газов, м2 с–1 |
| ρg | плотность газов, кг/м3 |
| ρM | плотность материала (кокса), кг/м3 |
| ψ | степень заполнения печи твердым материалом |
ИНДЕКСЫ
Список литературы
Rohani A., Sharifi K., Golpasha R. Calcinations of Petroleum Coke // Proc. 3rd International Conference on Chemical, Ecology and Environmental Sciences. 2014. P. 3.
Martins M.A., Oliveira L.S., Franca A.S. Modeling and simulation of coke calcination in rotary kilns // Fuel 80. 2001. P. 1611.
Борисов И.Н. Пути повышения эффективности цепных завес во вращающихся печах // Цем. его примен. 2003. № 3. С. 17.
Скрибнер Н.Г. Анализ движения сыпучих материалов во вращающихся барабанах // Хим. пром-сть. 1979. С. 232.
ASTM E1131. Standard Test Method for Compositional Analysis by Thermogravimetry.
ASTM D3172. Standard Practice for Proximate Analysis of Coal and Coke.
Sharikov F.Yu., Bazhin V.Yu. The study and modeling of coals and cokes behaviour with applying thermal analysis technique // Proceedings of XIX International Coal Preparation Congress. New Dehli, 2019. V. 1. P. 105.
Sharikov F.Yu., Sharikov Yu.V., Titov O.V. Application of heat-flow calorimetry for developing mathematical models of reactor processes // // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 225.
Laye P.G. Differential thermal analysis and differential scanning // Principles of Thermal Analysis and Calorimetry / Ed. Haines P.J. Cambridge: Royal Society of Chemistry, 2002. P. 55. https://doi.org/10.1039/9781847551764-00055
Sharikov Y.V., Sharikov F.Y., Titov O.V. Optimization of process conditions in a tubular rotary kiln with applying TG/DSC technique and mathematical modeling // J. Therm. Anal. Calorim. 2015. V. 122. P. 1029.
Navrotsky A. Progress and New Directions in High Temperature Calorimetry // Phys. Chem. Miner. 1997. V. 24. P. 222.
Wilthan B. Uncertainty budget for high temperature heat flux DSCs // J. Therm. Anal. Calorim. 2014. V. 118. P. 603. https://doi.org/10.1007/s10973-014-3671-0
Шариков Ю.В., Белоглазов И.Н. Моделирование систем. Часть 1. СПб.: Санкт-Петербургский государственный горный университет, 2011.
Шариков Ю.В., Белоглазов И.Н. Моделирование систем. Часть 2. СПб.: Санкт-Петербургский государственный горный университет, 2012.
Ходоров Е.И., Екимов В.А., Лимонов Б.С. Исследование длительности пребывания материала на открытой поверхности слоя во вращающейся печи // Производство глинозема. Труды ВАМИ. Л.: ВАМИ, 1974. № 88. С. 48.
Borisov I.N. Some features of the behavior of sludge on the drying circuit // Cem. Its Appl. 2002. № 5. P. 26.
Kossoy A., Sheinman I. Evaluating thermal explosion hazard by using kinetics-based simulation approach // Process Saf. Environ. Prot. 2004. V. 82. № 6. P. 421.
Benin A., Kossoy A., Sheinman I., Grinberg P. Evaluating Thermal Explosion Hazard of Self-Reactive Substances by Using Kinetics-Based Simulation Approach // Int. J. Self-Propag. High-Temp. Synth. 2006. V. 15. № 4. P. 297.
Ножко С.И., Веригин А.А., Демичев Д.Н., Гуляев А.В. Некоторые аспекты прокалки сырых нефтяных коксов для нужд алюминиевой промышленности // Сист. Методы Технол. 2017. № 4(36). С. 127. https://doi.org/10.18324/2077-5415-2017-4-127-133
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


