Теоретические основы химической технологии, 2021, T. 55, № 4, стр. 506-516
Динамика процесса тепломассообмена при инжектировании диспергированного адсорбента в парогазовый поток
М. И. Шиляев a, *, Е. М. Хромова a
a Томский государственный архитектурно-строительный университет
Томск, Россия
* E-mail: shmi2005@mail.ru
Поступила в редакцию 02.07.2020
После доработки 27.01.2021
Принята к публикации 27.01.2021
Аннотация
Проведено физико-математическое моделирование процесса адсорбции газовых компонентов на адсорбент, инжектируемый в паровоздушный поток в цилиндрической трубе и трубе Вентури. Проведены расчетные оценки адсорбции CO2 на алюмосиликат с масс-медианным размером частиц 50 мкм с использованием коэффициента фазового равновесия, найденного авторами в [1] методом сравнения расчетных и экспериментальных данных работы [2]. Проведен анализ процесса адсорбции в рассматриваемых условиях и сделаны практические выводы.
ВВЕДЕНИЕ
В литературе, посвященной очистке промышленных и, в частности, дымовых газов от SO2, CO2, NOx широко обсуждается вопрос об эффективности и экономичности применения адсорбентов как в сухом, так и в суспензионном виде на основе использования летучей золы (fly ash), являющейся продуктом сжигания угольного топлива, в комбинации с гашеной известью (Са(ОН)2). В [3] представлена схема мокрой газоочистки дымовых газов скруббером в системе тепловой электростанции с помощью подачи в скруббер суспензированного адсорбента. Далее исследуются физико-химические свойства таких адсорбентов (их структура, размер частиц, химический состав и пр.), различные способы их применения. В [4] доказывается преимущество введения (инжектирования) сухого адсорбента в газовой поток как более экономичного в сравнении с мокрыми способами его использования в скрубберах. В этой работе проводятся исследования удельной поверхности и удельного объема адсорбента, устанавливается их линейная связь между собой, определяются в статических условиях в суспензионном состоянии адсорбента эффективности извлечения SO2 из раствора в течение нескольких часов при различном весовом соотношении Са(ОН)2/fly ash. Так, например, при экспозиции 16 часов при весовом соотношении 70/30 достигнуто извлечение SO2 0.375 г на 1 г сорбента. Для этого сорбента удельная поверхность пор составила 42.4 м2/г сорбента. В работе [5] рассматривается проблема применения летучей золы в качестве сорбента для очистки загрязненных вод. Изучается извлечение Zn(II) на два сорбента из летучей золы fly ash (FAI) из водного раствора. Рассматриваются кинетические модели, термодинамика процесса, различные модели изотерм адсорбции (Ленгмюра, Фрейндлиха, Темкина) в аспекте применимости к изучаемым процессам. Показано, для исследуемых образцов сорбента по Zn(II) теплота сорбции изменяется от 0.86 до 3.35 кДж/моль, что представляет собой по сравнению с теплотой испарения–конденсации воды порядка 2500 кДж/кг незначительную величину, которой можно пренебречь в условиях парогазового потока.
В [2] обсуждается вопрос очистки дымовых газов тепловых электростанций, работающих на ископаемом топливе и вырабатывающих более 85% энергии для производственных и бытовых нужд населения планеты, от диоксида углерода СО2, являющимся основным источником парниковых газов. Показано в результате анализа большого количества литературных данных, что использование различных адсорбентов на основе алюмосиликатов может быть весьма высокоэффективным по его извлечению из парогазового потока, выбрасываемого в атмосферу. Так, для одного из образцов такого типа адсорбентов извлечение CO2 в зависимости от температуры (80–0°С) достигается соответственно пределах 58.1–140.8 мг CO2/г адсорбента. В работе приведены результаты экспериментального исследования различных образцов летучей золы на основе алюмосиликатов (fly ash based alumino-silicates) при продувке адсорбента, помещенного в трубку, 15% CO2, сбалансированного азотом N2, при температурах от 30 до 75°С. Получена эффективность извлечения CO2 от 10.8 до 34.82 мг CO2/г адсорбента. При этом последняя величина получена при 3% водяных паров. Время продувки адсорбента в трубке составляла до 20 мин. Кроме этого, в этой работе сняты для различных образцов адсорбента изотермы N2, одной из которых мы воспользуемся в настоящей работе.
В статье [6] рассматривается возможность извлечения CO2 из высокотемпературных (400–750°С) газовых выбросов тепловых станций и промышленных предприятий с помощью сухих адсорбентов, вводимых в поток, что невозможно осуществить при мокрой газоочистке. При таких высоких температурах эффективность извлечения CO2 достигнута порядка 12.5%. Рассмотрены вопросы регенерации сорбента. Развитие вопросов, затронутых в этой работе, в плоскости применения может быть перспективно осуществлено в направлении разработки технологий газоочистки при сжигании твердых бытовых отходов.
Работа [7] посвящена исследование извлечения NOx дымовых газов на адсорбент из частиц летучей золы. Представлены функции распределения по размерам частиц золы. Показано, что извлечение NOx на такой сорбент при продувке в трубке достигается более 20 мг на 1 г сорбента за время экспозиции порядка 4 мин.
В [8] экспериментально изучались в специальном реакторе тенденции извлечения SO2, NO с водяным паром в смеси из дымовых газов на адсорбент, приготовленный из угольной летучей золы, оксида кальция и сульфата кальция, и влияние на эти тенденции их концентраций в смеси.
В [9, 10] формулируется идея сухой очистки дымовых газов от SO2 с помощью прямого инжектирования диспергированного адсорбента в газовый поток и обсуждаются преимущества такого способа в сравнение с мокрыми методами. В [9] приводятся результаты экспериментального исследования извлечения SO2 на адсорбент, представляющий собой смесь гашеной извести Са(ОН)2 с летучей угольной золой в весовом соотношении 1/3. Опыты осуществлялись в специальном реакторе – адсорбере. Условия их проведения и приготовления адсорбента и имитатора дымовых газов приводятся в предшествующих работах авторов [11–15]. Дополнительные сведения, относящиеся к теме исследования, приводятся в работах [16–18].
В [9] построена математическая модель, состоящая из двух нестационарных дифференциальных балансовых уравнений для газовой и твердой фазы, экспериментально найдены соотношения для источниковых членов для условий проведения опытов, получено удовлетворительное согласование с экспериментальными данными. Проводится анализ влияния влажности потока и его температуры на эффективность извлечения SO2 на данной адсорбент. Показано, что эффективность извлечения SO2 обеспечивается достаточно высокой 90–80% за период времени реакции в адсорбере до 5–10 мин соответственно. Из экспериментальных и теоретических зависимостей видно, что с увеличением температуры и влажности процесс адсорбции ухудшается, в то время как из других экспериментальных работ наблюдается как совпадающая, так и противоположная тенденция [2]. Это обстоятельство указывает на необходимость более тщательного системного как экспериментального, так и теоретического изучения этого вопроса.
В [10] обсуждается циклическая технология извлечения СO2 на адсорбент, приготовляемый на основе СаО. Сообщается, что даже при очень высоких температурах до 920°С извлечение СO2 достигается равным 0.23 г (СO2)/г (СаО) после 30 циклов прогонки газа через адсорбент.
Из анализа рассмотренных работ следует: 1) При определенных условиях взаимодействия кальцийсодержащих сухих адсорбентов с SO2, CO2 последние могут извлекаться из парогазовых потоков достаточно эффективно и обеспечивать очистку дымовых газов от этих компонентов до санитарных норм выбросов в атмосферу. 2) Однако заявленный способ введения диспергированного адсорбента непосредственно в очищаемой газовый поток с помощью инжектирования в динамике никаким образом не рассматривался и не изучался. Это не дает возможности оценить термодинамические и конструктивные параметры реализации такого способа с тем, чтобы иметь все необходимые обоснования для разработки технологии этого способа сухой адсорбционной газоочистки.
Настоящая работа посвящена рассмотрению этой проблемы с помощью математического моделирования процесса абсорбции газовых компонентов, извлекаемых на сухой диспергированный адсорбент, инжектируемый непосредственно в парогазовой поток.
ПОСТАНОВКА ЗАДАЧИ. ДОПУЩЕНИЯ
Сформулируем систему дифференциальных уравнений, описывающих тепломассообмен частиц адсорбента с парогазовым потоком в цилиндрической трубе или в диффузоре трубы Вентури (ТВ). Будем считать, что размер частиц δр в процессе их движения с потоком остается постоянным. При этом отвлечемся от полидисперсности адсорбента и примем его монодисперсным с размерами частиц, равными масс-медианному размеру полидисперсного распределения. На входе в трубу или диффузор ТВ поток подаётся со следующим начальными параметрами: температурой парогазового потока – Т00, К; температурой частиц – Тр0, К; скоростью парогазового потока – U0, м/с; расходной массовой концентрацией частиц – μ0, кг/кг; влагосодержанием – dw0, кг (вод. пара)/кг (сух. части потока); газосодержанием целевого компонента (SO2, CO2) – di0, кг (SO2, CO2)/кг (сух. части потока). Запишем уравнения сохранения в общем виде в стационарной одномерной постановке, что является достаточно обоснованным для пневмотранспортных условий движения пылегазового потока в трубах [19].
Уравнение движения частицы адсорбента переменной массы за счёт поглощения ей целевого компонента в пренебрежении силы тяжести в сравнении с инерционными силами
(1)
$\begin{gathered} {{V}_{p}}\frac{{{\text{d}}{{V}_{p}}}}{{{\text{d}}x}} = {{R}_{с}} - \frac{{V_{p}^{2}}}{{{{m}_{p}}}}\frac{{{\text{d}}{{m}_{p}}}}{{{\text{d}}x}}, \\ {{V}_{p}} = {{V}_{{p0}}}\,\,{\text{при}}\,\,х = 0, \\ \end{gathered} $(2)
${{R}_{с}} = - \tilde {\xi }\frac{{{{V}_{p}} - U}}{{{{\tau }_{p}}}},\,\,\,\,{{\tau }_{p}} = \frac{{\rho _{p}^{'}\delta _{p}^{2}}}{{18\eta }},$(3)
$\begin{gathered} \tilde {\xi } = 1 + 0.197\operatorname{Re} _{p}^{{0.63}} + 2.6 \times {{10}^{{ - 4}}}\operatorname{Re} _{p}^{{1.38}}, \\ {{\operatorname{Re} }_{p}} \leqslant {{10}^{5}}, \\ \end{gathered} $Rep – число Рейнольдса обтекания частицы:
(4)
${{\operatorname{Re} }_{p}} = \frac{{\left| {{{V}_{p}} - U} \right|{{\delta }_{p}}\rho }}{\eta },$ρ, η, U – плотность, динамическая вязкость, продольная скорость парогазового потока; ${{m}_{p}} = \frac{{\pi \delta _{p}^{3}}}{6}\rho _{p}^{'}$ – текущая масса частицы, $\rho _{p}^{'}$ – текущая (с учетом сорбирования частицей целевого компонента и конденсации водяных паров) плотность частицы.
Плотность ρ парогазового потока является суммой парциальных плотностей его компонентов ρi – нереагирующего компонента, целевого и водяных паров:
Парциальные плотности ρi будем определять из уравнений состояний для идеальных газов:
где Рi и Mi – парциальные давления и молекулярные массы i-х компонентов; R = 8.314 × × 103 Дж/(кмоль К) – универсальная газовая постоянная, Т – температура потока, К.В соответствии с законом Дальтона
где В – барометрическое давление.В свою очередь, изменение массы частицы адсорбента является суммой изменений ее массы за счет поглощения отдельных i-х компонентов, включая водяной пар:
(8)
$\frac{{{\text{d}}{{m}_{p}}}}{{{\text{d}}\tau }} = \sum {\frac{{{\text{d}}{{m}_{{pi}}}}}{{{\text{d}}\tau }}} {{n}_{p}}.$Для каждого i-го компонента запишем уравнение неразрывности (сохранения массы) в полном виде:
(9)
$\frac{{\partial {{\rho }_{i}}}}{{\partial \tau }} + {\text{div}}\left( {{{\rho }_{i}}\overrightarrow U } \right) = - \frac{{{\text{d}}{{m}_{{pi}}}}}{{{\text{d}}\tau }}{{n}_{p}},$В стационарной одномерной постановке уравнение (9) примет следующий вид:
(10)
$\begin{gathered} \frac{{{\text{d}}\left( {{{\rho }_{i}}U} \right)}}{{{\text{d}}x}} = - {{V}_{p}}\frac{{{\text{d}}{{m}_{{pi}}}}}{{{\text{d}}x}}{{n}_{p}}, \\ {{\rho }_{i}} = {{\rho }_{{i0}}},\,\,\,\,U = {{U}_{0}}\,\,\,\,{\text{при}}\,\,\,\,x = 0; \\ \end{gathered} $(11)
${{n}_{p}} = \frac{{{{M}_{p}}}}{{\frac{{\pi \delta _{p}^{3}}}{6}\rho _{m}^{'}{{V}_{p}}{{S}_{x}}}},$Для цилиндрического канала Sx = S0, для диффузора ТВ
(12)
${{S}_{x}} = \frac{{\pi D_{x}^{2}}}{4},\,\,\,\,{{D}_{x}} = {{D}_{0}} + 2x{\text{tg}}\frac{\alpha }{2},$Скорость парогазового потока будем вычислять по скорости нейтрального компонента (например, сухого воздуха):
(13)
$U = {{U}_{0}}\frac{{{{\rho }_{{g0}}}}}{{{{\rho }_{g}}}}{{\left( {\frac{{{{D}_{0}}}}{{{{D}_{x}}}}} \right)}^{2}},$Для нейтрального компонента уравнение неразрывности имеет вид в одномерной стационарной постановке:
(15)
$\frac{{{\text{d}}\left( {{{\rho }_{g}}U} \right)}}{{{\text{d}}x}} = 0,\,\,\,\,{{\rho }_{g}} = {{\rho }_{{g0}}},\,\,\,\,U = {{U}_{0}}\,\,\,\,{\text{при}}\,\,\,\,х = 0.$Уравнение массообмена частицы с i-м реагирующим компонентом запишем в виде
(16)
$\frac{{{\text{d}}{{m}_{{pi}}}}}{{{\text{d}}\tau }} = - {{\beta }_{i}}\pi \delta _{p}^{2}\left( {{{\rho }_{{wi}}} - {{\rho }_{i}}} \right),$или в стационарной одномерной постановке
(17)
$\begin{gathered} {{V}_{p}}\frac{{{\text{d}}{{m}_{{pi}}}}}{{{\text{d}}x}} = - {{\beta }_{i}}\pi \delta _{p}^{2}\left( {{{\rho }_{{wi}}} - {{\rho }_{i}}} \right),\,\,\,{{m}_{{pi}}} = {{m}_{{p0}}}, \\ {{V}_{p}} = {{V}_{{p0}}}\,\,{\text{при}}\,\,х = 0;\,\,\,{{m}_{{p0}}} = \frac{{\pi \delta _{{p0}}^{3}}}{6}{{\rho }_{m}}\left( {1 - \varepsilon } \right), \\ {{\delta }_{p}} = {{\delta }_{{p0}}} = {\text{const}}. \\ \end{gathered} $В (17) βi – коэффициент массоотдачи, м/с.
При этом парциальное давление у поверхности частицы ρwi определяется по температуре насыщения, равной температуре частицы Тр:
где Pwi – парциальное давление у поверхности частицы, Тр – температура адсорбента. Pwi будем вычислять по экспериментальной изотерме Ленгмюра для адсорбата на конкретный адсорбент: где k и b – константы, определяются по опытным данным аппроксимацией изотермы вида (19); gi – концентрация адсорбата в адсорбенте (опытные данные), кг/кг. В последующем для азота N2 примем Рsi = 770 мм рт. ст. = 104720 Па.Для изучения структуры частиц адсорбента – удельной поверхности пор, их удельного объёма, приходящихся на 1 г адсорбента – определяют изотерму адсорбции N2 как нейтрального (нереагирующего) компонента. Такие изотермы в выше цитируемых работах для ряда адсорбентов приведены. Непосредственно для SO2 и CO2 таких изотерм при изучении адсорбции этих компонентов в этих работах не представлено. Поэтому в дальнейшем будем исходить из линейной закономерности поведения изотермы адсорбции N2 на конкретный адсорбент при невысоких концентрациях адсорбата, поименованный как FAS-AMP-30 – летучая зола на основе алюмосиликатов (fly ash based alumino-silicates) со следующим процентным элементным содержанием: SiО2 – 62.27; Al2O3 – 30.96; Fe2O3 – 1.25; TiO2 – 1.67; CaO – 3.02; Na2O – 0.12; K2O – 0.41; LOI – 0.29. Эту изотерму представим в виде табличных данных (табл. 1 [2]).
Таблица 1.
Изотерма N2 на FAS-AMP-30 [2]
| ${{{{P}_{{w,{{{\text{N}}}_{2}}}}}} \mathord{\left/ {\vphantom {{{{P}_{{w,{{{\text{N}}}_{2}}}}}} {{{P}_{{s,{{{\text{N}}}_{2}}}}}}}} \right. \kern-0em} {{{P}_{{s,{{{\text{N}}}_{2}}}}}}}$ | g, г(N2)/г(сорбента) |
|---|---|
| 0.1 | 0.020 |
| 0.2 | 0.025 |
| 0.3 | 0.03 |
| 0.5 | 0.036 |
| 0.6 | 0.039 |
| 0.7 | 0.043 |
| 0.8 | 0.052 |
| 0.9 | 0.07 |
Используя изотерму для N2 оценим работоспособность модели и сделаем оценочные расчеты адсорбции CO2 на FAS-AMP-30 с использованием коэффициентов фазового равновесия, установленных в [1].
Для паров воды на границе раздела фаз будем использовать известную аппроксимацию [20]:
(20)
${{P}_{w}} = {{P}_{{{\text{кр}}}}}\exp \left[ {{{A}_{1}}\ln \left( {\frac{{{{T}_{p}}}}{{{{T}_{{{\text{кр}}}}}}}} \right) + {{A}_{2}}{{f}_{2}}} \right],$Порозность частиц определим через экспериментальные данные для конкретного адсорбента:
(21)
$\varepsilon = \frac{{{{{10}}^{{ - 3}}}{{\upsilon }_{1}}{{\rho }_{m}}}}{{1 + {{{10}}^{{ - 3}}}{{\upsilon }_{1}}{{\rho }_{m}}}},$В (2)
где mр – вычисляется из уравнений массообмена при условии (8).В (16) βi будем рассчитывать по тем же формулам для сферических частиц, полагая что процесс массообмена между частицей адсорбента и потоком в основном лимитируется эмпирической изотермой Ленгмюра при определении Рwi:
(23)
${{\beta }_{i}}\,\,{\text{ = }}\,\,{\text{N}}{{{\text{u}}}_{i}}\frac{{{{D}_{i}}}}{{{{\delta }_{p}}}},\,\,\,{\text{N}}{{{\text{u}}}_{i}} = 2\left( {1 + 0.276\operatorname{Re} _{p}^{{0.5}}{\text{Sc}}_{i}^{{0.33}}} \right){{K}_{c}},$(24)
${{K}_{c}} = \frac{{{{P}_{{wi}}} + {{P}_{i}}}}{{2B}},\,\,\,\,{\text{S}}{{{\text{c}}}_{i}} = \frac{\eta }{{\rho {{D}_{i}}}},$(25)
$\begin{gathered} {{D}_{i}} = {{D}_{{i0}}}\frac{B}{{{{B}_{0}}}}{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}^{{1.75}}},\,\,\,{{В}_{0}} = 0.{\text{1}}\,\,{\text{МПа}}, \\ {{Т}_{0}} = {\text{273}}\,\,{\text{К}}\,\,\left[ {{\text{21}}} \right]. \\ \end{gathered} $В (23) Kс – поправка на стефановский поток.
Для азота (N2) Di0 = 13.2 × 10–6 м2/с; для паров воды (Н2О) Di0 = 22.0 × 10–6 м2/с при диффузии этих компонентов в воздухе.
Уравнение теплообмена парогазового потока с частицами адсорбента (для определения температуры парогазового потока) запишем в виде
(26)
$\rho U\frac{{{\text{d}}\left[ {c\left( {T - {{T}_{0}}} \right)} \right]}}{{{\text{d}}x}} = {{\alpha }_{p}}\pi \delta _{p}^{2}\left( {{{T}_{p}} - T} \right){{n}_{p}},$сi – теплоемкость i-х газовых компонентов, кДж/(кг К).
Коэффициент теплоотдачи будем аналогично рассчитывать как и для сферических частиц по формуле Дрейка:
(28)
$\begin{gathered} {\text{N}}{{{\text{u}}}_{p}} = \frac{{{{\alpha }_{p}}{{\delta }_{p}}}}{\lambda } = \\ = \,\,2 + 0.459\operatorname{Re} _{p}^{{0.55}}{{\Pr }^{{0.33}}},\,\,\,\,\Pr = \frac{{\eta c}}{\lambda }, \\ \end{gathered} $Приближенно для мелких частиц адсорбента можно принять
а также Sci = Pr ≈ 1. Коэффициенты η и λ будем вычислять как для воздуха.
Для определения температуры частиц адсорбента запишем уравнение их теплообмена с парогазовым потоком:
(30)
$\begin{gathered} {{V}_{p}}\frac{{{\text{d}}\left( {{{c}_{m}}{{m}_{p}}{{T}_{p}}} \right)}}{{{\text{d}}x}} = - {{\alpha }_{p}}\pi \delta _{p}^{2}\left( {{{T}_{p}} - T} \right) + \sum {{{r}_{i}}\frac{{{\text{d}}{{m}_{{pi}}}}}{{{\text{d}}x}}{{V}_{p}}} , \\ {{T}_{p}} = {{T}_{{p0}}}\,\,\,\,{\text{при}}\,\,\,\,x = 0, \\ \end{gathered} $Для алюмосиликата FAS-AMP-30 по справочным данным для расчетов примем ρm = 3000 кг/м3, сm = 785 Дж/(кг К). Для азота N2сi = 1.0 кДж/(кг К) (как для воздуха).
Эффективность извлечения целевого газового компонента будем вычислять по формуле
где l – длина цилиндрической трубы или диффузора ТВ.РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ
Расчеты будем проводить в условиях снятия изотермы N2 на адсорбент FAS-AMP-30: Тр0 = 293 К, Т00 = 328 К, δр = 50 мкм, ρi0(N2) = 0.15 кг (N2)/кг сух. возд., ρi0(Н2О) = 0.03 кг (Н2О)/кг сух. возд. Молекулярные массы компонентов: Мвозд. = 29 кг/кмоль, ${{M}_{{{{{\text{H}}}_{2}}{\text{O}}}}} = 18$ кг/кмоль, ${{M}_{{{{{\text{N}}}_{2}}}}} = 28$ кг/кмоль, υ1 = = 0.2070041 см3/г, Sуд = 91.3743 м2/г [2], для этих условий примем ε = 0.383 (почти как для плотной упаковки шаров).
При аппроксимации изотермы N2 на адсорбент FAS-AMP-30, как покажут последующие расчеты, концентрация адсорбируемого N2 в адсорбенте составляет менее 0.01 кг (N2)/кг адс. Это обстоятельство позволяет изотерму (19) в области малых концентраций аппроксимировать линейной зависимостью в виде закона Генри:
где k ≈ 13.53 в соответствие с табл. 1 довольно в широком диапазоне концентраций gwg до 0.1 [1].Расчеты проводились методом Рунге–Кутты с точностью 10–6.
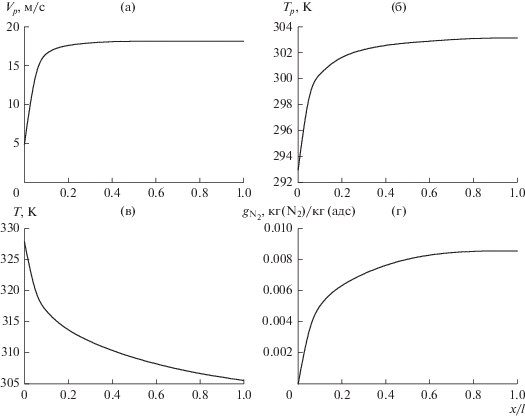
На рис. 1 представлены результаты расчета параметров частиц адсорбента и парогазового потока вдоль цилиндрической трубы длиной l = 1 м, диаметром D = 0.04 м при μ0 = 0.5 кг/кг парогазового потока при выше приведенных параметрах и U0 = 20 м/с, Vp0 = 4 м/с. Эффективность извлечения N2 оказалась равной ${{\eta }_{{{{{\text{N}}}_{2}}}}} = 3.16\% .$
Рис. 1.
Результаты расчета адсорбции N2 на адсорбент FAS-AMP-30 в круглой трубе (параметры расчета в тексте статьи), ${{\eta }_{{{{{\text{N}}}_{2}}}}} = 3.16\% .$
Аналогичный расчет проведен для адсорбции N2 на капли диспергированной воды тех же размеров в соответственных первому расчету условиях на основе данных по коэффициентам фазового равновесия N2 на воду [21] с использованием модели авторов [22]. Получена эффективность η = 6.4 × 10–4%, ничтожно малая величина, как и должно быть, иначе бы весь азот вымыло дождями из воздуха атмосферы.
Если сопоставить коэффициент фазового равновесия Генри для N2 и Н2О с соответствующим коэффициентом для N2 и FAS-AMP-30, то первый будет в 104 раз большим второго.
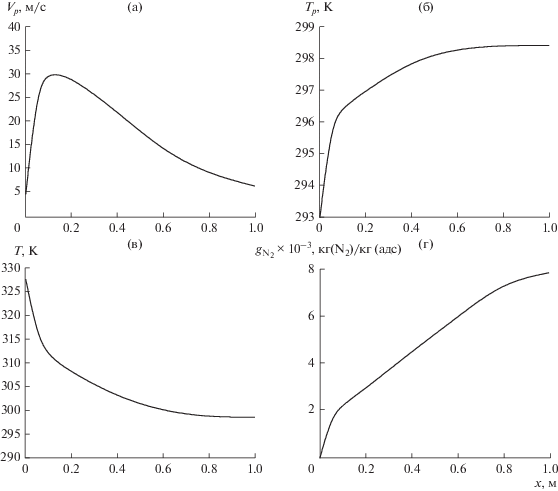
На рис. 2 приведены результаты расчета параметров частиц адсорбента и парогазового потока вдоль диффузора ТВ длиной l = 0.4 м, диаметром горловины D0 = 0.02 м, углом расширения α = 6° при μ0 = 2 кг адс./кг парогазового потока, скорости в горловине ТВ U0 = 60 м/с, δ = 50 мкм, Vp0 = = 4 м/с, Тр0 = 293 К, Т00 = 328 К, dw0 = 0.03, dw2 = 0.15. На длине l = 0.4 м достигнута эффективность η = = 12.2%. Как видно из рисунка, процесс адсорбции N2 далеко не завершается на заданной длине диффузора l = 0.4 м.
Рис. 2.
Результаты расчета адсорбции N2 на адсорбент FAS-AMP-30 в трубе Вентури (параметры расчета в тексте статьи), $\eta = 12.2\% .$
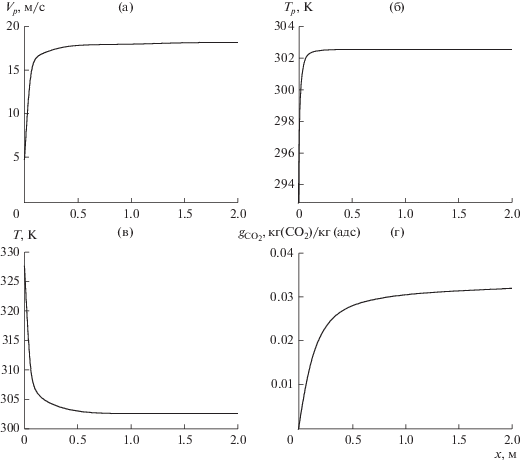
На рис. 3 приведены результаты расчета адсорбции CO2 в круглой трубе диаметром 0.04 м при параметрах: μ0 = 2 кг (адс.)/кг (парогазового потока); δр = 50 мкм; Vp0 = 4 м/с; U0 = 20 м/с; Т00 = = 328 К (55°С); Тр0 = 293 К (20°С). Коэффициенты фазовых равновесий для СО2 на данный адсорбент в зависимости от температуры были установлены в работе [1] и использованы в настоящем расчете. Так, коэффициент Генри (отнесенный к массовой концентрации) ${{m}_{{pc,{\text{C}}{{{\text{O}}}_{2}}}}} = 0.5 \times {{10}^{6}}$ Па для температуры парогазовой смеси 55°С. Парциальные плотности компонентов парогазовой смеси задавались следующими (так же как и в работе [1]): ${{\rho }_{{{\text{С}}{{{\text{О}}}_{2}},0}}} = 0.2445$ кг/м3, ${{\rho }_{{{{{\text{H}}}_{2}}{\text{O,0}}}}} = 0.02$ кг/м3, ${{\rho }_{{{{{\text{N}}}_{2}}{\text{,0}}}}} = 0.82$ кг/м3. Так что плотность смеси на входе была равной ${{\rho }_{{\text{0}}}} = 1.0845$ кг/м3. Из рис. 3 видно, что полное насыщение адсорбента при данных условиях достигается на длине трубы 2 м и соответствует концентрации 0.03 г (CO2)/г (адс.). При этом эффективность извлечения СO2 из потока парогазовой смеси обеспечивается предельной и равной ${{\eta }_{{{\text{С}}{{{\text{О}}}_{2}}}}} = 25\% .$ При l = 0.4 м ${{\eta }_{{{\text{С}}{{{\text{О}}}_{2}}}}} = 20.6\% ,$ при l = 0.8 м ${{\eta }_{{{\text{С}}{{{\text{О}}}_{2}}}}} = 23.8\% ,$ при l = = 1.5 м ${{\eta }_{{{\text{С}}{{{\text{О}}}_{2}}}}} = 24.9\% .$
Рис. 3.
Результаты расчета адсорбции CO2 в круглой трубе: (а) – скорость частиц адсорбента; (б) – температура частиц адсорбента; (в) – температура парогазового потока; (г) – концентрация CO2 в адсорбенте.
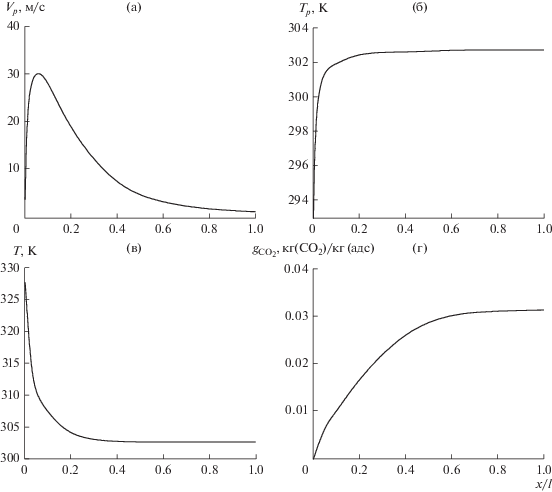
Аналогичные расчеты при тех же параметрах проведены для модельной трубы Вентури (ТВ) с диаметром горловины dг = 0.02 м и углом расширения диффузора α = 6°, результаты представлены на рис. 4. Начальная скорость парогазового потока в горловине ТВ задавалась равной U0 = 60 м/с, начальная скорость частицы адсорбента Vp0 = 4 м/с. Как видно из рис. 4, полное насыщение адсорбента компонентом CO2 достигается на длине 0.8 м и соответствует той же предельной концентрации CO2 в адсорбенте 0.03 кг (CO2)/кг (адс.) при эффективности извлечения CO2 из парогазовой смеси равной 27%. На длине диффузора l = 0.4 м ${{\eta }_{{{\text{С}}{{{\text{О}}}_{2}}}}} = 23\% .$ Из результатов расчета следует, что полное завершение процесса адсорбции в ТВ при данных условиях происходит на длине x/dг = 40 и значительно превышает рекомендуемую в [21] x/dг = 10–15.
Рис. 4.
Результаты расчета адсорбции CO2 в трубе Вентури (обозначения параметров те же, что и на рис. 3).
Следует отметить, что в круглой трубе эффективность ${{\eta }_{{{\text{С}}{{{\text{О}}}_{2}}}}}$ получена равной 25% при концентрации адсорбента на входе μ0 = 2, при меньших μ0 эффективность будет пропорционально меньшей. Величина μ0 = 2 практически соответствует условиям взвешенного трубопроводного пневмотранспорта, требующим скоростей движения в трубе не менее 20 м/с с тем, чтобы не происходило завала адсорбента и его выпадения на дно трубопровода при горизонтальном его расположении. Процесс адсорбции можно осуществлять во взвешенном кипящем слое адсорбента более эффективно. Для расчета такого процесса надо в уравнение (1) добавить правую часть силу тяжести и учесть специфические закономерности динамики такого слоя, такие как эффекты влияния высокой концентрации частиц адсорбента на гидравлическое сопротивление и тепломассообмен в потоке. Это должно представлять собой предмет самостоятельного исследования.
Расчёты, проведенные при Nui = Nup = 2 во всех случаях дали практически те же результаты, что и с использованием формул (23) и (28).
Проведены расчеты адсорбирования N2 в ТВ по параметрам рис. 2 при Т00 = 373 К (100°С) и тех же остальных параметрах и том же коэффициенте фазового равновесия. Получена эффективность чуть меньшая – η = 11.7%. Однако здесь не учтена за неимением экспериментальной информации зависимость коэффициента фазового равновесия от температуры, что должно быть предметом специальных исследований. Расчеты при повышенном влагосодержании ρid(H2O) = 0.13 кг/м3 вместо 0.03 и всех остальных тех же параметрах рис. 2 дали эффективность извлечения N2 на адсорбент η = 15.1%. Обе тенденции противоположны экспериментальным данным [9]. Однако из работы [2] следует, что присутствие водяного пара в потоке повышает эффективность адсорбирования.
ЗАКЛЮЧЕНИЕ
Сформулирована физико-математическая модель процесса адсорбции газовых компонентов на сухой диспергированный адсорбент, инжектируемый непосредственно в очищаемой парогазовой поток. Результаты расчетов показали, что на алюмосиликатный адсорбент на основе летучей золы в смеси с гашеной известью может быть достигнута эффективность очистки дымовых газов от CO2 при его введении в поток в диспергированном состоянии до 30% при размере частиц адсорбента менее 50 мкм на пути движения такого потока в круглой трубе до 2 м. В трубе Вентури эффективность может быть достигнута более высокой и на меньших длинах диффузора. Математическая модель позволяет рассчитать оптимальные параметры процесса адсорбции как в круглой трубе, так и в ТВ и их габариты при максимально возможной эффективности извлечения целевого компонента из потока.
Определение коэффициентов фазового равновесия для конкретных пар адсорбент–адсорбат в зависимости от температуры может быть осуществлен экспериментально с использованием предложенной модели в рамках решения обратной задачи [23].
ОБОЗНАЧЕНИЯ
| В | барометрическое давление, Па |
| сi | теплоемкость i-х газовых компонентов, кДж/(кг К) |
| сm | удельная теплоемкость частицы адсорбента с поглощенными его газовыми компонентами и парами воды, кДж/(кг К) |
| D0 | диаметр горловины ТВ, м |
| Dx | текущий диаметр диффузора ТВ, м |
| di0 | газосодержание целевого компонента (SO2, CO2), кг (SO2, CO2)/кг (сух. части потока) |
| dw0 | влагосодержание, кг (вод. пара)/кг (сух. части потока) |
| G0 | массовый расход парогазового потока на входе, кг/с |
| gi | концентрация адсорбата в адсорбенте, кг/кг |
| l | длина цилиндрической трубы или диффузора ТВ |
| Mi | молекулярные массы i-х компонентов, кг/кмоль |
| Мр | массовый расход адсорбента, кг/с |
| mp | текущая масса частицы, кг |
| ${{m}_{{pc,{\text{C}}{{{\text{O}}}_{2}}}}}$ | коэффициент фазового равновесия Генри СО2, отнесенный к массовой концентрации в адсорбенте, Па |
| np | счетная концентрация частиц адсорбента в потоке при их движении |
| Рi | парциальные давления i-х компонентов, Па |
| Pwi | парциальное давление у поверхности частицы, Па |
| Rс | сила аэродинамического сопротивления частицы адсорбента, приходящаяся на единицу ее массы, м/с2 |
| R | универсальная газовая постоянная, Дж/(кмоль К) |
| ri | удельные теплоты фазовых переходов – испарения–конденсации воды, адсорбции–десорбции газовых компонентов, кДж/кг |
| S0 | начальная площадь поперечного сечения канала (цилиндрической трубы, горловины ТВ), м2 |
| Sx | площадь текущего сечения канала, м2 |
| Т | текущая температура потока, К |
| Т00 | начальная температура парогазового потока, К |
| Тр | текущая температура адсорбента, К |
| Тр0 | начальная температура частиц, К |
| U | текущая продольная скорость парогазового потока, м/с |
| U0 | начальная скорость парогазового потока, м/с |
| Vр | скорость движения частицы в направлении продольной координаты, м/с |
| Vр0 | начальная скорость частицы, м/с |
| α | угол расширения диффузора, град |
| βi | коэффициент массоотдачи, м/с |
| δр | размер частиц, м |
| ε | порозность адсорбента |
| η | динамическая вязкость парогазового потока, Па с |
| λ | коэффициент теплопроводности парогазового потока, Вт/(м К) |
| μ0 | расходная массовая концентрация частиц, кг/кг |
| $\rho _{m}^{'}$ | плотность адсорбента с учетом пористости, кг/м3 |
| $\rho _{p}^{'}$ | текущая (с учетом сорбирования частицей целевого компонента и конденсации водяных паров) плотность частицы, кг/м3 |
| ρ | плотность парогазового потока, кг/м3 |
| ρ0 | начальная плотность парогазового потока, кг/м3 |
| ρg0 | парциальная плотность нейтрального компонента на входе, кг/м3 |
| ρm | истинная плотность адсорбента, кг/м3 |
| ρwi | парциальное давление i-го компонента у поверхности частицы, кг/м3 |
| $\tilde {\xi }$ | относительный коэффициент аэродинамического сопротивления частицы адсорбента |
| τ | время, с |
| υ1 | удельный объем пор в частицах адсорбента, см3/г |
| Rep | число Рейнольдса обтекания частицы |
Список литературы
Шиляев М.И., Хромова Е.М. Моделирование процесса адсорбции CO2 из дымовых газов ТЭС в насадочной колонне // Материалы XVIII Международной научной конференции “Качество внутреннего воздуха и окружающей среды”. М., 2020. С. 13.
Kumar V., Labhsetwar N., Meshram S., Rayalu S. Functionalized fly ash based alumino-silicates for capture of carbon dioxide // Energy Fuels. 2011. V. 25. P. 4854.
Rashidi N.A., Yusup S. An overview on the potential of coal-based bottom ash as low-cost adsorbents // ACS Sustainable Chem. Eng. 2016. https://doi.org/10.1021/acsuschemeng.5b01437
Lin R.-B., Shih S.-M., Liu C.-F. Structural properties and reactivities of Ca(OH)2/Fly Ash Sorbents for flue gas desulfurization // Ind. Eng. Chem. Res. 2003. V. 42. P. 1350.
Adamczuk A., Kolodynska D. Utilization of fly ashes from the coal burding processes to produce effective low-cost sorbents // Energy Fuels. 2017. https://doi.org/10.1021/acs.energyfuels.6b02921
Sanna A., Maroto-Valer M. CO2 capture at high temperature using fly ash-derived sodium silicates // Ind. Eng. Chem. Res. 2016. https://doi.org/10.1021/acs.iecr.5b047-80
Lu G.-Q., Do D.D. Adsorption properties of fly ash for NOx removal from flue gases // Fuel Process. Technol. 1991. V. 27. P. 95.
Tsuchial H., Ishizuka T., Nakamura H., Veno T., Hattori H. Removal of sulfur dioxide from flue gas by the absorbent prepared from coal ash: effects of nitrogen oxide and water vapor // Ind. Eng. Chem. Res. 1996. V. 35. P. 851.
Garea A., Viguri J.R., Irabien J.A. Desulfurization rate at low temperatures using calcium hydroxide and fly ash // Coal Sci. Technol. 1995. V. 24. P. 1863.
Feng Y., Jiang J., Li K., Tian S., Liu Z., Shi J., Chen X., Fei Z., Lu Y. Cyclic performance of waste-derived SiO2 stabilized, CaO-based sorbents for fast CO2 capture // ACS Sustainable Chem. Eng. 2016. https://doi.org/10.1021/acsuschemeng.6b01903
Garea A, Renedo M.J., Fernandez J., Ortiz M.I., Viguri J.R., Irabien J.A. Desulfurization yield of calcium hydroxide/fly-ash mixtures. Thermogravimetric determination // Thermochim. Acta. 1996. V. 286. № 1. P. 173.
Irabien A., Cortabitarte F., Viguri J., Ortiz L. Kinetic model for desulfurization at low temperatures using calcium hydroxide // Chem. Eng. Sci. 1990. V. 45. P. 3427.
Ortiz A., Garea A., Irabien F. Cortabitarte. Flue gas desulfurization at low temperatures. Characterization of the structural changes in the solid sorbent // Powder Technol. 1993. V. 75. № 2. P. 167.
Irabien A., Cortabitarte F., Ortiz M.I. Kinetics of flue gas desulfurization at low temperatures: nonideal surface adsorption model // Chem. Eng. Sci. 1992. V. 47. № 7. P. 1533.
Muzio L.J., Offien G.R. Assessment of Dry Sorbent Emission Control Technologies Part I. Fundamental Processes // J. Air Pollut. Control Assoc. 1987. V. 37. № 5. P. 642.
Klingspor J., Karlsson H., Bjerle I. A kinetic study of the dry SO2-limestone reaction at low temperature // Chemical Engineering Communications. 1983. V. 22. № 1-2. P. 81.
Peterson J.R., Rochelle G.T. Aqueous reaction of fly ash and calcium hydroxide to produce calcium silicate absorbent for flue gas desulfurization // Environ. Sci. Technol. 1988. V. 22. № 11. P. 1299.
Jorgensen C., Chang J.C.S., Brna T.G. Evaluation of sorbents and additives for dry SO2 removal // Environ. Prog. 1987. V. 6. № 2. P. 26.
Шваб В.А. Течение сжимаемой пылегазовой среды в трубах при некоторых тепловых и структурных режимах // Инж.-физ. журн. 1968. Т. 16. № 5. С. 826.
Богословский В.Н., Поз М.Я. Теплофизика аппаратов утилизации тепла систем отопления, вентиляции и кондиционирования воздуха. М.: Стройиздат, 1983.
Рамм В.М. Абсорбция газов. М.: Химия, 1976.
Shilyaev M.I., Khromova E.M. Modeling of heat and mass transfer and absorption-condensation dust and gas cleaning in jet scrubbers // Mass Transfer – Advances in Sustainable Energy and Environment Oriented Numerical Modeling. 2013. P. 163.
Шиляев М.И., Хромова Е.М., Богомолов А.Р., Широкова С.Н. Адаптация модели абсорбционной очистки газов в форсуночных скрубберах на хемосорбционные процессы // Изв. высш. учебн. завед. Строит. 2015. № 3. С. 52.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


