1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 55, № 5, 2021

Теоретические основы химической технологии, 2021, T. 55, № 5, стр. 559-566

Анализ процессов экстракционно-хроматографического разделения в каскаде смесительно-отстойных экстракторов

А. Е. Костанян a, *, Н. А. Милевский a, А. А. Вошкин a

a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия

* E-mail: kost@igic.ras.ru

Поступила в редакцию 21.05.2021
После доработки 26.05.2021
Принята к публикации 26.05.2021

Полный текст (PDF)

Аннотация

Проведен анализ процессов экстракционного разделения смеси компонентов в каскаде смесительно-отстойных экстракторов, работающих в режиме элюентной хроматографии, для условий, когда разделяемая смесь компонентов загружается в каскад в виде серии последовательных, разделенных короткими интервалами времени, импульсных вводов. Приведены аналитические зависимости, необходимые для моделирования периодических и непрерывных процессов разделения и примеры моделирования таких процессов. Показано, что использование серийного импульсного ввода раствора смеси компонентов позволяет более чем на порядок повысить как концентрацию в разделенных фракциях компонентов, так и производительность экстракционно-хроматографических процессов разделения.

Ключевые слова: выделение и очистка целевых компонентов из растворов, жидкостная экстракция, жидкость-жидкостная хроматография, каскад смесительно-отстойных экстракторов

ВВЕДЕНИЕ

В современных химико-технологических процессах экстракция широко используется как для выделения индивидуальных компонентов из смесей [1, 2], так и для очистки различных систем от примесных соединений [3]. Исследователи не только решают проблемы по повышению экологичности [4, 5] и удешевлению самих экстракционных систем [6, 7], но и разрабатывают более эффективное аппаратурное оформление и схемы проведения процессов разделения [8, 9].

Экстракционно-хроматографические процессы разделения и очистки веществ, разработанные в 1960-е годы [10], являются одними из самых перспективных с точки зрения повышения эффективности разделения веществ, в связи с чем получили широкое развитие. Эффективность работы хроматографических устройств, как и экстракционных аппаратов, определяется скоростью межфазного массообмена и степенью продольного перемешивания в обеих фазах. В отличие от промышленных процессов противоточной экстракции, в жидкость-жидкостной хроматографии процессы массопереноса не стационарны, и одна из фаз, называемая неподвижной, не выводится из хроматографической колонки. Она удерживается в колонке с помощью центробежных сил, возникающих при вращении барабана или пакета дисков с каскадом контактных камер, смонтированных на валу обычной центрифуги, или барабанов с намотанными спиральными колонками планетарной центрифуги [11–29]. Жидкость-жидкостная хроматография, получившая название жидкостная хроматография со свободной неподвижной фазой (ЖХСНФ) в отечественной литературе и противоточная или центробежная распределительная хроматография (centrifugal partition chromatography) в зарубежных публикациях, применяется главным образом в препаративных целях для выделения и очистки фармацевтических продуктов растительного происхождения [30]. Однако методы и аппаратура ЖХСНФ малопроизводительны, поскольку объемы известных аппаратов не превышают нескольких литров [31–33], и не могут быть использованы в промышленных целях, в частности в гидрометаллургии, где требуется переработка больших объемов технологических растворов. В то же время по сравнению с методами экстракции методы ЖХСНФ обладают рядом преимуществ: позволяют разделить большое число компонентов в одной технологической операции; обеспечивают получение продуктов высокой чистоты; более экологичны, поскольку используются относительно малые объемы органических растворителей; менее материало- и энергоемки, так как сокращается количество технологических операций и используемых реагентов [34–36].

В ИОНХ им. Н.С. Курнакова РАН разрабатываются комбинированные экстракционно-хроматографические процессы разделения, сочетающие преимущества обоих методов [37–39]. Важно отметить, что для реализации разрабатываемых процессов разделения используется широко применяемое в промышленности экстракционное оборудование: каскад многоступенчатых (секционированных) экстракционных колонн; каскад смесительно-отстойных экстракторов. В первом случае неподвижная, а точнее – непроточная, фаза экстрагента удерживается на перфорированных тарелках колонн благодаря силам вязкости и поверхностного натяжения. Удерживание фазы экстрагента в каскаде смесительно-отстойных экстракторов достигается путем ее полной рециркуляции между отстойником и смесителем в каждой ступени каскада. В обоих случаях, в отличие от противоточной экстракции, ступени каскада соединены только по потоку водной фазы. Возможны различные схемы и режимы проведения рассматриваемых процессов разделения. В настоящей работе для повышения производительности экстракционно-хроматографических процессов разделения в каскаде смесительно-отстойных экстракторов, работающих в режиме элюентной хроматографии, предлагается вместо широко распространенного в аналитике метода однократного впрыска пробы использовать серию последовательных, разделенных короткими интервалами времени, импульсных вводов разделяемой смеси компонентов. Как будет показано ниже, предлагаемый метод кроме повышения производительности позволяет получать высококонцентрированные фракции разделенных компонентов. Для практической реализации этих новых процессов разделения необходимо их теоретическое описание. Задачей настоящей работы является теоретический анализ экстракционно-хроматографических процессов разделения в каскаде смесительно-отстойных экстракторов при использовании серийного импульсного ввода раствора смеси компонентов в первую ступень каскада.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭКСТРАКЦИОННО-ХРОМАТОГРАФИЧЕСКИХ ПРОЦЕССОВ РАЗДЕЛЕНИЯ В КАСКАДЕ СМЕСИТЕЛЬНО-ОТСТОЙНЫХ ЭКСТРАКТОРОВ ПРИ СЕРИЙНОМ ИМПУЛЬСНОМ ВВОДЕ РАЗДЕЛЯЕМОЙ СМЕСИ

Как отмечалось выше, в каждой ступени каскада организован режим полной рециркуляции органической фазы между отстойником и смесителем, и ступени каскада соединены только по потоку водной фазы. Регулируя скорость рециркуляции, можно изменять соотношение фаз в смесителе и устанавливать, какая фаза будет дисперсной. Целесообразно устанавливать такую скорость рециркуляции органической фазы, чтобы доля объема, занимаемая этой фазой в смесителе (S), была в пределах 0.5 ≤ S ≤ 0.8. В таких условиях водная фаза будет дробиться в органической, что предпочтительно с точки зрения уноса непроточной органической фазы с потоком проточной водной фазы. Кроме того, при этом можно поддерживать минимальный объем водной фазы в отстойнике, что будет способствовать повышению эффективности экстракционно-хроматографических процессов разделения в каскаде. Экстракционно-хроматографическая установка снабжена автоматическим устройством для импульсного ввода заданных объемов раствора разделяемых компонентов через определенные интервалы времени в первую по ходу движения потока водной фазы ступень каскада экстракторов. Процесс проводится следующим образом. После установления стабильного гидродинамического режима в первую ступень каскада экстракторов в момент времени τ = 0 начинается серия импульсных вводов раствора компонентов. После завершения стадии загрузки раствора смеси происходит разделение компонентов смеси при ее движения через каскад, и из последней ступени выводятся фракции разделенных компонентов.

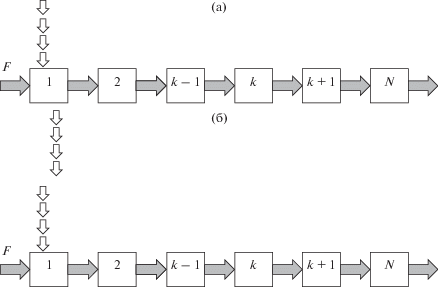
Рассмотрим два варианта организации процессов разделения: в периодическом и непрерывном режимах. Принимаем, что в каждой ступени каскада достигается равновесное распределение концентраций компонентов между двумя жидкими фазами, т.е. в каждой ступени достигается эффективность разделения, соответствующая одной теоретической ступени. На рис. 1 приведены схемы математических моделей для периодического и непрерывного вариантов организации процессов разделения.

Рис. 1.

Схемы математических моделей периодических (а) и непрерывных (б) экстракционно-хроматографических процессов разделения в каскаде смесительно-отстойных экстракторов.

Периодические процессы экстракционно-хроматографического разделения. На основании подходов, изложенных ранее [38], получено следующее уравнение, описывающее выходной профиль концентрации компонента с коэффициентом распределения KD после серийной загрузки, включающей n импульсных вводов раствора компонентов:

(1)
${{X}_{n}}\left( t \right) = \frac{{a\sqrt N }}{{\sqrt {2\pi } }}\sum\limits_{i = 1}^n {{{e}^{{ - {{{\left[ {1 + \left( {i - 1} \right)a{{t}_{{{\text{in}}}}} - at} \right]}}^{2}}N/2}}}} .~$

В уравнении (1) приняты следующие обозначения:

(2)
$a = \frac{1}{{1 - S + S{{K}_{D}}}};$

KD = y/x – коэффициент распределения, где x – концентрация в водной фазе, y – концентрация в органической фазе; N – число ступеней в каскаде; n – количество (номер) импульсных вводов смеси; S – доля объема, занимаемая в ступенях органической (непроточной) фазой; $X = {x \mathord{\left/ {\vphantom {x {\bar {x}}}} \right. \kern-0em} {\bar {x}}}$ – безразмерная концентрация; $\bar {x}$ = Q/Vс – средняя концентрация компонента в каскаде после загрузки одной порции раствора смеси (после одного импульсного ввода); Vс – общий объем каскада экстракционных ступеней; Q – количество компонента в одном загруженном объеме раствора компонентов; F – объемная скорость подачи в каскад водной фазы; $t = \frac{{\tau F}}{{{{V}_{c}}}}$ – безразмерное время; tin = τinF/Vc – безразмерный интервал времени между импульсными вводами в серийной загрузке раствора компонентов; τ – время.

Уравнение (1) описывает изменение во времени концентрации компонента с коэффициентом распределения KD на выходе из последней ступени N каскада при загрузке, состоящей из n импульсных вводов раствора компонентов в первую ступень каскада экстракторов в момент времени τ = 0.

Используя уравнение (1), рассмотрим несколько примеров периодических процессов разделения смесей компонентов при серийной загрузке разделяемой смеси. Для анализа и моделирования различных вариантов экстракционно-хроматографического разделения в каскаде смесительно-отстойных экстракторов удобно использовать стандартные расчетные программы. В настоящей работе использована программа Mathcad, в которой были записаны уравнения математических моделей и проведены численные исследования.

На рис. 2 приведены результаты численного моделирования процесса разделения двух четырехкомпонентных смесей: 1) KD1 = 0.5, KD2 = 1, KD3 = 1.75, KD4 = 2.75 и 2) KD1 = 1, KD2 = 2, KD3 = 3.5, KD4 = 5.5 в каскаде из ста ступеней (N = 100) при различных значениях параметра n: показаны рассчитанные по уравнению (1) профили концентраций компонентов после n импульсных вводов смесей.

Рис. 2.

Моделирование процесса разделения двух четырехкомпонентных смесей: (а) – KD1 = 0.5, KD2 = 1, KD3 = 1.75, KD4 = 2.75 и (б) – KD1 = 1, KD2 = 2, KD3 = 3.5, KD4 = 5.5 в каскаде из ста ступеней (N = 100) при различных значениях параметра n. Профили концентраций компонентов после n импульсных вводов смесей рассчитаны по уравнению (1).

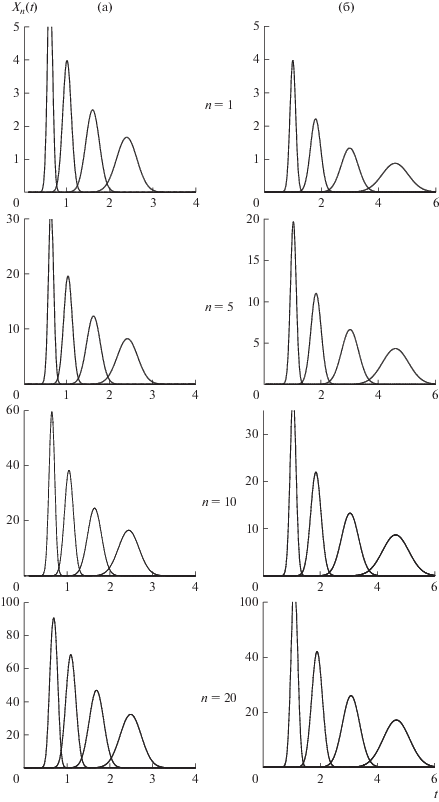
Как видно из рис. 2, с увеличением числа импульсных вводов раствора компонентов растет концентрация в разделенных фракциях компонентов; при увеличении n от 1 до 20 концентрация во фракциях компонентов увеличивается более чем на порядок. При этом качество разделения изменяется (ухудшается) незначительно. Кроме того, увеличение n от 1 до 20 соответствует двадцатикратному повышению производительности процесса разделения. Дальнейшего повышения производительности можно достичь при переходе от периодического к непрерывному режиму проведения процессов разделения.

Непрерывные процессы экстракционно-хроматографического разделения. Для моделирования непрерывных экстракционно-хроматографических процессов разделения с серийным импульсным вводом разделяемой смеси получено следующее уравнение:

(3)
${{X}_{n}}\left( t \right) = \frac{{a\sqrt N }}{{\sqrt {2\pi } }}\mathop \sum \limits_{j = 1}^m \mathop \sum \limits_{i = 1}^n {{e}^{{ - {{{\left[ {1 + \left( {i - 1} \right)a{{t}_{{in}}} + \left( {j - 1} \right)a{{t}_{{ins}}} - at} \right]}}^{2}}N/2}}},~~$
где m – число серийных загрузок; tins – безразмерный временной интервал между сериями загрузок.

Уравнение (3) описывает результирующий профиль концентрации компонента с коэффициентом распределения KD на выходе из последней ступени каскада после m серий загрузок раствора компонентов в установку. При этом каждая серия состоит из n импульсных вводов раствора компонентов.

Следует отметить, что для моделирования рассматриваемых непрерывных стационарных процессов достаточно иметь теоретическое описание выходных концентрационных профилей после двух последовательных серий загрузок. В этом случае уравнение (3) упрощается и приводится к следующему виду:

(4)
$\begin{gathered} {{X}_{n}}\left( t \right) = \frac{{a\sqrt N }}{{\sqrt {2\pi } }} \times \\ \times \,\,\mathop \sum \limits_{i = 1}^n \left[ {{{e}^{{ - {{{\left[ {1 + \left( {i - 1} \right)a{{t}_{{in}}} - at} \right]}}^{2}}{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}}}} + {{e}^{{ - {{{\left[ {1 + \left( {i - 1} \right)a{{t}_{{in}}} + a{{t}_{{ins}}} - at} \right]}}^{2}}{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}}}}} \right]. \\ \end{gathered} $

Уравнение (4) описывает два первых соседних профиля концентрации компонента с коэффициентом распределения KD, соответствующих первым двум последовательным сериям загрузок.

При использовании непрерывных стационарных процессов необходимо определить интервал между сериями загрузок исходного водного раствора компонентов (tins). Для достижения максимальной производительности этот интервал должен быть минимален, но достаточен для четкого разделения соседних концентрационных профилей, соответствующих двум последовательным сериям загрузок. Для определения минимальной величины интервала между сериями загрузок tins получено следующее уравнение:

(5)
${{t}_{{insm}}} = \frac{3}{N}~\left( {\frac{1}{{a_{l}^{2}}} + \frac{1}{{a_{h}^{2}}}} \right) + \frac{1}{{{{a}_{h}}}} - {{\frac{1}{a}}_{l}}~.~$

В уравнении (5) параметры ah и al рассчитываются по формуле (2): ah – для компонента смеси с максимальной величиной коэффициента распределения; al – для компонента смеси с минимальной величиной коэффициента распределения.

На рис. 3 и 4 приведены результаты моделирования непрерывных процессов разделения смесей, использованных при моделировании периодических процессов (рис. 2).

Рис. 3.

Моделирование непрерывных процессов разделения смесей, приведенных на рис. 2. Выходные профили концентраций компонентов после первых трех серийных загрузок рассчитаны по уравнениям (3) и (6).

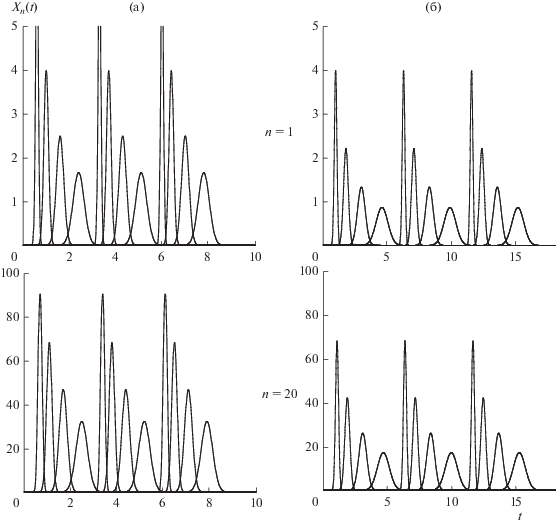
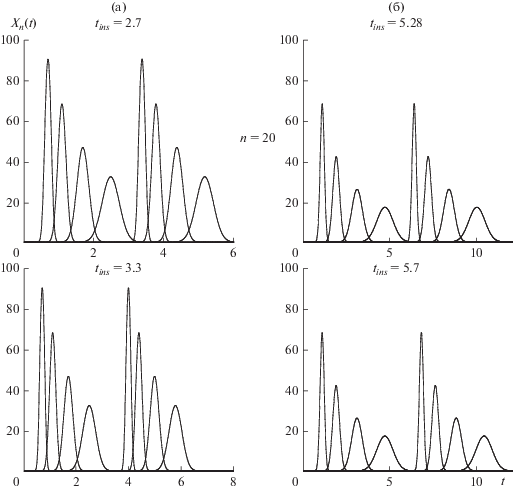
Рис. 4.

Выходные профили концентраций компонентов первой (а) и второй (б) смесей, рассчитанные по уравнению (4) для условий tins = tinsm и tins > tinsm.

На рис. 3 показаны выходные профили концентраций компонентов после первых трех серийных загрузок смеси, рассчитанные по уравнениям (3) и (5). Применительно к указанным выше четырехкомпонентным смесям уравнение (5) может быть записано в виде

(6)
$\begin{gathered} {{t}_{{inm}}} = \frac{3}{{\sqrt N }}~\left( {\frac{1}{{{{a}_{1}}}} + \frac{1}{{{{a}_{4}}}}} \right) + \frac{1}{{{{a}_{4}}}} - {{\frac{1}{a}}_{1}},~ \\ {{a}_{1}} = \frac{1}{{1 - S + S{{K}_{{D1}}}}},\,\,\,\,{{a}_{4}} = \frac{1}{{1 - S + S{{K}_{{D4}}}}}. \\ \end{gathered} $

Как видно из рис. 3, при расчете параметра tins по уравнению (6) достигаются оптимальные условия загрузки разделяемой смеси компонентов в каскад экстракторов – минимальный интервал между серийными загрузками и разделение соседних концентрационных профилей. Рассчитанная по уравнению (5) величина интервала для более слабоэкстрагируемой первой смеси компонентов (KD1 = 0.5, KD2 = 1, KD3 = 1.75, KD4 = 2.75) tinsm = 2.7, для второй смеси компонентов (KD1 = 1, KD2 = 2, KD3 = 3.5, KD4 = 5.5) tinsm = 5.28.

На рис. 4 приведены выходные профили концентраций компонентов первой и второй смесей, рассчитанные по уравнению (4) для условий tins = = tinsm и tins > tinsm.

ЗАКЛЮЧЕНИЕ

В настоящей работе для повышения производительности экстракционно-хроматографических процессов разделения предложено вместо применяемого в аналитике метода однократного впрыска пробы использовать серию последовательных, разделенных короткими интервалами времени, импульсных вводов разделяемой смеси компонентов. Предлагаемый метод кроме повышения производительности позволяет получать высококонцентрированные фракции разделенных компонентов. Проведен теоретический анализ экстракционно-хроматографических процессов разделения в каскаде смесительно-отстойных экстракторов, работающих в режиме элюентной хроматографии, при использовании серийного импульсного ввода раствора смеси компонентов в первую ступень каскада. Рассмотрены процессы разделения в периодическом и непрерывном режимах. Получены аналитические зависимости для моделирования таких экстракционно-хроматографических процессов разделения. Приведены примеры моделирования периодических и непрерывных процессов разделения.

Предлагаемый метод разделения может быть использован при разработке перспективных технологий получения чистых и особо чистых материалов, в частности, в производстве редкоземельных металлов.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований и Национального научного фонда Болгарии № 20-53-18007.

Список литературы

  1. Belova V.V., Voshkin A.A., Egorova N.S., Kholkin A.I. Solvent extraction of rare earth metals from nitrate solutions with di(2,4,4-trimethylpentyl)phosphinate of methyltrioctylammonium // J. Mol. Liq. 2012 V. 172. P. 144.

  2. Xing, W.D., Lee, M.S. A Process for the Separation of Noble Metals from HCl Liquor Containing Gold(III), Palladium(II), Platinum(IV), Rhodium(III), and Iridium(IV) by Solvent Extraction // Processes 2019. V. 7. P. 243.

  3. Solov’ev V.O., Zakhodyaeva Y.A., Voshkin, A.A. On the Influence of Additives of Polymer, Sodium Nitrate, and 1-Methyl-2-Pyrrolidone on the Extraction of Thiophene in an n-Hexane–Water System // Theor. Found. Chem. Eng. 2020. V. 54. P. 894.

  4. Voshkin A., Solov’ev V., Kostenko M., Zakhodyaeva Y., Pokrovskiy O. A doubly green separation process: merging aqueous two-phase extraction and supercritical fluid extraction // Processes. 2021. V. 9. V. 727.

  5. Perna F.M., Vitale P., Capriati V. Deep eutectic solvents and their applications as green solvents // Curr. Opin. Green Sustainable Chem. 2019. V. 21. P. 27.

  6. Zakhodyaeva Y.A., Zinov’eva I.V., Tokar E.S., Voshkin A.A. Complex Extraction of Metals in an Aqueous Two-Phase System Based on Poly(Ethylene Oxide) 1500 and Sodium Nitrate // Molecules. 2019. V. 24. P. 4078.

  7. Milevskiy N.A., Boryagina I.V., Karpukhina E.A., Kuznetsov V.N., Kabanova E.G. // J. Chem. Eng. Data. 2021. V. 66. P. 1021.

  8. Kostanyan A.E., Egorova N.S., Voshkin A.A., Zonov S.S. Extraction of uranyl, ytterbium, and lanthanum nitrates in a three-compartment multiphase extractor // Theor. Found. Chem. Eng. 2008. V. 42. № 5. P. 718.

  9. Gradov O.M., Voshkin A.A., Zakhodyaeva Y.A. Estimating the parameters of ultrasonically induced mass transfer and flow of liquids in the pseudomembrane method // Chem. Eng. Process. 2017. V. 118. P. 54.

  10. Ito Y., Weinstein M., Aoki I., Harada R., Kimura E., Nunogaki K. The coil planet centrifuge // Nature. 1966. V. 212. P. 985.

  11. Kostanyan A.A., Voshkin A.A., Belova V.V. Analytical, Preparative, and Industrial-Scale Separation of Substances by Methods of Countercurrent Liquid-Liquid Chromatography // Molecules. 2020. V. 25. P. 6020.

  12. Countercurrent Chromatography (Chromatographic Science Series. V. 82) / Eds. Menet J.M., Thiebaut D. New York: Marcel Dekker, 1999.

  13. Ito Y. Golden rules and pitfalls in selecting optimum conditions for high-speed counter-current chromatography // J. Chromatogr. A. 2005. V. 1065. P. 145.

  14. Berthod A., Maryutina T., Spivakov B., Shpigun O., Sutherland I.A. Countercurrent chromatography in analytical chemistry (IUPAC technical report) // Pure Appl. Chem. 2009. V. 81. P. 355.

  15. Conway W.D. Counter-current chromatography: Simple process and confusing terminology // J. Chromatogr. A. 2011. V. 1218. P. 6015.

  16. Morley R., Minceva M. Operating mode and parameter selection in liquid–liquid chromatography // J. Chromatogr. A. 2020. V. 1617. Article number 460479.

  17. Jerz G., Winterhalter P. The 10th International Conference on Countercurrent Chromatography held at Technische Universität Braunschweig, Braunschweig, Germany, August 1–3, 2018 // J. Chromatogr. A. 2020. V. 1617. Article number 460698.

  18. Friesen J.B., Ahmed S., Pauli G.F. Qualitative and quantitative evaluation of solvent systems for countercurrent separation // J. Chromatogr. A. 2015. V. 1377. P. 55.

  19. Bouju E., Berthod A., Faure K. Scale-up in centrifugal partition chromatography: The “free-space between peaks” method // J. Chromatogr. A. 2015. V. 1409. P. 70.

  20. Friesen J.B., McAlpine J.B., Chen S.-N., Pauli G.F. Countercurrent separation of natural products: An update // J. Nat. Prod. 2015. V. 78. P. 1765.

  21. Friesen J.B., McAlpine J.B., Chen S.-N., Pauli G.F. The 9th International Countercurrent Chromatography Conference held at Dominican University, Chicago, USA, August 1–3, 2016 // J. Chromatogr. A. 2017. V. 1520. P. 1.

  22. Peng A., Hewitson P., Sutherland I., Chen L., Ignatova S. How changes in column geometry and packing ratio can increase sample load and throughput by a factor of fifty in counter-current chromatography // J. Chromatogr. A. 2018. V. 1580. P. 120.

  23. Ignatova S., Sutherland I. The 8th International Conference on Counter-current Chromatography held at Brunel University, London, UK, July 23–25, 2014 // J. Chromatogr. A. 2015. V. 1425. P. 1.

  24. Guan Y.H., Hewitson P., van den Heuvel R., Zhao Y., Siebers R.P.G., Zhuang Y.-P., Sutherland I. Scale-up protein separation on stainless steel wide bore toroidal columns in the type-J counter-current chromatography // J. Chromatogr. A. 2015. V. 1424. P. 102.

  25. Roehrer S., Bezold F., García E.M., Minceva M. Deep eutectic solvents in countercurrent and centrifugal partition chromatography // J. Chromatogr. A. 2016. V. 1434. P. 102.

  26. Morley R., Minceva M. Trapping multiple dual mode centrifugal partition chromatography for the separation of intermediately-eluting components: throughput maximization strategy // J. Chromatogr. A. 2017. V. 1501. P. 26.

  27. Hopmann E.A. Development of a Centrifugal Partition Chromatographic Separation: From Molecule to Process. Munich: Dr. Hut, 2013.

  28. Ito Y. High-speed countercurrent chromatography // Nature. 1987. V. 326. P. 419.

  29. Ito Y. Origin and evolution of the coil planet centrifuge: a personal reflection of my 40 years of CCC research and development // Sep. Purif. Rev. 2005. V. 34. P. 131.

  30. Goll J., Frey A., Minceva M. Study of the separation limits of continuous solid support free liquid–liquid chromatography: Separation of capsaicin and dihydrocapsaicin by centrifugal partition chromatography // J. Chromatogr. A. 2013. V. 1284. P. 59.

  31. Sutherland I.A, Audo G., Bourton E., Couillard F., Fisher D. et al. Rapid linear scale-up of a protein separation by centrifugal partition chromatography // J. Chromatogr. A. 2008. V. 1190. P. 57.

  32. Sutherland I., Hewitson P., Ignatova S. New 18-l process-scale counter-current chromatography centrifuge // J. Chromatogr. A. 2009. V. 1216. P. 4201.

  33. Ignatova S., Wood P., Hawes D., Janaway L., Keay D., Sutherland I. Feasibility of scaling from pilot to process scale // J. Chromatogr. A. 2007. V. 1151. P. 20.

  34. Foucault A.P. Centrifugal Partition Chromatography. Abingdon: Taylor & Francis, 1995.

  35. Conway W.D. Countercurrent Chromatography: Apparatus, Theory, and Applications. Weinheim: Wiley-VCH, 1990.

  36. Countercurrent Chromatography: The Support-Free Liquid Stationary Phase (Comprehensive Analytical Chemistry. V. 38) / Ed. Berthod A. Amsterdam: Elsevier, 2002.

  37. Kostanyan A.E., Voshkin A.A. Support-free pulsed liquid-liquid chromatography‎ // J. Chromatogr. A. 2009. V. 1216. P. 7761.

  38. Kostanyan A.E., Voshkin A.A., Kodin N.V. Controlled-cycle pulsed liquid–liquid chromatography. A modified version of Craig’s counter-current distribution // J. Chromatogr. A. 2011. V. 1218. № 36. P. 6135.

  39. Kostanyan A., Martynova M. Modeling of two semi-continuous methods in liquid–liquid chromatography: Comparing conventional and closed-loop recycling modes // J. Chromatogr. A. 2020. V. 1614. Article number 460735.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал