Теоретические основы химической технологии, 2021, T. 55, № 6, стр. 754-763
Прогнозирование процесса электрохимического баромембранного разделения промышленных растворов на основе фрикционной теории
К. В. Шестаков a, *, С. И. Лазарев a, П. А. Хохлов a, К. К. Полянский b
a Тамбовский государственный технический университет
Тамбов, Россия
b Воронежский филиал Российского экономического университета им. Г.В. Плеханова
Воронеж, Россия
* E-mail: kostyanshestakov@mail.ru
Поступила в редакцию 17.04.2021
После доработки 13.05.2021
Принята к публикации 21.05.2021
Аннотация
Предложен усовершенствованный подход к определению кинетических характеристик электрохимического баромембранного разделения растворов, основанный на фрикционной теории Шпиглера с учетом суммарного воздействия химического и электрохимического потенциалов. На примере процесса электрохимического баромембранного разделения водных растворов CuSO4, Ni(NO3)2 и Fe(NO3)3 с концентрациями 1 × 10–2, 2 × 10–3 и 1 × 10–5 моль/л соответственно с помощью мембран МГА-95 и МГА-100 получены численные величины фрикционных коэффициентов взаимодействия систем растворитель–мембрана fωm, растворенное вещество (катионы)–мембрана f+m, растворенное вещество (катионы)–растворитель f+ω, а также найдены эмпирические коэффициенты для определения аппроксимирующих кривых. Выявлено увеличение абсолютных значений данных коэффициентов при повышении приложенного электрического потенциала практически во всех случаях. Исключением является массоперенос через прикатодные мембраны при разделении раствора Fe(NO3)3. Наименьшие абсолютные значения фрикционных коэффициентов характерны для разделения раствора CuSO4, наибольшие – для Fe(NO3)3. По полученным аппроксимационным зависимостям фрикционных коэффициентов от электрического потенциала решается обратная задача по нахождению значений коэффициентов задержания и выходного потока растворителя, что можно эффективно использовать для прогнозирования механизма массопереноса и расчета электромембранных установок.
ВВЕДЕНИЕ
Математическое моделирование не без основания является важным фактором в науке, одним из способов познания окружающего мира, который к тому же может дополнять экспериментально получаемые данные. Для того чтобы утверждать какой-либо факт, помимо убедительного эксперимента, необходима и математическая модель, способная описать и интерпретировать результаты этого эксперимента. Благодаря моделированию формируются различные гипотезы, в частности о механизме переноса веществ через полупроницаемые и ионообменные мембраны [1, 2].
За несколько десятилетий в области мембранного разделения растворов разработано достаточно большое количество математических моделей, описывающих различные аспекты массопереноса в мембранах. У каждой из них имеются как достоинства, так и недостатки, что в некоторой степени ограничивает область применения модели и сводит ее в рамки определенной технологии [3–11]. Это относится и к фрикционной модели Шпиглера, которая легла в основу предлагаемого в данной работе подхода к определению кинетических характеристик электрохимического баромембранного разделения растворов. К преимуществам фрикционной модели можно отнести более слабую зависимость фрикционных кинетических коэффициентов от концентрации электролита, их четкий физический смысл и независимость от выбранной системы отсчета.
Существующие научные работы в основном касаются мембранных и электрохимических мембранных процессов по отдельности, не затрагивая суммарное влияние всех составляющих электрохимического потенциала сразу [12–16]. Поэтому целью данной работы была разработка усовершенствованного подхода к прогнозированию кинетических характеристик электрохимического баромембранного разделения технологических растворов гальванопроизводств на основе фрикционной модели Шпиглера, который будет использован уже для электробаромембранного разделения в целом, учитывая комплексное влияние разности электрических потенциалов, давления, температуры и концентрации.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Фрикционная модель Шпиглера, представленная им в 1958 году, основана на том, что в рассматриваемой системе все компоненты перемещаются относительно друг друга под действием некоторых внешних сил, осуществляя при этом взаимное трение, в результате чего образуются фрикционные силы Fij. При этом все частицы движутся с постоянной скоростью, а в системе наблюдается баланс внешних сил и сил трения. Данные аспекты выражаются в уравнениях (1) и (2) [17, 18]:
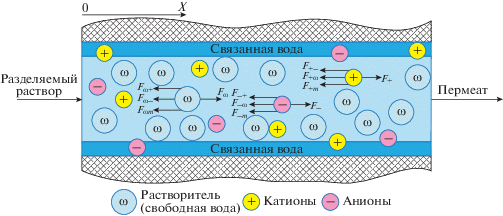
Взаимодействие всех приложенных к частицам сил в рассматриваемом объеме можно описать системой уравнений (3), где индексами +, –, ω, m обозначены катионы, анионы, растворитель и мембрана соответственно. На рис. 1 схематично изображены все силы, приложенные к каждому типу частиц в растворе.
Перед решением системы уравнений (3), следует ввести ряд допущений:
• поток жидкости стационарен, а режим течения – ламинарный;
• каждая среднестатистическая частица испытывает действие одних и тех же внешних сил, в следствие чего единичный объем не включает в себя элементы различных фаз;
• скорость электродных реакций намного выше скорости массопереноса;
• плотность тока существенно ниже критической;
• насос обеспечивает беспрерывную подачу разделяемого раствора в межмембранный канал;
• силы трения между катионами и анионами ничтожно малы и ими можно пренебречь.
Подставляя уравнение (1) в систему уравнений (3) и учитывая, что Fim= –fimciυi = –fimJi (из-за неподвижности стенок пор мембраны, υm = 0) [17, 18], получим систему уравнений следующего вида:
(4)
$\left\{ \begin{gathered} {{{\bar {c}}}_{ + }}{{F}_{ + }} - {{{\bar {c}}}_{ + }}{{f}_{{ + - }}}({{v}_{ + }} - {{v}_{ - }}) - {{{\bar {c}}}_{ + }}{{f}_{{ + \omega }}}({{v}_{ + }} - {{v}_{\omega }}) - {{f}_{{ + m}}}{{J}_{ + }} = 0, \hfill \\ {{{\bar {c}}}_{ - }}{{F}_{ - }} - {{{\bar {c}}}_{ - }}{{f}_{{ - + }}}({{v}_{ - }} - {{v}_{ + }}) - {{{\bar {c}}}_{{ - + }}}{{f}_{{ - \omega }}}({{v}_{ - }} - {{v}_{\omega }}) - {{f}_{{ - m}}}{{J}_{ - }} = 0, \hfill \\ {{{\bar {c}}}_{\omega }}{{F}_{\omega }} - {{{\bar {c}}}_{\omega }}{{f}_{{\omega + }}}({{v}_{\omega }} - {{v}_{ + }}) - {{{\bar {c}}}_{\omega }}{{f}_{{\omega - }}}({{v}_{\omega }} - {{v}_{ - }}) - {{f}_{{\omega m}}}{{J}_{\omega }} = 0, \hfill \\ {{{\bar {c}}}_{m}}{{F}_{m}} - {{{\bar {c}}}_{m}}{{f}_{{m + }}}{{v}_{ + }} - {{{\bar {c}}}_{m}}{{f}_{{m - }}}{{v}_{ - }} - {{{\bar {c}}}_{m}}{{f}_{{m\omega }}}{{v}_{\omega }} = 0. \hfill \\ \end{gathered} \right.$В данной системе неизвестны 12 коэффициентов трения между составляющими компонентами: f+–, f–+, f+ω, fω+, f+m, fm+, f–ω, fω–, f–m, fm–, fωm, fmω. Однако перекрестные коэффициенты трения могут быть выражены друг через друга за счет равенства перекрестных нормированных коэффициентов nij и nji, входящих в их состав (fij = cjnij) [18]. Это позволяет вывести следующее равенство:
(5)
${{\bar {c}}_{i}}{{f}_{{ij}}} = \,\,~{{\bar {c}}_{i}}{{\bar {c}}_{j}}{{n}_{{ij}}} = \,\,~{{\bar {c}}_{j}}{{\bar {c}}_{i}}{{n}_{{ji}}} = {{\bar {c}}_{j}}{{f}_{{ji}}}.$Данное равенство делает достаточным определение лишь одного коэффициента из каждой пары. При этом стоит отметить, что наибольший интерес представляют коэффициенты трения между каждым компонентом (катионы, анионы и растворитель) и мембраной f+m, f–m, fωm, а также между катионами и растворителем f+ω, анионами и растворителем f–ω.
На первом этапе решения системы уравнений (4) рассмотрим первые два уравнения и выразим перекрестные коэффициенты трения f+– и f–+ отдельно от остальных. В итоге получим следующие уравнения:
(6)
$\left\{ {\begin{array}{*{20}{c}} { - {{{\bar {c}}}_{ + }}{{f}_{{ + - }}}\left( {{{v}_{ + }} - {{v}_{ - }}} \right) = {{{\bar {c}}}_{ + }}{{f}_{{ + {{\omega }}}}}\left( {{{v}_{ + }} - {{v}_{{{\omega }}}}} \right) + {{f}_{{ + {\text{m}}}}}{{J}_{ + }} - {{{\bar {c}}}_{ + }}{{F}_{ + }},} \\ { - {{{\bar {c}}}_{ - }}{{f}_{{ - + }}}\left( {{{v}_{ - }} - {{v}_{ + }}} \right) = {{{\bar {c}}}_{ - }}{{f}_{{ - {{\omega }}}}}\left( {{{v}_{ - }} - {{v}_{{{\omega }}}}} \right) + {{f}_{{ - {\text{m}}}}}{{J}_{ - }} - {{{\bar {c}}}_{ - }}{{F}_{ - }}.} \end{array}} \right.$Учитывая выражения (5) и (6), получим следующее равенство:
(7)
$\begin{gathered} - {{{\bar {c}}}_{ + }}{{f}_{{ + {{\omega }}}}}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right) - {{f}_{{ + {\text{m}}}}}{{J}_{ + }} + {{{\bar {c}}}_{ + }}{{F}_{ + }} = \\ = {{{\bar {c}}}_{ - }}{{f}_{{ - {{\omega }}}}}\left( {{{v}_{ - }} - {{v}_{{{\omega }}}}} \right) + {{f}_{{ - {\text{m}}}}}{{J}_{ - }} - {{{\bar {c}}}_{ - }}{{F}_{ - }}. \\ \end{gathered} $Из данного равенства можно выразить коэффициент трения между коэффициент трения между анионами и растворителем f–ω:
(8)
${{f}_{{ - \omega }}} = \frac{{{{{\bar {c}}}_{ + }}{{F}_{ + }} - {{{\bar {c}}}_{ + }}{{f}_{{ + {{\omega }}}}}\left( {{{v}_{ + }} - {{v}_{{{\omega }}}}} \right) - {{f}_{{ + {\text{m}}}}}{{J}_{ + }} - {{f}_{{ - {\text{m}}}}}{{J}_{ - }} + {{{\bar {c}}}_{ - }}{{F}_{ - }}}}{{{{{\bar {c}}}_{ - }}\left( {{{v}_{ - }} - {{v}_{{{\omega }}}}} \right)}}.$Таким же образом, используя первое и третье уравнения из системы уравнений (4), выразим перекрестные коэффициенты трения f+ω и fω+:
(9)
$\left\{ {\begin{array}{*{20}{c}} { - {{{\bar {c}}}_{ + }}{{f}_{{ + \omega }}}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right) = {{{\bar {c}}}_{ + }}{{f}_{{ + - }}}\left( {{{v}_{ + }} - {{v}_{ - }}} \right) + {{f}_{{ + {\text{m}}}}}{{J}_{ + }} - {{{\bar {c}}}_{ + }}{{F}_{ + }},} \\ { - {{{\bar {c}}}_{\omega }}{{f}_{{\omega + }}}\left( {{{v}_{\omega }} - {{v}_{ + }}} \right) = {{{\bar {c}}}_{ - }}{{f}_{{\omega - }}}\left( {{{v}_{\omega }} - {{v}_{ - }}} \right) + {{f}_{{\omega {\text{m}}}}}{{J}_{\omega }} - {{{\bar {c}}}_{ - }}{{F}_{ - }}.} \end{array}} \right.$Далее с учетом выражения (5) выводим из системы уравнений (9) коэффициент трения между растворителем и анионами fω–:
(10)
${{f}_{{\omega - }}} = \frac{{{{{\bar {c}}}_{ + }}{{F}_{ + }} - {{{\bar {c}}}_{ + }}{{f}_{{ + - }}}\left( {{{v}_{ + }} - {{v}_{ - }}} \right) - {{f}_{{ + {\text{m}}}}}{{J}_{ + }} - {{f}_{{\omega {\text{m}}}}}{{J}_{\omega }} + {{{\bar {c}}}_{\omega }}{{F}_{\omega }}}}{{{{{\bar {c}}}_{\omega }}\left( {{{v}_{\omega }} - {{v}_{ - }}} \right)}}.$Из уравнений (8) и (10) в совокупности с выражением (5) получим выражение для коэффициента трения между катионами и анионами f+–:
(11)
${{f}_{{ + - }}} = \frac{{2{{{\bar {c}}}_{ + }}{{F}_{ + }} - {{{\bar {c}}}_{ + }}{{f}_{{ + \omega }}}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right) - 2{{f}_{{ + {\text{m}}}}}{{J}_{ + }} - {{f}_{{ - {\text{m}}}}}{{J}_{ - }} + 2{{{\bar {c}}}_{ - }}{{F}_{ - }} - {{f}_{{\omega {\text{m}}}}}{{J}_{\omega }}}}{{{{{\bar {c}}}_{ + }}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right)}}.$Для дальнейшего расчета необходимо прибегнуть к одному из допущений, введeнных ранее. Так, в связи с ничтожно малой силой трения между катионами и анионами ею можно пренебречь. Из этого следует, что f+– = 0, а вместе с этим и числитель выражения (11). Так как четвертое уравнение системы уравнений (4) тоже равняется 0, то приравняем его к числителю выражения (11) и получим
(12)
$\begin{gathered} 2{{{\bar {c}}}_{ + }}{{F}_{ + }} - {{{\bar {c}}}_{ + }}{{f}_{{ + \omega }}}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right) - 2{{f}_{{ + {\text{m}}}}}{{J}_{ + }} - \\ - \,\,{{f}_{{ - {\text{m}}}}}{{J}_{ - }} + 2{{{\bar {c}}}_{ - }}{{F}_{ - }} - {{f}_{{\omega {\text{m}}}}}{{J}_{\omega }} = \\ = {{{\bar {c}}}_{{\text{m}}}}{{F}_{{\text{m}}}} + {{{\bar {c}}}_{{\text{m}}}}{{f}_{{{\text{m}} + }}}{{v}_{ + }} - {{{\bar {c}}}_{{\text{m}}}}{{f}_{{{\text{m}} - }}}{{v}_{ - }} - {{{\bar {c}}}_{{\text{m}}}}{{f}_{{{\text{m}}\omega }}}{{v}_{\omega }}. \\ \end{gathered} $С помощью равенства (5) преобразуем правую часть выражения (12) и выразим коэффициент трения между катионами и растворителем f+ω:
(13)
$\begin{gathered} {{{\bar {c}}}_{ + }}{{f}_{{ + \omega }}}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right) = 2{{{\bar {c}}}_{ + }}{{F}_{ + }} - 2{{f}_{{ + {\text{m}}}}}{{J}_{ + }} - \\ - \,\,{{f}_{{ - {\text{m}}}}}{{J}_{ - }} + 2{{{\bar {c}}}_{ - }}{{F}_{ - }} - {{f}_{{\omega {\text{m}}}}}{{J}_{\omega }} - \\ - \,\,{{{\bar {c}}}_{{\text{m}}}}{{F}_{{\text{m}}}} + {{{\bar {c}}}_{ + }}{{f}_{{ + {\text{m}}}}}{{v}_{ + }} - {{{\bar {c}}}_{ - }}{{f}_{{ - {\text{m}}}}}{{v}_{ - }} - {{{\bar {c}}}_{\omega }}{{f}_{{\omega {\text{m}}}}}{{v}_{\omega }}.~ \\ \end{gathered} $Мембранная система неподвижна, следовательно, сумма всех приложенных к ней сил равна нулю ${{\bar {c}}_{ + }}{{F}_{ + }} + {{\bar {c}}_{ - }}{{F}_{ - }} + {{\bar {c}}_{\omega }}{{F}_{\omega }} + {{\bar {c}}_{{\text{m}}}}{{F}_{{\text{m}}}} = 0$, откуда выразим ${{\bar {c}}_{{\text{m}}}}{{F}_{{\text{m}}}} = - {{\bar {c}}_{ + }}{{F}_{ + }} - {{\bar {c}}_{ - }}{{F}_{ - }} - {{\bar {c}}_{\omega }}{{F}_{\omega }}$. Учитывая Ji = ciυi, приведем выражение (13) к виду
(14)
${{\bar {c}}_{ + }}{{f}_{{ + \omega }}}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right) = 3{{\bar {c}}_{ + }}{{F}_{ + }} + 3{{\bar {c}}_{ - }}{{F}_{ - }} + {{\bar {c}}_{\omega }}{{F}_{\omega }} - 3{{f}_{{ + {\text{m}}}}}{{J}_{ + }}.$Подставим выражение (14) в первое уравнение системы уравнений (6) и получим следующее выражение:
(15)
$ - {{\bar {c}}_{ + }}{{f}_{{ + - }}}\left( {{{v}_{ + }} - {{v}_{ - }}} \right) = 2{{\bar {c}}_{ + }}{{F}_{ + }} + 3{{\bar {c}}_{ - }}{{F}_{ - }} + {{\bar {c}}_{\omega }}{{F}_{\omega }} - 2{{f}_{{ + {\text{m}}}}}{{J}_{ + }}.$Так как f+– = 0, то правая часть выражения (15) тоже будет равняться нулю. Следовательно, можно выразить расчетное уравнение для коэффициента трения между катионами и поверхностью мембраны f+m, которое не будет зависеть от других коэффициентов трения:
(16)
${{f}_{{ + {\text{m}}}}} = \frac{{2{{{\bar {c}}}_{ + }}{{F}_{ + }} + 3{{{\bar {c}}}_{ - }}{{F}_{ - }} + {{{\bar {c}}}_{\omega }}{{F}_{\omega }}}}{{2{{J}_{ + }}}}.$Приняв во внимание уравнение (16), f+– = 0, υm = 0, а также то, что первое уравнение системы уравнений (4) равняется нулю, выразим расчетное уравнение для коэффициента трения между катионами и растворителем f+ω:
(17)
${{f}_{{ + \omega }}} = \frac{{{{{\bar {c}}}_{ + }}{{F}_{ + }} + {{{\bar {c}}}_{ + }}{{v}_{ + }}\left( {\frac{{2{{{\bar {c}}}_{ + }}{{F}_{ + }} + 3{{{\bar {c}}}_{ - }}{{F}_{ - }} + {{{\bar {c}}}_{\omega }}{{F}_{\omega }}}}{{2{{J}_{ + }}}}} \right)}}{{{{{\bar {c}}}_{ + }}\left( {{{v}_{ + }} - {{v}_{\omega }}} \right)}}.$В связи с тем что изначальное количество неизвестных коэффициентов было больше числа независимых уравнений в рассматриваемой системе, дальнейший расчет коэффициентов трения требовал введения дополнительного допущения, которое позволило бы получить расчетные формулы для оставшихся коэффициентов. Для этого было выдвинуто предположение, что между коэффициентами трения f+ω и f–ω есть некоторая взаимосвязь. Она заключается в том, что ионы растворенных веществ с различной молярной массой при прочих равных условиях будут по-разному скользить относительно ионов и молекул растворителя, так как сила трения скольжения прямо пропорциональна прижимающей силе (силе реакции опоры). Следовательно, через соотношение молярных масс катионов и анионов можно выразить соотношение и коэффициентов f+ω и f–ω, которое будет выглядеть следующим образом:
Расчет коэффициентов трения fω+ и fω– будет учитывать равенство (5) и уравнения (17) и (18):
(19)
${{f}_{{\omega + }}} = \frac{{{{f}_{{ + \omega }}}{{{\bar {c}}}_{ + }}}}{{{{{\bar {c}}}_{\omega }}}},$(20)
${{f}_{{\omega - }}} = \frac{{{{f}_{{ - \omega }}}{{M}_{ - }}{{{\bar {c}}}_{ - }}}}{{{{M}_{ + }}{{{\bar {c}}}_{\omega }}}}~.$Расчет коэффициента трения ${{f}_{{{{\omega m}}}}}~$ проводится следующим образом:
(21)
${{f}_{{{{\omega m}}}}} = \frac{{{{{\bar {c}}}_{\omega }}{{F}_{\omega }} - {{{\bar {c}}}_{\omega }}{{f}_{{\omega + }}}\left( {{{v}_{\omega }} - {{v}_{ + }}} \right) - {{{\bar {c}}}_{\omega }}{{f}_{{\omega - }}}\left( {{{v}_{\omega }} - {{v}_{ - }}} \right)}}{{{{J}_{\omega }}}}.$Для того чтобы окончательно решить систему уравнений (4) и рассчитать коэффициенты трения, необходимо также определить те внешние силы, которые входят в электрохимический потенциал и обусловливают движение частиц. Если рассматривать электробаромембранный процесс разделения, то перенос растворенных веществ (катионов и анионов) объясняется диффузионным RTd(lnas)/dx, электродиффузионным zsFdφ/dx и конвективным Vsdp/dx потоками. Перенос растворителя происходит из-за наличия осмотического RTd(lnaω)/dx, электроосмотического (${{\bar {c}}_{{{\omega }}}}$εξ0dφ)/(Lωηdx) и конвективного Vωdp/dx потоков [18–24]. Движущие силы для катионов, анионов и растворителя выразим через соответствующие электрохимические потенциалы и запишем в виде уравнений (22), (23) и (24) соответственно [17, 18]:
(22)
${{F}_{ + }} = - \frac{{d{{\mu }_{ + }}}}{{dх}} = - RT\frac{{d\left( {\ln {{a}_{ + }}} \right)}}{{dх}} - {{z}_{ + }}F\frac{{d\varphi }}{{dx}} - {{V}_{ + }}\frac{{dp}}{{dx}},$(23)
${{F}_{ - }} = - \frac{{d{{\mu }_{ - }}}}{{dх}} = - RT\frac{{d\left( {\ln {{a}_{ - }}} \right)}}{{dх}} - {{z}_{ - }}F\frac{{d\varphi }}{{dx}} - {{V}_{ - }}\frac{{dp}}{{dx}},$(24)
${{F}_{\omega }} = - \frac{{d{{\mu }_{\omega }}}}{{dх}} = - RT\frac{{d\left( {\ln {{a}_{\omega }}} \right)}}{{dх}} - \frac{{{{{\bar {c}}}_{\omega }}\varepsilon {{\varepsilon }_{0}}{{\xi }_{0}}d\varphi }}{{{{L}_{\omega }}\eta dx}} - {{V}_{\omega }}\frac{{dp}}{{dx}}.$Граничные условия выбраны следующие:
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
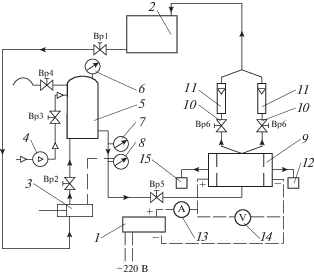
Все экспериментальные исследования, представленные в данной работе, проводились на электробаромембранной установке плоскокамерного типа с использованием ацетатцеллюлозных мембран МГА-95 и МГА-100. На рис. 2 представлена схема данной экспериментальной установки. Основными ее элементами являются электробаромембранная ячейка плоскокамерного типа, плунжерный насос, компрессор, ресивер и емкости с исходным раствором и пермеатом. Более подробно конструкция и принцип работы описаны в работах [25, 26].
Рис. 2.
Схема электробаромембранной установки: 1 – источник питания постоянного тока; 2 – исходная емкость; 3 – плунжерный насос; 4 – компрессор; 5 – ресивер; 6 – манометр; 7 – образцовый манометр; 8 – электроконтактный манометр; 9 – электрохимическая мембранная ячейка; 10 – дроссель; 11 – поплавковый ротаметр; 12 – емкость прикатодного пермеата; 13 – амперметр; 14 – вольтметр; 15 – емкость прианодного пермеата.
В качестве исследуемых растворов были выбраны модельные водные растворы солей трех металлов – CuSO4, Ni(NO3)2, Fe(NO3)3 с концентрациями 1 × 10–2, 2 × 10–3 и 1 × 10–5 моль/л соответственно. Остальные рабочие параметры экспериментов представлены в табл. 1.
Таблица 1.
Рабочие параметры экспериментов
| Параметр | Давление, Па | Напряжение, В | Рабочая площадь одной мембраны, м2 |
|---|---|---|---|
| Значение | 4 × 106 | 4–12 | 7.85 × 10–5 |
По результатам серии экспериментов по электробаромембранному разделению растворов получали значения коэффициентов задержания и плотностей потока веществ, проходящих через мембрану. После чего с помощью них и других рабочих параметров экспериментов рассчитывались дискретные значения интересующих фрикционных коэффициентов. Далее проводилась аппроксимация данных значений для последующего анализа и прогнозирования.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
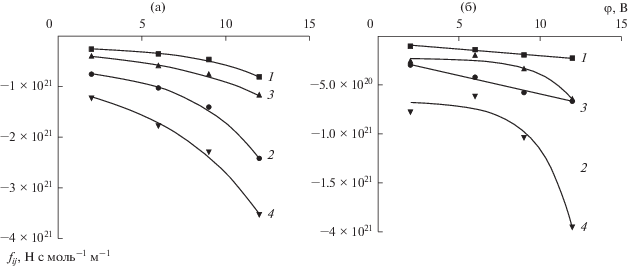
Наибольший интерес в ходе выполнения данной работы представили коэффициенты трения f+m, f+ω и fωm. Рассчитанные дискретные значения фрикционных коэффициентов f+m и f+ω (рис. 3а, 3б) представлены при разделении модельного водного раствора CuSO4 прианодными и прикатодными мембранами. Рассчитанные дискретные значения фрикционных коэффициентов указаны вместе с аппроксимирующими кривыми, необходимыми для прогнозирования изменения значений коэффициентов. Из рисунков видно, что с увеличением электрического потенциала происходит увеличение значений фрикционных коэффициентов. Причем для мембраны МГА-100 значения всех коэффициентов трения выше аналогичных значений мембраны МГА-95 на всем диапазоне применяемых значений электрического потенциала.
Рис. 3.
Зависимости фрикционных коэффициентов f+m и f+ω при разделении модельного водного раствора CuSO4 мембранами МГА-95 и МГА-100: (а) – прианодная мембрана; (б) – прикатодная мембрана; 1 – f+m (МГА-95); 2 – f+ω (МГА-95); 3 – f+m (МГА-100); 4 – f+ω (МГА-100).

Абсолютные значения фрикционных коэффициентов f+m и f+ω для раствора Ni(NO3)2 (рис. 4а, 4б) также увеличиваются, однако в отличие от раствора CuSO4 все значения коэффициентов отрицательные. Для прикатодных мембран наблюдается большее различие в значениях фрикционных коэффициентов f+m и f+ω при разделении раствора мембранами МГА-95 и МГА-100 по сравнению с прианодными.
Рис. 4.
Зависимости фрикционных коэффициентов f+m и f+ω при разделении модельного водного раствора Ni(NO3)2 мембранами МГА-95 и МГА-100: (а) – прианодная мембрана; (б) – прикатодная мембрана; 1 – f+m (МГА-95); 2 – f+ω (МГА-95); 3 – f+m (МГА-100); 4 – f+ω (МГА-100).
Фрикционные коэффициенты f+m при разделении раствора Fe(NO3)3, показанные на рис. 5, наибольшие среди всех растворов, прошедших процесс разделения. Следует отдельно отметить уменьшение абсолютных значений фрикционных коэффициентов для прикатодных мембран МГА-95 и МГА-100.
Рис. 5.
Зависимости фрикционных коэффициентов f+m и f+ω при разделении модельного водного раствора Fe(NO3)3 мембранами МГА-95 и МГА-100: (а) – прианодная мембрана; (б) – прикатодная мембрана; 1 – f+m (МГА-95); 2 – f+ω (МГА-95); 3 – f+m (МГА-100); 4 – f+ω (МГА-100).

Для определения аппроксимирующих кривых зависимости фрикционных коэффициентов от изменения приложенного электрического потенциала использовалось следующее экспоненциальное уравнение:
Все эмпирические коэффициенты b, c и d, необходимые для построения аппроксимирующей кривой и определения значения фрикционных коэффициентов при любом значении электрического потенциала, представлены в табл. 2.
Таблица 2.
Эмпирические коэффициенты для расчета коэффициентов трения f+m и f+ω
| Марка мембраны | Тип мембраны | Коэффициент трения | Раствор | Коэффициенты | ||
|---|---|---|---|---|---|---|
| b | c | d | ||||
| МГА-95 | Прианодная | f +m | CuSO4 | –1.64991 ×1019 | 1.58936 × 1019 | 0.16974 |
| f+ω | –3.53727 × 1019 | 3.40749 × 1019 | 0.16974 | |||
| Прикатодная | f +m | 1.13143 × 1020 | –1.18988 × 1020 | 0.10749 | ||
| f+ω | 2.42571 × 1020 | –2.55103 × 1020 | 0.10749 | |||
| МГА-100 | Прианодная | f +m | –7.98745 × 1019 | 6.85462 × 1019 | –0.04682 | |
| f+ω | –1.71246 × 1020 | 1.46959 × 1020 | –0.04682 | |||
| Прикатодная | f +m | 1.28778 ×1 020 | –1.40307 × 1020 | –0.06964 | ||
| f+ω | 2.76093 × 1020 | –3.00809 × 1020 | –0.06964 | |||
| МГА-95 | Прианодная | f +m | Ni(NO3)2 | –1.95792 × 1020 | –3.3706 × 1019 | 0.24162 |
| f+ω | –5.85187 × 1020 | –1.00741 × 1020 | 0.16754 | |||
| Прикатодная | f +m | 5.9148 × 1020 | –6.67202 × 1020 | 0.01681 | ||
| f+ω | 1.76783 × 1021 | –1.99415 × 1021 | 0.01681 | |||
| МГА-100 | Прианодная | f +m | –2.2699 × 1020 | –1.27077 × 1020 | 0.16754 | |
| f+ω | –6.78435 × 1020 | –3.7981 × 1020 | 0.16754 | |||
| Прикатодная | f +m | –2.2413 × 1020 | –1.40747 × 1018 | 0.47672 | ||
| f+ω | –6.69884 × 1020 | –4.20669 × 1018 | 0.47672 | |||
| МГА-95 | Прианодная | f +m | Fe(NO3)3 | –9.70957 × 1022 | –1.08692 × 1022 | 0.22357 |
| f+ω | –1.94191 × 1024 | –2.17385 × 1023 | 0.22357 | |||
| Прикатодная | f +m | –1.23477 × 1023 | 2.6025 × 1022 | –0.11151 | ||
| f+ω | –2.46955 × 1024 | 5.205 × 1023 | –0.11151 | |||
| МГА-100 | Прианодная | f +m | 1.56375 × 1024 | –1.67354 × 1024 | 0.05943 | |
| f+ω | 3.12751 × 1025 | –3.34707 × 1025 | 0.05943 | |||
| Прикатодная | f +m | –5.94188 × 1022 | –1.05401 × 1023 | –0.11323 | ||
| f+ω | –1.18838 × 1024 | –2.10803 × 1023 | –0.11323 | |||
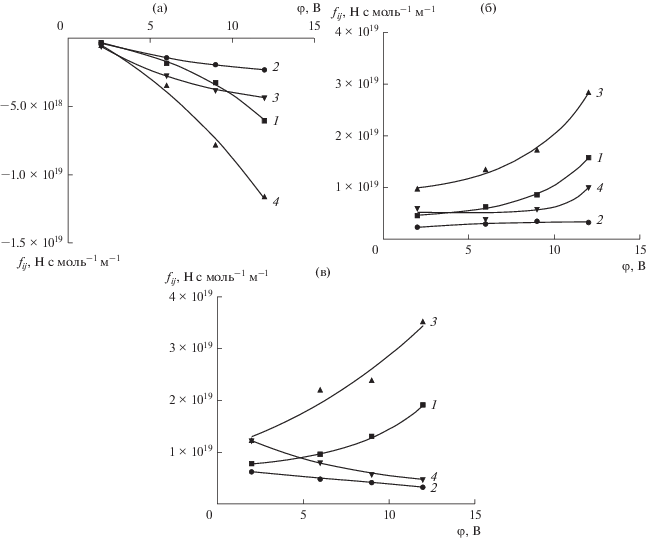
Зависимости фрикционных коэффициентов fωm при разделении всех модельных водных растворов, представленные на рис. 6, позволяют сделать вывод о некоторой схожести между кривыми зависимостей fωm при разделении растворов Ni(NO3)2 и Fe(NO3)3. Практически для всех мембран характерно увеличение абсолютных значений коэффициента трения fωm с увеличением приложенного электрического потенциала.
Рис. 6.
Зависимости фрикционных коэффициентов fωm при разделении модельных водных растворов: (а) – CuSO4; (б) – Ni(NO3)2; (в) – Fe(NO3)3; 1 – прианодная мембрана МГА-95; 2 – прикатодная мембрана МГА-95; 3 – прианодная мембрана МГА-100; 4 – прикатодная мембрана МГА-100.
Аппроксимация полученных дискретных значений fωm также проводилась по уравнению (25). Все определенные эмпирические коэффициенты сведены в табл. 3.
Таблица 3.
Эмпирические коэффициенты для расчета фрикционного коэффициента fωm
| Марка мембраны | Тип мембраны | Раствор | Коэффициенты | ||
|---|---|---|---|---|---|
| b | c | d | |||
| МГА-95 | Прианодная | CuSO4 | 1.28017 × 1018 | –1.24266 × 1018 | 0.14745 |
| Прикатодная | –3.11251 × 1018 | 3.60489 × 1018 | –0.12797 | ||
| МГА-100 | Прианодная | 9.007 × 1018 | –8.08773 × 1018 | 0.0787 | |
| Прикатодная | –5.3771 × 1018 | 6.56705 × 1018 | –0.15484 | ||
| МГА-95 | Прианодная | Ni(NO3)2 | 4.13351 × 1018 | 2.96826 × 1017 | 0.30554 |
| Прикатодная | 3.45439 × 1018 | –1.94219 × 1018 | –0.2655 | ||
| МГА-100 | Прианодная | 8.26647 × 1018 | 9.82721 × 1017 | 0.25069 | |
| Прикатодная | 5.11559 × 1018 | 6.5528 × 1014 | 0.74309 | ||
| МГА-95 | Прианодная | Fe(NO3)3 | 6.40931 × 1020 | 8.45083 × 1019 | 0.22559 |
| Прикатодная | –6.75726 × 1020 | 1.36871 × 1021 | –0.02579 | ||
| МГА-100 | Прианодная | –3.5432 × 1020 | 1.39779 × 1021 | 0.08329 | |
| Прикатодная | 2.57726 × 1020 | 1.32177 × 1021 | –0.15047 | ||
По полученным аппроксимационным зависимостям фрикционных коэффициентов от электрического потенциала решается обратная задача по нахождению значений коэффициентов задержания и выходного потока растворителя, что можно эффективно использовать для прогнозирования механизма массопереноса и расчета электромембранных установок. Применение представленного подхода возможно и в зависимости от другого параметра, оказывающего влияние на массоперенос через мембраны – трансмембранного давления или концентрации растворенного вещества.
ЗАКЛЮЧЕНИЕ
Предложен усовершенствованный подход к прогнозированию кинетических характеристик электробаромембранного разделения растворов на основе фрикционной модели Шпиглера. Рассчитанные таким способом численные величины фрикционных коэффициентов взаимодействия компонентов и последующая аппроксимация позволяют определить их изменение, вследствие чего возможно спрогнозировать кинетические характеристики электробаромембранного разделения растворов при желаемых исходных параметрах.
В работе представлен пример расчета фрикционных коэффициентов f+m, f+ω, fωm между катионами и поверхностью мембраны, катионами и растворителем, растворителем и поверхностью мембраны соответственно. Выявлено увеличение абсолютных значений данных коэффициентов при повышении приложенного электрического потенциала практически во всех случаях. Исключением является массоперенос через прикатодные мембраны при разделении раствора Fe(NO3)3. Наименьшие абсолютные значения фрикционных коэффициентов характерны для разделения раствора CuSO4, наибольшие – для Fe(NO3)3.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 20-38-90024.
ОБОЗНАЧЕНИЯ
| a | химическая активность, моль м–3 |
| b, c, d | эмпирические коэффициенты |
| $\bar {c}$ | концентрация частиц в единице объема системы, моль м–3 |
| F | постоянная Фарадея, Кл моль–1 |
| Fi | движущая сила к 1 молю частиц i, Н моль–1 |
| Fij | сила внутреннего фрикционного взаимодействия между частицами i и j в единице объема, Н м–3 |
| f | коэффициент трения, Н с моль–1 м–1 |
| J | плотность потока, моль м–2 c–1 |
| L | диагональный коэффициент проводимости, моль2 с–1 Дж–1 м–1 |
| M | молярная масса, г/моль |
| n | нормированный коэффициент, Н с м2 моль–2 |
| p | трансмембранное давление, Па |
| R | универсальная газовая постоянная, м2 кг с–2 К–1 моль–1 |
| T | температура, К |
| V | мольный объем, м3 моль–1 |
| z | заряд иона |
| ε | относительная диэлектрическая проницаемость растворителя |
| ε0 | электрическая постоянная, Ф м–1 |
| ζ0 | дзета-потенциал у стенок мембраны, В |
| η | динамическая вязкость растворителя, Н с м–2 |
| µ | электрохимический потенциал относительно растворенного вещества или растворителя, Н м моль–1 |
| $v$ | абсолютная скорость движения, м с–1 |
| φ | электрический потенциал, В |
ИНДЕКСЫ
Список литературы
Пушкарева Т.П. Математическое моделирование как необходимый компонент математической подготовки // Соврем. пробл. науки образ. 2014. № 5. С. 796.
Никоненко В.В., Письменская Н.Д., Pourcelly G., Larchet C. Моделирование явлений переноса в системах с ионообменными мембранами // Мембраны и мембранные технологии / Под ред. Ярославцева А.Б. М.: Научный мир, 2013. Гл. 7.
Узденова А.М. Моделирование электроконвекции в мембранных системах: анализ граничных условий у поверхности // Фундам. исслед. 2016. № 12 (5). С. 1010.
Zabolotskii V.I., Bugakov V.V., Sharafan M.V., Chermit R.K. Transfer of electrolyte ions and water dissociation in anion-exchange membranes under intense current conditions // Russ. J. Electrochem. 2012. V. 48. № 6. P. 650. [Заболоцкий В.И., Бугаков В.В., Шарафан М.В., Чермит Р.Х. Перенос ионов электролита и диссоциация воды в анионообменных мембранах при интенсивных токовых режимах // Электрохимия. 2012. Т. 48. № 6. С. 721.]
Miękisz J., Gomułkiewicz J., Miękisz S. Mathematical models of ion transport through cell membrane channels // Math. Appl. 2014. V. 42. № 1. P. 39.
Bhadauria R., Aluru N.R. Multiscale modeling of electroosmotic flow: Effects of discrete ion, enhanced viscosity, and surface friction // J. Chem. Phys. 2017. V. 146. № 18. P. 184106.
Zabolotskii V.I., Lebedev K.A., Urtenov M.K., Nikonenko V.V., Vasilenko P.A., Shaposhnik V.A., Vasil’eva V.I. Mathematical model describing voltammograms and transport numbers under intensive electrodialysis modes // Russ. J. Electrochem. 2013. V. 49. № 4. P. 369. [Заболоцкий В.И., Лебедев К.А., Уртенов М.Х., Никоненко В.В., Василенко П.А., Шапошник В.А., Васильева В.И. Математическая модель для описания вольт-амперных кривых и чисел переноса при интенсивных режимах электродиализа // Электрохимия. 2013. Т. 49. № 4. С. 416.]
Vorotyntsev V.M., Drozdov P.N., Vorotyntsev I.V. Mathematical modeling of the fine purification of gas mixtures by absorption pervaporation // Theor. Found. Chem. Eng. 2011. V. 45. № 2. P. 180. [Воротынцев В.М., Дроздов П.Н., Воротынцев И.В. Математическое моделирование процесса глубокой очистки газов методом абсорбционной первапорации // Теор. осн. хим. технол. 2011. Т. 45. № 2. С. 194.]
Миголь В.Г., Хамизов Р.Х., Аскерния А.А., Корабельников В.М. Влияние намывной фильтрации и сорбции на массоперенос соединений кремния через обратноосмотические мембраны. I. Модель процесса // Сорбционные хроматогр. процессы. 2011. Т. 11. № 6. С. 865.
Zabolotskii V.I., Lebedev K.A., Shel’deshov N.V. Ion-transfer across a membrane in the presence of a preceding slow homogeneous chemical reaction in the diffusion layer // Russ. J. Electrochem. 2017. V. 53. № 9. P. 966. [Заболоцкий В.И., Лебедев К.А., Шельдешов Н.В. Перенос ионов через мембрану в условиях предшествующей медленной гомогенной химической реакции в диффузионном слое // Электрохимия. 2017. Т. 53. № 9. С. 1083.]
Antipov S.T., Klyuchnikov A.I. Mathematical modeling of microfiltration in a rectangular channel // Theor. Found. Chem. Eng. 2019. V. 53. № 1. P. 83. [Антипов С.Т., Ключников А.И. Математическое моделирование процесса микрофильтрации в канале прямоугольного сечения // Теор. осн. хим. технол. 2019. Т. 53. № 1. С. 87.]
Turaev D.Yu. Use of membrane electrolysis for recovery of heavy metal ions // Russ. J. Appl. Chem. 2007. V. 80. № 1. P. 83. [Тураев Д.Ю. Применение метода мембранного электролиза для извлечения ионов тяжелых металлов // Журн. прикл. хим. 2007. Т. 80. № 1. С. 84.]
Vinther F., Pinelo M., Brøns M., Jonsson G., Meyer A.S. Statistical modelling of the interplay between solute shape and rejection in porous membranes // Sep. Purif. Technol. 2012. V. 89. P. 261.
Кругликов С.С., Тураев Д.Ю., Бузикова А.М. Регенерация раствора травления меди в производстве печатных плат методом мембранного электролиза // Гальванотех. обраб. поверхн. 2009. Т. 17. № 1. С. 59.
Unije U.V., Mücke R., Baumann S., Guillon O. Comparison of the Simplification of the Pressure Profiles Solving the Binary Friction Model for Asymmetric Membranes // Membranes (Basel, Switz.). 2017. V. 7. № 4. P. 58.
Metaiche M., Sanchez-Marcano J. Theoretical Considerations of Pressure Drop and Mass Transfer of Gas Flow in Spiral Wound Membrane Modules // Int. J. Membr. Sci. Technol. 2016. V. 3. № 1. P. 12.
Мулдер М. Введение в мембранную технологию. М.: Мир, 1999.
Заболоцкий В.И., Никоненко В.В. Перенос ионов в мембранах. М.: Наука, 1996.
Берд Р., Стьюард В., Лайтфут Е. Явления переноса. М.: Химия, 1974.
Кестинг Р.Е. Синтетические полимерные мембраны. М.: Химия, 1991.
Чалых А.Е. Диффузия в полимерных системах. М.: Химия, 1987.
Николаев H.И. Диффузия в мембранах. М.: Химия, 1980.
Бадесса Т.С. Перенос многозарядных ионов через ионообменные мембраны при электродиализе. Дис. … канд. хим. наук. Воронеж: ВГУ, 2015.
Вережников В.Н. Практикум по коллоидной химии поверхностно-активных веществ. Воронеж: Воронежский университет, 1984.
Лазарев С.И., Ковалев С.В., Казаков В.Г. Исследования кинетических и структурных характеристик электробаромембранной очистки промывных вод производства 2,2'-дибензтиазолилдисульфида // Изв. высш. учебн. завед. Хим. хим. технол. 2016. Т. 59. № 2. С. 34.
Ковалев С.В., Лазарев С.И., Лазарев К.С., Попов Р.В. Удельный поток и коэффициент задержания мембраны МГА-95 при электробаромембранном разделении водного раствора сульфата цинка // Вестн. Тамбов. гос. тех. унив. 2015. Т. 21. № 1. С. 112.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии