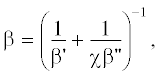Теоретические основы химической технологии, 2022, T. 56, № 2, стр. 148-157
Тепломассоперенос в плотном слое при дегидратации коллоидных и сорбционных капиллярно-пористых материалов в условиях нестационарного радиационно-конвективного энергоподвода
П. В. Акулич a, *, Д. С. Слижук a
a Институт тепло- и массообмена им. А.В. Лыкова НАН Беларуси
Минск, Беларусь
* E-mail: akul@hmti.ac.by
Поступила в редакцию 11.11.2021
После доработки 19.11.2021
Принята к публикации 03.12.2021
- EDN: SKOYTH
- DOI: 10.31857/S0040357122020026
Аннотация
Приведены результаты численного моделирования и экспериментального исследования тепломассопереноса в неподвижном продуваемом слое коллоидных капиллярно-пористых материалов растительного происхождения при циклическом радиационно-конвективном энергоподводе. Математическая модель состоит из уравнений сохранения массы газовой фазы, фильтрации, тепло- и массопереноса в фазах, которые учитывают внутреннее сопротивление переносу теплоты и влаги в частицах при определении коэффициентов тепло- и массоотдачи. Она учитывает зависимость удельной теплоты фазового перехода от влажности частиц, усадки частиц и высоты слоя в процессе дегидратации, зависимость эффективных коэффициентов теплопроводности газа и диффузии пара от скорости фильтрации. Приведены результаты моделирования дегидратации частиц картофеля в плотном слое при циклическом радиационно-конвективном энергоподводе. Показана возможность интенсификации дегидратации влаги и сокращения его продолжительности по сравнению с конвективным способом. Выполнено сравнение расчетных данных с опытными данными, подтверждающее адекватность модели. Приведены экспериментальные кинетические зависимости десорбции активированного угля и цеолита при конвективном и радиационно-конвективном энергоподводе. Результаты их сравнения свидетельствуют о заметном уменьшении длительности десорбции при дополнительном инфракрасном облучении, в частности для активированного угля процесс сокращается до двух раз.
ВВЕДЕНИЕ
В современных производствах и технологиях широкое распространение находят процессы сушки, термомеханохимической обработки и модификации материалов, которые характеризуются, как правило, высокой энергоемкостью и во многом определяют качество конечного продукта и его себестоимость. При этом с развитием экономики область их применения постоянно расширяется. К таким технологиям относятся переработка материалов растительного происхождения с получением сухих крупно- или мелкодисперсных продуктов, обезвоживание материалов в химической промышленности, в том числе регенерация различных сорбентов. Для сушки растительных материалов наиболее широкое распространение получили конвективные установки, в которых удельный расход теплоты достаточно велик и достигает 6–8 МДж/кг влаги и даже выше. Для интенсификации тепломассообменных процессов применяют способы воздействия электромагнитным излучением (инфракрасным, сверхвысокочастотным), вакуумирование среды, используют перегретый пар в качестве теплоносителя [1–6].
Основное отличие и преимущество терморадиационной сушки по сравнению с конвективной заключается в достижении больших удельных (на единицу площади) тепловых потоков. Оптические свойства материалов зависят как от свойств сухого скелета, так и в значительной степени от влажности и форм связи влаги, состояния поверхности и других свойств. Влагосодержание материала оказывает неоднозначное влияние на его оптические свойства. Отражательная способность материалов падает с повышением влажности для излучения с $\lambda $ = 1.4–15 мкм, что вызвано значительной поглощательной способностью воды в этом диапазоне длин волн [7]. Например, проникновение ИК-излучения в сырой картофель достигает 6 мм, а в сухой – 15–18 мм [8]. Глубина проникновения коротковолнового ИК-излучения в некоторые пищевые продукты достигает 7–30 мм [9]. Однако доля энергии излучения, проникающего даже на глубину 6 мм и более, сравнительно невелика. Вследствие больших плотностей потока ИК-излучения температура поверхностного слоя облучаемого материала обычно выше, чем при конвективной сушке, особенно в случае удаления связанной влаги. Растительные материалы термочувствительны и при повышении температуры теряют качество. В связи с этим находят дальнейшее развитие исследования с нестационарным циклическим воздействием энергетических полей, которые позволяют не только интенсифицировать тепломассообменные процессы и повысить их эффективность, но и снизить негативное тепловое влияние. В последнее время эти способы подвода энергии привлекают внимание исследователей, всесторонне изучаются и получают развитие и применение в новых технологиях и устройствах.
В работе [10] показано, что предварительное облучение ИК-излучением растительного сырья (например, яблок, айвы и дыни) перед сушкой сокращает длительность процесса и энергозатраты на 25–35% и улучшает качество конечного продукта, в частности приводит к уменьшению потерь витаминов.
В работе [11] приведены результаты исследования осциллирующей инфракрасной сушки семян овощных культур (огурцов, лука и др.). Показано, что применение данного способа при колебании температуры семян в процессе сушки от 34°С до 40°С вызывает стимуляцию семян, проявляющуюся в увеличении их энергии прорастания и всхожести. Наибольший стимулирующий эффект наблюдается при продолжительности осциллирующей инфракрасной сушки 40 мин.
В патенте [12] предложен импульсный инфракрасный способ сушки термолабильных материалов. Характерной особенностью данного способа является переменный по времени цикл “нагрев–охлаждение” с переменными в нем составляющими стадий нагрева и охлаждения. Этот режим достигается тем, что температура материала отслеживается бесконтактным пирометром и по достижении заданных значений максимальной и минимальной температур материала посредством регулирующего устройства осуществляется включение и отключение инфракрасных излучателей.
В обзоре [13] приводится критическое обсуждение применения и сравнительных характеристик инфракрасного излучения для сушки ряда пищевых материалов, включая зерно, фрукты, овощи и морепродукты. Отмечается, что радиационную сушку можно комбинировать с другими методами, такими как конвективный, вакуумный, сублимационный с целью увеличения скорости процесса, а также повышения эффективности. В [14] представлен обзор литературы за последние пять лет, посвященный разработке технологий сушки (микроволновой, инфракрасной, ультразвуковой) для фруктов и овощей. Отмечается, что эти методы сушки обеспечивают более высокую скорость процесса, термическую эффективность и позволяют получать высушенные продукты улучшенного качества (например, цвета, аромата, текстуры и сохранения питательных веществ) по сравнению с традиционной сушкой горячим воздухом. Кроме того, отмечается потребность в дальнейших исследованиях и разработках в этой области.
В работе [15] подчеркивается применимость и эффективность метода инфракрасной сушки для фруктов и овощей с высоким содержанием воды, в том числе, таких как киви, чеснок, различные разновидности грибов. Отмечается, что проводимые исследования в основном направлены на оптимизацию технологии сушки за счет изменения времени процесса и температуры, комбинирования различных способов энергоподвода для обеспечения высоких качественных показателей продуктов.
Моделирование кинетики и динамики процесса сушки осуществляют с применением различных подходов. Рассматривают одиночные частицы в условиях соответствующих по параметрам в сушильной камере [16]. Моделируют тепломассоперенос в дисперсном слое частиц на основе теории сплошной среды или метода Эйлера–Лагранжа, используют статистические методы и перколяционные модели. В работе [17] оценивается применимость метода инженерии химических реакций и равновесной энергии активации для моделирования инфракрасной и других способов сушки. В [18] приводятся двухфазные модели тепломассопереноса в плотном дисперсном слое при конвективном и комбинированном нагреве. Однако не учитывается диффузионное сопротивление во влажных частицах и сорбционные их свойства. В [19] рассматривается моделирование процесса сушки растительных материалов в ленточной установке на основе уравнений переноса и определения интенсивности испарения с использованием энергии активации.
Целью настоящей работы является исследование тепломассообмена при дегидратации растительных и сорбционных материалов в плотном слое при нестационарном радиационно-конвективном энергоподводе для выявления возможности интенсификации процесса и повышения его эффективности.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
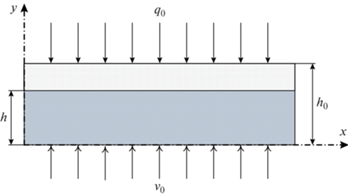
Постановка задачи. Сущность физической модели тепломассообмена влажного материала при нестационарном радиационно-конвективном воздействии состоит в следующем. Рассматривается слой дисперсного коллоидного капиллярно-пористого материала, который находится в неподвижном состоянии (рис. 2.1 ). Он может также перемещаться на движущейся ленте и принудительно перемешиваться. Слой материала продувается снизу вверх теплоносителем (нагретым воздухом) со скоростью ${{v}_{0}}.$ Такие способы обработки влажных материалов применяются в конвективных ленточных, конвейерных и камерных полочных установках. Для интенсификации тепломассообмена дисперсный слой сверху подвергается воздействию инфракрасного излучения.
Радиационное воздействие может быть как стационарным, так и циклическим (импульсным). При этом возможно ступенчатое или осциллирующее конвективное воздействие на различных этапах обработки. Эти режимы направлены на создание щадящих условий теплового воздействия и снижения удельного расхода теплоты на процесс удаления влаги.
Математическая модель. Описание тепломассопереноса в дисперсном слое учитывает процессы фильтрации, диффузии, десорбции и энергии связи влаги с материалом, фазовое превращение жидкости, межфазный обмен энергией и массой, термическое и диффузионное сопротивление внутри частиц, а также нестационарный радиационно-конвективный подвод энергии.
Модель включает следующие уравнения. Уравнение сохранения массы газовой фазы
(1)
$\frac{{\partial {{\rho }_{1}}}}{{\partial \tau }} + \nabla \cdot \left( {{{\rho }_{1}}{\mathbf{w}}} \right) = {{j}_{п}}.$Уравнение движения Дарси
где ${\mathbf{v}} = {\mathbf{w}}\varepsilon ,$ ${\mathbf{v}}$ – скорость газа, рассчитанная на соответствующую площадь поперечного сечения дисперсного слоя, т.е. скорость фильтрации, м/с.Тогда
(3)
$\frac{{\partial \left( {\rho _{1}^{^\circ }\varepsilon } \right)}}{{\partial \tau }} + \nabla \cdot \left( {\rho _{1}^{^\circ }{\mathbf{v}}} \right) = {{j}_{п}}.$Уравнение переноса пара в дисперсном (зернистом) слое
(4)
$\frac{{\partial \left( {\rho _{{\text{п}}}^{^\circ }\varepsilon } \right)}}{{\partial \tau }} + {\mathbf{v}}\nabla \rho _{п}^{^\circ } = \nabla \cdot \left( {{{D}_{{п.эф}}}\nabla \rho _{п}^{^\circ }} \right) + {{j}_{п}}.$Уравнение переноса теплоты в газовой фазе слоя
(5)
$\begin{gathered} {{c}_{1}}\rho _{1}^{^\circ }\left( {\varepsilon \frac{{\partial {{T}_{1}}}}{{\partial \tau }} + {\mathbf{v}}\nabla {{T}_{1}}} \right) = \\ = \,\,\nabla \cdot \left( {{{\lambda }_{{1эф}}}\nabla {{T}_{1}}} \right) - \alpha {{S}_{{уд}}}\left( {{{T}_{1}} - {{T}_{2}}} \right). \\ \end{gathered} $Зависимости эффективных коэффициентов теплопроводности газовой фазы и диффузии пара от скорости фильтрации учитывались с использованием следующих выражений в направлении соответствующих осей: ${{\lambda }_{{1y.эф}}}$ = ${{\lambda }_{1}}\left( {\varepsilon + 0.5\operatorname{Pe} } \right),$ ${{\lambda }_{{1x.эф}}}$ = ${{\lambda }_{1}}\left( {\varepsilon + 0.1\operatorname{Pe} } \right)$ и ${{D}_{{п.эф}}}$ = ${{D}_{п}}\varepsilon + 0.5{{d}_{ч}}{\mathbf{v}}$ [20, 21].
Уравнение переноса влаги в твердой фазе
(6)
$\left( {1 - \varepsilon } \right)\frac{{\partial U}}{{\partial \tau }} = \nabla \cdot \left( {{{D}_{{эф}}}\nabla U} \right) - {{j}_{п}}.$В случае, если слой дисперсного материала неподвижен, то величина эффективного коэффициента диффузии влаги мала и стремится к нулю. При принудительном перемешивании дисперсного слоя, например горизонтальной мешалкой, в рамках диффузионной модели эффективный коэффициент диффузии значительно возрастает. Его величину по высоте слоя можно оценить по соотношению ${{D}_{{x.эф}}} = {{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} {{{\tau }_{{cм}}}}}} \right. \kern-0em} {{{\tau }_{{cм}}}}},$ где ${{\tau }_{{cм}}}$ – характерное время смешения (характеризует время выравнивания концентрации влаги по высоте слоя). Для случая циклического (импульсного) перемешивания слоя коэффициент диффузии является функцией времени.
Уравнение переноса теплоты в твердой фазе слоя
(7)
$\begin{gathered} {{c}_{2}}{{\rho }_{c}}\left( {1 - \varepsilon } \right)\frac{{\partial {{T}_{2}}}}{{\partial \tau }} = \nabla \cdot \left( {{{\lambda }_{{2эф}}}\nabla {{T}_{2}}} \right) + \alpha {{S}_{{уд}}}\left( {{{T}_{1}} - {{T}_{2}}} \right) - \\ - \,\,{{r}_{п}}{{j}_{п}} + \left( {1 - \varepsilon } \right)I, \\ \end{gathered} $Влияние перемешивания слоя на перенос теплоты дисперсной фазой в рамках диффузионной модели можно учитывать за счет изменения величины эффективного коэффициента теплопроводности ${{\lambda }_{{2эф}}}.$ Процессы переноса в газовой фазе в меньшей степени зависят от скорости перемешивания слоя, поэтому его влиянием на эти процессы пренебрегается.
Интенсивность массоотдачи от твердой фазы в газовую фазу
(8)
${{j}_{п}} = {{\beta }_{u}}{{S}_{{уд}}}\left[ {u - {{u}_{р}}\left( {{{p}_{п}},{{T}_{1}}} \right)} \right].$Для описания изотермы сорбции (десорбции) материалов используется аппроксимационная формула [22]:
(9)
${{u}_{р}} = {{u}_{{0.5}}}\left( T \right){{\left( {\frac{{{{p}_{п}}}}{{{{p}_{н}} - {{p}_{п}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}},$Диффузионный перенос влаги в частицах материала учитывается в определении коэффициента массоотдачи. Последний определяется как коэффициент массопередачи, учитывающий сопротивление массоотдачи с поверхности частиц и внутридиффузионное сопротивление переносу влаги по формуле [24]:
где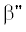 – коэффициент, учитывающий сопротивление диффузии влаги,
– коэффициент, учитывающий сопротивление диффузии влаги, 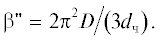
Плотность газовой смеси и водяных паров определяется по уравнению состояния идеального газа $\rho _{1}^{^\circ }$ = ${{p{{M}_{1}}} \mathord{\left/ {\vphantom {{p{{M}_{1}}} {\left( {R{\text{*}}{{T}_{1}}} \right)}}} \right. \kern-0em} {\left( {R{\text{*}}{{T}_{1}}} \right)}}$ и $\rho _{п}^{^\circ } = {{{{p}_{п}}{{M}_{п}}} \mathord{\left/ {\vphantom {{{{p}_{п}}{{M}_{п}}} {\left( {R{\text{*}}{{T}_{1}}} \right)}}} \right. \kern-0em} {\left( {R{\text{*}}{{T}_{1}}} \right)}}.$
Количество теплоты, выделяемое в частицах материала при воздействии инфракрасного излучения
(11)
$I = \delta \left( \tau \right)k{\kern 1pt} '{{q}_{0}}\left( {1 - {{R}_{{отр}}}} \right)\exp \left[ { - k{\kern 1pt} '\left( {1 - \varepsilon } \right)\left( {h - y} \right)} \right],$В процессе дегидратации коллоидных капиллярно-пористых материалов имеет место значительная деформация частиц и дисперсного слоя. При этом уменьшаются объем, размер частиц и высота слоя материала.
Скорость движения слоя материала по вертикальной координате вследствие усадки представим в виде [25]:
Скорость движения нижней границы слоя при $y = 0$ равна нулю ${{v}_{г}} = 0,$ а скорость верхней границы максимальна ${\text{v}} = {{v}_{г}}.$ Перемещение верхней границы слоя за время $\tau $ составит $\Delta h = {{h}_{0}} - h = {{{{v}_{г}}\tau y} \mathord{\left/ {\vphantom {{{{v}_{г}}\tau y} h}} \right. \kern-0em} h},$ где $0 \leqslant \tau \leqslant {{\tau }_{{к.у}}},$ ${{\tau }_{{к.у}}}$ – время завершения процесса усадки слоя, после достижения которого, усадкой слоя можно пренебречь. Процесс усадки происходит и в поперечном (горизонтальном) направлении вдоль оси x. Однако в промышленных аппаратах высота слоя обычно значительно меньше его ширины, причем продувка теплоносителем осуществляется в вертикальном направлении. Поэтому усадка слоя по горизонтальной оси не оказывает существенного влияния на процессы тепломассопереноса и ей можно пренебречь в данной задаче.
Уравнение переноса влаги в твердой фазе для двухмерного случая с учетом усадки слоя по высоте представим в виде
(13)
$\begin{gathered} \left( {1 - \varepsilon } \right)\left( {\frac{{\partial U}}{{\partial \tau }} + {\text{v}}\frac{{\partial U}}{{\partial y}}} \right) = \frac{\partial }{{\partial x}}\left( {{{D}_{{x.эф}}}\frac{{\partial U}}{{\partial x}}} \right) + \\ + \,\,\,\frac{\partial }{{\partial y}}\left( {{{D}_{{y.эф}}}\frac{{\partial U}}{{\partial y}}} \right) - {{j}_{п}}. \\ \end{gathered} $Среднеобъемное текущее значение влагосодержания слоя определяется по формуле
(14)
$\bar {U} = \frac{1}{{hl}}\int\limits_0^{h\left( \tau \right)} {\int\limits_0^l {U\left( {x,y,\tau } \right)} } dxdy,$Уравнение переноса теплоты в твердой фазе соответственно запишется
(15)
$\begin{gathered} c{{\rho }_{c}}\left( {1 - \varepsilon } \right)\left[ {\frac{{\partial {{T}_{2}}}}{{\partial \tau }} + {\text{v}}\frac{{\partial {{T}_{2}}}}{{\partial y}}} \right] = \frac{\partial }{{\partial x}}\left( {{{\lambda }_{{2x.эф}}}\frac{{\partial {{T}_{2}}}}{{\partial x}}} \right) + \\ + \,\,\frac{\partial }{{\partial y}}\left( {{{\lambda }_{{2y.эф}}}\frac{{\partial {{T}_{2}}}}{{\partial y}}} \right) + \alpha {{S}_{{уд}}}\left( {{{T}_{1}} - {{T}_{2}}} \right) - {{r}_{п}}{{j}_{п}} + \left( {1 - \varepsilon } \right)I. \\ \end{gathered} $Процессы переноса в газовой фазе в меньшей степени зависят от скорости деформации слоя, поэтому влиянием скорости деформации на эти процессы пренебрегается.
Усадка собственно объема частиц сырого картофеля учитывалась на основе опытных данных по зависимости $V = {{b}_{1}}u + {{b}_{2}},$ где $V$ – объем частицы, м3; ${{b}_{1}} = 4.76 \times {{10}^{{ - 8}}},$ ${{b}_{2}} = 9.95 \times {{10}^{{ - 8}}}$ – эмпирические постоянные.
Уменьшение высоты дисперсного слоя в процессе дегидратации описывалось эмпирическим уравнением $h = {{b}_{3}}u + {{b}_{4}},$ где ${{b}_{3}} = 0.0015,$ ${{b}_{4}} = 0.006$ – эмпирические постоянные. Зависимость высоты слоя от объемной концентрации влаги (влагосодержания) имеет вид $h = {{b}_{5}}{{U}^{2}} - {{b}_{6}}U + {{b}_{7}},$ где ${{b}_{5}} = 8 \times {{10}^{{ - 9}}},$ ${{b}_{6}} = 1 \times {{10}^{{ - 6}}},$ ${{b}_{7}} = 0.0062.$
Скорость перемещения верхней границы
Коэффициент влагопроводности находится по эмпирической формуле [26]:
(17)
$D(u,T) = {{a}_{0}}\exp ({{ - {{a}_{1}}} \mathord{\left/ {\vphantom {{ - {{a}_{1}}} u}} \right. \kern-0em} u})\exp ( - {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {T)}}} \right. \kern-0em} {T)}},$Удельная теплота испарения влаги находится из уравнения Клапейрона–Клаузиуса
(18)
${{r}_{п}} = \frac{{R{\text{*}}{{T}^{2}}}}{{{{M}_{п}}}}\left( {\frac{1}{{{{p}_{н}}}}\frac{{\partial {{p}_{н}}}}{{\partial T}} - \frac{{nu_{{0.5}}^{{n - 1}}}}{{u_{{0.5}}^{n} + u_{р}^{n}}}\frac{{\partial {{u}_{{0.5}}}}}{{\partial T}}} \right),$Давление насыщенного водяного пара ${{p}_{н}}$ в диапазоне температур от 0 до 100°С определяется по приближенной формуле Антуана
Коэффициент диффузии водяных паров в воздухе ${{D}_{п}} = {{D}_{0}}\left( {{{{{p}_{0}}} \mathord{\left/ {\vphantom {{{{p}_{0}}} p}} \right. \kern-0em} p}} \right){{\left( {{T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},$ где ${{D}_{0}} = 22 \times {{10}^{{ - 6}}}$ м2/с, ${{p}_{0}} = 101325$ Па, ${{T}_{0}} = 273$ К.
Коэффициент теплоотдачи в неподвижном зернистом слое определяется по выражению [27]:
где ${{\operatorname{Re} }_{э}} = {{v{{d}_{э}}} \mathord{\left/ {\vphantom {{v{{d}_{э}}} \nu }} \right. \kern-0em} \nu } = {{4v} \mathord{\left/ {\vphantom {{4v} {\left( {{{S}_{{уд}}}\nu } \right)}}} \right. \kern-0em} {\left( {{{S}_{{уд}}}\nu } \right)}}.$Коэффициент теплоотдачи рассчитывается с учетом термического сопротивления теплопроводности частиц по формуле [23]:
(21)
$\alpha = \frac{1}{{\frac{{{{d}_{э}}}}{{{{\lambda }_{ч}}{{{\operatorname{Nu} }}_{э}}}} + \frac{3}{2}\frac{{{{d}_{ч}}}}{{{{\pi }^{2}}{{\lambda }_{ч}}}}}}.$Допуская аналогию процессов тепло- и массообмена, коэффициент массоотдачи определяется по формуле подобной (20).
Система уравнений решалась при следующих граничных условиях (рис. 1). Для уравнения (3) сохранения массы газовой фазы: ${{\left. { - {\mathbf{n}} \cdot {\mathbf{v}}} \right|}_{{x = 0;x = l}}} = 0;$ ${{\left. { - {\mathbf{n}}\, \cdot {\mathbf{v}}} \right|}_{{y = 0}}} = {{v}_{0}};$ ${{\left. p \right|}_{{y = h}}} = {{p}_{0}}.$ Для уравнения (4) переноса пара: ${{\left. {{\mathbf{n}} \cdot \left( { - {{D}_{{п.эф}}}\nabla \rho _{п}^{^\circ } + \rho _{п}^{^\circ }{\mathbf{v}}} \right)} \right|}_{{x = 0;x = l}}} = 0$ – условие непроницаемости; ${{\left. {\rho _{п}^{^\circ }} \right|}_{{y = 0}}} = \rho _{{п0}}^{^\circ };$ ${{\left. {{\mathbf{n}} \cdot \left( { - {{D}_{{п{\kern 1pt} {\text{.}}эф}}}\nabla \rho _{п}^{^\circ }} \right)} \right|}_{{y = h}}}$ = = 0. Для уравнения (5) переноса теплоты в газовой фазе: ${{\left. {{{T}_{1}}} \right|}_{{y = 0}}} = {{T}_{{10}}},\,\,{{\left. {{\mathbf{n}} \cdot \left( { - {{\lambda }_{{1{\kern 1pt} эф}}}\nabla {{T}_{1}}} \right)} \right|}_{{y = h}}} = 0$, а остальные границы теплоизолированы. Для уравнений (6), (7) и соответственно (13), (15) переноса влаги и теплоты в твердой фазе ${{\left. {{\mathbf{n}} \cdot \left( { - {{\lambda }_{{2эф}}}\nabla {{T}_{2}}} \right)} \right|}_{{y = 0;\,\,y = h}}} = 0$, остальные границы тепло- и влагоизолированы.
Таким образом, получена замкнутая система дифференциальных уравнений тепло- и массопереноса в неподвижном и перемешиваемом дисперсном слое с учетом вышеуказанных явлений при нестационарном радиационно-конвективном энерговоздействии.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ И СРАВНЕНИЕ С ОПЫТНЫМИ ДАННЫМИ
Исследовался тепломассоперенос в неподвижном слое частиц картофеля сорта “Скарб”. Слой продувался нагретым воздухом снизу вверх. Частицы представляли собой кубики размером ~7 × 7 × × 7 мм. Влажный материал укладывался на сетчатую решетку в два слоя частиц, при этом начальная высота слоя ${{h}_{0}}$ составляла около 14 мм. После усадки частицы материала располагались в один ряд по высоте. Дисперсный слой влажного материала продувался теплоносителем (нагретым воздухом) с небольшой скоростью в режиме фильтрации. Скорость воздуха, рассчитанная на сечение слоя, в среднем составляла около 0.5 м/с, а его температура на входе в слой – 50–60°С. Лучистый поток направлялся на слой материала сверху по нормали к нему. Для предотвращения перегрева материала инфракрасным излучением воздействовали циклически (импульсно) во времени. Через заданные промежутки времени определялась масса слоя. В результате были получены кривые кинетики сушки. Для аналогичных условий получено численное решение вышеприведенной системы уравнений с использованием программы “Comsol” для нестационарного двухмерного тепломассопереноса в слое с учетом деформации (усадки) частиц и слоя по высоте при радиационно-конвективном энергоподводе.
Основные параметры, при которых выполнялись расчеты: $k = 1 \times {{10}^{{ - 8}}}$ м2; ${{\mu }_{1}} = 20 \times {{10}^{{ - 6}}}$ Па ∙ с; ${{c}_{1}} = 1.006$ кДж/(кг ∙ К); ${{\lambda }_{1}} = 0.029$ Вт/(м ∙ К); ${{D}_{{эф}}} = 5 \times {{10}^{{ - 12}}}$ м2/с; $R* = 8314.2$ Дж/(кмоль ∙ К); ${{M}_{п}} = 18.02$ кг/кмоль; ${{\rho }_{c}} = 175$ кг/м3; u0 = 5.2 кг/кг; ${{U}_{0}} = 910$ кг/м3 твердой фазы; ${{S}_{{уд}}} = 428.6$ м2/м3; ${{v}_{0}} = 0.5$ м/с; ${{h}_{0}} = 0.014$ м; ${{T}_{{10}}} = 333$ К; q0 = 8.8 × × 103 Вт/м2; ${{R}_{{отр}}} = 0.05;$ $k{\kern 1pt} ' = 220;$ $\varepsilon = 0.5.$
На рис. 2 отчетливо видно, что циклическое воздействие инфракрасным излучением на дисперсный слой материала приводит к увеличению скорости дегидратации и сокращению его продолжительности по сравнению с конвективным способом за счет интенсификации тепломассообменных процессов. Сопоставление результатов численного моделирования с опытными данными свидетельствует об их удовлетворительном соответствии. Более заметное расхождение наблюдается в первый период процесса. Это, по-видимому, связано с неравномерностью газораспределения по сечению слоя в экспериментальном исследовании вследствие небольшой высоты слоя материала. Форма кривой дегидратации с большой долей периода падающей скорости указывает на преобладающее влияние внутридиффузионного переноса влаги на продолжительность процесса.
Рис. 2.
Кинетические зависимости дегидратации частиц сырого картофеля при конвективном и радиационно-конвективном энергоподводе в продуваемом слое: 1 – циклический радиационно-конвективный энергоподвод: время ~0–20 мин, (${{\tau }_{{изл}}}$ + ${{\tau }_{п}}$) × количество циклов: (2 + 1) × 6; ~20–40 мин: (1 + 2) × 6 и далее конвективный подвод теплоты; 2 – расчетная кривая; 3 – конвективный энергоподвод. ${{t}_{1}} = 60^\circ {\text{С,}}$ $v = 0.5$ м/с; начальная высота слоя материала ${{h}_{0}} = 14$ мм.

Влагосодержание частиц по высоте слоя в процессе дегидратации отличается незначительно. При этом влагосодержание частиц в верхней области слоя снижается несколько быстрее в первом периоде.
В начальный момент времени дисперсный слой имеет равномерное распределение температуры частиц ${{t}_{2}} = 20^\circ {\text{C}}{\text{.}}$ Вследствие радиационного и конвективного энергоподвода происходит более быстрый прогрев слоя по сравнению с конвективным подводом теплоты. При этом температура частиц в слое носит колебательный характер с возрастанием амплитуды с течением времени (рис. 3).
Рис. 3.
(a) Зависимости температуры частиц в дисперсном слое от времени: 1 – $y = 0;$ 2 – $y = 0.5h;$ 3 – $y = h.$ $x = 0.06$ м. (б) Зависимости температуры газа в дисперсном слое от времени: 1 – $y = 0;$ 2 – $y = 0.5h;$ 3 – $y = h.$ $x = 0.06$ м.
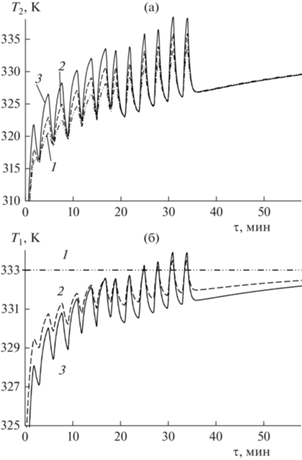
В начале процесса в периоды воздействия инфракрасного излучения температура частиц не достигает максимально допустимой температуры и только после прогрева слоя и снижения влагосодержания температура частиц в циклах повышается, однако носит кратковременный характер. Как видно, в периоды отключения инфракрасного излучения температура частиц быстро снижается и стремится к температуре мокрого термометра или газа. Видно, что по истечении 30–40 мин при радиационном облучении температура слоя быстро возрастает, поэтому целесообразно применение циклического (импульсного) воздействия. Отметим, что для предотвращения перегрева частиц продолжительность периодов облучения уменьшалась после прогрева слоя. В периоды инфракрасного воздействия температура частиц в верхних областях слоя выше, чем в нижних его областях (рис. 4).
Рис. 4.
(а) Температурное поле твердой фазы дисперсного слоя в цикле охлаждения при $\tau = 1970$ с. (б) Температурное поле твердой фазы дисперсного слоя в цикле нагрева при $\tau = 2030$ с.
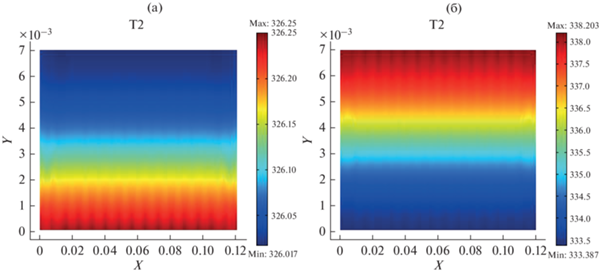
Однако эта разница незначительна. Наибольшая разность наблюдается при прогреве слоя. Во время охлаждения температура слоя заметно снижается, причем температура слоя по его высоте различается незначительно. Высота слоя вследствие усадки частиц заметно уменьшается, что видно по изменению вертикальной координаты y.
Температура газа на входе в слой задавалась постоянной и равной ${{t}_{1}} = 60^\circ {\text{C}}{\text{.}}$ На рис. 3 видно, что температуры газа и частиц внутри дисперсного слоя имеют подобные периодические зависимости. При этом температура газа на поверхности слоя в начале процесса ниже, чем в середине слоя, а затем становится выше. Максимальная температура газа в активные периоды облучения несколько ниже, чем температура частиц.
Концентрация водяных паров быстро возрастает в начальный период процесса и становится выше в верхних сечениях слоя. С течением времени она снижается, имея колебательную зависимость, и стремится к значению на входе в слой (рис. 5).
Рис. 5.
Зависимости концентрации водяных паров в дисперсном слое от времени: 1 – $y = 0;$ 2 – $y = 0.5h;$ 3 – $y = h.$ $x = 0.06$ м.

Интересные зависимости получены для градиента концентрации влаги в дисперсной фазе от времени, которые имеют максимум (рис. 6).
Рис. 6.
Зависимости градиента концентрации влаги в дисперсной фазе слоя от времени: 1 – $y = 0;$ 2 – $y = 0.5h;$ 3 – $y = h.$ $x = 0.06$ м.

При этом величина максимума существенно возрастает при переходе в верхние слои (кривая 3) и смещается в область больших времен. Градиент влагосодержания оказывает влияние на деформацию частиц и представляет интерес для задач, в которых это обстоятельство имеет важное значение.
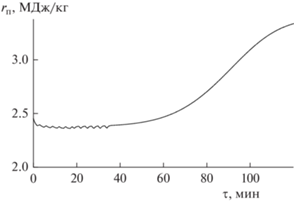
На рис. 7 видно, что удельная теплота испарения связанной влаги заметно изменяется с течением времени, вследствие уменьшения влагосодержания частиц. В начале процесса она несколько уменьшается, что вызвано ростом температуры частиц. При переходе к удалению связанной влаги удельная теплота испарения заметно возрастает, что обусловлено энергией связи влаги с материалом. Вследствие малого перепада влагосодержания частиц по высоте слоя теплота испарения также незначительно изменяется по вертикальной координате.
Исследования усадки дисперсного слоя, приведенные на рис. 8а свидетельствуют о том, что изменение высоты слоя происходит преимущественно при дегидратации свободной влаги. Далее изменение высоты слоя не столь значительно. На рис. 8б приведено изменение объема частиц в зависимости от их влагосодержания. Результаты экспериментальных данных аппроксимировались линейной зависимостью. Видно, что высота слоя материала и объем частиц значительно уменьшаются в процессе дегидратации, что следует учитывать при моделировании таких процессов.
Рис. 8.
(a) Зависимости усадки дисперсного слоя: 1 – $y = 0;$ 2 – $y = 0.5h;$ 3 – $y = h.$ (б) Зависимости усадки частиц.

Выполнены экспериментальные исследования кинетики сушки сорбционных материалов активированного угля и цеолита CaX. Процессы сушки (десорбции) имеют место при регенерации активированного угля, используемого для очистки воды. Гранулированный цеолит в технологиях сушки находит применение для осушки воздуха, при этом его необходимо регенерировать путем десорбции. Десорбция материалов проводилась радиационно-конвективным способом следующим образом. Диаметр шарообразных частиц активированного угля лежит в диапазоне 1‒2.2 мм, а гранулы цеолита цилиндрической формы имеют диаметр ~3 мм и высоту 4‒5 мм. Влажный материал насыпался на сетчатую решетку в виде слоя небольшой высоты. Высота слоя активированного угля составляла около 5 мм, а цеолита ~7 мм. При конвективной десорбции слой материала продувался нагретым воздухом с температурой на входе 150°С. Скорость фильтрации воздуха составляла около 0.2 м/с. При радиационно-конвективном энергоподводе слой влажного материала продувался нагретым до 150°С воздухом и облучался сверху инфракрасным излучением. В качестве излучателя служил керамический нагреватель ICH-101 фирмы “Номакон”. Мощность излучателя 1 кВт, температура поверхности ~690°С, расстояние расположения излучателя от слоя 300 мм. Кинетические зависимости при указанных способах энергоподвода приведены на рис. 9.
Рис. 9.
(a) Экспериментальные кинетические зависимости десорбции активированного угля: 1 ‒ при конвективном подводе теплоты; 2 ‒ радиационно-конвективном энергоподводе. (б) Экспериментальные кинетические зависимости десорбции цеолита: 1 ‒ при конвективном подводе теплоты; 2 ‒ радиационно-конвективном энергоподводe.
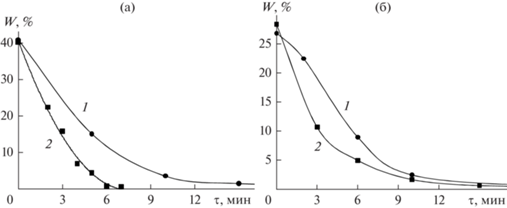
Из их сравнения видно, что воздействие инфракрасным излучением на слой материала позволяет заметно сократить продолжительность процесса десорбции, так для активированного угля до двух раз при данном режиме.
Радиационно-конвективный способ десорбции может быть использован для регенерации сорбентов при осушке воздуха в сушильных установках, в том числе для материалов растительного происхождения.
ЗАКЛЮЧЕНИЕ
В результате численного моделирования и экспериментальных исследований установлены зависимости кинетики дегидратации и усадки частиц, тепломассообмена в неподвижном слое коллоидных капиллярно-пористых материалов растительного происхождения, на примере частиц сырого картофеля, при конвективном и циклическом радиационно-конвективном энергоподводе. Показана адекватность расчетных результатов опытным данным и возможность значительной интенсификации процесса дегидратации и сокращения его продолжительности.
Экспериментально получены кинетические зависимости десорбции активированного угля и цеолита при конвективном и радиационно-конвективном энергоподводе. Результаты их сравнения свидетельствуют о заметном уменьшении длительности десорбции при дополнительном инфракрасном облучении, в частности для активированного угля процесс сокращается до двух раз.
ОБОЗНАЧЕНИЯ
| $c$ | удельная теплоемкость, Дж/(кг · К) |
| ${{c}_{c}},{{c}_{ж}}$ | удельная теплоемкость сухих частиц и жидкости, Дж/(кг · К) |
| ${{d}_{ч}},{{d}_{э}}$ | эквивалентный диаметр частиц и каналов, м |
| $h$ | высота слоя материала, м |
| $k$ | коэффициент проницаемости слоя частиц, м2 |
| $k{\kern 1pt} '$ | показатель поглощения |
| $M$ | молекулярная масса, кг/кмоль |
| ${{p}_{п}}$ | парциальное давление водяных паров в слое, Па |
| ${{q}_{0}}$ | плотность потока инфракрасного излучения падающего на поверхность слоя, Вт/м2 |
| ${{r}_{п}}$ | удельная теплота парообразования, Дж/кг |
| $R{\text{*}}$ | универсальная газовая постоянная, Дж/(кмоль · К) |
| ${{R}_{{отр}}}$ | коэффициент отражения |
| ${{R}_{п}}$ | газовая постоянная для водяного пара, Дж/(кг · К) |
| ${{S}_{{уд}}}$ | удельная поверхность слоя, м2/м3 |
| $T$ | температура, К |
| $u$ | влагосодержание частиц, кг/кг, $u = {U \mathord{\left/ {\vphantom {U {{{\rho }_{c}}}}} \right. \kern-0em} {{{\rho }_{c}}}}$ |
| $U$ | объемное влагосодержание, кг/м3 частицы |
| ${\mathbf{v}}$ | скорость фильтрации газа, м/с |
| ${\mathbf{w}}$ | скорость газа в зазорах между частицами слоя, м/с |
| $W$ | влажность материала, кг влаги/кг влажного материала или % |
| $x$ и $y$ | горизонтальная и вертикальная координаты, м |
| $\alpha $ | коэффициент теплоотдачи, Вт/(м2 ∙ К) |
| ${{\beta }_{u}} = {{\beta }_{p}}{{\Delta {{p}_{п}}} \mathord{\left/ {\vphantom {{\Delta {{p}_{п}}} {\Delta u}}} \right. \kern-0em} {\Delta u}}$ | коэффициент массоотдачи, отнесенный к разности влагосодержаний, кг/(м2 · с · кг/кг) |
| ${{\beta }_{p}} = {\beta \mathord{\left/ {\vphantom {\beta {\left( {{{R}_{п}}\bar {T}} \right)}}} \right. \kern-0em} {\left( {{{R}_{п}}\bar {T}} \right)}}$ | коэффициент массоотдачи, отнесенный к разности парциальных давлений пара, кг/(м2 · с · Па) |
| $\beta {\kern 1pt} '$ | коэффициент массоотдачи, отнесенный к разности концентраций, кг/(м2 · · с · кг/м3) |
| $\varepsilon $ | порозность слоя |
| $\chi = {{{{\rho }_{ж}}} \mathord{\left/ {\vphantom {{{{\rho }_{ж}}} {{{\rho }_{п}}}}} \right. \kern-0em} {{{\rho }_{п}}}}$ | равновесное соотношение плотностей жидкости и пара |
| $\lambda $ | коэффициент теплопроводности, Вт/(м · К) |
| ${{\mu }_{п}}$ | динамический коэффициент вязкости пара, Па · с |
| $\rho _{1}^{^\circ }$ и ${{\rho }_{1}}$ | истинная и приведенная плотность газовой фазы (сухого воздуха и водяных паров), кг/м3, ${{\rho }_{1}} = \varepsilon \rho _{1}^{^\circ }$ |
| ${{\rho }_{2}}$ и ${{\rho }_{c}}$ | плотность влажных и сухих частиц, кг/м3 |
| $\tau $ | время, с |
| ${{\tau }_{{изл}}},{{\tau }_{п}}$ | продолжительность облучения и пауза в цикле, с |
| ${{\operatorname{Re} }_{э}}$ | число Рейнольдса |
| ${{\operatorname{Nu} }_{э}} = {{{{\alpha {\kern 1pt} '{{d}_{э}}} \mathord{\left/ {\vphantom {{\alpha {\kern 1pt} '{{d}_{э}}} \lambda }} \right. \kern-0em} \lambda }}_{1}},$$\operatorname{Nu} _{э}^{'} = {{\beta {{d}_{э}}} \mathord{\left/ {\vphantom {{\beta {{d}_{э}}} {{{D}_{п}}}}} \right. \kern-0em} {{{D}_{п}}}}$ | тепловое и диффузионное числа Нуссельта |
| $\Pr = {\nu \mathord{\left/ {\vphantom {\nu a}} \right. \kern-0em} a}$ | число Прандтля |
ИНДЕКСЫ
Список литературы
Акулич П.В. Расчеты сушильных и теплообменных установок. Минск: Беларуская навука, 2010.
Акулич П.В., Акулич А.В. Конвективные сушильные установки: методы и примеры расчета. Минск: Вышэйшая школа, 2019.
Акулич П.В., Слижук Д.С. Тепловлагоперенос в неподвижном дисперсном слое растительных материалов при комбинированном энергоподводе // Инж.-физ. журн. 2020. Т. 93. № 4. С. 800.
Нестеров А.В. Сушка. Санкт Петербург. Процессы и аппараты химической технологии. 2020.
Тепляшин В.Н., Ченцова Л.И., Невзоров В.Н. Технологии и оборудование для сушки растительного сырья [Электронный ресурс]: учеб. пособие; Краснояр. гос. аграр. ун-т. Красноярск, 2019.
Kumar C. Microwave-convective drying of food materials: A critical review // Critical Review in Food Science and Nutrition. 2019. V. 59. Issue 3. P. 379.
Гинзбург А.С. Основы теории и техники сушки пищевых продуктов. М.: Пищевая пром-сть, 1973.
Атаназевич В.И. Сушка пищевых продуктов: Справочное пособие. М.: ДеЛи, 2000.
Гинзбург А.С. Инфракрасная техника в пищевой промышленности. М.: Пищевая пром-сть, 1966.
Снежкин Ю.Ф., Боряк Л.А., Избасаров Д.С. Энергосбережение и интенсификация процесса сушки импульсным ИК-облучением // Промышленная теплотехника. 2001. Т. 23. № 4–5. С. 90.
Рудобашта С.П., Зуева Г.А., Зуев А.И. Осциллирующая инфракрасная сушка и стимуляция семян // Тезисы докладов и сообщений XV Минского межд. форума по тепло- и массообмену 23–26 мая 2016. Минск, 2016. Т. 3. С. 191.
Григорьев И.В., Рудобашта С.П. Способ импульсной инфракрасной сушки термолабильных материалов. Патент 2 393 397 C2 RU, МПК F26B 3/06, 3/30/; заявка 2009119751/06, заявл. 2009.05.26; опубл. 2010.06.27.
Sakare P., Prasad N., Thombare N., Singh R. and Sharma S.C. Infrared Drying of Food Materials: Recent advances // Food Engineering Reviews. 2020. V. 12. P. 381. https://doi.org/10.1007/s12393-020-09237-w
Li K., Zhang M., Mujumdar A.S., Chitrakar B. Recent developments in physical field-based drying techniques for fruits and vegetables // Drying Technology. 2019. V. 37. Issue 15. P. 1954. https://doi.org/10.1080/ 07373937.2018.1546733
Zartha Sossa J.W, Orozco G.L, García Murillo L.M., Peña Osorio M. and Sánchez Suarez N. // Infrared Drying Trends Applied to Fruit. Front. Sustain. Food Syst. 2021. V. 5. P. 650690. https://doi.org/10.3389/fsufs.2021.650690
Рудобашта С.П., Карташов Э.М., Зуева Г.А. Тепломассоперенос при сушке пластины в непрерывно действующем электромагнитном поле высокой и сверхвысокой частоты // Теор. осн. хим. технол. 2021. Т. 55. № 2. С. 195.
Putranto A., Chen X.D. Reaction engineering approach modeling of intensified drying of fruits and vegetables using microwave, ultrasonic and infrared-heating // Drying Technology. 2020. V. 38. Issue 5–6. P. 747. https://doi.org/10.1080/07373937.2019.1708750
Календерьян В.А., Бошкова И.Л. Тепломассоперенос в аппаратах с плотным слоем дисперсного материала. Киев: Издательский Дом “Слово”, 2011.
Сороковая Н.Н., Снежкин Ю.Ф., Шапарь Р.А., Сороковой Р.Я. Математическое моделирование и оптимизация процесса непрерывной сушки термолабильных материалов // Инж.-физ. журн. 2019. Т. 92. № 5. С. 2218.
Amiri A., Vafai K. Analysis of dispersion effect and non-thermal equilibrium, non-Darcian, variable porosity incompressible flow through porous media // Int. J. Heat and Mass Transfer. 1994. V. 37. № 6. P. 939.
Байков В.И., Павлюкевич Н.В. Термодинамика и статистическая физика: учебное пособие. Минск: Вышэйшая школа, 2018.
Горобцова Н.Е. Метод описания и расчета изотерм сорбции-десорбции, общий для различных материалов // Тепломассообмен-V1. Материалы VI Всесоюзной конференции по тепломассообмену. Т. VII. Минск, 1980. С. 60.
Гришин М.А., Атаназевич В.И., Семенов Ю.Г. Установки для сушки пищевых продуктов. М.: Агропромиздат, 1989.
Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М.: Наука, 1987.
Рудобашта С.П., Карташов Э.М., Зуева Г.А. Матаматическое моделирование процесса конвективной сушки материалов с учетом их усадки // Инж.-физ. журн. 2020. Т. 93. № 6. С. 1446.
Sablani S., Rahman S., Al-Habsi N. Moisture diffusivity in foods – an over view. Drying Technology in Agrieulture and Food Sciences / Editor Arun S. Mujumdar. Science Publishers, Inc. Enfield (NH), USA. P. 35.
Аэров М.Э., Тодес О.М., Наринский Д.А. Аппараты со стационарным зернистым слоем. Ленинград: Химия, 1979.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии