Теоретические основы химической технологии, 2022, T. 56, № 2, стр. 158-166
Поиск оптимальных режимных параметров каталитического процесса на основе эволюционных вычислений
Е. В. Антипина a, *, С. А. Мустафина b, А. Ф. Антипин a
a Стерлитамакский филиал Башкирского государственного университета
Стерлитамак, Россия
b Башкирский государственный университет
Уфа, Россия
* E-mail: stepashinaev@ya.ru
Поступила в редакцию 21.10.2020
После доработки 18.12.2021
Принята к публикации 30.12.2021
- EDN: BMPCHY
- DOI: 10.31857/S0040357122020038
Аннотация
Сформулирован численный алгоритм поиска оптимального температурного режима химического процесса в реакторе идеального смешения, основанный на эволюционных вычислениях. Эволюционные алгоритмы позволили получить приближенное решение задачи поиска оптимальной температуры за приемлемое время, что является крайне важным в случае управления каталитическим процессом в режиме реального времени. Приведена постановка задачи оптимального управления каталитическим процессом в реакторе идеального смешения, где управляющим параметром является температура хладоагента. Описан пошаговый алгоритм решения поставленной задачи, в основу которого положен метод искусственных иммунных систем. Одной из отличительных особенностей данного метода является независимость решения оптимизационной задачи от начальной точки поиска решения. На основе разработанного алгоритма создана программа, позволяющая получить численное решение задачи поиска оптимального температурного режима процесса в реакторе идеального смешения. С помощью приложения проведен вычислительный эксперимент для реакции димеризации α-метилстирола в присутствии цеолитного катализатора NaHY. Приведена математическая модель данного каталитического процесса в реакторе идеального смешения, и на ее основе сформулирована задача оптимального управления. Вычислены оптимальные концентрации реагентов и оптимальный температурный режим процесса димеризации α-метилстирола в реакторе идеального смешения, обеспечивающий в конечный момент времени протекания реакции максимальный выход ее продуктов – линейных димеров.
ВВЕДЕНИЕ
В настоящее время одной из важнейших задач математического моделирования химико-технологических процессов является задача определения оптимальных условий их ведения, обеспечивающих достижение заданных показателей процесса. Применение методов математического моделирования дает возможность повысить производительность технологической схемы процесса и получить конкретные количественные результаты, имитируя натурный и лабораторный эксперименты с помощью компьютерных программ.
Однако при реализации численных методов решения задач управления часто возникает ряд трудностей, связанных с нелинейностью математических моделей, описывающих динамику течения процессов. Нелинейность процесса ограничивает применение методов линейного программирования [1–3]. Высокая размерность задач, связанная с участием в химической реакции большого количества промежуточных веществ, затрудняет использование динамического программирования ввиду высоких вычислительных затрат [4–6]. Применение принципа максимума требует дополнительной проверки найденного решения на оптимальность, что, в свою очередь, является ресурсоемкой задачей [7, 8]. Наличие фазовых ограничений затрудняет использование методов вариационного исчисления [9]. Помимо этого, решения оптимизационных задач, найденных с помощью численных методов, зависит от выбора начального приближения решения, что в свою очередь требует от исследователя знания некоторого приближения этой начальной точки хотя бы из физических соображений поставленной задачи.
В качестве методов решения оптимизационных задач и задач управления можно использовать эволюционные вычисления, которые представляют собой интеллектуальные системы извлечения новых знаний и ориентированы на автоматическое накопление и формирование знаний с использованием процедур анализа и обобщения данных [10, 11]. Эволюционные алгоритмы позволяют получить приближенное решение оптимизационной задачи за приемлемое с практической точки зрения время, что является крайне важным для управления проведением каталитической реакции в режиме реального времени.
Одним из эволюционных методов оптимизации является метод искусственных иммунных систем. Его отличительная особенность заключается в наличии механизма памяти, который передает информацию о найденных ранее наилучших решениях, т.е. механизм памяти повышает эффективность глобального поиска решения оптимизационной задачи. Решения, найденные с помощью метода искусственных иммунных систем, не зависят от начальной точки поиска решения, т. к. итеративная процедура поиска начинается с генерирования начальной популяции из набора случайных значений. Метод является прямым методом оптимизации нулевого порядка, то есть для его работы не требуется вычисления производной целевой функции, а также отсутствует требование непрерывности целевой функции и ее производных. Метод искусственных иммунных систем можно легко настраивать при изменении количества фазовых переменных, что позволяет применять его для решения задач оптимального управления различными процессами.
Целью данной работы является разработка численного алгоритма поиска оптимального управления каталитическим процессом в реакторе идеального смешения, основанный на эволюционном методе искусственных иммунных систем.
ПОСТАНОВКА ЗАДАЧИ
Сформулируем задачу поиска оптимального температурного режима каталитического процесса в реакторе идеального смешения в общем виде.
Пусть каталитический процесс протекает в реакторе идеального смешения периодического действия, то есть реактор одновременно загружается смесью всех реагентов и через определенное время, необходимое для достижения заданной степени завершенности процесса, выгружают смесь продуктов реакции. Процесс функционирования реактора состоит из периодически повторяющихся циклов.
При составлении математического описания каталитического процесса в реакторе идеального смешения приняты следующие допущения:
общая масса в реакторе идеального смешения постоянна, остальные характеристики (состав, температура) изменяются лишь во времени;
отсутствует градиент свойств реакционной среды во всем объеме реакционного пространства в данный момент времени; процесс предполагается проводить при достаточно энергичном перемешивании (500–600 об./мин);
реакция проводится для свежего катализатора, то есть не учитывается процесс дезактивации катализатора;
процессы внутренней и внешней диффузии не тормозят протекание процесса, что объясняется использованием мелкодисперсного катализатора с диаметром зерна ~0.1 мм. Наличие катализатора учитывается в значениях кинетических констант реакции.
Уравнения материального баланса представляются кинетической моделью реакции, то есть системой дифференциальных уравнений [12]
с начальными условиями
где x(t) = (x1(t), x2(t), …, xn – 1(t))T – вектор концентраций веществ, xn(t) – относительное изменение числа молей реакционной среды, T – температура реакционной смеси, t – время, f(x(t),T,t) = = (f1(x(t),T,t), f2(x(t),T,t), …, fn(x(t),u(t),t))T – непрерывная вместе со своими частными производными вектор-функция.Пусть [0, tend] – промежуток времени функционирования системы. Уравнение теплового баланса имеет вид
(3)
${{C}_{p}}\frac{{dT}}{{dt}} = \sum\limits_{i = 1}^n {{{Q}_{i}}{{W}_{i}}(x,T)} + \frac{{{{\alpha }_{x}}{{S}_{x}}}}{{{{C}_{0}}}}({{T}_{h}} - T),$с начальными условиями
где Cp – мольная теплоемкость реакционной смеси, Qi – тепловой эффект i-й стадии реакции, Wi – приведенная скорость i-й стадии реакции, αx – коэффициент теплопередачи, Sx – удельная поверхность теплосъема, C0 – начальная мольная плотность реакционной среды (начальная суммарная концентрация), T – температура реакционной смеси, Th – температура хладоагента.В системе дифференциальных уравнений (1), (3) с начальными условиями (2), (4) переменными состояния является вектор x(t) = (x1(t), x2(t), …, xn(t))T и температура реакции T, параметром управления – температура хладоагента Th.
Пусть на температуру реакционной смеси и температуру хладоагента наложены ограничения вида
где ${{T}^{a}},$ ${{T}^{b}},$ $T_{h}^{a},$ $T_{h}^{b}$ – нижняя и верхняя допустимые границы температур смеси и хладоагента соответственно, которые часто задаются из технологических соображений.Пусть в качестве критерия оптимальности выступает функционал вида
Тогда задача поиска оптимального управления процессом в реакторе идеального смешения формулируется следующим образом: требуется определить оптимальный температурный режим $T_{h}^{*}(t)$ каталитического процесса, описываемого системой дифференциальных уравнений (1), (3) с начальными условиями (2), (4), с учетом ограничений (5), (6), доставляющий экстремум критерию оптимальности (7).
Для определенности будем рассматривать задачу на максимум критерия оптимальности (7).
АЛГОРИТМ РЕШЕНИЯ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ В РЕАКТОРЕ ИДЕАЛЬНОГО СМЕШЕНИЯ
В основе метода искусственных иммунных систем заложены принципы функционирования иммунной системы живого организма. Основное назначение иммунной системы состоит в уничтожении чужеродных тел, проникающих в живой организм, и совершенствовании борьбы с ними на основе предыдущего опыта. Основные понятия метода [13, 14]:
антиген – чужеродное вещество, от которого организм пытается защититься с помощью антител;
антитело – вещество, которое распознает и уничтожает антиген;
клетка памяти – иммунная клетка, реализующая механизм памяти путем накопления информации о новых антителах, способных распознать антиген, и обеспечивающая эффективную работу в случае попадания в организм подобного антигена;
функция приспособленности – целевая функция оптимизационной задачи. Соответствует приспособленности иммунной клетки живого организма к борьбе с антигенами, т.е. способности вырабатывать антитела.
Сформулируем пошаговый алгоритм метода искусственных иммунных систем для решения оптимизационной задачи в реакторе идеального смешения. Введем в рассмотрение в качестве популяции иммунных клеток набор из l векторов температуры хладоагента:
В качестве функции приспособленности примем критерий оптимальности (7). Для работы алгоритма необходимо определение наихудшего и наилучшего значений функции приспособленности иммунной клетки. Поскольку рассматривается задача на поиск максимума целевой функции (7), то наихудшему значению функции приспособленности соответствует наименьшее значение критерия оптимальности (7), а наилучшему – его наибольшее значение. Чем больше значение критерия оптимальности (7), тем больше соответствующая ей иммунная клетка приспособлена, то есть способна вырабатывать антитела, и подходит в качестве решения.
Шаг 1. Генерирование начальной популяции температуры хладоагента.
Установить размер популяции (количество иммунных клеток) l, количество иммунных клеток с наихудшим значением функции приспособленности count_bad, количество клеток-родителей для селекции count_pat, количество клонов для оператора клонирования count_clone, параметр оператора мутации m, общее количество итераций алгоритма count_iter. Значение переменной-счетчика итераций принять равным нулю num_iter.
Заполнить случайным образом значения иммунных клеток начальной популяции $T_{h}^{j}(0),$ $j = \overline {1,l,} $ из диапазона допустимых значений $\left[ {T_{h}^{a},T_{h}^{b}} \right].$
Шаг 2. Решение прямой кинетической задачи.
Для каждой иммунной клетки $T_{h}^{j}(0)$ вычислить значение функции приспособленности (7). Для этого необходимо решить прямую кинетическую задачу, т.е. найти численное решение системы дифференциальных уравнений (1), (3) с начальными условиями (2), (4) явным или неявным методом.
Шаг 3. Клонирование.
Из текущей популяции с номером num_iter выбрать count_pat клеток с наилучшим значением функции приспособленности. Выбранные клетки являются родительскими клетками, к каждой из которых применяют оператор клонирования, т.е. создаются ее клоны, количество которых равно count_clone.
Шаг 4. Мутация.
Для каждой j-й клетки-родителя (j = = $\overline {1,count\_clone} )$ сгенерировать случайные числа ${{s}_{1}} \in [0,T_{h}^{b} - T_{{hi}}^{j}(num\_iter)],$ s2 ∈ $[0,T_{{hi}}^{j}(num\_iter)$ – – $[0,T_{{hi}}^{j}(num\_iter) - T_{h}^{a}],$ $i = \overline {1,nt} .$ Сгенерировать случайным образом число p на интервале [0, 1].
Если p > 0.5, то $T_{{hi}}^{r}(num\_iter): = $ $T_{{hi}}^{r}(num{\kern 1pt} \_{\kern 1pt} iter)$ + + s1m, иначе $T_{{hi}}^{r}(num\_iter): = $ $T_{{hi}}^{r}(num{\kern 1pt} \_{\kern 1pt} iter) - {{s}_{2}}m,$ где $r = \overline {1,count\_clone} ,$ m – параметр оператора мутации.
Шаг 5. Решение прямой кинетической задачи.
Для каждого клона-мутанта вычислить $T_{h}^{r}(num{\kern 1pt} \_{\kern 1pt} iter)$ $(r = \overline {1,count\_clone)} $ решить систему дифференциальных уравнений (1), (3) с начальными условиями (2), (4), и подставить полученные значения фазовых переменных в целевую функцию (7).
Шаг 6. Селекция и обновление популяции.
Для каждой клетки-родителя найти клона-мутанта с наилучшим значением функции приспособленности. Если значение функции приспособленности клетки-родителя меньше значения функции приспособленности клона-мутанта, то заменить родительскую клетку клоном-мутантом. В противном случае оставить в популяции родительскую клетку.
Шаг 7. Переход к новой популяции.
Сгенерировать случайным образом на интервале $\left[ {T_{h}^{a},T_{h}^{b}} \right]$ новые иммунные клетки количеством count_bad, для которых рассчитать значения функции приспособленности. Из текущей популяции $T_{h}^{j}(num\_iter)$ $(j = \overline {1,l)} $ выбрать count_bad иммунных клеток с наихудшим значением функции приспособленности (7), которые заменить вновь созданными клетками.
Шаг 8. Проверка условий окончания поиска решения.
Если num_iter<count_iter, то перейти к шагу 3, иначе завершить поиск решения. В качестве решения задачи поиска оптимального температурного режима каталитического процесса в реакторе идеального смешения выбрать из последней популяции клетку $T_{h}^{*}$ с наилучшим значением функции приспособленности.
Отличительной особенностью предложенного алгоритма является то, что в качестве иммунной клетки рассматривается вектор, координаты которого соответствуют значениям температуры в каждый момент времени протекания процесса. То есть решение на каждой итерации алгоритма строится не путем перехода от точки к точке, а путем перехода от вектора к вектору, т.е. построения температурной кривой на всем интервале времени. Кроме того, одним из отличий алгоритма является наличие блоков решения прямой кинетической задачи.
Сформулированный алгоритм реализован в виде программного средства в среде визуального программирования Delphi и позволяет пользователю получить численное решение задачи поиска оптимального температурного режима процесса в реакторе идеального смешения.
ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
С помощью разработанного алгоритма решим задачу поиска оптимального температурного режима в реакторе идеального смешения периодического действия для каталитической реакции димеризации α-метилстирола в присутствии цеолитного катализатора NaHY. Линейные и циклические димеры, являющиеся продуктами реакции, широко применяются в качестве пластификаторов, модификаторов полимеров, каучуков, в производстве синтетических масел и др.
Механизм реакции димеризации α-метилстирола в присутствии цеолитного катализатора NaHY и соответствующие уравнения скоростей стадий имеют вид [15]:
(8)
$\begin{array}{*{20}{c}} {2{{X}_{1}} \leftrightarrow {{X}_{2}},}&{{{w}_{1}}(C,T) = {{k}_{1}}(T)C_{1}^{2} - {{k}_{{10}}}(T){{C}_{2}},} \\ {2{{X}_{1}} \leftrightarrow {{X}_{3}},}&{{{w}_{2}}(C,T) = {{k}_{2}}(T)C_{1}^{2} - {{k}_{{11}}}(T){{C}_{3}},} \\ {2{{X}_{1}} \to {{X}_{4}},}&{{{w}_{3}}(C,T) = {{k}_{3}}(T)C_{1}^{2},} \\ {{{X}_{2}} \leftrightarrow {{X}_{3}},}&{{{w}_{4}}(C,T) = {{k}_{4}}(T){{C}_{2}} - {{k}_{{12}}}(T){{C}_{3}},} \\ {{{X}_{2}} \to {{X}_{4}},}&{{{w}_{5}}(C,T) = {{k}_{5}}(T){{C}_{2}},} \\ {{{X}_{3}} \to {{X}_{4}},}&{{{w}_{6}}(C,T) = {{k}_{6}}(T){{C}_{3}},} \\ {{{X}_{1}} + {{X}_{2}} \to {{X}_{5}},}&{{{w}_{7}}(C,T) = {{k}_{7}}(T){{C}_{1}}{{C}_{2}},} \\ {{{X}_{1}} + {{X}_{3}} \to {{X}_{5}},}&{{{w}_{8}}(C,T) = {{k}_{8}}(T){{C}_{1}}{{C}_{3}},} \\ {{{X}_{1}} + {{X}_{4}} \to {{X}_{5}},}&{{{w}_{9}}(C,T) = {{k}_{9}}(T){{C}_{1}}{{C}_{4}},} \end{array}$При построении математической модели данного процесса необходимо учитывать изменение реакционного объема (числа молей реакционной смеси) в процессе протекания реакции. Поэтому кинетическая модель димеризации α-метилстирола представляет собой систему дифференциальных уравнений:
(10)
$\begin{gathered} \frac{{d{{x}_{i}}}}{{dt}} = \frac{{{{F}_{i}}(x,T) - {{x}_{i}}{{F}_{n}}(x,T)}}{{{{x}_{6}}}}, \\ {\text{где}}\,\,\,\,{{F}_{i}} = \sum\limits_{j = 1}^9 {{{\gamma }_{{ij}}}{{W}_{j}}} ,\,\,\,\,i = \overline {1,5} , \\ \end{gathered} $(11)
$\frac{{d{{x}_{6}}}}{{dt}} = {{F}_{n}}(x,T),\,\,\,\,{\text{где}}\,\,\,\,{{F}_{n}} = \sum\limits_{j = 1}^9 {{{W}_{j}}} \sum\limits_{i = 1}^5 {{{\gamma }_{{ij}}}} ,$с начальными условиями:
где xi – концентрация вещества Xi $(i = \overline {1,5} )$ (мольная доля), x6 – переменный реакционный объем, x6 = C/C0, ${{C}_{0}} = \sum\limits_{i = 1}^5 {{{C}_{i}}(0)} $ – начальная суммарная концентрация веществ (кмоль/м3), (γij) – матрица стехиометрических коэффициентов веществ $(i = \overline {1,5} ,\,\,j = \overline {1,9} ),$ ${{W}_{j}} = {{{{w}_{j}}} \mathord{\left/ {\vphantom {{{{w}_{j}}} {{{C}_{0}}}}} \right. \kern-0em} {{{C}_{0}}}}$ – приведенная скорость j-й стадии реакции (1/ч) $(j = \overline {1,9} ).$Уравнение теплового баланса рассматриваемого процесса имеет вид:
(13)
${{C}_{p}}\frac{{dT}}{{dt}} = \sum\limits_{j = 1}^9 {{{Q}_{j}}{{W}_{j}}} + \frac{{{{\alpha }_{x}}{{S}_{x}}}}{{{{C}_{0}}}}({{T}_{h}} - T),$с начальными условиями
где Сp – мольная теплоемкость реакционной смеси (кДж/(кмоль К)), Qj – тепловой эффект j-й стадии реакции $(j = \overline {1,\,12} )$ (кДж/моль), Wj = wj/C0 – приведенная скорость j-й стадии реакции $(j = \overline {1,{\kern 1pt} \,12} )$ (1/ч), αx – коэффициент теплопередачи (кДж/(м2 К)), Sx – удельная поверхность теплосъема (1/м), T – температура протекания реакции (К), Th – температура хладоагента (К).Численные значения кинетических параметров химического процесса приведены в табл. 1 [16].
Таблица 1.
Кинетические параметры процесса димеризации α-метилстирола (T = 373 K)
| № | kj(373), м3/(кгkat ∙ ч) | Ej, кДж/моль |
|---|---|---|
| 1 | 61.357 | 196 |
| 2 | 8.9534 | 263 |
| 3 | 7.7916 | 259 |
| 4 | 1.1693 | 238 |
| 5 | 0.11922 | 275 |
| 6 | 0.12041 | 127 |
| 7 | 0.019308 | 247 |
| 8 | 41.556 | 194 |
| 9 | 0.03662 | 115 |
| 10 | 0.04547 | 279 |
| 11 | 0.0995 | 204 |
| 12 | 0.05132 | 138 |
Тепловые эффекты стадий реакции димеризации α-метилстирола равны (кДж/моль) [16]: Q1 = = 22.6, Q2 = 20.0, Q3 = 39.0, Q4 = –2.63, Q5 = 16.4, Q6 = 19.0, Q7 = 17.3, Q8 = 19.9, Q9 = 0.92. Начальная суммарная концентрация С0 = 7.72 кмоль/м3, коэффициент теплопередачи αx = 5.31 кДж/(м2 К).
Значения теплофизических параметров процесса димеризации α-метилстирола приведены в табл. 2 [16].
Таблица 2.
Термодинамические параметры компонентов реакционной смеси процесса димеризации α-метилстирола
| Наименование параметров | α-метил-стирол | α-димер | β-димер | Циклический димер | Tример |
|---|---|---|---|---|---|
| Брутто-формула | С9H10 | C18H20 | C18H20 | C18H20 | C27H30 |
| Молекулярная масса, М (г/моль) | 118.1 | 236.2 | 236.2 | 236.2 | 354.3 |
| Стандартная теплота образования при 298 К, $\Delta {{H}^{0}}$ (кДж/моль) | 27.0 | 31.4 | 34.0 | 15.0 | 41.1 |
| Константы в ряду теплоемкости, Cp (кДж/(моль К)) | |||||
| A | –5.811 | –21.98 | –22.82 | –26.72 | –35.49 |
| B × 103 | 165.6 | 369.4 | 364.5 | 392.5 | 567.6 |
| C × 106 | –108.2 | –243.6 | –236.0 | –264.3 | –378.5 |
| D × 109 | 28.2 | 60.03 | 57.27 | 66.1 | 93.97 |
Теплоемкости компонентов и мольная теплоемкость реакционной смеси определяются следующим образом:
Параметром управления является температура хладоагента Th, на которую наложены ограничения
На температуру реакционной смеси T также наложены ограничения вида
Поскольку целевыми продуктами реакции (8) являются линейные димеры X1 и X2, зададим в качестве критерия оптимальности их максимальный выход в конечный момент времени:
(17)
$J\left( {x,T,t} \right) = {{x}_{2}}\left( {{{t}_{{end}}}} \right) + {{x}_{3}}\left( {{{t}_{{end}}}} \right) \to {\text{max}}.$Тогда оптимизационная задача формулируется следующим образом. Необходимо для процесса, описываемого системой дифференциальных уравнений (10), (11), (13) с начальными условиями (12), (14) с учетом ограничений (16) определить оптимальный температурный режим $T_{h}^{*}(t)$ c ограничениями (15), обеспечивающий максимум критерию оптимальности (17).
В ходе решения оптимизационной задачи проведена серия вычислительных экспериментов с различными наборами параметров алгоритма искусственных иммунных систем (табл. 3).
Таблица 3.
Значение критерия оптимальности (17) при различных наборах параметров алгоритма искусственных иммунных систем
| № | l | count_bad | count_pat | count_сlone | m | count_iter | J(x,T,t), % |
|---|---|---|---|---|---|---|---|
| 1 | 50 | 10 | 10 | 20 | 0.3 | 800 | 80.6 |
| 2 | 50 | 20 | 20 | 10 | 0.5 | 600 | 81.2 |
| 3 | 50 | 30 | 30 | 20 | 0.7 | 400 | 82.6 |
| 4 | 50 | 10 | 40 | 10 | 0.3 | 200 | 80.2 |
| 5 | 50 | 20 | 10 | 20 | 0.5 | 800 | 81.9 |
| 6 | 60 | 10 | 30 | 20 | 0.3 | 400 | 81.2 |
| 7 | 60 | 20 | 40 | 10 | 0.5 | 200 | 80.4 |
| 8 | 60 | 30 | 10 | 20 | 0.7 | 800 | 81.6 |
| 9 | 60 | 10 | 20 | 10 | 0.3 | 600 | 82.4 |
| 10 | 60 | 20 | 30 | 20 | 0.5 | 400 | 82.8 |
| 11 | 70 | 10 | 10 | 20 | 0.3 | 800 | 80.4 |
| 12 | 70 | 20 | 20 | 10 | 0.5 | 600 | 83.3 |
| 13 | 70 | 30 | 30 | 20 | 0.7 | 400 | 81.5 |
| 14 | 70 | 10 | 40 | 10 | 0.3 | 200 | 80.2 |
| 15 | 70 | 20 | 10 | 20 | 0.5 | 800 | 81.6 |
| 16 | 80 | 10 | 30 | 20 | 0.3 | 400 | 83.1 |
| 17 | 80 | 20 | 40 | 10 | 0.5 | 200 | 80.1 |
| 18 | 80 | 30 | 10 | 20 | 0.7 | 800 | 82.8 |
| 19 | 80 | 10 | 20 | 10 | 0.3 | 600 | 83.1 |
| 20 | 80 | 20 | 30 | 20 | 0.5 | 400 | 81.7 |
В результате проведенных расчетов установлено, что наибольшие значения критерий оптимальности (17) обеспечивает следующий набор параметров алгоритма: количество иммунных клеток l = 70, количество иммунных клеток с наихудшим значением функции приспособленности count_bad = 20, количество клеток-родителей для селекции count_pat = 20, количество клонов для оператора клонирования count_clone = 10, параметр оператора мутации m = 0.5, общее количество итераций алгоритма count_iter = 600.
В ходе работы алгоритма решение системы дифференциальных уравнений (10), (11), (13) проводилось неявным методом прогноза и коррекции с начальными условиями:
В качестве начального приближения решения задачи оптимального управления рассматривалось 70 векторов, каждый из которых состоял из 95 сгенерированных случайным образом значений температуры хладоагента из диапазона допустимых значений (15) (приложение 1 ).
Пошаговая работа алгоритма приведена в приложении 2 .
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В результате расчетов с помощью алгоритма метода искусственных иммунных систем вычислены оптимальные концентрации веществ и оптимальный температурный режим процесса димеризации α-метилстирола в реакторе идеального смешения продолжительностью 2.5 ч. В результате расчетов установлено, что для достижения максимального выхода линейных димеров, равного 83.3% (73.7% – α-димера, 9.6% – β-димера) при начальной температуре реакционной смеси, равной 303 К (минимальной допустимой температуре), необходимо изменять температуру хладоагента следующим образом:
1) На протяжении 0.5 ч удерживать на уровне 403 К.
2) Через 0.5 ч резко снизить температуру до 303 К и 1.1 ч поддерживать ее на этом же уровне.
4) Резко поднять до 403 К и удерживать ее на этом уровне до конца времени протекания процесса (рис. 1).
Рис. 1.
Оптимальный температурный режим процесса димеризации α-метилстирола: 1 – температура хладоагента, 2 – температура реакционной смеси.
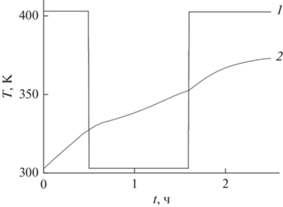
Полученный температурный режим позволит увеличить выход линейных димеров. Однако технологически будет затруднительно его получить, а именно для реализации такого режима необходимо изменить структуру подачи тепла для реактора и съема тепла в виде создания дополнительного кожуха реактора.
На рис. 2 показана динамика значений выхода линейных димеров при некоторых постоянных значениях температуры хладоагента.
Рис. 2.
Динамика концентраций линейных димеров при разных температурных режимах (1 – рассчитанный оптимальный температурный режим, 2 – T = 383 К, 3 – T = 403 К, 4 – T = 333 К).

Из рис. 2 видно, что значение выхода линейных димеров, вычисленное при оптимальном температурном режиме (0.83 мольных долей), выше вычисленных значений при произвольных допустимых значениях температуры хладоагента. Поэтому можно сделать вывод о корректной работе разработанного алгоритма метода искусственных иммунных систем.
ЗАКЛЮЧЕНИЕ
Таким образом, разработанный алгоритм позволяет находить решение задачи поиска оптимальных режимных параметров химических процессов в реакторе идеального смешения с ограничениями на параметр управления. В качестве параметра управления рассматривается температура хладоагента. Работа численного алгоритма основана на применении метода искусственных иммунных систем, благодаря чему решения оптимизационных задач, найденные с его помощью, не зависят от начального приближения, которое требуется указывать при применении других численных методов из физического смысла задачи. Независимость решения задачи от начального приближения обусловлено тем, что на первом шаге алгоритма задается начальная популяция векторов, элементами которых являются случайные значения из области допустимых значений управления. Данная особенность алгоритма существенно облегчает пользователю процесс поиска решения.
С помощью программы, реализующей сформулированный алгоритм, проведен вычислительный эксперимент для реакции димеризации α-метилстирола в присутствии цеолитного катализатора NaHY. Вычислены оптимальные концентрации реагентов и оптимальный температурный режим процесса в реакторе идеального смешения, обеспечивающий максимальный выход продуктов реакции – линейных димеров. Время решения задачи оптимального управления для реакции димеризации α-метилстирола с помощью программного средства, реализующего алгоритм искусственных иммунных систем, составило 2 мин 2 с при следующих технических характеристиках компьютера: процессор AMD Athlon II X2 245 с частотой 2.9 гГц, ОЗУ 4 Гб, операционная система Windows 7.
Разработанный алгоритм поиска оптимального температурного режима процесса в реакторе идеального смешения можно применять для решения задач оптимального управления и с другими управляющими параметрами путем модификации этапа задания популяции иммунных клеток.
Исследование выполнено в рамках государственного задания Министерства науки и высшего образования Российской Федерации (код научной темы FZWU-2020-0027).
ОБОЗНАЧЕНИЯ
| Обозначения теоретической части | |
| Сp | мольная теплоемкость реакционной смеси, кДж/(кмоль К) |
| count_bad | количество иммунных клеток с наихудшим значением функции приспособленности |
| count_clone | количество клонов для оператора клонирования |
| count_iter | общее количество итераций |
| count_pat | количество клеток-родителей для селекции |
| l | размер популяции |
| m | параметр оператора мутации |
| max | максимальное значение |
| nt | количество точек разбиения временного интервала; |
| num_iter | счетчик итераций |
| Sx | удельная поверхность теплосъема, 1/м |
| T | температура, К |
| t | время, с |
| Q | тепловой эффект реакции, кДж/моль |
| x | концентрация вещества, мольная доля |
| αx | коэффициент теплопередачи, кДж/(м2 К) |
| Обозначения вычислительного эксперимента | |
| C | концентрация вещества, кмоль/(м3 ч) |
| Сp | мольная теплоемкость реакционной смеси, кДж/(кмоль К) |
| k | константа скорости реакции, м3/(кмоль ч) |
| max | максимальное значение |
| Sx | удельная поверхность теплосъема, 1/м |
| T | температура, К |
| t | время, с |
| Q | тепловой эффект реакции, кДж/моль |
| W = w/C0 | приведенная скорость стадии реакции, 1/ч |
| w | скорость стадии реакции, кмоль/(м3 ч) |
| X | вещество |
| x | концентрация вещества, мольная доля |
| x6 = C/C0 | переменный реакционный объем |
| αx | коэффициент теплопередачи, кДж/(м2 К) |
| (γ) | матрица стехиометрических коэффициентов веществ |
ИНДЕКСЫ
| Индексы теоретической части | |
| 0 | начальное значение |
| a | нижняя допустимая граница температуры |
| b | верхняя допустимая граница температуры |
| end | конечное значение |
| h | хладоагент |
| i | номер стадии реакции |
| j | номер вектора популяции |
| Индексы вычислительного эксперимента | |
| 0 | начальное значение |
| 1 | α-метилстирол |
| 2 | α-димер |
| 3 | β-димер |
| 4 | циклический димер |
| 5 | тримеры |
| 6 | переменный реакционный объем |
| a | нижняя допустимая граница температуры |
| b | верхняя допустимая граница температуры |
| end | конечное значение |
| h | хладоагент |
| i | номер вещества |
| j | номер стадии реакции |
Список литературы
Tsirlin A.M., Akhremenkov A.A. Optimal heat transfer during the change of phase of a refrigerating medium // Theor. Found. Chem. Eng. 2018. V. 52. № 5. P. 812. [Цирлин А.М., Ахременков А.А. Оптимальный теплообмен при изменении фазового состояния хладагента // Теор. осн. хим. технол. 2018. Т. 52. № 5. С. 1.]
Santos L., Villas-Boas F., Oliveira A.R.L., Perin C. Optimized choice of parameters in interiorpoint methods for linear programming // Comput. Optimization and Applications. 2019. V. 73. P. 535.
Ziyatdinov N.N., Emel’yanov I.I., Lapteva T.V., Ryzhova A.A., Ignat’ev A.N. Method of automated synthesis of optimal heat exchange network (hen) based on the principle of fixation of variables // Theor. Found. Chem. Eng. 2020. V. 54. № 2. P. 258. [Зиятдинов Н.Н., Емельянов И.И., Лаптева Т.В., Рыжова А.А., Игнатьев А.Н. Метод автоматизированного синтеза оптимальных систем теплообмена на основе принципа закрепления переменных // Теор. осн. хим. технол. 2020. Т. 54. № 2. С. 144.]
Biegler L.T. Integrated Optimization Strategies for Dynamic Process Operations // Theor. Foundations of Chem. Engineering. 2017. V. 51. № 6. P. 910.
Dadebo S.A., Mcauley K.B. Dynamic optimization of constrained chemical engineering problems using dynamic programming // Comput. & Chem. Eng. 1995. V. 19. № 5. P. 513.
Pan Y., Fei Z.-S., Zhao L., Liang J. Dynamic optimization for chemical process based on improved iterative dynamic programming algorithm // J. East China University of Science and Technology. 2013. № 1. P. 61.
Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии. М.: Химия, 1975.
Островский Г.М., Волин Ю.М. Методы оптимизации сложных химико-технологических схем. М.: Химия, 1970.
Lindborg H., Eide V., Unger S., Henriksen S.T., Jakobsen H.A. Parallelization and performance optimization of a dynamic PDE fixed bed reactor model for practical applications // Comput. Chem. Eng. 2004. № 28. P. 1585.
Антипина Е.В., Мустафина С.А., Антипин А.Ф. Численный алгоритм решения задачи оптимального управления с терминальными ограничениями для динамических систем // Автометрия. 2020. № 6. С. 132.
Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой: учеб. пособие. М.: МГТУ им. Н.Э. Баумана, 2014.
Царева З.М., Орлова Е.И. Теоретические основы химической технологии. Киев: Вища шк., 1986.
Wei Y., Wang J. An Artificial Immune System Approach to Business Process Mining // Advanced Materials Research. 2012. V. 472. P. 35.
Колоколов А.А., Леванова Т.В., Поздняков Ю.С. Алгоритмы искусственной иммунной системы для вариантной задачи размещения телекоммуникационных центров // Изв. Иркут. гос. ун-та. Серия Математика. 2013. Т. 6. Вып. 1. С. 35.
Степашина Е.В., Байтимерова А.И., Мустафина С.А. Программный комплекс автоматизации процедуры уточнения механизма химической реакции на основе DRGEP-метода // Баш. хим. журн. 2011. Т. 18. № 3. С. 112.
Байтимерова А.И. Математическое моделирование и численное исследование каталитических процессов в каскаде реакторов. Дис. … канд. физ.-мат. наук. Уфа: БашГУ, 2009.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


