Теоретические основы химической технологии, 2022, T. 56, № 2, стр. 183-196

Самоподдерживающиеся процессы умягчения-опреснения воды: хлоридно-сульфатные системы

Р. Х. Хамизов^a, *, И. В. Комарова^a, Н. К. Галкина^a, А. Г. Прудковский^a

^a Институт геохимии и аналитической химии им. В.И. Вернадского РАН
Москва, Россия

Поступила в редакцию 13.07.2021
После доработки 07.10.2021
Принята к публикации 08.12.2021

EDN: IBWNOQ
DOI: 10.31857/S0040357122020099

Аннотация

Методом численного эксперимента исследована возможность организации стационарных самоподдерживающихся (СМП) процессов умягчения–опреснения солоноватых вод на примере многокомпонентных модельных растворов, содержащих хлориды и сульфаты натрия и кальция. В СМП процессах умягченная с помощью катионита вода подвергается опреснению, а образующийся при этом рассол, без добавления каких-либо дополнительных химических реагентов, используется для регенерации катионита в повторяющихся циклах сорбции–десорбции. Интерес к самоподдерживающимся процессам связан с новыми технологическими возможностями создания систем водоподготовки нового поколения, например мобильных автономных установок или систем с высокой степенью извлечения пресной воды. Проведены расчеты динамики ионного обмена для многих десятков последовательных циклов умягчения–опреснения при изменении варьируемых параметров, в частности, соотношения компонентов в исходном растворе и состава опресненной воды. Показаны условия, при которых формируются или не достигаются стационарные режимы. На основании результатов численных экспериментов предложено критериальное соотношение для предварительной оценки реализуемости самоподдерживающихся процессов.

Ключевые слова: самоподдерживающиеся процессы, умягчение, опреснение, катионит, сорбция, регенерация, стационарный режим

ВВЕДЕНИЕ

Самоподдерживающиеся (СМП) процессы умягчения-опреснения соленых вод были предсказаны почти полвека назад, что было весьма актуально в связи с растущей индустрией опреснения морских и других природных соленых вод [1]. Суть СМП процесса легко пояснить с помощью простейшей схемы, представленной на рис. 1а.

Рис. 1.

Самоподдерживающиеся процессы умягчения-опреснения в хлоридных (а) и хлоридно-сульфатных системах (б). Процессы: I – Na-катионирование; II – опреснение; III –удаление сульфата. Потоки: 1 – исходная соленая вода; 2 – умягченная соленая вода; 3 – опресненная вода; 4 – рассол без ионов жесткости; 5 – рассол после регенерации.

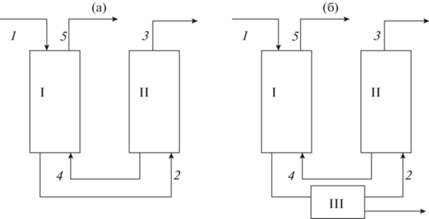
В повторяющемся циклическом процессе через колонну с катионитом в Na-форме пропускается соленая вода, и ионы жесткости, например, кальция, сорбируются в результате реакции ионного обмена, умягченная вода подвергается глубокому опреснению без опасности образования отложений слаборастворимых веществ, рассол, содержащий только соли натрия, накапливается и возвращается на регенерацию катионита после его отработки для вытеснения катионов жесткости и обратного перевода катионита в Na-форму. При использовании двух колонн, работающих в противофазе, можно организовать процесс, в котором непрерывно осуществляются умягчение и регенерация. Интерес к теории СМП-процессов [2–4] связан с технологическими возможностями создания систем водоподготовки нового поколения, например, не требующих привозных реагентов мобильных автономных установок опреснения соленых или солоноватых вод или систем с высокой степенью извлечения пресной воды и концентрирования рассола. В связи с новыми возможностями, которые открывает создание самоподдерживающихся процессов, или просто процессов умягчения-опреснения с рециркуляцией рассолов для частичной или полной регенерации катионита, интенсивно проводятся практические исследования в этой области [6–8]. В работах [3, 5] была показана реализуемость таких процессов для морской воды с использованием специальных неорганических ионообменников, получаемых пока в лабораторных масштабах. В работе [4], посвященной анализу возможности осуществления СМП-процессов для хлоридных растворов с меньшей минерализацией, были рассмотрены фундаментальные основы самоподдерживающихся (СМП)-процессов и показано, что возможность таких процессов связана с явлением электроселективности в ионном обмене и с нелинейными эффектами формирования концентрационных фронтов при обмене разнозарядных ионов. Были представлены результаты моделирования большого количества последовательных циклов умягчения-опреснения водных растворов смесей хлоридов кальция и натрия. Численные эксперименты показали осуществимость стационарных (повторяющихся) самоподдерживающихся процессов с использованием промышленного сильнокислотного катионита. Было показано влияние различных факторов на возможность осуществления и характеристики циклических самоподдерживающихся процессов на стадиях сорбции и регенерации: соотношения концентраций одно- и двухзарядных ионов в исходном растворе, суммарной концентрации этих растворов, степени концентрирования возвратных рассолов по сравнению с исходными растворами, потерь однозарядных ионов, “уносимых” с опресненной водой.

В настоящей работе рассматриваются сульфатсодержащие системы, более близкие к реальным природным соленым и солоноватым водам. По сравнению с двухкомпонентной смесью хлоридов натрия и кальция сульфатсодержащие системы имеют некоторые особенности:

1) комплексообразование (образование молекул сульфата кальция) влияет на ионообменные свойства катионита на стадии сорбционного умягчения;

2) в процессе сорбции идет накопление кальция к фазе катионита, что приводит к опасности осадкообразования при пропускании через кальциевую форму ионита исходного раствора с повышенным содержанием сульфата;

3) процесс опреснения раствора, содержащего ионы кальция и сульфата, может осложняться отложением гипса на теплопроводящих поверхностях или мембранах в зависимости от типа опреснителя;

4) десорбция кальция и регенерация натриевой формы катионита невозможны сульфатсодержащим концентратом после опреснения из-за образования осадка гипса в колонне с катионитом.

Проблемы 3) и 4) могут быть решены, если проводить извлечение сульфата из умягченной воды перед ее опреснением, как это показано на рис. 1б. Такое удаление может быть сделано ионообменным способом на анионите в хлоридной форме, что требует регенерации, например, хлоридом натрия, и что автоматически выводит такой процесс из класса самоподдерживающихся процессов. В данной работе рассмотрено удаление сульфата с помощью метода нанофильтрации, позволяющей разделять двух и однозарядные анионы в процессах, практически аналогичных рассматриваемым [9, 10].

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

В работе [3] для проведения динамических расчетов в циклических процессах на МЦА была использована общая модель многокомпонентного ионного обмена с линейными кинетическими уравнениями разностного типа. Авторы [11] предложили более сложную модель расчета катионирования на цеолитах, учитывающую конвективные процессы продольной дисперсии. В данной работе мы используем т. н. послойную (тарельчатую) модель динамики ионного обмена, которая, с одной стороны, лучше всего апробирована для процессов ионообменной сорбции и регенерации в поточном и противоточном режимах на сильнокислотном катионите [4, 12], с другой стороны, она обеспечивает быстрый счет большого количества последовательных циклов с изменяющимися характеристиками (до выхода на стационарный режим).

Решается задача о прохождении элюента через сорбционную колонну заданной длины L и сечения S, равномерно наполненной сорбентом. Предполагается, что раствор движется по колонне с постоянной скоростью v. Обозначим через ${{\bar {c}}_{i}}(x,t)$ концентрации (моль-экв/л) веществ в сорбенте, традиционно рассчитывающиеся на единицу объема колонны, а через ${{c}_{i}}(x,t)$ концентрации веществ в растворе, движение которых описываемые уравнениями переноса:

(1)

$\frac{{\partial {{c}_{i}}}}{{\partial t}} + v\frac{{\partial {{c}_{i}}}}{{\partial x}} + \frac{1}{\varepsilon }\frac{{\partial {{{\bar {c}}}_{i}}}}{{\partial t}} = {{D}_{{Li}}}\frac{{{{\partial }^{2}}{{c}_{i}}}}{{\partial {{x}^{2}}}}$

с граничными условиями первого рода на входе c_i(0, t) = f_i(t), условиями второго рода на выходе из колонны $\frac{{\partial {{c}_{i}}(L,t)}}{{\partial x}} = 0$ и некоторыми начальными условиями при t = 0: ${{c}_{i}}(x,0) = {{c}_{{i0}}}(x);$ ${{\bar {c}}_{i}}(x,0) = {{\bar {c}}_{{i0}}}(x).$ Обмен ионов между раствором и неподвижным сорбентом описывается в приближении квазистационарности:

(2)

$\frac{{{{{\bar {c}}}_{i}}}}{{{{c}_{i}}}} = K_{{\text{H}}}^{{Cat,i}}{{\left( {\frac{{{{{\bar {c}}}_{{\text{H}}}}}}{{{{c}_{{\text{H}}}}}}} \right)}^{{{{z}_{i}}}}},$

(3)

${{c}_{{{\text{OH}}}}} + \sum\limits_{j = 1}^m {{{c}_{j}}} = {{c}_{{\text{H}}}} + \sum\limits_{i = 1}^n {{{c}_{i}}} ,$

(4)

${{\bar {c}}_{{\text{H}}}} + \sum\limits_{i = 1}^n {{{{\bar {c}}}_{i}}} = {{\bar {c}}_{\Sigma }},$

(5)

$\varepsilon {{c}_{i}} + {{\bar {c}}_{i}} = {{\hat {c}}_{i}},$

где (2) – уравнение ионного обмена с коэффициентом равновесия определенного катиона c зарядом z_i на ион гидроксония $K_{{\text{H}}}^{{Cat,i}};$ (3) – уравнение электронейтральности в жидкой фазе, ($\sum\limits_{j = 1}^m {{{c}_{j}}} $ – суммарная концентрация (моль-экв/л) сопутствующих анионов); (4) – уравнение электронейтральности в неподвижной фазе; (5) – уравнение сохранения количества вещества ${{\hat {c}}_{i}}$ – суммарная концентрация i-ого вещества в слое; ${{\bar {c}}_{\Sigma }}$ – емкость ионита. Предполагается, что: ${{c}_{{\text{H}}}}{{c}_{{{\text{OH}}}}} = {{10}^{{ - 14}}}.$

Молекулярные комплексы

В рассматриваемых в данной работе системах присутствуют ионы Ca²⁺ и ${\text{SO}}_{4}^{{2 - }},$ а также молекулярные комплексы, образуемые в соответствии с равновесиями: ${\text{CaS}}{{{\text{O}}}_{4}} \leftrightarrow {\text{C}}{{{\text{a}}}^{{2 + }}} + {\text{SO}}_{4}^{{2 - }},$ характеризующимися концентрационными константами устойчивости.

(6)

$\frac{{{{c}_{{{\text{CaS}}{{{\text{O}}}_{{\text{4}}}}}}}}}{{c_{{{\text{Ca}}}}^{{2 + }} \cdot c_{{{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}^{{2 - }}}} = {{K}_{{{\text{CaS}}{{{\text{O}}}_{{\text{4}}}}}}}\,\,\,({1 \mathord{\left/ {\vphantom {1 {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}}).$

Табличные значения соответствующей константы устойчивости [13]:

$\lg {{K}_{{{\text{CaS}}{{{\text{O}}}_{{\text{4}}}}}}} = 2.31,\,\,\,(K_{{{\text{CaS}}{{{\text{O}}}_{{\text{4}}}}}}^{{ - 1}} = 0.004898).$

Из (6) получаем систему уравнений относительно $x = {{c}_{{{\text{CaS}}{{{\text{O}}}_{{\text{4}}}}}}}{\text{:}}$

(7)

$\begin{gathered} xK_{{{\text{CaS}}{{{\text{O}}}_{{\text{4}}}}}}^{{ - 1}} = \left( {{{c}_{{{\text{Ca}}}}} - x} \right)\left( {{{c}_{{{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} - x} \right) \Rightarrow x = \\ = \frac{{{{c}_{{{\text{Ca}}}}} + {{c}_{{{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} + K_{S}^{{ - 1}}}}{2} - \sqrt {{{{\left( {\frac{{{{c}_{{{\text{Ca}}}}} + {{c}_{{{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} + K_{S}^{{ - 1}}}}{2}} \right)}}^{2}} - {{c}_{{{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}}{{c}_{{{\text{Ca}}}}}} . \\ \end{gathered} $

Концентрацию ионов кальция и сульфата можно теперь рассчитать по формулам:

(8)

$c_{{{\text{Ca}}}}^{ + } = {{c}_{{{\text{Ca}}}}} - x;\,\,\,\,c_{{{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}^{ - } = {{c}_{{{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} - x.$

Для расчета ионообменных процессов были модифицированы разработанные нами ранее математическая модель и созданная на ее основе программа “Createscheme” [4, 14], базирующаяся на решении дифференциальных уравнений, описывающих эти процессы в приближении квазистационарности. Решение системы (2)–(5) совместно с уравнениями (6), (7) производится с помощью метода последовательных приближений при каждом акте сорбции на каждом шаге программы. Отличительной особенностью представленной здесь задачи является учет концентраций комплекса CaSO₄, которые не участвуют в процессах ионного обмена, но могут снижать эффективность умягчения, способствуя переносу двухзарядных ионов в слое катионита.

Нанофильтрация

Процесс удаления сульфата с помощью нанофильтрации (НФ) также требует учета концентрации незаряженного комплекса CaSO₄, который проходит свободно сквозь наномембрану и не участвуeт в процессах фильтрации. Фильтрацию оставшихся ионов можно моделировать с помощью приведенного далее несложного алгоритма.

Основным параметрoм НФ являeтся: степень концентрирования:

(9)

${{Q}_{N}} = {{{{V}_{{KN}}}} \mathord{\left/ {\vphantom {{{{V}_{{KN}}}} {{{V}_{S}}}}} \right. \kern-0em} {{{V}_{S}}}};\,\,\,\,{{V}_{S}} = {{V}_{{KN}}} + {{V}_{{PN}}},$

где V_S – исходный объем подаваемого на НФ раствора (в нашем случае – объем умягченной воды), V_KN – объем концентрата нанофильтрации, ${{V}_{{PN}}}$ – объем пермеата. А селективность мембран обычно выражается через степень удерживания заряженных ионов (анионов) компонента в процентах (Retentionpercentage) [15, 16], или в безразмерных долях:

(10)

${{R}_{{N,i}}} = {{({{c}_{{S,i}}} - {{c}_{{PN,i}}})} \mathord{\left/ {\vphantom {{({{c}_{{S,i}}} - {{c}_{{PN,i}}})} {{{c}_{{S,i}}},}}} \right. \kern-0em} {{{c}_{{S,i}}},}}$

где c_S,_i – исходная концентрация ионов i-го компонента в умягченной воде, c_PN,_i – концентрация ионов компонента в пермеате после нанофильтрации или в виде массового коэффициента селективности:

(11)

${{R}_{{M,i}}} = \frac{{{{c}_{{KN,i}}}{{V}_{{KN}}}}}{{{{c}_{{S,i}}}{{V}_{S}}}}.$

Для каждого из компонентов раствора выпишем соотношения баланса (выраженные в моль-экв):

(12)

${{V}_{S}}{{c}_{{S,i}}} = {{V}_{{PN}}}{{c}_{{PN,i}}} + {{V}_{{KN}}}{{c}_{{KN,i}}}.$

Используя (12), можно установить формулу связи концентрационного (10) и массового (11) коэффициентов селективности мембраны:

${{R}_{{M,i}}} = {{Q}_{N}} + {{R}_{{N,i}}} - {{Q}_{N}}{{R}_{{N,i}}}.$

С учетом высокой селективности многих НФ-мембран к двухзарядным ионам и практического отсутствия у них селективности к простым однозарядным ионам [15, 16] для концентраций катионов и анионов, задерживаемых наномембраной, получим:

(14)

${{c}_{{PN,i}}} = {{c}_{{S,i}}}\left( {1 - {{R}_{{N,i}}}} \right);\,\,\,\,{{c}_{{KN,i}}} = \frac{{{{c}_{{S,i}}}{{V}_{S}} - {{c}_{{PN,i}}}{{V}_{{PN}}}}}{{{{V}_{{KN}}}}}.$

В нашем случае наномембрана определяет концентрации двухзарядного иона SO₄ и двухзарядного иона Ca, при этом однозарядные ионы Cl и ионы Na проходят сквозь мембрану практически свободно. В связи с тем, что при катионировании концентрации анионов не изменяются в умягченной воде, поступающей на наномембрану, суммарная концентрация ионов кальция много меньше концентрации сульфат-иона, поэтому заряд вещества, задержанного при фильтрации, будет отрицательным и может быть скомпенсирован только положительными ионами натрия. Откуда следует, что концентрации хлорид ионов, свободно проходящих сквозь наномембрану, не меняются ${{c}_{{PN,{\text{Cl}}}}} = {{c}_{{KN{\text{,Cl}}}}} = {{c}_{{S,{\text{Cl}}}}} = {{c}_{{0,{\text{Cl}}}}}.$ А концентрации ионов натрия, компенсирующих отрицательный заряд вещества, задержанного наномембраной и пропущенного сквозь нее, можно найти из соотношений электронейтральности:

(15)

$\begin{gathered} {{c}_{{PN,{\text{Na}}}}} = {{c}_{{PN,{\text{Cl}}}}} + {{c}_{{PN,{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} - {{c}_{{PN,{\text{Ca}}}}}, \\ {{c}_{{KN,{\text{Na}}}}} = {{c}_{{S,{\text{Cl}}}}} + {{c}_{{KN,{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} - {{c}_{{KN,{\text{Ca}}}}}. \\ \end{gathered} $

Учитывая, что в пермеате концентрации сульфата и кальция малы, справедлива оценка:

(16)

${{c}_{{PN,{\text{Na}}}}} \approx {{c}_{{S,{\text{Cl}}}}} = {{c}_{{0,CL}}}.$

В данной работе моделируется стационарные режимы работы системы, при которых состояние системы стабильно повторяется от цикла к циклу. Такие стабильные режимы полностью определяются граничными условиями и практически не зависят от начальных условий. Соответственно, такие режимы слабо реагируют на случайные ошибки, возвращая систему в прежний режим через несколько циклов. Таким образом, несмотря на длительность счета, накопления ошибок не происходит, что также показано в работе [4], где эта проблема исследована путем введения в процесс искусственных однократных возмущений. Однако, в случае повторяющихся (из цикла в цикл) однотипных малых возмущений такое воздействие может быть существенным, что следует учитывать в будущих исследованиях.

УСЛОВИЯ ПРОВЕДЕНИЯ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Для расчетов выбраны следующие параметры: диаметр слоя катионита в колонне – 0.5 м (площадь сечения – 0.196 м²); высота слоя – 1 м; объем слоя сорбента – 0.196 м³; скорость пропускания растворов на стадиях сорбции – 5 колоночных объемов в час (0.980 м³/ч); скорость пропускания растворов на стадиях регенерации – 1 колоночный объем в час (0.196 м³/ч).

Предполагается, что катионит загружен в колонну так, что отсутствует жидкость вне слоя. Свободный объем жидкости определяется только порозностью (межзерновым пространством) стационарного слоя.

Виртуальный циклический процесс осуществляется в соответствии со схемой, показанной на рис. 2.

Рис. 2.

Схема виртуальной установки для численных экспериментов по СМП-процессу. Модули: 1 – Na-катионирования, 2 – нанофильтрации, 3 – опреснения; 4–6 – емкости: 4 – умягченной воды, 5 – регенерирующего раствора, 6 – раствора, вытесняемого из слоя катионита. Потоки: I – исходная вода, II –вытесняемый из слоя раствор, III – умягченная вода, IV – опресненная вода, V – концентрат после опреснителя; VI – регенерирующий раствор, VII – сброс, VIII – концентрат нанофильтрации, IX – добавка раствора NaCl.

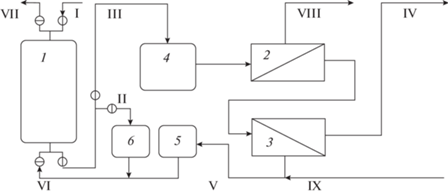
В каждом цикле стадия сорбции начинается с вытеснения рассола, который остался в межзерновом пространстве слоя катионита после предыдущего цикла регенерации. Также в каждом цикле стадия регенерации начинается с т. н. частичной регенерации с использованием этого рассола, полученного после указанной выше операции вытеснения при сорбции. Циклы удобнее описывать по цепочке: вытеснение (и частичная сорбция) – основная сорбция – частичная регенерация – основная регенерация.

Нулевой цикл. Катионит находится в исходной Na – форме. Исходная вода заданного состава $\left( {{{c}_{\Sigma }} = \sum {{{c}_{{0,i}}}} } \right)$ поступает сверху вниз в колонну 1 с катионитом, и умягченная вода собирается в емкости 4. Стадия умягчения заканчивается в момент заданного проскока кальция на выходе из колонны. Весь объем умягченной воды V_S из емкости 4 подается в нанофильтрационный модуль 2. Задаются два параметра нанофильтрации: степень концентрирования Q_N и селективность мембран R_N,_i, R_M,_i в соответствии с формулами (9–11).

Концентрат после нанофильтрации, представляющий собой сульфат натрия или смесь сульфата натрия с небольшой примесью хлорида натрия, является побочным продуктом и удаляется из процесса. Пермеат нанофильтрации объемом V_PN, практически не содержащий двухзарядных ионов и представляющий собой раствор хлорида натрия, поступает на опреснительный модуль 3. На схеме он приведен так, как обычно рисуют обратно-осмотический модуль. На самом деле, может быть использован опреснитель любого, в том числе дистилляционного типа. Задаются концентрации регенерационного раствора c_{R, Na} и потери натрия с опресненной водой c_{W, Na}; определяются: степень концентрирования рассола после опреснителя (используемого в качестве регенерационного раствора для катионита) k_R = c_R,_Na/c_PN,_Na, учитывая, что в силу (16) c_{PN, Na} = c_{0, Cl} имеем k_R = c_R,_Na/c_{0, Cl}, а коэффициент k_W = c_W,_Na/c_{0, Cl} определяет потери натрия с опресненной водой, тогда объем раствора на регенерацию V_R будет равен:

(17)

${{V}_{R}} = {{V}_{{PN}}}{{Q}_{R}};\,\,\,{{Q}_{R}} = {{(1 - {{k}_{W}})} \mathord{\left/ {\vphantom {{(1 - {{k}_{W}})} {({{k}_{R}} - {{k}_{W}}),}}} \right. \kern-0em} {({{k}_{R}} - {{k}_{W}}),}}$

где величина Q_R – степень концентрирования опреснителя. Рассол после опреснителя поступает в емкость 5 и далее подается на регенерацию в колонну в направлении снизу-вверх, после того, как прошла стадия частичной регенерации раствором, подаваемым из емкости 6. После стадии регенерации в слое катионита остается такой же объем рассола, который находился в емкости 6, поэтому объем раствора на регенерацию в каждом цикле остается равным V_R.

Первый и последующие циклы проводятся по иному алгоритму, включающему вытеснение и частичную сорбцию: на стадии сорбции, по достижению заданной концентрации ионов натрия на выходе, завершается процесс вытеснения рассола в емкость 6, и поток умягченной воды собирается в 4, откуда подается в нананофильтрационный модуль 2 для получения побочного продукта – концентрата и пермеата, который поступает в опреснитель 3 для получения основного продукта – пресной воды и рассола для регенерации, собираемого в емкости 5. Во всех циклах на стадии регенерации частичная регенерация проводится вытесненным рассолом из 6, а основная – рассолом после опреснения из 5. Для осуществления циклического процесса в случаe, когда в численном эксперименте с определенным количеством циклов не удается получить стабильный и повторяющийся СМП-процесс, проводится виртуальная операция по добавлению в емкость 5 определенного дополнительного количества раствора хлорида натрия той же концентрации, что и в 5 для завершения процесса регенерации катионита. Такой процесс не считается самоподдерживающимся.

В численных экспериментах были использованы следующие равновесные параметры – характеристики сульфокатионита КУ-2 (полученные экспериментально и апробированные ранее в расчетах [12]), полная обменная емкость (ПОЕ): ${{\bar {c}}_{\Sigma }}$ = 2 моль-экв/л. Константы равновесия ионного обмена: $K_{{\text{H}}}^{{{\text{Na}}}} = 1.2;$ $K_{{\text{H}}}^{{{\text{Ca}}}} = 5.3.$

Были использованы следующие критерии окончания различных стадий: критерий завершения стадии сорбции – проскок ионов Ca²⁺ = = 0.005 моль-экв/л. Критерий завершения процесса вытеснения – проскок ионов Na⁺ = = 0.15 моль-экв/л.

Завершением стадии регенерации считалось пропускание всего объема рассола из емкости 5 через колонну снизу вверх. Накопление концентрата, полученного после регенерации, и дальнейшая его переработка не рассматривались в рамках настоящих численных экспериментов.

Были использованы количественные характеристики нанофильтрационных мембран и процессов с их использованием, опубликованные в работах [15, 16]. В соответствии с этими работами, большинство промышленных НФ мембран характеризуется процентом удерживания двухзарядных ионов (Retention percentage) в диапазоне 89–98%. Для расчетов выбирали среднее значение коэффициента, рассчитываемого по формуле (10), равным: R_N,_i = 0.938. При оценке по массам, а не концентрациям двухзарядных ионов, это значение в соответствии с (13) соответствует коэффициенту селективности R_M,_i = 0.95.

В табл. 1 представлены составы модельных растворов, использованные в численных экспериментах.

Таблица 1.

Составы модельных растворов, моль-экв/л

Ионы	Na⁺– 0.025 Ca²⁺ – 0.025	Na⁺– 0.04 Ca²⁺– 0.01	Na⁺– 0.01 Ca²⁺– 0.04	Na⁺– 0.045 Ca²⁺– 0.005
Cl^– – 0.025 ${\text{SO}}_{4}^{{2 - }}$ – 0.025	K1A1	K2A1	K3A1	K4A1
Cl^– – 0.04 ${\text{SO}}_{4}^{{2 - }}$ – 0.01	K1A2	K2A2	K3A2	K4A2
Cl^– – 0.01 ${\text{SO}}_{4}^{{2 - }}$ – 0.04	K1A3	K2A3	K3A3	K4A3

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Реализуемость СМП-процессов для 4-х компонентных растворов

На рис. 3 приведены зависимости количества умягченной воды (в единицах колоночных объемов) в циклическом процессе сорбции-регенерации в зависимости от номера цикла для исходного раствора К4А1 (табл. 1). Эти зависимости рассчитаны для циклических процессов умягчения – опреснения, в которых часть хлорида натрия “теряется” с опресненной водой, в данном случае – для 0.01 М концентрации в ней соли. Кривая 1 соответствует самоподдерживающемуся процессу, в ходе формирования которого наблюдается уменьшение объема умягченной воды от цикла к циклу, а затем процесс полностью стабилизируется.

Рис. 3.

Зависимость числа колоночных объемов умягченной воды от номера цикла для раствора К4А1 с исходным содержанием компонентов (моль-экв/л): c_{0, Ca} (Ca²⁺ + CaSO₄) – 0.005, c_{0, Na} – 0.045, c_{0, Cl} – 0.025, ${{c}_{{{\text{0,S}}{{{\text{O}}}_{{\text{4}}}}}}}$ (${\text{SO}}_{4}^{{2 - }}$ + CaSO₄) – 0.025. Добавка 1 М раствора NaCl к такому же раствору, возвращаемому на регенерацию в СМП- процессе (%): 1 – 0; 2 – 50; 3 – 100.

Кривые 2 и 3 соответствуют процессам, в которых в каждом цикле в растворы, возвращаемые на регенерацию, дополнительно добавляются разные количества раствора хлорида натрия. Эти процессы, в частности, процесс описываемый зависимостью 2, также являются реагент-сберегающими по сравнению с традиционными ионообменными процессами умягчения, однако они не являются самоподдерживающимися.

На рис. 4а приведены несколько выходных кривых стадии умягчения (сорбции кальция) для процессов, переходящих в самоподдерживающийся и описываемых рассмотренной выше зависимостью 1. Кривые рассчитаны для предельного “проскока” кальция, равного 1.2 × 10^–3 моль-экв/л. Видно, что в стабилизированном процессе по сравнению с процессами в нулевом и первом циклах не только уменьшается емкость слоя катионита по кальцию, но и изменяется качество умягченной воды. Расчеты показывают, что для стабилизированного СМП-процесса усредненная концентрация кальция в объеме умягченной воды становится равной 1.5 × 10^–4 моль-экв/л кальция (3 мг/л), что составляет 3% от его содержания в исходной воде. Зависимости для распределения ионов кальция и натрия вдоль слоя катионита после стадий сорбции, приведенные на рис. 4б, показывают, что во всех циклах эти распределения повторяются с высокой точностью и кроме конечных сечений слоя определяются только равновесием между фазами ионита и исходного раствора независимо от распределения компонентов перед сорбцией.

Рис. 4.

Характеристики стадий сорбции для модельного раствора К4А1. а – Выходные кривые кальция в нулевом (1), первом (2) и тридцатом (3) циклах. б – Распределение ионов Ca²⁺ (1) и Na⁺ (2) вдоль слоя в нулевом, первом и тридцатом (стабильном) циклах.

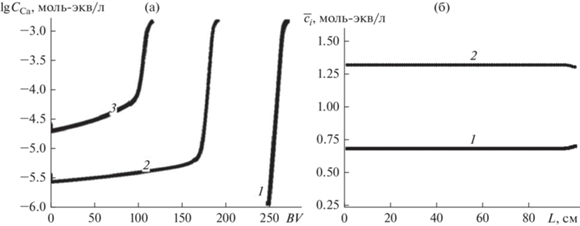
В связи с тем, что лишь часть полной обменной емкости слоя катионита “работает” и участвует в Na⁺ ↔ Ca²⁺ – обмене в самоподдерживающемся циклическом процессе, в ходе стабилизации СМП-процесса устанавливается существенно меньший расход регенерирующего (в нашем случае – 1 М раствора NaCl) по сравнению с его расходом в начальных циклах. Это хорошо видно на зависимости 1, приведенной на рис. 5. Зависимости 2 и 3 соответствуют зависимостям с такими же номерами для процессов сорбции, проиллюстрированных на рис. 3.

Рис. 5.

Зависимость числа колоночных объемов регенеранта от номера цикла переработки раствора К4А1. Добавка 1 М раствора NaCl (%): 1 – 0; 2 – 50; 3 – 100.

Выходные кривые десорбции кальция и регенерации катионита для некоторых циклов – нескольких точек зависимости 1 приведены на рис. 6.

Рис. 6.

Характеристики стадий регенерации для модельного раствора К4А1. а – выходные кривые компонентов в нулевом, первом, и в тридцатом циклах, соответственно: для кальция – 2, 4, 6; для натрия – 1, 3, 5; б – распределение ионов вдоль слоя катионита в нулевом, первом и тридцатом (стабильном) циклах, соответственно: 2, 4, 6 для Ca²⁺ и 1, 3, 5 для Na⁺.

Выходные кривые регенерации (рис. 6а) 4.6 и 3.5 на начальном этапе совпадают, однако имеют разную продолжительность циклов выходные кривые первого цикла 2.58 колоночных объемов, а стабильного цикла 1.59 объемов.

Отличительная особенность стабилизированного СМП-процесса по сравнению с процессами в начальных циклах состоит в том, что концентрация катионных компонентов в первых фракциях выходящего из колонны концентрата резко возрастает. На рис. 6б приведены кривые распределения компонентов вдоль слоя колонны после стадии регенерации для различных циклов. При сравнении однотипных рис. 4б и 6б, следует иметь ввиду, что координата длины слоя L = 0 – это его верхнее сечение, что соответствует входу потока воды в слой для стадии сорбции и выходу из него жидкого концентрата для стадии регенерации. На рис. 6б видно, что в установившемся самоподдерживающемся процессе, например, в 30-ом цикле, как и в начальных циклах, внизу слоя, т.е. на входе в него регенерирующего раствора хлорида натрия, концентрация кальция становится равной нулю, но толщина части слоя с нулевой концентрацией кальция становится ничтожной.

В результате проведения численных экспериментов получено, что самоподдерживающийся процесс реализуется из рассмотренных двенадцати модельных растворов только для шести: K4A1, K4A2, K4A3, K2A2, K2A1, K1A2 (табл. 2).

Таблица 2.

Зависимость количества умягченной воды (в колоночных объемах) от потерь натрия с опресненной водой при стабилизации

Раствор	Потери натрия с опресненной водой, моль-экв/л
Раствор	0	0.005	0.01	0.015
K4A1	246	200	116	54
K4A2	287	278	263	241
K4A3	62	31.5	0.46	–
K2A2	129	119	105	86
K2A1	76	30	–	–
K1A2	25	8	–	–

Причем, для модельных растворов K4A1, K4A2, K2A2 самоподдерживающийся режим осуществляется при всех значениях потерь натрия с опресненной водой. Для модельных растворов K2A1 и K1A2 СМП процесс реализуется только при нулевых потерях и при потерях, равных 0.005 моль-экв/л. Для модельного раствора K4A3 СМП процесс реализуется только при нулевых потерях (табл. 2).

Среди факторов, влияющих на возможность осуществления самоподдерживающегося процесса, наиболее важными являются соотношение компонентов в исходном растворе и величина “уноса” (потерь) ионов натрия из системы вместе с опресненной водой. Влияние последнего фактора видно при сравнении приведенных на рис. 7 зависимости количества умягченной воды (в колоночных объемах) от потерь натрия с опресненной водой для растворов разного состава, а на рис. 8 зависимостей, рассчитанных для раствора К2А1 (табл. 1).

Рис. 7.

Зависимость количества умягченной воды (в колоночных объемах) от потерь натрия с опресненной водой для растворов разного состава: 1 – K4A1, 2 – K4A2, 3 – K4A3, 4 – K2A2, 5 – K2A1, 6 – K1A2.

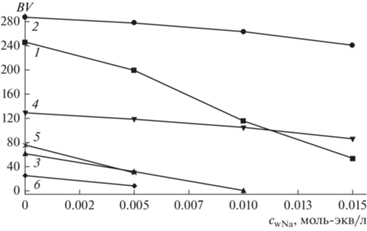
Рис. 8.

Зависимость числа колоночных объемов умягченной воды от номера цикла для раствора К2А1 с исходным содержанием компонентов (моль-экв/л): с_{0, Ca} = 0.01, c_{0, Na} = 0.04, c_{0, Cl} = 0.025, ${{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}$ = 0.025. Концентрация Na⁺ в опресненной воде (моль-экв/л): 1 – 0; 2 – 0.005.

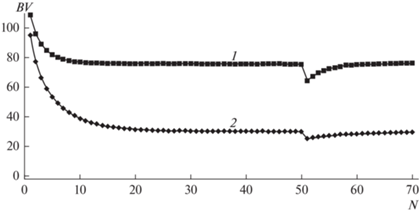
Потери ионов натрия с опресненной водой резко снижают объем раствора, который может быть умягчен в стабилизированном цикле, что очевидно связано со степенью регенерации катионита.

Соотношение компонентов в исходном растворе является существенно более сильным фактором. Его влияние на СМП-процесс можно увидеть, если сравнить зависимости, приведенные на рис. 3 (кривая 1) и рис. 8 (кривая 2).

Увеличение соотношения c_{0, Ca}/c_{0, Na} от значения 0.005/0.045 = 1/9 (рис. 1) до 0.01/0.04 = 1/4 в стабилизированном процессе, показанном на рис. 8, многократно уменьшает объем раствора, который может быть умягчен в одном цикле, при том, что потери Na⁺ c опресненной водой в этом процессе в два раза меньше.

Изломы на зависимостях, показанных на рис. 8, являются результатом специальных возмущений, вносимых в расчеты для последовательных циклов с целью установления истинности эффекта стабилизации. В этом случае, процессы самопроизвольно восстанавливаются, как показано на рисунке.

Дальнейшее увеличение соотношения c_{0, Ca}/c_{0, Na} может привести к невозможности осуществления самоподдерживающегося процесса. Такой пример показан на рис. 9, где представлены зависимости для исходного раствора К1А1 (табл. 1) с равной эквивалентной концентрацией этих компонентов.

Рис. 9.

Зависимость числа колоночных объемов умягченной воды от номера цикла для раствора К1А1 с исходным содержанием компонентов (моль-экв/л): с_{0, Ca} = 0.025, c_{0, Na} = 0.025, c_{0, Cl} = 0.025, ${{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}$ = 0.025, потери натрия с опресненной водой 0.015 моль-экв/л, регенерирующий раствор 1.5 M NaCl. Добавка 1.5 М раствора NaCl к раствору, возвращаемому на регенерацию в СМП-процессе (%): 1 – 100; 2 – 87.5; 3 – 75; 4 – 50; 5 – 0.

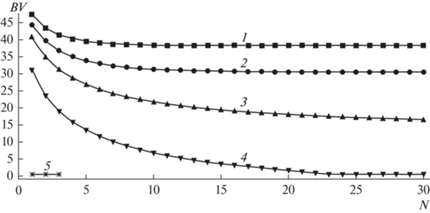
Как видно из представленных результатов, для раствора такого состава не реализуется не только СМП-процесс, но и стабильный процесс сорбции-регенерации при малых добавках раствора соли (менее 87.5%) к оборотному регенерационному раствору.

Как показано ниже, влияние остальных параметров, в том числе, исходного содержания сульфата в перерабатываемом растворе, имеет более сложный характер.

Критерий реализуемости СМП-процессов

Представляет интерес априорная оценка возможности осуществления самоподдерживающегося процесса, исходя из известных данных по составу перерабатываемой воды и значений варьируемых параметров. Очевидно, что смысл такого приближенного количественного критерия, достаточного для инженерных расчетов, должен состоять в достижении какого-то критического значения соотношения количеств ионов натрия и кальция в замкнутом цикле сорбции– регенерации.

Вывод критерия осуществимости стабилизированного СМП-процесса с повторяющимися циклами может быть сделан на основе оценок материального баланса в цикле сорбции–регенерации.

1. Поступающая в умягченный раствор масса ионов натрия в одном цикле (в моль-экв):

– из исходной воды: c_{0, Na}V_S, где V_S – объем умягченной воды;

– из сорбента: ${{\bar {c}}_{{S,{\text{Na}}}}}{{\bar {V}}_{b}} = {{c}_{{0,{\text{Ca}}}}}{{V}_{S}};$ где ${{\bar {c}}_{{S,{\text{Na}}}}}$ – концентрация натрия в слое катионита перед умягчением, ${{\bar {V}}_{b}}$ – объем слоя ионита;

2. Потери натрия в одном цикле (в моль-экв):

– потери с сульфатом при нанофильтрации (все количество анионов сульфата, которое задерживается при нанофильтрации, находится в виде натриевой соли): ${{R}_{M}}{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}{{V}_{S}};$ где, например, R_M = = 0.95 – коэффициент селективности НФ-мембраны;

– потери с хлоридом при нанофильтрации (концентрация хлорида (и эквивалентная ему часть концентрации натрия) примерно одинаковая в пермеате и концентрате НФ): ${{c}_{{0,{\text{Cl}}}}}{{V}_{{k,N}}},$ где V_k,_N – объем концентрата нанофильтрации;

– потери ионов натрия с опресненной водой (в моль-экв):

– ${{c}_{{w,{\text{Na}}}}}{{V}_{w}},$ где ${{c}_{{w,{\text{Na}}}}}$ – концентрация натрия в опресненной воде, V_w – объем опресненной воды в цикле.

Общая масса ионов натрия (в моль-экв), которой можно пользоваться в одном цикле для десорбции кальция и регенерации катионита:

(18)

$\begin{gathered} {{M}_{{{\text{Na}}}}} = {{c}_{{0,{\text{Na}}}}}{{V}_{S}} + {{c}_{{0,{\text{Na}}}}}{{V}_{S}} - {{R}_{M}}{{c}_{{0,{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}}{{V}_{S}} - \\ - \,\,{{c}_{{0,{\text{Cl}}}}}{{V}_{{k,{\text{N}}}}} - {{c}_{{w,{\text{Na}}}}}{{V}_{w}}. \\ \end{gathered} $

Общая масса ионов кальция (в моль-экв), которую необходимо десорбировать в одном цикле:

(19)

${{M}_{{{\text{Ca}}}}} = {{c}_{{0,{\text{Ca}}}}}{{V}_{S}}.$

Формулу критерия удобно представить в виде:

(20)

$\begin{gathered} Rc = \frac{{{{M}_{{{\text{Na}}}}}}}{{{{M}_{{{\text{Ca}}}}}}} = \frac{{{{c}_{{0,{\text{Na}}}}}{{V}_{S}} + {{c}_{{0,{\text{Ca}}}}}{{V}_{S}} - {{R}_{M}}{{c}_{{0,{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}}{{V}_{S}} - {{c}_{{0,{\text{Cl}}}}}{{V}_{{k,N}}} - {{c}_{{w,{\text{Na}}}}}{{V}_{w}}}}{{{{c}_{{0,{\text{Ca}}}}}{{V}_{S}}}} = \\ = \,\,\frac{{{{c}_{\Sigma }} - {{R}_{M}}{{c}_{{0,{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} - {{{{c}_{{0,{\text{Cl}}}}}{{V}_{{k,N}}}} \mathord{\left/ {\vphantom {{{{c}_{{0,{\text{Cl}}}}}{{V}_{{k,N}}}} {{{V}_{S}} - {{{{c}_{{w,{\text{Na}}}}}{{V}_{w}}} \mathord{\left/ {\vphantom {{{{c}_{{w,{\text{Na}}}}}{{V}_{w}}} {{{V}_{S}}}}} \right. \kern-0em} {{{V}_{S}}}}}}} \right. \kern-0em} {{{V}_{S}} - {{{{c}_{{w,{\text{Na}}}}}{{V}_{w}}} \mathord{\left/ {\vphantom {{{{c}_{{w,{\text{Na}}}}}{{V}_{w}}} {{{V}_{S}}}}} \right. \kern-0em} {{{V}_{S}}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}, \\ \end{gathered} $

где: ${{c}_{\Sigma }} = {{c}_{{0,{\text{Na}}}}} + {{c}_{{0,{\text{Ca}}}}}.$

Рассмотрим параметры: ${{{{V}_{{k,N}}}} \mathord{\left/ {\vphantom {{{{V}_{{k,N}}}} {{{V}_{S}}}}} \right. \kern-0em} {{{V}_{S}}}}$ и ${{{{V}_{w}}} \mathord{\left/ {\vphantom {{{{V}_{w}}} {{{V}_{S}}}}} \right. \kern-0em} {{{V}_{S}}}}.$ Первый представляет собой величину степени концентрирования при нанофильтрации (Q_N). Этот параметр подбирается, исходя из состава умягченного раствора, свойств НФ мембран и рациональных условий нанофильтрации. В наших расчетах он выбирался практически равным: Q_N = 0.192. Второй параметр Q_R рассчитывается в соответствии с формулой (17) и зависит от соотношения концентраций NaCl при разделении раствора на опресненную воду и регенерационный раствор:

${{{{V}_{w}}} \mathord{\left/ {\vphantom {{{{V}_{w}}} {{{V}_{S}} = ({{{{V}_{{k,N}}}} \mathord{\left/ {\vphantom {{{{V}_{{k,N}}}} {{{V}_{S}})({{{{V}_{w}}} \mathord{\left/ {\vphantom {{{{V}_{w}}} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}} \right. \kern-0em} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}}}} \right. \kern-0em} {{{V}_{S}})({{{{V}_{w}}} \mathord{\left/ {\vphantom {{{{V}_{w}}} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}} \right. \kern-0em} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}}}}}} \right. \kern-0em} {{{V}_{S}} = ({{{{V}_{{k,N}}}} \mathord{\left/ {\vphantom {{{{V}_{{k,N}}}} {{{V}_{S}})({{{{V}_{w}}} \mathord{\left/ {\vphantom {{{{V}_{w}}} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}} \right. \kern-0em} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}}}} \right. \kern-0em} {{{V}_{S}})({{{{V}_{w}}} \mathord{\left/ {\vphantom {{{{V}_{w}}} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}} \right. \kern-0em} {{{V}_{{k,N}}}) = (1 - {{Q}_{N}})(1 - {{Q}_{R}}).}}}}}}$

С учетом этого можно записать:

(21)

$\begin{gathered} Rc = \\ = \,\,\frac{{{{c}_{\Sigma }}\, - {{R}_{M}}{{c}_{{0,{\text{S}}{{{\text{O}}}_{{\text{4}}}}}}} - {{Q}_{N}}{{c}_{{0,{\text{Cl}}}}}\, - (1 - {{Q}_{N}})(1 - {{Q}_{R}}){{c}_{{w,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}. \\ \end{gathered} $

При использовании критерия (21) задаются исходные концентрации компонентов в перерабатываемой воде и расчет проводится для различных предполагаемых параметров: c_{w, Na} = 0, 0.005, 0.01, 0.015, ${{c}_{{R,{\text{Na}}}}} = 1.$ В силу (16) ${{c}_{{PN,{\text{Na}}}}} \approx {{c}_{{0,{\text{Cl}}}}},$ ${{k}_{R}} = \frac{{{{c}_{{R,{\text{Na}}}}}}}{{{{c}_{{PN,{\text{Na}}}}}}} = \frac{1}{{{{c}_{{0,{\text{Cl}}}}}}}$ и ${{k}_{w}} = \frac{{{{c}_{{w,{\text{Na}}}}}}}{{{{c}_{{PN,{\text{Na}}}}}}} = \frac{{{{c}_{{w,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Cl}}}}}}},$ в соответствии с (17) имеем формулу для критерия Q_R:

${{Q}_{R}} = {{(1 - {{k}_{W}})} \mathord{\left/ {\vphantom {{(1 - {{k}_{W}})} {({{k}_{R}} - {{k}_{W}}).}}} \right. \kern-0em} {({{k}_{R}} - {{k}_{W}}).}}$

Однако, для того, чтобы знать, при каких значениях критерия Rc реализуется самоподдерживающийся процесс, оценим его значение, используя результаты проведенных численных экспериментов, которые сведены в табл. 2 для случаев, когда такой процесс стабилен – табл. 3 и нестабилен – табл. 4.

Таблица 3.

Исходные данные и результаты численных экспериментов для стационарных СМП-процессов

Растворы ${{C}_{\Sigma }}$ = 0.05		Потери с водой ${{c}_{{w,{\text{Na}}}}}$	Объемы на разных стадиях цикла в колоночных объемах (объем колонны 0.196 м³)			Q_R	(1 – Q_N) (1 –Q_R)	Rc
Растворы ${{C}_{\Sigma }}$ = 0.05		Потери с водой ${{c}_{{w,{\text{Na}}}}}$	V_S	${{V}_{{k,{\text{N}}}}}$	${{V}_{w}}$	Q_R	(1 – Q_N) (1 –Q_R)	Rc
K4A1	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 9 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 1	0	246	47	193	0.025	0.788	4.29
		0.005	200	38	158	0.02	0.792	3.5
		0.010	116	22	92	0.015	0.796	2.7
		0.015	54	10	43	0.01	0.8	1.89
K2A2	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{C}}}}}}}$ = 4 $\frac{{{{c}_{{0,{\text{C}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 4	0	130	25	101	0.04	0.775	3.28
		0.005	119	23	92	0.035	0.779	2.89
		0.010	105	20	82	0.03	0.783	2.50
		0.015	86	16	68	0.025	0.787	2.10
K2A1	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 4 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 1	0	76	14.6	60	0.025	0.788	2.14
K2A1		0.005	29	5.6	23	0.02	0.796	1.75
K1A2	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 1 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 4	0	24	4.7	19	0.025	0.776	1.31
K4A2	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 9 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 4	0	287	55	222	0.04	0.776	6.56
		0.005	277	53	216	0.035	0.78	5.78
		0.01	262	50	205	0.03	0.784	5.0
		0.015	240	50	190	0.025	0.787	4.2
K4A3	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 9 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}} = \frac{1}{4}$	0	62	12	50	0.01	0.8	2.02
K4A3		0.005	31	6	25	0.0005	0.804	1.21

Таблица 4.

Расчет значений критерия Rc по исходным составам растворов и при задаваемых параметрах Q_N = = 0.192 для случаев, когда не реализуются СМП-процессы

Растворы c_Σ = 0.05		Потери	Q_R	(1 – Q_N)(1 – Q_R)	Rc
K1A1	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 1 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 1	0	0.025	0.788	0.86
		0.005	0.02	0.792	0.70
		0.01	0.015	0.796	0.54
		0.015	0.01	0.8	0.38
K1A3	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 1 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}} = \frac{1}{4}$	0	0.01	0.8	0.40
		0.005	0.0005	0.8	0.24
		0.01
K2A3	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}}$ = 4 $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}} = \frac{1}{4}$	0	0.01	0.8	1.00
		0.005	0.0005	0.8	0.60
		0.01	0	0.81	0.2
K3A1	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}} = \frac{1}{4}$ $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 1	0	0.025	0.788	0.54
		0.005	0.02	0.792	0.44
		0.01	0.015	0.796	0.34
		0.015	0.01	0.8	0.24
K3A2	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}} = \frac{1}{4}$ $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}}$ = 4	0	0.04	0.776	0.82
		0.005	0.035	0.78	0.72
		0.01	0.03	0.784	0.63
		0.015	0.025	0.787	0.53
K3A3	$\frac{{{{c}_{{0,{\text{Na}}}}}}}{{{{c}_{{0,{\text{Ca}}}}}}} = \frac{1}{4}$ $\frac{{{{c}_{{0,{\text{Cl}}}}}}}{{{{c}_{{0,{\text{S}}{{{\text{O}}}_{4}}}}}}} = \frac{1}{4}$	0	0.01	0.8	0.25
		0.005	0.0005	0.8	0.15
		0.01	0	0.81	0.05

Минимальное значение критерия Rc = 1.21 соответствует наименьшему объему умягченной воды, получаемой в одном повторяющемся цикле СМП-процесса: V_S = 31 колоночных объемов. При этом исходный раствор имеет состав, приведенный в последней строке таблицы, а опресненная вода содержит 0.005 моль-экв/л (292.5 мг/л) хлорида натрия.

В табл. 4 приведены данные для случаев, когда численные эксперименты показывают невозможность реализации самоподдерживающихся процессов. Значения параметров Q_N, Q_R и c_w, Na при этом заданы такими же, как для стационарных СМП-процессов.

Как видно из представленных данных, для всех рассмотренных примеров значения критерия: Rc < 1.

Полученные результаты показывают возможность проведения приближенных инженерных расчетов для априорной оценки реализуемости самоподдерживающихся процессов умягчения- опреснения.

ЗАКЛЮЧЕНИЕ

Проведенные численные эксперименты на примере модельных растворов хлоридов и сульфатов натрия и кальция и анализ полученных результатов показывает осуществимость на практике стационарных циклических самоподдерживающихся процессов умягчения–опреснения с использованием сильнокислотного катионита, в которых регенерация катионита в каждом цикле осуществляется только за счет возвратного рассола, получаемого при опреснении умягченной воды.

Для реализации СМП-процессов переработки сульфатсодержащих растворов необходимо разделение сульфатов и хлоридов в умягченной воде, направляемой на опреснение с одновременным получением рассола для регенерации катионита. Для такого разделения можно использовать метод нанофильтрации.

Численные эксперименты показывают, что наличие сульфата в растворе резко сужает диапазон составов соленых вод и условий для осуществления СМП-процессов по сравнению с хлоридными системами, изученными ранее [4].

Численные эксперименты для исследования большого количества последовательных циклов умягчения-опреснения, трудноосуществимые обычными экспериментальными методами, позволяют увидеть распределение катионов в слое катионита и выходные кривые компонентов на любой стадии процессов. Показано, что на характеристики самоподдерживающихся процессов, а именно количество циклов до выхода на стационарный режим, а также продолжительность этих циклов на стадиях сорбции и регенерации, оказывают влияние: соотношение концентраций двух- и однозарядных ионов в исходном растворе, а также относительные потери однозарядных ионов, “уносимые” с опресненной водой.

На основе анализа результатов большого количества составов модельных растворов солоноватых вод при изменении варьируемых условий предложено критериальное соотношение для инженерных расчетов с целью априорной оценки реализуемости СМП-процессов.

Проведенный анализ показывает методологию расчетов рациональных условий организации СМП-процессов в реальных условиях переработки природных и техногенных вод. Это дает возможность заложить технологические основы для создания автономных стационарных и передвижных систем водоподготовки при использовании СМП-процесса для переработки подземных солоноватых, а также сточных вод, не требующих привозных реагентов и, соответственно, вспомогательных устройств для хранения реагентов и приготовления регенерационных растворов.

ОБОЗНАЧЕНИЯ

А, В	компоненты раствора, участвующие в ионном обмене
BV	колоночный объем (в наших примерах 0.196 м³)
c	концентрация в растворе (моль-экв/л)
$\bar {с}$	концентрации в фазе ионита на объем слоя (моль-экв/л)
${{\hat {с}}_{i}}$	средняя концентрация i-ого компонента в сечении слоя катионита (моль-экв/л) (с учетом жидкой и твердой фазы)
D	коэффициент диффузии (см²/с)
K	концентрационная константа (коэффициент) равновесия ионного обмена
k_R, k_W	степень концентрирования при разделении на регенерационный раствор и опресненную воду
L	высота слоя катионита (см)
N	номер сорбционного цикла
Q_N, Q_R	объемные критерии концентрирования при фильтрации и опреснении
${{R}_{{N,i}}}{{R}_{{M,i}}}$	селективность наномембраны по концентрациям и по массе
Rc	критерий реализуемости СМП-процесса
S	площадь сечения слоя катионита, (м²)
t	время, мин (с, ч)
V	объемы на разных стадиях цикла (л)
$v$	линейная скорость, (см/мин)
X	координата точки концентрационного фронта вдоль слоя катионита
x	координата по высоте колонны, отсчитываемая от точки входа раствора
W	объемная скорость раствора (м³/ч)
z	заряд иона
ε	порозность (доля межзернового пространства в слое катионита)

ИНДЕКСЫ

Br	“проскоковая” концентрация
i, j	ионные компоненты
Σ	суммарная концентрация в растворе или сорбенте (емкость сорбента);
PN	пермеат нанофильтрации
KN	концентрат нанофильтрации
S	сорбция (умягчение)
R	регенерация
W	потери натрия с опресненной водой

Список литературы

Klein G., Vermeulen T. Cyclic performance of layered beds for binary ion exchange// AIChESymp. Ser. 1975. V. 71. № 152. P. 69.
Barba D., Brandani V., Foscolo P.U. A method based on equilibrium theory for a current choice of cationic resin in sea water softening // Desalination. 1983. V. 48. № 2. P. 133.
Tokmachev M.G., Tikhonov N.A., Khamizov R.Kh. Investigation of cyclic self-sustaining ion exchange process for softening water solutions on the basis of mathematical modeling // React. Funct. Polym. 2008. V. 68. P. 1245.
Хамизов Р.Х., Комарова И.В., Галкина Н.К., Прудковский А.Г. Самоподдерживающиеся процессы умягчения-опреснения воды. Простые двухкомпонентные системы // Теор. основы хим. технологии. 2020. Т. 54. № 5. С. 649.
MuravievD.N., Khamizov R.Kh., Tikhonov N.A., Morales J.G. Clean (“Green”) IonExchangeTechnologies. IV. High-Ca-selectivityion-exchange material for self-sustaining decalcification of mineralized waters process // Ind. Eng. Chem. Res. 2004. V. 43. № 8. P. 1868.
US Patent Appl.Publ. 2011/0278225.Method for purifying water by cyclic ionic exchange // Boodo F., Publ. Nov. 17, 2011.
Flodman H.R., Dvorak B.I. Brine reuse in ion-exchange softening: salt discharge, hardness leakage, and capacity tradeoffs // Water Environm.Res. 2012. V. 84. № 6. P. 535.
Патент РФ 2 686 147 Способ переработки природных солоноватых вод на ионитах с получением растворов сложных минеральных удобрений и установка для его осуществления (варианты) // Хамизов Р.Х., Хамизов С.Х. – опубл. 24.04.2019, Бюлл. № 12.
Tang S., Brinchak L, Cohen Y., Lahav O. Selective separation of divalent ions from seawater using an integrated ion-exchange/nanofiltration approach // Chem. Eng.Proc.-Proc.Inetens. 2018. V. 126. P. 8.
Brinchak L., Keller O., Tang S., Fridman-Bishop N., Lahav O. A membrane-based recycling process for minimizing environmental effects inflicted by ion-exchange softening applications // Sep. Purific. Technol. 2019. V. 223. P. 23.
Safonyk A., Prysiazhniuk I., Prysiazhniuk O., Naumchuk O. Mathematical modeling singularly perturbed processes of water softening on sodium-cationite filters // IAPGOS. 2019. № 1. P. 37.
Комарова И.В., Галкина Н.К., Прудковский А.Г. Вычислительный эксперимент как способ оценки эффективности работы водоподготовительных установок при поточной и противоточной регенерации ионообменных фильтров // Сорбц. Хроматограф. Процессы. 2018. Т. 18. № 5. С. 776.
Лурье Ю.Ю. Справочник по аналитической химии. М.: Химия, 1989. С. 448.
Комарова И.В., Галкина Н.К., Прудковский А.Г., Хамизов Р.Х. Математическое моделирование и расчет процесса деминерализации воды в промышленном фильтре Сообщение 1. Гидродинамика регенерации и отмывки промышленного фильтра // Сорбционные и хроматографические процессы. 2017. Т. 17. № 1. С. 10.
Amir Abbas Izadpanah, Asghar Javidnia. The Abilityofa Nanofiltration Membraneto Remove Hardnessand Ionsfrom Diluted Seawater // Water. 2012. V. 4. P. 283.
Bargeman G., Steensma M., ten Kate A., Westerink J.B., Demmer R.L.M., Bakkenes H., Manuhutu C.F.H. Nanofiltration as energy-efficient solution for sulfate waste in vacuum salt production // Desalination. 2009. V. 245. P. 460.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал