1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 56, № 2, 2022

Теоретические основы химической технологии, 2022, T. 56, № 2, стр. 197-204

Применение метода искусственных нейронных сетей для анализа данных о равновесии жидкость–жидкость в трехкомпонентных системах

Г. Х. Мисиков a, А. В. Петров a, А. М. Тойкка a, *

a Санкт-Петербургский государственный университет, Институт химии, кафедра химической термодинамики и кинетики
Санкт-Петербург, Россия

* E-mail: a.toikka@spbu.ru

Поступила в редакцию 17.11.2021
После доработки 22.11.2021
Принята к публикации 30.11.2021

Полный текст (PDF)

Аннотация

Рассмотрена возможность применения искусственных нейронных сетей для описания фазовых равновесий жидкость–жидкость в тройных системах при политермических условиях. Исследование проведено на примере 10 трехкомпонентных систем, включающих бинарные расслаивающиеся подсистемы вода–сложные эфиры карбоновых кислот, что определяет расслоение и в тройных системах (третий компонент – спирт или карбоновая кислота). Представлены особенности выбранной архитектуры сети, результаты, с критической оценкой точности расчетов, приведены в таблицах. Проведено сравнение аппроксимаций на основе искусственных нейронных сетей с расчетами по модели NRTL.

Ключевые слова: равновесие жидкость–жидкость, тройные системы, искусственные нейронные сети, моделирование, NRTL

ВВЕДЕНИЕ

Современные методы анализа данных существенно расширили возможности расчетов, моделирования, аппроксимации и представления свойств сложных физико-химических систем. Это особенно важно для развития новых подходов к анализу термодинамических свойств, включая такие значимые для химической технологии характеристики, как параметры фазовых равновесий. Среди указанных методов можно выделить искусственные нейронные сети (ИНС), популярность которых как метода представления и анализа данных определяется новыми возможностями учета большого числа параметров при работе со значительными объемами информации, описывать сложные функциональные зависимости, применимостью в различных областях знаний [1–5].

Для анализа и расчетов фазовых равновесий используются различные подходы, такие как модели локального состава (уравнение Вильсона, NRTL, UNIQUAC), групповые модели (UNIFAC), модели ассоциированных флюидов (PC-SAFT), и другие [6–10]. Вместе с тем, даже строгие теоретические подходы и расчетные методы часто не позволяют найти аналитические решения при анализе сложных физико-химических систем, в первую очередь, в силу необходимости учета большого числа внешних и внутренних факторов, специфических взаимодействий между компонентами. В этом отношении выигрышное место занимает метод ИНС, в основу которого заложены возможности работы с большими базами данных, описывать закономерности, связанные с большим числом переменных.

Определенный опыт применения искусственных нейронных сетей для описания равновесий жидкость–пар (см., например, [11–14]) позволяет выделить положительные и отрицательные стороны применения ИНС для анализа фазовых равновесий в целом, включая равновесия жидкость–жидкость. Одно из центральных мест занимает проблема относительно малого объема данных для фазовых равновесий конкретных систем: как правило, экспериментально исследуется не более нескольких десятков составов многокомпонентных систем. Для сравнения укажем, что, например, при моделировании свойств природного газа различных месторождений методом ИНС объем используемой эмпирической информации охватывал до 30 000 значений [15, 16]. Однако, в рамках подхода, предложенного Фокке [17] и развитого в дальнейших в работах [13, 14], было показано, что нейронные сети могут использоваться для моделирования равновесий жидкость–пар с удовлетворительной точностью. Отмечено, что хотя в основу применения ИНС для анализа фазовых равновесий не положена определенная физическая модель, при определенной архитектуре сети метод ИНС может быть представлен как некоторое обобщение уравнений моделей Вильсона и NRTL, имеющих физическое обоснование [13, 17]. Что касается равновесий жидкость–жидкость, то в ряде работ представлены возможности расчетов параметров таких систем с применением ИНС [18–21]. Рассматриваются многие варианты, связанные с физико-химической природой систем, числом компонентов, разной структурой сети, представлением входных и выходных данных, практическими задачами. В нашей работе представлен анализ возможностей и аспекты применения метода ИНС для описания фазовых равновесий жидкость–жидкость на примере тройных систем, содержащих карбоновую кислоту, спирт, сложный эфир и воду, включая результаты конкретных расчетов.

РАСЧЕТНАЯ ЧАСТЬ

Применение ИНС требует определенной исходной базы данных о системах конкретного типа. В настоящей работе рассматриваются тройные смеси, включающие бинарные подсистемы вода–сложный эфир, а именно системы с расслаиванием, которые вызывают расслоение и трехкомпонентных растворов. Третьими компонентами являлись карбоновые кислоты или спирты, т.е. тройные системы являлись подсистемами четверных смесей с реакциями синтеза сложного эфира. Список систем и литературные источники для данных, использованных при построении ИНС, представлены в табл. 1.

Таблица 1.  

Список тройных систем, выбранных для расчетов по ИНС, и ссылки на источники экспериментальных данных

Система Ссылки
Уксусная кислота–этилацетат–вода [23, 26, 27]
Этанол–этилацетат–вода [23, 26, 27]
Уксусная кислота–пропилацетат–вода [28, 29]
Пропанол–пропилацетат–вода [25, 28–30]
Уксусная кислота–бутилацетат–вода [31–36]
Уксусная кислота – бутанол – вода [31–34]
Бутанол–бутилацетат–вода [31–34]
Уксусная кислота–пентилацетат–вода [24, 37]
Уксусная кислота–пентанол–вода [24, 37]
Пентанол–пентилацетат–вода [24, 37]

Архитектура сети была построена согласно методу многослойного перцептрона, который является одним из самых распространенных и, в то же время, простых способов преобразования входной информации в выходную [22]. Он обеспечивает передачу информации только в одном направлении: от входного слоя к выходному через системы скрытых слоев. Таким образом, число слоев в такой схеме не может быть меньше трех (входной, выходной и хотя бы один скрытый), каждый из которых представлен набором нейронов, число которых во входном и выходном слоях диктуется спецификой получаемых данных, в то время как число нейронов в скрытом слое может быть подобрано для каждого конкретного случая. Одним из важных параметров ИНС является функция активации, определяющая выходные значения в зависимости от результата взвешенной суммы входов и порогового значения. Обычно используют стандартные функции, например, сигмоиду, гиперболический тангенс и другие.

В нашем случае, для исследования бинодалей в тройных системах, точнее, равновесных составов, имеются наборы данных о сосуществующих фазах, условно – водной (обогащенной водой) и органической. Решается задача об описании соотношения концентраций в фазах с применением многослойного перцептрона. В качестве входной информации принимались состав органической фазы и температура, соответственно, выходными данными являлись составы равновесной водной фазы, т.е. составы, отвечающие нодам жидкость–жидкость при данной температуре. Таким образом, входной слой содержал 4 нейрона (это 3 мольные доли компонентов в органической фазе и температура), а выходной – 3 нейрона (3 мольные доли компонентов водной фазы). Отметим, что несмотря на известную связь между мольными долями компонентов $\sum\limits_{i = 1}^n {{{x}_{i}}} = 1,$ в расчетах по ИНС каждый параметр (количества веществ) должен вносить независимый вклад в скрытый слой [13, 14, 17]. Вместо абсолютной температуры для нейронной сети использовалась приведенная температура (t), которая вычислялась по формуле:

(1)
$t = \,\,~\frac{{T - \,\,~{{T}_{{{\text{min}}}}}}}{{{{T}_{{{\text{max}}}}} - ~\,\,{{T}_{{{\text{min}}}}}}},$
где T – абсолютная температура, Tmin и Tmax – минимальная и максимальная температуры в исследуемом диапазоне равновесий. Значение приведенной температуры, как видно из формулы (1), меняется в диапазоне от 0 до 1, как и мольные доли компонентов. Таким образом исключается формальная возможность преимущественного вклада температуры из-за того, что ее численные значения T на несколько порядков больше величин мольных долей.

Один скрытый слой содержал 5 нейронов. Такое количество было выбрано опытным путем – при меньшем количестве нейронов в скрытом слое сеть не способна описать рассматриваемые данные с достаточной точностью, близкой к экспериментальной.

Таким образом, предлагаемая ИНС отвечает формуле:

(2)
${{y}_{i}} = \sum\limits_{j = 1}^c {\left( {{{k}_{{ij}}}f\left( {\sum\limits_{m = 1}^s {\left( {{{w}_{{mj}}}{{z}_{m}}} \right)} + ~{{b}_{j}}} \right)} \right)} ~,$
где zm – нейрон входного слоя (при m = 1,2,3, zm = = xi – мольная доля компонента (i = m) в органической фазе; z4 = t – приведенная температура), yi – мольная доля компонента i в водной фазе (выходные данные), kij – вес j-нейрона скрытого слоя в i-нейроне выходного слоя, wmj – вес m-нейрона входного слоя в j-нейроне скрытого слоя, bj – свободный член, f – функция активации, s – число нейронов во входном слое (s = 4), c – число нейронов в скрытом слое (c = 5). В качестве функции активации был выбран гиперболический тангенс (f(x) = tanh(x)) как наиболее оптимальный параметр, используемый обычно при создании ИНС:

(3)
${\text{tanh}}\left( x \right) = ~\frac{{{{e}^{{2x}}} - 1}}{{{{e}^{{2x}}} + 1}}~.$

Схема сети ИНС, отвечающая соотношению (2), представлена на рис. 1.

Рис. 1.

Схема расчетов с помощью ИНС. Входные нейроны: x1, x2, x3 – мольные доли компонентов в органической фазе, t – приведенная температура. Выходные нейроны: y1, y2, y3 – мольные доли компонентов в водной фазе. kij – вес j-нейрона скрытого слоя в i-нейроне выходного слоя, wmj – вес m-нейрона входного слоя в j-нейроне скрытого слоя, bj – свободный член, f – функция активации.

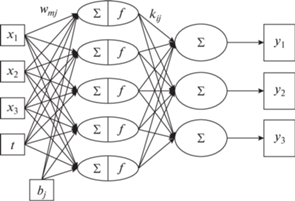
В случае трехкомпонентных систем уравнение (2) может быть переписано в виде системы уравнений, где в явном виде указана активационная функция:

(4)
$\left\{ {\begin{array}{*{20}{c}} {{{y}_{1}} = \sum\limits_{j = 1}^c {~\left( {{{k}_{{1j}}}{\text{tanh}}\left( {\mathop \sum \limits_{m = 1}^s \left( {{{w}_{{mj}}}{{z}_{m}}} \right) + ~\,\,{{b}_{j}}} \right)} \right)} ~} \\ {{{y}_{2}} = \sum\limits_{j = 1}^c {\left( {{{k}_{{2j}}}{\text{tanh}}\left( {\mathop \sum \limits_{m = 1}^s \left( {{{w}_{{mj}}}{{z}_{m}}} \right) + ~\,\,{{b}_{j}}} \right)} \right)} ~} \\ {{{y}_{3}} = \sum\limits_{j = 1}^c {~\left( {{{k}_{{3j}}}{\text{tanh}}\left( {\mathop \sum \limits_{m = 1}^s \left( {{{w}_{{mj}}}{{z}_{m}}} \right) + \,\,~{{b}_{j}}} \right)} \right)} } \end{array}} \right..$

Оптимизацию параметров проводили до минимизации среднеквадратичного отклонения (СКО), рассчитанного по формуле:

(5)
${\text{СКО}} = \sqrt {\frac{{\sum\limits_{r\, = \,1}^d {\sum\limits_{i~ = ~1}^n {{{{\left( {y_{{ri}}^{{{\text{calc}}}}~ - ~y_{{ri}}^{{{\text{ex}}p}}~} \right)}}^{2}}} } }}{{nd - 1}}} ,$
где n – число нейронов в выходном слое (n = 3), d – число составов (экспериментальных точек), $y_{i}^{{{\text{calc}}}}$ – рассчитанное значение мольной доли в водной фазе, $y_{i}^{{{\text{exp}}}}$ – экспериментальное значение мольной доли в водной фазе. Оценку результатов проводили на основе СКО.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Результаты расчетов и сравнения с моделью NRTL приведены в табл. 2, полученные параметры для избранных систем приведены в табл. 3.

Таблица 2.  

Данные, полученные методом ИНС в сравнении с расчетами по модели NRTL

Система Диапазон температур, K СКО (ИНС), мол. % СКО (NRTL), мол. %
Уксусная кислота–этилацетат–вода 293.15–333.15 0.4 2.0 [26]
Этанол–этилацетат–вода 293.15–333.15 0.7 3.3 [26]
Уксусная кислота–пропилацетат–вода 293.15–333.15 0.3 0.9 [29]
Пропанол–пропилацетат–вода 293.15–353.15 0.8 0.9 [29]
Уксусная кислота–бутилацетат–вода 298.15–366.15 1.2 0.9 [31]
Уксусная кислота–бутанол–вода 298.15–328.15 0.7 2.0 [31]
Бутанол–бутилацетат–вода 298.15–328.15 0.5 0.7 [31]
Уксусная кислота–пентилацетат–вода 293.15–323.15 0.4 0.5 [24]
Уксусная кислота–пентанол–вода 293.15–323.15 0.5 0.5 [24]
Пентанол–пентилацетат–вода 293.15–323.15 0.2 0.5 [24]
Таблица 3.  

Параметры ИНС для некоторых тройных систем

j w1j w2j w3j w4j bj k1j k2j k3j
Уксусная кислота–этилацетат–вода
1 1.023 4.924 1.230 0.098 5.151 0.227 0.318 0.432
2 –0.518 2.556 0.929 4.790 1.095 –0.066 1.321 0.684
3 –2.953 1.082 1.460 2.719 0.075 0.120 –1.853 0.223
4 0.378 1.358 1.501 0.003 –0.367 –0.800 0.022 –0.332
5 –2.294 0.864 1.234 5.237 0.142 0.449 –0.332 –4.303
Пропанол–пропилацетат–вода
1 1.093 0.874 1.162 0.999 1.128 0.566 0.692 0.580
2 0.954 1.095 0.888 0.811 0.938 0.050 –0.531 –0.162
3 0.932 1.833 0.338 0.803 1.103 –0.604 0.408 0.589
4 0.955 1.546 0.896 0.885 1.398 0.243 –0.543 –0.174
5 0.942 1.876 0.303 0.787 1.121 –0.241 –1.276 –1.414
Уксусная кислота–бутанол–вода
1 1.018 0.989 1.082 0.949 1.089 0.229 0.488 0.323
2 1.052 0.938 1.248 0.971 1.239 0.233 –0.580 0.377
3 0.609 2.361 0.049 0.763 1.020 –0.240 0.682 0.323
4 0.971 1.432 1.152 0.822 1.555 0.023 –0.580 –0.217
5 0.609 2.361 0.049 0.763 1.020 –0.240 –1.360 –1.216
Уксусная кислота–пентилацетат–вода
1 1.027 1.046 1.033 0.973 1.107 –0.030 0.179 0.390
2 1.029 1.153 1.035 0.963 1.217 –0.144 0.068 0.348
3 1.015 1.022 1.038 1.015 1.074 0.244 –0.624 0.398
4 0.221 1.131 0.350 0.021 –0.304 –0.465 0.174 –0.270
5 1.011 1.022 1.030 1.011 1.062 0.254 –1.217 –1.421

На рис. 2–5 для этих же систем приведены ноды и результаты расчетов по ИНС.

Рис. 2.

Ноды жидкость–жидкость в системе уксусная кислота–этилацетат–вода при 313.15 K: а – эксперимент [26], б – результаты расчета состава водной фазы по ИНС, А – этилацетат, B – уксусная кислота, C – вода.

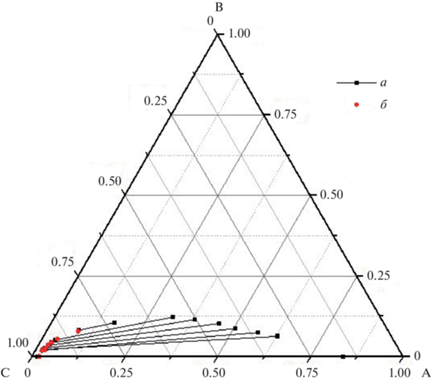
Рис. 3.

Ноды жидкость–жидкость в системе пропанол–пропилацетат–вода при 353.15 K: а – эксперимент [25], б – результаты расчета состава водной фазы по ИНС, А – пропилацетат, B – пропанол, C – вода.

Рис. 4.

Ноды жидкость–жидкость в системе уксусная кислота–бутанол–вода при 308.15 K: а – эксперимент [31], б – результаты расчета состава водной фазы по ИНС, А – бутанол, B – уксусная кислота, C – вода.

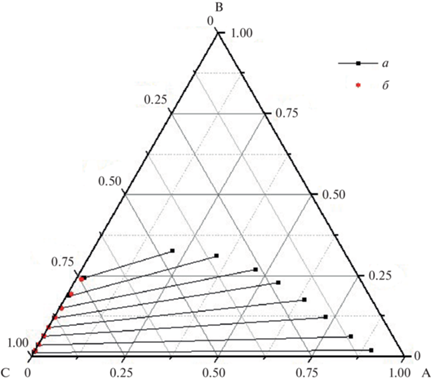
Рис. 5.

Ноды жидкость–жидкость в системе уксусная кислота–пентилацетат–вода при 293.15 K: а – эксперимент [37], б – результаты расчета состава водной фазы по ИНС, А – пентилацетат, B – уксусная кислота, C – вода.

Данные табл. 2 показывают, что СКО для всех систем изменяются в относительно небольшом интервале от 0.2 мол. % для системы пентанол–пентилацетат–вода до 1.2 мол. % в случае системы уксусная кислота–пентилацетат–вода. Эти значения находятся на уровне экспериментальной погрешности определения состава фазы (≈0.5 мол. %) [23–26]. Таким образом, значения СКО, близкие к экспериментальной точности, свидетельствуют о том, что данный подход может быть применен для описания равновесий жидкость–жидкость в рассматриваемых системах в практических целях.

Сравнение с результатами расчетов по уравнениям модели NRTL, представленными в работах [23–37], показывает, что точность этих двух подходов к описанию равновесий жидкость–жидкость находится на одном уровне, а в некоторых случаях метод ИНС дает лучшие результаты. Кроме того, метод ИНС позволяет включить температуру в качестве параметра в архитектуру сети, соответственно, дает возможность анализировать совместно данные при разных температурах, тогда как модель NRTL обычно используется для аппроксимации данных в изотермических условиях.

ЗАКЛЮЧЕНИЕ

В результате проведенного исследования получили дополнительное обоснование возможности применения метода ИНС для расчета и анализа равновесий жидкость–жидкость в трехкомпонентных расслаивающихся системах. Результаты расчетов для 10 тройных систем сложный эфир–вода карбоновая кислота (спирт) в политермических условиях имели точность, близкую к экспериментальной и достаточную для прикладных целей (CKO в пределах 0.2–1.2 мол. %). Более того, сравнение с расчетами по уравнениям модели NRTL показывает, что для ряда систем расчеты по ИНС дают лучшие результаты и позволяют учитывать большее число параметров в ходе моделирования, в частности, температуру. В целом, учитывая необходимость привлечения больших массивов экспериментальных параметров, применение ИНС в исследованиях систем жидкость–жидкость может быть рекомендовано, в первую очередь, для аппроксимации данных о равновесии.

Работа выполнена при финансовой поддержке Российского научного фонда (грант № 21-13-00038). Авторы благодарны В. Кочербитову (Университет Мальмо, Швеция) за полезные консультации. Исследования проведены с использованием вычислительных ресурсов Научного парка СПбГУ – РЦ “Вычислительный центр СПбГУ”.

ОБОЗНАЧЕНИЯ

b свободный член
c число нейронов в скрытом слое
d число экспериментальных составов
f функция активации
k вес нейрона скрытого слоя в нейроне выходного слоя
n число нейронов в выходном слое
s число нейронов во входном слое
T абсолютная температура, K
t приведенная температура
w вес нейрона входного слоя в нейроне скрытого слоя
x мольная доля компонента в органической фазе
y мольная доля компонента в водной фазе
z входной нейрон

ИНДЕКСЫ

calc рассчитанное значение
exp экспериментальное значение
i номер компонента, соответственно, и нейрона выходного слоя
j номер нейрона скрытого слоя
m номер нейрона входного слоя
r нумерация экспериментальных составов

Список литературы

  1. Muravyev N.V., Luciano G., Ornaghi H.L., Svoboda R., Vyazovkin S. Artificial neural networks for pyrolysis, thermal analysis, and thermokinetic studies: The status quo // Molecules. 2021. V. 26. № 12. P. 1.

  2. Li F., Gu Z., Ge L., Sun D., Deng X., Wang S., Hu B., Xu J. Application of artificial neural networks to X-ray fluorescence spectrum analysis // X-Ray Spectrom. 2019. V. 48. № 2. P. 138.

  3. Santos I., Castro L., Rodriguez-Fernandez N., Torrente-Patiño Á., Carballal A. Artificial Neural Networks and Deep Learning in the Visual Arts: a review // Neural Computing and Applications. 2021. V. 23. № 1. P. 121.

  4. Kumar R., Aggarwal R.K., Sharma J.D. Comparison of regression and artificial neural network models for estimation of global solar radiations // Renew. Sustain. Energy Rev. 2015. V. 52. P. 1294.

  5. Haglin J.M., Jimenez G., Eltorai A.E.M. Artificial neural networks in medicine // Health and Technol. 2019. V. 9. № 1.

  6. Wilson G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing // J. Am. Chem. Soc. 1964. V. 86. № 2. P. 127.

  7. Renon H., Prausnitz J.M. Local Compositions in Thermodynamic Excess Functions for Liquid Mixtures // AICHE J. 1968. V. 14. № 1. P. 135.

  8. Fredenslund A., Jones R.L., Prausnitz J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures // AIChE J. 1975. V. 21. № 6. P. 1086.

  9. Abrams D.S., Prausnitz J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems // AIChE J. 1975. V. 21. № 1. P. 116. https://doi.org/10.1002/aic.690210115

  10. Gross J., Sadowski G. Reply to Comment on “perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules // Ind. Eng. Chem. Res. 2019. V. 58. № 14. P. 5744.

  11. Nguyen V.D., Tan R.R., Brondial Y., Fuchino T. Prediction of vapor-liquid equilibrium data for ternary systems using artificial neural networks // Fluid Phase Equilib. 2007. V. 254. № 1–2. P. 188.

  12. Roosta A., Hekayati J., Javanmardi J. Application of artificial neural networks and genetic programming in vapor–liquid equilibrium of C 1 to C 7 alkane binary mixtures // Neural Comput. Appl. 2019. V. 31. № 4. P. 1165.

  13. Argatov I., Kocherbitov V. A note on artificial neural network modeling of vapor-liquid equilibrium in multicomponent mixtures // Fluid Phase Equilib. 2019. V. 502. P. 112282.

  14. Toikka A.M., Misikov G.K., Petrov A.V. Analysis of Data on Vapor–Liquid Equilibrium in Multicomponent Systems Using Artificial Neural Networks // Theor. Found. Chem. Eng. 2021. V. 55. № 3. P. 403.

  15. Farzaneh-Gord M., Mohseni-Gharyehsafa B., Ebrahimi-Moghadam A., Jabari-Moghadam A., Toikka A., Zvereva I. Precise Calculation of Natural Gas Sound Speed Using Neural Networks : An Application in Flow Meter Calibration // Flow Meas. Instrum. 2018. V. 64. P. 90

  16. Farzaneh-Gord M., Rahbari H.R., Mohseni-Gharesafa B., Toikka A., Zvereva I. Accurate determination of natural gas compressibility factor by measuring temperature, pressure and Joule-Thomson coefficient : Artificial neural network approach // J. Pet. Sci. Eng. 2021. V. 202. P. 108427.

  17. Focke W.W. Mixture models based on neural network averaging // Neural Comput. 2006. V. 18. № 1. P. 1.

  18. Sarlak F., Pirhoushyaran T., Shaahmadi F., Yaghoubi Z., Bazooyar B. The Development of Intelligent Models for Liquid–Liquid Equilibria (LLE) Phase Behavior of Thiophene/Alkane/Ionic Liquid Ternary System // Sep. Sci. Technol. 2018. V. 53. № 18. P. 2935. https://doi.org/10.1080/01496395.2018.1495734

  19. Cavalcanti R.N., Oliveira M.B., Meirelles A.J.A. Liquid-liquid equilibria for systems containing fatty acid ethyl esters, ethanol and glycerol at 333.15 and 343.15 K: Experimental data, thermodynamic and artificial neural network modeling // Brazilian J. Chem. Eng. 2018. V. 35. № 2. P. 819.

  20. Reynel-Ávila H.E., Bonilla-Petriciolet A., Tapia-Picazo J.C. An artificial neural network-based NRTL model for simulating liquid-liquid equilibria of systems present in biofuels production // Fluid Phase Equilib. 2019. V. 483. P. 153.

  21. Bekri S., Özmen D., Türkmenoğlu A., Özmen A. Application of deep neural network (DNN) for experimental liquid-liquid equilibrium data of water + butyric acid + + 5-methyl-2-hexanone ternary systems // Fluid Phase Equilib. 2021. V. 544–545.

  22. Haykin S. Neural Networks: A Comprehensive Foundation. New Jehsey: Prentice-Hall, 1999.

  23. Trofimova M., Sadaev A., Samarov A., Golikova A., Tsvetov N., Toikka M., Toikka A. Liquid-liquid equilibrium of acetic acid – ethanol – ethyl acetate – water quaternary system: Data review and new results at 323.15 K and 333.15 K // Fluid Phase Equilib. 2020. V. 503.

  24. Toikka M., Vernadskaya V., Samarov A. Solubility, liquid-liquid equilibrium and critical states for quaternary system acetic acid – n-amyl alcohol – n-amyl acetate – water at 303.15 K and atmospheric pressure // Fluid Phase Equilib. 2018. V. 471. P. 68.

  25. Samarov A.A., Toikka M.A., Naumkin P.V., Toikka A.M. Chemical equilibrium and liquid-phase splitting in acetic acid + n-propanol + n-propyl acetate + water system at 293.15 and 353.15 K // Theor. Found. Chem. Eng. 2016. V. 50. № 5. P. 739.

  26. Toikka M., Samarov A., Trofimova M., Golikova A., Tsvetov N., Toikka A. Solubility, liquid-liquid equilibrium and critical states for the quaternary system acetic acid-ethanol-ethyl acetate-water at 303.15 K and 313.15 K // Fluid Phase Equilib. 2014. V. 373. P. 72.

  27. Trofimova M., Toikka M., Toikka A. Solubility, liquid-liquid equilibrium and critical states for the quaternary system acetic acid-ethanol-ethyl acetate-water at 293.15 K // Fluid Phase Equilib. 2012. V. 313. P. 46.

  28. Toikka M., Samarov A., Toikka A. Solubility, liquid-liquid equilibrium and critical states for the system acetic acid + n-propanol + n-propyl acetate + water at 293.15 K and 303.15 K // Fluid Phase Equilib. 2014. V. 375. P. 66.

  29. Toikka M., Sadaev A., Lobacheva O., Golikova A. Experimental Liquid-Liquid Equilibrium and Solubility Study of an Acetic Acid- n-Propyl Alcohol- n-Propyl Acetate-Water System at 323.15 and 333.15 K // J. Chem. Eng. Data. 2020. V. 65. № 11.

  30. Toikka M.A., Tsvetov N.S., Toikka A.M. Splitting of the liquid solution and the compositions of liquid phases in the water-n-propanol-n-propyl acetate system at 293.15, 303.15, and 313.15 K // Theor. Found. Chem. Eng. 2011. V. 45. № 4. P. 429.

  31. Samarov A., Toikka M., Toikka A. Liquid-liquid equilibrium and critical states for the system acetic acid + n‑butanol + n-butyl acetate + water at 308.15 K // Fluid Phase Equilib. 2015. V. 385. P. 129.

  32. Smirnov A., Sadaeva A., Podryadova K., Toikka M. Quaternary liquid-liquid equilibrium, solubility and critical states: Acetic acid – n-butanol – n-butyl acetate – water at 318.15 K and atmospheric pressure // Fluid Phase Equilib. 2019. V. 493. P. 102.

  33. Toikka M., Smirnov A., Samarov A. Liquid-liquid equilibrium, solubility, and critical states in an acetic acid-n-butyl alcohol-n-butyl acetate-water system at 328.15 K and 101.3 K: Topology of phase diagrams and nrtl modeling // J. Chem. Eng. Data. 2021. V. 66. № 3. P. 1466.

  34. Ruiz Bevia F., Prats Rico D., Gomis Yagües V., Varo Galvañ P. Quaternary liquid-liquid equilibrium: water-acetic acid-1-butanol-n-butyl acetate at 25°C // Fluid Phase Equilib. 1984. V. 18. № 2. P. 171.

  35. Ince E., Kirbaşlar Ş.I. Liquid-liquid equilibria of the water-acetic acid-butyl acetate system // Brazilian J. Chem. Eng. 2002. V. 19. № 2. P. 243.

  36. Wang L., Cheng Y., Li X. Liquid-liquid equilibria for the acetic acid + water + amyl acetate and acetic acid + water + 2-methyl ethyl acetate ternary systems // J. Chem. Eng. Data. 2007. V. 52. № 6. P. 2171.

  37. Trofimova M., Misikov G., Samarov A., Prikhodko I., Toikka M. Solubility in the system acetic acid – n-amyl alcohol – n-amyl acetate – water at 293.15 K, 303.15 K, 313.15 K and 323.15 K and atmospheric pressure // J. Chem. Thermodyn. 2021. V. 161. P. 106515.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал