Теоретические основы химической технологии, 2022, T. 56, № 3, стр. 282-299
Оптимизация процесса парового риформинга метана в водородофильтрующем мембранном модуле с никелевым катализатором и фольгой из паладиевых сплавов
В. Н. Бабак a, *, Л. П. Диденко a, Л. А. Семенцова a, Ю. П. Квурт a
a Институт проблем химической физики РАН
г. Черноголовка, Московская область, Россия
* E-mail: tabor47@mail.ru
Поступила в редакцию 27.07.2021
После доработки 08.02.2022
Принята к публикации 15.02.2022
- EDN: NARYUW
- DOI: 10.31857/S0040357122030034
Аннотация
Предложена модель парового риформинга метана в каталитическом реакторе, рабочая часть которого – две цилиндрические камеры, разделенные фольговой палладиевой мембраной составов Pd, Pd–23% Ag, Pd–6% Ru, Pd–10% Ru, Pd–6% In–0.5% Ru, Pd–6% In. Верхняя камера вакуумирована, а в нижней поддерживается атмосферное давление. При равномерной подаче сырья в нижнюю камеру проблема сведена к нахождению потоков СН4, Н2О, СО2, СО и Н2 из решения системы нелинейных обыкновенных дифференциальных уравнений первого порядка. Показано, что 100% конверсия метана достигается только при условии, когда отношение входных потоков водяного пара и метана больше двух. Расчеты проводили в интервале температур 700 K $ < T < $ 1000 K при отношениях входных потоков пар/метан, принадлежащих интервалу [2, 10]. Найдены оптимальные значения потоков сырья на входе, при которых выход водорода и конверсия метана достигают 100%. Показано, что при оптимальных расходах и фиксированной температуре максимальный поток водорода через мембрану наблюдается при минимально допустимых значениях отношений входных потоков пара и метана.
ВВЕДЕНИЕ
Современная экономика испытывает острую потребность в водороде из-за его широкого потребления в химической промышленности, нефтехимии, металлургии и других отраслях. Водород является экологически чистым моторным топливом, применяется в топливных элементах и т.д. [1, 2].
В настоящее время Н2 получают из природного сырья, среди которого ∼50% приходится на природный газ, ∼30% – на тяжелые попутные нефтяные газы, ∼20% – на газификацию угля [3, 4].
Во многих процессах с использованием Н2 предъявляются высокие требования к его чистоте, поэтому получаемый различными способами водород должен подвергаться дальнейшей очистке, которую чаще всего осуществляют методом абсорбции–десорбции при переменном давлении с помощью криогенной дистилляции или селективных мембран [4, 5].
Основной промышленный способ получения Н2 – это паровой риформинг природного газа, состоящего в зависимости от месторождения из метана (∼90–85% по объему) и примесей более высоких гомологов С2+ (этан, пропан, бутан). Так как высокую конверсию метана удается достичь только при температурах ∼1000 K, то предварительно смесь превращают с помощью процесса предриформинга при более низких температурах (≤700 K) в нормализованный газ, состоящий из метана, водорода и окислов углерода [5]. Процессы чаще всего проводят в трубчатых аппаратах, используя катализаторы. Стенки аппаратов – это водородопроводящие, высокоселективные мембранные элементы.
При паровой конверсии углеводородов в качестве катализаторов используют такие металлы, как Pt, Rh, Ru, Ni, нанесенные на оксидные носители (Al2O3, ZnO2, Cr2O3). Большинство из этих металлов дороги, поэтому более экономично их использовать (для повышения активности и устойчивости к примесям) в виде добавок к более дешевым никелевым катализаторам.
Идея совмещения каталитических и мембранных процессов была предложена академиком В.Я. Грязновым в последней четверти прошлого столетия [6]. Первые мембраны, используемые для дегидрирования углеводородов, – это тонкостенные палладиевые трубки [7]. Стоимость таких трубок даже при минимально допустимой толщине (∼100 мкм) достаточно велика. Поэтому были начаты поиски более дешевых, но и более сложных в изготовлении, так называемых композитных мембран, основу которых составляют подложки толщиной в несколько миллиметров. В качестве подложек используют пористое стекло [8], керамические материалы (оксиды Al, Cr) [9], пористые металлы (сталь, ниобий, ванадий, тантал и т.д.) [10–13]. На поверхность подложек наносятся тонкие слои Pd (5–20 мкм) различными методами (электрохимическое покрытие, химическое нанесение из паровой фазы, магнетронное напыление). Уменьшая толщину подложки, удается получать мембраны с высокой водородопроницаемостью, но при этом снижается механическая прочность. К недостаткам композитных мембран можно отнести трудности с обеспечением сплошности нанесенных слоев как при изготовлении, так и в процессе эксплуатации, что снижает селективность по отношению к Н2. Существуют проблемы с термостойкостью этих мембран и их утилизацией, так как извлечение дорогостоящего Pd – это сложная и многостадийная операция. Проводимость композитных мембран зависит как от проводимости Pd-слоев, так и подложек. Однако чистый палладий для изготовления мембран не используют, так как при $T \leqslant 600$ K и давлении менее 20 ат он не устойчив из-за разрушения его решетки (переход $\alpha $-фазы в $\beta $-фазу). Замечено, что сплавление Pd c Ag (Pd–23% Ag) уменьшает критическую температуру перехода и, кроме того, увеличивает проницаемость по водороду и улучшает механическую прочность [14]. Однако сплавы с благородными металлами удорожают стоимость изделия. Поэтому особый интерес представляют палладиевые сплавы, не содержащие Ag и Au. Легирующими добавками к Pd, увеличивающими водородопроницаемость, являются Pt, Y, Ru, In, Cu, которые образуют с ним двойные или тройные твердые растворы [15–17]. При этом увеличиваются термостойкость, время эксплуатации и снижается охрупчивание мембраны в среде водорода. Коммерческий интерес представляют сплавы Pd с более дешевыми добавками (медью, Ru). Максимальная водородопроницаемость сплавов Pd с медью наблюдается при весовой доли Cu порядка 40% [18–20].
В природном газе и попутных нефтяных газах кроме метана и его высших гомологов, как правило, присутствуют в небольших количествах так называемые яды – газообразные соединения, способные дезактивировать мембрану и катализатор. Это могут быть сульфиды (H2S, SO2), хлориды, окислы углерода и т.д. Например, сероводород при контакте с чистым Pd образует на его поверхности тонкую пленку Pd4S, препятствующую проникновению Н2. На поверхности сплавов Pd/Cu, Pd/Ru подобные процессы не наблюдаются [21–23].
Паровую конверсию углеводородов обычно проводят в традиционных трубчатых аппаратах, стенки которых не проницаемы для H2 или изготовлены из пористого материала с нанесенным тонким слоем палладия (∼2–5 мкм). В отделение ретантата засыпают чаще всего никелевый катализатор, а в отделении пермиата для увеличения движущей силы используют отгонные газы (N2, Ar) или же понижают давление (∼1–3 мм рт. ст.).
Для достижения необходимой мощности (по водороду) из-за ограниченности пропускной способности мембран габариты таких установок могут быть внушительными (∼5–10 м). Все это осложняет расчет аппаратов, так как требуется решение уравнений гидродинамики, конвективной диффузии и теплопередачи для пористой среды [24, 25]. Даже при равномерной подаче сырья и пренебрежении концентрационными эффектами в поперечном направлении в промышленных установках необходим учет изменения температуры из-за тепловых эффектов каталитических реакций [26, 27]. Учитывая, что природные газы представляют из себя смеси метана с небольшими примесями его гомологов, паровому риформингу чистого метана в литературе уделяется особое внимание [28–30].
Проводились исследования по паровому риформингу чистых С2+ алканов [31–35]. Это дает возможность понять основные закономерности, которые наблюдаются при паровом риформинге природных газов.
В лабораторной практике находят широкое применение каталитические реакторы небольших размеров (до одного метра) с высокопроводящими палладиевыми мембранами, в которых легко поддерживать постоянную температуру и давление. Они позволяют исследовать при фиксированных $p$ и $T$ водородопроводимость мембран, влияние на них продуктов парового риформинга (СО, СО2, СН4), водяного пара [36–38], а также кинетику реакций на различных катализаторах [39].
Несмотря на широкое применение композитных мембран и успехи в области технологии их получения всегда существовал спрос и на фольговые палладиевые мембраны. Преимущество последних – это термостойкость (они выдерживают температуру ∼1200 K), высокая селективность по водороду, продолжительное время эксплуатации, а также простота утилизации: отработанная фольга просто отправляется на переплавку.
Минимальная толщина фольговых мембран (∼7–15 мкм) получена с помощью осаждения ионов из раствора на металлические поверхности с последующим удалением этих поверхностей [40]. Основным разработчиком фольговых палладиевых сплавов в России является Институт металлургии и материаловедения им. А.А. Байкова (ИМЕТ РАН). Фольга изготовляется методом холодного проката с промежуточным отжигом в инертной среде. Минимальная толщина фольги составляет ∼10 мкм [41].
В Институте проблем химической физики (ИПФХ) РАН разработан многофункциональный мембранный модуль (ММ), рабочей частью которого являются две цилиндрические камеры, разделенные перегородкой (фольговая водородопроницаемая мембрана или не проницаемая для Н2 пластина) [36].
С помощью ММ были изучены разделительные свойства фольговых мембран из сплавов Pd–6% Ru, Pd–10% Ru, Pd–6% In, Pd–6% In–0.5% Ru, а также влияние продуктов парового риформинга (СО, СО2, СН4 и водяного пара) на скорость проникновения Н2 через мембрану [17].
Засыпая в нижнюю камеру ММ никелевый катализатор, был исследован риформинг чистого метана с фольгой состава Pd–6% Ru при $m = 3$. Сравнивая расчеты с экспериментальными данные, была обоснована предложенная теоретическая модель процесса [42].
В настоящей работе проведено исследование парового риформинга метана в ММ с фольговыми мембранами Pd–6% Ru, Pd–10% Ru, Pd–6% In, Pd–6% In–0.5% Ru в широкой области изменения температур (700 K $ \leqslant T \leqslant $ 1000 K) при различных допустимых значениях отношения потоков пара и метана на входе ($m > 2$). При фиксированных T и m найдены объемные скорости подачи сырья (смесь метана и паров воды), характерные для данного реактора, при которых конверсия метана и выход водорода достигают 100%. Эти режимы парового риформинга будем называть оптимальными. При более высоких скоростях на выходе нижней камеры будут присутствовать водород и метан.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Установки представлена на рис. 1. Мембранный модуль (ММ) выполнен из нержавеющей стали марки 12х18Н10Т. Реакционная ячейка находится внутри ММ и представляет из себя две одинаковые цилиндрические камеры (высота 3.5 мм), разделенные фольговой мембраной из палладиевого сплава, избирательно пропускающей только молекулы H2. Фольга (диск площадью 15.2 см2, толщиной 30 мкм) помещалась между стальными сетками тонкого плетения для механической прочности. В нижней камере поддерживали постоянное давление (∼1 ат). Верхнюю камеру вакуумировали (∼2–4 мм рт. ст.) с помощью безмасляного диафрагменного мембранного вакуумного насоса марки MZ 2CNT (Германия). В нижнюю камеру помещали 2 см3 (3.35 г) промышленного никелевого катализатора марки НИАП-03-01. Мембранный модуль помещали внутри металлического кожуха с электрическим обогревом (внешний диаметр 17.6 см, высота 41.5 см). Водяной пар (температура ∼200°С) смешивали с метаном, поддерживая отношение мольных потоков пар/метан равное m (∼2-–10). Контроль за температурой внутри кожуха осуществляли с помощью хромель-алюмелевых термопар. Продукты риформинга из нижней камеры отводили через центральное отверстие (радиус ∼1 мм) и пропускали через холодильник (змеевик), где при комнатной температуре из смеси удаляли непрореагирующую воду. Объемную скорость “сухих” газов (СО, СО2, СН4, H2) после холодильника измеряли пенным расходомером и подавали в хроматограф (Кристалл – 5000 с ПИД и детектором по теплопроводности). Содержание H2 в продуктах реакции определяли на колонке с молекулярными ситами 13Х (2 мм × 2 м, газ-носитель – аргон). Углеводородный состав (СН4) продуктов определяли на колонке HP-Al/KCl (0.5 мм × 30 м, газ-носитель – гелий). Содержание СО и СО2 определяли на колонке с активированным углем (2 мм × 2 м, газ-носитель – гелий). Расходы газовых потоков контролировали регуляторами РРГ-12 (“Электроприбор”, г. Зеленоград).
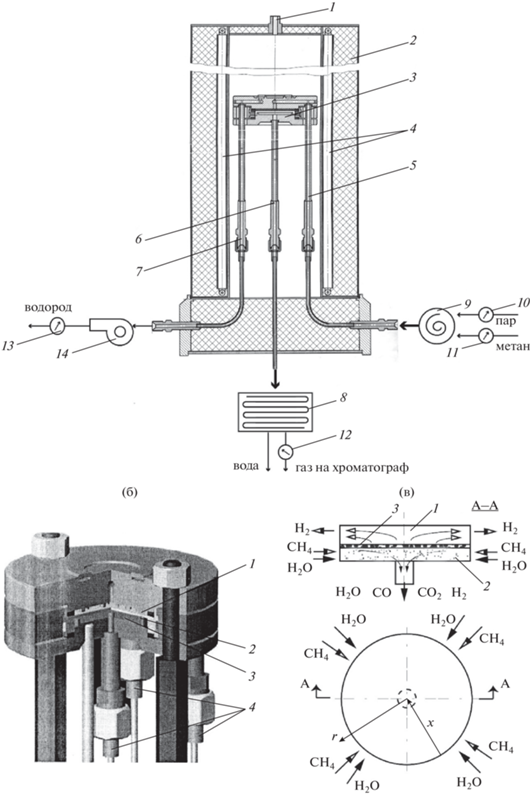
Рис. 1.
Экспериментальная установка. (а) Вертикальное сечение. 1 – отверстие для трубки с термопарой, 2 – внешняя стенка, 3 – мембранный модуль, 4 – электронагреватель, (5–7) – стальные трубки для подачи сырья и выхода продуктов из нижней и верхней камер, 8 – холодильник, 9 – смеситель, (10–13) – ротаметры, 14 – вакуумный насос. (б) Мембранный модуль. 1 – верхняя камера, 2 – мембрана, 3 – нижняя камера, 4 – трубки для подвода сырья и выхода продуктов реакций. (в) Схема реакционной ячейки. 1 – верхняя вакуумированная камера, 2 – нижняя камера с катализатором, 3 – мембрана. Kрадиальная координата, $x$, $y$ – безразмерные координаты в радиальном направлении.
МОДЕЛИРОВАНИЕ ПАРОВОГО РИФОРМИНГА МЕТАНА
При достаточно высоких температурах на никелевой поверхности протекают следующие обратимые химические реакции [43–45]:
(1)
${\text{С}}{{{\text{H}}}_{{\text{4}}}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}} = {\text{CO}} + 3{{{\text{H}}}_{2}}~\,\,\,\,({{K}_{1}}),$(2)
${\text{СO}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}} = {\text{C}}{{{\text{O}}}_{2}} + {{{\text{H}}}_{2}}~\,\,\,\,({{K}_{2}}).$При равномерной подаче сырья (смесь СН4 и Н2О) по периметру нижней камеры концентрации компонентов смеси зависят только от радиальной координаты $r{\kern 1pt} '$ (рис. 1). Пренебрегая диффузией по оси $r{\kern 1pt} '$ и интегрируя уравнения конвективной диффузии по вертикальной координате $z{\kern 1pt} '$, для расчета мольных интегральных потоков $N_{i}^{'}$ получаем уравнение [42]:
(3)
$\frac{{dN_{i}^{'}}}{{dr{\kern 1pt} '}} = (2\pi r{\kern 1pt} '){{\rho }_{{{\text{КАТ}}}}}{{\varphi }_{i}} - (2\pi r{\kern 1pt} '){{I}_{{i,{\text{П}}}}},$Выше обозначено: ${{I}_{{i,{\text{П}}}}}$ – потоки компонентов у поверхности мембраны, $N_{i}^{'}$ – мольные потоки по оси $r{\kern 1pt} '$, ${{N}_{i}}$ – интегральные потоки через цилиндрические поверхности ($r{\kern 1pt} ' = {\text{const}}$) в нижней камере, ${{\varphi }_{i}}$ – источник (сток) i-го компонента. Индекс “П” – поверхность фольги, i = 1 – метан, 2 – Н2О, 3 – СО, 4 – СО2, 5 – Н2.
Если ввести безразмерные координаты $y$ и $x$, отсчитываемые от внешней границы фольги: $r{\kern 1pt} ' = r_{{\max }}^{'}(1 - y)$, $x = 2y - {{y}^{2}}$, то уравнения для расчета потоков ${{N}_{i}}$ примут вид:
(4)
$\frac{{d( - {{N}_{i}})}}{{dx}} = {{w}_{{{\text{KAT}}}}}{{\varphi }_{i}} - S{{I}_{{i,{\text{П}}}}}.$Считается, что ${{I}_{{i,{\text{П}}}}} = 0$ для всех частиц, кроме Н2. Для потока водорода на поверхности фольги выполняется закон Сивертса [46]:
(5)
${{I}_{{{{{\text{H}}}_{{\text{2}}}}{\text{,П}}}}} = \frac{Q}{\delta }\exp ( - {E \mathord{\left/ {\vphantom {E {RT)(\sqrt {{{p}_{{{\text{HK}}}}}} - \sqrt {{{p}_{{{\text{BK}}}}}} )}}} \right. \kern-0em} {RT)(\sqrt {{{p}_{{{\text{HK}}}}}} - \sqrt {{{p}_{{{\text{BK}}}}}} )}},$Функции источников для газов имеют вид (см. (1), (2)):
(6)
$\begin{gathered} {{b}_{1}} = \frac{{{{{\tilde {k}}}_{1}}({{p}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - {{p_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}{{p}_{{{\text{CO}}}}}} \mathord{\left/ {\vphantom {{p_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}{{p}_{{{\text{CO}}}}}} {{{K}_{1}})}}} \right. \kern-0em} {{{K}_{1}})}}}}{{p_{{{{{\text{H}}}_{{\text{2}}}}}}^{{2.5}}(1 + {{k}_{{{\text{CO}}}}}{{p}_{{{\text{CO}}}}} + {{k}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \mathord{\left/ {\vphantom {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{)}^{2}}}}} \right. \kern-0em} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{)}^{2}}}}}}, \\ {{b}_{2}} = \frac{{{{{\tilde {k}}}_{2}}({{p}_{{{\text{CO}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - {{{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} {{{K}_{2}})}}} \right. \kern-0em} {{{K}_{2}})}}}}{{{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1 + {{k}_{{{\text{CO}}}}}{{p}_{{{\text{CO}}}}} + {{k}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \mathord{\left/ {\vphantom {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{)}^{2}}}}} \right. \kern-0em} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{)}^{2}}}}}}. \\ \end{gathered} $Температурные зависимости кинетических констант ${{\tilde {k}}_{1}}$, ${{\tilde {k}}_{2}}$, констант равновесия ${{K}_{1}}$, ${{K}_{2}}$ реакций (1), (2) и коэффициентов Лэнгмюра ${{k}_{i}}$ известны [43–45].
Потоки компонентов в нижней камере находим из системы пяти дифференциальных уравнений первого порядка:
(7)
$\begin{gathered} \frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = - {{b}_{1}}\left( {\frac{{{{w}_{{{\text{KAT}}}}}}}{{{{N}_{{{\text{ВХ}}}}}}}} \right),\,\,\,\,\,\frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{\partial x}} = - ({{b}_{1}} + {{b}_{2}})\left( {\frac{{{{w}_{{{\text{КАТ}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right), \\ \frac{{d{{n}_{{{\text{CO}}}}}}}{{dx}} = ({{b}_{1}} - {{b}_{2}})\left( {\frac{{{{w}_{{{\text{КАТ}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right),\,\,\,\,\frac{{\partial {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}}}{{\partial x}} = {{b}_{2}}\left( {\frac{{{{w}_{{{\text{КАТ}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right), \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dx}} = (3{{b}_{1}} + {{b}_{2}})\left( {\frac{{{{w}_{{{\text{КАТ}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right) - S{{{{I}_{{{{{\text{H}}}_{{\text{2}}}}{\text{,П}}}}}} \mathord{\left/ {\vphantom {{{{I}_{{{{{\text{H}}}_{{\text{2}}}}{\text{,П}}}}}} {{{N}_{{{\text{BX}}}}}}}} \right. \kern-0em} {{{N}_{{{\text{BX}}}}}}}. \\ \end{gathered} $Условия на входе ($x = 0$) равны:
(8)
${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 1,\,\,\,\,{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = m,\,\,\,\,{{n}_{{{\text{CO}}}}} = {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} = {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 0.$Выше введены безразмерные потоки ni = = Ni/NBX, ${{N}_{{{\text{BX}}}}}$ – интегральный поток СН4 при $x = 0$, $m$ – отношение входных потоков водяного пара и метана.
Используя начальные условия (8), комбинируя уравнения системы (7), можно показать, что потоки ${{n}_{{{\text{CO}}}}}$ и ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ линейно зависят от ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$:
(9)
$\begin{gathered} {{n}_{{{\text{CO}}}}} = 2(1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}) - (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}), \\ {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} = (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) - (1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}). \\ \end{gathered} $Для нахождения ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ получаем следующую систему из трех дифференциальных уравнений:
(10)
$\begin{gathered} \frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = - {{\alpha }_{1}}{{F}_{1}},\,\,\,\,\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dx}} = - {{\alpha }_{1}}{{F}_{1}} - {{\alpha }_{2}}{{F}_{2}}, \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dx}} + \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dx}} + 2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = - \beta \sqrt {{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \\ \end{gathered} $Здесь ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 1$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = m$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 0$ при $x = 0$.
Функции ${{F}_{1}}$, ${{F}_{2}}$, учитывая равенства (6) и зависимости
(11)
$\begin{gathered} {{X}_{i}} = {{{{n}_{i}}} \mathord{\left/ {\vphantom {{{{n}_{i}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}},\,\,\,\,{{n}_{\sum }} = {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} + {{n}_{{{\text{CO}}}}} + {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} + \\ + \,\,{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}, \\ \end{gathered} $можно выразить через потоки ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ [42]:
(12)
$\begin{gathered} {{F}_{1}} = \frac{{{{X}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}{{X}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - X_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}{{X}_{{{\text{CO}}}}}({{p_{{{\text{AT}}}}^{{}}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{{}}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})}}{{X_{{{{H}_{2}}O}}^{2}X_{{{{H}_{2}}}}^{{1/2}}{{{[1 + ...]}}^{2}}}} = \\ = \frac{{\sqrt {{{n}_{\sum }}} \left[ {{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - n_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}{{n}_{{{\text{CO}}}}}{{({{p_{{{\text{AT}}}}^{{}}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{{}}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})} \mathord{\left/ {\vphantom {{({{p_{{{\text{AT}}}}^{{}}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{{}}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})} {n_{\sum }^{2}}}} \right. \kern-0em} {n_{\sum }^{2}}}} \right]}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{[1 + ...]}}^{2}}}}, \\ {{F}_{2}} = \frac{{{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}\left[ {{{X}_{{{\text{CO}}}}}{{X}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{}}{{X}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})} \right]}}{{X_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}{{{[1 + ...]}}^{2}}}} = \\ = \frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}\left[ {{{n}_{{{\text{CO}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{}}{{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})} \right]}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}{{n}_{\sum }}{{{[1 + ...]}}^{2}}}}. \\ \end{gathered} $Безразмерные параметры ${{\alpha }_{1}}$, ${{\alpha }_{2}}$, $\beta $ в системе уравнений (10) определяются следующим образом:
(13)
$\begin{gathered} {{\alpha }_{1}} = \frac{{{{{\tilde {k}}}_{1}}}}{{k_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}\left( {\frac{{{{w}_{{{\text{КАТ}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right)\frac{1}{{p_{{{\text{AT}}}}^{{1/2}}}}, \\ {{\alpha }_{2}} = \frac{{{{{\tilde {k}}}_{2}}}}{{k_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}\left( {\frac{{{{w}_{{{\text{КАТ}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right){{p}_{{{\text{AT}}}}}, \\ \beta = S\left[ {\frac{{Q\exp ({{ - E} \mathord{\left/ {\vphantom {{ - E} {RT)}}} \right. \kern-0em} {RT)}}}}{\delta }} \right] \times {{10}^{2}}\sqrt {10} {{p_{{{\text{AT}}}}^{{1/2}}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{{1/2}}} {{{N}_{{{\text{BX}}}}}}}} \right. \kern-0em} {{{N}_{{{\text{BX}}}}}}}. \\ \end{gathered} $Квадратная скобка в знаменателях функций ${{F}_{1}}$ и ${{F}_{2}}$ равна:
Численные значения некоторых параметров при различных температурах для рассматриваемого ММ (${{w}_{{{\text{KAT}}}}} = 3.5$ г, $S = 15.2$ см2, $\delta = 30$ мкм) для фольги состава Pd–6% Ru можно получить из табл. 1.
Таблица 1.
К расчету безразмерных параметров и равновесных констант
| $T$, K | 673 | 773 | 823 | 873 | 973 | 1073 |
|---|---|---|---|---|---|---|
| ${{\alpha }_{1}}{{N}_{{{\text{BX}}}}}p_{{{\text{AT}}}}^{{1/2}}$, моль/с | 1.95 × 10–3 | 7.13 × 10–3 | 1.35 × 10–2 | 2.27 × 10–2 | 5.27 × 10–2 | 0.107 |
| ${{{{\alpha }_{2}}{{N}_{{{\text{BX}}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}{{N}_{{{\text{BX}}}}}} {{{p}_{{{\text{AT}}}}}}}} \right. \kern-0em} {{{p}_{{{\text{AT}}}}}}}$, моль/с | 20.46 | 1.61 | 0.58 | 0.22 | 0.047 | 0.013 |
| $({{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})p_{{{\text{AT}}}}^{{3/2}}$ | 1.05 × 104 | 2.4 × 102 | 46.3 | 10.44 | 0.895 | 0.121 |
| ${{(\beta {{N}_{{{\text{BX}}}}})} \mathord{\left/ {\vphantom {{(\beta {{N}_{{{\text{BX}}}}})} {p_{{{\text{AT}}}}^{{1/2}}}}} \right. \kern-0em} {p_{{{\text{AT}}}}^{{1/2}}}}$, моль/с | 0.8 × 10–4 | 1.15 × 10–4 | 1.3 × 10–4 | 1.5 × 10–4 | 1.8 × 10–4 | 2.1 × 10–4 |
| ${{({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})} \mathord{\left/ {\vphantom {{({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})} {{{p}_{{{\text{AT}}}}}}}} \right. \kern-0em} {{{p}_{{{\text{AT}}}}}}}$ | 0.46 × 10–1 | 0.14 × 10–1 | 0.05 × 10–1 | 0.64 × 10–2 | 0.32 × 10–2 | 0.2 × 10–2 |
| ${1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}$ | 8.4 × 10–2 | 0.20 | 0.29 | 0.39 | 0.67 | 1.03 |
| ${{p_{{{\text{AT}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{2}} {({{K}_{1}}{{K}_{2}})}}} \right. \kern-0em} {({{K}_{1}}{{K}_{2}})}}$ | 1.4 × 103 | 20 | 3.63 | 0.78 | 0.06 | 6.8 × 10–3 |
При фиксированном давлении в нижней камере параметрами, от которых зависит распределение потоков ${{n}_{i}}$, являются температура ($T$), поток СН4 на входе ${{N}_{{{\text{BX}}}}}$ и отношение $m$.
Обычно катализатор засыпают на 1/3–1/2 объема камеры (в наших экспериментах объем засыпки ∼2 см3, камеры ∼5.3 см3). Процесс протекает при хаотическом движении частичек катализатора для поддержания постоянной температуры и выравнивания концентраций по высоте при любом $r{\kern 1pt} '$. После каждого эксперимента проверяли равномерность засыпки катализатора в нижней камере.
Объемную скорость подачи сырья (смесь СН4 и Н2О) на входе в нижнюю камеру определим следующим образом [47]:
(14)
$\begin{gathered} G \cong {{{{{\dot {V}}}_{\sum }}} \mathord{\left/ {\vphantom {{{{{\dot {V}}}_{\sum }}} {{{V}_{{{\text{КАТ}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{КАТ}}}}}}} = 30{{{\dot {V}}}_{\sum }}\,\,\left[ {{1 \mathord{\left/ {\vphantom {1 {\text{ч}}}} \right. \kern-0em} {\text{ч}}}} \right],~ \\ {{{\dot {V}}}_{\sum }} = (1 + m)\dot {V} \\ \end{gathered} $Учитывая, что газовые смеси являются идеальными, поток метана ${{N}_{{{\text{BX}}}}}$ и объемная скорость $G$ связаны соотношением ($T$ ≅ 300 K):
(15)
$\begin{gathered} {{N}_{{{\text{BX}}}}} = \left[ {{{p}_{{{\text{AT}}}}}\frac{{G{{V}_{{{\text{KAT}}}}}}}{{900(1 + m)}}} \right] \times {{10}^{{ - 5}}}\,\,\left( {{{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}} \right) = \\ = \left[ {{{p}_{{{\text{AT}}}}}\frac{G}{{450(1 + m)}}} \right] \times {{10}^{{ - 5}}}\,\,\left( {{{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}} \right). \\ \end{gathered} $Распределения безразмерных потоков ${{n}_{i}}(x)$ внутри нижней камеры зависят от трех параметров ${{\alpha }_{1}}$, ${{\alpha }_{2}}$ и $\beta $ (табл. 1).
Ниже будет показано, что в рассматриваемой области изменения температур и при допустимых значениях отношений $m$ ($m > 2$) кинетические параметры ${{\alpha }_{1}}$, ${{\alpha }_{2}}$ намного больше единицы. Последнее означает, что в нижней камере существуют два участка изменения потоков: короткий начальный и основной [42].
Решение системы уравнений (10) на начальном участке. Разделив уравнения системы (10) на ${{\alpha }_{1}}$ и вводя безразмерную продольную координату $z = {{\alpha }_{1}}x$, преобразуем эту систему следующим образом:
(16)
$\begin{gathered} \frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dz}} = - {{F}_{1}},\,\,\,\,\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dz}} = - {{F}_{1}} - \left( {\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}}}}} \right){{F}_{2}}, \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dz}} + \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dz}} + 2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dz}} = - \left( {\frac{\beta }{{{{\alpha }_{1}}}}} \right)\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} . \\ \end{gathered} $Начальные условия равны:
(17)
${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 1,\,\,\,\,{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = m,\,\,\,\,{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 0,\,\,\,\,{\text{при}}\,\,\,\,z = 0.$При фиксированном значении давления в нижней камере (${{p}_{{{\text{AT}}}}} = 1$) коэффициенты системы (16), а следовательно и распределение потоков ${{n}_{i}}(z)$ зависят только от температуры. Интегрирование этой системы при $m = 3$ было проведено численно, используя схему Рунге–Кутта четвертого порядка [46, 51 ] .
Было показано, что в правой части последнего уравнения системы (16) на ограниченном участке $z$ членом $({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}})\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} $ можно пренебречь (таблица 1), а следовательно, используя начальные условия (17), поток водорода (также как ранее потоки ${{n}_{{{\text{CO}}}}}$ и ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ (9)) можно выразить через потоки ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$:
(18)
${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) + 2(1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}).$Потоки ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}(z)$ и ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}(z)$ являются убывающими функциями, а ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(z)$ – возрастающей функцией координаты $z$. При достаточно больших $z$ (практически при $z \geqslant 10$) производные ${{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \mathord{\left/ {\vphantom {{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} {dz}}} \right. \kern-0em} {dz}}$, ${{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}} \mathord{\left/ {\vphantom {{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}} {dz}}} \right. \kern-0em} {dz}}$, ${{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {dz}}} \right. \kern-0em} {dz}}$, а также функции ${{F}_{1}}(z)$ и ${{F}_{2}}(z)$ стремятся к нулю. Последнее означает, что реакции (1), (2) достигают равновесия, то есть скорости прямых и обратных процессов (см. числители в уравнениях (11)) становятся соизмеримыми. Участок $x \leqslant {{x}_{{{\text{нач}}}}} = {{10} \mathord{\left/ {\vphantom {{10} {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}}$ будем называть начальным. В дальнейшем будет показано, что размеры этого участка намного меньше единицы (${{x}_{{{\text{нач}}}}} \ll 1$). Следовательно в расчетах распределений потоков ${{n}_{i}}(x)$ на начальном участке нет необходимости, так как этот участок не оказывает практически влияния на переход Н2 через мембрану.
Для расчета распределений ${{n}_{i}}(x)$ на основном участке необходимо иметь информацию о потоках ${{n}_{i}}$ на выходе начального участка при $x = {{x}_{{{\text{нач}}}}}$. Эти потоки обозначим звездочкой $n_{i}^{*}$. Последние можно получить с помощью условия (18) и равенств ${{F}_{1}} = {{F}_{2}} = 0$ (см. (9) и (12)):
(19)
$\begin{gathered} n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} - n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*3}}\left[ {2(1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}) - (m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*})} \right] \times \\ \times \,\,{{\left( {{{p_{{{\text{AT}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{2}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{p_{{{\text{AT}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{2}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}} \right)} {n_{\sum }^{{*2}}}}} \right. \kern-0em} {n_{\sum }^{{*2}}}} = 0, \\ [2(1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}) - (m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}]n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} - n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} \times \\ \times \,\,\left[ {(m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}) - (1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*})} \right]\left( {{1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}} \right) = 0, \\ n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} = (m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}) + 2(1 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}). \\ \end{gathered} $Приведем алгоритм для численного решения этой системы алгебраических уравнений. Второе уравнение системы (19) представим в виде:
(20)
$n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*} = 1 - \Delta {\text{*}}\left( {\frac{{m - \Delta {\text{*}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}{{2m - 2\Delta + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}} \right),$(21)
$n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*} = \frac{{\left[ {{{p_{{{\text{AT}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{2}} {({{K}_{1}}{{K}_{2}})}}} \right. \kern-0em} {({{K}_{1}}{{K}_{2}})}}} \right]n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*4}}\Delta {\text{*}}}}{{(m - \Delta *)\left[ {2m - 2\Delta {\text{*}} + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} \right]{{{\left[ {1 + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + m - \Delta {\text{*}}} \right]}}^{2}}}},$(22)
$n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} = \left[ {\frac{{4m - 4\Delta {\text{*}} + 3n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}{{2m - 2\Delta {\text{*}} + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}} \right]\Delta {\text{*}}.$Из уравнения (22) нетрудно найти аналитическую зависимость отклонения потока пара $\Delta {\text{*}}$ от потока водорода $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$:
(23)
$\Delta * = \frac{{2m + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}\left[ {1 + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})} \right]}}{4} - \frac{1}{2}\sqrt {\frac{{{{{\left\{ {2m + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}\left[ {1 + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})} \right]} \right\}}}^{2}}}}{4} - n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}\left[ {2m + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} \right]} .$Знак (–) перед радикалом выбран из условия: $\Delta * \to 0$ при $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} \to 0$ (см. (20), (21)). Равновесные значения $\Delta {\text{*}}$, $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ находим из условия пересечения кривых $n_{{{\text{CH}}{}_{{\text{4}}}}}^{*}(n_{{{\text{H}}{}_{{\text{2}}}}}^{*})$ (формулы (20), (21)), в которых $\Delta {\text{*}}(n_{{{\text{H}}{}_{{\text{2}}}}}^{*})$ – зависимость (23). Переменная $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ “пробегает” значения от нуля с достаточно мелким шагом до точки пересечения кривых (20), (21). Потоки $n_{{{\text{CO}}}}^{*}$ и $n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*}$ находим по формулам (9). Расчетами было показано, что решение дифференциальных уравнений (10) при $\beta = 0$ стремится к $n_{i}^{*}$ при достаточно больших $z$ ($z \geqslant 5 - 10$) [42]. Физически это означает, что если палладиевую фольгу заменить на непроницаемую для Н2 перегородку, что третье уравнение системы (16) становится эквивалентным равенству (18) при любом $x$, а следовательно в таком немембранном процессе за пределами начального участка потоки газов остаются постоянными и равными $n_{i}^{*}$. При наличии мембраны на основном участке из-за проникновения Н2 в верхнюю камеру потоки $n_{i}^{{}}(x)$ будут отклоняться в ту или иную сторону от $n_{i}^{*}$. В частности, поток ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ при $x \cong {{x}_{{{\text{нач}}}}}$ проходит через максимум и в дальнейшем, по мере удаления от входа, уменьшается. Результаты расчетов потоков $n_{i}^{*}$ по указанному выше алгоритму в широкой области изменения температур (673–973 K) представлены в табл. 2 для ряда значений отношения $m$ из интервала 2–10. Соответствующие значения $\Delta {\text{*}}$, $n_{{{\text{CO}}}}^{*}$, $n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*}$, $n_{{{\text{CH}}{}_{{\text{4}}}}}^{*}$ приведены на рис. 2. Ниже будет показано, что параметр $m$ в случае парового риформинга метана не должен быть меньше двух.
Таблица 2.
Результаты расчета потока $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ на выходе начального участка
| $m$ | $T$, K | |||||||
|---|---|---|---|---|---|---|---|---|
| 673 | 773 | 823 | 873 | 923 | 973 | 1023 | 1073 | |
| 2 | 0.60 | 1.30 | 1.75 | 2.25 | 2.72 | 3.0 | 3.1 | 3.18 |
| 2.5 | 0.70 | 1.30 | 2.0 | 2.54 | 3.0 | 3.2 | 3.24 | 3.25 |
| 3 | 0.80 | 1.70 | 2.24 | 2.78 | 3.17 | 3.3 | 3.32 | 3.34 |
| 4 | 0.95 | 2.0 | 2.63 | 3.13 | 3.40 | 3.45 | 3.44 | 3.4 |
| 5 | 1.12 | 2.33 | 2.93 | 3.37 | 3.54 | 3.54 | 3.5 | 3.5 |
| 7 | 1.40 | 2.80 | 3.35 | 3.64 | 3.68 | 3.66 | 3.63 | 3.6 |
| 10 | 1.80 | 3.24 | 3.68 | 3.78 | 3.78 | 3.75 | 3.7 | 3.7 |
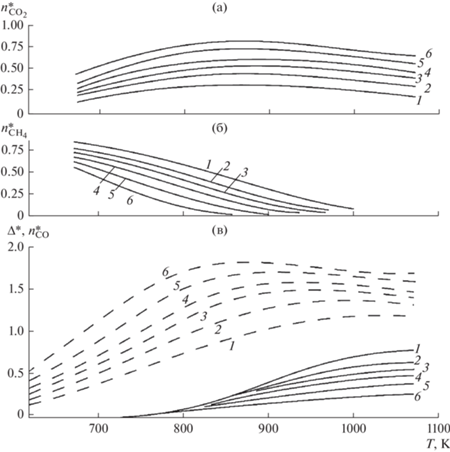
Рис. 2.
Равновесные значения потоков на выходе начального участка при различных $T$ и $m$. (а) – потоки $n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*}$; (б) – потоки $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$; (в) – потоки $\Delta {\text{*}}$ (штриховые линии), потоки $n_{{{\text{СO}}}}^{*}$ (сплошные линии). Кривые 1 – $m = 2$, 2 – 3, 3 – 4, 4 – 5, 5 – 7, 6 – $m = 10$.
Решение за пределами начального участка ($x > {{x}_{{{\text{нач}}}}}$). Предполагая, что на основном участке производные ${{\partial {{n}_{i}}} \mathord{\left/ {\vphantom {{\partial {{n}_{i}}} {\partial x}}} \right. \kern-0em} {\partial x}}$ ограничены (это будет показано ниже), при больших значениях параметров ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ должны выполняться неравенства ${{F}_{1}}$ ∼ ~ ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}} \ll 1$, ${{F}_{2}}$ ∼ ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{2}}}}} \right. \kern-0em} {{{\alpha }_{2}}}} \ll 1$ см. (10)). Физически это означает, что равновесия реакций, установившиеся на выходе начального участка, не нарушаются на основном участке несмотря на отвод водорода через мембрану. Зависимости ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ находим с помощью тех же формул (20), (21), в которых необходимо произвести замену $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} \to {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$, $n_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}^{*} \to {{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$, $\Delta * \to \Delta $: для любого фиксированного ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} < n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ переменная $\Delta \equiv (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})$ с достаточно малым шагом “пробегает” значения от $\Delta {\text{*}}$ до пересечения функций ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}(\Delta )$ (формулы (20), (21)). Потоки ${{n}_{{{\text{CO}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{\text{С}}{{{\text{O}}}_{{\text{2}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ после нахождения ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}) = m - \Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ определяем по общим формулам (9). Зависимости ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и $\Delta ({{n}_{{{{H}_{2}}}}})$ дают возможность рассчитать распределения потока водорода и других компонентов газовой смеси в нижней камере как функции переменной $x$. С этой целью последнее уравнение системы (10) преобразуем следующим образом:
(24)
$\begin{gathered} \int\limits_{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}^{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} {\frac{{\left( {2\frac{{\partial {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{\partial {{n}_{{{{H}_{2}}}}}}} + \frac{{\partial \Delta }}{{\partial {{n}_{{{{H}_{2}}}}}}} + 1} \right)\sqrt {\left( {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + m - \Delta } \right)} }}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} = \\ = \beta (x - {{x}_{{{\text{нач}}}}}). \\ \end{gathered} $Производные ${{\partial {{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}} \mathord{\left/ {\vphantom {{\partial {{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}} \partial }} \right. \kern-0em} \partial }{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ и ${{\partial \Delta } \mathord{\left/ {\vphantom {{\partial \Delta } \partial }} \right. \kern-0em} \partial }{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ находим в результате численного дифференцирования зависимостей ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ на основном участке. В качестве примера эти функции для случая $m = 3$ приведены на рис. 3 для ряда значений $T$ из интервала 673–973 K. Как видно, в результате перехода Н2 через мембрану потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ уменьшаются, а отклонение потока водяного пара от первоначального значения $m = 3$ продолжает увеличиваться ($\Delta \geqslant \Delta {\text{*}}$). При ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \to 0$ потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}} \to 0$, а $\Delta \to 2$ (см. (20)). Последнее означает, что при паровом риформинге метана поток водяного пара на входе как минимум вдвое должен превышать поток метана. В противном случае поток пара (${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = m - \Delta $) обращается в нуль (пар полностью расходуется) внутри камеры, реакции (1), (2) прекратятся и на выходе нельзя будет достичь 100% конверсии метана.
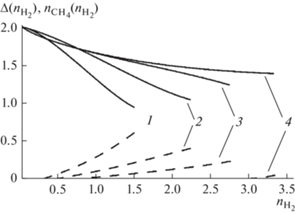
Рис. 3.
Функции ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ (штриховые линии) и $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ на основном участке при $m = 3$ и различных $T$. Кривые 1 – $T = $ 973 K, 2 – 873 K, 3 – 823 K, 4 – 773 K.
За пределами температурного интервала 773–973 K зависимости ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ при любом $m > 2$ можно получить аналитически. Покажем это для температур $T > 1000$ K. В этой области потоки $n_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$ на выходе начального участка при любом допустимом $m$ стремятся к нулю (рис. 2б), а произведение ${{p_{{{\text{AT}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{2}} {({{K}_{1}}{{K}_{2}}) \ll 1}}} \right. \kern-0em} {({{K}_{1}}{{K}_{2}}) \ll 1}}$ (см. табл. 1). Следовательно, как это видно из уравнения (21), на основном участке сохраняется равенство ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 0$. Функцию $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ можно найти из уравнения (20), где необходимо произвести замену $\Delta * \to \Delta $. В результате это уравнение сводится к квадратному относительно $\Delta $:
(25)
$\begin{gathered} \Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}) = \frac{{m + 2 + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{2} - \\ - \,\,\sqrt {\frac{{{{{\left[ {m + 2 + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}){{n}_{{{{H}_{2}}}}}} \right]}}^{2}}}}{4} - (2m + ({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} , \\ \end{gathered} $Знак (–) перед радикалом выбран из условия: $\Delta \to 2$ при ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \to 0$ (см. (20)). Равновесные значения $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ находим с помощью (25), где необходимо произвести замену $\Delta \to \Delta {\text{*}}$, $\Delta * = n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} - 2$, так как $n_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}^{*} \cong 0$ (см. (18)). В результате для $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ при высоких $T$ получаем квадратное уравнение:
(26)
$\begin{gathered} n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*2}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}} - 1) + \\ + \,\,n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}[m + 6 - 3({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})] - 4(m + 2) = 0. \\ \end{gathered} $Нетрудно проверить, что решение уравнения (26) совпадает с численными расчетами $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ при $T > 973$ K (см. табл. 2).
Получим зависимости $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ при температурах ($T < 700$ K). В этой области константа равновесия ${{K}_{2}} \gg 1$ (табл. 1), следовательно ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 1 - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}$ (см. (20)). Приравнивая потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}(\Delta )$ (формулы (20) и (21)), получим аналитическую зависимость ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ от $\Delta $ в области $\Delta \geqslant \Delta {\text{*}}$:
(27)
${{\left( {\frac{{2 - \Delta }}{\Delta }} \right)}^{{1/4}}}{{(m - \Delta )}^{{1/2}}}{{(m + 1 - \Delta )}^{{1/2}}} = \left( {\frac{{{{p}_{{{\text{AT}}}}}}}{{{{K}_{1}}{{K}_{2}}}}} \right){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}.$Равновесное значение $\Delta {\text{*}}$ находим из (27), где необходимо провести замену $\Delta \to \Delta {\text{*}}$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \to n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} = 2\Delta {\text{*}}$ (см. (18)):
(28)
${{\left( {\frac{{2 - \Delta {\text{*}}}}{{\Delta {\text{*}}}}} \right)}^{{1/4}}}{{\left( {\frac{{m - \Delta {\text{*}}}}{{\Delta {\text{*}}}}} \right)}^{{1/2}}}{{\left( {\frac{{m + 1 - \Delta {\text{*}}}}{{\Delta {\text{*}}}}} \right)}^{{1/2}}} = 2\left( {\frac{{{{p}_{{{\text{AT}}}}}}}{{{{K}_{1}}{{K}_{2}}}}} \right).$Нетрудно проверить, что решение уравнения (28) совпадает с численными расчетами при $T \leqslant 673$ K (рис. 2а).
Зависимости $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ в области $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{}} \leqslant n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ для $T = 673$ и 973 K и ряда значений $m$ (2, 3, 5, 7, 10) показаны на рис. 4а ($T = 673$ K) и рис. 4б (973 K). При $T = 673$ K поток ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 1 - {{\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})} \mathord{\left/ {\vphantom {{\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})} 2}} \right. \kern-0em} 2}$, а при $T = 973$ K, соответственно, ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 0$. Используя равновесные значения $\Delta {\text{*}}(m,T)$ и $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}(m,T)$ (см. (26), (28)), по формулам (25), (27) нетрудно рассчитать $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ на основном участке нижней камеры за пределами температурного интервала 673–973 K. Внутри этого интервала, как об этом сказано выше, необходимы численные расчеты, используя таблицы 1, 2, рис. 2в, а также формулы (20), (21), в которых заменяем $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} \to {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$, $n_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}^{*} \to {{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$, $\Delta * \to \Delta $.
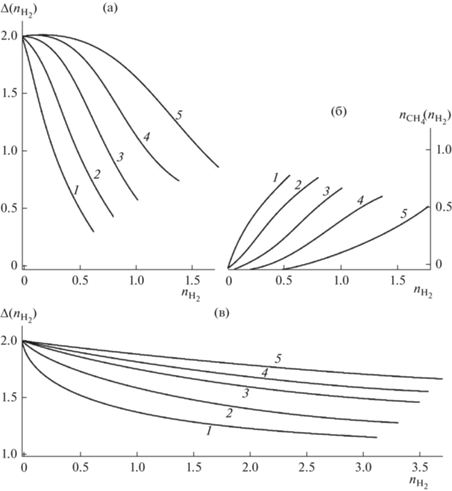
Рис. 4.
Зависимости $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ (а) и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ (б) на основном участке при $T = 673$ K; то же при $T = $973 K, ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}) \cong 0$ (в). Кривые 1 – $m = 2$, 2 – 3, 3 – 5, 4 – 7, 5 – $m = 10$.
При фиксированной температуре по мере увеличения параметра $m$ поток метана ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ как функция ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ уменьшается (см. рис. 4). Увеличение $T$ также способствует уменьшению этой зависимости, причем при $T \geqslant 1000$ K при любом $m > 2$ поток ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 0$. Аналогичные закономерности наблюдались и на выходе начального участка (см. рис. 2б). Отклонение потока водяного пара $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ от входной величины $m$ увеличивается при возрастании $m$. Очевидно, это связано с ростом скорости химического взаимодействия при увеличении избытка водяного пара (см. рис. 4а, 4б).
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ
Продифференцировав зависимости ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{{H}_{2}}O}}}({{n}_{{{{H}_{2}}}}})$ по переменной ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$, из уравнения (24) находим распределение потока водорода внутри нижней камеры ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$. Для примера результаты таких расчетов представлены на рис. 5 для температуры 823 K при $m = 3$. Потоки ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ на основном участке в отличие от начального зависят не только от температуры, но и от объемной скорости подачи сырья $G$ (см. (13), (15), (24)).
Рис. 5.
Распределение потока Н2 внутри нижней камеры ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ при $m = 3$ и $T = $ 823 K. Кривая 1 – $G = 1800$, 2 – 3600, 3 – 5400, 4 – $G = 9600$.
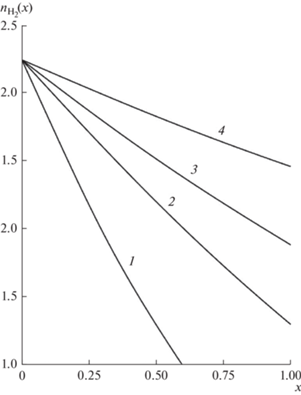
Поток водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ достигает своего максимального значения на выходе начального участка [42] и в дальнейшем монотонно уменьшается. Потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}(x)$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}(x)$ на основном участке ($x > {{x}_{{{\text{нач}}}}}$) также монотонно отклоняются от соответствующих значений $n_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$ (см. рис. 4а, 4б) в сторону уменьшения.
В качестве характеристики работы реактора используют конверсию метана $\alpha $ – отношение разности потоков СН4 на входе и выходе нижней камеры к его потоку на входе:
(29)
$\alpha = \frac{{{{N}_{{{\text{BX}}}}} - {{N}_{{{\text{ВЫХ}}}}}}}{{{{N}_{{{\text{BX}}}}}}} = 1 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}\,\,(1),$Другой важной характеристикой реактора является отвод водорода φ – отношение потока Н2 через мембрану к суммарному его потоку на выходе из верхней камеры (${{I}_{S}}$) и нижней ${{N}_{{{\text{BX}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)$:
(30)
$\varphi = \frac{{{{I}_{S}}}}{{{{I}_{S}} + {{N}_{{{\text{BX}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)}} = \frac{1}{{1 + \left( {\frac{1}{\beta }} \right)\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)}}{{\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} } dx}}}},$При $\alpha \to 1$ метан полностью расходуется внутри реактора, при $\varphi \to 1$ водород, получаемый в результате реакций, весь удаляется через мембрану.
При фиксированных Т и m, если объемный поток сырья $G$ “достаточно мал”, то Н2 полностью расходуется внутри нижней камеры на некотором расстоянии от входа ${{x}_{0}}$, при этом потоки ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}({{x}_{0}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{x}_{0}})$ в точке ${{x}_{0}}$ обращаются в нули (21). В этих случаях выход водорода φ и конверсия метана $\alpha $ равны единице (29), (30). С ростом $G$ заполнение камеры водородом увеличивается (рис. 5) и поток ${{I}_{S}}$ через мембрану растет. При некотором $G$ (в дальнейшем обозначим эту величину ${{G}_{{{\text{ОПТ}}}}}$) потоки ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ обращаются в нули на выходе нижней камеры (при $x = 1$). При данной температуре при дальнейшем увеличении $G$ ($G \geqslant {{G}_{{{\text{ОПТ}}}}}$) потоки метана и водорода на выходе становятся больше нуля, а следовательно, конверсия $\alpha $ и выход φ уменьшаются, то есть эффективность реактора ухудшается (см. (29), (30)). Решение парового риформинга при $G = {{G}_{{{\text{ОПТ}}}}}$ будем называть оптимальным. Сравнение расчетных и экспериментальных значений потоков ${{I}_{S}}$, выходов φ, а также конверсий $\alpha $ при $m = 3$ для мембраны Pd–6% Re приведены в табл. 3 [42]. В скобках указаны экспериментальные значения соответствующих величин. Несмотря на некоторые расхождения теории и эксперимента основные закономерности процесса риформинга получили теоретическое обоснование. Экспериментальные значения потоков Н2 через мембрану (${{I}_{S}}$) всегда занижены по сравнению с теоретическими (ошибка может достигать 20%). Основная причина, по-видимому, связана с дезактивацией мембраны окислами углерода и особенно водяными парами, как это отмечено ранее [38].
Таблица 3.
Сравнение теории и эксперимента для мембраны Pd–6% Ru при $m = 3$ [43]
| $T$, K | $G$, 1/ч | ${{I}_{S}} \times {{10}^{4}}$, моль/c | $\phi $ | $\alpha $ |
|---|---|---|---|---|
| 973 | 1800 3600 5400 9600 |
0.43 (0.33) 0.77 (0.62) 0.9 (0.7) 1.2 (0.95) |
1 (0.82) 1 (0.81) 0.92 (0.8) 0.65 (0.76) |
1 (1) 1 (1) 1 (0.98) 1 (0.96) |
| 823 | 1800 3600 5400 9600 |
0.4 (0.33) 0.7 (0.56) 0.79 0.84 |
1 (0.77) 0.92 (0.72) 0.75 0.52 |
1 (0.99) 1 (0.78) 0.9 0.8 |
| 773 | 1800 3600 5400 96 000 |
0.35 (0.3) 0.57 (0.46) 0.60 0.63 |
1 (0.79) 0.87 (0.68) 0.73 0.54 |
1 (0.75) 0.92 (0.7) 0.82 0.7 |
В общем случае при любом $m > 2$ оптимальное значение ${{G}_{{{\text{ОПТ}}}}}$ находится следующим образом (см. (13), (15)):
(31)
$\begin{gathered} {{\left( {{{{{G}_{{{\text{ОПТ}}}}}} \mathord{\left/ {\vphantom {{{{G}_{{{\text{ОПТ}}}}}} {{{{10}}^{3}}}}} \right. \kern-0em} {{{{10}}^{3}}}}} \right)}_{{{\text{ОПТ}}}}} = 4.5(1 + m) \times \\ \times \,\,{{\left[ {\frac{{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}}) \times {{{10}}^{6}}\sqrt {10} }}{\delta }} \right]} \mathord{\left/ {\vphantom {{\left[ {\frac{{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}}) \times {{{10}}^{6}}\sqrt {10} }}{\delta }} \right]} {{{\beta }_{{{\text{ОПТ}}}}}}}} \right. \kern-0em} {{{\beta }_{{{\text{ОПТ}}}}}}}, \\ \end{gathered} $(32)
$\begin{gathered} {{\beta }_{{{\text{ОПТ}}}}} = \int\limits_0^{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} {\left( {2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} - \frac{{d\Delta }}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)} \times \\ \times \,\,\left( {\sqrt {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + m - \Delta } } \right)\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}. \\ \end{gathered} $Распределение потока водорода в нижней камере ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ находим из уравнения (см. (24)):
(33)
$\begin{gathered} \frac{{\int\limits_{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{}}}^{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} {\left( {2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} - \frac{{d\Delta }}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)\left( {\sqrt {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + m - \Delta } } \right)\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}} }}{{\int\limits_0^{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} {\left( {2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} - \frac{{d\Delta }}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)\left( {\sqrt {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + m - \Delta } } \right)\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}} }} = \\ = (x - {{x}_{{{\text{нач}}}}}). \\ \end{gathered} $Оптимальные значения ${{\beta }_{{{\text{ОПТ}}}}}$ и соответствующие распределения ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ зависят только от температуры и отношения $m$, так как от этих величин зависят $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ и распределения ${{n}_{i}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ (см. таблицу 2 и (20), (21)). В табл. 4 приведены расчеты ${{\beta }_{{{\text{ОПТ}}}}}$ в широкой области температур (673–1073 K) при $m$ = 2, 3, 5, 10.
Таблица 4.
Расчеты ${{\beta }_{{{\text{ОПТ}}}}}$ при различных $T$ и $m$
| $T$, K | 673 | 773 | 823 | 873 | 923 | 973 | 1023 | 1073 |
|---|---|---|---|---|---|---|---|---|
| $m = 2$ | 13.51 | 9.43 | 8.26 | 7.46 | 7.19 | 6.99 | 6.62 | 6.62 |
| $m = 3$ | 14.81 | 10.42 | 9.26 | 8.62 | 8.20 | 7.87 | 7.81 | 7.81 |
| $m = 5$ | 16.5 | 11.63 | 10.31 | 9.9 | 9.71 | 9.52 | 9.52 | 9.52 |
| $m = 10$ | 17.86 | 13.51 | 13.16 | 12.98 | 12.99 | 12.99 | 12.99 | 12.99 |
Распределения ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$(x) при оптимальных режимах для трех температур 673, 823 и 973 K представлены на рис. 6. Нетрудно заметить, что безразмерные потоки водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ в нижней камере увеличиваются при возрастании температуры и потока сырья, что, по-видимому, связано с увеличением скоростей каталитических реакций (см. (12), (13)).
Рис. 6.
Распределения ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ при оптимальных режимах для различных $T$ и $m$. (а) температура 673 K, (б) 823 K, (в) 973 K. Кривые 1 – $m = 2$, 2 – 3, 3 – 5, 4 – $m = 10$.
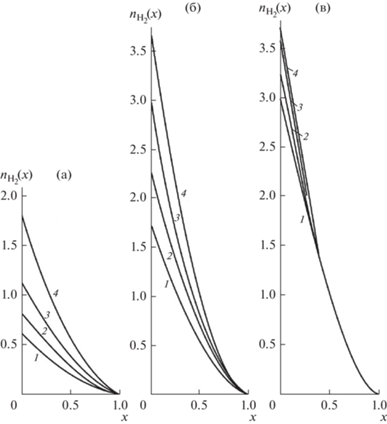
Оптимальные потоки Н2 через мембрану ${{I}_{S}}$ (на выходе верхней камеры) рассчитываются по формулам:
(34)
$\begin{gathered} {{I}_{S}} = \left( {{{N}_{{{\text{ВЫХ}}}}}\beta } \right)\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} dx} = \\ = S\left[ {\frac{{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}}) \times {{{10}}^{2}}\sqrt {10} \sqrt {{{p}_{{{\text{AT}}}}}} }}{\delta }} \right] \times \\ \times \,\,\left( {\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} dx} } \right), \\ \end{gathered} $Таблица 5.
Средняя движущаяся сила $\left( {\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} dx} } \right)$ при различных $T$ и $m$
| $T$, K | 673 | 773 | 823 | 873 | 923 | 973 | 1023 | 1073 |
|---|---|---|---|---|---|---|---|---|
| $m = 2$ | 0.296 | 0.427 | 0.478 | 0.515 | 0.564 | 0.594 | 0.60 | 0.607 |
| $m = 3$ | 0.285 | 0.415 | 0.403 | 0.467 | 0.48 | 0.509 | 0.509 | 0.509 |
| $m = 5$ | 0.245 | 0.335 | 0.308 | 0.40 | 0.4 | 0.4 | 0.4 | 0.4 |
| $m = 7$ | 0.29 | 0.3 | 0.35 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 |
| $m = 10$ | 0.197 | 0.265 | 0.315 | 0.316 | 0.316 | 0.316 | 0.316 | 0.316 |
При увеличении температуры (постоянное $m$) движущая сила увеличивается, что связано с ростом потока водорода в камере. В свою очередь, при увеличении $m$ (постоянная температура) движущая сила падает из-за увеличения избытка пара в смеси, так как в этом случае уменьшается мольная доля водорода ${{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}$. Оптимальная величина потока сырья ${{G}_{{{\text{ОПТ}}}}}$, в отличие от ${{\beta }_{{{\text{ОПТ}}}}}$ и ${{\left( {\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} dx} } \right)}_{{{\text{ОПТ}}}}}$, зависит от водородопроницаемости мембраны.
Для мембраны Pd–6% Ru в табл. 6 приведены расчеты ${{G}_{{{\text{ОПТ}}}}}$ в рассматриваемых интервалах температур и отношений $m$. При фиксированном $m$ с ростом температуры водородопроводимость мембраны и движущая сила увеличиваются, что позволяет увеличить подачу сырья на входе в нижнюю камеру.
Таблица 6.
Расчет оптимального потока сырья ${{G}_{{{\text{ОПТ}}}}}$ [1/ч] для мембраны состава Pd–6% Ru при различных $T$ и $m$
| $T$, K | 673 | 773 | 823 | 873 | 923 | 973 | 1023 | 1073 |
|---|---|---|---|---|---|---|---|---|
| $m = 2$ | 800 | 1650 | 2140 | 2660 | 3060 | 3460 | 3980 | 6620 |
| $m = 3$ | 970 | 1990 | 2550 | 3070 | 3580 | 4090 | 4530 | 4880 |
| $m = 5$ | 1310 | 2670 | 3430 | 4000 | 4530 | 5070 | 5370 | 5840 |
| $m = 10$ | 2220 | 4210 | 4930 | 5600 | 6210 | 6820 | 7430 | 8000 |
Соответствующие потоки на выходе верхней камеры для этой мембраны представлены на рис. 7. С ростом температуры (постоянное $m$) потоки ${{I}_{S}}$ увеличиваются как за счет увеличения водородопроводимости мембраны, так и движущей силы. При фиксированной температуре потоки ${{I}_{S}}$ уменьшаются с увеличением $m$, так как уменьшается движущая сила переноса Н2 через мембрану.
Рис. 7.
Потоки на выходе верхней камеры при оптимальных режимах для различных $T$ и $m$. Кривые 1 – $m = 2$, 2 – 3, 3 – 5, 4 – 7, 5 – $m = 10$.
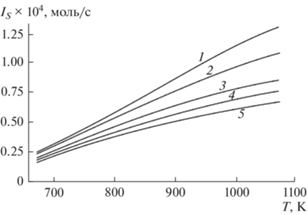
Из рис. 7 следует, что процесс парового риформинга необходимо проводить при достаточно высоких температурах, порядка 900–1000 K, и при как можно меньших отношениях $m$ (∼2–3). При низких температурах поток на выходе верхней камеры становится достаточно малым, а более высокие $T$ являются энергозатратными и не приводят к заметному увеличению ${{I}_{S}}$.
При оптимальных режимах парового риформинга метана на выходе нижней камеры мы получаем газовую смесь СО2 и Н2О, при этом безразмерные потоки компонентов смеси равны (см. (9) и (20)):
Соответствующий мольный состав равен:
После прохождения смеси на выходе нижней камеры через холодильник мы получаем практически чистый углекислый газ. На выходе в верхней камере присутствует только водород. Представленные выше экспериментальные и расчетные величины относятся к фольговой мембране состава Pd–6% Ru, для которой предъэкспоненциальный фактор и энергия активации перехода Н2 через мембрану равны ${{Q}_{{{\text{Ru}}}}} = 6.1 \times {{10}^{8}}$ [моль/м с Па] и ${{E}_{{{\text{Ru}}}}} = 13.9$ [кДж/моль], соответственно [17]. В работе [17] были приведены подобные характеристики для ряда палладиевых мембран (точнее плавов Pd c Ru, In, Ag). Соответствующие предъэкспоненты $Q$ и энергии активации $E$ представлены в табл. 7. Относительные водородопроводимости этих фольговых мембран по отношению к мембране состава Pd–6% Ru в интервале температур 573–1073 K, то есть отношение ${{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}})} \mathord{\left/ {\vphantom {{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}})} {{{Q}_{{{\text{Ru}}}}}\exp ( - {{{{E}_{{{\text{Ru}}}}}} \mathord{\left/ {\vphantom {{{{E}_{{{\text{Ru}}}}}} {RT}}} \right. \kern-0em} {RT}})}}} \right. \kern-0em} {{{Q}_{{{\text{Ru}}}}}\exp ( - {{{{E}_{{{\text{Ru}}}}}} \mathord{\left/ {\vphantom {{{{E}_{{{\text{Ru}}}}}} {RT}}} \right. \kern-0em} {RT}})}}$ заключено в интервале (0.3–3) (см. табл. 7), где первые значения относится к 573 K, а вторые – к 1073 K. Эти отношения монотонно зависят от температуры. Основные предположения, положенные в основу построения приближенной модели парового риформинга метана, остаются верными для всех представленных в таблице 7 мембран. В частности, можно проверить (см. таблицы 1, 4), что параметры ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ при $m > 2$ в интервале температур (673–1073 K) в районе оптимальных потоков подачи сырья $G$ намного больше единицы, а ${\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}} \ll 1$. Например, минимальное значение ${{\alpha }_{1}}$ для всех представленных выше мембран достигается при $m \cong 2$ и увеличивается с температурой. При $T = 673$ K это минимальное значение ∼102, а при $T = 1073$ K – порядка 103. Следовательно, предположения о коротком начальном и основном участках имеют место для всех исследованных мембран, при этом на выходе начального участка равновесные потоки $n_{i}^{*}$ остаются без изменения, так как они зависят только от температуры и отношения $m$ (см. табл. 2).
Таблица 7.
Предъэкспоненты $Q$ и энергии активации $E$ для различных мембран
| Cостав мембраны | $Q \times {{10}^{8}}$, моль/(м с Па) | $E$, кДж/моль | ${{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}})} \mathord{\left/ {\vphantom {{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}})} {{{Q}_{{{\text{Ru}}}}}}}} \right. \kern-0em} {{{Q}_{{{\text{Ru}}}}}}}\exp ( - {{{{E}_{{{\text{Ru}}}}}} \mathord{\left/ {\vphantom {{{{E}_{{{\text{Ru}}}}}} {RT}}} \right. \kern-0em} {RT}})$ |
|---|---|---|---|
| Pd | 0.88 | 10 | 0.3–0.2 |
| Pd–23% Ag | 1.5 | 10 | 0.5–0.4 |
| Pd–6% Ru | 6.1 | 13.9 | 1 |
| Pd–10% Ru | 13.4 | 15.4 | 1.7–1.9 |
| Pd–6% In | 9.5 | 11 | 2.8–2 |
| Pd–6% In–0.5% Ru | 23.1 | 16.7 | 2–2.8 |
Оптимальные значения подачи сырья и потока на выходе верхней камеры для представленных в табл. 7 мембран равны:
Учитывая, что ${{\beta }_{{{\text{ОПТ}}}}}$ и ${{\left( {\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} } dx} \right)}_{{{\text{ОПТ}}}}}$ зависят только от $T$ и $m$, то оптимальные значения потоков сырья на входе и потоков водорода на выходе верхней камеры для мембран состава Pd–10% Ru, Pd–6% Ru–0.5% In и Pd–6% In в два и более раз превышают соответствующие значения для мембраны Pd–6% Ru и на порядок больше, чем для мембраны из чистого Pd (табл. 7).
ЗАКЛЮЧЕНИЕ
Проведено моделирование парового риформинга метана в ММ с использованием фольговых палладиевых мембран различного состава (Pd, Pd–23% Ag, Pd–6% Ru, Pd–6% Ru–0.5% In, Pd–6% In). Доказано, что в нижней камере ММ, заполненной никелевым катализатором, существуют два несоизмеримых участка – начальный, размеры которого намного меньше радиуса камер, и основной. На начальном участке мембраны не оказывают влияние на протекающие химические процессы, причем на выходе этого участка реакции приходят к равновесию, а поток водорода максимален.
Влияние мембраны становится заметной на основном участке, где из-за слабого оттока водорода через мембрану химические равновесия практически не нарушаются.
Доказано, что при паровом риформинге метана отношение входных потоков Н2О и СН4 не должно быть менее двух. В противном случае водяной пар полностью расходуется внутри камеры, в дальнейшем реакция метана с водой не протекает и невозможно достичь 100% конверсии СН4 на выходе.
Расчеты были проведены в интервале температур ∼700–1000 K при отношениях потока воды и метана на входе 2–10.
Найдены оптимальные значения потока сырья на входе, при которых выход водорода и конверсия метана достигают 100%. Показано, что при оптимальных режимах и при фиксированной температуре максимальный поток H2 на выходе верхней камеры достигается при минимально допустимых отношениях входных потоков пара и метана равных двум.
При оптимальных режимах на выходе нижней камеры смесь практически состоит из водяных паров и СО2. После охлаждения (удаления Н2О) мы получаем чистый углекислый газ. В верхней камере присутствует только водород.
Поток водорода на выходе верхней камеры при фиксированной температуре можно увеличить за счет увеличения площади фольги, утоньшения ее, а также применяя мембраны с более высокой проницаемостью для водорода.
Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук, тема ИПХФ РАН 0089-2019-0018 (номер госрегистрации АААА-А19-119022690098-3).
ОБОЗНАЧЕНИЯ
| ${{b}_{1}}$, ${{b}_{2}}$ | скорости реакций 1. и 2., моль/кгКАТ с |
| $с_{i}^{'}$ | концентрации компонентов газа, моль/м3 |
| $D$ | коэффициент диффузии в зернистом слое, м2/с |
| ${{d}_{{{\text{KAT}}}}}$ | диаметр частиц катализатора, м |
| $E$ | энергия активации в уравнении Сивертса, Дж/моль |
| $G$ | объемная скорость подачи сырья, 1/ч |
| $h$ | высота камер, м |
| ${{I}_{{{{{\text{H}}}_{{\text{2}}}}{\text{,П}}}}}$ | локальный поток Н2 через мембрану, моль/м2 с |
| ${{I}_{{\text{П}}}}$ | суммарный поток Н2 через мембрану, моль/с |
| ${{K}_{1}}$ | константа равновесия реакции (1), ат2 |
| ${{K}_{2}}$ | константа равновесия реакции (2) |
| ${{\tilde {k}}_{1}}$ | кинетическая константа скорости реакции (1), моль ат1/2/кгКАТ с |
| ${{\tilde {k}}_{2}}$ | кинетическая константа скорости реакции (2), моль/ат кгКАТ с |
| ${{k}_{i}}$ | константа равновесия Лэнгмюра для СО, СН4, Н2, ат–1 |
| ${{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ | константа равновесия Лэнгмюра для пара Н2О |
| $m$ | отношение входных интегральных потоков пара и СН4 |
| $N_{i}^{'}$ | локальный мольный поток компонентов газа, моль/с м2 |
| ${{N}_{i}}$ | интегральный мольный поток компонентов, моль/с |
| ${{n}_{i}}$ | безразмерный локальный поток компонента i |
| ${{n}_{\sum }}$ | безразмерный поток газовой смеси |
| $n_{i}^{*}$ | равновесные потоки компонентов газа на выходе начального участка |
| ${{N}_{{{\text{BX}}}}}$, ${{N}_{{{\text{BЫ}}{\kern 1pt} {\text{X}}}}}$ | интегральные потоки СН4 на входе и выходе нижней камеры, моль/с |
| ${{p}_{{{\text{AT}}}}}$ | давление в нижней камере, ат |
| ${{p}_{i}}$ | парциальные давления компонентов смеси, ат |
| $Q$ | предъэкспоненциальный множитель в законе Сивертса, моль/м1/2 кг1/2 |
| $r{\kern 1pt} '$, $z{\kern 1pt} '$ | цилиндрические координаты, м |
| $r_{{\max }}^{'}$, $r_{{\min }}^{'}$ | радиусы мембраны и выходного отверстия, м |
| $R$ | универсальная газовая постоянная, Дж/моль град |
| $r$ | безразмерная координата, отсчитываемая от центра фольги |
| $S$ | площадь фольги, м2 |
| $T$ | температура, K |
| $\nu {\kern 1pt} '$, $u{\kern 1pt} '$ | компоненты скорости смеси, м/с |
| ${{v}_{{{\text{КАТ}}}}}$ | объем засыпки катализатора, см3 |
| ${{w}_{{{\text{КАТ}}}}}$ | масса засыпки катализатора, кг |
| $x$, $y$ | безразмерные координаты, отсчитываемые от периферии фольги |
| ${{X}_{i}}$ | мольная доля i-го компонента смеси |
| $z$ | безразмерная координата на начальном участке |
| $\alpha $ | конверсия метана |
| ${{\alpha }_{1}}$, ${{\alpha }_{2}}$ | безразмерные кинетические константы реакций (1) и (2) |
| $\beta $ | безразмерный параметр, учитывающий поток Н2 через мембрану |
| $\varepsilon $ | порозность |
| ${{\rho }_{{{\text{КАТ}}}}}$ | плотность катализатора, кг/м3 |
| φ | отвод водорода |
| ${{\phi }_{i}}$ | источник (сток) компонента i, моль/кгКАТ с |
| $\Delta $ | отклонение безразмерного потока Н2О от его значения на входе |
| $\delta $ | толщина мембраны, м |
Список литературы
Ramachandran R., Menon R.K. An overview of industrial uses of hydrogen // Int. J. Hydrogen Energy. 1998. V. 23. P. 593.
Kirillov V.A., Meshcheryakov V.D., Brizitskii O.F., Terent’ev V.Ya. Analysis of a power system based on low-temperature fuel cells and a fuel processor with a membrane hydrogen separator // Theor. Found. Chem. Eng. 2010. V. 44. № 3. P. 227.
Saeidi S., Fazlollahi F., Najari S., Iranshahi D., Klemes I.I., Baxter L.L. Hydrogen production: Perspectives, separation with special emphasis on kinetics of WGS reaction: A state-of-the-art review // J. Ind. and Bugin. Chem. 2017. V. 49. P. 1
Rahimpour M.R., Samimi F., Babapoor A., Tohiolian T., Mohebi S. Palladium membranes applications in reaction system for hydrogen separation and purification: A review // Chem. Eng. Proc.: Process Intensification. 2017. V. 121. P. 24.
Кириллов В.А., Амосов Ю.И., Шигаров А.Б., Кузин Н.А., Киреенков В.В., Пармон В.Н., Аристович Ю.В., Грицай М.А., Светов А.А. Экспериментальное и теоретическое исследование переработок попутного нефтяного газа в нормализованный газ посредством мягкого парового риформинга // Теорет. основы хим. технол. 2017. Т. 51. № 1. С. 15. (Kirillov V.A., Amosov Y.I., Shigarov A.B., Kireenkov V.V., Parmon V.N., Kuzin N.A., Aristovich Y.V., Gritsay M.A., Svetov A.A. Experimental and theoretical study of associated petroleum gas processing into normalized gas by soft steam reforming // Theoretical Foundations of Chemical Engineering. 2017. V. 51. № 1. P. 12.)
Gryaznov V.M. Hydrogen permeable palladium membrane catalyst. An aid to the efficient production of ultra pure chemicals and pharmaceuticals // Platinum Met. Rev. 1986. V. 36. P. 68.
Itoh N. Inorganic membranes for reaction and separation // AIChE J. 1987. V. 33. P. 1576.
Mazali I.O., Filho A.G., Viana B.C., Filho I.M., Alves O.L. Sizecontrollable synthesis of nanorized-TiO anatase using porous Vycor glass as template // J. Nanopart. Res. 2006. V. 8. P. 141.
Pizzi D., Worth R., Baschetti M.G., Sarfi G.C., Noda K. Hydrogen permeability of 2.5 μm palladium–silver membranes deposited on ceramic supports // J. Membr. Sci. 2008. V. 325. N 1. P. 446.
Tong I., Shirai R., Kashima Y., Matsumura Y. Preparation of a pinhole-free Pd–Ag membrane on a porous metal support for pure hydrogen separation // J. Membr. Sci. 2005. V. 260. № 1. P. 84.
Brenner I.R., Bhagat G., Vasa P. Hydrogen purification with palladium and palladium alloys on porous stainless steel membranes // Int. J. Oil, Gas and Coal Techn. 2008. V. 1. № 1–2. P. 109.
Tong I., Matsumura Y., Suda H., Hazaya K. Thin and dense Pd/CeO2/MPSS composite membrane for hydrogen separation and steam reforming of methane // Sep. Purif. Technol. 2005. V. 46. P. 1.
Shirasaki Y., Tsuneki T., Seki T., Yasuda I., Sato T., Itoh N. Improvement in hydrogen permeability of palladium membrane by alloying with transition metals // J. Chem. Eng. 2018. V. 51. P. 123.
Holleck G.L. Diffusion and solubility of hydrogen in palladium and palladium-silver alloys // J. Phys. Chem. 1970. V. 74. P. 503.
Fort D., Farr I., Hurris I.A. A comparison of palladium-silver and palladium-yttrium alloys as hydrogen separation membranes // J. Less-Common Met. 1975. V. 39. P. 293.
Sakamoto Y., Chen F., Furukawa H., Noguchi M. Permeability and diffusivity of hydrogen in palladium-rich Pd–Y(Cd)–Ag ternary alloys // J. Alloys Compd. 1992. V. 185. P. 191.
Диденко Л.П., Семенцова Л.А., Чижов П.Е., Бабак В.Н., Савченко В.И. Разделительные свойства фольги из сплавов Pd–(6%) In–(0.5%) Ru, Pd–(6%) Ru, Pd–(10%) Ru и влияние СО2, СО, СН4 и водяного пара на скорость потока Н2 через исследуемые мембраны // Изв. АН. Сер. Хим. 2016. № 8. С. 1997. (Didenko L.P., Sementsova L.A., Chizhov P.E., Babak V.N., Savchenko V.I. Separation performance of foils from Pd–In (6%)–Ru (0.5%), Pd–Ru (6%), and Pd–Ru (10%) alloys and influence of СО2, СН4, and water vapor on the Н2 flow rate through the test membranes // Russian Chemical Bulletin. 2016. V. 65. № 8. P. 1997–2003.)
Decaux C., Nyameni R., Solas D., Grigoriev S., Hiller P. Time and frequency domain analysis of hydrogen permeation across PdCu metallic membranes for hydrogen purification // Int. J. Hydrogen Energy. 2010. V. 35. P. 4883.
Howard H., Killmeyer R., Rothenberger K., Cugini A. Hydrogen permeance of palladium-cupper alloy membranes over a wide range of temperatures and pressure // J. Membr. Sci. 2004. V. 841. P. 207.
Acha E., Regnes I., Barrio V.I., Cambra I.F., Guemez M.R., Arias P.I., et al. PdCu membrane integration and lifetime in the production of hydrogen from methane // Int. J. Hydrogen Energy. 2013. V. 38. P. 7659.
Yuan L., Goldbach A., Xu H. Permition hysteresis in PdCu membranes // J. Phys. Chem. B. 2008. V. 112. P. 12692.
Haws H.W., Paglieri S.N., Marris C.C., Harall A., Way I.D. Application of Pd–Ru composite membrane to hydrogen production in a high temperature membrane reactor // Ser. Purif. Technol. 2015. V. 147. P. 388.
Kamakati P., Morreale B.D., Ciocco M.V. et al. Prediction of hydrogen flux through sulfur-tolerant binary alloy membranes // Science. 2005. V. 507. P. 569.
Coroneo H., Houtante G., Catalane I., Paglianti A. Modelling the effect of operating conditions on hydrodynamics and mass transfer in Pd–Ag membrane module for H2 purification // J. Membr. Sci. 2009. V. 343. P. 34.
Tiemersma T.P., Patie C.S., Annalong M.S., Kuipers I.A.M. Modelling of packed bed reactors for production of ultrapure hydrogen // Chem. Eng. Sci. 2006. V. 61. P. 1602.
Falco M., Paola L.D., Harrelli L. Heat transfer and hydrogen permeability in modelling industrial membrane reactors for methane steam reforming // Int. J. Hydrogen Energy. 2007. V. 32. P. 2902.
Gallici F., Comite A., Capannelli G., Basill A. Steam reforming of methane in a membrane reactor: An industrial case study // Ind. Eng. Chem. Res. 2006. V. 45. P. 2994.
Caravella A., Mario F.P., Renzo A. Optimization of membrane aria and catalyst distribution in a permeative – stall membrane reactor for methane steam reforming // J. Membr. Sci. 2008. V. 321. P. 209.
Wilde I., Fromet G.F. Computation fluid dynamics in chemical reactor analysis and design: Application to the zone flow reactor for methane steam reforming // Fuel. 2012. V. 100. P. 48.
Kim Ch.-H., Han I.-H., Lim H.-K., Kim D.-H., Ryi S.-K. Methane steam reforming in membrane reactor using high-permeable and low-selective Pd–Ru membrane // Korean J. Chem. Eng. 2017. V. 34. P. 1260.
Schädel B.T., Duisberg M., Deutschmann O. Steam reforming of methane, ethane, propane, butane, and natural gas over a rhodium-based catalyst // Catalysis Today. 2009. V. 142. P. 42.
Rakib M.A., Grade I.R. Steam reforming of propane in a fluidized bed membrane reactor for hydrogen production // Int. J. Hydrogen Energy. 2010. V. 35. P. 6276.
Didenko L.P., Sementsova L.A., Babak V.N., Chizhov P.E., Dorofeeva T.V., Kvurt Yu.P. Steam reforming of a n-butane in membrane reactor with industrial nickel catalyst and foil made of Pd–Ru alloy // Membrane and Membrane Technol. 2020. V. 10. № 2. P. 99. (Диденко Л.П., Семенцова Л.А., Бабак В.Н., Чижов П.Е., Дорофеева Т.В., Квурт Ю.П. Паровая конверсия н-бутана в мембранном реакторе с промышленным никелевым катализатором и фольгой из Pd-Ru сплава // Мембраны и мембранные технологии. 2020. Т. 10. № 2. С. 85.)
Диденко Л.П., Бабак В.Н., Семенцова Л.А., Чижов П.Е., Дорофеева Т.В. Паровая конверсия пропана в мембранном реакторе с промышленным никелевым катализатором // Нефтехимия. 2021. Т. 61. № 1. С. 103. (Didenko L.P., Babak V.N., Sementsova L.A., Chizhov P.E., Dorofeeva T.V. Steam convension of propane in a membrane reactor with industrial nickel catalyst // Petrolium chemistry. 2021. V. 61. № 1. P. 92)
Asci A.K., Trimm D.L., Arsoylu A.E., Önsan Z.I. Hydrogen production by steam reforming of n-butane over supported Ni and Pt–Ni catalysts // App. Catal. A Gen. 2004. V. 258. P. 255.
Didenko L.P., Voronetsky M.S., Sementsova L.A., Barelco V.V., Bikov L.A. et al. Technical characteristics of the hydrogen-filtering module on a base of the palladium foil // Int. Scientific J. Altern. Energy Ecol. 2010. № 10. P. 154.
Boeltken T., Wunsch A., Gietzeet T., Pfeifer P., Dittmeyer R. Ultra-compact microstructured methane steam reforming with integrated palladium membrane for on-site production of pure hydrogen: Experimental demonstration // Int. J. Hydrogen Energy. 2014. V. 30. P. 18058.
Бабак В.Н., Диденко Л.П., Квурт Ю.П., Семенцова Л.А. Извлечение водорода из бинарных газовых смесей с помощью мембранного модуля на основе палладиевой фольги с учетом дезактивации мембраны // Теорет. основы хим. технол. 2018. Т. 52. № 3. С. 318. (Babak V.N., Didenko L.P., Kvurt Y.P., Sementsova L.A. The recovery of hydrogen from binary gas mixtures using a membrane module based on a palladium foil taking into account the deactivation of the membrane // Theor. Found. Chem. Eng. 2018. V. 52. № 3. P. 371–385.)
Дубинин А.М., Тупоногов В.Г., Иконников И.С. Моделирование процесса производства водорода из метана // Теорет. основы хим. технол. 2013. Т. 47. № 6. С. 634. (Dubinin A.M., Tuponogov V.G., Ikonnikov I.S. Modeling the process of producing hydrogen from methane // Theor. Found. Chem. Eng. 2013. V.47. № 6. P. 697–701.)
Gradl S.R., Thoen P.M., Way I.D. Unsupported palladium alloy foil membranes fabricated by electroless plating // J. Membr. Sci. 2008. V. 316. P. 112.
Burkhanov G.S., Gorina N.B., Kolchugina N.B., Roshan N.R., Slovetsky D.I., Chistov E.M. Palladium-based alloy membranes for separation of high purity hydrogen from hydrogen-containing gas mixtures // Platinum Met. Rev. 2011. V. 55. № 1. P. 3.
Бабак В.Н., Диденко Л.П., Квурт Ю.П. Исследование паровой конверсии метана в каталитическом реакторе с мембраной из палладиевой фольги // Материалы международной конференции “Математические методы в технике и технологиях” (ММТТ-33). Казань. 2020. Т. 4. С. 65.
Xu I., Fromet G.F. Methane steam reforming. Methanation and water-gas shift, intrinsic kinetics // AIChE J. 1989. V. 35. № 1. P. 88.
Lin Y.M., Liu Sh.I., Chuang Ch.H., Chu Y.T. Effect of incipient removal of hydrogen through palladium membrane on conversion of methane steam reforming: Experimental and modelling // Catalysis Today. 2003. V. 82. № 1. P. 127.
Falko M., Marrelli P.L. Heat transfer and hydrogen permeability in modelling industrial membrane reactors for methane steam reforming // Int. J. Hydrogen Energy. 2007. V. 32. P. 2094.
Sieverts A., Krumbhaar W. Über die Löglich Keit von Gases in metallen und liqie Rungen // Ber. Deut. Chem. Gas. 1910. V. 43. S. 893.
Крылов О.В. Гетерогенный катализ. М.: ИКЦ Академкнига, 2004.
Демидович Б.П., Марон И.А., Шувалов Э.З. Численные методы анализа. М.: ГИФМЛ, 1963.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


