Теоретические основы химической технологии, 2022, T. 56, № 5, стр. 524-531
Метод случайных блужданий применительно к описанию структуры потоков в насадочно-каталитических колоннах
А. Н. Букин a, *, А. А. Романенко a, b, В. С. Мосеева a, С. А. Марунич a, Ю. С. Пак a, М. Б. Розенкевич a
a РХТУ им. Д.И. Менделеева
125047 Москва, Россия
b НИУ ВШЭ
Москва, Россия
* E-mail: aleks.bukin88@gmail.com
Поступила в редакцию 29.11.2021
После доработки 10.06.2022
Принята к публикации 11.06.2022
- EDN: VTSMSO
- DOI: 10.31857/S0040357122050013
Аннотация
В рамках настоящей работы предпринята попытка описания движения потока воды через смешанный слой гидрофобного катализатора и гидрофильной насадки по методу случайных блужданий. С использованием разработанной программы “Column” теоретически предсказано и экспериментально подтверждено, что для поддержания “пленочного” режима течения воды через смешанный слой предельное содержание гидрофобного катализатора в нем не должно превышать 20–25 об. %.
ВВЕДЕНИЕ
Основной сложностью моделирования и эксплуатации противоточных колонн с комбинированным слоем гидрофобного катализатора и гидрофильной насадки является оценка влияния структуры потоков на массообменные характеристики. Чередование гидрофобных и гидрофильных участков по сечению и высоте колонны приводит к пульсациям потоков газа и жидкости. Работы по моделированию структуры потоков направлены на изучение распределения жидкости в объеме насадочно-каталитического слоя, влияния смачиваемости материалов и расчета гидравлического сопротивления. Для описания гидродинамики потоков в насыпных колоннах обычно применяются следующие модели: полуэмпирический анализ на основе критериального подобия лабораторных и промышленных установок, метод случайных блужданий [1–3], теория перколяции [4, 5], метод компьютерной вычислительной гидродинамики (CFD) [6, 7]. Развитие вычислительных мощностей компьютеров позволило заметно повысить точность расчета и предсказания гидродинамических параметров насадочных регулярных и нерегулярных слоев. Сложность применения готовых программных решений заключается в необходимости точного знания большого количества физически трудно измеряемых констант. На практике для повышения точности расчетных моделей в их алгоритмы закладывают критериальные выражения, полученные при исследовании процесса на лабораторных установках.
В рамках настоящей работы в качестве основного инструмента моделирования структуры потока жидкости в насыпных колоннах было предложено использовать метод случайных блужданий по трехмерной решетке, узлами которой являются насадочные элементы и частицы катализатора. Целью работы стал поиск максимально возможного количества катализатора в колонне, выше которого исчезает понятие пленочного движения жидкости. Добавление любого количества гидрофобного катализатора всегда приводит к разрыву пленки жидкости, образованной потоком на поверхности насадки, и переходу к частично струйному типу течения. При струйном течении жидкости снижается доля смоченной (активной) поверхности, что негативно сказывается на массообменных характеристиках. Граничным значением “пленочного” режима можно условно считать порог перколяции (проникновения жидкости) для неподвижной решетки. В условиях разделительной колонны полного прекращения движения жидкости достигнуть сложно: жидкость будет проникать и через колонну, заполненную только катализатором, деформируя каталитический слой и образуя в нем каналы для течения. Под порогом перколяции в таких условиях будет считать объемную долю катализатора, которая оказывает существенное влияние на гидродинамические характеристики потока (коэффициент продольного перемешивания Dax, критерий Боденштейна Bo).
МЕТОДИЧЕСКАЯ ЧАСТЬ
Описание математической модели. Для описания движения потока жидкости через насадочно-каталитический слой (рис. 1а) была разработана математическая модель процесса перколяции – “Column”. Центральным элементом модели является трехмерная упрощенная (рис. 1б и 1в) структура насыпного слоя, которая представляет собой простую кубическую решетку со стороной a, равной эквивалентному диаметру насадочного элемента deq. Кубическая решетка вписана в цилиндрическую колонну, при этом диаметр D и высота Н колонны кратны габариту a элементарной ячейки:
Рис. 1.
Модель насадочно-каталитического слоя: а – внешний вид разделительной колонны со смешанной загрузкой; б – фото насыпного слоя на плоскости; в – модельное заполнение колонны.
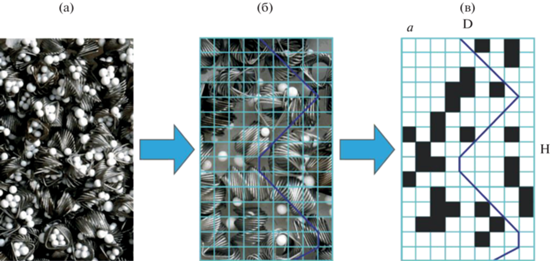
Ячейки, в которые попали гранулы гидрофобного катализатора, считаются заблокированными для потока жидкости, а ячейки с насадкой – свободными.
При орошении колонны поток жидкости под действием сил гравитации движется сверху вниз по свободным ячейкам. С математической точки зрения данная задача сводится к разработке модели проникновения (перколяции) или модели направленного (ориентированного) случайного блуждания по регулярной объемной решетке. Перемещение жидкости возможно только между свободными соседними ячейками: случайным образом из вышележащей ячейки в любую нижележащую соседнюю ячейку. Соседними называем те ячейки, связь между которыми установлена по плоскостям, ребрам или вершинам (рис. 2). Максимальное количество соседних ячеек в нижележащем слое равняется 9 (см. рис. 2). В рамках программы “Column” введено ограничение для направлений движения жидкости: запрещено движение жидкости в слое вбок и вверх. Также разработанный алгоритм заполнения решетки катализатором исключает ситуации типа “пробка”, когда движение жидкости невозможно.
Траектория движения потоков в объемной колонне представляет собой цепь Маркова, т.е. структура потока зависит от пространственных параметров каждой конкретной точки в насыпном слое и ее соседнего окружения. С увеличением расстояния между любыми двумя точками решетки резко снижается вероятность перехода элемента жидкости между ними, и в пределе этот параметр стремится к нулю [8]. Вероятность перехода потока жидкости между соседними насадочными элементами зависит от их расположения друг относительно друга, плотности упаковки разделительной колонны, а также наличия частиц гидрофобного катализатора. Для моделирования неравномерности орошения насадочного слоя или наличия застойных зон возможно отключение части узлов или связей между ними [9]. Физический смысл связи заключается в описании движения потока жидкости на микроуровне и может быть связан с шероховатостью материала насадки, его смачиваемостью или объемной долей катализатора. Например, в работе [10] показано, что по мере увеличения доли гидрофобного катализатора снижается вязкое сопротивление потоку (статическая составляющая), а силы инерционного взаимодействия становятся преобладающими (динамическая составляющая).
Для построения траектории движения жидкости и расчета плотности ее распределения в рамках настоящей модели приравняем такие параметры, как вероятность перехода между соседними узлами решетки и поток орошения Li. Т.е. при переходе с i-ого уровня на i + 1 уровень поток орошения равномерно распределяется между доступными для движения ячейками. Если же допустить, что перед началом эксперимента динамическая задержка по жидкой фазе ΔHdyn равномерно распределена во всем объеме насадки, то получаем выражение для расчета времени пребывания потока (трассера) в k-ой ячейке:
При описании движения трассера через колонну следует учитывать, что трассер может покинуть ячейку с потоком динамической задержки или остаться в ячейке, перейдя в статическую задержку. Тогда вероятность покинуть ячейку (e) определяется отношением динамической задержки к статической (f) и рассчитывается по уравнению:
(4)
$e = \frac{{\Delta {{H}_{{{\text{dyn}}}}}}}{{\Delta {{H}_{{{\text{dyn}}}}} + \Delta {{H}_{{{\text{stat}}}}}}} = \frac{f}{{f + 1}}.$Величина f характеризует структуру потоков в слое катализатора и насадки и зависит от объемной доли катализатора. Согласно данным работы [11] наблюдается линейная зависимость критерия Bo от величины f до соотношения f > 8. По мере увеличения доли статической задержки увеличивается разброс по временам пребывания частиц потока в колонне, возрастает дисперсия и снижается величина критерия Боденштейна. Параметры f и e, входящие в настоящую модель, определяли на основании экспериментальных данных.
На основании принятых в рамках модели “Column” допущений можно предложить, что кривая отклика на импульсный ввод трассера в поток жидкости в колонне E(t) будет соответствовать функции распределения времени пребывания частиц трассера при его импульсном вводе в насыпную колонну:
Подробное описание методики экспериментального исследования структуры потоков по методу импульсного ввода трассера представлено в работах [12–14] и частично изложено в методическом разделе настоящей статьи. Снижение статистической погрешности при построении функции распределения времени пребывания элементов жидкости в колонне в расчетной модели достигается за счет увеличения числа рассматриваемых траекторий движения n. Результаты численного моделирования на программе “Column” плотности распределения времени пребывания в зависимости от числа траекторий n представлены на рис. 3. При величине n равной 100 000 погрешность в измерении коэффициента продольного перемешивания составила ±5%.
Рис. 3.
Результаты численного моделирования плотности распределения времени пребывания потока в колонне в зависимости от числа рассматриваемых траекторий n.

Методика расчета. Верификация модели была выполнена в разделительной колонне (D = 46 мм, H = 150 мм), заполненной смесью гидрофильной спирально–призматической насадки (спн) 3 × 3 × 0.2 мм, изготовленной из нержавеющей стали, и гидрофобного платинового катализатора с использованием носителя сополимера стирола и дивинилбензола (СДВБ, размер гранул 0.8–1.2 мм). Для экспериментального определения времени пребывания элементов потока жидкости в разделительной колонне использовали импульсный ввод трассера (0.5 мл 0.1 М раствора NaCl). Кривая отклика на внесенное возмущение определялась сразу на выходе из колонны с помощью проточной кондуктометрической ячейки (RCL-метра). Способ постановки эксперимента соответствует закрыто-закрытой схеме (ввод трассера и его измерение производится вне основного потока, что исключает обратную диффузию) [15]. Обработка экспериментальных данных проводилась по методу моментов [14].
Первый момент распределения τ характеризует среднее время пребывания трассера или частиц потока в колонне:
Второй момент функции распределения σ2 является дисперсией случайной величины и характеризует степень размытия кривой отклика:
(7)
${{\sigma }^{2}} = \int\limits_0^\infty {{{{\left( {t - \tau } \right)}}^{2}}} ~E\left( t \right)dt.$Сравнение различных загрузок катализатора и насадки велось по величине критерия Боденштейна Bo в приближении для закрыто-закрытых систем:
(8)
$\frac{{{{\sigma }^{2}}}}{{{{\tau }^{2}}}} = \frac{2}{{Bo}} - \frac{2}{{B{{o}^{2}}}}(1 - {{e}^{{ - Bo}}}),$Неопределенность измерения коэффициента продольного перемешивания определялась для серии параллельных измерений (не менее 20) для каждой точки. Наибольший вклад в погрешность вносит способ подготовки насадочно-каталитического слоя перед началом измерений: ±18.4% для предварительно высушенного слоя и ±5.6% для предварительно затопленного слоя. Все дальнейшие гидродинамические измерения проведены в режиме предварительного затопления насыпной колонны.
В реальной колонне при измерении коэффициента продольного перемешивания под действием потока воды происходит перемещение катализатора в объеме насадочно-каталитического слоя. Для исключения данного явления исследуемая загрузка отверждалась в эпоксидной смоле (параметры образца: D = 44 мм и H = 50 мм). В таком случае проводящей средой выступал материал насадки, а порог перколяции определялся по величине электрического сопротивления R слоя: добавление гранул катализатора приводит к изоляции отдельных точек контакта между насадочными элементами, а при некотором пороговом содержании катализатора слой становится диэлектрическим.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Расчетные значения плотности распределения частиц трассера по времени их пребывания в насадочно-каталитической колонне коррелируют с экспериментальными данными (рис. 4) при объемном содержания катализатора в колонне до 20%. Отклонение модели от эксперимента по величине коэффициента продольного перемешивания в этой области не превышает 20–30% (рис. 5).
Рис. 4.
Сопоставление модельной и экспериментальной кривых отклика (εcat = 20%, e = 0.42): 1 – модель “Column” (a = 2 мм, m = 23 шт., k = 75 шт., Dax.mod = 1.51 × 10–4 м2/с); 2 – эксперимент (deq = 1.95 мм, Dcol = 46 мм, Hcol = 150 мм, Dax.exp= 1.23 × 10–4 м2/с).

Рис. 5.
Зависимость коэффициента продольного перемешивания Dax и электрического сопротивления слоя R от объемной доли катализатора.
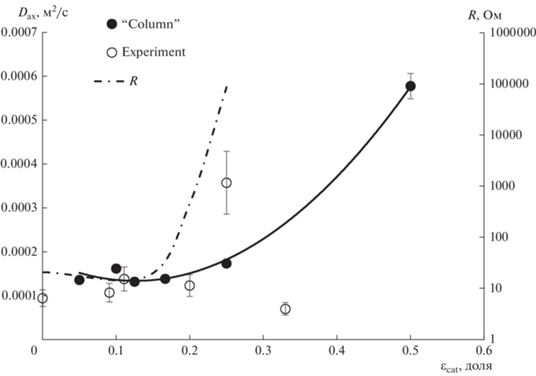
При дальнейшем увеличении количества катализатора в колонне (εcat ≥ 20 об. %) наблюдается расхождение как по абсолютной величине Dax, так и по характеру зависимости. Модельная зависимость Dax от εcat имеет полиноминальный вид и непрерывно возрастает, а на экспериментальной зависимости наблюдается максимум при объемной доле катализатора 25% (рис. 5). Данное явление объясняется различным поведением модели и реальной колонны с ростом доли катализатора. Алгоритм расчета модели исключает возможность полного перекрывания путей для движения жидкости, выборочно удаляя мешающие потоку частички катализатора из сетки. В реальной колонне застойные зоны возможны, но под действием силы тяжести потока легкие гранулы катализатора на основе СДВБ перераспределятся в слое насадки, а жидкость продолжит движение в струйном режиме по освободившемуся каналу. Движение в канале характеризуется меньшими значениями коэффициента продольного перемешивания Dax, чем движение в псевдопленочном режиме через насадочно-каталитический слой. Наблюдаемая экспериментальная зависимость может означать, что объемная доля катализатора в колонне около 20–25% является верхней границей, выше которой в слое преобладает струйное течение.
Об изменении характера движения жидкости свидетельствуют и данные по удерживающей способности насыпного слоя. С увеличением содержания катализатора в колонне (от 0 до 33 об. %) объем суммарной задержки снижается незначительно, однако происходит перераспределение жидкости между статической и динамической составляющими задержки (рис. 6). Добавление гидрофобных гранул катализатора, с одной стороны, препятствует нормальному смачиванию насадочных элементов (снижается статическая задержка), а, с другой стороны, приводит к накоплению жидкости в малоподвижных зонах (увеличивается динамическая задержка).
Рис. 6.
Экспериментальная зависимость задержки в насыпной колонне от объемного содержания гидрофобного катализатора: 1 – суммарная задержка; 2 – статическая задержка; 3 – динамическая задержка.
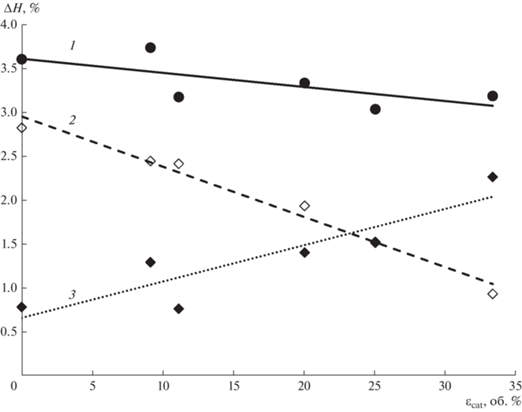
Эксперименты с измерением электрического сопротивления R отвержденного слоя показывают, что порог перколяции наступает при меньших значениях εcat. Логарифмический рост электрического сопротивления R начинается при доле катализатора 15–20 об. % (рис. 5).
ЗАКЛЮЧЕНИЕ
В рамках настоящей работы была разработана и экспериментально верифицирована модель перколяции потока жидкости через комбинированный слой катализатора и насадки. На основании полученных данных можно сделать вывод, что любое добавление катализатора в насадочный слой оказывает определенное влияние на режим течения жидкости. Однако в исследованных условиях невозможно добиться полной остановки потока (образования мертвой зоны) и достичь порога перколяции в его классическом понимании. Условным порогом перколяции, в зависимости от подвижности частиц катализатора в слое насадки, можно считать объемную долю катализатора, равную 20–25%. Рост объемной доли катализатора приводит не к остановке потока, а к перераспределению катализатора в колонне и к переходу от “пленочного” течения жидкости к “струйному”. Превышение порога перколяции в насадочно-каталитической колонне создаст гидродинамические затруднения для движения жидкости и снизит эффективность массообмена. Дальнейшая модификация программы “Column” будет направлена на снятие ограничений, связанных с направлением движения жидкости, наличием застойных зон, а также характером перераспределения катализатора под действием потока жидкости. Это позволит оптимизировать способ загрузки насадочно-каталитических колонн на стадии проектирования и выбора контактных элементов.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-08-00452 А.
ОБОЗНАЧЕНИЯ
| a | сторона кубической решетки |
| D | диаметр, м |
| d | диаметр насадочного элемента, м |
| e | вероятность покинуть ячейку |
| f | характеристика структуры потоков (отношение статической задержки к динамической) |
| H | высота насадочно-каталитической части, м |
| L | поток воды, кг/ч |
| k | количество слоев в моделируемой колонне |
| m | количество столбцов в моделируемой колонне |
| n | число рассматриваемых траекторий движения |
| R | сопротивление, Ом |
| t | время, с |
| w | линейная скорость, м/с |
| ε | доля катализатора, % |
| τ | первый момент, с |
| σ2 | второй момент, с2 |
| с(t) | количество частиц трассера, прошедших модельную колонну в момент времени t, или экспериментально измеренная концентрация трассера, моль/л |
| E(t) | функция распределения времени пребывания частиц трассера в колонне |
| $Bo$ | критериальное число Боденштейна |
| Dax | коэффициент продольного перемешивания, м2/с |
| ΔH | задержка, м3/м3 |
ИНДЕКСЫ
Список литературы
Badreddlne A.A., Henrlk P. Very Large Lattice Model of Liquid Mixing in Trickle Beds Badreddlne // Ind. Eng. Chem. Fundam. 1986. V. 25. № 1. P. 108.
Barnett V. Simple Random Walk on Parallel Axes Moving at Different Rates // J. Appl. Probab. 1975. V. 12. № 3. P. 466.
Daw C.S., Halow J. Random walk model for biomass particle mixing in bubbling fluidized beds // Ind. Eng. Chem. Res. 2014. V. 53. № 41. P. 15836.
Platzer B. Hydrodynamics of Trickle-Beds. The Percolation Theory // Chem. React. Des. Technol. 1986. V. 82. № 8. P. 539.
Kraub T., Hofmann H. Some experiences with the application of the percolation concept for modelling trickle-bed fluid dynamics // Chem. Eng. Process. 1994. V. 33. № 2. P. 67.
Gorshkova E. et al. Three-phase CFD-model for trickle bed reactors // Int. J. Nonlinear Sci. Numer. Simul. 2012. V. 13. № 6. P. 397.
Amini Y., Nasr Esfahany M. CFD simulation of the structured packings: A review // Sep. Sci. Technol. 2019. V. 54. № 15. P. 2536.
Brener A.M. Adaptation of random walk methods to the modelling of liquid distribution in packed columns // Adv. Fluid Mech. 2002. V. 32. P. 291.
Crine M., Marchot P., L’Homme G. Mathematical Modelling of the Liquid Trickling Flow Through a Packed Bed Using the Percolation Theory. // J. Microw. Power. 1979. V. 2. P. 994.
Rangwala H.A. et al. Mass transfer in a trickle-bed column packed with a mixture of hydrophobic and hydrophilic spheres // Can. J. Chem. Eng. 1990. V. 68. № 2. P. 237.
Swaaij W.P.M. Van, Charpentier J.C., Villermaux J. Residence time distribution in the liquid phase of trickle flow in packed columns // Chem. Eng. Sci. 1969. V. 24. P. 1083.
Macias-Salinas R., Fair J.R. Axial mixing effects in packed gas-liquid contactors // Ind. Eng. Chem. Res. 2002. V. 41. № 14. P. 3429.
Bukin A.N. et al. Application of the Pulse Tracer Injection Method for Estimating the Mass Transfer Efficiency at Extremely Low Irrigation Densities for the Case of Structured CY Sulzer Packing // Theor. Found. Chem. Eng. 2018. V. 52. № 3. P. 326.
Bukin A.N. et al. Mass transfer and hydrodynamics in a mixed bed of a hydrophobic catalyst and a hydrophilic packing // Fusion Eng. Des. 2021. V. 171. P. 112595.
Levenspiel O. Tracer Technology. Modeling the Flow of Fluids / Eds. Moreau Madylam R. New York: Springer, 2019.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии



