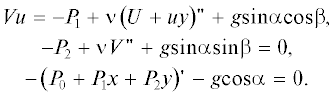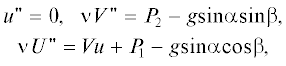1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 56, № 5, 2022

Теоретические основы химической технологии, 2022, T. 56, № 5, стр. 532-538

Неоднородное течение Нуссельта–Куэтта–Пуазейля

Н. В. Бурмашева a, *, Е. Ю. Просвиряков a, **

a Институт машиноведения УрО РАН
г. Екатеринбург, Россия

* E-mail: nat_burm@mail.ru
** E-mail: evgen_pros@mail.ru

Поступила в редакцию 16.03.2022
После доработки 02.05.2022
Принята к публикации 09.06.2022

Полный текст (PDF)

Аннотация

Изучен новый тип установившегося пленочного течения жидкости, стекающей по наклонной плоскости. Рассмотрены двумерные по скоростям неоднородные течения типа Нуссельта. В зависимости от граничных условий на свободной границе, которая полагается недеформируемой, неоднородные течения жидкости обобщают точные решения Нуссельта, Куэтта и Пуазейля. Рассмотренные в статье обобщения и модификации классических течений описываются переопределенной системой, состоящей из уравнений Навье–Стокса и уравнения непрерывности. Указано нетривиальное точное решение переопределенной системы, которое характеризует неоднородное движение вертикальной завихренной жидкости. Проанализированы скорости и касательные напряжения, которые описываются полиномами. Исследование гидродинамических полей показало, что они имеют сложную стратификацию. Поток жидкости, движущейся по наклонной плоскости, может содержать четыре области с противотоками. Касательные напряжения имеют разный знак по толщине слоя и могут дважды менять знак.

Ключевые слова: точное решение, уравнения Навье–Стокса, неоднородное сдвиговое течение, течение Нуссельта, течение Куэтта, течение Пуазейля, противотечения

ВВЕДЕНИЕ

При описании гидродинамических явлений в химической технологии важным типом движений жидкой фазы является пленочное течение [1–8]. Исследование стекания жидких пленок является важной задачей для создания миниатюрных охлаждающих устройств в микроэлектронике [9–13], при проектировании аппаратов химической технологии для сушки, выпаривания и теплообменных агрегатов [1, 5, 6], для разработки различных контактных колонн [1, 5, 6], при нанесении краски на поверхность и многих других движений тонких слоев жидкости, стекающих по наклонной поверхности под действием сил гравитации [1, 5–8]. К настоящему времени описание дрейфа пленок основывается на точном решении Нуссельта, описывающем однонаправленный поток [1, 5, 6]. Изучение свойств точного решения Нуссельта и его обобщений приведено в статьях [1, 4, 5]. Особо отметим статьи, где описывается возможность установившегося и нестационарного течения многослойных пленок [4].

С течением Нуссельта связаны известные экспериментальные исследования Капицы, согласно которым возникла необходимость методами гидродинамической устойчивости найти условие возникновения волн на свободной границе для первоначально установившегося пленочного течения с недеформируемой границей [14–16]. В гидродинамике тонких слоев жидкости известны точные решения, которые описывают трансформацию однонаправленного напорного течения Нуссельта в двумерное (плоское) движение жидкости [4, 7]. Очевидно, что такие решения представляют интерес не только для теоретической, но и для физико-химической гидродинамики, поскольку позволят интенсифицировать потоки для создания новых типов аппаратов химической технологии.

В данной статье предполагается обобщить и модифицировать точные решения, представленных в научных работах [1, 4, 5, 7], рассмотрев течение пленки в бесконечно протяженном горизонтальном наклонном слое. Установившееся течение тонкого слоя будет описываться двумерным полем скоростей, зависящим от трех координат [17, 18]. Неоднородные течения типа Куэтта и Пуазейля, рассмотренные в статьях [17, 18] в точной постановке, позволили объяснить ряд новых физических эффектов, в том числе регистрацию режима вращения без предварительной закрутки и объяснения существования застойных точек. Теоретическое изучение неоднородного течения Нуссельта для различных классов граничных условий (задания скоростей и давления) необходимо для разработки новых способов исследования гидродинамической устойчивости с последующим внедрением полученных знаний в повседневное применение новых технологических решений.

ПОСТАНОВКА КРАЕВОЙ ЗАДАЧИ

Рассмотрим сдвиговое (двумерное по скоростям) установившееся изотермическое течение вязкой несжимаемой жидкости в бесконечно протяженном наклонном слое заданной толщины h. Толщину слоя считаем постоянной, то есть пренебрегаем деформацией свободной границы. Такое допущение справедливо для установившихся крупномасштабных течений жидкости [17]. Система уравнений, традиционно используемая для описания такого рода течений, состоит из векторного уравнения Навье–Стокса и уравнения непрерывности (несжимаемости). Указанные уравнения в проекциях на оси системы координат принимают вид:

$\begin{gathered} {{V}_{x}}\frac{{\partial {{V}_{x}}}}{{\partial x}} + {{V}_{y}}\frac{{\partial {{V}_{x}}}}{{\partial y}} = \\ = - \frac{{\partial P}}{{\partial x}} + \nu \left( {\frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{z}^{2}}}}} \right) + gsin\alpha cos\beta , \\ \end{gathered} $
$\begin{gathered} {{V}_{x}}\frac{{\partial {{V}_{y}}}}{{\partial x}} + {{V}_{y}}\frac{{\partial {{V}_{y}}}}{{\partial y}} = \\ = - \frac{{\partial P}}{{\partial y}} + \nu \left( {\frac{{{{\partial }^{2}}{{V}_{y}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{V}_{y}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{V}_{y}}}}{{\partial {{z}^{2}}}}} \right) + gsin\alpha sin\beta , \\ \end{gathered} $
(1)
$\frac{{\partial P}}{{\partial z}} + gcos\alpha = 0,$
(2)
$\frac{{\partial {{V}_{x}}}}{{\partial x}} + \frac{{\partial {{V}_{y}}}}{{\partial y}} = 0.$

В системе (1), (2) символами ${{V}_{x}},{{V}_{y}}$ обозначены ненулевые проекции вектора скорости $V$; $P$ – нормированное на среднюю плотность жидкости $\rho $ отклонение давления от гидростатического, $\nu $ – кинематическая вязкость; g – ускорение свободного падения.

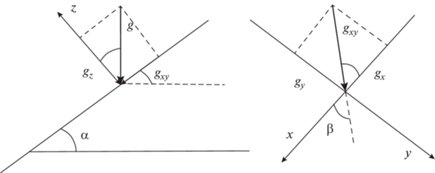
Прямоугольная система координат Oxyz выбрана таким образом, что по плоскости Oxy течет жидкость, а ось Oz направлена перпендикулярно к этой плоскости вверх. Наклон рассматриваемого слоя по отношению к горизонту определяется величиной угла α (рис. 1). Оси Ox, Oy в наклонной плоскости ориентированы таким образом, что положительное направление осей отвечает течению жидкости вниз по данной плоскости (рис. 1). Угол $\beta $ – это угол между положительным направлением оси Ox и проекцией нормированной на плотность удельной силы тяжести на плоскость течения (рис. 1). Если положить в уравнениях (1) $\beta = 0$, то рассматриваемая задача сводится к двумерному течению Нуссельта. Введение дополнительного угла $\beta $ обусловлено не только изучением неоднородного сдвигового течения жидкости, а также возможностью конструирования новых технических гидродинамических систем с управлением потоками стекающих тонких слоев.

Рис. 1.

Геометрия течения.

Система (1), (2) квадратично нелинейных уравнений в частных производных является переопределенной: она содержит четыре уравнения для определения трех неизвестных функций (давления $P$ и скоростей ${{V}_{x}},{{V}_{y}}$).

Будем далее искать точное решение уравнений (1) и (2) в следующем виде [18–22].

(3)
${{V}_{x}} = U\left( z \right) + u\left( z \right)y,\,\,\,\,{{V}_{y}} = V\left( z \right).$

Выражения (3) описывают неоднородное сдвиговое течение жидкости. Структура точного решения такова, уравнение несжимаемости (2) автоматически выполняется.

Давление также будем представлять в виде линейной формы:

(4)
$P = {{P}_{0}}\left( z \right) + {{P}_{1}}\left( z \right)x + {{P}_{2}}\left( z \right)y.$

Гидродинамические поля, описываемые формулами (3) и (4), принадлежат классу точных решений Линя–Сидорова–Аристова [23–25]. Заметим, что для переопределенных систем вида (1), (2) выражения (3) и (4) являются простейшим нетривиальным семейством точных решений [17, 18]. В статьях [7, 26–28] указаны способы “размножения” (например, преобразование поворота) решения (3) и (4) для трехмерного течения. В этих же статьях было показано, что при тиражировании простейшего точного решения поле скоростей (3) не приобретает новых физически важных свойств.

Далее изучим течения, которые индуцируются не только силой тяжести, но и неоднородным распределением скоростей на верхней недеформируемой границе слоя $z = h$:

(5)
${{V}_{x}}\left( h \right) = Wcos\varphi + \Omega y,\,\,\,\,{{V}_{y}}\left( h \right) = Wsin\varphi $
и заданием отсчетного значения давления и его горизонтальных (продольных) градиентов:

(6)
$P\left( h \right) = {{p}_{0}} + {{p}_{1}}x + {{p}_{2}}y.$

На нижней границе $z = 0$ полагаем выполнение традиционного для гидродинамики ньютоновской жидкости условия прилипания:

(7)
${{V}_{x}}\left( 0 \right) = 0,\,\,\,\,{{V}_{y}}\left( 0 \right) = 0.$

Краевая задача (1), (2) и (5)–(7) описывает неоднородное течение типа Куэтта–Пуазейля–Нуссельта. В случае если рассматривается безградиентное течение, то его можно классифицировать как неоднородное течение Куэтта–Нуссельта, в противном случае будет изучаться неоднородное течение Пуазейля–Нуссельта. Далее все типы течений будут проанализированы.

ТОЧНОЕ РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ

После подстановки выражений (3), (4) в систему уравнений (1), (2) и проведения элементарных преобразований придем к системе обыкновенных дифференциальных уравнений, производная в которых берется по переменной z:

(8)

В виду независимости пространственных переменных x и y, первое и третье уравнения в (8) распадаются на несколько уравнений:

(9)
(10)
$P_{0}^{'} = - gcos\alpha ,\,\,\,\,P_{1}^{'} = 0,\,\,\,\,P_{2}^{'} = 0.$

Заметим, что первые два уравнения системы (9) и уравнения системы (10) являются изолированными, поскольку их решение может быть найдено вне зависимости от решений других уравнений:

(11)
$\begin{gathered} {{P}_{0}} = - gcos\alpha z + {{c}_{0}},\,\,\,\,{{P}_{1}} = {\text{const}}, \\ {{P}_{2}} = {\text{const,}} \\ \end{gathered} $
(12)
$u = {{c}_{1}}z + {{c}_{2}},\,\,\,\,V = \frac{{{{P}_{2}} - gsin\alpha sin\beta }}{{2\nu }}{{z}^{2}} + {{c}_{3}}z + {{c}_{4}}.$

Точное решение оставшегося (третьего) уравнения системы (9) легко получается интегрированием после подстановки выражений (11), (12):

(13)
$\begin{gathered} U = \frac{{\left( {{{P}_{2}} - gsin\alpha sin\beta } \right){{c}_{1}}}}{{40{{\nu }^{2}}}}{{z}^{5}} + \\ + \,\,\frac{{{{P}_{2}} - gsin\alpha sin\beta + 2\nu {{c}_{1}}{{c}_{3}}}}{{24{{\nu }^{2}}}}{{z}^{4}} + \frac{{\left( {{{c}_{1}}{{c}_{4}} + {{c}_{3}}{{c}_{2}}} \right)}}{{6\nu }}{{z}^{3}} + \\ + \,\,\frac{{\left( {{{c}_{2}}{{c}_{4}} + \nu \left( {{{P}_{1}} - gsin\alpha cos\beta } \right)} \right)}}{{2\nu }}{{z}^{2}} + {{c}_{5}}z + {{c}_{6}}. \\ \end{gathered} $

Постоянные интегрирования ${{c}_{i}}$ в общем решении (11)–(13) определяются из краевых условий (5)–(7), которые согласно формулам (3) и (4) можно переписать в виде:

(14)
$\begin{gathered} U\left( 0 \right) = u\left( 0 \right) = V\left( 0 \right) = 0,\,\,\,\,{{P}_{0}}\left( h \right) = {{p}_{0}}, \\ {{P}_{1}}\left( h \right) = {{p}_{1}},\,\,\,\,{{P}_{2}}\left( h \right) = {{p}_{2}}, \\ U\left( h \right) = Wcos\varphi ,\,\,\,\,u\left( h \right) = \Omega ,\,\,\,V\left( h \right) = Wsin\varphi {\kern 1pt} . \\ \end{gathered} $

Частное решение (11), (12), отвечающее условиям (14), имеет вид:

(15)
$\begin{gathered} u = \Omega Z, \\ V = \left[ {Wsin\varphi - \frac{{{{h}^{2}}\left( {sin\alpha sin\beta g - {{p}_{2}}} \right)}}{{2\nu }}\left( { - 1 + Z} \right)} \right]Z, \\ U = Z\left[ {Wcos\varphi + {{h}^{2}}\frac{{sin\alpha cos\beta g - {{p}_{1}}}}{{2\nu }}\left( {1 - Z} \right)} \right. + \\ + \,\,\frac{{{{h}^{2}}\Omega Wsin\varphi }}{{12\nu }}\left( { - 1 + {{Z}^{3}}} \right) + \\ + \,\,\left. {{{h}^{4}}\Omega \frac{{sin\alpha sin\beta \Omega - {{p}_{2}}}}{{120{{\nu }^{2}}}}\left( { - 2 + 5{{Z}^{3}} - 3{{Z}^{4}}} \right)} \right], \\ {{P}_{0}} = {{p}_{0}} - ghcos\alpha \left( {Z - 1} \right). \\ \end{gathered} $

В полиномиальных выражениях (15) введена безразмерная координата $Z = {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}$ для единообразия описания слоев разной толщины.

АНАЛИЗ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ

Проанализируем поле скоростей (15). Заметим, что функция $ - u$ является вертикальной компонентой завихренности жидкости:

${{\Omega }_{z}} = {{\left( {rotV} \right)}_{z}} = \frac{{\partial {{V}_{y}}}}{{\partial x}} - \frac{{\partial {{V}_{x}}}}{{\partial y}} = - u.$

Таким образом, формулы (15) описывают течение жидкости с вертикальной закруткой без приложения силы Кориолиса. Согласно найденному точному решению, вихрь вокруг оси Oz не меняет в слое своего направления.

Поток жидкости, движущейся вдоль оси Oy, описывается профилем Куэтта–Пуазейля, который может один раз сменить направление, если полином

$Wsin\varphi - \frac{{{{h}^{2}}\left( {sin\alpha sin\beta g - {{p}_{2}}} \right)}}{{2\nu }}\left( { - 1 + Z} \right)$
имеет корень внутри интервала $\left( {0,1} \right)$ (рис. 2). Последнее имеет место, если выполнено неравенство:

$Wsin\varphi \left[ {Wsin\varphi + \frac{{{{h}^{2}}\left( {sin\alpha sin\beta g - {{p}_{2}}} \right)}}{{2\nu }}} \right] < 0.$
Рис. 2.

Профиль скорости V при наличии противотечения.

Если для горизонтального градиента давления выполняется равенство ${{p}_{2}} = sin\alpha sin\beta g$, то скорость ${{V}_{y}} = V = Wsin\varphi Z$ описывается профилем Куэтта. Таким образом, существует комбинация углов, при которой градиентное течение жидкости трансформируется в слоистое.

Наибольший интерес представляет исследование фоновой скорости U, поскольку отвечающий ей полином имеет наибольшую (пятую) степень. Скорость U определяется линейной суперпозицией нескольких потоков. Если положить в (15) $\alpha = \beta = 0$ и ${{p}_{1}} = {{p}_{2}} = 0$, то эти формулы описывают пространственно неоднородное течение Куэтта

${{V}_{x}} = Z\left[ {Wcos\varphi + \frac{{{{h}^{2}}\Omega Wsin\varphi }}{{12\nu }}\left( { - 1 + {{Z}^{3}}} \right)} \right] + \Omega Zy,$
изученное в [17, 18]. Это течение характеризует тем, что в жидкости регистрируются противотечения. Поле скорости стратифицируется на два встречных потока, которые контактируют по границе, параболической формы [17, 18, 29]. Если в качестве вторичных движений учитывать градиентные потоки в горизонтальном слое жидкости, то соответствующие неоднородные течения Пуазейля были рассмотрены в статьях [29]. В этих работах было показано, что учет горизонтальных градиентов давления может привести к расслоению поля скорости на три зоны, существование которых определяется двумя нулевыми значениями полинома

$\begin{gathered} U = Z\left[ {Wcos\varphi - \frac{{{{p}_{1}}{{h}^{2}}}}{{2\nu }}\left( {1 - Z} \right) + \frac{{{{h}^{2}}\Omega Wsin\varphi }}{{12\nu }}} \right. \times \\ \times \,\,\left. {\left( { - 1 + {{Z}^{3}}} \right) - \frac{{{{p}_{2}}{{h}^{4}}\Omega }}{{120{{\nu }^{2}}}}\left( { - 2 + 5{{Z}^{3}} - 3{{Z}^{4}}} \right)} \right]. \\ \end{gathered} $

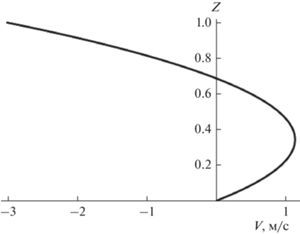
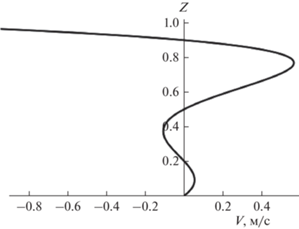
В формуле (15) полиномы $Wcos\varphi z$ и $\frac{{{{h}^{2}}\left( {sin\alpha sin\beta g - {{p}_{2}}} \right)}}{{2\nu }}\left( {1 - Z} \right)Z$ описывают вклад профилей Куэтта и Пуазейля соответственно. Вторичные течения $\frac{{{{h}^{2}}\Omega Wsin\varphi }}{{12\nu }}\left( { - 1 + {{Z}^{3}}} \right)Z$ и ${{h}^{4}}\Omega \frac{{sin\alpha sin\beta \Omega - {{p}_{2}}}}{{120{{\nu }^{2}}}}\left( { - 2 + 5{{Z}^{3}} - 3{{Z}^{4}}} \right)$ обусловлены учетом сил инерции в уравнениях Навье–Стокса (неоднородным распределением скоростей). Среди этих полиномов только многочлен $\left( { - 2 + 5{{Z}^{3}} - 3{{Z}^{4}}} \right)$ принимает экстремальное значение внутри слоя (при $Z = {4 \mathord{\left/ {\vphantom {4 5}} \right. \kern-0em} 5}$). В области монотонности этого полинома, согласно [30], скорость U может иметь до трех нулевых точек. Соответствующий профиль приведен на рис. 3, иллюстрирующем расслоение поля скорости на четыре зоны с чередованием направления течения.

Рис. 3.

Профиль скорости U, иллюстрирующий стратификацию скорости.

Таким образом, учет наклона слоя жидкости приводит к появлению дополнительной точки стратификации (увеличивается количество зон с возвратным течением). Заметим, что суммирование фонового течения с потоком $uy = \Omega Zy$ в выражении для скорости ${{V}_{x}}$ не приводит к появлению дополнительных противотечений.

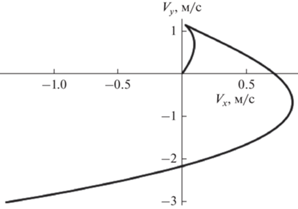
Если изобразить годограф скоростей (рис. 4), то стекающий по наклонной плоскости поток жидкости имеет спиралевидный характер. Такой характер движения обусловлен неоднородным течением жидкости и учетом сил инерции при изучении сдвигового течения жидкости.

Рис. 4.

Годограф вектора скорости.

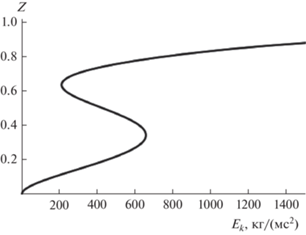
Для иллюстрации сложности топологии течения приведем график удельной кинетической энергии (рис. 5), которая имеет несколько локальных экстремумов, обусловленных стратификацией поля скорости. Варьируя значения параметров задачи, можно добиться того, что единственная нулевая точка скорости Vy будет одной из нулевых точек скорости Vx. Другими словами, будет наблюдаться глобальная застойная точка течения. После прохождения этой точки течение либо повернется в обратную сторону либо сохранит направление, но после прохождения данной точки кинетическая энергия (в виду квадратичной зависимости от компонент проекций скорости) будет нарастать.

Рис. 5.

Удельная кинетическая энергия неоднородного течения.

Опираясь на свойства поля скорости (15) и их интерпретацию (рис. 2, 3), можно заметить, что поле касательных напряжений

$\begin{gathered} {{\tau }_{{xz}}} = h\eta \left[ {Wcos\varphi + \frac{{Wsin\varphi {{h}^{2}}\Omega }}{{12\nu }}\left( {4{{Z}^{3}} - 1} \right)} \right. - \\ - \,\,\frac{{\left( {g\cos \beta \sin \alpha - {{P}_{1}}} \right){{h}^{2}}}}{{2\nu }}\left( { - 1 + 2Z} \right) - \\ \left. { - \,\,\frac{{\left( {g\sin \alpha \sin \beta - {{P}_{2}}} \right){{h}^{4}}\Omega }}{{120{{\nu }^{2}}}}\left( {2 - 20{{Z}^{3}} + 15{{Z}^{4}}} \right)} \right], \\ \end{gathered} $
${{\tau }_{{yz}}} = h\eta \left[ {Wsin\varphi - \frac{{\left( {gsin\alpha sin\beta - {{P}_{2}}} \right){{h}^{2}}}}{{2\nu }}\left( { - 1 + 2Z} \right)} \right]$
также может стратифицироваться. Например, касательное напряжение ${{{{\tau }_{{yz}}}h} \mathord{\left/ {\vphantom {{{{\tau }_{{yz}}}h} \eta }} \right. \kern-0em} \eta }$ ($\eta $ – динамическая вязкость жидкости) может расслаиваться на две зоны (рис. 6, штриховая линия), а касательное напряжение ${{{{\tau }_{{xz}}}h} \mathord{\left/ {\vphantom {{{{\tau }_{{xz}}}h} \eta }} \right. \kern-0em} \eta }$ – на четыре зоны (рис. 6, сплошная линия). Причем каждый раз при переходе из любой такой зоны в соседнюю зону соответствующее напряжение меняет знак (меняет тип с растягивающего на сжимающее или наоборот).

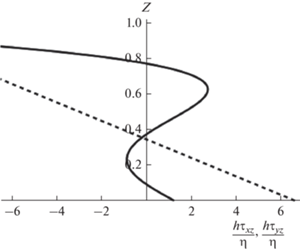
Рис. 6.

Профили касательного напряжения ${{{{\tau }_{{yz}}}h} \mathord{\left/ {\vphantom {{{{\tau }_{{yz}}}h} \eta }} \right. \kern-0em} \eta }$ (штриховая линия) и касательного напряжения ${{{{\tau }_{{xz}}}h} \mathord{\left/ {\vphantom {{{{\tau }_{{xz}}}h} \eta }} \right. \kern-0em} \eta }$ (сплошная линия).

ЗАКЛЮЧЕНИЕ

Найдены точные решения уравнений гидродинамики для описания неоднородного сдвигового течения в поле силы тяжести. Движение жидкости индуцируется распределением скоростей на горизонтальной свободной границе бесконечно протяженного наклонного слоя и заданием горизонтальных градиентов давления. Проведен анализ гидродинамических полей скорости и напряжений. Установлено, что удельная кинетическая энергия имеет немонотонный профиль и принимает нулевой значение в точке, располагающейся внутри слоя. Иными словами, эта точка не соответствует границе, на которой задано условие прилипания, что иллюстрирует застойную точку в потоке и существование противотечений до четырех вторичных потоков. Существование встречных потоков сопровождается сменой знаков касательных напряжений в неоднородном течении Нуссельта–Куэтта–Пуазейля.

ОБОЗНАЧЕНИЯ

${\mathbf{g}}$ вектор ускорения свободного падения, м/с2
$h$ толщина слоя жидкости, м
$P$ отклонение давления от гидростатического, деленное на среднюю плотность жидкости, м2/с2
${{p}_{0}}$, ${{p}_{1}}$, ${{p}_{2}}$ задаваемые на границе области течения значения
$U$, $V$, $u$, ${{P}_{0}}$, ${{P}_{1}}$, ${{P}_{2}}$ функции, входящие в класс решений (3), (4)
${{V}_{x}}$, ${{V}_{y}}$ компоненты вектора скорости течения жидкости, м/с
W значение скорости на верхней границе, м/с
$x$, $y$, $z$ декартовы координаты, м
$Z$ безразмерная координата
$\alpha $ угол, характеризующий наклон плоскости, рад
$\beta $ угол между положительным направлением оси Ox и проекцией вектора ускорения свободного падения на наклонную плоскость, рад
$\eta $ динамическая вязкость, кг/(м с)
$\nu $ кинематическая (молекулярная) вязкость жидкости, м2/с
${{\tau }_{{xz}}}$, ${{\tau }_{{yz}}}$ компоненты тензора напряжений
$\varphi $ угол, определяющий направление течения по отношению к положительному направлению оси Ox, рад
$\Omega $ градиент скорости ${{V}_{x}}$, 1/с
${{\Omega }_{z}}$ вертикальная компонента завихренности, 1/с

Список литературы

  1. Polyanin A.D., Kutepov A.M., Vyazmin A.V., Kazenin D.A. Hydrodynamics, Mass and Heat Transfer in Chemical Engineering. London: Taylor & Francis, 2002.

  2. Стародубцева И.П., Павленко А.Н., Володин О.А., Суртаев А.С. Особенности динамики повторного смачивания перегретой поверхности стекающей пленкой криогенной жидкости // Теплофиз. и аэромех. 2012. Т. 19. № 3. С. 347.

  3. Andreev V.K. On Nusselt’s solution and its generalizations // AIP Conf. Proc. 2021. V. 2448.

  4. Drazin P.G. Introduction to hydrodynamic stability. Cambridge: Cambridge University Press, 2002.

  5. Bird R.B., Stewart W.E., Lightfoot E.N. Transport phenomena. New York: John Wiley and Sons, 1960.

  6. Левич В.Г. Физико-химическая гидродинамика. М.: Физматгиз, 1959. [Levich V.G. Physicochemical hydrodynamics. Englewood Cliffs, N.J., Prentice-Hall, 1962.]

  7. Аристов С.Н., Князев Д.Е., Полянин А.Д. Точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двухпространственных переменных // Теорет. основы хим. технологии. 2009. Т. 43. № 5. С. 547. [Aristov S.N., Knyazev D.V., Polyanin A.D. Exact solutions of the Navier-Stokes equations with the linear dependence of velocity components on two space variables // Theor. Found. Chem. Eng. 2009. V. 43. № 5. P. 642.]

  8. Ershkov S.V., Prosviryakov E.Y., Burmasheva N.V., Christianto V. Towards understanding the algorithms for solving the Navier-Stokes equations // Fluid Dyn. Research. 2021. V. 53. № 4. 044501.

  9. Роньшин Ф.В., Чиннов Е.А., Дементьев Ю.А., Кабов О.А. Мостиковый режим течения в микроканалах // Докл. РАН. Физика, техн. науки. 2021. Т. 499. № 1. С. 43.

  10. Zheng W., Chen T., Sen P., Bai B., Gatapova E.Y., Kabov O.A. Subcooled jet impingement boiling enhanced by porous surface with microcolumn array // J. Enhanced Heat Transfer. 2021. T. 28. № 5. P. 1.

  11. Karchevsky A.L., Cheverda V.V., Marchuk I.V., Gigola T.G., Kabov O.A., Sulyaeva V.S. Heat flux density evaluation in the region of contact line of drop on a sapphire surface using infrared thermography measurements // Microgravity Sci. and Technology. 2021. T. 33. № 4.

  12. Люлин Ю.В., Кабов О.А., Кузнецов Г.В., Феоктистов Д.В., Пономарев К.О. Влияние протяженности межфазной поверхности на интенсивность испарения горизонтального слоя жидкости под действием потока газа // Теплофиз. и аэромех. 2020. Т. 27. № 1. С. 121. [Lyulin Y.V., Kabov O.A., Feoktistov D.V., Kuznetsov G.V., Ponomarev K.O. The effect of the interface length on the evaporation rate of a horizontal liquid layer under a gas flow // Thermophysics and Aeromechanics. 2020. Т. 27. № 1. P. 117.]

  13. Kochkin D.Y., Zaitsev D.V., Kabov O.A. Thermocapillary rupture and contact line dynamics in the heated liquid layers // Interfacial Phenomena and Heat Transfer. 2020. T. 8. № 1. P. 1.

  14. Капица П.Л. Волновое течение тонких слоев вязкой жидкости. Свободный поток // Журн. эксперимент. и техн. физ. 1948. Т. 18. № 1. С. 3.

  15. Пухначев В.В. К теории катящихся волн // Журн. прикл. мех. и техн. физ. 1975. № 5. С. 47. [Pukhnachev V.V. On the theory of rolling waves // J. Applied Mech. and Technical Phys. 1975. V. 16. № 5. Р. 703.]

  16. Benjamin T. Wave formation in laminar flow down an inclined plane // J. Fluid Mech. 1957. V. 2. № 6. P. 554.

  17. Аристов С.Н., Просвиряков Е.Ю. Неоднородные течения Куэтта // Нелин. динам. 2014. Т. 10. № 2. С. 177.

  18. Просвиряков Е.Ю., Спевак Л.Ф. Пространственно неоднородные слоистые течения вязкой несжимаемой жидкости // Теорет. основы хим. технологии. 2018. Т. 52. № 5. С. 483. [Prosviryakov E.Y., Spevak L.F. Layered three-dimensional nonuniform viscous incompressible flows // Theor. Found. Chem. Eng. 2018. Т. 52. № 5. Р. 765.]

  19. Аристов С.Н., Просвиряков Е.Ю. Новый класс точных решений трехмерных уравнений термодиффузии // Теорет. основы хим. технологии. 2016. Т. 50. № 3. С. 294. [Aristov S.N., Prosviryakov E.Y. A new class of exact solutions for three-dimensional thermal diffusion equations // Theor. Found. Chem. Eng. 2016. V. 50. № 3. P. 286.]

  20. Просвиряков Е.Ю. Новый класс точных решений уравнений Навье–Стокса со степенной зависимостью скоростей от двух пространственных координат // Теорет. основы хим. технологии. 2019. Т. 53. № 1. С. 112. [Prosviryakov E.Y. New class of exact solutions of Navier–Stokes equations with exponential dependence of velocity on two spatial coordinates // Theor. Found. Chem. Eng. 2019. V. 53. № 1. P. 10.7.]

  21. Бурмашева Н.В., Просвиряков Е.Ю. Термокапиллярная конвекция вертикально завихренной жидкости // Теорет. основы хим. технологии. 2020. Т. 54. № 1. С. 114. [Burmasheva N.V., Prosviryakov E.Yu. Thermocapillary convection of a vertical swirling liquid // Theor. Found. Chem. Eng. 2020. V. 54. № 1. Р. 230.]

  22. Burmasheva N.V., Prosviryakov E.Yu. Convective layered flows of a vertically whirling viscous incompressible fluid. Velocity field investigation // J. Samara State Technical Univ., Ser. Phys. and Math. Sci. 2019. V. 23. № 2. P. 341.

  23. Lin C.C. Note on a class of exact solutions in magneto-hydrodynamics // Arch. Rational Mech. Anal. 1958. V. 1. P. 391.

  24. Сидоров А.Ф. О двух классах решений уравнений механики жидкости и газа и их связи с теорией бегущих волн // Прикл. мех. и теорет. физ. 1989. № 2. С. 34. [Sidorov A.F. Two classes of solutions of the fluid and gas mechanics equations and their connection to traveling wave theory // J. Appl. Mech. Tech. Phy. 1989. V. 30. № 2. P. 197.]

  25. Аристов С.Н. Вихревые течения в тонких слоях жидкости: дис. … д-р. физ.-мат. наук. Владивосток: ИАПУ, 1990.

  26. Полянин А.Д., Аристов С.Н. Новый метод построения точных решений трехмерных уравнений Навье–Стокса и Эйлера // Теорет. основы хим. технологии. 2011. Т. 45. № 6. С. 696. [Polyanin A.D., Aristov S.N. A new method for constructing exact solutions to three-dimensional Navier-Stokes and Euler equations // Theor. Found. Chem. Eng. 2011. V. 45. № 6. P. 885.]

  27. Aristov S.N., Polyanin A.D. New classes of exact solutions and some transformations of the Navier-Stokes equations // Russian J. Math. Physics. 2010. V. 17. № 1. P. 1.

  28. Аристов С.Н., Полянин А.Д. Точные решения трехмерных нестационарных уравнений Навье–Стокса // Докл. АН. 2009. Т. 427. № 1. С. 35. [Aristov S.N., Polyanin A.D. Exact solutions of unsteady three-dimensional Navier-Stokes equations // Doklady Physics. 2009. V. 54. № 7. P. 316.]

  29. Горулева Л.С., Просвиряков Е.Ю. Неоднородное сдвиговое течение Куэтта–Пуазейля при движении нижней границы горизонтального слоя // Химич. физ. и мезоскопия. 2021. №4. С. 403.

  30. Бурмашева Н.В., Просвиряков Е.Ю. Исследование стратификации гидродинамических полей для слоистых течений вертикально завихренной жидкости // Diagnostics, Resource and Mechanics of materials and structures. 2020. № 4. С. 62.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал