Теоретические основы химической технологии, 2022, T. 56, № 5, стр. 596-606
Применение статистического анализа к расчетам по топохимической кинетике фторидно-аммониевой переработки золошлаковых техногенных отходов ТЭЦ
А. А. Пушкин a, *, В. С. Римкевич a, И. В. Гиренко a
a Институт геологии и природопользования ДВО РАН
г. Благовещенск, Россия
* E-mail: pushkin@ascnet.ru
Поступила в редакцию 25.11.2021
После доработки 02.06.2022
Принята к публикации 14.06.2022
- EDN: AJHNIX
- DOI: 10.31857/S0040357122050165
Аннотация
Статья посвящена вычислению кинетических характеристик химических реакций в технологической цепи фторидно-аммониевой переработки алюмосиликатного сырья с целью извлечения полезных компонентов. Изучаются реакция фторирования золы гидродифторидом аммония и реакция разложения с сублимацией фтораммониевых солей. В работе для расчета кинетических характеристик используется параметрический регрессионный и корреляционный анализы. Расчет кинетики реакции фторирования проводится по степенному закону, а реакции разложения с сублимацией фтораммониевых солей – по уравнению Ерофеева–Авраами. Исследуются дифференциальные и интегральные кинетические кривые обеих реакций, строятся расчетные функции отклика. Построенная линейная регрессионная модель подвергается проверке при помощи пяти статистических гипотез, а именно гипотез об однородности дисперсии воспроизводимости, об адекватности регрессионной модели, о значимости коэффициентов регрессии, о практической значимости функции отклика и о значимости коэффициента корреляции. Для расчетов используется созданная нами программа на языке Visual Basic. Объектом исследования в данной работе являются продукты сжигания углей из золоотвала Благовещенской ТЭЦ.
ВВЕДЕНИЕ
В настоящее время в ИГиП ДВО РАН разрабатывается фторидно-аммониевая (ФА) технология комплексной переработки силикатного и алюмосиликатного сырья, которая, используя твердофазные реакции с гидродифторидом NH4HF2 и фторидом NH4F аммония, позволяет извлекать полезные компоненты из вышеупомянутого сырья при значительном уменьшении материальных и энергетических затрат. Достоинством этой технологии является использование сублимации гексафторосиликата аммония, который образуется после фторирования исходного сырья. Преимуществом химического обогащения с применением сублимации гексафторосиликата аммония является отсутствие образования отходов, что улучшает экологию, уменьшает затраты на хранение и утилизацию отходов [1–4]. Основным сдерживающим фактором в развитии ФА технологии переработки алюмосиликатов являлось отсутствие ее реализации в промышленном масштабе, поэтому эта технология приобретает новый импульс в связи с проблемой импортозамещения. Так, например, UC Rusal до 2023 г. начнет опытно-промышленное производство глинозема из каолиновых руд на Ачинском глиноземном комбинате. А к 2024 г. UC Rusal построит завод мощностью 1 млн т глинозема в год [5].
Большой интерес в РФ вызывают накапливающиеся золошлаковые отходы промышленных предприятий теплоэнергетики. При сжигании углей содержание многих полезных компонентов в золошлаковых отходах возрастает в 5–6 раз: оксидов алюминия до (15–25%), железа до (6–15%), кремния до (40–60%), кроме того, в золе наблюдаются в виде микродобавок около 50 элементов периодической системы. По сложности и многокомпонентности вещественного состава отходы ТЭЦ соответствуют техногенным месторождениям нерудных и рудных полезных ископаемых, находящихся на поверхности и не требующих расходов на добычу из недр, причем их запасы значительны и постоянно увеличиваются [6–9]. В Благовещенске Амурской области, например, в результате сжигания угля в 4-х котлах Благовещенской ТЭЦ ежегодное поступление золы составляет 150 тыс. тонн, а ее общее накопление в золоотвале – 3.5 млн тонн [10, 11].
Изучение кинетики ХР требует математической обработки результатов экспериментов с целью сравнения их с ХР, изучавшимися ранее [12, 13].
Целью данной работы является расчет кинетических характеристик топохимических (ТХ) реакций фторирования гидродифторидом аммония (ГДФА) золы из Золоотвала Благовещенской ТЭЦ (ЗБТЭЦ), и реакций разложения с сублимацией фтораммониевых солей в процессе термообработки. Компьютерный расчет проводится с применением параметрического регрессионного и корреляционного анализа (РКА) [14, 15].
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
ХР фторирования алюмосиликатов является ТХ поскольку среди реагентов (Р) и продуктов (П), обязательно присутствуют твердые вещества [16]. Интегральные кинетические кривые (ИКК) изучаемых ХР монотонно возрастают или убывают в ходе реакции, поэтому в качестве параметрических функций (ПФ) ${{{{\alpha }}}^{i}}\left( t \right)$ выберем степенной (i = 0) и экспоненциальный (i = 2) законы, относящиеся к ТХ уравнениям ускоряющегося типа, а также ТХ уравнение Ерофеева–Авраами (i = 1) сигмоидного типа
(1)
$\left\{ \begin{gathered} {{\alpha }^{0}}\left( t \right) = {{с}_{r}}{{t}^{{{{c}_{s}}}}},\,\,\,\,~i = 0 \hfill \\ {{\alpha }^{1}}\left( t \right) = 1 - \exp ( - {{с}_{r}}{{t}^{{{{c}_{s}}}}}),\,\,\,\,~i = 1 \hfill \\ {{\alpha }^{2}}\left( t \right) = 1 - \exp \left( { - {{с}_{r}}t} \right),\,\,\,\,~i = 2, \hfill \\ \end{gathered} \right.,$Регрессионные модели (РМ), строящиеся на основе нелинейных ПФ, также нелинейны. После проведения замен (2) и (3), аналогичных заменам в [12],
(2)
${{x}^{i}} = \left\{ \begin{gathered} \ln \left( t \right),\,\,\,\,~i = 0,~1 \hfill \\ t,\,\,\,\,~i = 2 \hfill \\ \end{gathered} \right.$(3)
${{y}^{i}} = \left\{ \begin{gathered} \ln \left( {{{\alpha }^{0}}\left( t \right)} \right),\,\,\,\,~i = 0 \hfill \\ \ln \left( { - \ln \left( {1 - {{\alpha }^{1}}\left( t \right)} \right)} \right)~,\,\,\,\,~i = 1,~ \hfill \\ \ln \left( {1 - {{\alpha }^{2}}\left( t \right)} \right),~\,\,\,\,~~i = 2 \hfill \\ \end{gathered} \right.$Точечные оценки коэффициентов ЛРМ $\left( {b_{0}^{*}} \right)_{j}^{i}\,\,~{\text{и}}\,\,\left( {b_{1}^{*}} \right)_{j}^{i}$ рассчитываются методом наименьших квадратов (МНК) по уравнению (4), в котором $x_{{jk}}^{i} = {{\left. {{{x}^{i}}(t)} \right|}_{{t = {{t}_{{jk}}}}}},$ а $y_{{jk}}^{i} = \left. {{{y}^{i}}(t)} \right|_{{t = {{t}_{{jk}}}}}^{{{{\alpha }^{i}} = {{\alpha }_{{jk}}}}}~$, индекс $j~\,\,\left( {j = 0,~1,~ \ldots ,~~m} \right)$ нумерует исследуемые температуры ${{T}_{j}}$, $k\,~\left( {k = 0,~1,~ \ldots ,~{{n}_{j}}} \right)$ – моменты отсчетов времени (МОВ), ${{t}_{{jk}}}~\,\,{\text{и}}\,\,~{{\alpha }_{{jk}}}$ – массивы экспериментальных значений МОВ и степеней превращения вещества (СПВ), в общем случае размерностей $\left( {{{n}_{j}};~m} \right)$, ${{n}_{j}}~и~m~$ – количества МОВ при температуре ${{T}_{j}}$ и количество исследуемых температур ${{T}_{j}}$.
Точечные оценки $(с_{r}^{*})_{j}^{i}$ и $(с_{s}^{*})_{j}^{i}$ кинетических параметров ${{с}_{r}}$ и ${{c}_{s}}$, соответственно, для i-ой ЛРМ при температуре ${{T}_{j}}~$ вычисляются по формулам
(5)
$\left\{ \begin{gathered} (с_{r}^{*})_{j}^{i} = {{({{x}^{i}})}^{{ - 1}}}(b_{0}^{*})_{j}^{i},~\,\,\,\,(с_{s}^{*})_{j}^{i} = (b_{1}^{*})_{j}^{i},~\,\,\,\,~i = 0,~1 \hfill \\ (с_{r}^{*})_{j}^{i} = ~(b_{1}^{*})_{j}^{i},\,\,\,\,i = 2. \hfill \\ \end{gathered} \right.$После подстановки точечных оценок параметров $(с_{r}^{*})_{j}^{i}$ и $(с_{s}^{*})_{j}^{i}$ в i-ую ПФ ${{\alpha }^{i}}\left( t \right)$ получим i-ую функцию отклика (ФО) $\alpha _{j}^{i}\left( t \right)$ при температуре ${{T}_{j}}$
(6)
$\left\{ \begin{gathered} \alpha _{j}^{0}\left( t \right) = (с_{r}^{*})_{j}^{0}{{t}^{{(с_{s}^{*})_{j}^{0}}}},\,\,\,\,~i = 0 \hfill \\ \alpha _{j}^{1}\left( t \right) = 1 - \exp \left( { - (с_{r}^{*})_{j}^{1}{{t}^{{(с_{s}^{*})_{j}^{1}}}}} \right),\,\,\,\,~i = 1 \hfill \\ \alpha _{j}^{2}\left( t \right) = 1 - \exp \left( { - (с_{r}^{*})_{j}^{2}t} \right),\,\,\,\,~i = 2.~~ \hfill \\ \end{gathered} \right..$Энергию активации (ЭА) ${{E}^{i}}$ вычисляют по уравнению Аррениуса для КС [19], которое представимо в виде уравнения ЛРМ без свободного члена (7)
(7)
$ln\left( {\left( {{{c}_{r}}} \right)_{j}^{i}} \right) = - \frac{{{{E}^{i}}}}{R}\left( {\frac{1}{{{{T}_{j}}}}} \right).$Предварительный выбор между ЛРМ при каждой температуре выполняем по минимуму погрешностей аппроксимаций (ПА) [20], которые рассчитываются как относительные средние ошибки аппроксимации
(8)
$\varepsilon _{j}^{i} = \frac{1}{{{{n}_{j}}{\text{\;}}}}~\mathop \sum \limits_{k = 0}^{{{n}_{j}}} \left| {\frac{{{{\alpha }_{{jk}}}\left( {{{t}_{{jk}}}} \right) - {{{\left. {\alpha _{j}^{i}\left( t \right)} \right|}}_{{t = {{t}_{{jk}}}}}}}}{{{{\alpha }_{{jk}}}\left( {{{t}_{{jk}}}} \right)}}} \right|,$Расчет погрешностей коэффициентов ЛРМ, имеющих интервальные оценки, осуществляется в соответствии с [21]
(9)
$\left[ {\left( {b_{0}^{*}} \right)_{j}^{i} - {{t}_{\beta }}\frac{{\sqrt p }}{{\sigma _{\varepsilon }^{*}}}\left( {b_{0}^{*}} \right)_{j}^{i}~;\,\,\left( {b_{0}^{*}} \right)_{j}^{i} + {{t}_{\beta }}\frac{{\sqrt p }}{{\sigma _{\varepsilon }^{*}}}\left( {b_{0}^{*}} \right)_{j}^{i}} \right]$(10)
$\left[ {\left( {b_{1}^{*}} \right)_{j}^{i} - {{t}_{\beta }}\frac{{\sqrt p \sigma _{x}^{*}}}{{\sigma _{\varepsilon }^{*}}}\left( {b_{1}^{*}} \right)_{j}^{i}~;\,\,\left( {b_{1}^{*}} \right)_{j}^{i} + {{t}_{\beta }}\frac{{\sqrt p \sigma _{x}^{*}}}{{\sigma _{\varepsilon }^{*}}}\left( {b_{1}^{*}} \right)_{j}^{i}} \right],$Погрешности кинетических параметров связаны с погрешностями коэффициентов ЛРМ, в частности, погрешности КФ $\left( {{{c}_{s}}} \right)_{j}^{i}$ для i = 0, 1 и погрешности КС $\left( {{{c}_{r}}} \right)_{j}^{i}$ для i = 2 совпадают с погрешностями коэффициентов ЛРМ $\left( {{{b}_{1}}} \right)_{j}^{i}$. Относительные погрешности КС $\left( {{{c}_{r}}} \right)_{j}^{i}$ для i = 0, 1 в силу ее связи со свободным членом $\left( {{{b}_{0}}} \right)_{j}^{i}$ по формуле: $\left( {{{b}_{0}}} \right)_{j}^{i} = {\text{ln}}\left( {\left( {{{c}_{r}}} \right)_{j}^{i}} \right)$, равны абсолютным погрешностям $\left( {{{b}_{0}}} \right)_{j}^{i}$ и вычисляются в соответствии с (9) по формуле
(11)
$\frac{{\Delta \left( {{{c}_{r}}} \right)_{j}^{i}}}{{\left( {{{c}_{r}}} \right)_{j}^{i}}} = {{t}_{\beta }}\frac{{\sqrt p }}{{\sigma _{\varepsilon }^{*}}}.~$После предварительного отбора модели реакции и последующего расчета по этой модели статистических характеристик ХР проводится статистическая проверка гипотез РКА с возможной коррекцией отбора модели, а, следовательно, и соответствующих характеристик.
В первую очередь, проверяется однородность дисперсии воспроизводимости (ДВ) с целью установления допустимости применения РКА. В качестве нулевой выбираем следующую гипотезу Н0: ДВ равны по всему факторному пространству (ФП). Проверка гипотезы выполняется методом Снедекора–Фишера: 1) рассчитываются оценки ДВ ${{\left( {\sigma _{{jk}}^{*}} \right)}^{2}}$ путем проведения ${{l}_{{jk}}}$ измерений в каждой точке ФП $\left( {{{t}_{{jk}}},~{{\alpha }_{{jk}}}} \right)$; 2) строится F-отношение максимальной и минимальной ДВ ${{\left( {f{\text{*}}\left( {{{h}_{1}};{{h}_{2}}} \right)} \right)}_{j}} = {{\left( {\frac{{{{{\left( {\sigma _{{{\text{max}}}}^{*}} \right)}}^{2}}}}{{{{{\left( {\sigma _{{{\text{min}}}}^{*}} \right)}}^{2}}}}} \right)}_{j}}$ по всему ФП при каждой температуре Tj. Критическое значение ${{f}_{\beta }}\left( {{{h}_{1}};{{h}_{2}}} \right)$ выбирается по таблице F-распределения на уровне значимости β и числах степеней свободы (ЧСС) h1 и h2 для ${{\left( {{{{\left( {\sigma _{{{\text{\;max}}}}^{*}} \right)}}^{2}}} \right)}_{j}}$ и ${{\left( {{{{\left( {\sigma _{{{\text{min}}}}^{*}} \right)}}^{2}}} \right)}_{j}}$, соответственно. Нулевая гипотеза принимается, если
(12)
${{\left( {f{\text{*}}\left( {{{h}_{1}};{{h}_{2}}} \right)} \right)}_{j}} < {{f}_{\beta }}\left( {{{h}_{1}};{{h}_{2}}} \right).$Для проверки адекватности ЛРМ при помощи F-отношения Снедекора–Фишера сравниваются остаточная дисперсия (ОД) $(\sigma _{R}^{2})_{j}^{i}$ и общая ДВ $(\sigma _{y}^{2})_{j}^{i}$. ОД вычисляется по формуле $(\sigma _{R}^{2})_{j}^{i} = \frac{{{{{\sum\limits_{k = 1}^{{{n}_{j}}} {{{{\left( {y_{{jk}}^{i} - y_{{jk}}^{{i*}}} \right)}}^{2}}} }}^{2}}}}{p}$, где $\left( {y_{{jk}}^{i} - y_{{jk}}^{{i*}}} \right)$ – отклонения значений обобщенной ординаты $y_{{jk}}^{i}$ в точке ${{t}_{{jk}}}$ от ее ординаты регрессии $y_{{jk}}^{{i*}}$. ДВ – по формуле $\left( {\sigma _{y}^{2}} \right)_{j}^{i} = \frac{{\sum\limits_{k = 0}^{{{n}_{j}}} {\sum\limits_{l = 0}^{{{l}_{{jk}}}} {{{{\left( {y_{{jkl}}^{i} - \overline {y_{{jk}}^{i}} } \right)}}^{2}}} } }}{{{{n}_{j}}\left( {{{l}_{{jk}}} - 1} \right)}}$, где $\left( {y_{{jkl}}^{i} - \overline {y_{{jk}}^{i}} } \right)$ – отклонение экспериментальных значений переменной $y_{{jkl}}^{i}$ от их математических ожиданий $\overline {y_{{jk}}^{i}} $ в каждой точке ФП, индексы j и k нумеруют каждое из ${{l}_{{jk}}}$ измерений в каждой из $\mathop \sum \limits_{j = 0}^m {{n}_{j}}$ точек ФП.
Рассчитываются статистики $\left( {f{\text{*}}\left( {{{p}_{1}},~{{p}_{2}}} \right)} \right)_{j}^{i} = \frac{{\left( {\sigma _{y}^{2}} \right)_{j}^{i}}}{{\left( {\sigma _{R}^{2}} \right)_{j}^{i}}}$, если $\left( {\sigma _{y}^{2}} \right)_{j}^{i} > \left( {\sigma _{R}^{2}} \right)_{j}^{i}$, где p1 и p2 – ЧСС для ОД и ДВ; или $\left( {f{\text{*}}\left( {{{p}_{1}},~{{p}_{2}}} \right)} \right)_{j}^{i} = \frac{{\left( {\sigma _{R}^{2}} \right)_{j}^{i}}}{{\left( {\sigma _{y}^{2}} \right)_{j}^{i}}}$, если $\left( {\sigma _{R}^{2}} \right)_{j}^{i} > \left( {\sigma _{y}^{2}} \right)_{j}^{i}$, где p1 и p2 – ЧСС для ДВ и ОД, соответственно. Нулевая гипотеза Н0: дисперсии равны $\left( {\sigma _{y}^{2}} \right)_{j}^{i} = \left( {\sigma _{R}^{2}} \right)_{j}^{i}$, альтернативная гипотеза Н1: дисперсии не равны $\left( {\sigma _{y}^{2}} \right)_{j}^{i} \ne \left( {\sigma _{R}^{2}} \right)_{j}^{i}$. Далее проверяем
(13)
$\left\{ \begin{gathered} \left( {\sigma _{y}^{2}} \right)_{j}^{i} > \left( {\sigma _{R}^{2}} \right)_{j}^{i}~ \to \left( {f{\text{*}}\left( {{{p}_{1}},~{{p}_{2}}} \right)} \right)_{j}^{i} < {{f}_{\beta }}\left( {{{p}_{1}},~{{p}_{2}}} \right) \to {\text{гипотеза}}~\,\,\,\,{{H}_{0}}~\,\,\,\,{\text{не\;отклоняется}}, \hfill \\ \left( {\sigma _{R}^{2}} \right)_{j}^{i} > \left( {\sigma _{y}^{2}} \right)_{j}^{i}~ \to \left( {f{\text{*}}\left( {{{p}_{1}},~{{p}_{2}}} \right)} \right)_{j}^{i} > {{f}_{\beta }}\left( {{{p}_{1}},~{{p}_{2}}} \right) \to \,\,~{\text{гипотеза}}\,\,\,\,~{{H}_{1}}\,\,\,\,~{\text{принимается}}, \hfill \\ \end{gathered} \right.$Значимость коэффициентов ЛРМ проверяется с применением t-критерия Стьюдента. Нулевая гипотеза Н0: коэффициент ЛРМ $\left( {{{b}_{{{\gamma }}}}} \right)_{j}^{i} = 0$, (γ = 0, 1). Рассчитывается статистика $t{\text{*}}\left( {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right) = \frac{{\left( {b_{\gamma }^{*}} \right)_{j}^{i}}}{{\sigma {\text{*}}\left[ {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right]}}$, где $\left( {b_{\gamma }^{*}} \right)_{j}^{i}$ и $\sigma {\text{*}}\left[ {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right]$ – ТО $\left( {{{b}_{{{\gamma }}}}} \right)_{j}^{i}$ и его стандартной ошибки $\sigma \left[ {\left( {{{b}_{{{\gamma }}}}} \right)_{j}^{i}} \right]$. Расчетное значение статистики $t{\text{*}}\left( {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right)$ сравнивается с табличным значением ${{t}_{\beta }}$. Коэффициент считается значимым, если
(14)
$t{\text{*}}\left( {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right) \geqslant {{t}_{\beta }}.$ЛРМ имеет практическую ценность, если коэффициент корреляции (КК) и показатель согласованности Стьюдента (ПСС), $\left( {{{r}_{{xy}}}} \right)_{j}^{i} = $ $ = \,\frac{{\sum\limits_{k = 0}^{{{n}_{j}}} {x_{{jk}}^{i}y_{{jk}}^{i}} - ~\frac{1}{{{{n}_{j}}}}\left( {\sum\limits_{k = 0}^{{{n}_{j}}} {x_{{jk}}^{i}} } \right)\left( {\sum\limits_{k = 0}^{{{n}_{j}}} {y_{{jk}}^{i}} } \right)}}{{\sqrt {\left[ {\sum\limits_{k = 0}^{{{n}_{j}}} {{{{\left( {x_{{jk}}^{i}} \right)}}^{2}}} \, - \,\frac{1}{{{{n}_{j}}}}{{{\left( {\sum\limits_{k = 0}^{{{n}_{j}}} {x_{{jk}}^{i}} } \right)}}^{2}}} \right]\left[ {\sum\limits_{k = 0}^{{{n}_{j}}} {{{{\left( {y_{{jk}}^{i}} \right)}}^{2}}} \, - \,\frac{1}{{{{n}_{j}}}}{{{\left( {\sum\limits_{k = 0}^{{{n}_{j}}} {y_{{jk}}^{i}} } \right)}}^{2}}} \right]} }}$ и $~\left( {{{t}_{r}}} \right)_{j}^{i} = \left( {{{r}_{{xy}}}} \right)_{j}^{i}\sqrt {\frac{{{{n}_{j}} - 2}}{{1 - r_{{xy}}^{2}}}} $, соответственно, удовлетворяют неравенствам
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Фторируемым Р для ХР спекания выбрана электромагнитная фракция (ЭФ) золы состава в мас. %: SiO2 – 54.27; Al2O3 – 21.01; Fe3O4 – 7.82; TiO2 – 0.66; CaO – 8.24; MnO – 0.30; MgO – 2.49; Na2O – 0.40; K2O – 1.23; P2O5 – 0.08; SO3 – 0.27; п.п.п. – 2.91 [10]. ЭФ составляет 88.7 мас. % пробы золы из ЗБТЭЦ и характеризуется высоким содержанием глинозема и низким содержанием серы. По данным минералогического анализа, в электромагнитной фракции преобладают прозрачные и полупрозрачные частицы раскристаллизованого пузырчатого стекла силикатного состава и их шлакоподобные агрегаты, присутствуют зерна полевых шпатов и кварца с включениями магнетита и гематита [11]. Исходное сырье перед фторированием истиралось в планетарной мельнице “Пульверизетте 5” до размеров частиц менее 25 мкм, в которой происходило постоянное перемешивание мелющихся частиц и мелющих тел, в результате чего воздействие мелющих тел на частицы, находящиеся в равных условиях и испытывающих большое количество ударов, усредняется, и частицы приобретают приблизительно форму сфер с диаметром около 25 мкм.
В качестве фторирующего Р использовался ГДФА (NH4HF2) марки ч. д. а., который при комнатной температуре менее агрессивен и более экологичен, например, чем фтор или плавиковая кислота. Но при нагревании выше точки плавления (126.8°С), становится химически активным реагентом.
Р, взятые в заданных соотношениях, растирали, перемешивали и помещали в фарфоровые чашки. ФА обработку осуществляли внутри сушильного шкафа SNOL 20/300, поддерживающего температуру с точностью 0.1%, неравномерность температуры внутри сушильного шкафа составляла менее 4%.
Спекание происходило при фторирования золы ГДФА и продолжалось в течение 0.5–4.5 ч при температурах 50–200°С. В ходе ХР образовывался по данным рентгенофазового анализа порошок спекшихся гексафторосиликата (ГФСА) (SiO2 + 3NH4HF2 = (NH4)2SiF6 + NH3↑ + 2H2O↑), гексафтороалюмината (ГФАА) (Аl2O3 + 6NH4HF2 = = 2(NH4)3AlF6 + 3H2O↑) и небольшого количества гексафтортитаната (ГФТА) (TiO2 + 3NH4HF2 = = (NH4)2TiF6 + 2H2O↑ + NH3↑) аммония, минерала (Ca, Y)F2 (СaO + NH4HF2 = CaF2 + H2O↑ + + NH3↑), гематита (4Fe3O4 + O2 = 6Fe2O3) и незначительного количества фторидов щелочных металлов NaF и KF (Na2O + NH4HF2 = 2NaF + + H2O↑ + NH3↑ и K2O + NH4HF2 = 2KF + H2O↑ + + NH3↑), а также улетучивались аммиак (NH3), фтороводород (HF) и пары воды (H2O).
Термообработка получившегося после фторирования спека при температурах 350–550°С с разложением ГФАА (2(NH4)3AlF6 = 2AlF3 + + 6NH3↑ + 6HF↑) и сублимацией ГФСА ((NH4)2SiF6 = (NH4)2SiF6↑) и незначительного количества ГФТА ((NH4)2TiF6 = (NH4)2TiF6↑) проводилась в платиновых тиглях. В работе [22] ГФТА и ГФСА разделялись пирогидролизом при температуре при температурах 500–800°С в течение 3–5 ч. Сублимирующий ГФСА оседал на стенках сосуда при температурах 270–25°С, а улетучивающиеся после разложения ГФАА аммиак и фтороводород отводились через отверстие в крышке при помощи трубки в сосуд с водой. Оставшийся после улетучивания твердый осадок представлял собой смесь фторида алюминия, гематита и минерала (Ca, Y)F2 и незначительного количества фторидов щелочных металлов (NaF и KF). Этот твердый осадок после выщелачивания водой с растворением щелочных фторидов, подвергался выщелачиванию соляной кислотой при T = 50–60°С и выдержке 3 ч. В результате образовывался раствор хлорида железа FeCl3 (Fe2O3 + 6HCl = 2FeCl3 + 3H2O), который отделялся фильтрованием от нерастворимого в соляной кислоте осадка фторидов алюминия и кальция. Хлорид железа гидролизовался под действием аммиачной воды (25 мас. % NH3) при T = = 80°C и pH = 7–8 с образованием красного железооксидного пигмента Fe2O3 (2FeCl3 + + 6NH4OH = Fe2O3↓ + 6NH4Cl + 3H2O), который выпадал в осадок, выдерживался при заданной температуре не менее 1 ч и отделялся путем фильтрования от хлорида аммония NH4Cl.
Осадок фторидов кальция и алюминия подвергался фторированию ГДФА при температуре 180°С, после чего образовавшийся растворимый ГФАА отделялся водой от непрореагировавшего обогащенного редкими и другими элементами минерала-концентратора (Ca, Y)F2. Раствор ГФАА гидролизовался аммиачной водой с образованием гидроксида алюминия ((NH4)3AlF6 + + 3NH4ОН = Al(OH)3↓ + 6NH4F), из которого кальцинацией получался глинозем (2Al(OH)3 = = Al2O3 + 3H2O). Осадок ГФСА в конденсаторе гидролизовался аммиачной водой с образованием мелкодисперсного аморфного кремнезема ((NH4)2SiF6 + 4NH4ОН = SiO2↓ + 6NH4F + + 2H2O).
В процессе комплексной переработки 100 кг золы на выходе получались 54.26 кг аморфного кремнезема, 21.01 глинозема, 8.09 кг красного железооксидного пигмента, а также 11.47 кг обогащенного редкими элементами минерала-концентратора (Ca, Y)F2 [11].
Исходное сырье, промежуточные фазы и конечные продукты исследовали химическим, рентгенофазовым, спектральным и другими видами анализов. Химический анализ на содержание элементов (Si, Al, Fe, Na, K и др.) в пробах проводили на спектрометре BRUKER S4 PIONEER. Концентрацию фтора определяли ионометрическим методом, аммиака – титрованием. Для рентгенофазового анализа применяли рентгеновский дифрактометр MAXIMA XRD-700 (CuKα-излучение, λ = 1.5406 Å) с базой данных для фазового анализа ICDD PDF 2008. Эмиссионный спектральный анализ микропримесей выполняли на спектрографе СТЭ-1 со скрещенной дисперсией со стандартным определением 44 элементов. Измерение содержания редких элементов осуществляли методом icp-ms на масс-спектрометре ICP-MS Elan 9000.
В ХР фторирования при исследуемой температуре Т в момент времени t измерялись убыли масс навесок. На основании данных химического анализа на элементы данные по убыли массы навесок m пересчитывались в СПВ по формуле $\alpha ~\,\, = ~\,\,\left( {{m \mathord{\left/ {\vphantom {m {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}}} \right) \times 100\% $ (${{m}_{0}}$ – теоретически возможное количество вещества). Зависимость СПВ $\alpha $ от МОВ t изображена в виде ИКК на рис. 1а. Из рисунка видно, что реакция при трех нижних температурах продолжалась в течение всего эксперимента, а при верхней – прекращалась к 2 часам. Такое различие между длительностями реакции при различных температурах согласуется с соотношением значений констант скоростей в табл. 1: скорость реакции при верхней температуре примерно в 5 раз выше, чем при нижней.
Рис. 1.
Графики экспериментальных кинетических кривых для реакции спекания образца золы с ГДФА при температурах: 1 – 50°C, 2 – 100°C, 3 – 150°C, 4 – 200°C: (a) интегральная кинетическая кривая α(t); (б) дифференциальная кинетическая кривая ∆α(t)/∆t. Штриховой линией показан теоретический уровень степени превращения выделившегося аммиака.
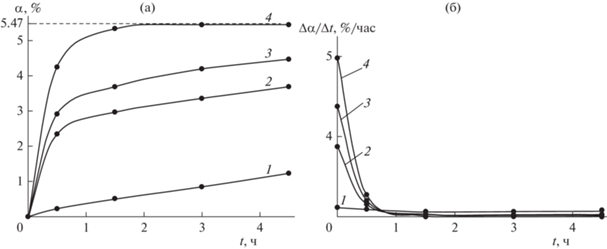
Таблица 1.
Кинетические и статистические характеристики, полученные в результате предварительного отбора по величине погрешностей аппроксимаций, для реакции спекания золы из ЗБТЭЦ с ГДФА
| Температура ${{T}_{j}}$, °С | 50 | 100 | 150 | 200 |
| Константа скорости $\left( {{{c}_{r}}} \right)_{j}^{i}$, мин–1 | 0.000804 | 0,002356 | 0.003131 | 0.003787 |
| Коэффициент формы $\left( {{{c}_{s}}} \right)_{j}^{i}$ | 0.76 | 0.16 | 0.39 | 0.48 |
| Погрешность аппроксимации $\varepsilon _{j}^{i}$ | 3 | 4 | 3 | 3 |
| Энергия активации ${{E}^{i}}$, кДж/моль | 13 | 13 | 13 | 13 |
| Уравнение реакции ${{\alpha }^{i}}\left( t \right)$ | Степ | Степ | Степ | Степ |
| Зона реакции | Д | Д | Д | Д |
| Статистика Фишера для однородности дисперсии $f_{j}^{*}\left( {{{h}_{1}};{{h}_{2}}} \right)$ | 4.74 | 4.21 | 1.64 | 3.75 |
| Коэффициент Фишера для однородности дисперсии ${{f}_{\beta }}\left( {{{h}_{1}};{{h}_{2}}} \right)$ | 19.37 | 19,37 | 19.37 | 19.37 |
| Статистика Фишера для адекватности регрессии $\left( {f{\text{*}}} \right)_{j}^{i}\left( {{{p}_{1}},~{{p}_{2}}} \right)$ | 2.0 | 3,59 | 2.9 | 3.72 |
| Коэффициент Фишера для адекватности регрессии ${{f}_{\beta }}$(${{p}_{1}};{{p}_{2}}$) | 4.46 | 4,46 | 4.46 | 4.46 |
| Статистика для свободного члена $t{\text{*}}\left( {{{b}_{0}}} \right)_{j}^{i}~$ | 94.28 | 25.36 | 12.83 | 1,12 |
| Статистика для углового коэффициента $t{\text{*}}~\left( {{{b}_{1}}} \right)_{j}^{i}$ | 39.19 | 7.66 | 12.19 | 4,4 |
| Коэффициент корреляции $\left( {{{r}_{{xy}}}} \right)_{j}^{i}$ | 1 | 0.97 | 0.99 | 0.91 |
| Показатель согласованности Стьюдента $\left( {{{t}_{r}}} \right)_{j}^{i}$ | 27.71 | 5.42 | 9,25 | 3.11 |
| Коэффициент Стьюдента (${{t}_{\beta }}$) | 4.3 | 4.3 | 4.3 | 4.3 |
Дифференциальные кинетические кривые (ДКК) изучаемой ХР спекания изображены на рис. 1б, из которого видно, что ДКК 2, 3 и 4, начинаются с высоких значений скоростей реакции, обусловленных большими количествами контактирующих частиц Р в начале реакции, но в течение получаса скорость реакции уменьшается из-за израсходования атомов Р: ДКК убывают на порядок величины. Но вследствие увеличения площади реакционной зоны [23] реакция не прекращается: ИКК 2, 3 и 4 только уменьшают свой наклон. К моменту 2 ч от начала опыта ДКК 4 обращается в 0, а ДКК 2 и 3 сохраняют неравные нулю значения до конца реакции, ИКК 2 и 3 не выходят на плато до конца реакции. ХР при ИТ 2, 3 и 4, вначале протекающие за счет химического взаимодействия между частицами, замедляются по мере уменьшения числа частиц Р. В результате увеличивается среднее расстояние между частицами и увеличивается роль диффузии частиц Р через обедненные частицами области. Низкие значения скоростей реакции на протяжении длительного времени (рис. 1б) говорит о протекании реакции в зоне диффузии [23], что подтверждается значениями энергии активации в табл. 1.
Термическая обработка в восстановительных условиях при температурах 350–550°С полученного порошкообразного спека приводит к образованию нелетучего остатка, который состоит по данным рентгенофазового анализа из фторида алюминия AlF3, минерала (Ca, Y)F2 и гематита Fe2O3, а также небольшого количества щелочных фторидов, и улетучивающихся аммиака, фтороводорода, водяного пара и оседающего на стенках конденсатора сублимирующего ГФСА. В ХР разложения с сублимацией при исследуемой температуре Т в момент времени t измерялись убыли массы навесок аналогично тому, как это делалось в экспериментах по фторированию и пересчет убылей массы навесок в СПВ проводился по той же формуле.
На рис. 2а показаны ИКК реакции разложения с сублимацией фтораммониевых солей, полученные по данным убыли массы нелетучего остатка в процессе термообработки в восстановительных условиях, а на рис. 2б показаны соответствующие ДКК. Из рис. 2а видно, что реакция не прекращается при нижней температуре до конца эксперимента, тогда как при верхней протекает в течение 20–25 мин. Кривая 1 на рис. 2б только к концу эксперимента незначительно убывает, что говорит о малой скорости реакции, в то время как кривая 3 на рис. 2б быстро (в течение 20–25 мин) убывает практически до нуля, что свидетельствует об израсходовании реагирующих частиц. Из табл. 2 следует, что реакция разложения с сублимацией при всех температурах протекает в переходной зоне [24, 25].
Рис. 2.
Графики экспериментальных кинетических кривых улетучивания для термообработки порошкообразного спека в восстановительных условиях при температурах: 1 – 350°C, 2 – 450°C, 3 – 550°C: (a) интегральная кинетическая кривая α(t); (б) дифференциальная кинетическая кривая ∆α(t)/∆t.
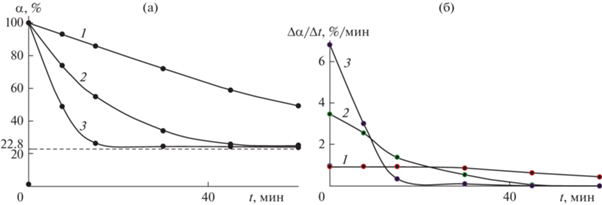
Таблица 2.
Кинетические и статистические характеристики, полученные в результате предварительного отбора по величине погрешностей аппроксимаций, для процесса термообработки спека золы из ЗБТЭЦ с ГДФА
| Температура ${{T}_{j}}$, °С | 350 | 450 | 550 |
| Константа скорости $\left( {{{c}_{r}}} \right)_{j}^{i}$, мин–1 | 0.017579 | 0.05915 | 0.071877 |
| Коэффициент формы $\left( {{{c}_{s}}} \right)_{j}^{i}$ | 0.97 | 0.51 | 0.19 |
| Погрешность аппроксимации $\varepsilon _{j}^{i}$ | 2 | 2 | 4 |
| Энергия активации ${{E}^{i}}$, кДж/моль | 30.8 | 30.8 | 30.8 |
| Уравнение реакции ${{\alpha }^{i}}\left( t \right)$ | ЕА | ЕА | ЕА |
| Зона реакции | П | П | П |
| Статистика Фишера для однородности дисперсии $f_{j}^{*}\left( {{{h}_{1}};{{h}_{2}}} \right)$ | 2.91 | 7.38 | 12.14 |
| Коэффициент Фишера для однородности дисперсии ${{f}_{\beta }}\left( {{{h}_{1}};{{h}_{2}}} \right)$ | 19 | 19 | 19 |
| Статистика Фишера для адекватности регрессии $\left( {f{\text{*}}} \right)_{j}^{i}\left( {{{p}_{1}},~{{p}_{2}}} \right)$ | 5.42 | 2.42 | 1.49 |
| Коэффициент Фишера для адекватности регрессии ${{f}_{\beta }}$(${{p}_{1}};{{p}_{2}}$) | 10 | 10 | 10 |
| Статистика для свободного члена $t{\text{*}}\left( {{{b}_{0}}} \right)_{j}^{i}~$ | 4.05 | 34.27 | 20.65 |
| Статистика для углового коэффициента $t{\text{*}}~\left( {{{b}_{1}}} \right)_{j}^{i}$ | 67.08 | 20.61 | 6.61 |
| Коэффициент корреляции $\left( {{{r}_{{xy}}}} \right)_{j}^{i}$ | 1 | 0.99 | 0.95 |
| Показатель согласованности Стьюдента $\left( {{{t}_{r}}} \right)_{j}^{i}$ | 51.96 | 15.96 | 5.12 |
| Коэффициент Стьюдента (${{t}_{\beta }}$) | 3.18 | 3.18 | 3.18 |
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Как отмечалось выше, при математическом моделировании химических реакций нами по форме кинетических кривых выбраны три параметрических функции: степенной и экспоненциальный законы и уравнение Ерофеева–Авраами. Все эти уравнения получены, исходя из предположений о правильной форме зерен исходного вещества и сферической формы зародышей [16]. Как показывают данные минералогического анализа с учетом процедуры подготовки сырья истиранием в планетарной мельнице, приблизительно эти условия выполняются. Дополнительно следует обсудить уравнение Ерофеева–Авраами. Следует заметить, что уравнение Ерофеева–Авраами, в силу того, что при замене переменных в нем возникает двойной логарифм, сглаживающий многие отклонения экспериментальных точек от линейной регрессии, обладает “широкой описательной способностью”. Поэтому его применение должно быть осторожным и, в частности, недопустимо в случае противоречия с его физическим смыслом, например, при наличии диффузионного торможения или в случае ускорения реакции в результате образования жидкой фазы [16]. В нашем случае, в реакции спекания золы с ГДФА фторирующий реагент ГДФА плавится при третьей и четвертой температурах. Поскольку в эксперименте при двух верхних температурах присутствовала жидкая фаза применение уравнения Ерофеева–Авраами для реакции спекания недопустимо при этих температурах. Кроме того, при расчете по t-критерию Стьюдента статистика для свободного члена при 100°С для уравнения Ерофеева–Авраами меньше коэффициента Стьюдента $t{\text{*}}\left( {{{b}_{0}}} \right)_{1}^{1} = 0.25 < {{t}_{\beta }} = ~\,\,4.3~$, т.е. свободный член незначим (для сравнения $t{\text{*}}\left( {{{b}_{0}}} \right)_{1}^{0} = 25.36 > {{t}_{\beta }} = ~\,\,4.3$), а при 50°С погрешность аппроксимации меньше для степенного закона ($\varepsilon _{0}^{0} = 3\% < \varepsilon _{0}^{1} = 4\% $). Для реакции разложения с сублимацией фтораммониевых солей применение уравнения Ерофеева–Авраами возможно и будет конкурировать с другими параметрическими функциями по величине погрешностей аппроксимации и значениям статистических характеристик.
Математическая обработка данных по кинетике исследуемой реакции проводилась с использованием разрабатываемой нами расчетной программы на языке Visual Basic [26], являющейся одним из результатов исследования.
В программе используются два типа координат: естественные относительные двумерные координаты Time(j, k) и Alpha(j, k), получаемые нормировкой МОВ ${{t}_{{jk}}}$ и СПВ ${{\alpha }_{{jk}}}$, и обобщенные трехмерные переменные abs(i, j, k) и ord(i, j, k), обозначаемые в работе ${{x}^{i}}$ и ${{y}^{i}}$, соответственно, и получаемые по формулам (2) и (3) из естественных относительных координат и параметрических функций ${{\alpha }^{i}}\left( t \right)$ и принимающие значения $x_{{jk}}^{i}$ и $y_{{jk}}^{i}$.
В программе вычисляются точечные оценки коэффициентов ЛРМ в уравнении (4) по МНК. Затем по формулам (5) вычисляем точечные оценки КС $\left( {с_{r}^{*}} \right)_{j}^{i}$ и КФ $\left( {с_{s}^{*}} \right)_{j}^{i}$, по формулам (6) – ФО $\alpha _{j}^{i}$, а по уравнению (7) – ЭА ${{E}^{i}}$ для каждого из законов. Выбор закона протекания реакции (ее ФО $\alpha _{j}^{i}$) при исследуемой температуре ${{T}_{j}}$ происходит по минимуму ПА, вычисляемых по формуле (8) для каждой ФО $\alpha _{j}^{i}$ при каждой исследуемой температуре ${{T}_{j}}$.
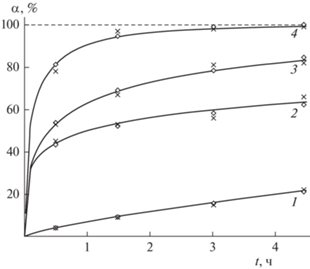
Расчет показал, что реакция фторирования образца золы ГДФА при всех температурах протекает по степенному закону с энергией активации 13 кДж/моль (табл. 1). Зона реакции – диффузионная [27] (13 < 20 кДж/моль). Выбранные ПФ с параметрами $\left( {{{c}_{r}}} \right)_{{{{j}_{0}}}}^{{{{i}_{0}}}}$ и $\left( {{{c}_{s}}} \right)_{{{{j}_{0}}}}^{{{{i}_{0}}}}$ (строки 2 и 3 в таблице 1) для каждой температуры представляют собой функции отклика $\alpha _{{{{j}_{0}}}}^{{{{i}_{0}}}}\left( t \right)$ (формула (6)) для данной температуры, которые показаны на рис. 3. Из рисунка видно хорошее соответствие между экспериментальными и теоретическими значениями.
Рис. 3.
Графики расчетных функций отклика α(t) для реакции спекания образца золы с ГДФА. Температуры: 1 – 50°C, 2 – 100°C, 3 – 150°C, 4 – 200°C. Ромбиками показаны значения точек, рассчитанные по степенному закону, крестиками экспериментальные точки. Штриховой линией показан теоретический уровень степени превращения выделившегося аммиака, соответствующий теоретическим 5.47% нелетучего остатка.
Проверка достоверности полученных предварительных результатов расчета осуществляется путем сравнения значений соответствующих статистик для каждой из 5 статистических гипотез: для первых двух гипотез – статистик из строк 8 и 10 табл. 1 с коэффициентами Фишера из строк 9 и 11 той же таблицы по формулам (12) и (13) – первые две гипотезы достоверны. Сравнение по формулам (15) значений КК и ПСС из 14-ой и 15-ой строк с числом 0.7 и коэффициентом Стьюдента из строки 16, соответственно, означает высокую степень связи между входными и выходными данными и статистическую значимость коэффициента корреляции.
Сравнение статистик для коэффициентов ЛРМ из строк 12 и 13 с коэффициентом Стьюдента из строки 16 по формуле (14) показывает, что все коэффициенты значимы за исключением свободного члена при четвертой температуре (1.12 < 4.3). Значения коэффициента корреляции из 14 строки говорят о наличии корреляции между входными и выходными данными, а значения показателя согласованности в 15 строке о достоверности коэффициента корреляции, во всех случаях кроме четвертой температуры ($\left( {{{t}_{r}}} \right)_{3}^{0} = 3.1 < {{t}_{\beta }} = ~\,\,4.3~$, хотя значение показателя согласованности и близко к значению коэффициента корреляции. Значения статистических характеристик, рассчитанных по экспоненциальному закону не лучше, при этом погрешности аппроксимаций больше. Поэтому продолжаем считать реакцию при 200°С протекающей по степенному закону.
Расчет реакции разложения с сублимацией фтораммониевых солей показал, что она протекает при температурах 350–550°С по уравнению Ерофеева–Авраами с энергией активации 30.8 кДж/моль в переходной зоне [27].
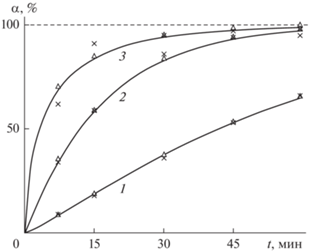
Константы скоростей и коэффициенты формы кинетических кривых указаны в табл. 2. Значения статистических характеристик в таблице 2 показывают, что для данной реакции статистические гипотезы об однородности дисперсии $f_{j}^{*}\left( {{{h}_{1}};{{h}_{2}}} \right) < {{f}_{\beta }}\left( {{{h}_{1}};{{h}_{2}}} \right) = 19$ и об адекватности регрессионной модели $\left( {f{\text{*}}} \right)_{j}^{1}\left( {{{p}_{1}},~{{p}_{2}}} \right) < {{f}_{\beta }}\left( {{{p}_{1}};{{p}_{2}}} \right) = 10$ достоверны при любой температуре, статистики для свободного члена $t{\text{*}}\left( {{{b}_{0}}} \right)_{j}^{1}~$ и для углового коэффициента $t{\text{*}}\left( {{{b}_{1}}} \right)_{j}^{1}~$ превышают при любой температуре значения коэффициента Стьюдента ${{t}_{\beta }} = \,\,~4.3$. Значения коэффициента корреляции близки к 1, что говорит о хорошей корреляции, а значения показателя согласованности Стьюдента $\left( {{{t}_{r}}} \right)_{j}^{1}$ больше, чем коэффициент Стьюдента ${{t}_{\beta }} = \,\,~4.3$ при всех температурах. Функции отклика процесса улетучивания для температур 350–550°С изображены на рис. 4.
Рис. 4.
Графики расчетных функций отклика α(t) для реакции разложения с сублимацией фтораммониевых солей в ходе термообработки в восстановительных условиях при температурах: 1 – 350°C, 2 – 450°C, 3 – 550°C. Крестиками показаны экспериментальные значения, треугольниками – расчетные по уравнению Ерофеева–Авраами. Пунктиром показан теоретический уровень улетучившихся продуктов реакции, соответствующий теоретическим 22.8% нелетучего остатка.
ЗАКЛЮЧЕНИЕ
В работе проведено исследование кинетики топохимических реакций фторирования золы ГДФА и реакции разложения фтораммониевых солей с сублимацией. Изучены экспериментально и теоретически интегральные и дифференциальные кинетические кривые обеих реакций, определены кинетические параметры кривых, зоны протекания обеих реакций, уравнения обеих реакций (степенное для реакции фторирования и Ерофеева–Авраами для реакции разложения с сублимацией) и построены функции отклика в изучаемых температурных интервалах 50–200°С и 350–550°С. В ходе топохимических расчетов проводилась проверка статистических гипотез РКА. Для реакции спекания все проверяемые гипотезы достоверны за исключением реакции при температуре 200°С. При этой температуре оказываются незначимыми свободный член по t-критерию Стьюдента и коэффициент корреляции по значению показателя согласованности Стьюдента. Поскольку применение уравнения Ерофеева–Авраами при этой температуре недопустимо, а экспоненциальный закон показывает не лучшую статистику, по-видимому, потребуется введение в рассмотрение других параметрических функций. Реакция разложения с сублимацией протекает при всех температурах по уравнению Ерофеева–Авраами с кинетическими и статистическими характеристиками из таблицы 2. Проверка статистических гипотез показывает, что гипотезы об однородности дисперсии, об адекватности регрессионной модели выполняются, коэффициенты регрессии и корреляции значимы, коэффициент корреляции близок к 1.
ОБОЗНАЧЕНИЯ
| $\alpha $ | степень превращения вещества |
| ${{{{\alpha }}}^{i}}\left( t \right)$ | i-ая параметрическая функция |
| $\alpha _{j}^{i}\left( t \right)$ | i-ая функция отклика при j-ой температуре |
| ${{\alpha }_{{jk}}}$ | массив значений СПВ при j-ой температуре в k-ый МОВ |
| $\left( {{{b}_{0}}} \right)_{j}^{i}$ | первый коэффициент i-ой ЛРМ при температуре ${{T}_{j}}$ |
| $\left( {b_{0}^{*}} \right)_{j}^{i}$ | точечная оценка первого коэффициента i-ой ЛРМ при ${{T}_{j}}$ |
| $\left( {{{b}_{1}}} \right)_{j}^{i}$ | второй коэффициент i-ой ЛРМ при ${{T}_{j}}$ |
| $\left( {b_{1}^{*}} \right)_{j}^{i}$ | точечная оценка второго коэффициента i-ой ЛРМ при ${{T}_{j}}$ |
| $(b_{\gamma }^{*})_{j}^{i}$ | общее обозначение для $\left( {b_{0}^{*}} \right)_{j}^{i}$ и $\left( {b_{1}^{*}} \right)_{j}^{i}$, $\gamma = 0,~1$ |
| ${{с}_{r}}$ | константа скорости ХР |
| ${{c}_{s}}$ | коэффициент формы кинетической кривой |
| ${{E}^{i}}$ | энергия активации для i-ой ЛРМ |
| ${{\left( {f{\text{*}}\left( {{{h}_{1}};{{h}_{2}}} \right)} \right)}_{j}}$ | статистика Снедекора–Фишера для гипотезы об однородности ДВ при температуре ${{T}_{j}}$ с ЧСС h1 и h2 |
| $\left( {f{\text{*}}\left( {{{p}_{1}},~{{p}_{2}}} \right)} \right)_{j}^{i}$ | статистика Снедекора–Фишера для гипотезы об адекватности i-ой ЛРМ при температуре ${{T}_{j}}$ с ЧСС p1 и p2 |
| ${{f}_{\beta }}\left( {{{h}_{1}},~{{h}_{2}}} \right)$ | коэффициент Фишера для гипотезы об однородности ДВ при температуре ${{T}_{j}}$ с ЧСС h1 и h2 на уровне значимости $\beta $ |
| ${{f}_{\beta }}\left( {{{p}_{1}},~{{p}_{2}}} \right)$ | коэффициент Фишера для гипотезы об адекватности i-ой ЛРМ при температуре ${{T}_{j}}$ с ЧСС p1 и p2 на уровне значимости $\beta $ |
| ${{l}_{{jk}}}$ | количество измерений в точке ФП с МОВ ${{t}_{{jk}}}$ |
| $m$ | количество исследуемых температур |
| ${{m}_{0}}$ | теоретически возможная убыль массы навески |
| ${{m}_{{jk}}}$ | убыль массы навески к МОВ ${{t}_{{jk}}}$ |
| ${{n}_{j}}$ | количество отсчетов времени при j-ой температуре |
| p | число степеней свободы |
| $R$ | универсальная газовая постоянная ($8.31\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {\left( {{\text{моль}}\,\,{\text{К}}} \right)}}} \right. \kern-0em} {\left( {{\text{моль}}\,\,{\text{К}}} \right)}}$) |
| $\left( {{{r}_{{xy}}}} \right)_{j}^{i}$ | коэффициент корреляции для i-ой ЛРМ при j-ой температуре |
| $\sigma _{\varepsilon }^{*}$ | точечная оценка среднеквадратического отклонения экспериментальных значений ординат от ЛРМ |
| ${{\left( {\sigma _{{jk}}^{*}} \right)}^{2}}$ | точечная оценка ДВ в МОВ ${{t}_{{jk}}}$ |
| ${{\left( {\sigma _{{{\text{\;}}{\kern 1pt} {\text{max}}}}^{*}} \right)}^{2}}$ | максимальное значение ДВ при данной температуре |
| ${{\left( {\sigma _{{{\text{\;}}{\kern 1pt} {\text{min}}}}^{*}} \right)}^{2}}$ | минимальное значение ДВ при данной температуре |
| $\left( {\sigma _{y}^{2}} \right)_{j}^{i}$ | дисперсия воспроизводимости, |
| $\left( {\sigma _{R}^{2}} \right)_{j}^{i}$ | дисперсия остаточная. |
| $\sigma \left[ {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right]$ | стандартная ошибка коэффициента $\left( {b_{\gamma }^{*}} \right)_{j}^{i}$ |
| $\sigma {\text{*}}\left[ {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right]$ | ТО стандартной ошибка коэффициента $(b_{\gamma }^{*})_{j}^{i}$ |
| t | текущее время |
| ${{t}_{\beta }}$ | коэффициент Стьюдента |
| ${{t}_{{jk}}}$ | k-ый МОВ при j-ой температуре |
| $\left( {{{t}_{r}}} \right)_{j}^{i}$ | показатель согласованности Стьюдента, |
| $t{\text{*}}\left( {\left( {b_{\gamma }^{*}} \right)_{j}^{i}} \right)$ | статистика для t-критерия Стьюдента |
| ${{T}_{j}}$ | j-ая исследуемая температура |
| $x_{{jk}}^{i}~$ | обобщенная абсцисса |
| $\overline {x_{{jk}}^{i}} $ | среднее значение обобщенной абсциссы |
| $y_{{jk}}^{i}$ | обобщенная ордината |
| $y_{{jk}}^{{i*}}$ | обобщенная ордината линейной регрессии |
| $\overline {y_{{jk}}^{i}} $ | среднее значение обобщенной ординаты |
ПРИМЕЧАНИЯ К ТАБЛИЦАМ
В таблицах используются следующие сокращения:
| ЗР | зона реакции |
| Степ | степенной закон |
| ЕА | уравнение Ерофеева–Авраами |
| Д | диффузионная зона |
| П | переходная зона |
Коэффициенты Стьюдента и Фишера приводятся в соответствии с [28].
Список литературы
Мельниченко Е.И. Фторидная переработка редкометальных руд Дальнего Востока. Владивосток: Дальнаука. 2002.
Римкевич В.С., Пушкин А.А., Маловицкий Ю.Н., Еранская Т.Ю., Гиренко И.В. Физико-химические процессы фторидной переработки алюминиевых руд // Теорет. основы хим. технологии. 2010. Т. 44. № 6. С. 626. [Rimkevich V.S., Pushkin A.A., Malovitskii Yu.N., Eranskaya T.Yu., Girenko I.V. Physicochemical processes of the fluoride processing of aluminum ores // Theor. Found. Chem. Eng. 2010. V. 44. № 6. P. 844]
Макаров Д.В., Беляевский А.Т., Меньшиков Ю.П., Нестеров Д.П., Юсупов М.Ф. Исследование механизма и кинетики взаимодействия порошкового нефелина с гидродифторидом аммония // Журн. прикл. химии. 2007. Т. 80. № 2. С. 177.
Андреев В.А., Буйновский А.С., Андреев А.А., Дьяченко А.Н. Обескремнивание топазового концентрата // Известия Томского политехнического университета. 2007. Т. 311. № 3. С. 30.
UC Rusal хочет отказаться от импортного сырья – Ведомости (vedomosti.ru)
Фомина Е.Ю., Артемова О.С. Исследование возможности переработки золошлаковых отходов ТЭС металлургическими методами // ГИАБ. 2011. № 8. С. 273.
Кондратьев В.В., Немчинова Н.В., Иванов Н.А., Ершов В.А., Сысоев И.А. Новые технологические решения по переработке отходов кремниевого и алюминиевого производств // Металлург. 2013. № 5. С. 92.
Лебедев В.В., Рубан В.А., Шпирт М.Я. Комплексное использование углей. М.: Недра, 1980. 387 с.
Сорокин А.П., Конюшок А.А. Распределение редких металлов и редкоземельных элементов в буроугольных месторождениях Верхнего и Среднего Приамурья // ДАН. 2018. № 6. С. 658–661.
Римкевич В.С., Пушкин А.А., Чарушова О.В. Комплексная переработка угольной золы ТЭЦ // Горный информационно-аналитический бюллетень. 2015. № 6. С. 250.
Римкевич В.С., Сорокин А.П., Пушкин А.А., Гиренко И.В. Физико-химические исследования распределения полезных компонентов в техногенных отходах предприятий теплоэнергетики// Физико-технические проблемы разработки полезных ископаемых. 2020. № 3. С. 152. [Rimkevich V.S., Sorokin A.P., Pushkin A.A., Girenko I.V. Physicochemical analysis of distribution of useful components in waste in the thermal energy sector // J. mining science. 2020. № 3. P. 464]
Пушкин А.А., Римкевич В.С. Статистическая обработка экспериментов по кинетике химических реакций // Журн. успехи современного естествознания. 2020. № 3. С. 76.
Пушкин А.А., Римкевич В.С., Гиренко И.В. Кинетика фторидно-аммониевой переработки золы углей предприятий теплоэнергетики // Современные наукоемкие технологии. 2021. № 5. С. 114.
Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. 8-е изд., стер. М.: Высш. шк., 2002.
Колемаев В.А., Староверов С.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. Учеб. пособие для экономических специальностей вузов. М.: Высш. шк, 1991.
Розовский А.Я. Кинетика топохимических реакций. М.: Химия, 1974.
Свиридова Т.В. Химия твердого тела. Топохимическая кинетика. Электронное учебное пособие. Минск, 2011.
Новый справочник химика и технолога. Электродные процессы. Химическая кинетика и диффузия. Коллоидная химия. С.-Пб.: АНО НПО “Профессионал”. 2004.
Еремин Е.Н. Основы химической кинетики: Учеб. Пособие для университетов и химико-технологических вузов. 2-е изд., доп. М.: Высш. Шк., 1976.
Балдин К.В, Башлыков В.Н., Рукосуев А.В. Основы теории вероятностей и математической статистики. Учебник. 4-е издание. М.: Флинта. 2016. 489 с.
Балдин К.В., Башлыков В.Н., Рукосуев А.В. Теория вероятностей и математическая статистика. Учебник. 2-е изд. М.: Издательско-торговая корпорация “Дашков & К0", 2014. 473 с.
Мельниченко Е.И., Эпов Д.Г., Щека С.А., Крысенко Г.Ф. Способ переработки титансодержащего минерального сырья. RU2136771C1 Российский патент 1999 года по МПК C22B34/12 C22B1/02 C01G23/04.
Продан Е.А., Павлюченко М.М., Продан С.А. Закономерности топохимических реакций. Минск: Наука и техника. 1976.
Бочкарев В.В. Теория химико-технологических процессов органического синтеза. Гетерофазные и гетерогенно-каталитические реакции. Учебное пособие. Томск: Издательство ТПУ, 2005.
Евдокимов А.Н. Теория химико-технологических процессов органического синтеза. Ч. 1. Гетерофазные реакции. Учебное пособие. Санкт-Петербург, 2011.
Дукин А.Н., Пожидаев А.А. Самоучитель Visual Basic 2010. Санкт-Петербург: БХВ-Петербург. 2010.
Стромберг А.Г., Семченко Д.П. Физическая химия. 4-е изд., испр. М.: Высшая школа, 1999.
Статистические таблицы. URL: https://math.semestr.ru/corel/table.php.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


