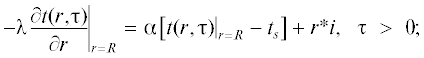Теоретические основы химической технологии, 2022, T. 56, № 5, стр. 648-657

Тепломассоперенос при сушке цилиндрического тела в непрерывно действующем электромагнитном поле высокой и сверхвысокой частоты

С. П. Рудобашта^a, *, Э. М. Карташов^b, Г. А. Зуева^c

^a Российский государственный аграрный университет – МСХА им. К.А. Тимирязева
Москва, Россия

^b Российский технологический университет – МИРЭА (Институт тонких химических технологий им. М.В. Ломоносова) Россия
Москва, Россия

^c Ивановский государственный химико-технологический университет
Иваново, Россия

^* E-mail: srudobashta@rgau-msha.ru

Поступила в редакцию 11.04.2021
После доработки 10.06.2022
Принята к публикации 16.06.2022

EDN: NBVWDB
DOI: 10.31857/S0040357122050190

Полный текст (PDF)

Аннотация

Рассмотрен тепломассоперенос в теле цилиндрической формы при его сушке в электромагнитном поле высокой и сверхвысокой частоты. Сформулирована и аналитически решена линейная (постоянство параметров процесса) задача нагрева цилиндрического тела при этих видах энергоподвода в условиях его конвективной сушки и с учетом его конвективного тепло- и массообмена с внешней газовой средой – как в общем случае, так и при сушке в первом периоде. В первом случае интенсивность сушки описана на основе аналитического решения задачи массопроводности (диффузии влаги) при условии, что фазовые превращения происходят у поверхности тела. Во втором случае принято, что вся подводимая к телу теплота расходуется на испарение влаги и поэтому нагрев тела не происходит и что парциальное давление пара у поверхности цилиндра равно давлению насыщенного пара при температуре поверхности цилиндра. При этом зависимость давления насыщенного пара от температуры описана уравнением Антуана. Решения задач нагрева получены применительно к локальной и средней по объему цилиндра температуре. На их основе проведено численное моделирование процесса нагрева тела и его влияния на кинетику сушки гранул цилиндрической формы (прутков из полиамида PA-6), показывающее методику расчета кинетики сушки зональным методом с использованием полученных уравнений. Применительно ко второй задаче выполнен численный расчет процесса испарения пленочной влаги с поверхности прутка из полиамида PA-6.

Ключевые слова: сушка, электромагнитный нагрев, токи высокой и сверхвысокой частоты, конвективный тепломассообмен, аналитическое решение

ВВЕДЕНИЕ

Сушке материалов в электромагнитном поле высокой и сверхвысокой частоты в последние годы уделяется большое внимание [1–3]. Это объясняется тем, что при этих видах энергоподвода имеет место объемное поглощение теплоты телом, что приводит к существенной интенсификации сушки вследствие того, что среднеобъемная температура тела в ходе процесса оказывается более высокой, чем при чисто конвективной сушке, при которой теплота к телу подводится через его поверхность. Кроме того, при электромагнитном теплоподводе токами высокой и сверхвысокой частоты температурный градиент направлен по внутренней нормали к поверхности тела, а не по внешней, как при конвективной сушке, что также способствует увеличению скорости сушки, т.к. перенос влаги по механизму термовлагопроводности происходит по потоку тепла [4], который при конвективной сушке направлен против потока влаги и, следовательно, тормозит процесс сушки, а при сушке токами высокой и сверхвысокой частоты оба потока по направлению совпадают. Сушка токами высокой и сверхвысокой частоты уже достаточно широко применяется в промышленности – как самостоятельный процесс, так и в комбинации с конвективной сушкой [1–3].

Для термолабильных материалов для сохранения их качества электромагнитный энергоподвод осуществляется, как правило, в прерывистом режиме [5–15], который позволяет не перегревать материал. Математические модели, описывающие прерывистый процесс конвективной, электромагнитной и комбинированной сушки, приведены в [6, 7, 11, 15–21].

Осциллирующий подвод электромагнитной энергии, как отмечено выше, необходим при сушке термолабильных материалов. Однако, на практике высушивается достаточно большое количество материалов, которые таковыми не являются. Кроме того, как показано в [22], при надлежащем выборе мощности электромагнитного источника теплоты при непрерывном электромагнитном энергоподводе можно также создавать режимы, не приводящие к перегреву материала при его сушке – и-за стока теплоты на испарение влаги. Для расчета и анализа тепломассопереноса при непрерывной ТВЧ- и СВЧ- сушке материала необходимы математические модели, описывающие их непрерывный электромагнитный нагрев с учетом стока теплоты на испарение влаги. В [23] приведены математические модели для “чистого” (без массообмена) нагрева тела в форме пластины – при постоянном внутреннем источнике теплоты. В [22] представлена математическая модель, описывающая тепломассоперенос при сушке тел пластинчатой формы в непрерывно действующем электромагнитном поле высокой и сверхвысокой частоты.

Целью данной работы является разработка аналитических математических моделей, описывающих тепломассоперенос при сушке цилиндрических тел в непрерывно действующем электромагнитном поле высокой и сверхвысокой частоты с учетом стока теплоты на испарение влаги и конвективный теплообмен поверхности тел с внешней газовой средой, в процессе которого может происходить либо дополнительный нагрев тела (при температуре внешней среды выше температуры поверхности тела), либо его охлаждение, когда температура поверхности тела ниже температуры внешней среды. В сочетании с представленным в работе математическим описанием массообмена эти модели позволят рассчитывать кинетику сушки.

Постановка задачи нагрева цилиндрического тела при испарении из него влаги

При сушке дисперсных материалов в аппарате, в котором происходит облучение материала по всей поверхности частиц, можно принять, что при ТВЧ- и СВЧ сушке в силу большой глубины проникновения электромагнитного поля (ЭМП) во все частицы (тела) внутренний объемный источник теплоты ${{q}_{{\text{v}}}}$ (Вт/м³) в каждой частице (теле) постоянен. Величину внутреннего объемного источника теплоты qv можно определить из теплового баланса аппарата, содержащего этот источник

(1)

${{N}_{{em}}}{{\eta }_{t}} = {{q}_{V}}V~ = {{q}_{V}}{{V}_{{rab}}}\left( {1 - \varepsilon } \right),$

откуда получаем

(2)

${{q}_{{\text{v}}}} = {{{{N}_{{em}}}{{\eta }_{t}}} \mathord{\left/ {\vphantom {{{{N}_{{em}}}{{\eta }_{t}}} {({{V}_{{rab}}}\left( {1 - \varepsilon } \right),}}} \right. \kern-0em} {({{V}_{{rab}}}\left( {1 - \varepsilon } \right),}}$

где N_em – действующий внутри аппарата источник электромагнитной энергии, Вт; η_t – термический кпд источника; V, V_rab – внутренний и рабочий объем аппарата соответственно, м³; (1 – ε) – доля рабочего объема, занятого материалом, м³/м³. При известных размерах цилиндрического тела количество цилиндрических тел одинакового размера, загруженных в аппарат, составляет:

$n = {{V}_{{rab}}}{{(1 - \varepsilon )} \mathord{\left/ {\vphantom {{(1 - \varepsilon )} {{{V}_{{\text{т}}}}}}} \right. \kern-0em} {{{V}_{{\text{т}}}}}},$

где V_т – объем одного тела, а.

Примем, что все цилиндрические тела, загруженные в аппарат, имеют одинаковые размеры и что длина цилиндрического тела намного больше его диаметра. С учетом вышеизложенного сформулируем задачу нагрева влажного бесконечного цилиндра при его сушке в поле токов высокой и сверхвысокой частоты, приняв следующие условия и допущения:

– объемный источник теплоты в теле постоянен: q_v = const;

– у поверхности цилиндра имеет место его конвективный тепло-и массообмен с внешней газовой средой в соответствии с граничными условиями теплообмена [23] и массообмена [24] 3-го рода;

– температура внешней среды постоянна;

– в момент начала процесса температура в цилиндре распределена равномерно;

– все теплофизические характеристики процесса постоянны;

– цилиндр равномерно облучается по поверхности;

– испарение влаги происходит у поверхности цилиндра (внутренние фазовые стоки теплоты отсутствуют);

– термовлагопроводность пренебрежимо мала;

– усадка цилиндра отсутствует.

С учетом изложенного сформулируем линейную одномерную (температура и влагосодержание тела изменяются только по радиальной координате) задачу электромагнитного нагрева цилиндра, поместив начало координат на его центральной оси, в виде

(3)

$\frac{{\partial {\kern 1pt} t}}{{\partial {\kern 1pt} {{\tau }}}} = a\left( {\frac{{{{\partial }^{2}}t}}{{\partial {\kern 1pt} {{r}^{2}}}} + \frac{1}{r}\frac{{\partial t}}{{\partial r}}} \right) + q_{{\text{v}}}^{*},\,\,\,\,0 < r < R,\,\,\,\,\tau > 0;$

(4)

${{\left. {t(r,\,{{\tau }})} \right|}_{{\tau = 0}}} = {{t}_{n}},\,\,\,\,0 \leqslant r \leqslant R;$

(5)

(6)

${{\left. {\frac{{\partial t(r,\tau )}}{{\partial r}}} \right|}_{{r = 0}}} = 0,\,\,\,\,{{\tau }} \geqslant 0.$

Когда температура цилиндра больше температуры внешней среды (за счет электромагнитного энергоподвода), то левая часть уравнения (5) положительна и, поскольку ${{\left. {t(x,{{\tau }})} \right|}_{{r = R}}} - {{t}_{s}}$ > 0, то имеет место теплоотдача с поверхности цилиндра во внешнюю более холодную среду, кроме того, отводимая от цилиндра теплота расходуется на испарение влаги: $r{\text{*}}i(\tau ).$ При ${{\left. {t(r,{{\tau }})} \right|}_{{r = R}}} - {{t}_{s}}$ < 0 (температура внешней среды больше температуры цилиндра) теплота из этой среды подводится к цилиндру, часть ее расходуется на испарение влаги у поверхности, а оставшаяся часть идет на нагрев цилиндра. Таким образом, уравнение (5) учитывает как теплопотери в окружающую холодную среду, так и комбинированный нагрев цилиндра за счет электромагнитного энергоподвода и подвода теплоты конвекцией от внешней горячей среды. В обоих случаях учитывается сток теплоты на испарение влаги.

Интенсивность сушки i изменяется в ходе процесса, ее можно представить в зависимости от скорости сушки $\left| {\frac{{d\bar {u}}}{{d{{\tau }}}}} \right|$ в виде [24]: $i = \left| {\frac{{d\bar {u}}}{{d{{\tau }}}}} \right|{{R}_{{\text{V}}}}{{{{\rho }}}_{{\text{0}}}},$ где ${{R}_{{\text{V}}}}$ – отношение объема тела к его поверхности (для цилиндра R_V = R/2). Воспользуемся аналитическим решением линейной задачи массопроводности для среднеобъемного влагосодержания в цилиндре при граничном условии масообмена 3-го рода [24]

(7)

$\begin{gathered} \bar {E} = \frac{{\bar {u} - u_{r}^{ * }}}{{{{u}_{n}} - u_{r}^{ * }}} = \\ = \sum\limits_{k = 1}^\infty {\frac{{2{\text{Bi}}_{m}^{2}}}{{\mu _{k}^{2}\left( {{\text{Bi}}_{m}^{2} + \mu _{k}^{2} + {\text{B}}{{{\text{i}}}_{m}}} \right)}}} \exp \left( { - \mu _{k}^{2}{\text{F}}{{{\text{o}}}_{m}}} \right), \\ \end{gathered} $

из которого найдем $\left| {\frac{{d\bar {u}}}{{d{{\tau }}}}} \right|$ и далее, имея ввиду, что ${\text{F}}{{{\text{o}}}_{m}} = {\text{Lu}}\,{\text{Fo}}$, запишем i(Fo)в виде

(8)

$i({\text{Fo}}) = \left[ {\frac{{{{{{\rho }}}_{{\text{0}}}}a}}{{2R}}{\text{Lu}}\sum\limits_{k = 1}^\infty {{{B}_{k}}{{\mu }}_{k}^{2}\exp ( - {{\mu }}_{k}^{2}{\text{LuFo}})} } \right]({{\bar {u}}_{n}} - u_{r}^{ * }),$

где

(9)

${{B}_{k}} = \frac{{2{\text{Bi}}_{m}^{2}}}{{{{\mu }}_{k}^{2}\left( {{\text{Bi}}_{m}^{2} + {{\mu }}_{k}^{2} + {\text{B}}{{{\text{i}}}_{m}}} \right)}},$

${{{{\mu }}}_{k}}$ – корни характеристического уравнения

(10)

$\frac{{{{J}_{0}}({{\mu }_{k}}{\text{)}}}}{{{{J}_{{\text{1}}}}({{{{\mu }}}_{k}}{\text{)}}}} = \frac{{{{{{\mu }}}_{k}}}}{{{\text{B}}{{{\text{i}}}_{m}}}}.$

Здесь J₀, J₁ – функции Бесселя первого рода нулевого и первого порядка соответственно. Задача (3)–(6) представляет собой параболическую модель нестационарной теплопроводности. Отметим, что наряду с параболическими моделями нестационарной теплопроводности в последнее время развиваются гиперболические модели – для быстро протекающих процессов теплообмена [24].

Найдем решение задачи (3)–(6), считая a, $q_{{\text{V}}}^{*} = \frac{{{{q}_{{\text{V}}}}}}{{c\rho }}$, λ, r*, α, R, t_n, k, t_s, $u_{r}^{ * }$ = const. В случае линейной равновесной зависимости: $u_{r}^{ * } = {{u}_{r}},$ а в случае нелинейной величина $u_{r}^{ * }$ находится через равновесное влагосодержание $u_{r}^{{}}$ по методике, описанной в [25].

Решение.

Введем безразмерные переменные:

$\begin{gathered} \rho = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R};\,\,\,\,{\text{Fo}} = {{a\tau } \mathord{\left/ {\vphantom {{a\tau } {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}};\,\,\,\,W(\rho ,\,{\text{Fo)}} = \frac{{t{\text{(}}r{\text{, }}\tau {\text{)}} - {{t}_{n}}}}{{{{t}_{s}} - {{t}_{n}}}}; \\ {\text{Bi}} = {{\alpha R} \mathord{\left/ {\vphantom {{\alpha R} \lambda }} \right. \kern-0em} \lambda };\,\,\,\,{{Q}_{{\text{v}}}} = \frac{{q_{{\text{v}}}^{ * }{{R}^{2}}}}{{a\,({{t}_{s}} - {{t}_{n}})}};\,\,\,\,{{R}_{{\text{0}}}} = \frac{{r{\text{*}}iR}}{{\lambda ({{t}_{s}} - {{t}_{n}})}}. \\ \end{gathered} $

Тогда задача (3)–(6) будет иметь вид:

(11)

$\frac{{\partial {\kern 1pt} W}}{{\partial {\kern 1pt} {\text{Fo}}}} = \frac{{{{\partial }^{2}}W}}{{\partial {\kern 1pt} {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial W}}{{\partial \rho }} + {{Q}_{{\text{v}}}},\,\,\,\,0 < \rho < 0,\,\,\,{\text{Fo}} > 0;$

(12)

${{\left. {W(\rho ,\,{\text{Fo}})} \right|}_{{{\text{Fo}} = 0}}} = 0,\,\,\,\,0 \leqslant \rho \leqslant 1;$

(13)

$\begin{gathered} {{\left. {\frac{{\partial W(\rho ,{\text{Fo}})}}{{\partial \rho }}} \right|}_{{\rho = 1}}} = \\ = - {\text{Bi}}\left[ {{{{\left. {W(\rho ,\,{\text{Fo}})} \right|}}_{{\rho = 1}}} - 1} \right] - {{R}_{0}},\,\,\,\,{\text{Fo}} > 0; \\ \end{gathered} $

(14)

${{\left. {\frac{{\partial W(\rho ,\,{\text{Fo}})}}{{\partial \rho }}} \right|}_{{\rho = 0}}} = 0,\,\,\,\,{\text{Fo}} > 0.$

Задачу (11)–(14) решаем методом интегральных преобразований по таблицам Карташова [26, 27]. Запишем три формулы:

интегральное преобразование:

(15)

$\overline W ({{{{\mu }}}_{n}},{\text{Fo)}} = \int\limits_0^1 {\rho {{J}_{0}}({{\mu }_{n}}\rho )W(\rho ,{\text{Fo}})} {\text{d}}\rho ;$

изображение оператора $\Delta W(\rho ,\,{\text{Fo}}) = \frac{{{{\partial }^{2}}W}}{{\partial {\kern 1pt} {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial W}}{{\partial \rho }}:$

(16)

$\begin{gathered} \int\limits_0^1 {\rho {{J}_{0}}({{\mu }_{n}}\rho )} \left( {\frac{{{{\partial }^{2}}W}}{{\partial {\kern 1pt} {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial W}}{{\partial \rho }}} \right){\text{d}}\rho = \\ = {{J}_{0}}({{\mu }_{n}}\rho ){{\left( {\frac{{\partial W}}{{\partial \rho }} + {\text{Bi}}W} \right)}_{{\rho = {\text{0}}}}} - \mu _{n}^{2}\bar {W}({{\mu }_{n}},{\text{Fo);}} \\ \end{gathered} $

формулу обращения:

(17)

$W(\rho ,\,{\text{Fo}}) = 2\sum\limits_{n = 1}^\infty {\frac{{{{\mu }}_{n}^{2}{{J}_{0}}({{\mu }_{n}}\rho )\bar {W}({{{{\mu }}}_{n}},{\text{Fo)}}}}{{({{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}})J_{{_{0}}}^{2}({{\mu }_{n}})}}} .$

Здесь ${{\mu }_{n}}$ > 0 – корни уравнения ${{\mu }}{{J}_{1}}({{\mu }}) = {\text{Bi}}\,{{J}_{0}}({{\mu }})$, ${{J}_{0}}(\mu ),\;{{J}_{1}}(\mu )$ – функции Бесселя 1-го рода, нулевого и первого порядка соответственно.

Далее учтем также, что

(18)

$\int\limits_0^1 {\rho {{J}_{0}}({{\mu }_{n}}\rho )} {\text{d}}\rho = \frac{1}{{{{\mu }_{n}}}}{{J}_{1}}({{\mu }_{n}}).$

Решение для локальной температуры в безразмерных переменных имеет вид:

(19)

$\begin{gathered} W(\rho ,Fo) = 2({\text{Bi}} - {{R}_{0}}) \times \\ \times \,\,\sum\limits_{n = 1}^\infty {\frac{{{{J}_{0}}({{\mu }_{n}}\rho )(1 - \exp ( - \mu _{n}^{2}{\text{Fo}}))}}{{(\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}){{J}_{0}}({{\mu }_{n}})}}} + \\ + \,\,2{{Q}_{{\text{v}}}}\sum\limits_{n = 1}^\infty {\frac{{{{J}_{1}}({{\mu }_{n}}){{J}_{0}}({{\mu }_{n}}\rho )(1 - \exp ( - \mu _{n}^{2}{\text{Fo)}})}}{{{{\mu }_{n}}(\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}})J_{0}^{2}({{\mu }_{n}})}}} . \\ \end{gathered} $

Среднее значение решения $W(\rho ,{\text{Fo}})$ вычислим по формуле:

(20)

$\overline W ({\text{Fo)}} = 2\int\limits_0^1 {\rho W(\rho ,{\text{Fo}})} {\text{d}}\rho .$

Получим:

(21)

$\begin{gathered} \overline W ({\text{Fo)}} = 4({\text{Bi}} - {{R}_{{\text{0}}}}) \times \\ \times \,\,\sum\limits_{n = 1}^\infty {\frac{{{{J}_{1}}({{{{\mu }}}_{n}})(1 - \exp ( - {{\mu }}_{n}^{2}{\text{Fo))}}}}{{{{{{\mu }}}_{n}}({{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}){{J}_{0}}({{{{\mu }}}_{n}})}}} + \\ + \,\,4{{Q}_{{\text{V}}}}\sum\limits_{n = 1}^\infty {\frac{{J_{1}^{2}({{\mu }_{n}})(1 - \exp ( - {{\mu }}_{n}^{2}{\text{Fo))}}}}{{{{\mu }}_{n}^{2}({{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}})J_{0}^{2}({{\mu }_{n}})}}} {\text{.}} \\ \end{gathered} $

Решение при i = const.

При i = const имеет место первый период сушки. Найдем для него отдельное решение задачи электромагнитного нагрева цилиндра в процессе сушки, приняв, что в периоде постоянной скорости сушки вся подводимая теплота расходуется на испарение влаги и поэтому температура пластины во времени не изменяется. Сформулируем для этого случая задачу в виде

(22)

$a\left( {\frac{{{{d}^{2}}t}}{{d{\kern 1pt} {{r}^{2}}}} + \frac{1}{r}\frac{{\partial t}}{{\partial r}}} \right) + q_{{\text{v}}}^{ * } = 0,\,\,\,\,0 < r < R;$

(23)

$ - {{\lambda }}{{\left. {\frac{{dt(r)}}{{dr}}} \right|}_{{r = R}}} = {{\alpha }}\left[ {{{{\left. {t(r)} \right|}}_{{r = R}}} - {{t}_{s}}} \right] + r*{{i}_{1}},\,\,\,\,t > 0;$

(24)

$\frac{{dt}}{{dr}}\left| \begin{gathered} \hfill \\ r = 0 \hfill \\ \end{gathered} \right. = 0,\,\,\,\,r = {\text{ }}0,$

где a, $q_{{\text{v}}}^{ * }$, r* λ, α, i₁, R, t_s = const.

Получим решение задачи (22)–(24). Введем безразмерные переменные:

$\begin{gathered} \rho = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R};\,\,\,\,{\text{Bi}} = {{\alpha R} \mathord{\left/ {\vphantom {{\alpha R} \lambda }} \right. \kern-0em} \lambda };\,\,\,\,W(\rho {\text{)}} = \frac{{t{\text{(}}r)}}{{{{t}_{s}}}}; \\ {{Q}_{{\text{v}}}} = \frac{{q_{{\text{v}}}^{ * }{{R}^{2}}}}{{a{{t}_{s}}}};\,\,\,\,{{R}_{{\text{0}}}} = \frac{{r{\text{*}}{{i}_{1}}R}}{{\lambda {{t}_{s}}}}. \\ \end{gathered} $

Задача (22)–(24) будет иметь вид:

(25)

$\frac{{{{d}^{2}}W}}{{d{\kern 1pt} {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{dW}}{{d\rho }} + {{Q}_{{\text{v}}}} = 0,\,\,\,\,0{\text{ }} < \rho < 0;$

(26)

${{\left. {\frac{{dW(\rho )}}{{d\rho }}} \right|}_{{\rho = 1}}} = - {\text{Bi}}\left[ {{{{\left. {W(\rho )} \right|}}_{{\rho = 1}}} - 1} \right] - {{R}_{0}},\,\,{\text{Fo}} > 0;$

(27)

${{\left. {\frac{{dW(\rho )}}{{d\rho }}} \right|}_{{\rho = 0}}} = 0.$

Уравнение (25) – это обыкновенное линейное дифференциальное уравнение второго порядка, его можно записать в виде

$\frac{1}{\rho }\frac{d}{{d\rho }}\left( {\rho \frac{{dW}}{{d\rho }}} \right) = - {{Q}_{{\text{v}}}},\,\,\,\,0 < \rho < 0.$

Интегрируя последовательно и используя граничные условия (26), (27), находим

(28)

$W({{\rho }}) = - ({{{{Q}_{{\text{v}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{\text{v}}}}} 4}} \right. \kern-0em} 4}){{{{\rho }}}^{2}} + \frac{{({\text{Bi}} + 2){{Q}_{{\text{v}}}}}}{{4{\text{Bi}}}} - \frac{{{{R}_{0}} - {\text{Bi}}}}{{{\text{Bi}}}},$

среднее значение:

(29)

$\overline W = \frac{{{{Q}_{{\text{v}}}} - 2({{R}_{0}} - {\text{Bi)}}}}{{4{\text{Bi}}}}.$

Численный анализ полученных решений.

Пример 1.

Для иллюстрации развитых математических моделей рассмотрим процесс сушки прутка из полиамида марки PA-6, равномерно облучаемого по поверхности электромагнитным полем. Примем, что длина прутка намного больше его диаметра, поэтому будем его рассматривать как цилиндр бесконечной длины. При переработке полиамида в изделия начальное влагосодержание, ввиду гигроскопичности этого материала, может составлять 4.5%, а высушить его, согласно технологическому регламенту, необходимо до остаточного влагосодержания ~0.05%. Из-за окисляемости полиамида для исключения его контакта с кислородом применяют две технологии сушки [28]: сушку в токе азота при температуре азота до 140°С и сушку в вакууме. Примем в данном примере, что сушка осуществляется в токе азота. Пусть диаметр прутка равен d = 3 мм и l/d = 5, его начальное влагосодержание ${{\bar {u}}_{{\text{н}}}} = 0.045$ кг/(кг сух. м-ла), конечное – ${{\bar {u}}_{{\text{к}}}} = 0.05 \times {{10}^{{ - 2}}}$ кг/(кг сух. м-ла), начальная температура прутка t_н = 18°C, температура сушильного агента (азота), обдувающего пруток, в разных вариантах расчета различна. Теплофизические характеристики полиамида ПА-6 [29]: λ = = 0.28 Вт/(м К); c = 2100 Дж/(кг К); ρ = 1120 кг/м³ (следовательно, a = 0.12 × 10^–6 м²/с); максимально допустимая температура нагрева прутка t_max = = 140°C, т.к в противном случае начинается размягчение материала, которое может приводить к слипанию гранул в аппарате. Проанализируем влияние мощности электромагнитного источника и температуры сушильного агента на кинетику нагрева прутка и кинетику его сушки.

Для обеспечения глубокой сушки полиамида необходимо использовать осушенный азот, примем в этом расчете для его упрощения влагосодержание азота равным нулю. Интенсивность сушки рассчитывали по уравнению (8). Установлено [25, 30], что при глубокой сушке гранулированных полимеров, в том числе полиамида ПА-6, кинетика сушки контролируется внутренней диффузией. Поэтому в уравнении (7) значения B_k и β_k находили как для внутренней задачи, соответствующей условию ${\text{B}}{{{\text{i}}}_{m}} \to \infty $. Для этого случая уравнения (9) и (10) трансформируются соответственно к виду [25]

а именно:

(32)

${{B}_{k}} = \frac{4}{{{{\mu }}_{k}^{2}}},$

(33)

${{J}_{0}}\left( {{{{{\mu }}}_{k}}} \right) = 0.$

Примем далее в расчете N_em = 75 × 10³ Вт; η_t = 0.9; ε = 0.8 (такая порозность может иметь место при сушке гранул полиамидного прутка в виброожиженном слое); r * = 2400 × 10³ Дж/кг; V= 1.0 × 0.5 × × 0.4 = 0.2 м³. Коэффициент теплоотдачи будем считать равным α = 10 Вт/(м² К) – с ориентацией на данные [28], расчет числа Bi при этом дает значение: Bi = 0.054 – чисто внешняя задача теплообмена.

Полиамид PA-6 относится к числу непористых полимеров, перенос влаги в которых происходит путем молекулярной диффузии [25, 30, 31]. Поэтому коэффициент массопроводности k в данном случае является эффективным коэффициентом молекулярной диффузии влаги: $k \equiv {{D}_{e}}$. Он существенно зависит от влагосодержания и температуры материала, причем температурная зависимость подчиняется уравнению Аррениуса [27, 30]

(34)

${{D}_{e}} = {{D}_{{\infty .u}}}\exp \left[ { - \frac{{{{E}_{{D.u}}}}}{{R{\kern 1pt} {\text{*}}T}}} \right]{\text{,}}$

где ${{D}_{{\infty .u}}} = {{D}_{0}}{{e}^{{ - b{\kern 1pt} ' \cdot u}}}$ – формальное значение коэффициента диффузии при $T \to \infty $ и любом u. В [27] для полиамида PA-6 было найдено: ${{D}_{0}} = 94.0 \times {{10}^{{ - 4}}}$ м²/с; $b{\kern 1pt} ' = 31.7;$ ${{E}_{{D.u}}} = 65.0 \times {{10}^{3}}(1 - 2.87u)$ ${{кДж} \mathord{\left/ {\vphantom {{кДж} {кмоль}}} \right. \kern-0em} {кмоль}}.$

Кинетику сушки в примере рассчитывали зональным методом [25], разбивая весь диапазон удаляемой из полимера влаги на три концентрационные зоны: ${{\bar {u}}_{{n{\text{.}}i}}} - {{\bar {u}}_{{k{\text{.}}i}}}) \times {{10}^{{ - 2}}}:$ (4.5–2.5), (2.5–1.0), (1.0–0.05) кг/(кг сух. м-ла) и используя в каждой из них средние значения коэффициента диффузии ${{D}_{e}}$ на интервалах ${{\bar {u}}_{i}} \in ({{\bar {u}}_{{k{\text{.}}i}}},{{\bar {u}}_{{n.i}}})$, т.е. при ${{\bar {u}}_{{{\text{sr}}{\text{.}}i}}} = {{({{{\bar {u}}}_{{n{\text{.}}i}}} + {{{\bar {u}}}_{{k.i}}})} \mathord{\left/ {\vphantom {{({{{\bar {u}}}_{{n{\text{.}}i}}} + {{{\bar {u}}}_{{k.i}}})} 2}} \right. \kern-0em} 2}.$ Влияние температуры материала на величину коэффициента диффузии учитывали по средней температуре материала в зоне: ${{\bar {t}}_{{{\text{s}}r.i}}} \in ({{\bar {t}}_{{n.i}}},{{\bar {t}}_{{k{\text{.}}i}}}).$

Расчет проводили методом приближений в следующей последовательности: 1) задавали продолжительность сушки прутка в рассматриваемой концентрационной зоне τ_i, 2) используя полученное аналитическое решение (21), рассчитывали соответствующую этому времени конечную среднеобъемную температуру прутка, 3) рассчитывали для рассматриваемого промежутка времени среднее значение среднеобъемной температуры прутка ${{\bar {t}}_{{sr.i}}}$, 4) по этой температуре и среднему значению влагосодержания материала на рассматриваемом концентрационном интервале ${{\bar {u}}_{{{\text{sr}}{\text{.}}i}}}$ определяли значение коэффициента диффузии ${{D}_{{{\text{e}}{\text{.}}i}}}$, 5) по уравнению (35) рассчитывали продолжительность сушки прутка в i-той зоне τ_i, 6) сопоставляли рассчитанное значение τ_i с предварительно принятым и при значительной разнице повторяли расчет с найденным значением τ_i.

Формула для расчета времени сушки в i-той концентрационной зоне для ограниченного цилиндра имеет вид [25]

(35)

${{\tau }_{i}} = \frac{1}{{{{D}_{{e.i}}}\left( {\frac{{\mu _{{ts.i}}^{2}}}{{R_{{ts}}^{2}}} + \frac{{\mu _{{pl.i}}^{2}}}{{R_{{pl}}^{2}}}} \right)}}{\text{ln}}\frac{{{{{\rm B}}_{{ts.i}}}{{{\rm B}}_{{pl,i}}}}}{{{{{\bar {E}}}_{i}}}},\,\,\,\,i = {\text{ }}1, \ldots ,n,~$

где коэффициенты ${{{\rm B}}_{{ts.i}}}\;{\text{и}}\;{{{\rm B}}_{{pl,i}}}$ согласно рекомендациям [25] приняли равными единице. Первые положительные корни характеристических уравнений $\mu _{{ts .i}}^{{}}$и $\mu _{{pl.i}}^{{}}$ для внутренней задачи массообмена равны [25]: для цилиндрической поверхности ${{{{\mu }}}_{{ts{\text{.}}i}}} = {{{{\mu }}}_{{ts{\text{.1}}}}} = 2.4048;$ для плоской поверхности (торцы цилиндра) ${{\mu }_{{pl.i}}} = {{\mu }_{{pl.1}}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2};$ ${{R}_{{ts}}} \equiv R;$ ${{R}_{{pl}}} = {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2};$ ${{\bar {E}}_{i}} = \frac{{{{{\bar {u}}}_{{k{\text{.}}i}}} - {{u}_{{r.i}}}}}{{{{{\bar {u}}}_{{n.i}}} - {{u}_{{r.i}}}}}$ (в этом расчете ${{u}_{{r.i}}} = 0$).

Средняя по времени τ_i среднеобъемная температура прутка ${{\bar {t}}_{{sr.i}}}$ определяется выражением

(36)

${{\bar {t}}_{{sr.i}}} = \frac{1}{{{{{{\tau }}}_{i}}}}\int\limits_0^{{{\tau }_{i}}} {{{{\bar {t}}}_{i}}} {\kern 1pt} d{{\tau ,}}$

где функция ${{\bar {t}}_{i}}$ находится из уравнения (21).

Результаты расчетов приведены на рис. 1, 2 и в табл. 1. На рис. 1 показано изменение температуры на поверхности прутка (линия 1), на оси прутка (линия 2) и его среднеобъемной температуры (линия 3). Как видно из рисунка, все три температуры плавно возрастают во времени от начального значения t_n = 18°C до некоторого стабилизированного значения, которое максимально на оси прутка и минимально у его поверхности. Это объясняется тем, что температура сушильного агента, с которым контактирует пруток в этом примере низка (t_s = 20°C), поэтому вскоре после подъема температуры прутка начинается его охлаждение сушильным агентом, что в конечном счете стабилизирует температуру. Этот пример показывает нецелесообразность в данном случае чисто электромагнитного энергоподвода.

Рис. 1.

Изменение температуры прутка во времени: 1 – на его поверхности, 2 – в центре, 3 – среднеобъемной температуры (N_em, = 75 × 10³ Вт; t_n = 18°C; t_s = = 20°C).

Рис. 2.

Изменение температуры прутка во времени: 1 – на его поверхности, 2 – в центре, 3 – среднеобъемной температуры (N_em, = 5 × 10³ Вт; t_n = 18°C; t_s = = 127°C).

Таблица 1.

Расчеты кинетики сушки прутка из полиамида PA-6

№ зоны	$({{\bar {u}}_{{n{\text{.}}i}}} - {{\bar {u}}_{{k{\text{.}}i}}})$ × 10²	$\begin{gathered} {{{\bar {u}}}_{{{\text{s}}r{\text{.}}i}}} = \\ = {{({{{\bar {u}}}_{{n{\text{.}}i}}} + {{{\bar {u}}}_{{k{\text{.}}i}}})} \mathord{\left/ {\vphantom {{({{{\bar {u}}}_{{n{\text{.}}i}}} + {{{\bar {u}}}_{{k{\text{.}}i}}})} 2}} \right. \kern-0em} 2} \\ \end{gathered} $	${{\bar {t}}_{{sr.i}}}$, °C	${{D}_{{\infty .u}}} \times {{10}^{2}}$	E_D.u×10^–4	${{D}_{{e.i}}}$ ×10¹⁰, м²/с	${{\tau }_{i}} \times {{10}^{{ - 3}}},$ с	${{{{\tau }}}_{{\text{с}}}} = \sum\limits_{\text{1}}^{\text{3}} {{{{{\tau }}}_{i}}} ,$
i = 1	(4.5–2.5)	3.5^{× 10^–2}	128	0.31	5.84	0.7581	2.965	2.960 × 10⁴ с = 8.22 ч
i = 2	(2.5–1.0)	1.75 × 10^–2	132	0.54	6.17	0.5844	5.998
i = 3	(1.0–0.05)	1.0525 × 10^–2	134.5	0.67	6.30	0.5552	20.640

Рассмотрим далее комбинированный конвективно-электромагнитный энергоподвод, при котором теплота к прутку подводится как конвективно – с помощью предварительно нагретого до температуры t_s = 127°C сушильного агента, так и от электромагнитного источника мощностью N_em = 5 × 10³ Вт. Остальные параметры – те же. Результаты этих расчетов приведены на рис. 2. Как видно из рис. 2, при указанных параметрах процесса температурные кривые для оси прутка, его поверхности и для среднеобъемной температуры практически сливаются. Это является следствием того, что при выбранных условиях проведения процесса режим теплообмена является внешним (число Bi = 0.054), а электромагнитный источник мал, чтобы вносить в распределение температуры по радиусу большие коррективы. Отметим, что при таком комбинированном энергоподводе, энергия, подводимая от электромагнитного источника, не теряется на нагрев сушильного агента.

В табл. 1 приведены результаты расчета кинетики сушки прутка из полиамида PA-6 при t_s = = 127°C, N_em = 5 × 10³ Вт и указанных выше остальных условиях. Как видно из таблицы, средняя на каждом временном интервале температура прутка ${{\bar {t}}_{{sr.i}}}$ от первой к третьей концентрационной зоне возрастает (так как уменьшается интенсивность сушки), но остается меньше 140°С, что важно для предотвращения слипаемости гранул.

Проиллюстрируем далее применение решения (28), полученного при i = const.

Пример 2.

При глубокой сушке прутков из полиамида PA-6 на сушку могут поступать прутки после их промывки водой от внешних загрязнений (например, при вторичной переработке гранулята). В этом случае процесс сушки состоит из двух стадий: 1) испарение пленки воды с внешней поверхности прутка, 2) его глубокая сушка от ${{\bar {u}}_{{\text{н}}}}$ до ${{\bar {u}}_{{\text{к}}}}$. Расчет продолжительности первой стадии при электромагнитном энергоподводе можно рассчитать по уравнению (28). Примем те же исходные данные, что и в предыдущем примере, а именно: d = 3 мм; l/d = 5; N_em = 5 × 10³ Вт; η_t = 0.9; ε = 0.8; r* = 2400 × 10³ Дж/кг; V_rab = 1.0 × 0.5 × 0.4 = 0.2 м³; α = 10 Вт/(м² К). Пусть толщина пленки на поверхности прутка равна δ = 0.1 мм, тогда ее масса составляет M_w = πd(l + d/2)δρ_w = 1.48 × 10^–5 кг, где ρ_w = 1000 кг/м³ – плотность воды.

Продолжительность испарения пленки воды найдем из соотношения ${{{{\tau }}}_{{\text{1}}}} = {{{{M}_{w}}} \mathord{\left/ {\vphantom {{{{M}_{w}}} {({{i}_{1}}F)}}} \right. \kern-0em} {({{i}_{1}}F)}},$ где ${{i}_{1}}$ – интенсивность испарения влаги, кг/(м²с); F – поверхность прутка, равная: F= πd(l + d/2) = 1.55 × ×10^–4 м². Интенсивность испарения определяется уравнением массоотдачи

(37)

${{i}_{1}} = {{\beta }_{с}}({{C}_{s}}_{{.p}}--{{C}_{s}}) = {{\beta }_{p}}({{p}_{{par}}}_{{.p}}--{{p}_{{par}}}_{{.s}}){\text{ }},$

где β_с, β_p – коэффициенты массоотдачи, отнесенные соответственно к разности концентраций пара в сушильном агенте (кг/(м² с (кг/м³)) и к разности парциальных давлений пара (кг/(м² с Па); C_s.p, C_s – концентрация пара соответственно у поверхности тела и в ядре потока внешней фазы (в среде), кг/м³; p_par.p, p_par.s – давление пара соответственно у поверхности испарения и в ядре потока внешней фазы (в среде), Па. В соответствии с принятым в расчете условием, что сушильный агент является абсолютно сухим, имеем: C_s = p_par.s = 0.

Коэффициент массоотдачи β_с пересчитаем из коэффициента теплоотдачи, используя соотношение [32]:

(38)

$\frac{{{\alpha }}}{{{{{{\beta }}}_{с}}}} = {{\rho }}{{c}_{p}}\frac{{P - {{p}_{{par.sr }}}{\text{ }}}}{P},$

где p_par.sr – среднее парциальное давление пара в пограничном слое, Па, которое принимаем равным: p_par.sr = (p_par.p + p_par.s)/2 = p_par.p/2; ρc_p – объемная изобарная теплоемкость азота (Дж/(м³ К). Для сухого азота в расчетном температурном интервале приняли ρс_p = 1300 Дж/(м³ К) [33].

Коэффициент масоотдачи β_с, пересчитываем в коэффициент массоотдачи β_p по соотношению [32, 34]:

(39)

${{{{\beta }}}_{p}} = {{{{{{\beta }}}_{с}}} \mathord{\left/ {\vphantom {{{{{{\beta }}}_{с}}} {(R_{{par}}^{ * }{{T}_{{sr}}})}}} \right. \kern-0em} {(R_{{par}}^{ * }{{T}_{{sr}}})}},$

где ${{T}_{{sr}}} = \frac{{{{T}_{p}} + {{T}_{s}}}}{2}$ – средняя температура пограничного слоя, К [34].

Парциальное давление пара у поверхности испарения будем находить по уравнению Антуана [35], считая пар насыщенным (p_par.p = p _nas ):

(40)

${{р}_{{nas}}} = {{10}^{5}}\exp {{\left( {{{A - B} \mathord{\left/ {\vphantom {{A - B} {\left( {T - C} \right)}}} \right. \kern-0em} {\left( {T - C} \right)}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{A - B} \mathord{\left/ {\vphantom {{A - B} {\left( {T - C} \right)}}} \right. \kern-0em} {\left( {T - C} \right)}}} \right)} {760}}} \right. \kern-0em} {760}},$

где р_nas – давление насыщенного пара при температуре t_p, Па; А, В, С – константы, для воды равные: А = 18.3036; В = 3816.44; С = 46,13; Т = t + + 273, K.

Расчет интенсивности испарения по уравнению (37) будем проводить методом последовательных приближений в следующей последовательности: 1) задаем произвольно температуру поверхности тела t_p; 2) по этой температуре по уравнению Антуана рассчитываем давление насыщенного пара р_nas; 3) по уравнению (38) пересчитываем коэффициент теплоотдачи α в коэффициент массоотдачи β_с, который затем пересчитываем в коэффициент β_p по уравнению (39); 4) по уравнению (37) рассчитываем интенсивность испарения i₁; 5) по уравнению (28) определяем температуру поверхности тела t_p и сопоставляем ее с предварительно заданной; 6) при несовпадении рассчитанной температуры t_p с предварительно принятой по рассчитанной температуре t_p по уравнению Антуана определяем новое значение р_nas и повторяем расчет (вторая итерация). Итерации повторяем до нужного совпадения предыдущего и последующего значений t_p; 7) получив необходимое совпадение значений t_p, по уравнению (37) находим окончательно интенсивность испарения i₁.

По данной методике была рассчитана интенсивность испарения пленки воды толщиной δ = 0.1 мм с поверхности прутка полиамида PA-6 и продолжительность этого процесса для двух случаев проведения этого процесса (при температурах t_s = = 20°С и t_s = 127°С), результаты расчетов приведены в табл. 2.

Таблица 2.

Влияние электромагнитного энергоподвода на интенсивность сушки в первом периоде

t_s, ^оС	N_em = 0 кВт			N_em = 5 кВт
t_s, ^оС	t_m.t, ^оС	i₁, г/(м² ч)	τ_1, с	t_p, ^оС	i_1.em, г/(м² ч)	τ_1.em, с
20	6.8	199	1731	10.9	262	1313
127	37	1067	322	42.0	1402	245

Приведенные в табл.2 результаты расчетов показывают, что наложение электромагнитного поля в рассматриваемом примере приводит к интенсификации испарения как при низкой, так и при высокой температуре сушильного агента – за счет повышения температуры поверхности материала. Сравнительно небольшая мощность N_em (5 кВт) существенно повышает интенсивность испарения и, соответственно, сокращает продолжительность процесса. Это показывает целесообразность применения комбинированного (конвективно-электромагнитного) подвода для удаления поверхностной влаги.

ЗАКЛЮЧЕНИЕ

1. Развиты аналитические математические модели, описывающие нагрев цилиндра в условиях его сушки (для общего случая и для периода постоянной скорости сушки) при действующем внутри тела непрерывном постоянном электромагнитном источнике энергии и при конвективном тепло-и массообмене поверхности цилиндра с внешней газовой средой.

2. На основе полученных решений выполнен численный анализ процесса тепло- и массообмена применительно к глубокой сушке прутков полиамида PA-6, показывающий работоспособность полученных зависимостей как в условиях “чисто” электромагнитного, так и комбинированного “электромагнитно-конвективного” энергоподвода.

ОБОЗНАЧЕНИЯ

A_r = u_r/С_s	коэффициент распределения функции концентрационного равновесия, (кг/(кг сух. м-ла)/(кг/м³)
a	коэффициент температуропроводности цилиндра, м²/с
C_s	концентрация пара в ядре потока внешней фазы (в среде), кг/м³
c	массовая теплоемкость цилиндра, Дж/(кг К)
c_p	изобарная массовая теплоемкость азота, Дж/(кг К)
D_e	эффективный коэффициент диффузии влаги в непористых полимерах, м²/с
d =2R	диаметр прутка, м
F	поверхность прутка, м²
i	интенсивность сушки, кг/(м² с)
k	коэффициент массопроводности, м²/с
l	длина прутка, м
M	масса, кг
N_em	мощность электромагнитного источника, Вт
${{q}_{{\text{v}}}} = \frac{{{{N}_{{em}}}\eta }}{{V(1 - {{\varepsilon )}}}}$	внутренний объемный источник теплоты в цилиндре, Вт/м³
$q_{{\text{v}}}^{ * } = \frac{{{{q}_{v}}}}{{c{{\rho }}}}$	внутренний объемный источник теплоты в цилиндре, отнесенный к его объемной теплоемкости, °С/с
P = 0.98 × 10⁵	общее давление сушильного агента, Па
R	радиус цилиндра, м
R_v	отношение объема цилиндра к его поверхности, м
R* = 8.31	кДж(кмоль К) универсальная газовая постоянная
$R_{{par}}^{ * }$ = 462	газовая постоянная водяного пара, Дж/(кг К)
V	внутренний объем аппарата, м³
$r{\text{*}}$	теплота парообразования, включая теплоту десорбции влаги, Дж/кг
t	локальная температура в цилиндре, °С
$\bar {t}$	среднеобъемная температура цилиндра, °С
T	температура, К
$u,{\kern 1pt} \,\bar {u}$	локальное и среднее по объему цилиндра влагосодержание соответственно, кг/(кг сух. м-ла)
$u_{r}^{ * }$	приведенное равновесное влагосодержание, кг/(кг сух. м-ла)
r	радиальная координата, м
α	коэффициент теплоотдачи, Вт/(м² К)
β_с	коэффициент массоотдачи, отнесенный к разности концентраций пара в сушильном агенте, (кг/(м² с (кг/м³))
β_p	коэффициент массоотдачи, отнесенный к разности парциальных давлений пара, (кг/(м² с Па)
ε	доля свободного объема аппарата, м³/м³
δ	толщина пленки воды на поверхности прутка, м
$\lambda $	коэффициент теплопроводности цилиндра, Вт/(м К)
ρ	плотность материала цилиндра, кг/м³
ρ₀	плотность абсолютно сухого материала, кг/м³
w	вода
τ	время, с
${\text{Bi}} = \frac{{{{\alpha }}R}}{{{\lambda }}}$	число Био тепловое, безразмерное
${\text{B}}{{{\text{i}}}_{m}} = \frac{{{{{{\beta }}}_{c}}R}}{{k{{{{\rho }}}_{{\text{0}}}}{{A}_{r}}}}$	число Био массообменное, модифицированное, безразмерное
$\bar {E} = \frac{{\bar {u}({{\tau )}} - {{u}_{r}}}}{{{{u}_{n}} - {{u}_{r}}}}$	среднеобъемное относительное влагосодержание цилиндра, безразимерное
$Fo = {{a\tau } \mathord{\left/ {\vphantom {{a\tau } {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$	число Фурье тепловое, безразмерное
$F{{o}_{m}} = {{k\tau } \mathord{\left/ {\vphantom {{k\tau } {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$	число Фурье массообменное, безразмерное
Lu = k/a	число Лыкова, безразмерное
R_v	отношение объема тела к его поверхности, м

ИНДЕКСЫ

em	электромагнитный
k	конечный
m	массообменный
m.t	мокрый термометр
n	начальный
nas	состояние насыщения
p	поверхность цилиндра
par	пар
pl	пластина
r	равновесный
rab	рабочий
s	сушильный агент
sr	среднее значение
ts	цилиндр
v	отнесен к объему
w	вода
1	первый период сушки

Список литературы

Kudra T., Strumillo Cz. Thermal Processing of Bio-materials. Amsterdam: Gordon and Breach Science Publishers, 1998.
Акулич П.В., Драгун В.Л., Куц П.С. Технологии и техника сушки и термообработки материалов. Минск: Белорусская наука, 2006.
Ratti C., Mujumdar A. S. Handbook of Industrial Drying. 3rd edition. A.S. Mujumdar (Ed). Boca Raton, FL.: CRC Press, 2007.
Лыков А.В. Теория сушки. М.: Энергия, 1968.
Gunasekaran S. Pulsed microwave-vacuum drying of food materials // Drying Technology. 1999. V. 17. Is. 3. P. 395.
Bon J., Kudra T. Enthalpy-Driven Optimization of Intermittent Drying // Drying Technology. 2007. V. 25. Is. 4. P. 523.
Vaquiro H. A., Clemente G., Garcia-Perez J. V., Mulet A., Bonb J. Enthalpy-driven optimization of intermittent drying of Mangifera indica L. // Chemical engineering research and design. 2009. V. 87. P. 885.
Soysal Y., Arslan M., Keskin M. Intermittent microwave-convective air drying of Oregano // Food Science and Technology International. 2009. V. 15. Is. 4. P. 397.
Рудобашта С.П., Григорьев И.В. Импульсная инфракрасная сушка семян // Пром. теплотехника. 2011. Т. 33. № 8. С. 85.
Рудобашта С.П., Карташов Э.М., Зуев Н.А. Тепломассоперенос при сушке в осциллирующем электромагнитном поле // Теорет. основы хим. технологии. 2011. Т. 45. № 6. С. 641.
Esturk O. Intermittent and continuous microwave-convective air-drying characteristics of sage (Salvia officinalis) leaves // Food and Bioprocess Technology. 2012. V. 5. Is. 5. P. 1664.
Zhao D., An K., Ding S., Liu L., Xu Z., Wang Z. Two-stage intermittent microwave coupled with hot-air drying of carrot slices: Drying kinetics and physical quality // Food and Bioprocess Technology. 2014. V. 7. Is. 8. P. 2308.
Kumar C., Karim M.A., Joardder M.U.H. Intermittent drying of food products: A critical review // Journal of Food Engineering. 2014. V. 121. P. 48.
Kumar C., Joardder M.U.H., Farrell T.W., Millar G.J., Karim M.A. Mathematical model for intermittent microwave convective drying of food materials // Drying technology. 2016. V. 34. № 8. P. 962.
Гринчик Н.Н., Акулич П.В., Адамович А.Л., Куц П.С., Кундас С.П. Моделирование неизотермического тепло- и влагопереноса в капиллярнопористых средах при периодическом микроволновом нагреве // Инж.- физ. журнал. 2007. Т. 80. № 1. С.
Акулич П.В. Тепломассообмен капли раствора при комбинированном энергетическом воздействии и углублении зоны испарения // Инж.- физ. журн. 2016. Т. 89. № 3. С. 527.
Акулич П.В., Темрук А.В., Акулич А.В. Моделирование и эксперименталь ное исследование тепло- и влагопереноса при СВЧ-конвективной сушке растительных материалов. Инж.-физ. журн. 2012. Т. 85. № 5. С. 951.
Rudobashta S.P., Zueva G.A. Heat and mass transfer when drying a spherical particle in an oscillating electromagnetic field // Theor. Found. Chem. Eng. 2016. V. 50. Is. 5. P. 718.
Rudobashta S.P., Zueva G.A., Kartashov E.M. Heat and mass transfer in the drying of a cylindrical body in an oscillating electromagnetic field // J. Engineering Physics and Thermophysics. 2018. V. 91. № 1. January. P. 227.
Rudobashta S., Zueva G., Zuev N. Mathematical Modeling and Numerical Simulation of Oscillating Infrared Seeds Drying Process // Drying Technology. 2014. V. 32. № 11. P. 1352.
Rudobashta S., Zueva G. Drying of seeds through oscillating infrared heating // Drying Technology. 2016. V. 34. № 5. P. 505.
Rudobashta S.P., Kartashov E.M., Zueva G.A. Heat and Mass Transfer in Drying of a Plate in a Continuous High- and Superhigh-Frequency Electromagnetic Field // Theoret. Found. of Chem. Eng. 2021. V. 55. № 2. P. 261.
Лыков А.В. Теория теплопроводности. Москва: Высшая школа. 1968.
Карташов Э.М. Аналитические решения гиперболических моделей нестационарной теплопроводности // Тонкие химические технологии. 2018. Т. 13. № 2. С. 81.
Рудобашта С.П. Массоперенос в системах с твердой фазой. М.: Химия, 1980.
Рудобашта С.П., Карташов Э.М. Химическая технология: диффузионные процессы. Часть 1. М: Юрайт, 2015.
Рудобашта С.П., Карташов Э.М. Химическая технология: диффузионные процессы. Часть 2. М: Юрайт, 2015.
Рудобашта С.П., Зуева Г.А., Зайцев В.А. Моделирование процесса глубокой сушки гранулированного полиамида при конвективно-инфра- красном энергоподводе // Изв. вузов. Химия и хим. технология. 2019. Т. 62. Вып. 12. С. 94.
Справочник по пластическим массам. Под ред. М.И. Гарбара, М.С. Акутина, Н.М. Егорова. М.: Химия. 1967.
Rudobashta S.P., Dmitriev V.M. Kinetics and apparatus-technological arrangement of convective drying of disperse polymer materials // J. Eng. Phys. Thermophys. 2005. V. 78. № 3. P. 463.
Рудобашта С.П., Плановский А.Н. Исследование кинетики сушки при переносе влаги в материале по закону молекулярной диффузии // Теорет. основы хим. технологии. 1976. Т. X. № 2. С. 197.
Krischer O. Die wissenchaftlichen Grundlagen der Trocknung Technick. Heidelberg: Springer-Verlag, 1957.
Рабинович О.М. Сборник задач по технической термодинамике. М.: Машиностроение, 1969.
Лыков А.В. Теория сушки. М.-Л.: Госэнергоиздат, 1950.
Рид Р., Праусниц Дж., Шервуд Т. Свойства газов и жидкостей. Л.: Химия, 1982.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал