Теоретические основы химической технологии, 2022, T. 56, № 5, стр. 633-647
Синтез и уплотнение нитрида циркония, используя оксид циркония и подачу воздуха
А. А. Марков *
Институт проблем механики им. А.Ю. Ишлинского РАН РФ
119526 Москва, пр-т Вернадского, д. 101, корп. 1, Россия
* E-mail: markov.ipm@yandex.ru
Поступила в редакцию 06.04.2021
После доработки 06.04.2022
Принята к публикации 16.06.2022
- EDN: MPCVKP
- DOI: 10.31857/S0040357122050116
Аннотация
Развита многотемпературная модель сопряженного теплообмена синтеза нитрида циркония. Модель включает температуру твердой фазы состоящей из микронных частиц ${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}$, ${\text{C}}$, ${\text{ZrN}}$, температуру газовой фазы компонент ${\text{CO,C}}{{{\text{O}}}_{{\text{2}}}},{{{\text{O}}}_{{\text{2}}}},{{{\text{N}}}_{2}}$, температуру корпуса реактора из пористого графита и температуру слоя вольфрамового сплава к электродам которого приложена разность потенциалов. Исследованы режимы работы с многостадийным потоком воздуха на входе в реактор с целью снижения примеси углерода. Продемонстрировано снижение пористости на три порядка по сравнению со значением в начальный момент времени. Результаты удовлетворительно согласуются с экспериментальными данными.
ВВЕДЕНИЕ
Нитрид циркония привлекает все больше и больше внимания в последнее десятилетие благодаря сочетанию в себе превосходных термических, механических и электрических свойств, высокой температуры плавления, твердости и высоких прочностных характеристик [1]. Также нитрид циркония применяется в качестве защитных износостойких покрытий деталей, контактирующих с агрессивными средами, является заменителем нитрида урана для оптимизации параметров процесса изготовления нитридного топлива, которое используются в космических энергетических реакторах [1, 2] и для усовершенствования аварийно-стойкого топлива для реакторов [3, 4]. Керамика на основе нитрида циркония применятся в электротехнике и атомном материаловедении. Карбид циркония ${\text{ZrC}}$ и керамика ${\text{ZrN}}$ представляют интерес для использования при экстремально высоких температурах, ${\text{ZrC}}$ и ${\text{ZrN}}$ обладают ценными характеристиками, такими как высокая теплопроводность и электропроводность. Представленные в литературе данные часто страдают разбросом из-за различий в методах обработки и сложности определения стехиометрии синтеза нитрида и карбида циркония, что существенно влияет на теплофизические свойства [1]. Однако методы обработки этих материалов могут изменить содержание примесей, таких как кислород в ${\text{ZrC}}$ и кислород и углерод в ${\text{ZrN}}$ [1–7]. Цирконий обладает замечательной способностью гореть в кислороде воздуха (температура самовоспламенения – 250°С) практически без дыма и с высокой скоростью. При этом развивается самая высокая температура для металлических топлив (4650°С). Были проведены эксперименты по использованию горения циркония в качестве источника света для накачки лазера. Нитриды циркония и гафния тугоплавки (>2500°С) и близки по твердости к сверхтвердым материалам [5, 6]. Эти материалы, обладая высокой тепло- и электропроводностью [1, 6, 7], находят применение в микроэлектронике [6, 8].
Для получения ${\text{ZrC}}$ и ${\text{ZrN}}$ используется метод самораспространяющегося высокотемпературного синтеза (СВС) [9–11] и метод химического осаждения из газовой фазы [1, 7, 8]. Осуществлен способ получения нитрида циркония на основе СВС путем обжига смеси, состоящей из оксида циркония и энергетического компонента, в присутствии азотирующего агента. При этом промежуточные продукты тушат, прерывая процесс горения через 20–90 с после инициирования, а в экзотермическую смесь дополнительно вводят активирующую добавку нанопорошка оксидов. Синтез карбидных и нитридных материалов обычно включает прямую реакцию с металлом, гидридом металла или оксидом металла, при этом оксид металла является основным прекурсором при переработке отработавшего топлива [1, 9–19].
Метод синтеза оксидов сжиганием углерода (CCSO) [20] стимулировал теоретические исследования [21–26]. Разработана вычислительная методика численного моделирования тепловых процессов [22]. С помощью численного моделирования были предсказаны движение теплового фронта и динамика газового потока, а также скорость роста частиц при CCSO. Предложены модели осреднения на основе взаимопроникающих континуумов, в которых утраченная детальная информация на микромасштабах, такая как конфигурация межфазных границ и др., представляется в виде коэффициентов тепло- и массообмена [27–33]. Концентрационная и тепловая дисперсия важны в усредненных уравнениях наряду с молекулярной диффузией тепла и вещества [27–33]. Рассеяние массы и тепла вызываются флуктуациями массового и теплового потока в осредненном движении, а диффузия – движением молекул. В работах [25–33] изучались различные модели тепловой дисперсии. Наряду с упомянутыми моделями осреднения развивается и прямое моделирование течения в пористой структуре – см., например, [34].
Моделирование синтеза материалов развивалось в работах [21–26] в приближении постоянных размеров пор, заданных априори. Следует отметить, что размеры пор, как правило, распределены в реакторе синтеза неравномерно, размеры пор изменяются во времени, влияя на потоки тепла и массы реагентов и продуктов через пористую среду. Градиенты температуры и концентрации приводят к изменению объема и возникновению смещений и напряжений в твердой фазе. В [35–38] рассмотрены модели спекания и синтеза порошковых смесей твердой фазы с учетом взаимного влияния процессов объемных изменений в процессе спекания. Тепловое расширение является важной характеристикой композиционного топливного материала, такого как UN, диспергированного в ZrN. К сожалению, в литературе мало исследований механизма карботермического восстановления и азотирования ${\text{ZrN}}$ с использованием в качестве реагента оксида ${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}$ [1–3, 13–19]). Отмечалось зарождение фракций ${\text{Zr}}{{{\text{C}}}_{x}}{{{\text{N}}}_{y}}$ и диффузии углерода в реакционный слой, что приводит к удалению углерода до появления ядра из ${\text{ZrN}}$.
В работах [35, 37] исследуется эффект концентрационного расширения твердой фазы в условиях межфазного тепломассообмена. Учтено объемное изменение при синтезе титаната бария ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ на основе двухфазной модели теплового и массового рассеяния [37, 38]. Предложена теоретическая модель, позволяющая прогнозировать характеристики волны горения, движущейся в образце переменной пористости, при поверхностном типе горения. Моделирование синтеза титаната бария проведено в осесимметричном реакторе искрового плазменного спекания (SPS-spark plasma sintering) [2, 4, 19], с каналом для подачи газа и с электропроводящим слоем вольфрамового сплава для нагрева смеси реагентов и инициирования горения, уплотнения и спекания продукта синтеза. Используется формула нестационарного изменения пористости в зоне синтеза при заданном распределении пористости в начальный момент времени [38]. Изучено влияние переменной пористости на процессы синтеза микронных частиц с термическим и массовым рассеянием, сопровождающимся конвективным и кондуктивным тепломассообменом.
В данной работе обобщается модель реактора SPS с графитовой оболочкой малой пористости и с подачей газа по каналу, специально расположенному в реакторе вблизи границы зоны синтеза, заполненной мелкодисперсным реагентом. Рассмотрен двух-стадийный процесс получения нитрида циркония, основанный на сжигании смеси, состоящей из циркония и азотирующего потока воздуха,который пропускают над смесью реагентов синтеза нитридов. Инициирование синтеза, уплотнения и спекания нитрида циркония осуществляется за счет регулируемого во времени тепловыделения при пропускании электрического тока через вольфрамовый канал. Степень азотирования регулируется интенсивностью потока воздуха (смеси азота и кислорода), подаваемого на входе в реактор. Для моделирования синтеза нитрида циркония наряду с уплотнением и спеканием применяются результаты теплового и концентрационного расширения [37, 38] и результаты термопластичности [40–43]. Моделирование мелкодисперсных частиц нитрида циркония в реакторе рассмотрено на основе уравнений макро-сохранения, записанных в безразмерных переменных. Проведено моделирование синтеза нитрида циркония методом горения и уплотнения на основе модели Олевского [42] в осесимметричном реакторе. Полученные результаты показывают существенное влияние объемных изменений твердой фазы. Предложенная модель позволяет анализировать скорость синтеза, уплотнения и распределение продукта в зоне синтеза, а также уменьшать примесь углерода в нитриде циркония. В данной работе представлены результаты моделирования для частиц размером более микрона. Это исследование обобщает результаты [39] в следующих направлениях. Рассмотрена модель синтеза нитрида циркония, основанная на многоступенчатой подаче воздуха вместо чистого дорогостоящего азота и оксида циркония вместо чистого циркония. Исследованы режимы синтеза для различных входных данных. Представлены результаты моделирования, демонстрирующие устранение примесей углерода в синтезированном продукте.
Отметим, что для микронных размеров синтезированных частиц характерное значение числа Кнудсена мало, а эффекты скольжения и скачков температуры [44] пренебрежимо малы. Однако при субмикронных размерах частиц и пор влияние слоев Кнудсена в газе вблизи поверхности пор становится существенным и необходимо учитывать эффекты скольжения [21].
ОПИСАНИЕ МОДЕЛИ
В исследованиях механизма карботермического восстановления и азотирования ${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}$ [18, 45–49] сообщалось о стадии азотирования ${\text{ZrC}}$ в атмосфере 10% легированного ${{{\text{H}}}_{{\text{2}}}}{\kern 1pt} - {\kern 1pt} {{{\text{N}}}_{{\text{2}}}}$ при 1800–1873 K в течение 4–24 ч. Заметим, что кинетика синтеза ${\text{ZrN}}$ характеризуется широким диапазоном применения стехиометрии [1–3, 13–18]. Азотирование ${\text{ZrN}}$ и спекание ${\text{ZrN}}$ сопровождается многостадийной подачей связанного азота [6, 45–49]. Интересно, что применение высокого давления приводит к увеличению отношения азота в порошках. Предполагается, что холодное прессование с повышенной нагрузкой до применения процесса SPS приводит к увеличению площади контакта с частицами, что приводит к уменьшению количества открытых пор, которые воздействуют на быструю диффузию азота [12]. Предлагаемая модель основана на синтезе нитрида циркония в SPS реакторе, дополненном протоком для подачи газа [39].
Кинетика синтеза ZrN. В модели компонентами газовой и твердой фазы являются соответственно: ${{{\text{N}}}_{{\text{2}}}}{\text{(g),}}\,{{{\text{O}}}_{2}}{\text{(g),}}$ $\,{\text{CO(g)}},\,{\text{C}}{{{\text{O}}}_{2}}{\text{(g)}}$ и ${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}{\text{(s),}}$ ${\text{C(s),}}$ ${\text{Zr}}{{{\text{O}}}_{{{\text{2}}{{x}_{\nu }}}}}$. ${{{\text{N}}}_{{4{{x}_{\nu }}/3}}}{\text{(s)}},{\text{ZrN(s)}}$. Рассмотрены следующие реакции
(1)
$\begin{gathered} \left( {{\text{2}}{\kern 1pt} - {\kern 1pt} {\text{2}}{{{\text{a}}}_{{{{{\text{O}}}_{{\text{2}}}}}}}} \right){\text{Zr}}{{{\text{O}}}_{{\text{2}}}}{\text{(s)}}\,\,{\text{ + }}\,\,\left( {{\text{1}}{\kern 1pt} - {\kern 1pt} {{{\text{a}}}_{{{{{\text{O}}}_{{\text{2}}}}}}}} \right){{{\text{N}}}_{{\text{2}}}}{\text{(g)}}\,\,{\text{ + }}{\kern 1pt} \\ {\text{ + }}\,\,{{{\text{a}}}_{{{{{\text{O}}}_{{\text{2}}}}}}}{{{\text{O}}}_{{\text{2}}}}{\text{(g)}}\,\,{\text{ + }}\,\,\left( {{\text{4}}{\kern 1pt} - {\kern 1pt} {\text{2}}{{{\text{a}}}_{{{{{\text{O}}}_{{\text{2}}}}}}}} \right){\text{C(s)}} \to \\ \to \left( {{\text{2}}{\kern 1pt} - {\kern 1pt} {\text{2}}{{{\text{a}}}_{{{{{\text{O}}}_{{\text{2}}}}}}}} \right){\text{ZrN(s)}}\,\,{\text{ + }}\,\,\left( {{\text{4}}{\kern 1pt} - {\kern 1pt} {\text{2}}{{{\text{a}}}_{{{{{\text{O}}}_{{\text{2}}}}}}}} \right){\text{CO(g),}} \\ \end{gathered} $(2)
${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}{\text{(s)}}\,\,{\text{ + }}\,\,{\text{CO}}\left( {\text{g}} \right) \to {\text{ZrO}}\left( {\text{g}} \right)\,\,{\text{ + }}\,\,{\text{C}}{{{\text{O}}}_{{\text{2}}}}\left( {\text{g}} \right),$(3)
${\text{ZrO}}\left( {\text{g}} \right)\,\,{\text{ + }}\,\,{\text{CO}}\left( {\text{g}} \right) \to {\text{Zr}}{{{\text{C}}}_{{{{x}_{\nu }}}}}{{{\text{O}}}_{{{{y}_{\nu }}}}}\left( {\text{s}} \right)\,\,{\text{ + }}\,\,{\text{C}}{{{\text{O}}}_{{\text{2}}}}\left( {\text{g}} \right),$(5)
${\text{2CO(g)}}\,\,{\text{ + }}\,\,{{{\text{O}}}_{2}}{\text{(g)}} \to {\text{2C}}{{{\text{O}}}_{2}}{\text{(g),}}$(6)
${\text{Zr}}{{{\text{C}}}_{{{{x}_{\nu }}}}}{{{\text{O}}}_{{{{y}_{\nu }}}}}\left( {\text{s}} \right) \to {{x}_{\nu }}{\text{ZrC}}\,\,{\text{ + }}\,\,{\text{0}}{\text{.5}}{{y}_{\nu }}{{{\text{O}}}_{2}}{\text{(g)}}{\text{.}}$В реакциях компоненты твердой фазы диффундируют и перемещаются в твердой фазе [1, 5].
Коэффициенты расширения. Определяющая система уравнений включает уравнения сохранения массы, энергии и импульса для газовой фазы и уравнения термоупругости и термопластичности, основанные на соотношениях Дюамеля–Неймана и модели [35] для твердой фазы. Используем для компонент тензора напряжений обобщенные соотношения Дюамеля–Неймана (для изотропного линейно упругого тела соотношения Дюамеля–Неймана, представляют закон Гука)
Положим $\left( {2{{\mu }_{{S1}}} + 3{{\mu }_{{S2}}}} \right) = 3{{\mu }_{S}}$, тогда
Переменная пористость смеси реагентов и продукта синтеза титаната бария находится с учетом эффектов теплового и концентрационного расширения компонент газовой и твердой фазы по формуле [38, 39]
(7)
$\chi (t,x,r) = \frac{{\chi (0,x,r)}}{{\chi (0,x,r) + \left( {1 - \chi (0,x,r)} \right)\left( {1 + E(t,x,r)} \right)}},$(8)
${{\zeta }_{p}} = - \frac{K}{{P(0,x,r)}}\left( {{{\omega }_{T}}(0,x,r) + {{\omega }_{S}}(0,x,r)} \right).$Определяющее уравнение термопластичности для SPS. Электропластичность обычно изучалась путем измерения напряжения, необходимого для деформации полностью плотных металлических образцов с электрическим током и без него при низких или высоких температурах [7, 8]. Предполагаем, что пластическая деформация материала активируется термически, скорость деформации $\dot {\gamma }$ может быть выражена следующим образом [40, 43]: $\dot {\gamma } = {{\dot {\gamma }}_{0}}\exp \left( {\frac{{ - E_{{pl}}^{{}}}}{{RT}}} \right)$, где – $E_{{pl}}^{{}}$ энергия активации (кДж/моль), Т, абсолютная температура (К). Далее применяется модель [40], основанная на степенном законе пластичности $\sigma \left( W \right) = {{A}_{m}}{{W}^{m}}$, для пористого вязкого материала, ${{A}_{m}} = \frac{{{{A}_{0}}T}}{{{{r}_{p}}}}{{\left( {\frac{d}{b}} \right)}^{p}}\exp \left( {\frac{{ - E_{{pl}}^{{}}}}{{RT}}} \right)$, где $d = 1,$ $b = 0.05,$ $p = 1,1$, ${{A}_{0}}$,${{A}_{m}}$, – коэффициенты ползучести для степенного закона, ${{r}_{p}}$ – размер частиц, ${{r}_{p}} \sim 5 \times {{10}^{{ - 7}}}$, T – абсолютная температура, R – газовая постоянная, $E_{{pl}}^{{}}$ – энергия активации ползучести [42]. Далее считаем, $\frac{{\sigma \left( W \right)}}{W} = {{r}_{p}}A_{m}^{m}{{W}^{{m - 1}}}$ где W – эквивалентная скорость деформации. Скорость уплотнения $\dot {\gamma }$ и изменения формы $\dot {e}$ являются функциями компонентов тензора скорости деформации ${{\dot {\varepsilon }}_{{ij}}}$ [41]
Величина эквивалентной скорости деформации W для пористого материала определяется следующим образом:
Для степенной скорости деформации, эквивалентной пластичности (ползучести,) пористого твердого тела вводятся две функции пористости: нормализованный модуль сдвига $\varphi = {{\left( {1 - \chi } \right)}^{2}}$ и нормализованный модуль объемной упругости $\psi = \frac{2}{3}\frac{{{{{\left( {1 - \chi } \right)}}^{3}}}}{\chi }$. Основываясь на континуальной теории спекания [41–43], определяющее уравнение, описывающее горячее прессование нелинейно-вязкого пористого материала с жесткой матрицей, выражается как:
(9)
${{\sigma }_{{ij}}} = \frac{{\sigma \left( W \right)}}{W}\left[ {\varphi {{{\dot {\varepsilon }}}_{{ij}}} + \left( {\psi - \frac{1}{3}\varphi } \right)\left( {{{P}_{{ex}}} + {{P}_{g}}} \right){{\delta }_{{ij}}}} \right] + {{P}_{L}}{{\delta }_{{ij}}}.$Рассмотрим ${{\dot {\varepsilon }}_{r}} = 0$ [42], в этом случае для скорости уменьшения пористости при уплотнении (также называемой определяющим уравнением для нелинейно-вязкого уплотнения) справедливо следующее соотношение
(10)
$\dot {\chi } = - A_{m}^{{ - 1}}{{\left( {\frac{{3\chi }}{2}} \right)}^{{\frac{{m + 1}}{{2m}}}}}{{\left( {1 - \chi } \right)}^{{\frac{{m - 3}}{{2m}}}}}{{\left( {\frac{{{{\sigma }_{{tot}}}}}{{{{r}_{p}}}}} \right)}^{{\frac{1}{m}}}}.$Расчет изменения пористости в двухстадийном реакторе синтеза-уплотнения проводится по формулам
(11)
$\begin{gathered} \dot {\chi }(t,x,r) = {{{\dot {\chi }}}_{1}}(t,x,r) + {{{\dot {\chi }}}_{2}}(t,x,r), \\ \chi (0,x,r) = {{\chi }_{0}}, \\ \end{gathered} $(12)
$\begin{gathered} {{\chi }_{1}}(t,x,r) = \\ = \frac{{{{\chi }_{0}}\left( {1 + {{\omega }_{g}}(t,x,r)} \right)}}{{{{\chi }_{0}}\left( {1 + {{\omega }_{g}}(t,x,r)} \right) + \left( {1 - {{\chi }_{0}}} \right)\left( {1 + E(t,x,r)} \right)}}, \\ \end{gathered} $(13)
$\begin{gathered} {{{\dot {\chi }}}_{2}}(t,x,r) = - \left[ {\frac{{{{r}_{p}}}}{{{{A}_{0}}T}}{{{\left( {\frac{b}{d}} \right)}}^{p}}\exp \left( {\frac{{ - Q}}{{RT}}} \right)} \right] \times \\ \times \,\,{{\left( {\frac{{3\chi }}{2}} \right)}^{{\frac{{m + 1}}{{2m}}}}}{{\left( {1 - \chi } \right)}^{{\frac{{m - 3}}{{2m}}}}}{{\left( {\frac{{{{\sigma }_{z}}}}{{{{r}_{p}}}}} \right)}^{{\frac{1}{m}}}}. \\ \end{gathered} $Безразмерные переменные. Применяем ниже безразмерные переменные, отмеченные тильдой [38, 39],
(14)
$\begin{gathered} {{{\tilde {c}}}_{{pg}}} = \frac{{{{C}_{{pg}}}}}{{{{c}_{p}}}},\,\,\,\,\tilde {D} = \frac{D}{{{{D}_{0}}}};\,\,\,\,{{\mu }_{0}} = {{\rho }_{0}}{{\nu }_{{air}}},\,\,\,\,{{\rho }_{{1S}}} = {{\rho }_{C}}, \\ {{\rho }_{{2S}}} = {{\rho }_{{{\text{Zr}}{{{\text{O}}}_{{\text{2}}}}}}},\,\,\,\,{{\rho }_{{3S}}} = {{\rho }_{{{\text{ZrC}}}}}, \\ {{\rho }_{{4S}}} = {{\rho }_{{{\text{Zr}}{{{\text{C}}}_{{\text{x}}}}{{{\text{N}}}_{{\text{y}}}}}}},\,\,\,\,{{\rho }_{{5S}}} = {{\rho }_{{{\text{ZrN}}}}}, \\ {{{\tilde {\rho }}}_{{lS}}} = \frac{{{{\rho }_{{lS}}}}}{{{{\rho }_{{0{\text{Zr}}}}}}},\;\;\,l = 1,...,5; \\ {{\rho }_{S}} = {{\rho }_{{1S}}} + ... + {{\rho }_{{5S}}},\,\,\,\,{{\rho }_{g}} = {{\rho }_{{1g}}} + ... + {{\rho }_{{4g}}}, \\ {{{\tilde {c}}}_{{pg}}} = \frac{{{{C}_{{pg}}}}}{{{{c}_{p}}}},\,\,\,\,{{{\tilde {D}}}_{m}} = \frac{{{{D}_{m}}}}{{{{D}_{0}}}},\,\,\,\,{{{\tilde {\lambda }}}_{g}} = \frac{{{{\lambda }_{{air}}}}}{{{{\lambda }_{0}}}}, \\ {{{\tilde {\lambda }}}_{S}} = \frac{{{{\lambda }_{S}}}}{{{{\lambda }_{0}}}},\,\,\,{{{\tilde {c}}}_{S}} = \frac{{{{C}_{S}}}}{{{{c}_{p}}}},\,\,\,{\text{M}}{{{\text{a}}}^{{ - 2}}} = \frac{{{{\gamma }_{{air}}}{{p}_{0}}}}{{{{\rho }_{0}}u_{0}^{2}}}, \\ \operatorname{Re} = \frac{{l_{0}^{2}\,\,}}{{{{t}_{0}}{{\nu }_{{air}}}}},\,\,\,\,{{\operatorname{R} }_{{solid}}} = {{p}_{0}}{{\left( {{{\zeta }_{p}}{{\mu }_{{S0}}}} \right)}^{{ - 1}}}, \\ \end{gathered} $Здесь ${{t}_{9}} = 1{\kern 1pt} - {\kern 1pt} 10\left( {\text{s}} \right),$ ${{l}_{0}} = 0.018\,\,\left( {\text{m}} \right)$, $A = l_{0}^{2}\,\,({{{\text{m}}}^{2}})$, $V = l_{0}^{3}\,\,({{{\text{m}}}^{3}})$, ${{c}_{p}} = {{C}_{{p,air}}} = $ $ = 1114\,\,({{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{K}}}} \right. \kern-0em} {\text{K}}}}}} \right. \kern-0em} {{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{K}}}} \right. \kern-0em} {\text{K}}}}})$, ${{\rho }_{0}} = {{\rho }_{{air}}} = 0.4\,\,({\text{kg}}\,{{{\text{m}}}^{{ - 3}}}),$ ${{\lambda }_{0}} = {{\lambda }_{{air}}} = 0.06\;({{\text{W}} \mathord{\left/ {\vphantom {{\text{W}} {{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{K}}}} \right. \kern-0em} {\text{K}}}}}} \right. \kern-0em} {{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{K}}}} \right. \kern-0em} {\text{K}}}}})$, ${{D}_{0}} = 2 \times {{10}^{{ - 5}}}\,\,({{{{{\text{m}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\text{m}}}^{2}}} {\text{s}}}} \right. \kern-0em} {\text{s}}})$, ${{\mu }_{{S0}}} = 2 \times {{10}^{9}}\,\,\left( {{\text{Pa}}} \right)$, ${{\nu }_{{air}}} = $ $ = 9.7\, \times \,{{10}^{{ - 5}}}\,({{{{{\text{m}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\text{m}}}^{2}}} {\text{s}}}} \right. \kern-0em} {\text{s}}}),$ ${{\lambda }_{{el}}}\, = \,178\,({\text{W}}{{{\text{m}}}^{{ - 1}}}\,{{{\text{K}}}^{{ - 1}}}),$ ${\text{P}}{{{\text{e}}}_{{el}}} = $ $ = 0.000945,$ ${{j}_{0}} = 3500\,\,\left( {\text{A}} \right)$, ${\text{P}}{{{\text{e}}}_{{gr}}} = 3.132$, ${{\rho }_{{el}}} = $ $ = 1.93 \times {{10}^{4}}\;({\text{kg}}\,{{{\text{m}}}^{{ - 3}}}),$ ${{c}_{{p,el}}} = 24.27\;({\text{J}}\,\,{\text{mo}}{{{\text{l}}}^{{ - 1}}}\,\,{{{\text{K}}}^{{ - 1}}}),$ ${{E}_{{el,0}}} = 100\,\,({\text{V}}\,\,{{{\text{m}}}^{{ - 1}}})$, ${{\varphi }_{0}} = {{l}_{0}}{{E}_{{el,0}}}\,\,\left( {\text{V}} \right)$, ${{\sigma }_{{el,0}}} = $ $ = {{{{j}_{0}}} \mathord{\left/ {\vphantom {{{{j}_{0}}} {{{E}_{{el,0}}}}}} \right. \kern-0em} {{{E}_{{el,0}}}}}\,({{{\text{m}}}^{{ - 1}}}\,\,{\text{O}}{{{\text{m}}}^{{ - 1}}})$, ${{R}_{{el}}}\, = \,2\, \times \,{{10}^{{ - 7}}}{\kern 1pt} - {\kern 1pt} 2\, \times \,{{10}^{{ - 5}}}\,\left( {{\text{m}}\,{\text{Om}}} \right)$, ${{j}_{0}} = 3500\,\,\left( {\text{A}} \right)$.
${{T}_{g}},\,{{T}_{S}}$ – температура газа и смеси твердых компонентов, ${{T}_{{gr}}},\,{{T}_{{el}}}$ – температура графитовой оболочки вольфрамового канала . Температура находится по формуле
Величина $\beta = {{{{R{{T}_{0}}} \mathord{\left/ {\vphantom {{R{{T}_{0}}} E}} \right. \kern-0em} E}}_{{comb}}}$ – безразмерный параметр, характеризующий энергию активации горения ${{E}_{{comb}}}$, ${{\beta }_{{pl}}} = {{R{{T}_{0}}} \mathord{\left/ {\vphantom {{R{{T}_{0}}} {{{E}_{{pl}}}}}} \right. \kern-0em} {{{E}_{{pl}}}}}$ – безразмерный параметр, характеризующий энергию активации пластичности, $\beta = 0.084,$ ${{\beta }_{{pl}}} = 0.05$. Величины $R,\,E,\,Q$ – газовая постоянная, энергия активации, тепловой эффект горения; $p = {{\rho }_{g}}{{T}_{0}}\left( {1 + \beta {{{\tilde {T}}}_{g}}} \right)$ – давление газа; ${{\kappa }_{0}}$ – безразмерный коэффициент теплоотдачи; ${{\tilde {c}}_{S}},\,{{\tilde {c}}_{{pg}}}$ – теплоемкость; ${{\tilde {\lambda }}_{{{\kern 1pt} S}}},{{\tilde {\lambda }}_{{{\kern 1pt} g}}}$ – теплопроводность, $\tilde {D}$ – коэффициент диффузии; ${\text{Ma}},\;\operatorname{Re} $ – числа Маха и Рейнольдса; ${\text{P}}{{{\text{e}}}_{{{\kern 1pt} T}}},\,{\text{P}}{{{\text{e}}}_{{{\kern 1pt} 1}}}$ – тепловое и диффузионное числа Пекле, индекс относится к параметрам воздуха при нормальных условиях.
Приведем основные уравнения в виде, допускающем регулярный предельный переход $\chi \to 0$ и $\chi \to 1$, [38, 39]. Система уравнений представлена ниже в безразмерных переменных, знак тильды опущен.
Уравнения сохранения плотности фаз
(15)
$\begin{gathered} \frac{{\partial \chi {{\rho }_{g}}}}{{\partial t}} + \nabla \cdot \left( {\chi {{\rho }_{g}}{\mathbf{u}}} \right) = - {{J}_{{g \to S}}}, \\ \frac{{\partial \left( {1 - \chi } \right){{\rho }_{S}}}}{{\partial t}} = {{J}_{{g \to S}}},\,\,\,\,{{J}_{{g \to S}}} = \frac{{{{M}_{{1g}}}}}{{{{M}_{{1S}}}}}{{J}_{{1S}}}. \\ \end{gathered} $Уравнение сохранения массы для компонента азота
(16)
$\frac{{\partial \chi {{\rho }_{g}}}}{{\partial t}} + \nabla \cdot \left( {\chi {{\rho }_{g}}{\mathbf{u}}} \right) = - \frac{{{{M}_{{1g}}}}}{{{{M}_{{1S}}}}}J_{{1S}}^{{}},\,\,\,\,{{\rho }_{{N2}}} = {{\rho }_{g}}.$В реакциях для компонентов твердой фазы реагенты не смешиваются на молекулярном уровне, диффундируют и перемещаются внутри твердой фазы. Уравнение сохранения массы твердой фазы можно записать в виде
(17)
$\frac{{\partial \left( {1 - \chi } \right){{\rho }_{{1S}}}}}{{\partial t}} = - J_{{1S}}^{{}},\,\,\,\,\frac{{\partial \left( {1 - \chi } \right){{\rho }_{{2S}}}}}{{\partial t}} = \frac{{{{M}_{{2S}}}}}{{{{M}_{{1S}}}}}J_{{1S}}^{{}},$Уравнение движения газа в порах [19–22] имеет вид:
(18)
$\begin{gathered} \frac{{\partial \chi {{\rho }_{g}}{\mathbf{u}}}}{{\partial t}} + \nabla \cdot \left( {\chi {{\rho }_{g}}{\mathbf{uu}}} \right) + {\text{M}}{{{\text{a}}}^{{ - 2}}}\nabla p = \\ = {{\operatorname{Re} }^{{ - 1}}}\nabla \cdot {\mathbf{\tau }} + {{{\mathbf{S}}}_{{\mathbf{V}}}}, \\ {\mathbf{\tau }} = \mu \left[ {\nabla {\mathbf{u}} + {{{\left( {\nabla {\mathbf{u}}} \right)}}^{T}} - \frac{2}{3}\left( {\nabla \cdot {\mathbf{u}}} \right){\mathbf{I}}} \right], \\ \end{gathered} $Запишем уравнение фазы движения твердого тела в простейшем случае, пренебрегая влиянием работы механических напряжений на температурное поле [38, 39]
(19)
$\begin{gathered} \frac{{\partial \left( {1 - \chi } \right){{\rho }_{S}}\,{{{\text{V}}}_{{solid}}}}}{{\partial \,t}} + \nabla \cdot \left[ {\left( {1 - \chi } \right){{\rho }_{S}}{{{\text{V}}}_{{solid}}}{{{\text{V}}}_{{solid}}}} \right] = \\ = \operatorname{R} _{{solid}}^{{ - 1}}\nabla \cdot \sigma ,\,\,\,\,{{\sigma }_{{ij}}} = 2{{\mu }_{{S1}}}{{\varepsilon }_{{ij}}} + {{\delta }_{{ij}}}\left( {{{\mu }_{{S2}}}\sum\limits_k {{{\varepsilon }_{{kk}}}} - K\omega } \right), \\ \end{gathered} $Уравнение теплового баланса газовой фазы с учетом дисперсии записывается в виде
(20)
$\begin{gathered} {{\rho }_{g}}{{c}_{{pg}}}\chi \left( {\frac{{\partial {{T}_{g}}}}{{\partial t}} + {\mathbf{u}} \cdot \nabla {{T}_{g}}} \right) + {{c}_{g}}{{T}_{g}}\chi {{J}_{{S \to g}}} = \\ = \nabla \cdot \left( {\chi \frac{{{{{\text{D}}}_{{{\text{Tg}}}}}}}{{{\text{P}}{{{\text{e}}}_{{Tg}}}}}\nabla {{T}_{g}}} \right) - \kappa \chi \left( {1 - \chi } \right)\left( {{{T}_{g}} - {{T}_{S}}} \right) + \chi {{Q}_{r}}, \\ \end{gathered} $${{Q}_{r}} = Q_{r}^{0}{{\chi }^{2}}\left( {1 - \chi } \right){{\left( {\frac{{{{\rho }_{{1g}}}}}{{{{M}_{{1g}}}}}} \right)}^{2}}{{k}_{1}}\exp \left( {\frac{{{{T}_{g}}}}{{\beta {{T}_{g}} + 1}}} \right)$ – тепловой поток химического превращения, ${{{\text{D}}}_{{{\text{Tg}}}}} = \left( {\begin{array}{*{20}{c}} {{{\lambda }_{{{\kern 1pt} 1g}}}}&0 \\ 0&{{{\lambda }_{{{\kern 1pt} 2g}}}} \end{array}} \right)$, ${{\lambda }_{{{\kern 1pt} 1g}}} = {{\lambda }_{g}}\left[ {\xi + {{\varphi }_{{{\kern 1pt} 1}}}\left( {{\text{P}}{{{\text{e}}}_{{{\kern 1pt} 1t}}}} \right)} \right],$ ${{\lambda }_{{{\kern 1pt} 2g}}} = {{\lambda }_{g}}\left[ {\xi + {{\varphi }_{{{\kern 1pt} 2}}}\left( {{\text{P}}{{{\text{e}}}_{{{\kern 1pt} 2t}}}} \right)} \right]$ – тензор [38] учитывающий продольную и поперечную дисперсию.
Уравнение теплового баланса твердой фазы имеет вид
(21)
$\begin{gathered} {{\rho }_{S}}{{c}_{S}}\left( {1 - \chi } \right)\left( {\frac{{\partial \,{{T}_{S}}}}{{\partial \,t}} + {{{\text{V}}}_{{solid}}} \cdot \nabla {{T}_{S}}} \right) = \\ = \nabla \cdot \left[ {\left( {1 - \chi } \right)\frac{{{{\lambda }_{S}}}}{{{\text{P}}{{{\text{e}}}_{{Ts}}}}}\nabla {{T}_{S}}} \right] + \\ + \,\,\kappa \chi \left( {1 - \chi } \right)\left( {{{T}_{g}} - {{T}_{S}}} \right) + \left( {1 - \chi } \right){{Q}_{r}}. \\ \end{gathered} $Коэффициент теплообмена между газовой и твердой фазами описывается формулой Левека [22, 53] в виде $\kappa = {{\kappa }_{0}}\left( {1 + \operatorname{Re} _{{loc}}^{{0.3}}{\text{Pe}}_{{Tloc}}^{{0.3}}} \right)$. Здесь ${{\operatorname{Re} }_{{loc}}} = \operatorname{Re} \left| {\mathbf{u}} \right|{{\rho }_{g}}$, ${\text{P}}{{{\text{e}}}_{{Tloc}}} = {\text{P}}{{{\text{e}}}_{{Tg}}}\left| {\mathbf{u}} \right|{{\rho }_{g}}$ – локальные числа Рейнольдса и Пекле [22], (скорость и плотность безразмерны!).
Уравнение теплового баланса в графитовой оболочке имеет вид
(22)
${{\rho }_{{gr}}}{{c}_{{gr}}}\left( {\frac{{\partial {{T}_{{gr}}}}}{{\partial t}}} \right) = \nabla \cdot \left( {\frac{{{{\lambda }_{{gr}}}}}{{{\text{P}}{{{\text{e}}}_{{gr}}}}}\nabla {{T}_{{gr}}}} \right).$Уравнение теплового баланса в вольфрамовом канале имеет вид
(23)
$\begin{gathered} {{\rho }_{{Wr}}}{{c}_{{Wr}}}\left( {\frac{{\partial {{T}_{{Wr}}}}}{{\partial t}}} \right) = \nabla \cdot \left( {\frac{{{{\lambda }_{{Wr}}}}}{{P{{e}_{{Wr}}}}}\nabla {{T}_{{Wr}}}} \right) + {{Q}_{{J,Wr}}}, \\ Q_{{J,Wr}}^{{}} = {{\sigma }_{{Wr}}}j_{{Wr}}^{2}. \\ \end{gathered} $Уравнения электрического поля, основанные на законе Ома, имеют вид
(24)
$\nabla \cdot \nabla \varphi = 0,\,\,\,\,{{j}_{{Wr}}} = - {{\sigma }_{{Wr}}}{\kern 1pt} \nabla \varphi ,$Граничные и начальные условия. Для реактора, состоящего из зон 1, …, 6, установлены соотношения: Графитовое тело представлено зонами 1, 2, 3, вольфрамовый сплав инициирования горения – зоной 4, канал подачи ${{{\text{N}}}_{{\text{2}}}}$, ${{{\text{O}}}_{{\text{2}}}}$ показана зоной 5, а пористая область синтеза, состоящая из частиц ${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}{\text{(s),}}$ ${\text{C(s),}}$ ${\text{Zr}}{{{\text{O}}}_{{{\text{2}}{{x}_{\nu }}}}}{{{\text{N}}}_{{4{{x}_{\nu }}/3}}}{\text{(s)}},$ ${\text{ZrN(s)}}$ и ${{{\text{N}}}_{{\text{2}}}}{\text{(g),}}$ ${{{\text{O}}}_{2}}{\text{(g),}}$ ${\text{CO(g)}},$ ${\text{C}}{{{\text{O}}}_{2}}{\text{(g)}}$, представлена зоной 6 (см. рис. 1a).
Рис. 1.
Схема реактора СПС (рис. 1а). Показана область моделирования, состоящая из зон 1–6. Зона 1: Зона 2: Зона 3: – графитовый корпус реактора. Зона 4: – вольфрамовый слой. Зона 5: – канал подачи воздуха. Зона 6: – пористая зона смеси реагентов и продуктов синтеза. На рис. 1в приводится зависимость от времени силы тока, пропускаемого через вольфрамовый слой (зона 4, рис. 1а). Рис. 1в и рис. 1г иллюстрируют сравнение с экспериментальным [6]. Воспламенение циркония инициировалось нагревом электрическим током слоя вольфрама (область 4 на рис. 1ф). На рис. 1г показано сравнение динамики температуры в зоне 6 рис. 1а с символами эксперимента. Символы экспериментов 1 и 2 относятся к цирконию массой 4б5 г (М = 0.5 моль) и массой 9.1 г (М = 0.1 моль) соответственно. Сплошными линиями 1.2 показана динамика температуры твердой фазы в зоне 6 рис. 1б в точках с координатами (5/7.0.5) и (5/7.0.25) соответственно.
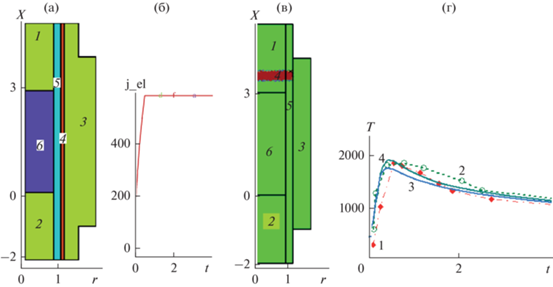
Граничные условия на графитовом теле (зоны 1, 2, 3).
$x = - 2,$ $0 < r < 1 - d$; $x = 5,$ $0 < r < 1 - d$; $ - 2 < x < 5,$ $r = 1 + \delta $; и внешней границе зоны 3 граничные условия следующие
(25)
$\begin{gathered} \frac{{\partial {{T}_{{gr}}}}}{{\partial n}} = {{\alpha }_{{ex}}}\left( {{{T}_{{ex}}} - {{T}_{{gr}}}} \right),\,\,\,\,{\text{при}} \\ - 2 < x < 0,\,\,\,\,r = 1 - d. \\ \end{gathered} $На границе $x = - 2,$ $0 < r < 1 - d$; $3 < x < 5,$ $r = 1 - d$; условие теплового излучения/поглощения задавалось по закону Стефана–Больцмана, который в безразмерных переменных имеет вид
(26)
$\begin{gathered} \frac{{\partial {{T}_{g}}}}{{\partial n}} = - {{q}_{{g,rad}}},\,\,\,\,\frac{{\partial {{T}_{S}}}}{{\partial n}} = - {{q}_{{S,rad}}}, \\ {{q}_{{g,rad}}} = {{\varepsilon }_{\Sigma }}\frac{{{{A}_{W}}}}{\beta }\left[ {{{{\left( {1 + \beta {{T}_{W}}} \right)}}^{4}} - {{{\left( {1 + \beta {{T}_{g}}} \right)}}^{4}}} \right], \\ {{q}_{{S,rad}}} = {{\varepsilon }_{\Sigma }}\frac{{{{A}_{W}}}}{\beta }\left[ {{{{\left( {1 + \beta {{T}_{W}}} \right)}}^{4}} - {{{\left( {1 + \beta {{T}_{{gr}}}} \right)}}^{4}}} \right], \\ \end{gathered} $где ${{T}_{{gr}}}$ – температура графитового тела на внутренней границе между зонами 3, 4; – постоянная Больцмана в безразмерных переменных [54 ] , ${{A}_{{{\kern 1pt} W}}} = \frac{{2\chi l_{0}^{2}}}{{{{r}_{p}}}}\frac{{{{\sigma }_{B}}}}{{{{\lambda }_{0}}}}T_{0}^{3}.$
На внутренней границе между зонами 4, 5: $ - 2 < x < 5,\,\,r = 1 + \delta $ граничное условие имеет вид
(27)
$\begin{gathered} \frac{{\partial {{T}_{{gr}}}}}{{\partial n}} = - {{q}_{{gr,rad}}}, \\ {{q}_{{gr,rad}}} = {{\varepsilon }_{\Sigma }}\frac{{{{A}_{W}}}}{\beta }\left[ {{{{\left( {1 + \beta {{T}_{{el}}}} \right)}}^{4}} - {{{\left( {1 + \beta {{T}_{{gr}}}} \right)}}^{4}}} \right]. \\ \end{gathered} $На границе зоны 4 (сплав вольфрама) задается потенциал электрического поля $\varphi \left( t \right)$, зависящий от времени, что позволяет генерировать напряжение электрического поля $E(t)$ и электрический ток $j(t)$ и управлять инициированием горения и тепловым режимом уплотнения нитрида циркония.
На внутренней границе между зонами 4, 5: $ - 2 < x < 5,\,\,r = 1 + \delta $ граничное условие имеет вид
(28)
$\begin{gathered} \frac{{\partial {{T}_{g}}}}{{\partial n}} = - {{q}_{{g,rad}}}, \\ {{q}_{{g,rad}}} = {{\varepsilon }_{\Sigma }}\frac{{{{A}_{{{\kern 1pt} W}}}}}{\beta }\left[ {{{{\left( {1 + \beta {{T}_{{el}}}} \right)}}^{4}} - {{{\left( {1 + \beta {{T}_{g}}} \right)}}^{4}}} \right]. \\ \end{gathered} $Граничные условия на входе в зону реактора 5: $x = - 2,\,\,1 - d < r < 1$
(29)
$\begin{gathered} u = {{u}_{{in}}},\,\,\,\,{v} = 0,\,\,\,\,p = {{p}_{{in}}},\,\,\,\,\frac{{\partial {{T}_{g}}}}{{\partial n}} = - {{q}_{f}}\left( t \right), \\ \frac{{\partial {{\rho }_{g}}}}{{\partial n}} = - {{N}_{{2f}}}. \\ \end{gathered} $Граничные условия на выходе из зоны 5:
(30)
$\begin{gathered} t > 0;\,\,\,\,x = 5;\,\,\,\,1 - d < r < 1{\kern 1pt} :\,\,\frac{{\partial u}}{{\partial x}} = 0,\,\,\,\,{v} = 0, \\ p = {{p}_{{ex}}},\,\,\,\,\frac{{\partial {{T}_{g}}}}{{\partial n}} = {{\alpha }_{{ex}}}\left( {{{T}_{{ex}}} - {{T}_{g}}} \right),\,\,\,\frac{{\partial {{T}_{S}}}}{{\partial n}} = {{\alpha }_{{ex}}}\left( {{{T}_{{ex}}} - {{T}_{S}}} \right). \\ \end{gathered} $На внутренних границах зоны: $5{\kern 1pt} - \,2 < x < 0,$ $r = 1 - d$ и $ - 1 < x < 4,\,\,r = 1$ граничное условие имеет вид
(31)
$\begin{gathered} \frac{{\partial {{T}_{g}}}}{{\partial n}} = - {{q}_{{g,rad}}},\,\,\,\,\frac{{\partial {{T}_{S}}}}{{\partial n}} = - {{q}_{{S,rad}}}, \\ {{q}_{{g,rad}}} = {{\varepsilon }_{\Sigma }}\frac{{{{A}_{W}}}}{\beta }\left[ {{{{\left( {1 + \beta {{T}_{W}}} \right)}}^{4}} - {{{\left( {1 + \beta {{T}_{g}}} \right)}}^{4}}} \right]. \\ \end{gathered} $Граничные условия для зон 1, 2, 6 на оси симметрии реактора: $ - 2 < x < 5,\,\,r = 0$ имеют вид
(32)
$\begin{gathered} t > 0,\,\,\,\,r = 0{\kern 1pt} :\,\,{v} = 0, \\ \frac{{\partial {{T}_{g}}}}{{\partial n}} = 0,\,\,\,\,\frac{{\partial {{T}_{S}}}}{{\partial n}} = 0,\,\,\,\,\frac{{\partial {{T}_{{gr}}}}}{{\partial n}} = 0. \\ \end{gathered} $Условие на внутренней границе между каналом и зоной 6: $0 < x < 3,\,\,r = 1 - d$, ${\partial \mathord{\left/ {\vphantom {\partial {\partial n}}} \right. \kern-0em} {\partial n}}$ обозначает нормальную производную, ${{R}_{{{\kern 1pt} 1}}} = 1 - d$.
Первоначальные условия.
(33)
$\begin{gathered} t = 0,\,\,\,\,u = 0,\,\;{v} = 0,\,\,\,\,{{T}_{g}} = {{T}^{0}},\,\,\,\,{{T}_{S}} = {{T}^{0}}, \\ {{T}_{{gr}}} = {{T}^{0}},\,\,\,\,{{T}_{{el}}} = {{T}^{0}},\,\,\,\,{{T}_{g}} = {{T}^{0}},\,\,\,\,{{T}_{S}} = {{T}^{0}}, \\ t = 0;\,\,\,\,\,\,0 < x < 3;\,\,\,\,\,0 < r < 1 - d{\kern 1pt} :u = {{u}^{0}} \\ {v} = 0,\,\,\,\,{{\rho }_{g}} = \rho _{g}^{0},\,\,\,\,{{\rho }_{{jS}}} = \rho _{{jS}}^{0},\,\,\,\,j = 1,2, \\ \end{gathered} $где нулевой верхний индекс относится к значению переменной в начальный момент времени.
3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ И ОБСУЖДЕНИЕ
Был применен метод конечных элементов, апробированный в наших предыдущих работах [19–24]. Результаты моделирования были проверены с использованием различных сеток. Точность результатов моделирования проверялась с использованием различных сеток и адаптации сетки в зоне больших градиентов. Результаты были подтверждены сгущением сетки. Прогнозируемая температура при горении углерода в реакторах хорошо согласуется с экспериментальными измерениями [21]. Динамика уплотнения частиц синтеза нитрида циркония и прогрева в SPS реакторе удовлетворительно согласуется с экспериментами [42]. Результаты численного решения уравнений (10)–(19) с соотношениями (6)–(8), (20)–(28) представлены на рис. 1б, рис. 2, …, рис. 8 с использованием кинетики (1) … ,(6).
Рис. 2.
Сравнение с экспериментом. Сравнение пористости с экспериментом [42] для и см. формулу (8) показано на рис. 2б для повышения температуры со скоростью . Символы 1 относятся к рис. 2а и, рис. 2б соответственно. Сплошные линии 2, 3 на рис. 2а относятся к пористости в точках с координатами (0.9, 0.5), (1.42, 0.5) и линиях 2, 3 на рис. 2б относятся к пористости в точках с координатами (0.9, 0.75), (2.14, 0.75).
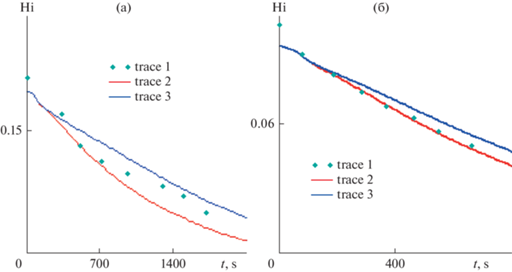
Рис. 3–8 показано влияние многоступенчатой подачи воздуха в зону реактора 5 в интервалах времени расход = 1, 0 < t < 0.2, 5 < t < 10, расход = 0, 0.2 < t < 5, t > 10. На рис. 5а показано изменение во времени плотности ${{{\text{O}}}_{{\text{2}}}}$ в точках с координатами (1/7, 0, 5), (5/77, 0, 5), (10/7, 0, 5), (15/7, 0, 5), (20/7, 0, 5). Отметим дефицит реагента ${{{\text{O}}}_{{\text{2}}}}$ в интервале времени 0, 0.2 < t < 0.8, приводящий к зоне постоянной во времени плотности оксида циркония (линии 2–6 на рис. 3б). Возобновление притока воздуха в интервале времени t > 1 активирует синтез нитрида циркония и выход на стационарную плотность (рис. 3в). Начальная плотность оксида циркония принимается за единицу, поэтому лимитирующим реагентом является ZrO2 (рис. 3б).
Рис. 3.
Проиллюстрирована динамика кислорода, оксида циркония и нитрида циркония при двухступенчатом режиме подачи воздуха. Рис. 5а, рис. 5б и рис. 5в показаны зависимости ${{{\text{O}}}_{{\text{2}}}}$, ${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}$и $Z{\text{rN}}$ от времени соответственно. Строки 1, …, 6 относятся к точкам с координатами (1/7, 0.5), (5/77, 0.5), (10/7, 0.5), (15/7, 0.5), (20/7, 0.5).
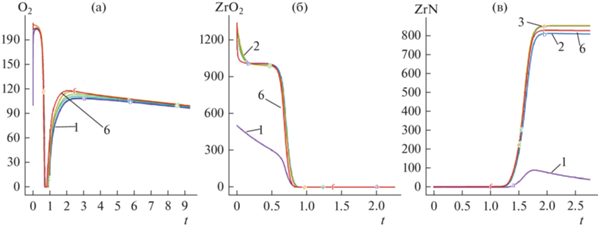
Рис. 4.
Динамика плотности ${\text{CO}}$ (рис. 14 а) и ${\text{C}}{{{\text{O}}}_{{\text{2}}}}$ (рис. 14 б) для начальной плотности ${{\rho }_{{{\text{Zr}}{{{\text{O}}}_{{\text{2}}}}}}}\left( {t,x,r} \right) = {{10}^{3}}$. Кривые на рис. 14 а и рис. 14 б относятся к положениям управления в реакторе, представленным на рис. 14 в и рис. 14 г с использованием горизонтального расположения оси симметрии. Строки 1, …, 6 относятся к контрольным точкам (x, r) с координатами; (0, 0.5) (0.14, 0.5), (0.9, 0.5), (1.42, 0.5), (2.14, 0.5), (2.86, 0.5) соответственно. Рис. 4в показано расположение контрольных точек в реакторе с горизонтальной осью симметрии.
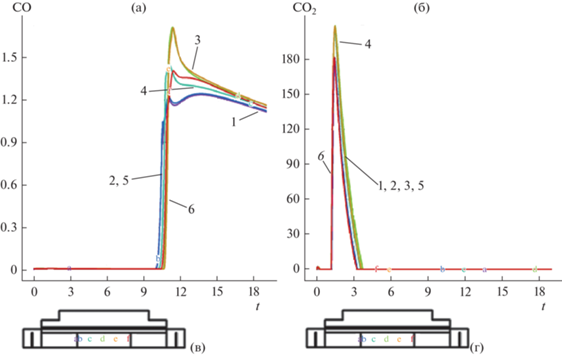
Рис. 5.
Проиллюстрирована динамика компонентов воздуха ${{{\text{N}}}_{{\text{2}}}}$ (рис. 15 а) и ${{{\text{O}}}_{{\text{2}}}}$ (рис. 15 б). Кривые на рис. 15 а и рис. 15 б относятся к положениям управления в реакторе, представленным на рис. 15 в и рис. 15г с использованием горизонтального расположения оси симметрии. Строки 1, …, 6 относятся к контрольным точкам (x, r) с координатами; (0, 0.5) (0.14, 0.5), (0.9, 0.5), (1.42, 0.5), (2.14, 0.5), (2.86, 0.5) соответственно.
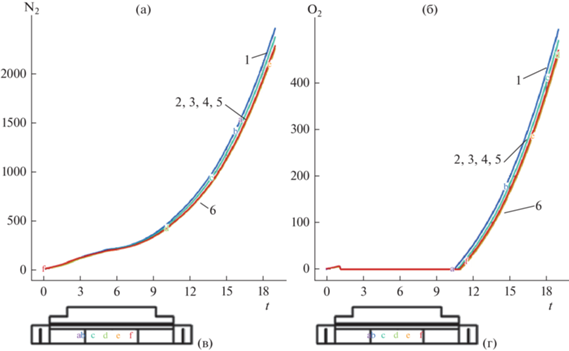
Рис. 6.
Динамика ${{\rho }_{{{\text{ZrN}}}}}\left( {t,x,r} \right)$ (рис. 16 а) и плотности углерода ${{\rho }_{{\text{C}}}}\left( {t,x,r} \right)$ (рис. 16 б) для ${{\rho }_{{{\text{Zr}}{{{\text{O}}}_{{\text{2}}}}}}}\left( {t,x,r} \right) = {{10}^{3}}$ проиллюстрирована. Кривые на рис. 16 а и рис. 16 б относятся к позициям управления в реакторе, представленным на рис. 16 в и рис. 16 г с использованием горизонтального расположения оси симметрии. Строки 1, …, 6 относятся к контрольным точкам (x, r) с координатами; (0, 0.5) (0.14, 0.5), (0.9, 0.5), (1.42, 0.5), (2.14, 0.5), (2.86, 0.5) соответственно.
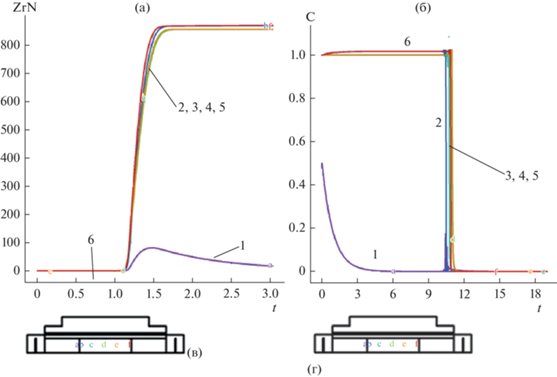
Рис. 7.
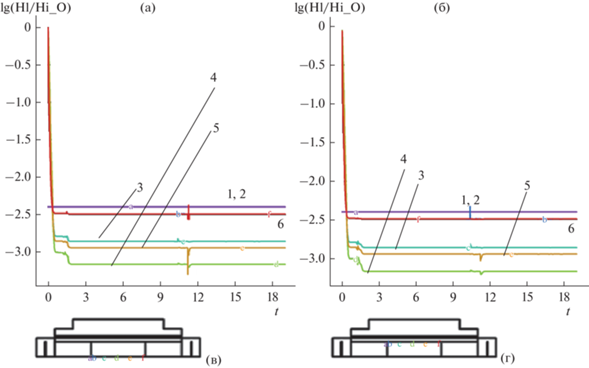
Представлена пористость$\chi \left( {t,x,r} \right)$ твердой фазы в процессе уплотнения, найденная по формулам (2) и (5). Рис. 1а и рис. 7б показано изменение во времени десятичного логарифма $\lg \left( {{{\chi (t,x,r)} \mathord{\left/ {\vphantom {{\chi (t,x,r)} {{{\chi }_{0}}}}} \right. \kern-0em} {{{\chi }_{0}}}}} \right)$ в точках с координатами (0, 0.75), (0.14, 0.75), (0.9, 0.75), (1.42, 0.75), (2.14, 0.75), (2.86, 0.75) и (0, 0) (0.14, 0), (0.9, 0), (1.42, 0), (2.14, 0), (2.86, 0.) соответственно.
Обратите внимание на интервал нулевой плотности кислорода на рис. 5в, иллюстрирующий недостаточную интенсивность нагнетаемого воздуха и соответствующую задержку синтеза нитрида циркония на рис. 5в и удаление углеродных примесей.
Синтез практически завершается к моменту времени t = 2 (рис. 6а), и в зоне синтеза остается значительное количество примеси углерода (рис. 6б). Рис. 7 представляет динамику уплотнения нитрида циркония. Относительная пористость $\lg \left( {{{\chi (t,x,r)} \mathord{\left/ {\vphantom {{\chi (t,x,r)} {{{\chi }_{0}}}}} \right. \kern-0em} {{{\chi }_{0}}}}} \right)$ в логарифмической шкале в контрольных точках с координатами (0, 0.75), (0.14, 0.75), (0.9, 0.75), (1.42, 0.75), (2.14, 0.75), (2.86, 0.75) и (0, 0.) (0.14, 0.), (0.9, 0.), (1.42, 0.), (2.14, 0.), (2.86, 0.) на рис. 7а и рис. 7в соответственно иллюстрирует уменьшение относительной пористости на три порядка.
ЗАКЛЮЧЕНИЕ
Излагаются результаты синтеза, уплотнения частиц нитрида циркония, не используя в качестве регентов чистый цирконий и чистый азот. Исследованы новые кинетические схемы синтеза нитрида циркония. Применен управляемый нагрев электрическим током, протекающем через область высокой электропроводимости (канал сплава вольфрама).
Представлены расчеты, включающие тепловое излучение, концентрационное расширение, тепловое и массовое рассеивание. Найдены коэффициенты концентрационного расширения в процессе горения циркония в пористой зоне реактора в зависимости от кинетики синтеза нитрида циркония при заданных начальных значениях газовой и твердой фазы для нестационарной подачи азота по газовому каналу. Подход позволяет контролировать скорость нитрирования.
Развита многотемпературная модель сопряженного теплообмена включающая температуру внутри смеси частиц ${\text{ZrC}},\,{\text{ZrN,}}\,{\text{Zr}}{{{\text{O}}}_{{\text{2}}}}{\text{,}}\,{\text{C}}$, и молекул ${{{\text{N}}}_{{\text{2}}}},\,{{{\text{O}}}_{{\text{2}}}}$,${\text{CO,}}\,\,{\text{C}}{{{\text{O}}}_{{\text{2}}}}$, температуру газовой фазы и температуру пористого графитового корпуса реактора при заданном изменении во времени плотности электрического тока. Продемонстрировано снижение пористости на три порядка по сравнению со значением в начальный момент времени. Управляемый нагрев электрическим током в проводящем слое позволяет оценить изменение температуры при синтезе и уплотнении в зависимости от исходного фазового состава, эффект нагрева на конечное распределение ${\text{ZrN}}$ в образце, а также на продолжительность процесса синтеза и величину примеси углерода.
Проведенное моделирование синтеза и уплотнения ${\text{ZrN}}$ свидетельствует о неравномерном пористости ${\text{ZrN}}$ в реакторе. Полученные результаты демонстрируют значительное влияние переменной пористости на синтез мелких частиц ${\text{ZrN}}$. Результаты для получение керамики на основе нитрида циркония можно применить для других материалов повышенной термостойкости.
Работа выполнена по теме государственного задания № госрегистрации АААА-А20-120011690135-5.
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
| $A$ | площадь ${{{\text{м}}}^{{\text{2}}}}$ |
| ${\text{ZrN}}$ | нитрид циркония |
| ${\text{ZrC}}$ | карбид циркония |
| ${\text{Zr}}{{{\text{O}}}_{{\text{2}}}}$ | оксид циркония |
| ${\text{Zr}}{{{\text{C}}}_{x}}{{{\text{N}}}_{y}}$ | фракция нитрида циркония |
| ${{b}_{0}},{{b}_{1}}$ | константы зависимости тензоров дисперсии от локального числа Пекле (безразмерные) |
| ${{c}_{p}}$,${{c}_{p}} = {{C}_{{p,air}}}$ | характерная теплоемкость газовой фазы при постоянном давлении, ${\text{Дж}}\,\,{\text{к}}{{{\text{г}}}^{{ - 1}}}\,\,{{{\text{K}}}^{{ - 1}}}$ |
| ${{\tilde {c}}_{S}},\,{{\tilde {c}}_{{pg}}},$${{\tilde {c}}_{S}} = {{{{C}_{S}}} \mathord{\left/ {\vphantom {{{{C}_{S}}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}$${{\tilde {c}}_{{pg}}} = {{{{C}_{{pg}}}} \mathord{\left/ {\vphantom {{{{C}_{{pg}}}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}$ | безразмерные теплоемкости твердой и газовой фазы |
| ${{C}_{j}},\,j = 1,2,3$ | массовые доли газовых компонент (безразмерные) |
| ${{B}_{{\lg }}} = \frac{{{{Y}_{{\lg }}}}}{{{{Y}_{{g,tot}}}}}$ | молярные доли (концентрации) газовых компонент (безразмерные) |
| ${{B}_{{jS}}} = \frac{{{{Y}_{{jS}}}}}{{{{Y}_{{S,tot}}}}}$ | молярные доли (концентрации) компонент твердой фазы (безразмерные) |
| ${{D}_{0}} = 2 \times {{10}^{{ - 5}}}$ | характерная величина коэффициента диффузии, ${{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 1}}}$ |
| $\tilde {D}$, $\tilde {D} = {D \mathord{\left/ {\vphantom {D {{{D}_{0}}}}} \right. \kern-0em} {{{D}_{0}}}}$ | безразмерный коэффициент диффузии |
| ${{{\text{D}}}_{{{\text{mg}}}}}$ | дисперсионный тензор диффузии массы, ${{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{D}_{L}}$, ${{D}_{{Tr}}}$ | компоненты продольной и поперечной дисперсии массы, ${{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{d}_{p}}$ | диаметр частиц (зерен), м |
| ${{{\text{D}}}_{{{\text{Tg}}}}}$ | дисперсионный тензор диффузии тепла ${\text{Вт}}\,{{{\text{м}}}^{{ - 1}}}\,{{{\text{К}}}^{{ - 1}}}$ |
| $J_{{iS}}^{{}},i = 1,...5$ | массовые потоки, ${\text{кг}}\,{{{\text{м}}}^{{ - 2}}}\,{{{\text{с}}}^{{ - 1}}}$ |
| $k$ | частотный фактор в формуле Аррениуса, ${{{\text{с}}}^{{ - 1}}}$ |
| $K$ | изотермический модуль всестороннего сжатия, ${\text{Па}}$ |
| $\,{{K}_{\alpha }}$ | параметр масштабирования коэффициентов концентрационного расширения (безразмерный) |
| ${{l}_{0}}$ | характерный размер, ${\text{м}}$ |
| ${\text{Ma}}$ | число Маха (безразмерное) |
| ${{M}_{0}}$ | характерная молярная масса, ${\text{кг}}\,{\text{мо}}{{{\text{л}}}^{{ - 1}}}$ |
| ${{M}_{{1g}}},\,{{M}_{{2g}}},\,{{M}_{S}}$ | молярные массы газовых компонент, ${\text{кг}}\,{\text{мо}}{{{\text{л}}}^{{ - 1}}}$ |
| ${{M}_{{iS}}},\,i = 1,...5\,$ | молярные массы компонент синтеза, ${\text{кг}}\,{\text{мо}}{{{\text{л}}}^{{ - 1}}}$ |
| ${{p}_{0}}$ | характерное давление, ${\text{Па}}$ |
| ${{p}_{g}}$ | давление газа, ${\text{Па}}$ |
| ${{P}_{L}}$ | эффективное напряжение свободного спекания (безразмерное) |
| ${{P}_{{ex}}}$, ${{P}_{g}}$ | внешнее давление, давление газа на границе поры, ${\text{Па}}$ |
| ${{P}_{{tot}}} = {{P}_{{ex}}} - {{P}_{g}}$ | общее давление, ${\text{Па}}$ |
| ${\text{P}}{{{\text{e}}}_{{\text{1}}}}$ | диффузионное число Пекле (безразмерное) |
| ${\text{P}}{{{\text{e}}}_{{{\text{1t}}}}}{\text{,}}\,{\text{P}}{{{\text{e}}}_{{{\text{2t}}}}}$ | локальные числа Пекле для продольной и поперечной дисперсии тепла, (безразмерные) |
| ${\text{P}}{{{\text{e}}}_{{{\text{Tg}}}}}{\text{,P}}{{{\text{e}}}_{{{\text{Ts}}}}}$ | тепловые числа Пекле для газовой и твердой фазы, (безразмерные) |
| $Q$ | тепловой эффект химической реакции, ${\text{Дж}}\,{\text{к}}{{{\text{г}}}^{{ - 1}}}$ |
| ${{Q}_{r}}$ | теплота химической реакции, ${\text{Вт}}\,{{{\text{м}}}^{{ - 2}}}$ |
| $\operatorname{Re} $ | число Рейнольдса (безразмерное); |
| $\begin{gathered} {{\operatorname{R} }_{S}} = \\ = {{p}_{0}}{{\left( {{{\zeta }_{p}}{{\mu }_{{S0}}}} \right)}^{{ - 1}}} \\ \end{gathered} $ | аналог числа Рейнольдса для твердой фазы (безразмерное) |
| ${\text{R}}{{{\text{e}}}_{{loc}}},\,{\text{P}}{{{\text{e}}}_{{Tloc}}}$ | локальные числа Рейнольдса и Пекле (безразмерные) |
| ${{{\mathbf{S}}}_{{\mathbf{V}}}}$ | слагаемое распределенного сопротивления газа в порах, ${\text{Па}}\,{{{\text{м}}}^{{ - 1}}}$ |
| ${{T}_{0}} = 1000$ | характерная температура, ${\text{К}}$ |
| ${{T}_{g}},\,{{T}_{S}}$ | температура газа и твердой фазы, ${\text{К}}$ |
| ${{\tilde {T}}_{g}}$,${{\tilde {T}}_{S}}$ | безразмерная температура. ${{T}_{g}} = {{T}_{0}}\left( {1 + \beta {{{\tilde {T}}}_{g}}} \right),\,\,{{T}_{S}} = {{T}_{0}}\left( {1 + \beta {{{\tilde {T}}}_{S}}} \right)$ |
| ${{t}_{0}}$ | характерное время, ${\text{с}}$ |
| $t$ | время, ${\text{с}}$ |
| $\tilde {t}$ | безразмерное время $\tilde {t} = {t \mathord{\left/ {\vphantom {t {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}$ |
| $V$ | удельный объем, ${{{\text{м}}}^{3}}$ |
| ${{V}_{{i,solid}}}$ | компоненты скорости твердой фазы, ${\text{м}}\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{Y}_{{\lg }}} = \frac{{{{\rho }_{{\lg }}}}}{{{{M}_{{\lg }}}}}$ | молярные плотности компонент фазы, ${\text{мол}}\,{{{\text{м}}}^{{ - 3}}};$ газовой |
| ${{Y}_{{jS}}} = \frac{{{{\rho }_{{jS}}}}}{{{{M}_{{jS}}}}}$ | молярные плотности компонент твердой фазы, ${\text{мол}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{Y}_{{g,tot}}} = \sum\limits_{l = 1}^4 {{{Y}_{{\lg }}}} $ | суммарная молярная плотность газовой фазы, ${\text{мол}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{Y}_{{S,tot}}} = \sum\limits_{j = 1}^5 {{{Y}_{{jS}}}} $ | суммарная молярная плотность твердой фазы, ${\text{мол}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{a}_{g}}$ | коэффициент температуропроводности газа, ${{{\text{м}}}^{{\text{2}}}}\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{\alpha }_{j}}$, $j = 1,2,3$ | коэффициенты в формуле распределенного сопротивления пористости ${{\eta }_{j}} = {{\alpha }_{j}}\left| {\text{u}} \right| + {{\varsigma }_{j}}$${\text{Па}}\,{{{\text{м}}}^{{ - 2}}}\,{\text{с}}$ |
| ${{\bar {\alpha }}_{{ig}}}$, ${{\bar {\alpha }}_{{iS}}}$ | коэффициенты концентрационного расширения (безразмерные) |
| $\beta $ | безразмерный параметр энергии активации горения $\beta = {{R{{T}_{0}}} \mathord{\left/ {\vphantom {{R{{T}_{0}}} E}} \right. \kern-0em} E}$ |
| ${{\varepsilon }_{{ij}}}$ | тензор деформаций (безразмерный) |
| ${{\rho }_{{jg}}}$, $j = 1,...,4$ | массовые плотности компонент газовой фазы ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| $\begin{gathered} {{\rho }_{g}} = \\ = {{\rho }_{{1g}}} + ... + {{\rho }_{{4g}}} \\ \end{gathered} $ | суммарная плотность компонент газовой фазы, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\rho }_{{lS}}}$, $\,l = 1,...,5$ | массовые плотности компонент твердой фазы, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| $\begin{gathered} {{\rho }_{S}} = \\ = {{\rho }_{{1S}}} + ... + {{\rho }_{{5S}}} \\ \end{gathered} $ | суммарная плотность компонент твердой фазы, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\rho }_{{tot}}} = {{\rho }_{g}} - {{\rho }_{S}}$ | суммарная массовая плотность, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| $E = \sum\limits_k {{{\varepsilon }_{{kk}}}} $ | первый инвариант тензора деформаций Коши безразмерный |
| ${{\sigma }_{{ij}}}$ | тензор напряжений в твердой фазе, ${\text{Па}}$ |
| $\,{{\eta }_{j}}$, $j = 1,2,3$ | компоненты распределенного сопротивления ${{\eta }_{j}} = {{\alpha }_{j}}\left| {\text{u}} \right| + {{\varsigma }_{j}},$${\text{Па}}\,{{{\text{м}}}^{{ - 1}}}$ |
| ${{\lambda }_{0}}\,$ | характерная величина коэффициента теплопроводности ${{\lambda }_{0}} = {{\lambda }_{{air}}} = 0.06,$${\text{Вт}}\,{{{\text{м}}}^{{ - 1}}}\,{{{\text{K}}}^{{ - 1}}}$ |
| $\,{{\tilde {\lambda }}_{g}}$, ${{\tilde {\lambda }}_{S}}$ | безразмерные коэффициенты теплопроводности газовой и твердой фаз; |
| $\mu $ | коэффициент динамической вязкости газа, ${\text{кг}}\,{{{\text{м}}}^{{ - 1}}}\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{\mu }_{{S1}}},{{\mu }_{{S2}}}$ | коэффициенты Ламе) твердой фазы, ${\text{Па}}$ |
| ${{\nu }_{{\lg }}} = \frac{{{{M}_{{\lg }}}}}{{{{\rho }_{{\lg }}}}}$ | молярный объем компонента газовой фазы, ${{{\text{м}}}^{3}}$ |
| ${{\nu }_{{jS}}} = \frac{{{{M}_{{jS}}}}}{{{{\rho }_{{jS}}}}}$ | молярный объем компонента твердой фазы, ${{{\text{м}}}^{3}}$ |
| ${{\varsigma }_{j}}$, $j = 1,2,3$ | компоненты распределенного сопротивления ${{\eta }_{j}} = {{\alpha }_{j}}\left| {\text{u}} \right| + {{\varsigma }_{j}},$${\text{Па}}\,{{{\text{м}}}^{{ - 1}}}$ |
| $\kappa $ | коэффициент теплообмена, ${\text{Вт}}\,{{{\text{K}}}^{{ - 1}}}\,{{{\text{м}}}^{{ - 2}}}$ |
| $\begin{gathered} \tilde {\kappa } = \\ = {{\kappa {{t}_{0}}A} \mathord{\left/ {\vphantom {{\kappa {{t}_{0}}A} {\left( {{{c}_{p}}{{\rho }_{0}}V} \right)}}} \right. \kern-0em} {\left( {{{c}_{p}}{{\rho }_{0}}V} \right)}} \\ \end{gathered} $ | безразмерный коэффициент межфазового теплообмена |
| ${{\kappa }_{0}}\,$ | размерный коэффициент в формуле Левека, ${\text{Вт}}\,{{{\text{K}}}^{{ - 1}}}{{{\text{м}}}^{{ - 2}}}$ |
| $\,\chi $ | коэффициент пористости (безразмерный) |
| ${{\chi }_{0}}$ | начальная пористость, (безразмерный) |
| $\begin{gathered} \omega = \\ = {{\omega }_{T}} + {{\omega }_{g}} + {{\omega }_{S}} \\ \end{gathered} $ | суммарный коэффициент объемного расширения,(безразмерный) |
| ${{\omega }_{T}}$ | вклад в расширение изменения температуры, (безразмерный) |
| ${{\omega }_{g}},\,{{\omega }_{S}}$ | эффект концентрационного расширения компонентов газовой и твердой фазы, (безразмерный) |
| ${{q}_{{g,rad}}}$ | тепловой поток излучения/поглощения тепла, ${\text{Вт}}\,{{{\text{м}}}^{{ - 2}}}$ |
| ${{A}_{W}}\, = \,\frac{{2\chi l_{0}^{2}}}{{{{r}_{p}}}}\frac{{{{\sigma }_{B}}}}{{{{\lambda }_{0}}}}T_{0}^{3}$ | постоянная Больцмана, коэффициент излучения |
| $\dot {\gamma }$ | пластическая деформация, скорость уплотнения. $\dot {\gamma } = {{\dot {\gamma }}_{0}}\exp \left( { - \frac{Q}{{RT}}} \right)\,$ |
| $E_{{pl}}^{{}}$ | энергия активации пластической деформации, кДж/моль |
| $\varphi = {{\left( {1 - \chi } \right)}^{2}}$ | нормализованный модуль сдвига (безразмерный) |
| $\psi = \frac{2}{3}\frac{{{{{\left( {1 - \chi } \right)}}^{3}}}}{\chi }$ | нормализованный объемный модуль (безразмерный) |
| $\sigma \left( W \right)$ | эквивалентное напряжение для степенного закона, $\sigma \left( W \right) = {{A}_{m}}{{W}^{m}}$ |
| ${{\sigma }_{{z,ole}}}$, ${{\dot {\chi }}_{{ole}}}$ | напряжение, скорость уплотнения |
| ${{\dot {\varepsilon }}_{{ij}}}$ | тензор скорости деформации (безразмерный) |
Список литературы
Harrison R.W., Lee W.E. Processing and properties of ZrC, ZrN and ZrCN ceramics,” Advances in Applied Ceramics, 2016. V. 115. № 5. P. 294– 307. https://doi.org/10.1179/1743676115Y.0000000061
Munir Z.A., Anselmi-Tamburini U., Ohyanagi M. The effect of electric field and pressure on the synthesis andconsolidation of materials: a review of the spark plasmasintering method // J. Mater. Sci. 2006. V. 41. № 3. P. 763–777.
Shijiao Zhao, Jingtao Ma, Rui Xu, Xuping Lin, Xing Cheng,Shaochang Hao, Xingyu Zhao, Changsheng Deng, Bing Liu. Synthesis and Characterization of Zirconium Nitride Nanopowders by Internal Gelation and Carbothermic Nitridation // Scientific Reports. (2019)9: 19199. https://doi.org/10.1038/s41598-019-55450-x
Hulbert D.M., Anders A., Andersson J., Lavernia E.J., Mukherjee A.K. A discussion on the absence of plasma inspark plasma sintering // Scr. Mater., 2009. V. 60. № 10. P. 835–838.
Jackson H.F., Lee W.E. Properties and characteristics of ZrC,” in Comprehensive nuclear materials, (Ed. R.J.M. Konings), 2012. P. 339–372, Oxford, Elsevier.
Дитц А.А. Оксинитридные керамические материалы на основе продуктов сжигания промышленных порошков металлов на воздухе // Диссертация ктн. Томск.2006. С. 163.
Самсонов Г.В. Нитриды / Г.В. Самсонов. К.: Наукова думка., 1969. С. 371
Химия синтеза сжиганием / Под. ред. Коидзуми. Перевод с янон. М.: Мир, 1998. С. 247
Мержанов А.Г. Самораспространяющийся высокотемпературный синтез / В кн.: Физическая химия. Современные проблемы. Ежегодник // Под. ред. акад. Колотыркина Я.М. М.: Химия. 1983. 224 с.
Сычев А.Е. Самораспросграняющийся высокотемпературный синтез наноматериалов / А.Е. Сычев, А.Г. Мержанов // Успехи химии. 2004. Т. № 2. С. 157–170.
Ch'ng H.N., Pan J. Cubic spline elements for modelling microstructural evolution of materials controlled by solid-state diffusion and grain-boundary migration. // J. Computational Physics. 2004. 20-5.
Russias J., Cardinal S., Esnouf C.Ю. Fantozzi G., Bienvenu K. Hot pressed titanium nitride obtained from SHS starting powders: influence of a pre-sintering heat-treatment of the starting powders on the densification process // J. Eur. Ceram. Soc. 2007. V. 27. № 1. P. 327–335.
Sakai T., Iwata M. Effect of oxygen on sintering of AlN // J. Mater. Sci. 1977. V. 12. № 8. P. 1659–1665.
Adachi J., Kurosaki K., Uno M., Yamanaka S. Thermal and electrical properties of zirconium nitride // J. Alloys Compd, 2005. 399. (12). 242–244.
Merja P., Masahide T., Tsuyoshi N. Sintering and characterization of (Pu,Zr)N // J. Nucl. Mater., 2014. V. 444. P. 421– 427.
Harrison R., Rapaud O., Pradeilles N., Maitre A., Lee W.E. On the fabrication of ZrCxNy from ZrO2 via two-step carbothermic reduction-nitridation // J. Eur. Ceram. Soc. 2015. V. 35. № 5. P. 1413–1421.
Aigner K., Lengauer W., Rafaja D., Ettmayer P. Lattice parameters and thermal expansion of Ti(CxNx), Zr(CxNx), Hf(CxN1 –x) and TiNx from 298 to 1473 K as investigated by high-temperature X-ray diffraction // J. Alloys Compd, 1994, 215, (1–2), 121–126.
Harrison R.W., Lee W.E. Processing and properties of ZrC, ZrN and ZrCN ceramics: Advances in Applied Ceramics, 2016. 115:5, 294–307, https://doi.org/10.1179/1743676115Y.0000000061
Lee G., Yurlova M.S., Giuntini D., Grigoryev E.G., Khasanov O.L., McKittrick J., Olevsky E.A. Densification of zirconium nitride by spark plasma sintering and high voltage electric discharge consolidation: A comparative analysis // Ceram. Int., V. 41. № 10. P. B. 2015. P. 14973–14987.
Martirosyan K.S., Luss D. Carbon Combustion Synthesis of Oxides Process Demonstration and Features // AIChE, V. J 51 10. 2005. P. 2801–2810.
Markov A.A., Hobossian M.A., Martirosyan K.S. Investigation of the synthesis of ferrites behind the combustion wave using models of sliding and temperature jumps and concentrations of the components of the gas phase on the surface of the pores of the solid phase // Physical-Chemical Kinetics in Gas Dynamics, 2015. V. 16. № 1. http://chemphys.edu.ru/issues/2015-16-1/articles/506/
[Марков А.А., Филимонов И.А., Мартиросян К.С. Моделирование синтеза сложных оксидов субмикронной дисперсности // Теорет. основы хим. технологии 2017 V. 51. № 1. С. 31.] Markov A., Filimonov I.A., Martirosyan K.S. Modeling of Submicron Complex Oxides Synthesis // Theor. Found. Chem. Eng. 2017. V. 51. № 1. P. 31. Markov, A. A., Filimonov, I. A., and Martirosyan, K. S. Carbon Combustion Synthesis of Oxides: Effect of Mach, Peclet, and Reynolds Numbers on Gas Dynamics // International J. Self Propagating High Temperature Synthesis, 2013. V. 22. № 1. P. 11–17.
Markov A.A., Filimonov I.A., Martirosyan K.S. Simulation of front motion in a reacting condensed two phase mixture // J. Comput. Phys. 2012. V. 231. № 20. P. 6714–6724.
Markov A.A. On Thermal and Mass Dispersion Effect on Barium Titanate Synthesis via CCSO // Physical-Chemical Kinetics in Gas Dynamics, 2019. V. 20. № 4. http://chemphys.edu.ru/issues/2019-20-4/articles/870/
Markov A.A. “On fine particles synthesis using three-zone reactor,” August 2020 // J. Physics: Conference Series, 1611:012047, 2020. https://doi.org/10.1088/1742-6596/1611/1/012047
Berre F., Doster E., Keilegavlen,Flow in fractured porous media: a review of conceptual models and discretization approaches, Transp. Porous Media. 2019. 130, 215–236.
Whitaker S. Transport equations for multi-phase systems // Chemical Engineering Scienc. 1973. V. 28. P. 139– 147.
Hsu C.T., Cheng P. Thermal dispersion in a porous medium // Int. J. Heat Mass Transf. V. 33. 1990. P. 1587–1597.
Fatehi M., Kaviany M., Role of gas-phase reaction and gas-solid thermal nonequilibrium in reverse combustion // Int. Heat Mass Transfer, 1997. V. 11. P. 2607–20.
Oliveira A.A.M., Kaviany M. Nonequilibrium in the transport of heat and reactants in combustion in porous media // Progress in Energy and Combustion Science, 2001. V. 27. P. 523– 45.
Pereira F.M., Oliveira A.A.M., Fachini F.F. Theoretical analysis of ultra-lean premixed flames in porous inert media // J. Fluid Mech. 2010. V. 657. P. 285–307.
Delgado J.M.P.Q. Longitudinal and transverse dispersion in porous media // Chem. Eng. Res. Des., Elsevier, 2007. V. 85. № 9. P. 1245–1252.
Betelin V.B., Galkin V.A., Shpilman A.V., Smirnov N.N. Digital core simulator – a promising method for developming hard-to-recover oil reserves technology // Materials Physics and Mechanics, из-во ФГБУ ИПМаш.РАН (Санкт-Петербург) 2020. Т. 44. С. 186–209.
Сорокова С.Н., Князева А.Г. Связанная модель спекания порошков системы Ti–TiAI3 // Изв. ТПУ. 2009. Т. 314(2) С. 96.
Князева А.Г. Введение в термодинамику необратимых процессов. Томск: Изд-во “Иван Федоров”, 2014. 170 с.
Markov A. Modeling the Synthesis of Barium Titanate Micron Particles in Axisymmetric Direct-Flow and Three-Zone Reactors // J. Eng. Phys. Thermophy, 2021. V. 94. P. 1312–1325. https://doi.org/10.1007/s10891-021-02412-8
[А.А. Марков. Эффект теплового и концентрационного расширения при синтезе титаната бария в прямоточном реакторе // Теорет. основы хим. технологии 2021 V. 55. № 5. С. 929–041.] Markov A.A. Thermal and Concentration Expansion in the Synthesis of Barium Titanate in a Once-Through Reactor // Theoretical Foundations of Chemical Engineering, 2021. V. 55. № 5. P. 929–941.
Markov A.A. Multitemperature model of a sps reactor for the synthesis and densification of zirconium nitride // Physical-Chemical Kinetics in Gas Dynamics 2021 V. 22(6). http://chemphys.edu.ru/issues/2021-22-6/articles/962/.
Lee G., Olevsky E.A., Maniere C., Maximenko A., Izhvanov O., Back C., McKittrick J. Effect of electric current on densification behavior of conductive ceramic powders consolidated by spark plasma sintering // Acta Materialia, 2017. https://doi.org/10.1016/j.actamat.2017.11.010
Olevsky E., Timmermans G., Shtern M., Froyen L., Delaey L. The permeable element method for modeling of deformation processes in porous and powder materials: Theoretical basis and checking by experiments // Powd. Technol. 1997. 93/2, 123–141.
Olevsky E.A. Theory of sintering: from discrete to continuum // Mater. Sci. & Eng. R: Reports. 1998. V. 23. № 2. P. 41–100.
Olevsky E., Tikare V., Garino T. Multi-scale modeling of sintering // Review,” J. Amer. Ceram. Soc. 2006. V. 89. № 6. P. 1914–1922.
Markov A.A. Jump-Slip simulation technique for combustion in submicron tubes and submicron pores // Computers and Fluids, 2014. V. 99. C. P. 83–92.
Xie Z., Fu Y., Wang S., Lee W., Niihara K. Synthesis of nanosized zirconium carbide powders by a combinational method of sol-gel and pulse current heating // J. Eur. Ceram. Soc., 2014. V. 34. № 1. P. 13e1–13e7.
Bardelle Ph., Warin D., Mechanism and kinetics of the uranium-plutonium mononitride synthesis // J. Nucl. Mater., 1992. V. 188. https://doi.org/10.1016/0022-3115(92)90451-p
Aigner K., Lengauer W., Rafaja D., Ettmayer P. Lattice parameters and thermal expansion of Ti(CxNx), Zr(CxNx), Hf(CxN1– x) and TiNx from 298 to 1473 K as investigated by high-temperature X-ray diffraction // J. Alloys Compd., 1994. V. 215. № 1–2. P. 121– 126.
Ortega A., Alcala M.D., Real C. Carbothermal synthesis of silicon nitride (Si3N4): kinetics and diffusion mechanism // J. Mater. Process. Technol., 2008. V. 195. № 13. P. 224– 231.
Weimer A.W., Eisman G.A., Susnitzky D.W. Beaman D.R., McCoy J.W. Mechanism and kinetics of the carbothermal nitridation synthesis of alpha-silicon nitride // J. Am. Ceram. Soc., 1997. V. 80. № 11. P. 2853–2863.
Боли Б., Уийиер Дж. Теория температурных напряжений. М.: Мир., 1964.
Conrad H. Electroplasticity in metals and ceramics // Mat. Sci. Eng. A., 2000. V. 287. № 2. P. 276–287.
Olevsky E., Tikare V., Garino T. Multi-scale modeling of sintering // Review, J. Amer. Ceram. Soc., 2006. 89(6). 1914–1922.
Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. M.: Наука (3-e, испр и доп). 1987.
Markov A.A., Filimonov I.A. Model of thermal radiation using heat absorption by CO2 in submicron pores with application to magnesium-zinc ferritefine disperse particles synthesis via combustion // APhM 2017 IOP Publishing IOP Conf. Series: J. Physics: Conf. Series 1009, 2018, 012040. https://doi.org/10.1088/1742-6596/1009/1/012040
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


