Теоретические основы химической технологии, 2022, T. 56, № 6, стр. 705-711

ВВЕДЕНИЕ

Растворение оксидов металлов в жидкости используется во многих технологиях и производственных процессах для самых разнообразных целей [1–3]. Из них большая группа приложений ставит целью интенсификацию процесса. Последняя может быть реализована разными способами, но к наиболее эффективным стимуляторам можно отнести применение адаптированных методов ультразвукового (УЗ) воздействия [4–11]. Оно обладает такими свойствами и особенностями, которые весьма точно соответствуют задачам ускорения взаимодействия молекул растворителя и оксидов металлов. Во-первых, своими осциллирующими во времени микропотоками ультразвук увеличивает возможности молекул растворителя приблизиться к атому металла и захватить его. Во-вторых, создаваемые им стационарные течения способствуют перемещению насыщенного металлом раствора, открывая доступ к металлу свежим порциям растворителя. Это является одним из решающих факторов стимуляции.

Многочисленные исследования нелинейных свойств ультразвука, обобщенные, например, в работах [4–11], указывают на следующие важные особенности этого явления. Акустические течения возникают как в свободном неоднородном УЗ поле, так и вблизи препятствий разного рода или в окрестности колеблющихся тел. При этом они всегда имеют вихревой характер и возникают только в вязкой среде. Скорость этих потоков возрастает с увеличением мощности ультразвука, но даже при наибольших интенсивностях, полученных в настоящее время, остается меньше амплитуды колебательной скорости в УЗ волне. Существующее разделение акустических течений на три вида оказывается полезным в целом ряде ситуаций, в частности, позволяет оценить возможные проявления нелинейности в большинстве практических схем использования ультразвука и внести соответствующие коррективы для достижения поставленных целей [12, 13]. К первому типу относят мелкомасштабные течения, возникающие вблизи препятствий или в вязком пограничном слое под воздействием ультразвука. Они впервые были исследованы Шлихтингом [14], обнаружившим их вихревой характер. Масштаб второго типа акустических течений сравним с длиной УЗ волны, они реализуются, например, между двумя плоскостями или в цилиндрической трубке. Их подробное описание принадлежит Рэлею [15] для стоячей УЗ волны. В свободном неоднородном УЗ поле возникающие акустические течения третьего типа имеют масштаб неоднородности, определяемый объемом, который занимает ультразвук, т.е. значительно превышает длину волны. Этот тип течений изучался Эккартом [16] и поэтому его иногда называют эккартовским по имени первого своего исследователя так же, как и течения первых двух типов называют по именам их первооткрывателей. Таким образом, практически в каждом рабочем объеме любой формы реализуются акустические течения того или иного типа в процессе использования мощного ультразвука для достижения самых разнообразных целей [17].

В настоящей работе выявлены основные закономерности растворения порошка оксида лития-кобальта(III), как самого распространенного типа катода литий-ионных аккумуляторов [18], в глубоком эвтектическом растворителе хлорид холина–сульфосалициловая кислота под воздействием ультразвука для любого вида возникающего в рабочем объеме акустического течения. При этом учет конкретных особенностей пространственного распределения акустического поля в каждом отдельном устройстве оказывается возможным с помощью численных коэффициентов, входящих в общую формулу, величина которых рассчитывается, исходя из особенностей выбранной схемы применения ультразвука. Выявленные различия в кинетике растворения отдельной частицы оксида металла и их скопления связаны с изменением свойств растворителя, проходящего сквозь слой частиц, в результате взаимодействия с ними. При этом случай растворения отдельной частицы применим для описания также и режима обработки разреженного скопления частиц в случае, когда плотность их пространственного распределения и скорость акустического течения не выходят за рамки установленных ограничений. Результаты выполненных экспериментов полностью подтверждают выводы теории.

МЕТОДИКА РАСЧЕТОВ И АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Растворение цельного куска оксида металла отличается от случая использования порошка такой же массы тем, что жидкость окружает каждую частицу и суммарная поверхность взаимодействия значительно увеличивается. При этом все частицы оксида металла в равной степени находятся под влиянием внешних факторов, например, одинаково испытывают УЗ воздействие. В результате интенсивность процесса оказывается существенно выше [19].

Применение ультразвука приводит к тому, что каждую частицу, представляющую собой сферу радиуса R, окружает осциллирующий с частотой ω во времени t поток жидкости, скорость которого u(t), направленная вдоль оси 0X, меняется по закону

Хорошо известно [20–22], что воздействие на шар радиусом R, оказываемое таким осциллирующим потоком, характеризуется силой F_s, являющейся обобщением известной формулы Стокса [21, 22] для стационарного обтекания на случай переменного во времени внешнего течения

Здесь ρ₀ – исходная плотность жидкости, η – ее коэффициент вязкости.

Под воздействием силы (2) частица оксида металла движется с некоторой скоростью u_p(t), величину которой можно вычислить из уравнения движения для нее. При этом относительная скорость u_p(t) – u(t) позволяет определить амплитуду осцилляторного движения ξ_m частицы оксида металла в жидкости. В УЗ диапазоне частот, когда для обычно применяемых при растворении жидкостей и порошков выполняется условие

Следует отметить, что рассмотрение поведения частиц в растворе под УЗ воздействием, выполненное в работе [20], существенно отличается от представляемого в настоящей работе тем, что в [20] исследовался процесс УЗ дробления капель несмачиваемой жидкости, которые под воздействием микропотоков (2) меняли форму и разбивались на более мелкие частицы. Здесь же анализируется возвратно-поступательное движение твердых сфер относительно жидкости в условиях, когда их радиус постепенно уменьшается из-за растворения оксида металла с их поверхности. Другой вид поведения частиц изучался в [23], где под влиянием акустического давления капли в несмачиваемой жидкости периодически сжимались и расширялись, ускоряя процесс экстракции в методе жидких мембран.

Динамика растворения отдельной частицы оксида металла под воздействием ультразвука

Рассмотрим частицу оксида металла сферической формы радиусом R, которая находится в жидкой среде под воздействием УЗ. Последнее означает, что жидкость вокруг нее представляет собой переменный во времени поток, испытывая смещение ξ(t), имеющее вид

(4)

$\xi (t) = {{\xi }_{{\text{m}}}}\cos (\omega t).$

Вызывающее этот процесс акустическое давление Р_а(t) связано со скоростью u(t) согласно [21, 24] следующим соотношением, справедливым в линейном приближении

(5)

${{Р}_{а}}(t) = {{Р}_{{\text{m}}}}\sin (\omega t),\,\,\,\,{{Р}_{{\text{m}}}} = {{с}_{0}}{{u}_{{\text{m}}}}{{r}_{0}}.$

Здесь с₀ – скорость звука в жидкости.

Перемещение жидкости в УЗ поле вдоль оси 0X в переменном направлении приводит к тому, что со сферой взаимодействует столб раствора объемом V, величина которого, согласно рис. 1, определяется формулой

(6)

$V = \pi {{R}^{2}}{{\xi }_{{\text{m}}}}.$

Рис. 1.

Схема взаимодействия частицы оксида металла с микропотоками в жидкости под воздействием ультразвука.

На рис. 1 пунктиром обозначен край жидкости, близкий к поверхности сферы, который в процессе осцилляций перемещается из позиции “А” в положение “В”. Таким образом, пространство между “А” и “В” заполняется жидкостью, ламинарно обтекающей шар и поступающей с противоположной его стороны.

Количество молекул оксида металла ΔN, контактировавших с молекулой растворителя, описывается выражением

(7)

$\Delta N = Vn \equiv \pi {{R}^{2}}n{{\xi }_{{\text{m}}}}.$

Здесь n – концентрация растворителя.

Если этот объем жидкости, обтекающий осцилляционно сферу оксида металла, не будет заменен свежим раствором, то количество извлеченного металла останется прежним и равным (7), так как все молекулы растворителя уже задействованы. Подобная замена осуществляется с помощью стационарных потоков, образуемых акустическими течениями, всегда сопровождающих воздействие ультразвука на те или иные жидкие объекты.

Как показывают исследования [4–10, 14–16, 20, 21], скорость акустического течения V_а во всех известных случаях можно связать с амплитудой u_m некоторым универсальным соотношением, справедливым для всех типов акустических течений

(8)

${{V}_{а}} = {{qu_{{\text{m}}}^{2}} \mathord{\left/ {\vphantom {{qu_{{\text{m}}}^{2}} {{{с}_{0}}}}} \right. \kern-0em} {{{с}_{0}}}}.$

Входящий в (8) численный коэффициент q является структурным фактором, связанным с пространственным распределением ультразвука, и определяется геометрическими особенностями конкретного устройства, в котором акустическое течение возбуждается.

Время Δt, за которое жидкость, обтекающая сферу, будет заменена на свежую порцию растворителя, зависит от радиуса R сферы и скорости акустического течения V_а поперек осцилляторного потока

(9)

$\Delta t = {{2R} \mathord{\left/ {\vphantom {{2R} {{{V}_{а}}}}} \right. \kern-0em} {{{V}_{а}}}}.$

Отрезок времени Δt значительно превышает период колебаний ультразвука (Т = 2π/ω) и определяет скорость уменьшения радиуса сферы на величину ΔR из-за того, что из ее кристаллической структуры удалено ΔN частиц в соответствии с формулой (7).

Если предположить, что растворенные атомы металла равномерно отдалялись от поверхности оксида металла, то изменение радиуса сферы ΔR связано, согласно (9), с изменением ΔN, произошедшим за отрезок времени Δt, следующим соотношением

(10)

${{4\pi {{R}^{2}}\Delta R{{r}_{{\text{М}}}}} \mathord{\left/ {\vphantom {{4\pi {{R}^{2}}\Delta R{{r}_{{\text{М}}}}} {{{М}_{а}}}}} \right. \kern-0em} {{{М}_{а}}}} = \Delta N = \pi {{R}^{2}}{{V}_{а}}n{{\xi }_{{\text{m}}}}{{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {2R}}} \right. \kern-0em} {2R}}.$

Здесь М_а – масса уходящих в раствор частиц металла.

Из (10) вытекает следующая зависимость радиуса частицы от времени

(11)

$R(t) = \sqrt {R_{0}^{2} - 0.25{{\xi }_{{\text{m}}}}{{V}_{a}}n{{\lambda }^{3}}t} ;\,\,\,\,{{R}_{0}} = R(t = 0).$

Здесь λ – характерный размер кристаллической решетки оксида металла. Время t₀, за которое частица полностью растворится, с помощью (11) можно записать в следующем виде

(12)

${{t}_{0}} = \frac{{4R_{0}^{2}}}{{{{\xi }_{{\text{m}}}}{{V}_{a}}n{{\lambda }^{3}}}}.$

Вполне понятно, что это время растет с увеличением размера частиц и падает с увеличением мощности УЗ воздействия и повышением концентрации растворителя. Графически эти зависимости показаны на рис. 2 для некоторых типичных значений характеристик процесса растворения.

Рис. 2.

Зависимость времени растворения частицы оксида металла от акустического давления и концентрации растворителя.

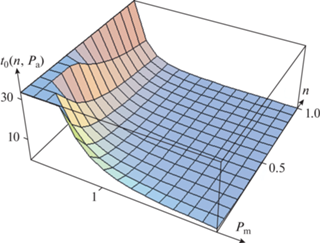
Согласно (12), время t₀ сильно зависит от интенсивности ультразвука, концентрации растворителя и параметров решетки оксида металла. Его кубическая зависимость от амплитуды акустического давления говорит о достаточно высокой чувствительности продолжительности процесса к изменениям в прикладываемой мощности внешнего воздействия. Рис. 2 дает некоторое общее представление о характере такой зависимости времени исчезновения частиц от значений этих двух исходных данных.

Особенности растворения скопления частиц оксида металла в поле ультразвука, действующего в кислотной среде

В случае поступления в раствор скопления частиц оксида металла, каждую из которых беспрепятственно и ламинарно обтекает акустическое течение, процесс растворения оксида металла получает определенные отличия от кинетики растворения отдельной частицы. Если ширина скопления частиц L в направлении, перпендикулярном вектору скорости осцилляторного движения жидкости, меньше характерного размера акустического вихря, т.е. четверти длины волны ультразвука, то все его области находятся в идентичных условиях, что упрощает получение исходного уравнения, описывающего кинетику растворения такого оксида металла. Для скопления частиц оксида металла с большой шириной L при относительно невысоких скоростях V_а акустического течения и сравнительно коротком времени растворения, когда растворитель в объеме жидкости, равном тому, который занимают частицы, успевает полностью прореагировать с оксидом металла за время прохождения сквозь него, можно проследить с использованием некоторых упрощений кинетику растворения оксида металла вплоть до полного исчезновения частиц. С этой целью следует определить, прежде всего, дистанцию l_r вдоль направления акустического течения (ось 0X), на которой поступающий в скопление частиц оксида металла поток растворителя с площадью сечения S прореагирует с оксидом металла. В реальности концентрация растворителя падает от края скопления частиц к точке х = l_r из-за взаимодействия с оксидом металла. Но для упрощения расчетов можно допустить пространственную однородность концентрации n на отрезке 0 ≤ x ≤ l_r, так что на этом участке оксид металла полностью растворится за время t₀ согласно формуле (12). Для определения значения l_r нужно приравнять количество молекул оксида металла в объеме S l_r, содержащихся в частицах, числу молекул растворителя, которые пересекли площадку с размером сечения S в течение времени t₀. В результате для l_r получается выражение

(13)

${{l}_{{\text{r}}}} = \frac{3}{{4\pi }}{{\left( {\frac{\lambda }{{{{R}_{0}}}}} \right)}^{3}}\frac{{{{n}_{{}}}{{t}_{0}}{{V}_{a}}}}{{{{N}_{{\text{p}}}}}}.$

Здесь N_р – количество частиц в единице объема раствора для исходной концентрации.

Если часть скопления частиц оксида металла с шириной l_r растворяется в растворителе за время t₀, то все скопление шириной L растворится за время t_с, определяемое согласно (13) формулой

(14)

${{t}_{{\text{c}}}} = {{t}_{0}}\frac{L}{{{{l}_{{\text{r}}}}}} = \frac{{4\pi }}{3}{{\left( {\frac{{{{R}_{0}}}}{\lambda }} \right)}^{3}}\frac{{{{N}_{{\text{p}}}}}}{n}\frac{1}{{QP_{{\text{m}}}^{2}}},\,\,\,\,Q = \frac{q}{{c_{0}^{3}\rho _{0}^{2}}}.$

Сравнение выражений (13) и (14) показывает разную зависимость времени t₀ растворения отдельной частицы и скопления частиц оксида металла из них t_с от их радиуса R₀ и интенсивности акустического давления Р_m, но связь с концентрацией растворителя у них одинакова.

На рис. 3 представлена зависимость времени растворения частиц оксида металла от их радиуса R₀ и величины акустического давления Р_m для тех же параметров, которые были использованы при построении рис. 2. Следует отметить, что характеристики растворения отдельной частицы (11), (12) применимы также и для скоплений таких частиц при выполнении определенных ограничений на их разреженность, когда все параметры удовлетворяют условию

(15)

$\pi R_{0}^{2}N_{{\text{p}}}^{{}}L < 1.$

Рис. 3.

Связь величины времени исчезновения скопления частиц из порошка оксида металла вследствие растворения в растворителе с размером частиц и с силовой составляющей УЗ воздействия.

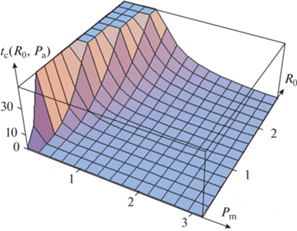
Таким образом, выполненный анализ позволяет охватить количественными характеристиками практически все реальные режимы растворения порошка оксида металла в глубоком эвтектическом растворителе под воздействием ультразвука для их дальнейшего использования с целью повышения эффективности технологического процесса. Для случаев же, когда значения параметров выходят за рамки принятых приближений, представленные вычисления могут оказаться полезными при выполнении соответствующих конкретных расчетов.

Зависимость от времени концентрации металла N_m(t) в растворе можно представить в виде очевидного соотношения

(16)

${{N}_{{\text{m}}}}\left( t \right) = 4\pi {{N}_{{\text{р}}}}{{r}_{{\text{М}}}}{{[R_{0}^{3} - {{R}^{3}}\left( t \right)]{\text{ }}} \mathord{\left/ {\vphantom {{[R_{0}^{3} - {{R}^{3}}\left( t \right)]{\text{ }}} {3{{М}_{а}}}}} \right. \kern-0em} {3{{М}_{а}}}}.$

Соответствующие теоретические и экспериментальные закономерности кинетики растворения оксида лития-кобальта(III) в глубоком эвтектическом растворителе хлорид холина–сульфосалициловая кислота (7 : 3) представлены на рис. 4. Экспериментальные данные были получены с использованием методики, описанной в статье [25].

Рис. 4.

Влияние ультразвука на растворение (а) – Co и (б) – Li в глубоком эвтектическом растворителе хлорид холина–сульфосалициловая кислота (7 : 3) с добавлением 10% воды. Линии – теория, маркеры – эксперимент.

Из рисунка видно, что применение УЗ воздействия значительно увеличивает скорость растворения LiCoO₂ в растворителе. Тенденция увеличения концентрации металла в глубоком эвтектическом растворителе наблюдалась как для Li, так и для Co. Рассмотренная схема растворения порошка оксида металлов применима к докавитационному режиму воздействия ультразвука. Использование УЗ кавитации существенно меняет картину процесса [26]. Характер, направление, мощность микропотоков и течений становятся совершенно другими, возникают ударные волны от схлопывающихся кавитационных пузырьков, меняется способ воздействия на кристаллическую структуру [5, 27]. Для количественного описания этого процесса требуется проведение самостоятельного детального исследования.

ЗАКЛЮЧЕНИЕ

Возможности ультразвука создавать осциллирующие микропотоки и стационарные вихревые течения позволяют с наибольшей эффективностью решать проблему стимуляции растворения оксидов металлов путем построения наивыгоднейших практических схем реализации процесса в каждой конкретной ситуации. В рассмотренном в настоящей работе варианте растворения оксида металлов, когда используется порошкообразный материал, можно выделить два различных режима реализации процесса, создаваемых путем изменения концентрации порошка. На практике таких режимов может быть гораздо больше из-за наличия огромного количества вариантов построения взаимодействия скоплений частиц оксида металла в растворе (которые могут быть различной формы и по-разному доставляться в рабочий объем), с очень разнообразными структурами акустических полей. Последние также могут сильно отличаться друг от друга в зависимости от требований каждой конкретной технологии. Таким образом, в действительности всегда можно подобрать условия и реализовать схему УЗ растворения порошка оксида лития-кобальта(III) с теми выходными данными, которые максимально приближены к требуемым значениям. Приведенные в настоящей работе примеры расчета параметров растворения порошка допускают относительно несложное обобщение на другие конкретные ситуации и могут оказаться полезными при разработке инновационных технологий УЗ растворения оксидов металлов.

Для ускорения процесса растворения можно эффективно использовать способность ультразвука разрушать кристаллическую решетку не только прямым силовым воздействием, но также с помощью усталостного механизма разрушения. В этом случае большое значение приобретает достижение выгодной взаимной ориентации между геометрической формой объекта растворения и направлением изменения УЗ давления. Кроме того, способность ультразвука в кавитационном режиме очищать поверхность металла от загрязнения, адгезионных пленок, окислов также может при надлежащем использовании оказаться весьма полезной для применения в технологиях растворения металла.

Исследование выполнено за счет гранта Российского научного фонда (проект № 20-13-00387).