Теоретические основы химической технологии, 2022, T. 56, № 6, стр. 712-723
О теплоотдаче трубчатого водо-водяного теплообменника и ее оценках по некоторым критериальным моделям
А. А. Коноплев a, *, Б. Л. Рытов a, Ал. Ал. Берлин a, С. В. Романов b
a Федеральное государственное бюджетное учреждение науки Федеральный исследовательский центр
химической физики им. Н.Н. Семенова Российской академии наук
119991 Москва, ул. Косыгина, 4, Россия
b ООО “НПП “Энергосистемы”
105094 Москва, Семеновская наб., 2/1, Россия
* E-mail: alexey.konoplyov@gmail.com
Поступила в редакцию 14.04.2022
После доработки 25.06.2022
Принята к публикации 03.07.2022
- EDN: YGNVDI
- DOI: 10.31857/S0040357122060082
Аннотация
Поскольку известно, что результаты расчетов по различным критериальным моделям конвективного теплообмена могут отличаться между собой, проведено сравнение экспериментальных данных по теплоотдаче, полученных в экспериментах на лабораторных водо-водяных трубчатых теплообменниках с гладкими трубками трех различных диаметров при нормальном давлении и умеренных температурах с результатами расчетов по критериальным моделям Б.С. Петухова, С.С. Кутателадзе, Нуссельта и М.А. Михеева. Эксперименты проводились на двумерной сетке расходов трубного и межтрубного канала, что позволяет, в соответствии с разработанной ранее методикой построить продольные профили теплообменных параметров. Результаты обработки экспериментальных данных по методу средних значений и по продольным профилям сравниваясь между собой, демонстрируют хорошее совпадение. Обнаружено, что отклонения данных экспериментов от результатов расчетов по критериальным моделям носят систематический характер, зависят от области определяющих параметров, т.е., чисел Рейнольдса и Прандтля Re–Pr, в которых они сравниваются, возрастают с ростом числа Re, а в зависимости от числа Pr имеют экстремум.
ВВЕДЕНИЕ
Трубчатые теплообменники, обладают, как известно, некоторыми определенными преимуществами перед другими видами теплообменного оборудования, что делает их применение, по крайней мере, для некоторых технологических задач теплообмена, предпочтительным.
Поэтому задача создания современного высокоэффективного и экономичного трубчатого теплообменного оборудования является сегодня весьма актуальной задачей. Для своего решения эта задача требует, с одной стороны разработки высокоэффективных и технологичных методов интенсификации конвективного теплообмена, с другой – достаточно точных методов ее оценки и расчета теплообменных характеристик.
В настоящее время большинство теплотехнических расчетов конвективного теплообмена осуществляется с помощью критериальных моделей конвективного теплообмена, точность которых в пределах 15–25% считается допустимой.
Будучи по сути своей моделями эмпирическими, т.е., когда соотношения между критериями определяемыми (например, критерий Нуссельта Nu) и критериями определяющими (например, критериями Рейнольдса Re и Прандтля Pr) находятся из экспериментов. Желая, по-видимому, добиться большей универсальности выстраиваемых моделей, эксперименты, которые проводятся для установления значений эмпирических модельных коэффициентов осуществляются с разными средами и при различных условиях. Таким образом, удалось построить несколько критериальных моделей для достаточно больших диапазонов изменения определяющих критериев, сужение же этих диапазонов позволяет несколько упростить модельные выражения (см., напр., [1, 2]). При этом, достаточно большие ошибки в расчетах по критериальным моделям считаются результатом плохо контролируемых условий проведения экспериментов – состоянием теплообменной поверхности, влиянием условий ввода потоков, начальных участков и т.п.
Поэтому, целью нашей работы являлось проведение экспериментов в водо-водяном трубчатом теплообменнике при нормальных давлении и температурах, и сравнении полученных результатов с результатами расчетов по некоторым хорошо известным критериальным моделям.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Теплотехнические эксперименты проводились на лабораторных трубчатых теплообменниках типа “труба в трубе” с гладкими медными трубками трех различных диаметров и длин. В том числе теплообменник с трубкой с внутренним диаметром D = 0.008 м, длиной L = 0.53 м и безразмерной длиной L/D = 66.25 (Т08), теплообменник с трубкой D = 0.014 м и безразмерной длиной L/D = 78 (Т14), теплообменник с трубкой D = = 0.02 м и L/D = 76.2 (Т20).
Греющими каналами могли быть как трубные, так и межтрубные. Входную температуру теплоносителей греющих каналов стремились поддерживать постоянной и равной приблизительно 70°С, а входная температура теплоносителей нагреваемых каналов определялась температурой воды в водопроводной сети.
Измерения экспериментальных параметров проводили по разработанной нами ранее методике в узлах двумерной сетки расходов трубного Gтр и межтрубного Gмт каналов, что в конечном итоге позволяет построить (точнее, приблизить) продольные профили теплотехнических параметров. Сущность этой методики, вкратце, заключается в следующем. Зафиксировав входные температуры теплоносителей трубного tтр, вх и межтрубного tмт, вх каналов (т.е., две из четырех независимых переменных теплообмена), для двух других независимых переменных, а именно, расходов каналов Gтр и Gмт можно построить уравнение теплового потока Q = Q(Gтр, Gмт). Анализ которого, позволяет из коэффициента теплопередачи K выделить коэффициенты теплоотдачи трубного αтр и межтрубного αмт каналов, а в предположении, что изменения коэффициентов теплоотдачи каналов по их длине могут быть приближены какой-либо подходящей функцией, например, полиномом, позволяет найти коэффициенты этой самой функции и построить продольные распределения искомых теплотехнических параметров. Средние значения параметров, при этом, могут быть получены осреднением этих самых распределений.
Таким образом, построение зависимостей теплотехнических параметров от расходов, например, αтр = f(Gтр, Gмт), или, произведя замену переменных, αтр = f(Reтр, Reмт), позволяет построить математическую модель процесса теплообмена, теплотехнические параметры которого могут быть представлены как средними их значениями, так и распределениями по длине. Подробнее о методике смотри в [1], а о ее применении, например, в [2].
Распределения параметров по длине канала позволяют более детально описать процесс теплообмена, увеличив при этом и объем определяемых данных, и область их определения Re–Pr. Очевидно, что использование распределений параметров наиболее эффективным может быть для длинных теплообменных каналов, т.е., таких, у которых безразмерная длина L/D достаточно велика, и может составлять величину вплоть до нескольких сотен единиц. Обычно, это промышленные, а не лабораторные теплообменники.
Конструктивные параметры теплообменных аппаратов Т08, Т14 и Т20 представлены в табл. 1. Там же приведены режимные и расходные параметры проведенных экспериментов, а также расчетов характеристик теплообмена для условий турбулентного режима течения теплоносителя трубного канала.
Таблица 1.
Параметры конструктивные теплообменников, режимные1) эксперимента и расходные для расчета турбулентного режима
| № п/п |
Теплообменник | L, м | D, м | Dн, м | Dк, м | Трубный канал |
tвх, °С | Эксперимент | Расчет | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gmin, л/с |
Gmax, л/с |
Сетка расходов Gтр × Gмт |
oQ, кВт |
Gmin, л/с |
Gmax, л/с |
Сетка расходов Gтр × Gмт |
||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 15 | |
| 1 | Т08 | 0.53 | 0.008 | 0.01 | 0.022 | Греющий | 70.2 9.6 |
0.012 0.062 |
0.111 0.214 |
8 × 8 | 0.0229 | 0.038 0.11 |
0.11 0.21 |
5 × 5 |
| Нагревамый | 3.3 70.7 |
0.034 0.02 |
0.218 0.112 |
8 × 8 | 0.0175 | 0.11 0.038 |
0.21 0.11 |
5 × 5 | ||||||
| 2 | Т14 | 1.092 | 0.014 | 0.016 | 0.022 | Греющий | 69.9 3.5 |
0.025 0.107 |
0.332 0.365 |
8 × 8 | 0.0149 | 0.17 0.18 |
0.33 0.36 |
5 × 5 |
| Нагревамый | 3.4 70 |
0.052 0.09 |
0.364 0.332 |
8 × 8 | 0.016 | 0.18 0.17 |
0.36 0.33 |
5 × 5 | ||||||
| 3 | Т20 | 1.524 | 0.02 | 0.024 | 0.035 | Греющий | 70 4.8 |
0.04 0.108 |
0.25 0.377 |
8 × 8 | 0.0128 | 0.11 0.23 |
0.25 0.37 |
5 × 5 |
| Нагревамый | 7.6 70 |
0.074 0.102 |
0.377 0.25 |
7 × 7 | 0.0141 | 0.23 0.11 |
0.37 0.25 |
5 × 5 | ||||||
На рисунке 1 в качестве иллюстрации приведены зависимости тепловых потоков Q = Q(Gтр, Gмт) для случаев греющего и нагреваемого трубных каналов теплообменника Т20 при минимальных и максимальных расходах теплоносителей по межтрубному каналу. В каждой точке экспериментальной сетки расходов проводились по три измерения, среднее значение из которых представлено на графиках. Среднее среднеквадратичное относительное отклонение oQ теплового потока Q определялось по этим осредненным значения. Значения oQ для всех шести проведенных экспериментов с разными теплообменниками представлены в табл. 1.
Рис. 1.
Теплообменник Т20, тепловой поток Q(Gтр, Gмт), в зависимости от расходов Gтр при минимальных и максимальных расходах Gмт: осредненные по трем измерениям экспериментальные значения трубного (точки) и межтрубного (кружки) каналов, и аппроксимирующие (штрих-пунктирные) кривые; (a) – трубный канал греющий, Gмт = = 0.108, (б) – то же, Gмт = 0.376, (в) – трубный канал нагреваемый, Gмт = 0.102, (г) – то же, Gмт = 0.25 л/с.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Для представления экспериментальных данных с помощью решения уравнения для теплового потока мы использовали сетку задаваемых расходов Gтр×Gмт, состоящую из 5×5 равноотстоящих узлов, что принято с целью не слишком большого увеличения объема рассматриваемых данных. При этом, все задаваемые расходы принадлежали непосредственно областям изменения расходов, имевших место быть в эксперименте, но выбирались такими образом, чтобы получаемые значения теплообменных параметров принадлежали только турбулентному режиму течения теплоносителя в трубном канале. Средние значения рассчитываемых таким образом параметров, определялись как значения, получаемые осреднением продольных распределений параметров по длине канала теплообменника.
Рассчитывались также значения параметра (Pr/Prw)0.25, который, как это предполагается (напр., в [5]), достаточно хорошо учитывает зависимость теплоотдачи от направления теплового потока. Полученные результаты для случаев минимальных и максимальных расходов теплоносителей представлены в качестве иллюстрации в табл. 2.
Таблица 2.
Распределения параметров теплообмена по длине трубного канала теплообменника1) и средние их значения при минимальных и максимальных расходах теплоносителей
| Теплообменник | l/L | Трубный канал греющий | Трубный канал нагреваемый | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gтр, л/с |
Gмт, л/с |
t, °С | K, кВт/(м2 К) |
Re × 10–3 | Pr | α, кВт/(м2 К) |
Nu | Pr/Prw | Gтр, л/с |
Gмт, л/с |
t, °С | K, кВт/(м2 К) |
Re × 10–3 | Pr | α, кВт/(м2 К) |
Nu | Pr/Prw | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Т08 | 0 | 0.038 | 0.11 | 58.73 | 2.11 | 12.42 | 3.02 | 5.84 | 71.09 | 0.899 | 0.11 | 0.038 | 3.3 | 1.77 | 10.91 | 12.09 | 9.13 | 131 | 1.12 |
| 0.25 | 61.54 | 2.06 | 12.96 | 2.89 | 5.68 | 68.74 | 0.898 | 4.21 | 1.8 | 11.23 | 11.7 | 9.52 | 136.1 | 1.119 | |||||
| 0.5 | 64.38 | 2.02 | 13.51 | 2.76 | 5.52 | 66.52 | 0.896 | 5.17 | 1.83 | 11.57 | 11.3 | 9.94 | 141.5 | 1.118 | |||||
| 0.75 | 67.26 | 1.97 | 14.07 | 2.64 | 5.36 | 64.42 | 0.895 | 6.17 | 1.87 | 11.94 | 10.9 | 10.37 | 147 | 1.117 | |||||
| 1 | 70.2 | 1.93 | 14.65 | 2.53 | 5.22 | 62.45 | 0.894 | 7.23 | 1.9 | 12.34 | 10.5 | 10.82 | 152.7 | 1.116 | |||||
| Srd | 64.41 | 2.02 | 13.52 | 2.77 | 5.52 | 66.61 | 0.897 | 5.2 | 1.83 | 11.59 | 11.3 | 9.95 | 141.6 | 1.118 | |||||
| 0 | 0.11 | 0.21 | 62.71 | 3.83 | 38.16 | 2.83 | 14.65 | 177.1 | 0.926 | 0.21 | 0.11 | 3.3 | 3.15 | 20.83 | 12.09 | 18.21 | 261.3 | 1.116 | |
| 0.25 | 64.59 | 3.75 | 39.21 | 2.75 | 14.41 | 173.7 | 0.927 | 4.2 | 3.19 | 21.44 | 11.7 | 18.91 | 270.3 | 1.113 | |||||
| 0.5 | 66.46 | 3.67 | 41.28 | 2.67 | 14.18 | 170.5 | 0.928 | 5.13 | 3.23 | 22.07 | 11.31 | 19.62 | 279.4 | 1.11 | |||||
| 0.75 | 68.32 | 3.59 | 41.34 | 2.6 | 13.96 | 167.5 | 0.928 | 6.09 | 3.26 | 22.74 | 10.94 | 20.35 | 288.6 | 1.107 | |||||
| 1 | 70.2 | 3.51 | 42.4 | 2.53 | 13.75 | 164.6 | 0.929 | 7.1 | 3.29 | 23.43 | 10.56 | 21.1 | 297.9 | 1.104 | |||||
| Srd | 66.45 | 3.67 | 40.28 | 2.68 | 14.19 | 170.6 | 0.928 | 5.15 | 3.23 | 22.09 | 11.32 | 19.63 | 279.5 | 1.11 | |||||
| Т14 | 0 | 0.17 | 0.18 | 58.68 | 2.65 | 31.73 | 3.03 | 7.47 | 159 | 0.898 | 0.18 | 0.17 | 3.4 | 2.7 | 10.24 | 12.04 | 5.71 | 143.3 | 1.243 |
| 0.25 | 61.5 | 2.63 | 33.11 | 2.86 | 7.35 | 155.7 | 0.9 | 6.06 | 2.79 | 11.13 | 10.94 | 6.04 | 149.9 | 1.229 | |||||
| 0.5 | 64.31 | 2.61 | 34.5 | 2.76 | 7.23 | 152.7 | 0.902 | 8.82 | 2.89 | 12.1 | 9.94 | 6.39 | 156.6 | 1.215 | |||||
| 0.75 | 67.12 | 2.6 | 35.9 | 2.65 | 7.12 | 149.8 | 0.904 | 11.69 | 2.98 | 13.14 | 9.02 | 6.75 | 163.4 | 1.201 | |||||
| 1 | 69.9 | 2.59 | 37.33 | 2.54 | 7.02 | 147.2 | 0.905 | 14.67 | 3.07 | 14.26 | 8.2 | 7.12 | 170 | 1.188 | |||||
| Srd | 64.31 | 2.62 | 34.51 | 2.77 | 7.24 | 152.8 | 0.902 | 8.9 | 2.89 | 12.15 | 10 | 6.4 | 156.6 | 1.215 | |||||
| 0 | 0.33 | 0.36 | 59.85 | 4.51 | 62.7 | 2.97 | 13.32 | 283 | 0.902 | 0.36 | 0.33 | 3.4 | 4.76 | 20.47 | 12.04 | 10.75 | 269.8 | 1.233 | |
| 0.25 | 62.38 | 4.47 | 65.11 | 2.85 | 13.13 | 278 | 0.904 | 5.79 | 4.89 | 22.07 | 11.05 | 11.3 | 280.8 | 1.221 | |||||
| 0.5 | 64.9 | 4.44 | 67.53 | 2.74 | 12.96 | 273.3 | 0.906 | 8.25 | 5.03 | 23.79 | 10.13 | 11.87 | 291.9 | 1.209 | |||||
| 0.75 | 67.41 | 4.42 | 69.98 | 2.64 | 12.79 | 268.9 | 0.907 | 10.79 | 5.17 | 25.62 | 9.29 | 12.46 | 302.9 | 1.197 | |||||
| 1 | 69.9 | 4.39 | 72.46 | 2.54 | 12.63 | 274.8 | 0.909 | 13.42 | 5.3 | 27.57 | 8.53 | 13.07 | 313.8 | 1.185 | |||||
| Srd | 64.89 | 4.45 | 67.55 | 2.74 | 12.96 | 273.5 | 0.906 | 8.31 | 5.03 | 23.87 | 10.19 | 11.89 | 291.9 | 1.209 | |||||
| Т20 | 0 | 0.11 | 0.23 | 52.39 | 1.34 | 13.02 | 3.37 | 2.82 | 86.6 | 0.863 | 0.23 | 0.11 | 7.6 | 1.31 | 10.43 | 10.37 | 3.33 | 117.1 | 1.169 |
| 0.25 | 56.55 | 1.33 | 13.91 | 3.14 | 2.75 | 83.92 | 0.861 | 9.39 | 1.35 | 11 | 9.74 | 3.47 | 121.2 | 1.169 | |||||
| 0.5 | 60.87 | 1.32 | 14.86 | 2.92 | 2.69 | 81.45 | 0.859 | 11.35 | 1.39 | 11.64 | 9.12 | 3.62 | 125.4 | 1.168 | |||||
| 0.75 | 65.36 | 1.31 | 15.86 | 2.72 | 2.63 | 79.18 | 0.857 | 13.47 | 1.43 | 12.35 | 8.52 | 3.79 | 129.8 | 1.167 | |||||
| 1 | 70 | 1.3 | 16.93 | 2.54 | 2.58 | 77.13 | 0.855 | 15.76 | 1.47 | 13.13 | 7.93 | 3.96 | 134.5 | 1.166 | |||||
| Srd | 60.99 | 1.32 | 14.9 | 2.93 | 2.69 | 81.6 | 0.859 | 11.47 | 1.39 | 11.69 | 9.13 | 3.63 | 125.5 | 1.168 | |||||
| 0 | 0.25 | 0.37 | 56.14 | 2.3 | 31.41 | 3.16 | 5.81 | 177.4 | 0.884 | 0.37 | 0.25 | 7.6 | 2.21 | 16.77 | 10.37 | 5.22 | 183.9 | 1.195 | |
| 0.25 | 59.5 | 2.3 | 33.07 | 2.99 | 5.72 | 173.7 | 0.884 | 9.63 | 2.27 | 17.82 | 9.66 | 5.46 | 190.6 | 1.189 | |||||
| 0.5 | 62.93 | 2.3 | 34.8 | 2.82 | 5.63 | 170.2 | 0.885 | 11.79 | 2.34 | 18.96 | 8.99 | 5.71 | 197.4 | 1.183 | |||||
| 0.75 | 66.43 | 2.3 | 36.6 | 2.67 | 5.55 | 167 | 0.885 | 14.06 | 2.4 | 20.19 | 8.36 | 5.97 | 204.3 | 1.177 | |||||
| 1 | 70 | 2.29 | 38.47 | 2.54 | 5.48 | 164.1 | 0.885 | 16.46 | 2.47 | 21.5 | 7.76 | 6.24 | 211.3 | 1.171 | |||||
| Srd | 62.98 | 2.3 | 34.85 | 2.83 | 5.64 | 170.4 | 0.885 | 11.87 | 2.34 | 19.03 | 9.02 | 5.72 | 197.5 | 1.183 | |||||
Найденные по экспериментальным данным значения критериальных чисел Nu = Nu(Re,Pr) соотносились со значениями NuКМ = NuКМ(Re,Pr) рассчитываемыми по критериальным моделям, в качестве которых рассматривались следующие.
Критериальная модель 1 (КМ1) – модель Б.С. Петухова-Кириллова, область применения которой определена как – 4 × 103 < Re < 5 × 106 и 0.5 < Pr < 5 × 105 [см., напр., 3]:
(1)
${\text{Nu}} = \frac{{\zeta \operatorname{Re} \Pr }}{{8 + {{7200} \mathord{\left/ {\vphantom {{7200} {\operatorname{Re} \,\, + 35.9\sqrt \zeta ({{{\Pr }}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} - 1)}}} \right. \kern-0em} {\operatorname{Re} \,\, + 35.9\sqrt \zeta ({{{\Pr }}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} - 1)}}}}.$Критериальная модель 2 (КМ2) – модель С.С. Кутателадзе, которая может быть использована для газов и неметаллических жидкостей в стабилизированном потоке при Pr > 0.5 [4]:
(2)
$\begin{gathered} {\text{Nu}} = \\ = \frac{{0.14\Pr \operatorname{Re} \sqrt \zeta }}{{\ln \operatorname{Re} \sqrt \zeta + 2\ln \frac{{1 + 5\Pr }}{{1 + 0.2\Pr }} + 2.4\Pr f(\Pr ) - 6.638}}, \\ \end{gathered} $Критериальная модель 3 (КМ3) – модель Нуссельта–Кроуссольда, которая, по мнению [4], дает неплохие результаты при 0.5 < Pr < 5:
Критериальная модель 4 (КМ4) – модель академика М.А. Михеева, получившая ныне, пожалуй, наиболее широкое распространение для проведения теплотехнических расчетов (см., напр., [3, 4, 6]):
Кроме того, значения Nu, найденные из экспериментов, мы непосредственно аппроксимировались степенной функцией, той самой, которая послужила основой для двух последних рассматриваемых нами моделей (3)–(4):
коэффициенты a, b и с для которой находились с точностью до 2-х, и с точностью до 5-ти значащих цифр. Эти аппроксимации обозначим как аппроксимационная модель 2 (АМ2), и аппроксимационная модель 5 (АМ5) соответственно.Значения чисел Nu, найденные из экспериментальных данных посредством расчетов как по средним значениям параметров теплообмена, так и по значениям их продольных профилей, сотносились со значениями NuКМ, рассчитываемым по моделям (1)–(5), в соответствующих для каждого проведенного эксперимента областях определения (Remin ≤ Re ≤ Remax)–(Prmin ≤ Pr ≤ Prmax) искомых параметров. Полученные результаты Nu/NuКМ = Nu/NuКМ(Re,Pr) представлены в табл. 3 в виде соответствующих средних значений Srd и среднеквадратичных отклонений oS от среднего значения Srd, а также среднеквадратичных отклонений o1 от значения, равного 1. Кроме того, эти результаты были аппроксимированы двумерной параболой, и среднеквадратичное отклонение аппроксимации oa также приведено в табл. 3.
Таблица 3.
Сравнение данных, полученных из экспериментов, с расчетами по критериальным моделям Nu/NuКМ для трубного канала в турбулентном режиме
| Теплообменник | Греющий канал | Критериальная модель | Расчет по средним значениям параметров теплообмена | Расчет по значениям продольных профилей параметров теплообмена | ||||||||||||
| n | 10–3 Re | Pr | Srd | oS | o1 | oa | n | 10–3 Re | Pr | Srd | oS | o1 | oa | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Т08 | Трубный | КМ1 | 25 | 13.3–40.79 | 2.63–2.82 | 1.009 | 0.008 | 0.012 | 0.0029 | 125 | 12.02–42.41 | 2.52–3.14 | 1.009 | 0.054 | 0.055 | 0.0071 |
| КМ2 | 1.021 | 0.012 | 0.024 | 0.0022 | 1.022 | 0.054 | 0.058 | 0.0042 | ||||||||
| КМ3 | 1.094 | 0.013 | 0.095 | 0.0010 | 1.097 | 0.059 | 0.113 | 0.0015 | ||||||||
| КМ4 | 1.163 | 0.014 | 0.164 | 0.0010 | 1.165 | 0.061 | 0.176 | 0.0016 | ||||||||
| AМ21) | 1.003 | 0.009 | 0.010 | 0.0008 | 0.995 | 0.052 | 0.052 | 0.0013 | ||||||||
| AМ57) | 1.0000 | 0.0011 | 0.0011 | 0.0003 | 1.0000 | 0.0010 | 0.0010 | 0.0009 | ||||||||
| Межтрубный | КМ1 | 25 | 11.58–22.1 | 10.85–11.64 | 1.25 | 0.053 | 0.255 | 0.0078 | 125 | 10.9–23.43 | 9.68–12.1 | 1.246 | 0.069 | 0.256 | 0.0079 | |
| КМ2 | 1.318 | 0.059 | 0.324 | 0.0063 | 1.316 | 0.072 | 0.324 | 0.0064 | ||||||||
| КМ3 | 1.369 | 0.069 | 0.376 | 0.0006 | 1.37 | 0.087 | 0.38 | 0.0015 | ||||||||
| КМ4 | 1.395 | 0.07 | 0.401 | 0.0007 | 1.395 | 0.09 | 0.406 | 0.0015 | ||||||||
| AМ22) | 0.999 | 0.046 | 0.046 | 0.0005 | 0.999 | 0.061 | 0.061 | 0.0011 | ||||||||
| AМ58) | 1.0000 | 0.0007 | 0.0007 | 0.0002 | 1.0000 | 0.0068 | 0.0068 | 0.0010 | ||||||||
| Т14 | Трубный | КМ1 | 25 | 33.69–68.96 | 2.67–2.85 | 1.06 | 0.013 | 0.061 | 0.0082 | 125 | 30.24–72.46 | 2.53–3.19 | 1.068 | 0.05 | 0.085 | 0.0117 |
| КМ2 | 1.085 | 0.011 | 0.086 | 0.0047 | 1.092 | 0.05 | 0.104 | 0.0069 | ||||||||
| КМ3 | 1.177 | 0.013 | 0.177 | 0.0005 | 1.18 | 0.059 | 0.189 | 0.0017 | ||||||||
| КМ4 | 1.25 | 0.014 | 0.25 | 0.0005 | 1.253 | 0.061 | 0.26 | 0.0018 | ||||||||
| AМ23) | 0.997 | 0.009 | 0.009 | 0.0004 | 0.996 | 0.047 | 0.047 | 0.0014 | ||||||||
| AМ59) | 1.0000 | 0.0007 | 0.0007 | 0.0003 | 1.0000 | 0.0015 | 0.0015 | 0.0014 | ||||||||
| Межтрубный | КМ1 | 25 | 12.14–23.87 | 9.48–10.7 | 1.269 | 0.02 | 0.269 | 0.0048 | 125 | 10.23–27.58 | 7.41–12.05 | 1.276 | 0.03 | 0.278 | 0.0085 | |
| КМ2 | 1.325 | 0.027 | 0.327 | 0.0038 | 1.334 | 0.027 | 0.335 | 0.0067 | ||||||||
| КМ3 | 1.402 | 0.035 | 0.403 | 0.0003 | 1.408 | 0.05 | 0.411 | 0.0013 | ||||||||
| КМ4 | 1.432 | 0.035 | 0.434 | 0.0003 | 1.439 | 0.055 | 0.442 | 0.0013 | ||||||||
| AМ24) | 0.996 | 0.018 | 0.018 | 0.0002 | 1.001 | 0.033 | 0.033 | 0.0009 | ||||||||
| AМ510 | 1.0000 | 0.0002 | 0.0002 | 0.0001 | 1.0000 | 0.0015 | 0.0015 | 0.0008 | ||||||||
| Теплообменник | Греющий канал | Критериальная модель | Расчет по средним значениям параметров теплообмена | Расчет по значениям продольных профилей параметров теплообмена | ||||||||||||
| n | 10–3 Re | Pr | Srd | oS | o1 | oa | n | 10–3 Re | Pr | Srd | oS | o1 | oa | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Т20 | Трубный | КМ1 | 25 | 14.65–35.44 | 2.77–2.99 | 1.152 | 0.01 | 0.153 | 0.0041 | 125 | 12.6–38.47 | 2.53–3.5 | 1.165 | 0.069 | 0.179 | 0.0094 |
| КМ2 | 1.169 | 0.009 | 0.169 | 0.0029 | 1.179 | 0.069 | 0.192 | 0.0057 | ||||||||
| КМ3 | 1.26 | 0.013 | 0.26 | 0.0008 | 1.266 | 0.08 | 0.277 | 0.0017 | ||||||||
| КМ4 | 1.337 | 0.014 | 0.337 | 0.0009 | 1.343 | 0.081 | 0.352 | 0.0018 | ||||||||
| AМ25) | 0.998 | 0.006 | 0.007 | 0.0006 | 0.992 | 0.06 | 0.061 | 0.0013 | ||||||||
| AМ511) | 1.0000 | 0.0007 | 0.0007 | 0.0004 | 1.0000 | 0.0013 | 0.0013 | 0.0012 | ||||||||
| Межтрубный | КМ1 | 25 | 11.68–19.02 | 8.65–9.47 | 1.103 | 0.016 | 0.105 | 0.0054 | 12 5 | 10.42–21.51 | 7.16–10.38 | 1.109 | 0.025 | 0.111 | 0.0072 | |
| КМ2 | 1.141 | 0.019 | 0.142 | 0.0041 | 1.146 | 0.022 | 0.148 | 0.0048 | ||||||||
| КМ3 | 1.212 | 0.024 | 0.214 | 0.0001 | 1.216 | 0.037 | 0.219 | 0.0010 | ||||||||
| КМ4 | 1.243 | 0.024 | 0.244 | 0.0001 | 1.247 | 0.04 | 0.25 | 0.0011 | ||||||||
| AМ26) | 1.003 | 0.016 | 0.016 | 0.0001 | 1.006 | 0.03 | 0.031 | 0.0009 | ||||||||
| AМ512) | 1.0000 | 0.0003 | 0.0003 | 0.0001 | 1.0000 | 0.0013 | 0.0013 | 0.0008 | ||||||||
| Примечания. | расчет по средним значениям: | расчет по значениям продольных профилей: | ||||||||||||||
| 1) – NuАМ2 = 0.022Re0.81Pr0.43; | NuАМ2 = 0.022Re0.81Pr0.44; | |||||||||||||||
| 2) – NuАМ2 = 0.023Re0.82Pr0.45; | NuАМ2 = 0.023Re0.82Pr0.45; | |||||||||||||||
| 3) – NuАМ2 = 0.021Re0.82Pr0.44; | NuАМ2 = 0.023Re0.81Pr0.46; | |||||||||||||||
| 4) – NuАМ2 = 0.022Re0.83Pr0.44; | NuАМ2 = 0.022Re0.83Pr0.44; | |||||||||||||||
| 5) – NuАМ2 = 0.023Re0.82Pr0.43; | NuАМ2 = 0.023Re0.82Pr0.44; | |||||||||||||||
| 6) – NuАМ2 = 0.021Re0.82Pr0.44; | NuАМ2 = 0.021Re0.82Pr0.44; | |||||||||||||||
| 7) – NuАМ5 = 4.3231 × 10–3Re0.8712Pr1.442; | NuАМ5 = 4.114 × 10–3Re0.87164Pr1.4886; | |||||||||||||||
| 8) – NuАМ5 = 6.7622 × 10–3Re1.0561Pr0.008289; | NuАМ5 = 6.4301 × 10–3Re1.0633; | |||||||||||||||
| 9) – NuАМ5 = 4.5366 × 10–3Re0.87692Pr1.3407; | NuАМ5 = 5.0777 × 10–3Re0.87176Pr1.2869; | |||||||||||||||
| 10) – NuАМ5 = 1.0709 × 10–2Re0.91431Pr0.39338; | NuАМ5 = 1.2693 × 10–2Re0.91914Pr0.30126; | |||||||||||||||
| 11) – NuАМ5 = 5.7577 × 10–3Re0.87746Pr1.19111; | NuАМ5 = 6.2645 × 10–3Re0.87185Pr1.1692; | |||||||||||||||
| 12) – NuАМ5 = 8.625 × 10–3Re0.92685Pr0.37831; | NuАМ5 = 1.0034 × 10–2Re0.93229Pr0.28686 | |||||||||||||||
Вычисление продольных распределений теплообменных параметров по длине трубного канала позволяют увеличивать не только объем получаемых из эксперимента данных (см., табл. 2), но и области их определения Re–Pr (см. табл. 3). Так даже для наших теплообменников при сравнительно небольших длинах теплообменных каналов, увеличение, как это следует из приведенных в таблице 3 данных, диапазона по числу Рейнольдса составляет для греющих каналов 1.11–1.24, для нагреваемых – 1.19–1.51 раза. По числу же Прандтля увеличение диапазона изменения гораздо больше, и составляет для греющих каналов 3.26–4.41, для нагреваемых – 3.06–3.93 раза.
Из приводимых в таблице 3 данных следует, что результаты расчетов по средним значениям параметров теплообмена и по продольным их профилям весьма близки. Несколько возрастают средние значения Srd, на доли процента, а также отклонения oS от значения Srd, величины которых при этом не превышают 7% (см. табл. 3). Таким образом, полученные результаты свидетельствует о применимости методики построения продольных профилей к оценке экспериментальных данных.
Наименьшее расхождение с результатами экспериментов во всех случаях имеют результаты расчетов по модели КМ1, наибольшее – по модели КМ4, результаты же расчетов по моделям КМ2 и КМ3 занимают промежуточное положение, а среднеквадратичные отклонения от среднего значения составляют лишь несколько процентов (см. табл. 3).
Аппроксимации экспериментальных данных моделями АМ2 и АМ5 приводят, естественным образом, к повышению точности при определении средних значений параметра Nu/NuКМ, что отражается в уменьшении величины параметра o1, характеризующего расхождения между экспериментом и расчетами. Коэффициенты модели АМ2 весьма близки по величине к коэффициентам моделей КМ3–КМ4, в то время, как коэффициенты модели АМ5 отличаются достаточно сильно, но они же и значительно точнее описывают эксперимент (см. табл. 3).
На рис. 2 и 3 в виде контурных графиков приведены аппроксимации значений Nu/NuКМ для критериальных моделей КМ1–КМ4 и модели АМ2 двумерной параболой.
Рис. 2.
Теплообменник Т08, трубный канал греющий. Теплоотдача относительная Nu/NuКМ: (a, в, д, ж, и) – расчет по средним значениям параметров теплообмена, область их определения – 10–3 Re = 13.3–40.79, Pr = 2.63–2.82; (б, г, е, з, к) – расчет по значениям продольных профилей параметров теплообмена, область их определения – 10–3 Re = 12.02–42.41, Pr = 2.52–3.14; (a, б) – Nu/NuКМ1, (в, г) – Nu/NuКМ2, (д, е) – Nu/NuКМ3, (ж, з) – Nu/NuКМ4, (и, к) – Nu/NuАМ2.
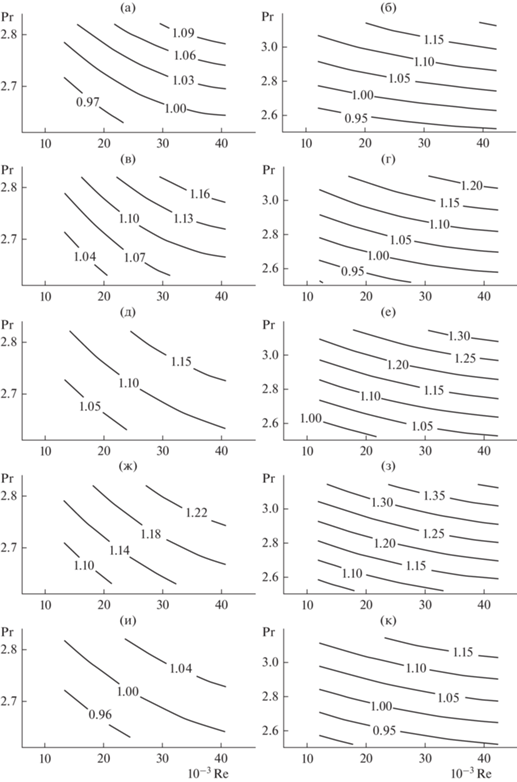
Рис. 3.
Теплообменник Т08, трубный канал нагреваемый. Теплоотдача относительная Nu/NuКМ: (a, в, д, ж, и) – расчет по средним значениям параметров теплообмена, область их определения – 10–3 Re = 11.58–22.1, Pr = 10.85–11.64; (б, г, е, з, к – расчет по значениям продольных профилей параметров теплообмена, область их определения – 10–3 Re = 10.9–23.43, Pr = 9.68–12.1; (a, б) – Nu/NuКМ1, (в, г) – Nu/NuКМ2, (д, е) – Nu/NuКМ3, (ж, з) – Nu/NuКМ4, (и, к) – Nu/NuАМ2.
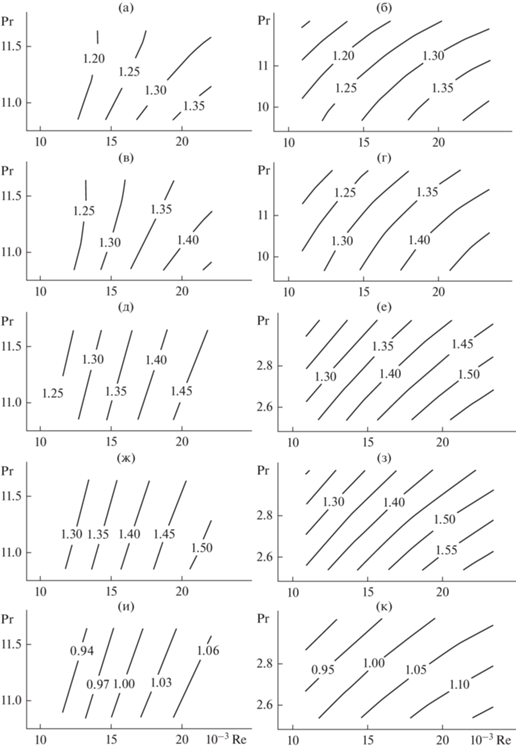
Из анализа приводимых данных следует, что рассогласования между экспериментом и расчетами по моделям носят скорее системный, а не случайный характер. Так во всех экспериментах и с греющим, и с нагреваемым трубными каналами, и для всех моделей, включая АМ2, с ростом числа Re расхождения увеличиваются. Это означает, что в нашем эксперименте теплоотдача растет быстрее, чем это следует из рассматриваемых моделей, в том числе и из модели АМ2.
С ростом числа Прандтля ситуация в случае греющего канала аналогична, а в случае нагреваемого – противоположна (см. рис. 2–3). Это означает, что с ростом числа Прандтля при малых его значениях теплоотдача в эксперименте растет быстрее, а при больших – медленнее, чем в расчетах по моделям, а также то, что зависимость Nu/NuКМ = = Nu/NuКМ(Re = const,Pr) имеет экстремум.
Эти обстоятельства указывают на то, значения коэффициентов критериальных моделей конвективного теплообмена, определяемых из экспериментов, зависят от условий проведения этих экспериментов и способов обработки их данных.
На рисунках 4–5 приведены сечения аппроксимаций Nu/NuКМ для теплообменников Т08 и Т20, еще более наглядно демонстрирующие сделанные выше заключения. Для сравнения приводятся сечения модели АМ5, демонстрирующие, практически, отсутствие зависимости значений Nu/NuКМ5 от изменений чисел Рейнольдса или Прандтля.
Рис. 4.
Теплообменник Т08. Теплоотдача относительная Nu/NuКМ трубного канала зависимости от чисел Re и Pr: (a–г) – расчет по средним значениям параметров теплообмена; (д–з) – расчет по значениям продольных профилей параметров теплообмена; (a, в, д, ж) – греющий канал; (б, г, е, з) – нагреваемый канал; (a, д) – Pr = 2.8; (б, е) – Pr = 11; (в–г, ж–з) – 10–3 Re = 20; 1 – Nu/NuКМ1; 2 – Nu/NuКМ2; 3 – Nu/NuКМ3; 4 – Nu/NuКМ4; 5 – Nu/NuАМ2; 6 – Nu/NuАМ5.

Рис. 5.
Теплообменник Т20. Теплоотдача относительная Nu/NuКМ трубного канала зависимости от чисел Re и Pr: (a–г) – расчет по средним значениям параметров теплообмена; (д–з) – расчет по значениям продольных профилей параметров теплообмена; (a, в, д, ж) – греющий канал; (б, г, е, з) – нагреваемый канал; (a, д) – Pr = 2.9; (б, е) – Pr = 9; (в–г, ж–з) – 10–3 Re = 18; 1 – Nu/NuКМ1; 2 – Nu/NuКМ2; 3 – Nu/NuКМ3; 4 – Nu/NuКМ4; 5 – Nu/NuАМ2; 6 – Nu/NuАМ5.

ЗАКЛЮЧЕНИЕ
Таким образом, из представленных результатов можно сделать вывод о том, что из рассмотренных критериальных моделей теплоотдачу трубчатых водо-водяных теплообменников при нормальном давлении и умеренных температурах наиболее точно описывает критериальная модель Б.С. Петухова-Кириллова, а наименее точно – модель М.А. Михеева. Связано это, по-видимому, с тем, что на определение эмпирических коэффициентов модели влияние оказывают не только условия проведения экспериментов (начальные участки, штуцеры, состояние теплообменной поверхности и т.д.), но и с областью их определения Re–Pr.
Как показывает сравнение результатов аппроксимации одних и тех же данных одной и той же функцией, но с различной точностью искомых коэффициентов (модели АМ2 и АМ5) повышение точности коэффициентов аппроксимации и, по-видимому, учет их зависимостей от определяющих критериев может заметно повысить точность расчетов параметров конвективного теплообмена по критериальным моделям.
ОБОЗНАЧЕНИЯ
| D | диаметр трубки внутренний, характерный размер, м |
| Dн | диаметр трубки наружный, м |
| Dк | диаметр кожуха внутренний, м |
| G | расход теплоносителя, л/с |
| К | коэффициент теплопередачи, кВт/(м2 К) |
| L | длина теплообмена, м |
| l | текущая длина теплообмена, м |
| n | число точек |
| Nu | критерий Нуссельта |
| oa | среднеквадратичное отклонение аппроксимации |
| oQ | среднеквадратичное относительное отклонение теплового потока |
| oS | среднеквадратичное отклонение от среднего значения |
| o1 | среднеквадратичное отклонение от значения, равного 1 |
| Pr | критерий Прандтля |
| Q | тепловой поток, кВт |
| Re | критерий Рейнольдса |
| Srd | среднее значения |
| t | температура, °С |
| α | коэффициент теплоотдачи, кВт/(м2 К) |
| ζ | коэффициент гидродинамического сопротивления |
ИНДЕКСЫ
Список литературы
Коноплев А.А., Алексанян Г.Г., Рытов Б.Л., Берлин Ал.Ал. Расчет локальных параметров интенсифицированного теплообмена // Теорет. основы хим. технологии. 2007. Т. 41. № 6. С. 692.
Коноплев А.А., Алексанян Г.Г., Рытов Б.Л., Берлин Ал.Ал. Об эффективности интенсификации теплообмена глубоким профилированием // Теорет. основы хим. технологии. 2012. Т. 46. № 1. С. 24.
Тепло- и массообмен. Теплотехнический эксперимент: Справочник / Под Ред. В.А. Григорьева и В.М. Зорина. М.: Энергоиздат, 1982.
Кутателадзе С.С. Теплопередача и гидравлическое сопротивление: Справочное пособие. М.: Энергоатомиздат, 1990.
Михеев М.А. Теплоотдача при турбулентном движении жидкости в трубах. Известия АН СССР, ОТН. 1952. № 10. С. 1448–1454.
Михеев М.А. Средняя теплоотдача при движении жидкости в трубах: Сборник “Теплопередача и тепловое моделирование”. М.: Изд-во АН СССР, 1959.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


