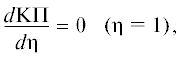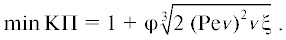Теоретические основы химической технологии, 2022, T. 56, № 6, стр. 724-728

Теоретический расчет концентрационной поляризации при ультрафильтрационной очистке технологических растворов, содержащих тринатрийфосфат

С. И. Лазарев^a, О. А. Абоносимов^a, С. И. Котенев^a, К. В. Шестаков^a, *

^a Тамбовский государственный технический университет
Тамбов, Россия

Поступила в редакцию 05.05.2021
После доработки 08.05.2022
Принята к публикации 03.07.2022

EDN: FSCXFC
DOI: 10.31857/S0040357122060094

Аннотация

Целями настоящей работы были математическое описание процесса образования слоя осадка на поверхности мембран за счет концентрационной поляризации на основе полуинтегрального метода решения уравнения конвективной диффузии, оптимизация процесса ультрафильтрации и определение слоя осадка на поверхности мембраны, расчет времени работы мембраны и объема фильтрата в стационарном режиме до проведения регенерации. Результаты минимизации показали, что наименьшее значение функции получено с помощью пакета Wolfram Mathematica, и оно составило 1.32583 и 1.32112 для концентраций Na₃PO₄ 0.5 и 1 кг/м³ соответственно. Установлено, что через 2.43 и 2.52 с после начала процесса разделения в конце канала КП достигнет максимально допустимого значения в 1.32583 и 1.298 для растворов с концентрацией 0.5 и 1 кг/м³ соответственно. Для того, чтобы концентрационная распространилась по всей длине канала, потребуется соответственно 5500 и 5710 с. После этого для поддержания требуемого уровня очистки потребуется регенерация мембран. За данные отрезки времени образуется 0.191 и 0.173 литров отфильтрованной жидкости.

Ключевые слова: полунтегральный метод, ультрафильтрация, мембрана, концентрационная поляризация, тринатрийфосфат, оптимизация

ВВЕДЕНИЕ

Одним из ключевых вызовов, стоящих перед предприятиями химической промышленности, является непрерывно возникающие экологические проблемы и загрязнение водного бассейна. Для решения данных проблем проводится поиск оптимальных режимов процесса очистки конкретных сточных вод и промышленных растворов, проводится подбор композиций химических реагентов, разрабатываются и совершенствуются очистные сооружения.

Среди множества очистных методов широкое распространение получила и ультрафильтрация. Как и другие методы, ультрафильтрация имеет свои преимущества и недостатки. Существенное негативное влияние на процесс фильтрации через ультрафильтрационную мембрану оказывает концентрационная поляризация (КП), представляющая собой слой загрязняющих веществ, скапливающихся на поверхности мембраны. С течением времени этот слой увеличивается, и происходит рост трансмембранного давления (ТМД) ΔР при постоянной удельной производительности. Таким образом расход фильтрующего продукта через мембрану зависит от гидродинамического сопротивления мембраны ТМД и толщины слоя осадка, возникшего за счет КП:

$J = f\left( {\Delta P} \right),$

$\Delta P\left( \tau \right) = f\left( \delta \right).$

Применение для удаления скопившихся загрязнений гидравлически обратной промывки малоэффективно. Наиболее эффективным способом удаления этих слоев с поверхности мембран являются специально подобранные композиции химических реагентов, но в этом случае нужен точный расчет КП.

Расчет КП обычно проводят в соответствии с моделями процесса массопереноса растворенного вещества через мембрану. Автором работы [1] предложена математическая модель процесса ультрафильтрации раствора высокомолекулярного соединения, в которой учитывается изменение положения точки начала образования геля, загрязняющего поверхность мембраны. В работе [2] представлен расчет КП согласно модели, описывающей перенос растворенного вещества в пограничном слое за счет молекулярной диффузии и конвекции. Эмпирическое выражение зависимости КП от проницаемости мембран и турбулентности потока применительно к ультрафильтрации молочного сырья получены в работе [3]. Авторами работы [4] показана математически возможность адаптации однопараметрической диффузионной модели к мембранному процессу разделения за счет учета проницаемости одной из стенок рассматриваемого канала прямоугольного сечения. В работе [5] рассматривается тупиковый режим нестационарного процесса фильтрации суспензии в канале, характерной для трубчатых и половолоконных мембранных элементов, а также аппаратов с тангенциальной фильтрацией. Другим научным коллективом [6, 7] предложен полуинтегральный метод определения нестационарной КП при ламинарной ультрафильтрации в плоском канале. В этих работах распределение концентрации в диффузионном пограничном слое определяется непосредственно из уравнения конвективной диффузии. В данном распределении неизвестным параметром является не произвольная величина, например, толщина диффузионного пограничного слоя, которая является определяющим параметром в чисто интегральном подходе, а физически четкий параметр потока.

Учитывая важность определения КП в процессах ультрафильтрации промышленных растворов и преимуществ полуинтегрального метода в ее определении, целями в настоящей работе были:

1) Математическое описание процесса образования слоя осадка на поверхности мембран за счет КП на основе полуинтегрального метода решения уравнения конвективной диффузии.

2) Оптимизация процесса ультрафильтрации и определение слоя осадка на поверхности мембраны.

3) Расчет времени работы мембраны и объема фильтрата в стационарном режиме до проведения регенерации.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

На основе полуинтегрального метода решения уравнения конвективной диффузии (1) при краевых условиях (2.1)–(2.3) получена инженерная формула (3), справедливая в широком диапазоне чисел Pev для мембран с неидеальной селективностью:

(1)

(2.1)

(2.2)

(2.3)

${\text{КП}} = 1\,\,\,\,{\text{ }}\left( {\xi = 0} \right),$

(3)

Следует отметить, что при φ = 1 выражение переходит в уравнение для расчета КП на стенке мембраны.

Для оптимизации процесса ультрафильтрации и определения слоя осадка на поверхности мембраны необходимо было организовать процесс очистки промышленных растворов в аппаратах плоскокамерного типа таким образом, чтобы за счет минимизации негативного воздействия КП можно было бы определить время до проведения регенерации мембран и максимальный объем фильтрата. Для минимизации КП формулу (3) представили в виде (4) с ограничениями (5):

(4)

$\min {\text{КП\; = \;1 + \;}}{{x}_{{\text{2}}}}\sqrt[3]{{2~x_{3}^{2}~{{x}_{1}}}}{\text{\;,}}$

(5)

$\begin{gathered} \min {{х}_{1}} \leqslant {{х}_{1}} \leqslant \max {{х}_{1}};\,\,\,\,\min {{х}_{2}} \leqslant {{х}_{2}} \leqslant \max {{х}_{2}}; \\ \min {{х}_{3}} \leqslant {{х}_{3}} \leqslant \max {{х}_{3}}, \\ \end{gathered} $

где х₁ = vξ_max; х₂ = φ; х₃ = Pev при v = const.

Безразмерную толщину диффузионного слоя δ, необходимую для расчета $\overline {{\delta }} $, определяли по формуле (6):

(6)

${{\delta }} = \frac{{\ln ~{\text{КП}}}}{{{\text{Pe}}~v}}.$

Толщину диффузионного слоя $\overline {{\delta }} $ определяли по формуле (7):

(7)

$\overline {{\delta }} = \delta h.$

Коэффициент массоотдачи рассчитывали по формуле (8):

(8)

$k = \frac{D}{{\overline {{\delta }} }}.$

Расчет времени работы мембраны и объема фильтрата V, который можно получить до начала процесса регенерации мембраны, производился в зависимости от длины канала разделения. При расчете времени работы мембраны применительно к каналам малой (l ≤ 0.13 м) использовали следующие выражения (9)–(12):

(9)

${\text{КП\; = \;1\; + \;\;}}\sqrt {2~{\text{Pe}}~{{v}^{2}}~{{\tau }}} {\text{\;}} \leqslant \left[ {{\text{КП}}} \right],$

(10)

${{\tau }} = \frac{{{{{({\text{КП}} - 1)}}^{2}}}}{{2~{\text{Pe\;}}~{{v}^{2}}}},$

(11)

${{t}_{{{\text{ст}}}}} = \frac{{{{\tau \;}}h}}{{\overline w }},$

(12)

${{t}_{{{\text{н}}{\text{.р}}}}} = {{t}_{{{\text{ст}}}}}\frac{l}{{\overline \delta }}.$

Количество отфильтрованной жидкости V определяли по уравнению (13):

(13)

$V = a~l~\tilde {v}~{{t}_{{{\text{н}}{\text{.р}}}}}.$

Расчет t_ст, t_н.р и V относительно каналов большой длины (l ≥ 0.29 м) так же возможно по выражениям (11)–(13), однако определение τ необходимо производить по формулам (14) и (15):

(14)

${\text{КП\; = \;Pe}}~{{v}^{2}}~{{\tau \;}} \leqslant \left[ {{\text{КП}}} \right],$

(15)

${{\tau }} = \frac{{{\text{КП}}}}{{~{\text{Pe\;}}{{v}^{2}}}}.$

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Один из этапов данного исследования был направлен на получение экспериментальных данных по очистке технологических растворов от Na₃PO₄ на лабораторной плоскокамерной баромембранной установке (рис. 1) с помощью мембран УАМ-150. Концентрация Na₃PO₄ в растворах составляла 0.5 и 1 кг/м³. Габаритные размеры камеры разделения – 0.13 × 0.06 × 0.001 м.

Рис. 1.

Лабораторная установка: 1 – емкость исходного раствора; 2 – насос-дозатор; 3 – гидроаккумулятор; 4 – воздушно-поршневой компрессор; 5 – манометр; 6 – образцовый манометр; 7 – электроконтактный манометр; 8 – плоскокамерный мембранный аппарат; 9 – емкости пермеата; 10 – дроссели; 11 – ротаметры.

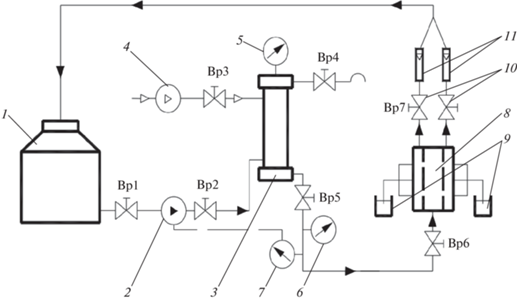
При разделении технологического раствора, содержащего Na₃PO₄, установка работала следующим образом: технологический раствор из емкости исходного раствора 1 при помощи насоса-дозатора 2 нагнетался в гидроаккумулятор 3, далее он попадал в плоскокамерный мембранный аппарат 8. Технологический раствор, содержащий Na₃PO₄, вышедший из плоскокамерного обратноосмотического аппарата 8 в виде ретентата, проходил через дроссели 10 и ротаметры 11 и возвращался обратно в емкость исходного раствора 1. Для снижения влияния пульсаций давления ультрафильтрационная установка оснащалась гидроаккумулятором 3 с установленным в специальном штуцере манометром 5. Гидроаккумулятор 3 заполнялся сжатым воздухом от 30 до 40% от рабочего давления при помощи воздушно-поршневого компрессора 4, что визуально фиксировалось показаниями манометра 5. Контроль давления в экспериментальной установке производился образцовым манометром 6, а для автоматического регулирования подачи раствора конструкция установки была оснащена электроконтактным манометром 7, который при помощи реле отключал насос дозатора 2 при превышении давления в установке выше рабочего. Пермеат, прошедший сквозь поры мембраны и выходящий из плоскокамерного аппарата 8, отводился самотеком в емкости пермеата 9.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Полученные экспериментальные данные по удельному потоку растворителя, коэффициенту задержания мембраны УАМ-150 и другим кинетическим характеристикам процесса разделения при ультрафильтрационной очистке технологических растворов от Na₃PO₄ были использованы для расчета КП, времени работы мембраны и объема фильтрата в стационарном режиме до проведения регенерации.

Процесс минимизации функции (4) был произведен двумя способами – с помощью программного математического пакета Wolfram Mathematica и методом штрафных функций [8]. Ограничения переменных x₁, x₂ и x₃, использованные при минимизации, не отличались между собой у обоих способов для одинаковой концентрации раствора. Для концентрации 0,5 кг/м³ они составили 0.00189 ≤ х₁ ≤ 0.01; 0.938 ≤ х₂ ≤ 0.96; 3.33 ≤ х₃ ≤ 100, а для концентрации 1 кг/м³ – 0.00189 ≤ х₁ ≤ 0.01; 0.929 ≤ х₂ ≤ 0.96; 2.955 ≤ х₁ ≤ 100.

Результаты минимизации (табл. 1) показали, что наименьшее значение функции получено с помощью пакета Wolfram Mathematica, и оно составило 1.32583 и 1.32112 для концентраций 0.5 и 1 кг/м³ соответственно. Максимальное расхождение между значениями КП, рассчитанными разными способами, не превышает 7.2%.

Таблица 1.

Минимизация функции

Метод	Wolfram Mathematica	Штрафных функций
0.5 кг/м³
КП	1.32583	1.37067
х₁	0.00189	0.00278
х₂	0.938	0.93811
х₃	3.33	3.3301
1 кг/м³
КП	1.298	1.3993
х₁	0.00189	0.00278
х₂	0.929	0.93811
х₃	2.955	3.25811

На основе полученного минимального значения КП были рассчитаны время работы мембраны и объем фильтрата в стационарном режиме до проведения регенерации (табл. 2) для канала малой длины (l ≤ 0.13 м). По данным расчета через 2.43 и 2.52 с после начала процесса разделения в конце канала КП достигнет максимально допустимого значения в 1.32583 и 1.298 для растворов с концентрацией Na₃PO₄ 0.5 и 1 кг/м³ соответственно. Для того, чтобы КП распространилась по всей длине канала, потребуется соответственно 5500 и 5710 с. После этого для поддержания требуемого уровня очистки потребуется регенерация мембран. За данные отрезки времени образуется 0.191 и 0.173 литров отфильтрованной жидкости.

Таблица 2.

Расчет параметров

Параметр	0.5 кг/м³	1 кг/м³
l, м	0.13	0.13
h, м	0.0005	0.0005
а, м	0.06	0.06
ξ_max	260	260
D, м²/с	0.493 × 10^–9	0.504 × 10^–9
Ре	0.115 × 10⁷	0.112 × 10⁷
v	0.290 × 10^–5	0.263 × 10^–5
$\tilde {v}$, м/с	0.328 × 10^–5	0.298 × 10^–5
$\bar {w}$, м/с	1.13186	1.13186
φ	0.938	0.929
τ	5500	5710
t_ст, с.	2.43	2.52
t_н.р, с.	7450	7430
$\overline {{\delta }} $, м	4.235 × 10^–5	4.413 × 10^–4
δ	0.0847	0.08827
КП	1.32583	1.298
k, м/с	0.116 × 10^–4	0.114 × 10^–4
V, дм³	0.191	0.173

ЗАКЛЮЧЕНИЕ

1. В работе математически описан процесс образования слоя осадка на поверхности мембран за счет КП на основе полуинтегрального метода решения уравнения конвективной диффузии, произведена оптимизация процесса ультрафильтрации методом штрафных функций и с помощью программногопакета Wolfram Mathematica, рассчитан слой осадка на поверхности мембраны. Максимальное расхождение между значениями КП, рассчитанными разными способами, не превышает 7.2%.

2. Произведен расчет времени работы мембраны и объема фильтрата в стационарном режиме до проведения регенерации. Установлено, что через 2.43 и 2.52 с после начала процесса разделения в конце канала КП достигнет максимально допустимого значения в 1.32583 и 1.298 для растворов с концентрацией Na₃PO₄ 0.5 и 1 кг/м³ соответственно. Для того, чтобы КП распространилась по всей длине канала, потребуется соответственно 5500 и 5710 с. После этого для поддержания требуемого уровня очистки потребуется регенерация мембран. За данные отрезки времени образуется 0.191 и 0.173 литров отфильтрованной жидкости.

ОБОЗНАЧЕНИЯ

a	ширина канала, м
C	концентрация целевого вещества, кг/м³
D	коэффициент диффузии, м²/с
H	полувысота плоского канала, мм
J	поток фильтрата через мембрану, м³/с
k	коэффициент массоотдачи, м/с
l	длина канала, м
ΔP	трансмембранное давление, Па
Pe	критерий Пекле
t	время, с
u = w/$\bar {w}$	безразмерная продольная составляющая скорости
v	безразмерная трансмембранная скорость
$\tilde {v} = v\bar {w}$	трансмембранная скорость, м/с
w	продольная составляющая скорости в канале, м/с
$\overline w {\text{ }}$	средняя скорость на входе в канал, м/с
x	текущая длина плоского канала, мм
y	текущая ширина плоского канала, мм
δ	безразмерная толщина слоя осадка, накопившегося до достижения критического значения ΔP_кр
η = y/h	безразмерная поперечная координата мембраны
ξ = x/h	безразмерная продольная координата мембраны
τ	безразмерное время выхода на стационарный режим
$v$	поперечная составляющая скорости в канале, м/с
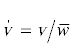	безразмерная поперечная составляющая скорости
φ	коэффициент задержания (селективность) мембраны

ИНДЕКС

исх	в исходном растворе
кр	критическое значение
м	в мембране
н.р	до начала регенерации
ст	выход на стационарный режим

Список литературы

Семенов А.Г. Развитие гелевого загрязнения мембраны при тангенциальной ультрафильтрации раствора высокомолекулярного соединения // Техн. и технол. пищ. произв. 2011. № 1(20). С. 79.
Дытнерский Ю.И. Баромембранные процессы. Теория и расчет. М.: Химия, 1986.
Полянский К.К., Родионова Н.С. Концентрационная поляризация при ультрафильтрации молочного сырья // Изв. ВУЗов. Пищ. технол. 1992. № 2. С. 43.
Антипов С.Т., Ключников А.И. Математическое моделирование процесса микрофильтрации в канале прямоугольного сечения // Теор. осн. хим. технологии. 2019. Т. 53. № 1. С. 87 [Antipov S.T., Klyuchnikov A.I. Mathematical modeling of microfiltration in a rectangular channel // Theor. Found. Chem. Eng. 2019. V. 53. № 1. P. 83].
Давыдова Е.Б., Ильин М.И., Тарасов А.В. Моделирование нестационарного процесса фильтрации суспензий в тупиковом канале // Теор. осн. хим. технологии. 2013. Т. 47. № 3. С. 352 [Davydova E.B., Il’in M.I., Tarasov A.V. Simulation of the unsteady-state filtration of suspensions in a dead-end channel // Theor. Found. Chem. Eng. 2013. V. 47. № 3. P. 295].
Байков В.И., Бильдюкевич А.В. Нестационарная концентрационная поляризация при ламинарной ультрафильтрации в плоском канале // Инж.-физ. журн. 1994. Т. 67. № 1–2. С. 103 [Baikov V.I., Bil’dyukevich A.V. Nonstationary concentration polarization in laminar ultrafiltration in a plane channel // J. Eng. Phys. Thermophys. 1994. V. 67. P. 773].
Байков В.И., Лучко Н.Н., Сидорович Т.В. Влияние гелеобразования на процесс ламинарной проточной ультрафильтрации // Инж.-физ. журн. 1998. №1. С.166 [Baikov V.I., Luchko N.N., Sidorovich T.V. Effect of gel formation on the process of laminar continuous-flow ultrafiltration // J. Eng. Phys. Thermophys. V. 71. P. 166].
Банди Б. Методы оптимизации. М.: Радио и связь. 1988.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал