Теоретические основы химической технологии, 2023, T. 57, № 1, стр. 71-80
Нестационарный массоперенос в гелях с микроорганизмами
Д. П. Храмцов a, b, *, О. А. Сулягина a, Б. Г. Покусаев a, b, А. В. Вязьмин a, b, Д. А. Некрасов a, b
a Московский политехнический университет
Москва, Россия
b РТУ МИРЭА – Российский технологический университет
Москва, Россия
* E-mail: dp@khramtsov.net
Поступила в редакцию 12.10.2022
После доработки 25.10.2022
Принята к публикации 25.10.2022
- EDN: BMCHBK
- DOI: 10.31857/S0040357123010074
Аннотация
Использование гидрогелей в качестве матрицы для инкубирования клеток и применение таких систем биоматериалов в качестве биочернил пригодным для 3D-биопечати является многообещающей перспективой в тканевой инженерии. Оптическими методами спектроскопии и микроскопии исследовались процессы тепло- и массообмена в гидрогелевых материалах на основе агарозы и желатина с инкубированными в объем геля модельными микроорганизмами. Проведено сравнение закономерности распространения фронта питательной среды в чистых желатиновых гидрогелях и смесевых гидрогелях на основе агарозы с добавлением желатина для определения диффузионных свойств смесевых гидрогелей, способных обеспечить доставку питательных компонентов к микроорганизмам. Получены новые данные о степени неоднородности роста микроорганизмов при их объемном инкубировании и разных температурных режимах инкубирования, что необходимо для управления свойствами биочернил при биопечати. Предложено аналитическое описание кривой роста клеток в геле и на ее основе получено выражение для определения скорости роста клеток. Разработана численная модель для описания процесса поглощения питательных веществ клетками в процессе их роста.
ВВЕДЕНИЕ
Активное развитие технологий трехмерной биопечати приводит к необходимости поиска новых материалов, пригодных для широкого спектра задач биопринтинга. Такие материалы должны обеспечивать условия для развития и роста иммобилизованных в них биообъектов, а именно сохранять форму в рабочих температурных режимах и иметь массопроводные свойства достаточные для обеспечения клеток всеми необходимыми питательными веществами [1]. Целесообразно использовать гидрогели с иммобилизованными клетками в качестве биочернил для биопринтинга. Такие гели отличаются тем, что более 99% их массы составляет жидкость. В качестве подобной жидкости может быть использована вода, однако больший интерес [2] представляет создание гелей на основе питательной среды. Такой гель будет служить не только структурой, в которой будет происходить рост клеточных структур, но также и обеспечивать клетки питанием.
Технология биопринтинга является ключевой в развитии перспективных подходов регенеративной медицины [3]. При этом необходимо получение новых данных по массопроводным и теплофизическим свойствам материалов, пригодных для биопечати и обеспечения благоприятных условий для иммобилизованных в таких материалах клеток. В связи со сложностью проведения натурных экспериментов, включая эксперименты со стволовыми клетками [4], необходимо использование модельных материалов, а также методов математического и численного моделирования. В качестве модельных клеток могут быть использованы дрожжевые культуры. Таким образом актуальной задачей является разработка подходов к проведению исследований для апробации новых регенеративных технологий.
В качестве основы для биочернил, используемых в биопринтинге было предложено использование агарозного геля [5], однако для улучшения характеристик геля, таких как массопроводность и прочность структуры, представляет интерес применения не чистой агарозы, а смесевых гелей на ее основе. В качестве такой примеси может быть использовал желатин. Добавление желатина в различных концентрациях позволяет регулировать вязкость чернил из гидрогеля, фиксировать форму печатных конструкций в качестве стабилизирующего агента, улучшает адгезию слоев при аддитивной биопечати и позволяет варьировать температуру гелеобразования чернил [6]. Благодаря вышеперечисленным свойствам желатин является хорошей добавкой для улучшения пригодности чернил для биопечати. На практике, гидрогели, модифицированные желатином, используют для создания сосудистой структуры [7], для изготовления повязок для заживления ран [8] и для регенерации костей и лечения переломов [9].
Гидрогели, как вид биоматериала, обладают хорошей биосовместимостью и широко используются в качестве материала для иммобилизации клеток с целью применения подобных каркасов для тканевой инженерии, в том числе с помощью биопринтинга [10, 11]. В процессе роста клетки формируют агломераты, увеличивающиеся в размере со временем по мере того, как идет процесс деления и роста клеток, возрастает потребность клеточных массивов в питательных веществах. Важно подчеркнуть, что для устойчивого развития микробиологических объектов в гидрогеле, обеспечение их питательными веществами и кислородом приобретает принципиальное значение. Кислород, питательные вещества, белки и другие биомолекулы легко проникают через набухшую в воде сеть гидрогелей, чтобы питать инкапсулированные клетки. Но среди факторов, препятствующих росту числа клеток в гидрогелевых образцах, необходимо учитывать следующие: недостаток питательной среды и кислорода при доставке к клеткам диффузионным путем, механическое сопротивление геля при росте микроорганизмов, выделение клетками продуктов метаболизма, ингибирующих их рост. Необходимость учитывать эти факторы приводит к постановке задачи исследования и возможности прогнозирования поведения микроорганизмов в гидрогелях, а также адаптации многообещающих гидрогелевых биоматериалов к использованию их в качестве биочернил, пригодным для 3D-печати, остается сложной задачей, на решение которой направленны исследования, представленные в статье.
Целью работы является, путем экспериментальных и численных исследований, определение влияния составов смесевых гелей на их массопроводные свойства и эффективность подачи питательных веществ к клеткам.
МЕТОДЫ И МАТЕРИАЛЫ
Для изучения распространения концентрационного фронта фуксина в гидрогелях был использован метод оптического зондирования. Данные метод был ранее использован авторами для определения глубины проникновения питательной среды и фуксина, моделирующего питательную среду. Схема стенда представлена в [12]. Исследование роста и адаптации микроорганизмов в гидрогелевых образцах микроскопическим методом поможет получить данные о фазах роста клеток в гидрогелях для выявления наиболее подходящего способа поддержания их жизнедеятельности. Для микроскопического исследования гидрогелевых систем с микроорганизмами был использован микроскоп биологический Биолам Д-1, предназначенный для исследования препаратов в проходящем свете в светлом поле с увеличением от 63 до 1350 крат, которое дает возможность наблюдать за изменением формы, количества микроорганизмов и клеточной структурой.
Для исследования процессов и массопереноса с целью определения факторов, влияющих на развитие микроорганизмов, использовались гидрогелевые образцы на основе агарозы 0.6 мас. % и желатина от 2 до 8 мас. %. В качестве клеточной культуры, инкубированной в гидрогель, использовались клетки культуры Pichia polymorpha Y-314 с концентрацией 0.04 мг/мл, ввиду того, что такие клетки близки к соматическим клеткам человека по размеру (20–25 мкм – размер клеток дрожжей [13] и 25 мкм) – размер гепатоцитов паренхимы печени человека [14] и по условиям жизнедеятельности. Дрожжевая культура, предварительно разбавленная в питательной среде до необходимой концентрации, добавлялась в гелеобразующий раствор на стадии охлаждения при температуре 40°С и тщательно перемешивалась. Культура хорошо растет при температуре от 30 до 42°С [15]. Необходимые микроэлементы для жизнеобеспечения клеток содержались в питательной среде, добавленной в гель на этапе его приготовления.
Для измерения оптического пропускания света через гидрогели с микроорганизмами была выбрана длина волны 540 нм. Особенностью многих биологических микроорганизмов является способность к поглощению света в диапазоне между 400 и 600 нм. Выбранная длина волны наиболее близка к поглощению гемоглобина – белка, содержащегося в эритроцитах [16]. Снижение оптического пропускания на выбранной длине волны отождествлялось с ростом микроорганизмов, так как при росте клетки увеличивают количество агломераций и свои размеры, что в целом снижает оптическое пропускание образца на выбранной для исследования длине волны.
Концентрация клеток в геле при их росте и развитии была установлена методом интерполяции значений оптической плотности гидрогеля с клетками, полученной в ходе эксперимента, по предварительно полученной оценке зависимости оптической плотности от концентрации клеток в гелях.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Математическое описание кривой роста клеток. Процесс развития живых культур можно разделить условно на 4 характерных стадии: лаг-фаза, когда клетки адаптируются к новой среде, экспоненциальная фаза роста соответствует фазе активного деления клеток, сменяющемуся стационарной фазой, когда не наблюдается существенного прироста новых клеток и популяции поддерживается примерно на постоянном уровне. Завершающая стадия – стадия отмирания, когда количество живых клеток стремительно уменьшается ввиду использование доступных питательных ресурсов [12]. Длительность каждой из стадий зависит от вида клеток. Так, например для дрожжевых клеток Pichia polymorpha Y-314, используемых в экспериментальных исследованиях, характерные времена представлены в табл. 1.
Таблица 1.
Характерные времена для стадий развития клеток
| Лаг-фаза | 2–6 ч |
| Экспоненциальный рост | 4–8 ч |
| Стационарная фаза | 2–4 ч |
| Фаза отмирания | 2–4 ч |
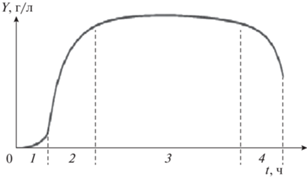
Кривая роста дает понимание, какой объем питательных веществ необходимо подводить к клеткам для обеспечения их метаболизма. Ввиду того, что кривая роста базируется на экспериментальных данных, имеет место вопрос о ее математическом описании с целью установления связи между временем и количеством живых клеток. Такое описание должно обладать минимальным количеством свободных параметров для простоты определения параметров кривой роста под конкретный вид живых культур. Существуют различные подходы для аппроксимации экспериментальных данных, такие как полиномиальная [17], кубическими сплайнами [18], а также использование функций специального вида (например, гиперболические и сигмоидные). Характер поведения кривой (рисунок 1) роста близок к сигмоидной функции. Такие функции активно применяются в задачах математического моделирования [19, 20].
Рис. 1.
Кривая роста микроорганизмов в общем случае: 1 – лаг-фаза; 2 – фаза активного роста; 3 – стационарная фаза; 4 – стадия отмирания.
Предложено описание кривой роста как линейной комбинации двух сигмоидных функций. Для ограничения кривой роста во времени в описании добавлена функция Хевисайда в качестве сомножителя. Такое ограничение необходимо ввиду того, что сигмоидная функция определена при любом времени, в то время как в реальных задачах накладываются указанные выше ограничения по времени – например, время проведения эксперимента или срок службы геля.
Такое описание кривой роста позволяет задать по одному свободному параметру для каждой стадии жизненного цикла клеток. Так, τ – время лаг-фазы; α – коэффициент экспоненциального роста, определяющий интенсивность увеличения количества клеток во время лаг-фазы и фазы роста; β – коэффициент, определяющий длительность стационарной фазы; ω – коэффициент характеризующий интенсивность отмирания клеток; tк (ч.) – окончание кривой роста. A (г/л клеток) –максимальное количество клеток, наблюдаемое во время стационарной фазы.
Выражение для скорости роста клеток. Используя полученную формулу для описания кривой роста, найдем выражение для определения изменения концентрации клеток. Возьмем производную Y(t) по времени без учета функции Хевисайда, выполняющую роль ограничения по времени. Также при нахождении производной не учитывается лаг фаза ввиду того, что в этот период рост микроорганизмов отсутствует. Полученное выражение для скорости роста клеток представлено ниже
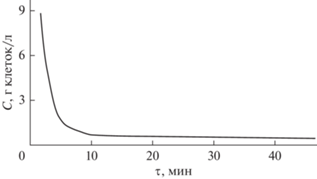
Зависимость скорости от времени демонстрирует экспоненциальную убывающую зависимость (рис. 2), где высокая скорость роста наблюдается на этапе экспоненциального роста с последующем замедлением. Во время стационарной фазы скорость роста меняется незначительно, что соответствует наблюдениям за кривой роста, когда масса клеток не претерпевает существенных изменений во время данной фазы.
Стоит отметить, что рассмотренная выше модель роста клеток представляет качественное описание обобщенного случая. В реальных экспериментах ввиду особенности роста и питания клеточных культур кривая роста может содержать, к примеру только фазу активного роста и стационарную фазу. Такая ситуация может возникнуть, если измерения проводятся начиная с момента адаптации клеток. В таком случае время лаг-фазы будет мало и им можно пренебречь. Аналогичным образом в случае, если экспериментальные замеры завершаются до начала стадии отмирания клеток, может не рассматриваться финальная стадия отмирания.
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Моделирование питания клеток. Наличие клеток в геле приводит к изменению концентрации питательного вещества с учетом его потребления. При этом увеличение количества клеток со временем приводит к изменению количества потребляемых веществ. Существует взаимосвязь между количеством клеток и объемом потребления питательных веществ.
Модель геля при наличии клеток рассматривается как модель на основе метода случайного блуждания, где клетки представлены в виде точечного источника поглощения питательных веществ (рис. 3), а скорость поглощения является функцией от кривой роста γ(R(t)). Параметры модели для чистого агарозного геля массовой концентрации 0.6 мас. % приведены в табл. 2.
Случай множества агломераций клеток. Случай роста клеток в геле с точечным агломератом клеток можно обобщить на случай произвольного количества агломератов ввиду того, что в экспериментальных исследованиях, как правило, наблюдается формирование нескольких кластеров клеток
Подобный подход дает лучшее понимание, как меняется фронт концентрации питательного вещества в зависимости от расположения агломератов клеток. Точечные клеточные агломераты могут быть заданы вручную с целью воспроизведения определенных условий роста клеток в геле, например, в задачах биопринтинга необходимо расположить клеточные культуры в определенных областях для формирования биологических тканей требуемой конфигурации. Альтернативным вариантом является расположение точечных клеточных агломератов согласно некоторому статистическому закону. Такой подход также актуален, так как экспериментальные исследования показывают, что заранее сложно определить в каких областях геля с клетками будут сформированы агломерации. В таком случае вероятностный подход является предпочтительным. В случае равномерного распределения клеток по гелю целесообразнее использовать гауссовый закон распределения. В случаях, когда, к примеру, клетки сконцентрированы в определенной области геля (например, у мениска) целесообразнее применять степенные законы распределения, такие как закон Пуассона или Мандельброта.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Ранее были получены закономерности и описаны зависимости распространения диффузионного фронта в чистых агарозных и смесевых гелях на её основе с добавлением желатина, где в качестве маркера для определения скорости диффузии был выбран краситель фуксин [12]. Для настройки модели прогнозирования диффузионных свойств гидрогелей были также проведены эксперименты с чистым желатиновым гелем концентраций от 2 до 8 мас. %. На основе полученных экспериментальных данных были найдены параметры для модели диффузии в геле (табл. 3). Полученные из эксперимента значения позволяют оценить, как меняются настройки модели при изменении составов смесевых гелей, включая предельные случаи чистых гелей (агароза, желатин).
Таблица 3.
Настройки модели для различных составов гелей
| Гель | r1 | r2 | r3 | K, ×104 |
|---|---|---|---|---|
| Агароза 0.6 мас. %, фуксин | 1.3 | 1.1 | 1.0 | 2.7 |
| Агароза 0.6 мас. %, питательная среда | 1.0 | 1.2 | 0.9 | 3.9 |
| Смесевой гель (агароза 0.6%, желатин 0.5%), питательная среда | 0.6 | 1.2 | 1.1 | 4.2 |
| Смесевой гель (агароза 0.6%, желатин 4%), питательная среда | 0.9 | 1.5 | 1.2 | 2.7 |
| Смесевой гель (агароза 0.6%, желатин 2%), питательная среда | 0.72 | 1.3 | 0.93 | 3.1 |
| Желатин 2% | 0.54 | 0.63 | 0.74 | 2.6 |
| Желатин 4% | 0.6 | 0.57 | 0.71 | 3.4 |
| Желатин 8% | 0.62 | 0.55 | 0.73 | 4.4 |
На рис. 4 представлена зависимость глубины проникновения от времени при диффузии фуксина в гидрогели на основе желатина, полученных методом оптического зондирования выбранной области.
Рис. 4.
Концентрационный фронт фуксина в геле на основе желатина различной концентрации от времени: 1 – желатин 2 мас. %; 2 – желатин 4 мас. %; 3 – желатин 6 мас. %; 4 – желатин 8 мас. % (точки – экспериментальные данные, линии – численное моделирование).
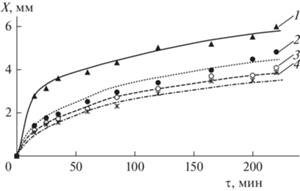
Анализ экспериментальных данных позволяет установить, что увеличение концентрации желатина в гидрогеле ведет к уменьшению расстояния глубины проникновения фуксина в гель. Для расчетной модели были определены параметры, соответствующие рассмотренным концентрациям желатина. Характер зависимостей имеет нелинейный характер и в случае минимальной концентрации (2%) наблюдается резкий скачок в области поверхности. Экспериментальные исследования показали, что концентрация желатина в 2 мас. % является минимально возможной для создания устойчивой гелевой структуры, а при дальнейшем уменьшении концентрации желатин не может сформировать устойчивых связей.
Сравнение характера распространения концентрационного фронта фуксина в чистых агарозном и желатиновом гелях, и смесевом геле, полученном на их основе, представлено на рис. 5.
Рис. 5.
Концентрационный фронт фуксина в геле на основе агарозы и желатина различной концентрации от времени: 1 – желатин 4 мас. %; 2 – агароза 0.6 мас. %; 3 – агароза 0.6 мас. % + желатин 4 мас. % (точки – экспериментальные данные, линии – численное моделирование).

Несмотря на то, что скорость диффузии в желатиновом геле значительно выше по сравнению с агарозным гелем, добавление желатина к агарозе снижает диффузионные свойства смесевого гидрогеля по сравнению с чистыми гелями соответствующих концентраций. Численное моделирование показало схожие результаты по сравнению с экспериментом. Во всех случаях наблюдается зависимость глубины проникновения пропорциональна квадратному корню времени процесса, что соответствует диффузионному процессу, протекающему согласно закону Фика.
На рис. 6 представлена глубина проникновения концентрационного фронта фуксина в чистых и смесевых гелях на основе агарозы и желатина через 220 мин после начала эксперимента.
Рис. 6.
Положение концентрационного фронта фуксина в гелях на основе агарозы и желатина в зависимости от содержания желатина спустя 220 мин от начала эксперимента: 1 – Чистые желатиновые гидрогели; 2 – Смесевые гидрогели на основе агарозы 0.6 мас. % с добавлением желатина.
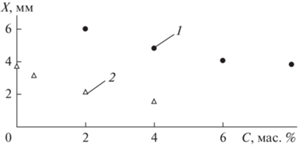
Установлено, что увеличение концентрации желатина как в чистых, так и в смесевых гелях приводит к снижению диффузионных свойств гидрогелей. Анализ полученных для численной модели параметров показывает, что в случае однокомпонентных гелей разброс параметров r1, r2, r3 становится меньше по сравнению со смесевыми гелями. Это может быть связано с тем, что смесевые гели обладают менее упорядоченной структурой.
Динамика роста клеток в гидрогелях различных составов и условиях. Обеспечение микроорганизмов питательными веществами и кислородом имеет принципиальное значение для их устойчивого метаболизма в гидрогеле. Далее приведены новые данные о динамике роста микроорганизмов при их объемном инкубировании при разных температурных условиях, различных составах гидрогелей и способах подачи кислорода. Интегральные спектроскопические методы исследования предоставляют возможность определения оптической плотности образцов, что косвенно позволяет судить об изменении метаболизма микроорганизмов, инкубированных в гидрогель. Но для детального анализа жизнедеятельности микроорганизмов, совокупно со спектроскопией, полезно применять метод световой микроскопии для визуальной оценки состояния клеток.
Световая микроскопия предназначена для исследования морфологии, размеров клеток, их взаимного расположения, структурной организации и других особенностей клеток, инкубируемых в гидрогеле. Изучение динамики роста микроорганизмов указанным методом проводилось в течении суток при различных температурных режимах инкубирования: при температуре 25°С, характеризующей завершение процесса гелеобразования [21] и температуре 36°С – оптимальной для роста клеток дрожжей Pichia polymorpha Y-314.Результаты микроскопического исследования образцов гидрогеля с концентрацией 0.6 мас. % агарозы при первоначальной концентрацией микроорганизмов 0.01 г/л геля, представлены на рис. 7.
Рис. 7.
Микроскопическое исследование динамики роста микроорганизмов, иммобилизированных в гидрогель на основе агарозы: а – после инкубирования; б – через 24 ч после инкубирования при Т = 25°С; в – через 24 часа после инкубирования при Т = 36°С; 1 – объединение микроорганизмов в цепочки (псевдомицелии) при их росте.
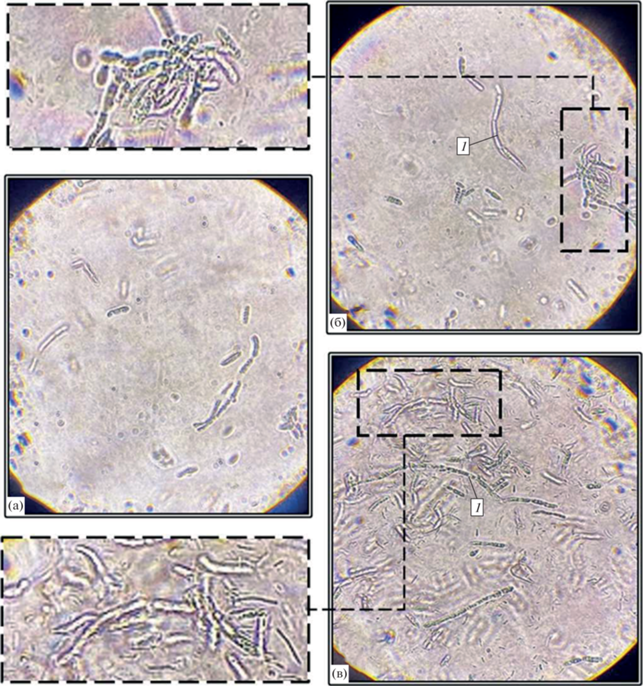
С помощью визуального наблюдения образцов с использованием метода микроскопии удалось установить, что клетки дрожжей Pichia polymorpha Y-314 могут быть инкубированы в объем гидрогеля (рис. 7a). При росте в агаризованной среде, в состав которой входят глюкоза и минеральные соли, культура образует колонии: белые, гладкие с ровным краем. С возрастом колонии приобретают бугристую поверхность и бежевый оттенок, характерный для возрастной культуры, что снижает интенсивность пропускания света через образец из-за увеличения количества микроорганизмов и изменения цвета колоний (рис. 7б, 7в). При благоприятных условиях, с достаточным количеством питательной среды, размножение использованного вида дрожжей происходит путем многостороннего почкования (рис. 7б, 7в). При этом, при повышенной до 36°С температуре и одинаковом времени инкубирования, в поле наблюдения отдельных и объединенных в цепочки (псевдомицелий) микроорганизмов больше (рис. 7в), чем при температуре 25°С (рис. 7б).
Результаты спектроскопии аналогичных образцов на длине волны проходящего света 540 нм представлены на рис. 8. Сканирование гелевых образцов проводилось в рабочей области, высота которой составляла 7 мм с отступом 2 мм от межфазной границы воздух-гель.
Рис. 8.
Динамика роста микроорганизмов, иммобилизированных в гидрогель на основе агарозы, от времени при различных температурах: 1 – 25; 2 – 36°С.

Рост микроорганизмов в геле наблюдался на небольшой глубине от границы раздела воздух-гель и был ограничен массопроводностью кислорода, зависящей от температуры. В экспериментах при температуре 36°С концентрации микроорганизмов в гидрогеле за первые сутки увеличилась почти в два раза от первоначального значения. Однако из-за ограниченного количества кислорода в объеме воздуха, заключенного в кювете, скорость роста микроорганизмов в последующие 24 ч снижалась. При температуре 25°С скорость роста микроорганизмов за все время эксперимента была практически одинаковой. Об этом свидетельствует линейный характер зависимости концентрации микроорганизмов от времени. При этом количество клеток увеличилось в 1.8 раз, не достигнув соответствующей концентрации по сравнению с температурным режимом 36°С.
Поскольку увеличение концентрации желатина в смесевых гелях снижает их массопроводные свойства, возникает необходимость изучения влияния желатина на кинетику размножения микроорганизмов, находящихся в объеме смесевого гидрогеля. Результаты такого исследования в смесевом гидрогеле на основе агарозы 0.6 мас. % с добавлением желатина 2 мас. % (в сравнении с чистым однокомпонентным агарозным гидрогелем 0.6 мас. %) при температуре инкубирования 25°С представлены на рис. 9.
Рис. 9.
Динамика роста микроорганизмов, иммобилизированных в гидрогель на основе агарозы с добавлением желатина, от времени: 1 – агароза 0.6 мас. %; 2 – агароза 0.6 мас. % + желатин 2 мас. %.
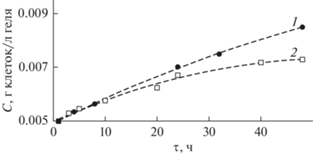
Как следует из рис. 9, увеличение концентрации желатина в смесевом гидрогеле приводит к подавлению роста микроорганизмов почти на 30% по сравнению с чистым агарозным гелем. Вероятно, это является следствием того, что увеличение концентрации желатина в смесевых гелях приводит к снижению диффузионных свойств гидрогелей и как следствие, недостаточности обеспечения клеток питанием и кислородом.
Важным условием метаболизма иммобилизованных микроорганизмов является доставка питательных веществ и кислорода именно в объем гелей, в противном случае, рост клеток будет происходить только на поверхности гелевого образца [12].
Доставка питательных сред и кислорода при объемном культивировании биологических микроорганизмов может быть осуществлена за счет формирования искусственных каналов внутри геля, которые аналогичны системе кровеносных капилляров в биологических тканях [22]. Задачей экспериментальных исследований являлось изучение роста микроорганизмов при разных способах подачи кислорода в объем геля. Эксперименты по исследованию процессов массопереноса в объем геля при наличии в нем живых микроорганизмов проводилась двумя способами подачи. В первом образце кислород из воздуха поступал к микроорганизмам через проточный канал диаметром d = 1 мм. Во втором образце подача кислорода к ним осуществлялась из свободного объема кюветы, заполненного воздухом, через границу раздела воздух–гель. В обоих образцах была выбрана одинаковая область для измерения концентрации микроорганизмов во времени методом определения интенсивности, проходящего через гелевый образец света. На рис. 10 показана зависимость интенсивности пропускания света от времени на длине волны 540 нм при температуре 36°С.
Рис. 10.
Динамика роста микроорганизмов, иммобилизированных в гидрогель на основе агарозы 0.6 мас. % и желатина 2 мас. %, от времени при температуре Т = = 36°С: 1 – подача кислорода через проточный канал с d = 1 мм; 2 – поступление кислорода через поверхность из свободного объема кюветы.

Как видно на рис. 10, при обеспечении микроорганизмов в гелевом образце непрерывной подачей кислорода через канал, интенсивность пропускания значительно уменьшилась по сравнению с подачей кислорода через границу раздела. Имеющиеся экспериментальные данные также показывают, что рост микробиологических объектов в объеме геля происходит и при температуре ниже оптимальной обычно используемой для выращивания выбранных микроорганизмов, но с меньшей интенсивностью.
Данные, представленные на рис. 9, были использованы для создания функциональных зависимостей кривых роста в модели учитывающей составы гелевых материалов. Цель – получение дополнительных данных, которые определить прямым экспериментальным путем не представлялось возможным. В модельной задаче рассматривался случай одиночного конгломерата клеток радиусом 5 мм, окруженный питательным раствором, при этом доступное количество питательных веществ принималось за 1 (100%). Далее проводился расчет изменения количества доступных питательных веществ вблизи клеточного агломерата от времени (рис. 11).
Рис. 11.
Изменение относительной концентрации питательной среды в области клеточного агломерата в процессе его роста: 1 – агароза 0.6 мас. %; 2 – агароза 0.6 мас. % + желатин 2 мас. %.
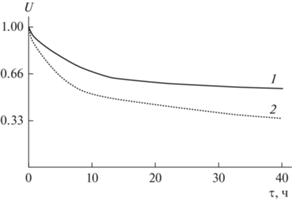
Таким образом, необходимость в питательных веществах увеличивается с ростом концентрации клеток, при том, что возможность подачи питательных веществ непосредственно к клеточному агломерату ограничено диффузионными свойствами гелевого материала. При этом с ростом концентрации клеток потребление питательного раствора увеличивается и для обоих составов гелевого материала наблюдается снижение концентрации питательного раствора в близи клеточного агломерата. Заметим, что для смесевого геля снижение концентрации более выражено, что согласуется с ранее полученными данными по глубине проникновения в него модельного вещества (рис. 5).
ЗАКЛЮЧЕНИЕ
Сведения о диффузионных свойствах гидрогелей необходимы для целенаправленного научно обоснованного выбора составов гидрогелей для применения в качестве рабочих материалов для 3D-биопечати с инкапсулированными клетками, для иммобилизации которых требуется доставка питательных веществ и кислорода. В совокупности полученные результаты позволяют предположить, что использование смесевых гидрогелей на основе агарозы 0.6 мас. %, модифицированных желатином, максимально обеспечат необходимую вязкость “чернил” для биопечати, поддержание формы печатных конструкций, улучшаат адгезию слоев при использовании аддитивной биопечати и позволит варьировать температуру гелеобразования. Важно, что добавление желатина существенно не препятствует росту и развитию микроорганизмов, инкубированных в смесевых гидрогелях. Применение в 3D-биопечати смесевых гидрогелей на основе агарозы и желатина имеет большой потенциал для разработки трехмерной архитектуры ткани.
Разработанная расчетная модель позволила получить данные об изменении концентрации питательного раствора в окрестностях клеточного агломерата, которое обусловлено влиянием массопроводных свойств гелевого материала на доступность питательных веществ к клеткам в процессе их роста. В случае как чистого агарозного геля, так и смесевого на основе агарозы и желатина наблюдается уменьшение концентрации питательного вещества в области роста клеток, при этом для случая смесевого геля недостаток питательных веществ более выражен, что соответствует меньшим массопроводным свойствами такого смесевого геля.
Авторский коллектив выражает благодарность Герман Людмиле Сергеевне за экспертную помощь по вопросам питания и жизнедеятельности микроорганизмов выбранных для проведения экспериментов.
Статья подготовлена в рамках выполнения базовой части государственного задания ФГАОУ ВО “Московский политехнический университет” (проект АААА-А20-120092190052-9).
ОБОЗНАЧЕНИЯ
| A | определяет максимальное количество клеток, наблюдаемое во время стационарной фазы, г/л клеток |
| α | количество питательных веществ подаваемых к агломерации клеток за единицу времени, г/ч |
| E | потребление клетками питательных веществ в единицу времени, г |
| N | количество агломераций в образце геля |
| P | закон случайного распределения агломераций и его параметры (равномерное, Гаусса, Пуассона, и т.п.) |
| tк | окончание кривой роста (может означать конец стадии отмирания или время завершения экспериментальных наблюдений), ч |
| W | исходное количество питательных веществ |
| Y | масса клеток, г/л |
| α | коэффициент экспоненциального роста, определяет интенсивность рост клеток во время лаг-фазы и фазы экспоненциального роста |
| β | коэффициент длительности стационарной фазы |
| γ(t) | количество питательных веществ потребляемых клетками за единицу времени, г/ч |
| θ(t) | функция Хевисайда (функция активации) |
| τ | время запаздывания, с |
| ω | характеризует интенсивность отмирания клеток |
| ИНДЕКСЫ | |
| i | номер агломерации клеток |
Список литературы
Wasupalli G.K., Verma D. Thermosensitive injectable hydrogel based on chitosan-polygalacturonic acid polyelectrolyte complexes for bone tissue engineering // Carbohydrate Polymers. 2022. V. 294. P. 119769.
Aljohani W., Ullah M.W., Zhang X., Yang G. Bioprinting and its applications in tissue engineering and regenerative medicine // International Journal of Biological Macromolecules. 2018. V. 107. Part A. P. 261.
Wang Z., Kapadia W., Li C., Lin F., Pereira R.F., Granja P.L., Sarmento B., Cui W. Tissue-specific engineering: 3D bioprinting in regenerative medicine // J. Controlled Release. 2021. V. 329. P. 237.
Leberfinger A.N., Ravnic D.J., Dhawan A., Ozbolat I.T. Concise Review: Bioprinting of Stem Cells for Transplantable Tissue Fabrication // Stem Cells Translational Medicine. 2017. V. 6. P. 1940.
Pokusaev B.G., Karlov S.P., Vyazmin A.V., Nekrasov D.A. Laws of the formation and diffusion properties of silica and agarose gels // Theoretical Foundations of Chemical Engineering. 2018. V. 52. № 2. P. 200. [Покусаев Б.Г., Карлов С.П., Вязьмин А.В., Некрасов Д.А. Закономерности формирования и диффузионные свойства силикатных и агарозных гелей // Теоретические основы химической технологии. 2018. Т. 52. № 2. С. 200.]
He Y., Yang F., Zhao H., Gao Q., Xia B., Fu J. Research on the printability of hydrogels in 3D bioprinting // Sci Rep. 2016. № 6. P. 29977
Hong S., Kim J.S., Jung B., Won C., Hwang C. Coaxial bioprinting of cell-laden vascular constructs using a gelatin–tyramine bioink // Biomater. Sci. 2019. № 7. P. 4578.
Chekini M., Krivoshapkina E., Shkodenko L., Koshel E., Shestovskaya M., Dukhinova M., Kheiri S., Khuu N., Kumacheva E. Nanocolloidal Hydrogel with Sensing and Antibacterial Activities Governed by Iron Ion Sequestration // Chemistry of Materials. 2020. № 32 (23). P. 10066.
Han X., He J., Wang Z., Bai Z., Qu P., Song Z., Wang W. Fabrication of silver nanoparticles/gelatin hydrogel system for bone regeneration and fracture treatment // Drug Delivery. 2021. № 28. P. 319.
Guiting L.,Yuan Z., Xianlong Z., Shaoyun G. Advances in hydrogels for stem cell therapy: regulation mechanisms and tissue engineering applications // J. Mater. Chem. B. 2022. № 10. P. 5520.
Bedell M.L. Human gelatin-based composite hydrogels for osteochondral tissue engineering and their adaptation into bioinks for extrusion, inkjet, and digital light processing bioprinting // Biofabrication. 2022. № 14. P. 045012.
Pokusaev B.G., Vyazmin A.V., Zakharov N.S., Khramtsov D.P., Nekrasov D.A. Unsteady mass transfer of nutrients in gels with channels of different spatial structures // Theoretical Foundations of Chemical Engineering. 2020. V. 54. P. 277. [Покусаев Б.Г., Вязьмин А.В., Захаров Н.С., Храмцов Д.П., Некрасов Д.А. Нестационарный массоперенос питательных веществ в гелях с каналами различной пространственной структуры // Теоретические основы химической технологии. 2020. Т. 54. № 2. С. 163.]
Меледина Т.В., Давыденко С.Г. Дрожжи Saccharomyces serevisiae. Морфология, химический состав, метаболизм. СПб.: Университет ИТМО, 2015.
Радченко В.Г., Шабров А.В., Зиновьева Е.Н., Ситкин С.И. Заболевания печени и желчевыводящих путей. СПб.: СпецЛит, 2011.
The Yeasts: A Taxonomic Study / Eds. Kurtzman C.P., Fell J.W., Boekhout T. Amsterdam: Elsevier, 2011.
Красников И.В., Привалов В.Е., Сетейкин А.Ю., Фотиади А.Э. Распространение оптического излучения в биологических тканях // Вестник Санкт-Петербургского университета. Медицина. 2013. № 4. С. 202.
Beck J.V., Blackwell B., Haji-Sheikh A. Comparison of some inverse heat conduction methods using experimental data // International J. Heat and Mass Transfer. 1996. V. 39. P. 3649.
Pottmann H., Leopoldseder S., Hofer M. Approximation with active B-spline curves and surfaces // Proc. 10th Pacific Conference on Computer Graphics and Applications, 2002. P. 8.
Iliev A., Kyurkchiev N., Markov S. On the approximation of the step function by some sigmoid functions // Mathematics and Computers in Simulation. 2017. V. 133. P. 223.
Kyurkchiev N., Markov S. Sigmoidal Functions: Some Computationaland Modelling Aspects // Biomath Communications. 2014. № 1/2.
Pokusaev B.G., Karlov S.P., Nekrasov D.A. Agarose gels with bioresorbable additives: The kinetics of the formation, structure, some properties // Chemical Engineering Transactions. 2019. V.74. P. 1171.
Jakab C., Norotte C., Marga F. Tissue engineering by self-assembly and bioprinting of living cells // Biofabrication. 2010. V. 2. № 2. P. 022001.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии